TTP 피복 경사식 구조물의 전달파고계수 산정에 관한 수리실험
Hydraulic Experiments on Wave Transmission Coefficients for Rubble Mound Structure Armored with Tetrapods
Article information
Abstract
본 연구에서는 상치콘크리트가 설치된 TTP 피복 경사식 구조물에 대한 전달파고계수 산정식을 도출하기 위하여 2차원 수리실험을 실시하였다. 기존에 제시된 경사식 구조물에 대한 전달파고계수 산정식은 대부분 국외에서 수행된 저천단 구조물에 대한 연구성과이다. 기존 연구에서는 피복재로 대부분 피복석이 적용되었고, 상치콘크리트가 설치되어 있지 않은 경우이다. 이로 인해 국내 경사제 설계시 적용되는 단면형상과는 많은 차이가 발생한다. 본 연구에서는 국내 경사식 구조물의 설계동향에 부합하는 전달파고계수 산정식을 제시하였으며, 파형경사의 영향 및 상치콘크리트 전면에 거치되는 TTP의 거치 열수에 따른 변화를 고려하였다.
Trans Abstract
Two-dimensional hydraulic model experiments on rubble mound structure armoring with the tetrapods and the superstructure were conducted to investigate wave transmission characteristics under irregular wave conditions. The previous studies about the wave transmission coefficients dealt with the low crested structures, therefore the rock was the main armor units and the superstructure was not constructed. In this study, the new empirical design formula for the wave transmission coefficient about rubble mound structure with the tetrapods and the superstructure was suggested and the effects of wave steepness and the row of the tetrapods in front of the superstructure could be considered.
1. 서 론
항만구조물을 설계함에 있어 구조물에 대한 반사계수와 전달계수 등을 산정 또는 예측하는 것은 기본적인 설계항목이며, 적절한 전달계수의 예측은 구조물의 마루높이 선정에 있어 중요한 역할을 한다. 마루높이의 선정은 항만의 기능 확보 및 경제성 확보 측면에서 중요한 설계인자이며, 입사파고, 허용 월파량 및 전달파고 관점에서 결정되는 것이 일반적이다.
전달파고계수 산정과 관련하여 설계기준서에서 제시하고 있는 대표적인 기법을 살펴보면, 우리나라의 항만 및 어항설계기준 · 해설(MOF, 2014)에서는 Goda et al.(1967) 및 Goda(1969)의 연구에 근거하여 직립제 및 혼성제에 대한 전달파고계수 산정기법이 제시되어 있으며, 경사제의 경우에는 Seelig(1980)이 제시한 산정기법이 수록되어 있다. Seelig(1980)의 경사제 전달계수 산정기법은 처오름높이와 여유고의 함수로 제시되어 있으며, 제체 투과파에 대한 영향은 고려되어 있지 않다. 미국의 CEM(USACE, 2006)에는 직립제에 대한 전달파고계수는 Goda et al.(1967), Goda(1969) 및 Takahashi(2002)의 연구성과가 제시되어 있으며, 경사제의 경우에는 저천단 구조물(low crested structure)을 대상으로 한 Allsop(1983), Powell and Allsop(1985) 및 van der Meer and d’Angremond(1991)의 결과가 제시되어 있다.
국내의 경우, 전달파고계수에 대한 연구는 Kim and Lee(2015)가 직립제에 대한 전달파고계수 산정식을 sine 함수의 형태로 제시하였다. 국외의 경우에 다양한 연구가 수행되었으나, 대부분 수중방파제 및 인공리프와 같은 저천단 구조물에 대한 연구이다(Hamer and Hamer, 1982; Powell and Allsop, 1985; van der Meer and Daemen, 1994; d’Angremond et al., 1996; Melito and Melby, 2002; Kramer et al., 2005; van der Meer et al., 2005; Wang et al., 2007). 전달파고계수 산정에 대한 연구성과는 월파량 산정기법 연구에 비해 상대적으로 많지 않으며, 전술한 바와 같이 직립제의 경우에 우리나라 및 미국에서 Goda의 연구결과를 설계지침에 적용하고 있는 상황이다.
본 연구에서는 TTP(Tetrapods)가 피복된 투과성 경사식구조물을 대상으로 불규칙파를 적용한 2차원 수리실험을 실시하였다. 입사파고, 주기, 수심 및 구조물 제원(상치콘크리트폭, 피복재 거치 열 수) 등을 변화시키면서 전달파고계수 산정을 위한 실험을 실시하였다. 본 연구에서는 수행된 수리실험결과를 이용하여 평균 전달파고계수 산정식을 제안하고, 각 설계요소(구조물 제원 및 파랑조건)의 영향을 고려할 수 있는 영향계수를 제시하고자 한다.
2. 수리모형실험
2.1 실험시설
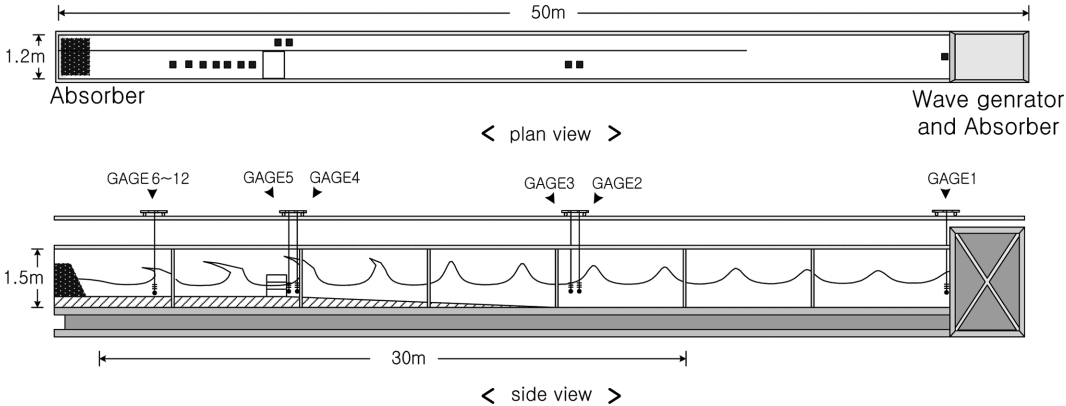
단면 수리실험은 한국건설기술연구원의 폭 1.2 m, 높이 1.5 m, 길이 50 m의 수로에서 수행되었으며, 단면수로에는 전기서보 피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다(Fig. 1 참조). 그리고 수로 내에서 구조물 설치로 인한 반사와 조파판에서 발생하는 재반사를 효과적으로 제어하기 위해 수로 폭 1.2 m를 폭 0.8 m(광폭수로)와 폭 0.4 m(협수로)로 분할하였다. 분할된 수로에서 실험모형은 폭 0.8 m의 수로에 설치하여 제반 자료를 취득하고, 폭 0.4 m의 수로에서는 입사파의 설정 및 계측을 수행하였다. 또한 흡수식 조파를 실시하여 구조물로부터 반사되어온 파가 조파기에서 재반사 되는 현상을 최소화하였다. 수로 전면 30 m 구간을 강화유리로 처리하여 실험장면 관찰이 용이하도록 되어있으며, 수로 양쪽 끝 부분에는 여러 겹의 다공성 구조로 형성된 소파장치가 설치되어 있다. 월파 및 투과파에 의한 전달파 발생시 구조물 배후면에서 순간적인 수위상승으로 인하여 구조물 전후 면의 수위차가 발생할 수 있다. 이를 저감하기 위하여 수로 끝단의 다공성 소파시설은 광폭수로와 협수로가 연결되어 있으며, 또한 수로 양쪽 끝단은 직경 0.3 m의 관으로 연결되어 있어 수위차의 발생이 최소화 될 수 있도록 하였다. 그리고 자유수면계측은 용량식 파고계를 사용하였다. Fig. 1과 같이 수로 좌측 끝단에는 소파제가 설치되어 있어 대부분의 반사파는 소파제에 의하여 흡수가 되지만, 광폭수로에 모형이 설치되고, 협수로는 통과파가 진행할 경우 협수로의 입사파가 광폭수로로 투과되어 파랑이 발생할 수 있다. 이러한 영향을 본 실험조건을 적용하여 무월파 및 무투과파 조건의 직립제를 대상으로 검증실험을 수행하였으며, 그 결과 협수로의 영향으로 최대 2%의 전달파고계수가 발생하는 것으로 계측되었으나, 보수적인 설계측면에서 이를 포함하여 결과를 분석하였다.
2.2 실험모형 및 실험조건
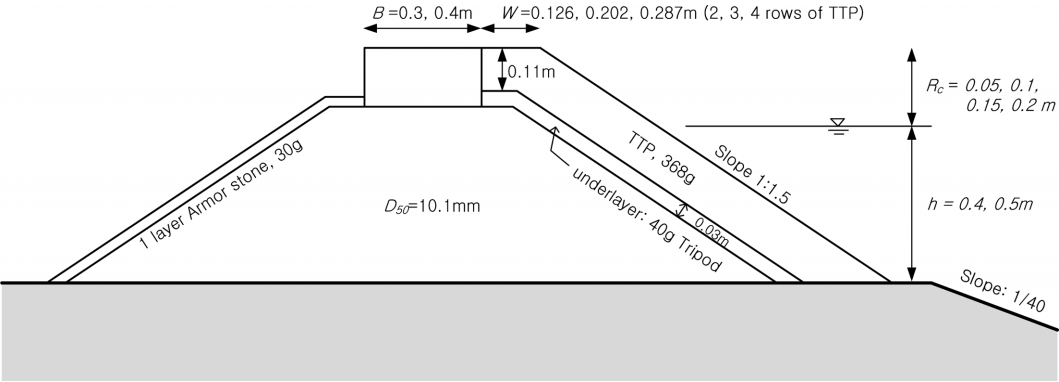
본 단면 수리실험에 적용된 실험단면은 TTP 피복 경사식 단면으로서 실험단면 형상은 Fig. 2와 같다. 경사식 구조물 외측에는 1:1.5의 경사로 중량 368 g의 TTP가 2층 피복되며, 내측에는 30 g의 피복석이 1층 피복된다.
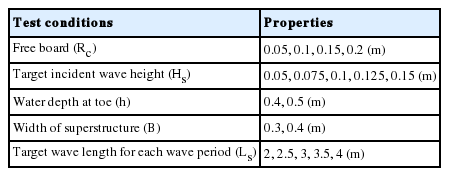
구조물 설치수심(h)은 h = 0.4m, 0.5m이며, 여유고는 Rc = 0.05 m, 0.1 m, 0.15 m, 0.2 m이고, 상치콘크리트의 폭(B)은 B = 0.3m와 0.4 m이다. 상치콘크리트 전면에 거치되는 TTP의 열수는 2열, 3열 및 4열로 변화시켰으며, 각각의 거치 열 수에 따른 TTP의 거치 폭(W)은 각각 0.126 m, 0.202 m, 0.278 m에 해당한다. 경사제 속채움 사석의 크기는 D50 = 10.1 mm이다. 그리고 구조물 전면에는 1:40의 경사면이 설치되어 있다.
실험파는 Bretschneider-Mitsuyasu 주파수 스펙트럼을 적용한 불규칙파 조건을 적용하였으며, 실험에 적용된 목표 유의파고(Hs)는 Hs = 0.05m, 0.075m, 0.1m, 0.125m 및 0.15 m이고, 유의주기(Ts)는 각각의 수심별로 유의파장(Ls)이 2 m, 2.5 m, 3 m, 3.5m 및 4 m가 되도록 설정하였다. 전달파고 계측을 위해 상치콘크리트 항내측 선단으로부터 0.5 m, 1 m, 2 m, 3 m, 3.5 m, 4 m 및 5 m 지점에 파고계를 설치하였고 (Fig. 1의 6번~12번 파고계), 입사파는 Fig. 1의 협수로 내 구조물 설치 위치에 파고계를 설치하고 2점법(Goda and Suzuki, 1976)을 적용하여 분석하였다(Fig. 1의 4번과 5번 파고계). Fig. 1의 1번 파고계는 흡수식 조파를 위하여 조파기에 설치된 파고계이다.
월파 발생시 구조물 후면의 수위가 순간적으로 상승할 수 있으므로, 전달파고는 수위 상승량을 제거하고 분석하였으며, Fig. 2와 Table 1은 각각 본 실험에서 적용한 실험모형 및 실험조건이다. Table 1에서 목표 파고(Hs)와 주기(Ls)는 구조물 설치 위치에서의 값이다. 실험에 적용된 실험수로와 계측장비 및 실험파 조건은 Kim and Lee(2015)와 동일하다.
3. 전달파고계수 분석 방법
경사제 전달계수 산정에 관한 기존 연구의 대부분은 국외에서 수행되었으며, 대상 구조물은 저천단 구조물이 대부분이다. 그리고 경사제에 피복되는 주피복재는 대부분 피복석(rock)이고, 상치콘크리트가 설치되지 않은 단면형상을 대상으로 하였다. Melito and Melby(2003)는 Core-loc을 주피복재로 하여 경사제에 대한 전달계수를 제시하였다.
항만 및 어항설계기준 · 해설(MOF, 2014)에 제시된 경사식 구조물에 대한 전달파고계수 산정식은 식(1)과 같다. 식(1)은 Seelig(1980)이 제안한 산정식으로서 Rc는 구조물의 여유고, R은 처오름 높이(runup height), B는 구조물 상단폭, h는 설치수심이며, ξ는 쇄파유사성 매개변수(surf similarity parameter)이다. 식(1)은 제체투과에 의한 영향은 고려되지 않은 월파에 의해서 발생하는 전달파고계수를 산정할 수 있는 식으로서 최대값은 Kt, max = 1이며, 최소값은 Kt, min = 0이다.
여기서,
van der Meer(1990a, b)는 Fig. 3 및 식(2)와 같이 저천단 구조물에 대한 전달파고계수 산정식을 선형 형태로 제안하였다. Fig. 3에서 여유고(Rc)의 음의 값은 구조물 상단이 정수면 아래에 위치함을 의미한다.
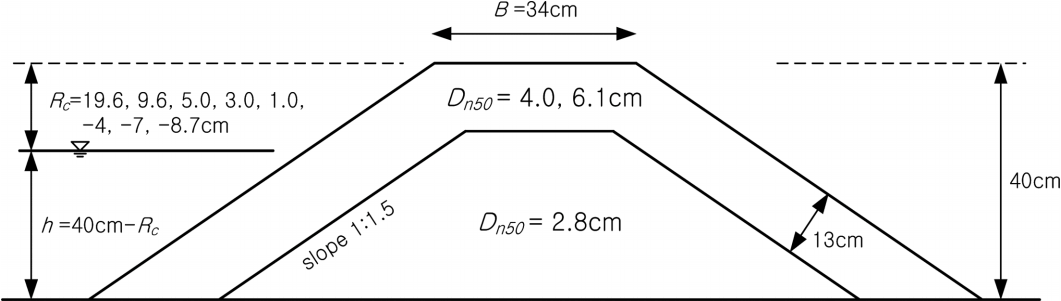
van der Meer and Daemen(1994)은 Fig. 4의 단면형상에 대하여 식(3)과 같이 전달파고계수 산정식을 제시하였다. 식(3)은 Fig. 3의 결과 및 Fig. 4의 단면에 대한 실험결과를 재분석한 것으로서 여유고와 피복석 입경의 비(Rc/Dn50)를 적용하여 식(3)과 같은 산정식을 제안하였다. 이 식을 적용함에 있어 적용범위는 1 < Hs/Dn50 < 6이고, 0.01 < s0 < 0.05이다. 여기서, s0(= Hs/L0)는 파형경사이며, L0는 심해파장이다.
여기서,
식(2)와 식(3)의 전달파고계수 산정식은 피복석을 대상으로 한 연구성과이며, Melito and Melby(2002)는 피복재로 Coreloc을 적용하여 전달파고계수 산정식을 제안하였다(식(4) 및 Fig. 5 참조). 전달파고계수 산정을 위한 분석방법은 van der Meer(1990a, b)가 제시한 방법과 유사하다. Melito and Melby(2002)의 실험단면은 주피복재로 272 g의 Core-loc을 사용하고, 중간피복석이 설치된 단면으로서 국내 설계시 적용되는 단면형상과 유사하지만 상치콘크리트가 설치되어 있지 않다.
전달파고계수는 월파로 인해 발생되는 전달파고계수(Kt, o)와 제체 투과파로 인해 발생하는 전달파고계수(Kt, t)로 구분할 수 있다. 그리고 이들 두 가지 요소에 의한 전달파고계수(Kt)는 식(5)와 같이 정의된다(Goda, 1969; Seelig, 1980; Powell and Allsop, 1985; Heijn, 1997; Takahashi, 2002).
식(5)의 관계에 대해 Goda et al.(1967), Goda(1969), Takahashi(2002), Kim and Lee(2015)는 직립제 및 혼성제를 대상으로 한 전달파고계수 산정식을 sine 함수 형태로 제안하였으며, Heijn(1997)은 지수함수의 형태로 제시하였다. 본 연구의 대상구조물인 경사제에 대한 전달파고계수는 제체 투과파가 포함된 결과이며, van der Meer(1990a, b) 및 Melito and Melby(2002) 등이 제시한 선형함수 형태로 전달파고계수를 분석하고자 한다.
4. 실험결과 및 분석
4.1 상치콘크리트 폭에 따른 전달파고계수 및 기존 연구와의 비교
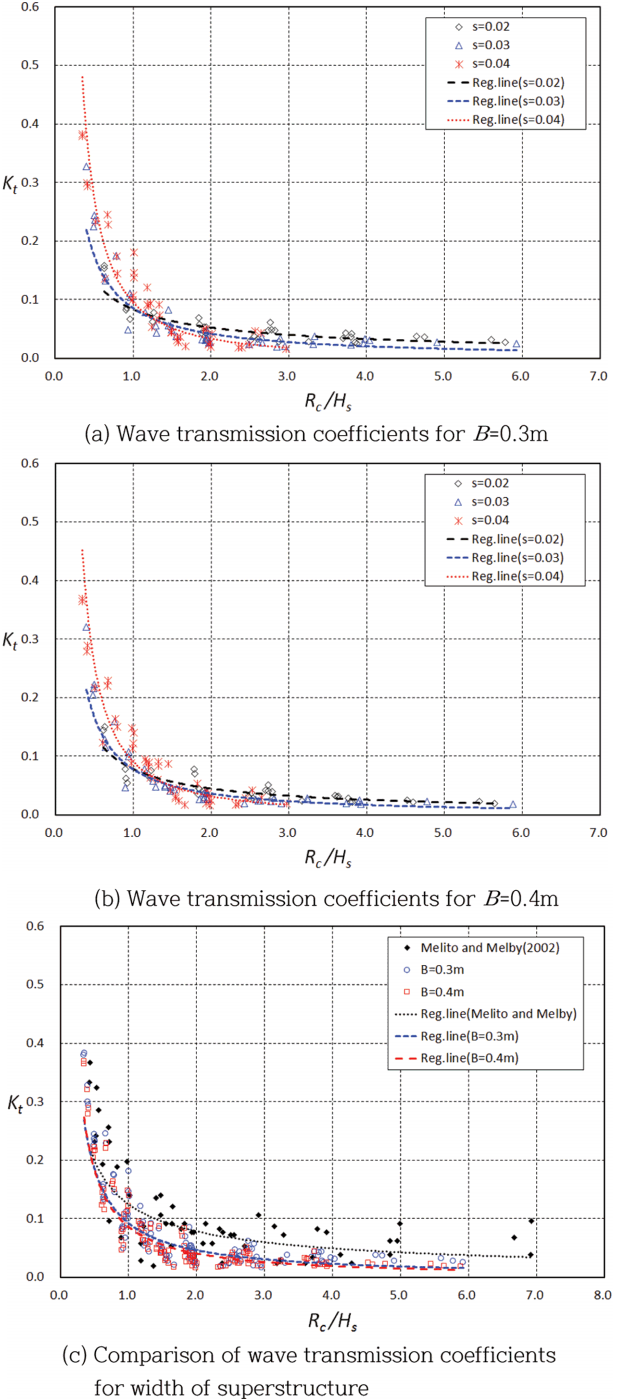
경사식 구조물에 대한 Seelig(1980)의 연구에 의하면 월파량이 많지 않을 경우에는 경사면에 거치된 소파블록 및 제체 내에서의 소파효과 등으로 인해 파형경사가 증가할수록 전달계수는 감소하는 경향이 나타나지만, 처오름 높이가 증가하여 상치콘크리트 높이를 초과하게 되면 상대적으로 많은 월파가 발생하게 되며, 이러한 경우에는 파형경사가 증가할수록 전달파고계수는 증가하는 경향을 보이는 것으로 분석하였다. 그러나 수중방파제의 경우에는 파형경사가 증가할수록 전달파고계수는 감소하고, 파형경사가 감소할 경우에는 전달파고계수가 증가하는 경향을 나타낸다.
Fig. 2의 단면에서 상치콘크리트 전면에 거치되는 TTP의 거치 열 수가 2개인 경사제 단면을 대상으로 상치콘크리트의 폭에 따른 전달파고계수를 비교하였다. 본 연구의 실험결과에서도 전반적으로 Seelig(1980)의 연구와 유사한 경향이 나타남을 알 수 있다. 즉, 상대여유고가 작은 경우, 즉 입사파고에 비하여 구조물의 마루높이가 낮을 때에는 파형경사가 증가할수록 전달파고계수가 크게 나타나며, 상대여유고가 큰 경우에는 파형경사가 작을 때 전달파고계수가 크게 나타났다(Fig. 6(a, b) 참조). Fig. 6(c)는 주피복재로 Core-loc을 사용한 실험결과(Melito and Melby, 2002)와 본 실험결과를 비교한 것이다. Fig. 6(c)에 의하면, 상치콘크리트의 폭에 따른 전달파고계수의 차이는 크지 않은 것으로 나타났으며, 이는 Seelig(1980)가 제시한 결과와도 유사한 경향이다. 즉, 상치콘크리트의 폭이 증가함에 따라 전달파고계수는 약간 감소하였으나, 그 차이는 매우 작은 것을 알 수 있다. 본 실험에서는 상치콘크리트의 폭이 넓어진 만큼 제체 폭이 넓어진 단면을 적용하였다. 본 실험에 적용한 실험조건 내에서 제체 폭의 변화에 따른 투과파가 전달파고계수에 대한 영향은 크지 않으며, 상치콘크리트에서의 월파량에 의한 전달파고계수가 지배적인 영향임을 알 수 있다.
상치콘크리트가 있는 본 실험의 단면형상(Fig. 2 참조)과 상치콘크리트가 없는 조건인 Melito and Melby(2002)의 단면형상(Fig. 5 참조)을 대상으로 전달파고계수를 직접 비교하는 것은 여의치 않으나, 전반적인 경향은 파악할 수 있다. 즉, 동일 상대여유고 조건에서 상치콘크리트의 설치 유무에 따른 전달파고계수를 비교해 보면, 상치콘크리트가 설치된 경우의 전달파고계수가 작게 나타나는 것을 알 수 있다. 그리고 상대여유고가 일정 수준 이상인 경우에는 상대여유고의 증가에 따른 전달파고계수의 차이는 크지 않음을 알 수 있으며, 이는 Melito and Melby(2002)의 실험결과와도 동일한 경향이다. 즉, 상대여유고(Rc/Hs)가 약 2 이상이 되면 상대여유고의 변화에 따른 전달파고계수의 차이는 거의 발생하지 않음을 알 수 있다.
국내 항만구조물 설계시 직립제 및 경사제의 마루높이 산정에 있어 마루높이는 설계조위 상에서 유의파고의 0.6배 이상으로 선정하고 있으며, 월파를 적극 억제하고자 할 경우에는 설계조위 상에서 1.25배로 결정하는 것이 일반적이다. 본 연구에서는 상대여유고 조건이 약 6인 경우까지 실험을 수행하였지만, 이 후 실험결과의 분석에서는 실제 설계에 적용할 수 있는 범위에 해당하는 조건(0.3 ≤ Rc/Hs ≤ 2)을 대상으로 결과를 분석하고자 한다.
Fig. 7은 Fig. 6에 제시된 본 연구의 실험결과와 기존 전달파고계수 산정식의 결과를 비교한 것이다. 결과에서 알 수 있는 바와 같이 상치콘크리트가 설치되지 않은 조건의 결과인 van der Meer(1990a, b)와 Melito and Melby(2002)의 결과가 본 실험결과보다 전달계수를 크게 예측하고 있는 것을 알 수 있다. 그리고 항만 및 어항설계기준 · 해설(MOF, 2014)에 제시된 Seelig(1980) 산정식의 결과는 본 실험결과의 중간 범위에 위치하는 것을 알 수 있으나, 상대여유고가 약 1보다 큰 경우에는 작은 전달파고계수가 나타남을 알 수 있다. 이는 전술한 바와 같이 제체 투과성분을 고려하지 않았기 때문으로 판단된다. Fig. 7에 도시된 실험결과를 살펴보면 동일 상대여유고 조건에서 파랑조건 및 제체형상 등에 따라 다양한 전달파고계수가 분포함을 알 수 있으며, 이에 대해서는 다음 절에서 분석 하고자 한다.
4.2 설계요소(파형경사)가 전달파고계수에 미치는 영향 분석
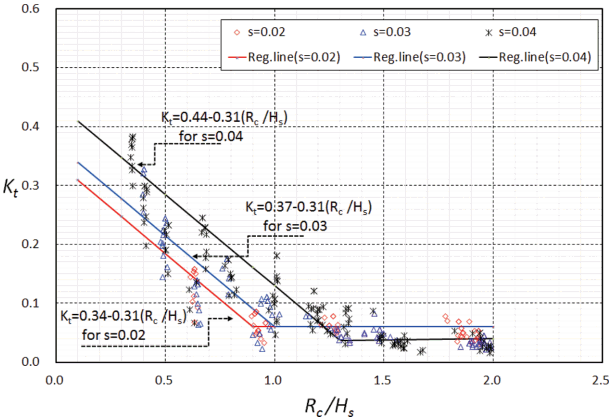
4.1절의 결과에서 적정 설계적용 범위(0.3 ≤ Rc/Hs ≤ 2)를 대상으로 van der Meer(1990a, b) 및 Melito and Melby(2002)가 적용한 선형분석 방법을 적용하여 본 실험결과를 다시 도시하면 Fig. 8과 같이 나타낼 수 있다. Seelig(1980)와 van der Meer and Daemen(1994)은 파형경사가 전달파고계수에 영향을 미치는 주요 변수로 분석하였다. 이에 따라 본 연구에서도 실험에 적용된 실험파 조건을 파형경사별로 구분하여 결과를 도시 하였다(Fig. 8 참조). van der Meer(1990a, b) 및 Melito and Melby(2002)는 상대여유고가 0에서부터 일정 구간까지 증가할 때 전달파고계수가 선형적으로 감소하며, 이후 상대여유고가 증가해도 전달파고계수의 변화는 크지 않은 것으로 결과를 제시하였다. 본 연구의 결과도 이와 동일한 경향이 나타나는 것을 알 수 있으며, 파형경사에 따른 전달파고계수를 분석하였다.
Fig. 8에서 각각의 파형경사에 대해 상대여유고가 증가함에 따라 감소하는 전달파고계수의 차이(기울기)는 유사한 것을 알 수 있다. 파형경사에 따른 전달파고계수는 4.1절에서 설명한 바와 같이 상대여유고 Rc/Hs ≈ 1.25를 기준으로 상대여유고가 작은 경우에는 파형경사가 증가함에 따라 전달파고계수가 증가하며, 상대여유고가 큰 경우에는 파형경사가 증가할수록 전달파고계수는 감소하는 것을 알 수 있다. 전체적으로 상대여유고에 따른 전달파고계수의 감소 차이(기울기)는 유사하며, y축 절편에 해당하는 전달파고계수가 파형경사에 따라 변하는 것을 알 수 있다. 따라서 파형경사를 고려한 전달파고계수 산정식은 식(6)과 같이 나타낼 수 있다. 식(6)에서 αs는 파형경사에 따른 zero-freeboard(Rc = 0)에서의 전달파고계수로서 도표의 y절편에 해당한다. 파형경사 s는 구조물 설치위치에서 입사파 분석을 통해 계산된 값으로 s = Hs/Ls이며, Ls는 구조물 위치에서의 유의파장이다.
Fig. 8에서 파형경사가 s = 0.04인 경우에 상대여유고(Rc/Hs)가 1.5 이상인 조건에서는 전달파고계수는 Kt ≈ 0.04이지만, 보수적인 측면에서 타 실험조건을 고려하여 최소 전달파고계수는 0.06으로 설정한 후 식(6)을 제안하고자 한다.
4.3 상치콘크리트 전면 TTP 거치열 수에 따른 전달파고계수
상치콘크리트의 안정성 확보 및 소파효과에 의한 월파량 저감, 이를 통한 마루높이의 조정 등을 목적으로 상치콘크리트 전면에 거치되는 TTP의 거치 열 수를 조정할 수 있다. 본 절에서는 상치콘크리트 전면에 거치되는 TTP의 거치 열 수에 따른 전달파고계수를 분석하였다. 특히 경사제에 TTP를 적용할 경우 설계에 많이 적용되는 사례를 감안하여 거치 열수가 2~4인 조건을 적용하였다. 그리고 결과의 분석을 위하여 거치열 수에 대한 설치폭(W)을 실험에 적용된 피복재의 공칭길이(Dn)로 무차원화하여 분석하였다.
실험결과에서 추세선(평균값)을 중심으로 일부 실험결과의 분산이 발생하고 있으나, 전체적인 경향은 TTP의 거치 열 수가 증가함에 따라 전달파고계수가 선형적으로 감소함을 알 수 있다(Fig. 9 참조). Fig. 9에 도시된 TTP의 거치 열 수에 따른 전달파고계수 변화를 식(6)과 같은 형태의 선형식으로 표시하면 식(7)과 같이 나타낼 수 있다. 식(7)에서 αrow는 상치콘크리트 전면 TTP의 거치 열 수에 따라 변하는 전달파고계수이다. 식(7)에서 Dn은 TTP의 공칭길이(

Wave transmission coefficients with the change of number of TTP rows in front of the superstructure.
4.4 TTP 피복 경사제에 대한 전달파고계수 산정식 제안
본 연구에서는 상치콘크리트가 설치된 TTP 피복 경사제에 대한 전달파고계수 산정식 도출을 위한 수리실험을 수행하여 실험결과를 Fig. 7~Fig. 9에 도시하고, 4.2절과 4.3절에서는 파형경사의 영향과 TTP 어깨폭의 영향을 고려한 전달파고계수 산정식을 각각 식(6)과 식(7)로 제시하였다. 식(6)과 식(7)로 제시된 전달파고계수 산정식을 통합하면 식(8)과 같이 정리할 수 있다. 식(8)에서 αs는 파형경사의 영향을 고려한 항이며, αrow는 상치콘트리트 전면에 거치되는 TTP 어깨폭에 따른 영향을 나타내는 항이다. 즉, 어깨폭이 증가하게되면 전달파고계수는 감소됨을 의미한다.
그리고 식(8)의 적용범위는 다음과 같다.
5. 결 론
기존에 수행된 경사식 구조물에 대한 전달파고계수는 대부분 저천단 구조물에 대한 연구성과로서 상치콘크리트가 설치되어 있지 않은 조건이고, 또한 주피복재로 대부분 피복석이 사용된 경우이다. 본 연구에서는 국내에서 경사제 설계시 가장 많이 적용되는 단면형상(TTP 거치, 상치콘크리트 설치, 사면경사 1:1.5)을 대상으로 전달파고계수 산정식을 제안하였다. 본 실험을 통하여 도출된 결과를 요약하면 다음과 같다.
1. 상치콘크리트의 폭에 따른 전달파고계수의 차이는 크지 않은 것으로 나타났으며, 동일 상대여유고 조건에서 상치콘크리트의 설치유무에 따른 전달파고계수는 상치콘크리트가 설치된 경우에 상대적으로 작게 나타났다.
2. 파형경사를 이용하여 전달파고계수를 분석하였으며, 기존 연구성과와 동일한 특성이 도출되었다.
- 상대여유고가 작은 경우, 즉 월파량이 많은 경우에는 파형경사가 증가할수록 전달파고계수가 증가하는 경향이 나타났다.
- 상대여유고가 큰 경우, 즉 월파량이 적은 경우에는 경사면에 거치된 소파블록 및 제체 내에서의 소파 등으로 인해 파형경사가 증가할수록 전달계수가 감소하는 경향이 나타났다.
3. 상치콘크리트가 설치된 TTP 피복 경사제 단면에 대한 전달파고계수 산정식을 van der Meer(1990a, b) 및 Melito and Melby(2002)의 제안식과 같은 선형함수 형태로 제시하였으며, 파형경사 및 상치콘크리트 전면에 거치되는 TTP의 거치 열 수(어깨 폭)에 따른 영향을 추가하였다.
4. 본 논문에서는 상치콘크리트의 높이와 거치 블록의 종류를 한가지로 고정한 조건에 대한 실험을 통하여 결과를 도출하였으며, 상치콘크리트의 높이 변화에 대한 추가 연구 및 분석이 필요할 것으로 생각된다. 본 연구의 성과는 TTP 피복 경사제에 있어 상치콘크리트와 TTP의 거치 높이가 동일한 조건에 대하여 개략적인 전달파고계수 산정에 이용될 수 있을 것이다.
Acknowledgements
본 논문은 2017년도 해양수산부 재원으로 한국해양과학기술진흥원의 연구비 지원(과제번호: 20110131)을 받아 수행된 연구이며, 연구비 지원에 감사드립니다.