Article information

Abstract

Trans Abstract

1. Introduction

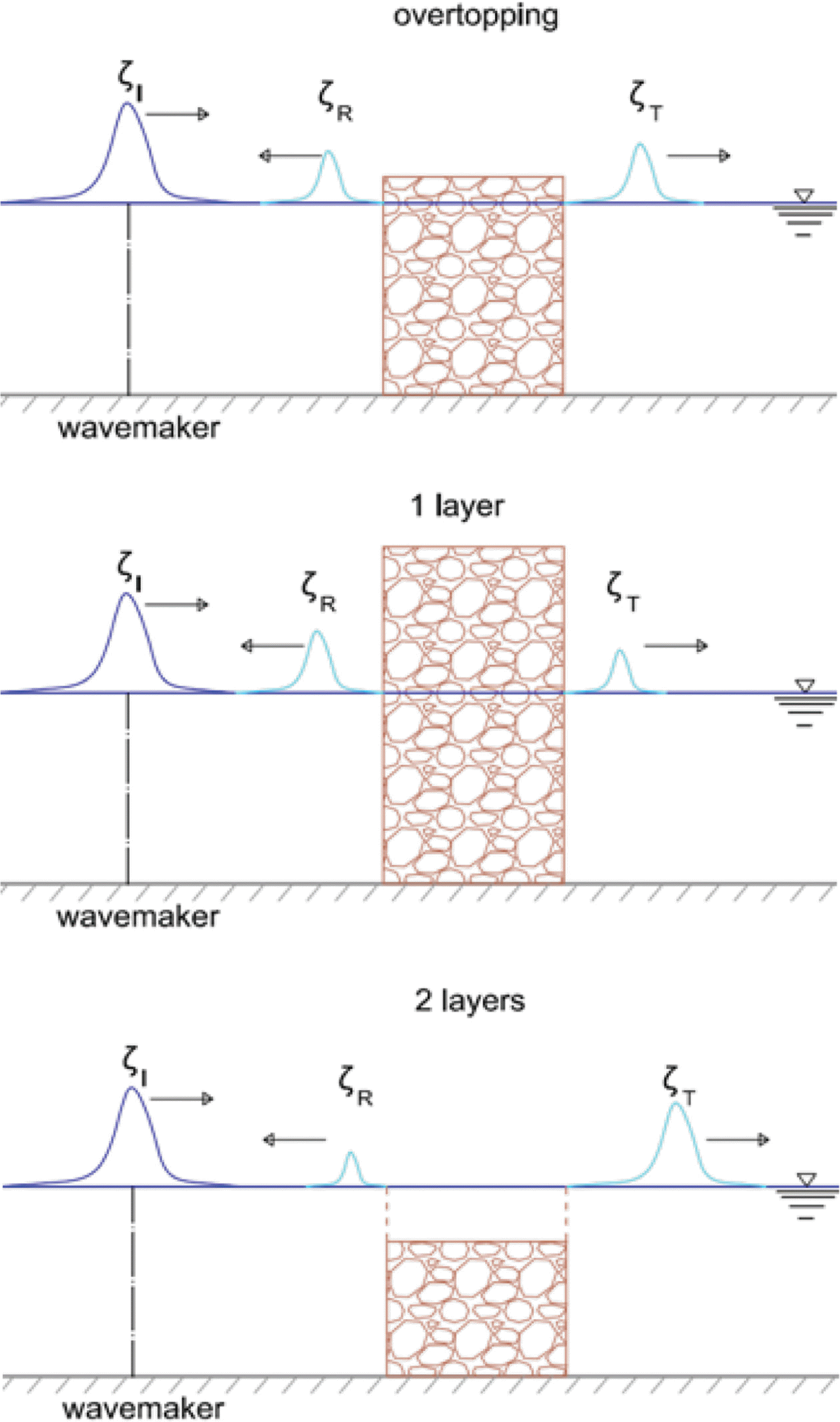
Wave overtopping on a breakwater may cause damage to coastal structures as well as injuries and life losses to people. In reality, wave overtopping is a three-dimensional phenomenon due to refraction and diffraction because usually waves propagate obliquely on coastal structures. Usually, people use three-dimensional equations such as the Reynolds Averaged Navier-Stokes equations, e.g., COBRAS(Lin and Liu, 1998) and CASMAS-SURF (CDIT, 2001) or the smooth particle hydrodynamics method (Gingold and Monaghan, 1977) to simulate wave overtopping. Simulation of the three-dimensional equations in a horizontal twodimensional domain requires so long running time. Hence, coastal engineers simulate wave overtopping only for normally incident waves. The Boussinesq equations are depth-averaged two-dimensional equations. Thus, simulation of the Boussinesq equations in a horizontal two-dimensional domain does not require so long running time. For waves overtopping on a porous breakwater, there may exist open space between the bottom and the water surface. The Boussinesq equations assume that there should not be any open space. Thus, in some case, the Boussinesq equations cannot simulate overtopping of waves on a porous breakwater. The Boussinesq equations were developed for waves on a porous bed by Cruz et al. (1997). The equations consider waves in two layers, i.e., a upper free layer and a lower porous layer. In the present study, we extend Cruz et al.’s Boussinesq equations to analyze waves in two porous layers with different porosities. Recently, the Boussinesq equations are developed for waves in a porous layer by Lee et al. (2014). The equations consider waves in one porous layer. The waves overtopping on a low-crested porous breakwater would experience energy dissipation more than waves through a high-crested breakwater and less than waves passing through a submerged porous breakwater. Thus, the height of waves overtopping on a low-crested porous breakwater which can be simulated using the Navier-Stokes equations (CDIT, 2001) is greater than that of waves passing through a high-crested porous breakwater which can be simulated using the one-layer Boussinesq equations (Lee et al., 2014) and also it is less than that of waves passing through a submerged breakwater which can be simulated using the two-layer Boussinesq equations(Cruz et al., 1997). Fig. 1 shows three cases of waves passing on porous breakwaters.

Fig. 1.

Waves overtopping and transmitting a porous breakwater.

In this study, we approximately obtain the heights of solitary waves overtopping on porous breakwaters using the one- and two-layer Boussinesq equations. In Section 2, we describe theory of the one-layer and two-layer Boussinesq equations and the Navier-Stokes equations. In Section 3, we conduct numerical experiments to find optimum values of the drag and inertial coefficients which are used in the Boussinesq equations and the Navier-Stokes equations and to find the height of waves overtopping on a low-crested porous breakwater is between that of waves passing through a high-crested porous breakwater and a submerged porous breakwater. In section 4, we summarize the present study and suggest the future study.

2. Theory

2.2 Governing equations of the Boussinesq equations and the Navier-Stokes equations

The one-layer Boussinesq equations (Lee et al., 2014) are derived from the continuity and boundary conditions in dimensionless form as

(4) μ2∇2Φ+∂2Φ∂z2=0,  -h≤z≤ɛζ

(5) μ2(β∂Φ∂t+αΦ+ζ)+ɛβ12[μ2(∇Φ)2+(∂Φ∂z)2]=0,      z=ɛζ

(6) ∂Φ∂z=μ2(∂ζ∂t+ɛ∇Φ⋅∇ζ),  z=ɛζ

(7) ∂Φ∂z=-μ2∇Φ⋅∇h,  z=-h

where Φ is the velocity potential, ζ is the water surface elevation, h is the mean water depth, ∇ (= (∂/∂x, ∂/∂y)) is the horizontal gradient operator, and μ (= h₀/l) and ε (= a/h₀) is the wave dispersiveness and nonlinearity parameters, respectively. Eq. (4) is the continuity equation, Eqs. (5) and (6) are the dynamic and kinematic boundary conditions on free surface and Eq. (7) is the bottom boundary condition. The velocity potential is expressed as a power series in vertical coordinate given by

(8) Φ(x,y,z,t)=∑n=0∞[z+h(x,y)]nϕn(x,y,t)

Following Cruz et al. (1997), Lee et al. (2014) derived the extended Boussinesq equations for deeper water in dimensional form as

(9) ∂ζ∂t+∇⋅[(h+ζ)u]=0

(10) (β∂∂t+α)u+βu⋅∇u+g∇ζ+16(β∂∂t+α)h2∇(∇⋅u)        -(12+γ)(β∂∂t+α)h∇[∇⋅(hu)]-γgh∇[∇⋅(h∇ζ)]=0

where u (= (u, v)) is the horizontal seepage velocity vector, γ (= 1/18) is a parameter to improve the dispersion relation in deeper waters, and Eqs. (9) and (10) are the continuity and momentum equations. For non-porous layer (i.e., β = 1 and α = 0), the momentum equation (10) becomes Madsen and Sørensen’s (1992) equation given by

(11) ∂u∂t+u⋅∇u+g∇ζ+16h2∇(∇⋅∂u∂t)           -(12+γ)h∇[∇⋅(h∂u∂t)]-γgh∇[∇⋅(h∇ζ)]=0

And further, if γ = 0, the momentum equation (11) becomes Peregrine’s (1967) equation given by

(12) ∂u∂t+u⋅∇u+g∇ζ+16h2∇(∇⋅∂u∂t)         -12h∇[∇⋅(h∂u∂t)]=0

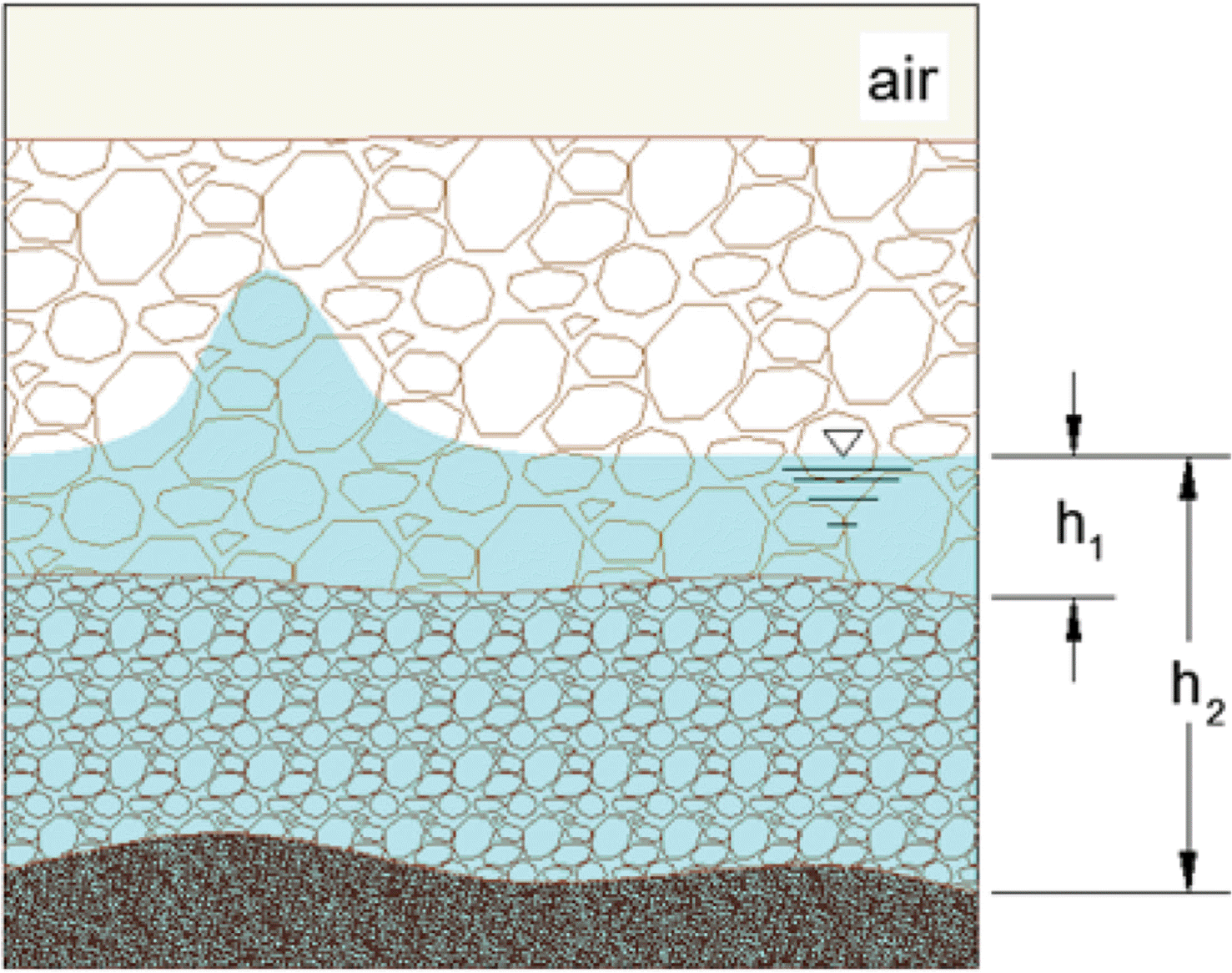
In the present study, we derive the Boussinesq equations for waves in two porous layers. For waves in two porous layers, there are two water depths h₁ and h₂ measured from the mean water level (see Fig. 2).

Fig. 2.

Water depth h₁ and h₂ for two porous layers.

The continuity and boundary conditions in dimensionless form are given below

(13) μ2∇2Φ1+∂2Φ1∂z2=0,  -h1≤z≤ɛζ

(14) μ2∇2Φ2+∂2Φ2∂z2=0,  -h2≤z≤−h1

(15) μ2(β1∂Φ1∂t+α1Φ1+ζ)          +ɛβ112[μ2(∇Φ1)2+(∂Φ1∂z)2]=0,  z=ɛζ

(16) ∂Φ1∂z=μ2(∂ζ∂t+ɛ∇Φ1⋅∇ζ),  z=ɛζ

(17) μ2(β1∂Φ1∂t+α1Φ1)+ɛβ112[μ2(∇Φ1)2+(∂Φ1∂z)2]             =μ2(β2∂Φ2∂t+α1Φ2)+ɛβ212[μ2(∇Φ2)2+(∂Φ2∂z)2],z=-h1

(18) λ1(∂Φ1∂z+μ2∇Φ1⋅∇h1)=λ2(∂Φ2∂z+μ2∇Φ2⋅∇h1),     z=-h1

(19) ∂Φ2∂z=-μ2∇Φ2⋅∇h2,  z=-h2

Eqs. (13) and (14) are the continuity equations for the upper and lower layers, respectively. Eqs. (15) and (16) are the dynamic and kinematic boundary conditions on free surface. Eqs. (17) and (18) are the dynamic and kinematic boundary conditions at the interface between the upper and lower layers. Eq. (19) is the bottom boundary condition. In Eqs. (13) to (19), the subscripts 1 and 2 imply the corresponding variables in the upper and lower layers, respectively. The velocity potentials are expressed as a power series in vertical coordinate given by

(20) Φ1(x,y,z,t)=∑n=0∞[z+h1(x,y)]nϕ1,n(x,y,t)

(21) Φ2(x,y,z,t)=∑n=0∞[z+h2(x,y)]nϕ2,n(x,y,t)

Following Cruz et al. (1997), we derive the extended Boussinesq equations for deeper water in dimensional form as

(22) ∂ζ∂t+∇⋅[(h1+ζ)u1]+λ2λ1∇⋅[(h2-h1)u2]=0

(23) (β1∂∂t+α1)u1+β1u1⋅∇u1+g∇ζ+12(β1∂∂t+α1)〈h123∇(∇⋅u1)-h1∇{λ2λ1∇⋅[(h2-h1)u2]}〉-(12+γ1)(β1∂∂t+α1)h1∇[∇⋅(h1u1)]-γ1gh1∇[∇⋅(h1∇ζ)]=0

(24) (β2∂∂t+α2)u2+β2u2⋅∇u2+g∇ζ+12(β2∂∂t+α2)      [-23(h2-h1)2∇(∇⋅u2)-(h2-h1)∇(∇h2-u2)      -(h2-h1)∇(h2-2h1)∇⋅u2+2∇h1∇h2⋅u2]      -12(β1∂∂t+α1)∇[∇⋅(h12u1)]      -[(1+γ2)(β1∂∂t+α1)+γ2(α2β1β2-α1)]      ∇{h1λ2λ1∇⋅[(h2-h1)u2]}      -γ2gβ1β2∇{h1λ2λ1∇⋅[(h2-h1)∇ζ]}=0

where γ₁ (= 1/18), γ₂ (= 1/18) are parameters to improve the dispersion relation in deeper waters. If β₁ = ₁, α1 = 0, λ1 = 1, then the upper layer is non-porous and thus Eqs. (22) to (24) become Cruz et al.’s (1997) Boussinesq equations. Cruz et al.’s equations can be applied for waves on porous beds and submerged breakwaters. The present equations can be applied further for waves in two porous layers with different porosities.

The continuity and momentum equations of the CADMASSURF(CDIT, 2001) can be expressed as

(25) ∇3⋅(λU)=λSp

(26) βcdUdt+λρ∇3(p+ρgz)+αcU=Su

where S_p and S_u are source terms in the continuity and momentum equations, respectively. At the free surface, the transport equation of F is used as

(27) λ∂F∂t+∇3⋅(λUF)=λSF

where F is the volume of fluid and S_F is the source term of F.

3. Numerical Experiments

Vidal et al. (1988) conducted hydraulic experiments to measure transmission coefficients of solitary waves passing through a porous breakwater. With the experimental conditions of Vidal et al., we find that the height of waves overtopping on a low-crested porous breakwater is between the heights of waves passing a high-crested porous breakwater and a submerged porous breakwater.

First, for solitary waves through a porous breakwater(i.e., one layer case), we compare numerical results of the Boussinesq equations and the CADMAS-SURF with the same conditions of the drag resistance coefficients. Experimental conditions investigated in the present study are water depth of h = 30 cm, breakwater width of b = 20 cm, porous material size of d = 1.43 cm, porosity of λ = 0.44, and wave nonlinearity is varied as a/h = 0.064, 0.144, 0.264. The drag resistance coefficients are α_l = 800 and αt = 3 in the Boussinesq equations and α_lE (= α_l/[λ(1 − λ)]) = 3250 and a_tE = 3 in the CADMAS-SURF.

For the whole experiments, the added mass coefficient which is used in the inertial resistance term is fixed in both the Boussinesq equations and the CADMAS-SURF as κ = 0.34 which was suggested by Lara et al. (2012) for waves in a porous breakwater. It should be known that κ = 0.5 and κ = 1 are for porous layer with spheres and circular cylinders, respectively.

Fig. 3 shows the variation of transmission coefficients with wave nonlinearity. In the figure, the drag resistance coefficients are the same between the Boussinesq equations and the CADMAS-SURF. The numerical solutions of the Boussinesq equations and CADMAS-SURF are compared against the experimental data of Vidal et al. The experimental data shows the decrease of transmission coefficient with the increase of wave nonlinearity. Numerical results of the Boussinesq equations are close to the experimental data because the drag resistance terms have been tuned to fit the numerical results to the experimental data (Vu et al., 2017). However, numerical results of the CADMAS-SURF are smaller than the experimental data which means that the drag resistance coefficients should be tuned to fit to the experimental data.

Fig. 3.

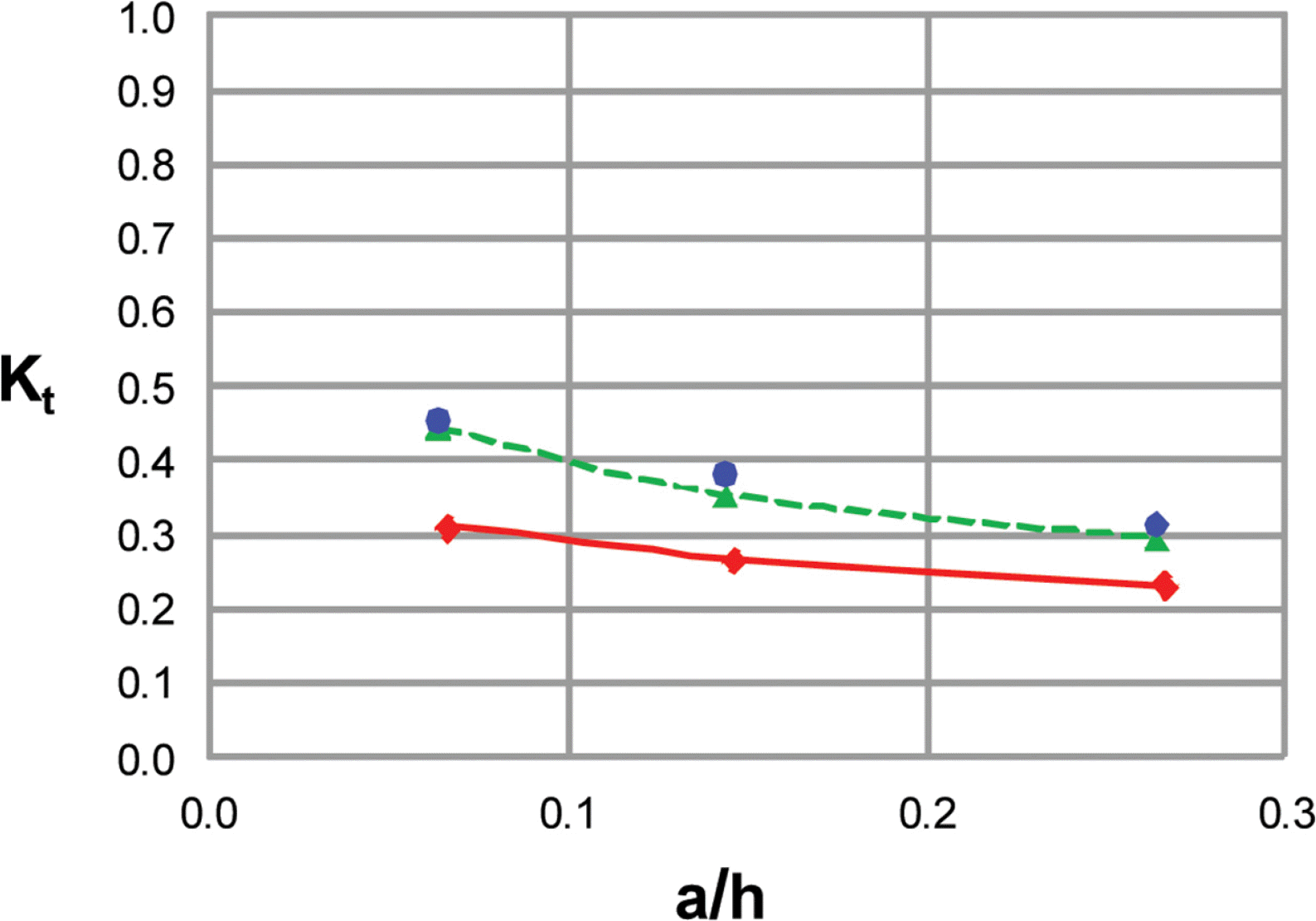
Variation of transmission coefficients with wave nonlineartiy (Drag resistance coefficients are the same between the Boussinesq equations and the CASMAS-SURF); circle = Vidal et al., solid line with diamond = CADMAS-SURF, dashed line with triangle = Boussinesq equations.

Second, for solitary waves through a porous breakwater(i.e., one layer case), values of the drag resistance coefficients are determined such that the transmission coefficients of numerical models (both the Boussinesq and Navier-Stokes equations) are close to experimental data. Fig. 4(a) shows that the transmission coefficients of numerical models become close to the experimental data after finding optimum values of the drag resistance coefficient (i.e., α_l = 800 and αt = 3 for the Boussinesq equations; α_lE = 2000 and α_tE = 0.7 for the CADMAS-SURF). We use these optimum values of the drag coefficient in later numerical experiments.

Fig. 4.

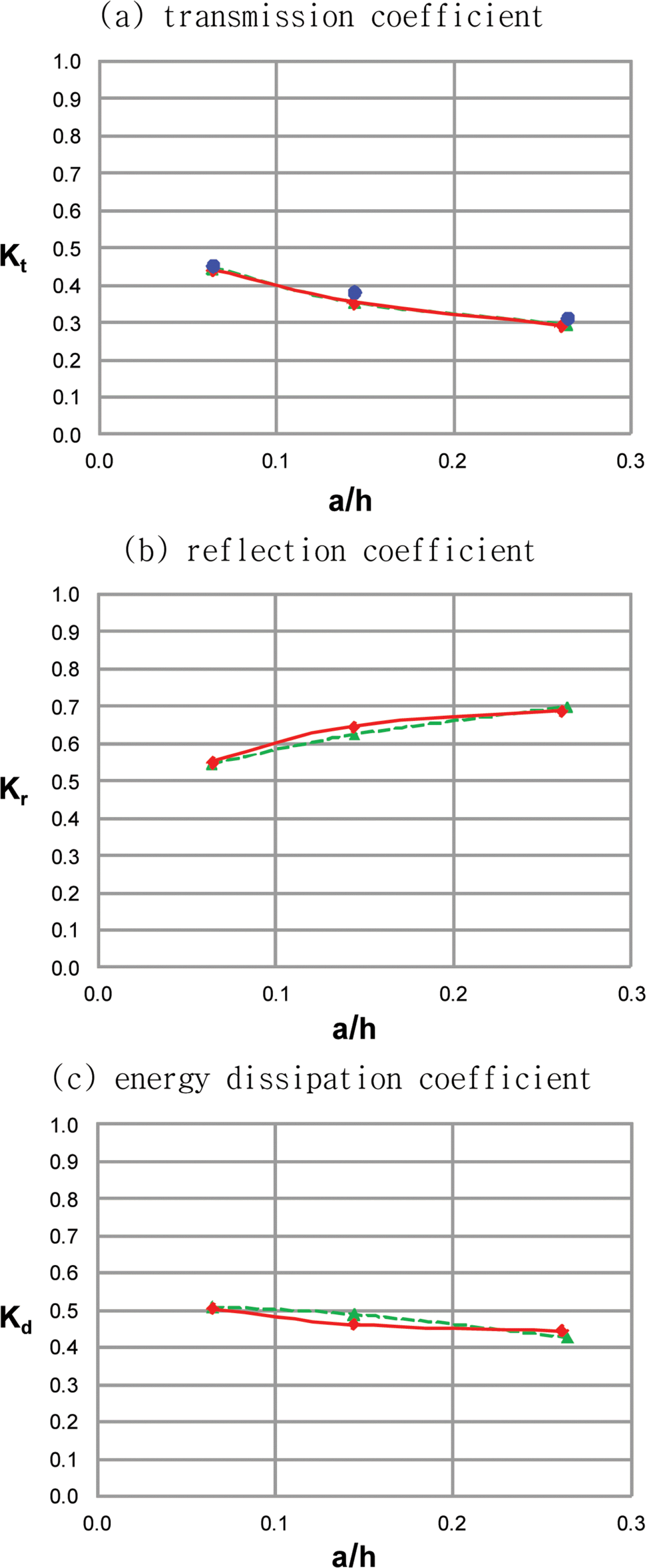
Variation of transmission, reflection, and energy dissipation coefficients with wave nonlinearity (Drag resistance coefficients are determined to fit experimental data); circle = Vidal et al., solid line with diamond = CADMAS-SURF, dashed line with triangle = Boussinesq equations.

Fig. 4(b) shows the variation of reflection coefficients with wave nonlinearity with the optimum values of the drag resistance coefficients. It is noticeable that, even without experimental data, the reflection coefficients are close to each other between the Boussinesq equations and the CADMAS-SURF. As wave nonlinearity increases, the reflection coefficient increases. That is because the area of reflection on the wall increases with the increase of wave nonlinearity.

We also investigate the energy dissipation coefficient for waves in a porous breakwater. The energy dissipation coefficient can be defined as

The energy is proportional to squared wave height and thus the transmission and reflection coefficients which are the ratios of wave heights are squared in Eq. (28).

Fig. 4(c) shows the variation of energy dissipation coefficients with wave nonlinearity with the optimum values of the drag resistance coefficients. It is noticeable that, even without experimental data, the energy dissipation coefficients are close to each other between the Boussinesq equations and the CADMAS-SURF. It is interesting that the energy dissipation coefficient decreases a little with the increase of wave nonlinearity. Figs. 4(a) to 4(c) show that, as wave nonlinearity increases, the increase of the reflection coefficient is more significant than the decrease of the transmission coefficient and thus the energy dissipation coefficient would decrease.

Third, for solitary waves overtopping on a porous breakwater, we find that, with the variation of wave nonlinearity, the height of waves overtopping a low-crested breakwater (obtained by the Navier-Stokes equations) are between the heights of waves passing a high-crested breakwater (obtained by the one-layer Boussinesq equations) and submerged breakwaters (obtained by the two-layer Boussinesq equations). See Fig. 1 for the concept. Three cases with the breakwater crest heights are h_c = 60 cm(high-crested breakwater), h_c = 1 cm (low-crested breakwater), and h_c = −2 cm (submerged breakwater). Experimental conditions are the same as those of Vidal et al. (1988), i.e., water depth of h = 30 cm, breakwater width of b = 20 cm, porous material size of d = 1.43 cm, porosity of λ = 0.44. Wave nonlinearity is varied as a/h = 0.064, 0.144, 0.264.

Fig. 5(a) compares the transmission coefficients among the one- and two-layer Boussinesq equations and the CADMAS-SURF. The transmission coefficients of waves overtopping a low-crested breakwater (obtained by the CADMAS-SURF) are greater than those of waves passing through a high-crested breakwater (obtained by the one layer Boussinesq equations) and less than those of waves passing through a submerged breakwater (obtained by the two layer Boussinesq equations). For waves with lower wave nonlinearity, overtopping waves can be more accurately predicted using the one-layer and two-layer Boussinesq equations. It is interesting that, with the increase of wave nonlinearity, the transmission coefficient by the one-layer Boussinesq equations decreases while the transmission coefficient by both the two-layer Boussinesq equations and the CADMAS-SURF increases. That is because, for waves over a low-crested breakwater and a submerged breakwater, more highly nonlinear waves have more area above the breakwater crest which would pass through the breakwater without energy dissipation and thus experience more transmission. However, for waves in a high-crested breakwater, more highly nonlinear waves have more area under the breakwater crest which would pass through the breakwater with energy dissipation and thus experience less transmission. As wave nonlinearity becomes smaller, the heights of transmitting waves become closer to each other between the one-layer and two-layer Boussinesq equations and thus become closer to the height of overtopping waves.

Fig. 5.

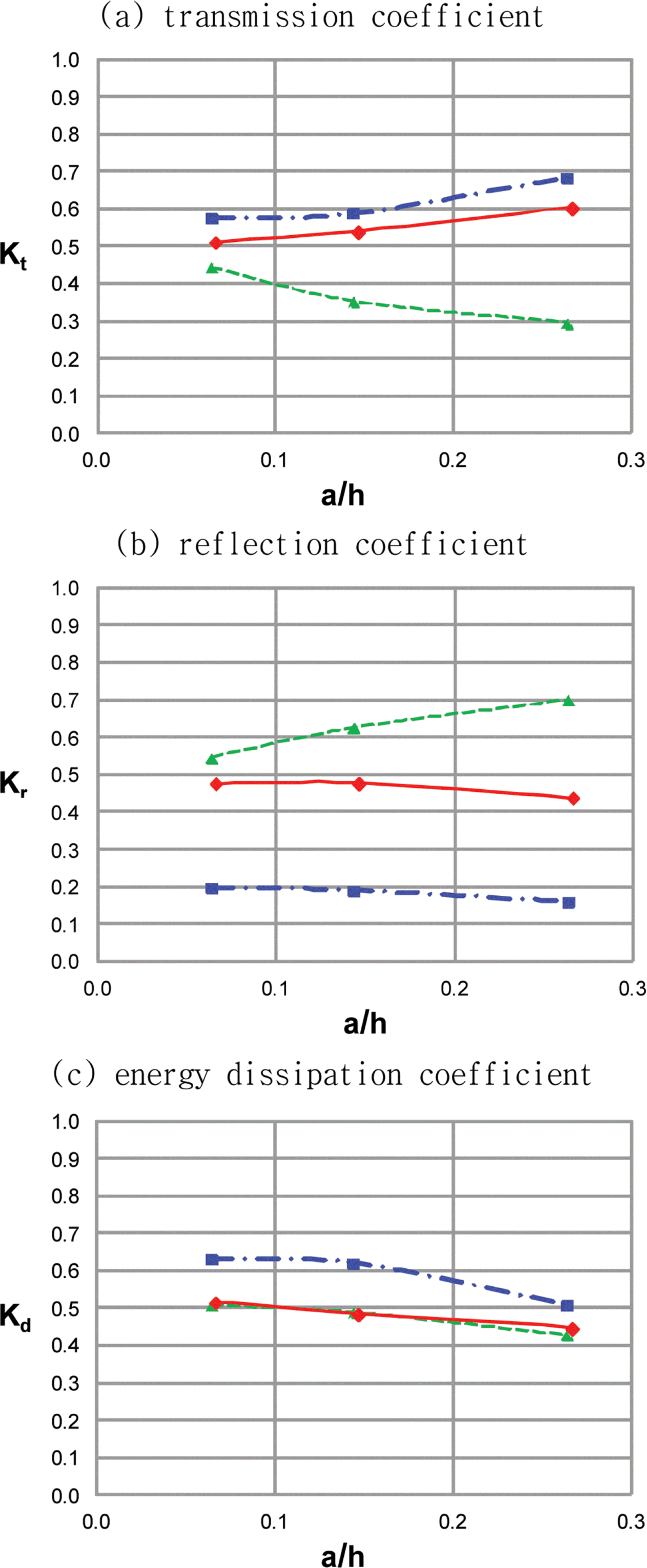
Comparison of transmission, reflection, and energy dissipation coefficients obtained by the one-layer and two-layer Boussinesq equations and the CADMAS-SURF (wave nonlinearity is varied); solid line with diamond = CADMAS, dashed line with triangle = one-layer Boussinesq equations, dash-dotted line with rectangle = two-layer Boussinesq equations.

Fig. 5(b) compares the reflection coefficients among the one-layer and two-layer Boussinesq equations and the CADMAS-SURF. The reflection coefficients of waves overtopping a low-crested breakwater are less than those of waves passing through a high-crested breakwater and greater than those of waves passing through a submerged breakwater. It is interesting that, with the increase of wave nonlinearity, the reflection coefficient by the one-layer Boussinesq equations increases while the reflection coefficient by both the two-layer Boussinesq equations and the CADMAS-SURF decreases. That is because, for waves over a low-crested breakwater and a submerged breakwater, more highly nonlinear waves have less area below the breakwater crest which would reflect from the breakwater wall and thus experience less reflection. However, for waves in a high-crested breakwater, more highly nonlinear waves have more area under the breakwater crest which would reflect from the breakwater wall and thus experience more reflection.

Fig. 5(c) compares the energy dissipation coefficients among the one-layer and two-layer Boussinesq equations and the CADMAS-SURF. The energy dissipation coefficients increase with the increase of wave nonlinearity. The energy dissipation coefficients are close to each other between the one-layer Boussinesq equations and the CADMAS-SURF. However, the energy dissipation coefficients by the twolayer Boussinesq equations are greater than the those by the one-layer Boussinesq equations and the CADMAS-SURF.

Fourth, for solitary waves overtopping on a porous breakwater, we find that, with the variation of breakwater width, the height of waves overtopping a low-crested breakwater are between the heights of waves passing a high-crested breakwater and a submerged breakwater. Three cases with the breakwater crest heights are h_c = 60 cm, 1 cm, −2 cm. Experimental conditions are the same as those of Vidal et al. (1988), i.e., water depth of h = 30 cm, porous material size of d = 1.43 cm, porosity of λ = 0.44. The breakwater width is reduced from d = 20m, to d = 15 m, 10 m, 5 m.

Figs. 6(a) and 6(b) compares transmission and reflection coefficients among the one-layer and two-layer Boussinesq equations and the CADMAS-SURF. As the breakwater width becomes narrower, both the transmission and reflection coefficients of overtopping waves of one-layer and two-layer results become close together. This implies that, for waves on breakwaters with narrower width, overtopping waves can be more accurately predicted using the one-layer and two-layer Boussinesq equations. Fig. 6(c) compares the energy dissipation coefficients among the one-layer and two-layer Boussinesq equations and the CADMAS-SURF. As the breakwater width becomes narrower, the energy dissipation would be negligibly smaller and thus the transmission and reflection coefficients would be near to unity and zero, respectively.

Fig. 6.

Comparison of transmission, reflection, and energy dissipation coefficients obtained by the one-layer and two-layer Boussinesq equations and the CADMAS-SURF (breakwater width is varied); solid line with diamond = CADMAS, dashed line with triangle = one-layer Boussinesq equations, dash-dotted line with rectangle = two-layer Boussinesq equations.

4. Conclusion

In the present study, we approximately obtain height of waves overtopping on a porous breakwater using both the one-layer and two-layer Boussinesq equations. We use the one-layer Boussinesq equations of Lee et al. (2014) and we derive the two-layer Boussinesq equations following Cruz et al. (1997). For solitary waves through a porous breakwater (i.e., one layer case), values of the drag resistance coefficients are determined such that the transmission coefficients of numerical models (both the Boussinesq and Navier-Stokes equations) are close to experimental data. Further, we find that the height of waves overtopping on a low-crested breakwater (obtained by the Navier-Stokes equations) are smaller than the height of waves passing through a high-crest breakwater (obtained by the one-layer Boussinesq equations) and larger than the height of waves passing through a submerged breakwater (obtained by the two-layer Boussinesq equations). As wave nonlinearity becomes smaller or the porous breakwater width becomes narrower, the heights of transmitting waves obtained by the one-layer and two-layer Boussinesq equations become closer to the height of overtopping waves obtained by the Navier-Stokes equations. If the water surface elevation is above the breakwater crest, the waves are in two layers, i.e., upper non-porous layer and lower porous layer. If the water surface elevation is below the breakwater crest, the waves are in one porous layer. In the future, we will directly simulate overtopping waves using both one-layer and twolayer Boussinesq equations simultaneously.

Article information Continued