3.1 Waves2FOAM 모델

본 연구에서는 OpenFOAM 기반의 공개 소프트웨어 Waves2FOAM을 이용하여 수치모델링을 수행하였다(Jacobson et al., 2012). OpenFOAM(Open Field Operation And Manipulation)은 C++ 언어로 작성된 CFD 소프트웨어로 프로그램 코드가 공개되어 누구나 수정 및 재배포가 가능하다. OpenFOAM은 1990년대 초반 영국 Imperial College에서 개발되기 시작하여 2004년 말부터 GNU-GPL(General Public License) 형태로 공개되었다. 다양한 유체역학 현상 해석을 위한 라이브러리(library) 및 솔버(solver)의 집합으로 구성되어 있으며, 대규모 병렬계산을 지원한다.

OpenFOAM은 라이센스 비용이 발생하지 않고, 해석하고자 하는 물리 현상 전용으로 개발되기 때문에 원시 코드(source code)의 최적화를 통해 독립적인 해석 모델을 구축할 수 있다는 장점이 있다. 반면, 프로그램 언어 및 사용 환경에 익숙해지는데 시간이 소요되며 라이브러리나 솔버가 충분히 개발되지 않은 현상에 대해서는 해석이 어렵다는 단점이 있다. Waves2FOAM은 현재 연안 및 해양공학 분야에서의 OpenFOAM 모델링에서 가장 기본적으로 활용되고 있는 라이브러리로서 여러 형태의 파랑 생성 및 소파 기능을 제공한다. 본 연구에서는 OpenFOAM ver. 2.4.0을 프로그램 개발에 사용하였다.

3.2 지배방정식

OpenFOAM의 지배방정식은 비압축성 Navier-Stokes 방정식이며 연속방정식과 운동량방정식으로 구성된다.

여기에서 U는 유동의 속도 벡터를 나타내고 t는 시간, p는 압력, ρ는 밀도, T는 점성응력텐서, f_b는 체적력을 나타낸다. 자유수면의 위치는 Eq. (3)~(5)에 의해 정의되는 VOF(Volume of Fluids)법으로 결정된다.

여기에서 α는 물의 비율을 나타내고 ρ_l과 ρ_g는 각각 액체와 기체의 밀도, μ_l과 μ_g는 각각 액체와 기체의 점성을 나타낸다. 위 식을 직접 계산하게 되면 수치적인 확산으로 α의 분포가 넓게 나타나 계산 정확도가 떨어질 수 있다. 따라서 수치확산을 감소시키기 위해 물과 공기의 속도 차이를 상대속도 U_r로 정의하여 식을 아래와 같이 나타낸다.

여기에서 U_l은 물의 속도, U_g는 공기의 속도를 나타낸다.

3.3 조파 및 소파 방법

OpenFOAM에 조파 및 소파 기능을 추가한 것이 Waves2FOAM(Jacobsen et al., 2012)이다. Waves2FOAM은 경계에서의 조파를 제공하며, 소파는 완화구간 (relaxation zone)을 통해 구현한다. 본 연구에서는 Waves2FOAM에서 제공하는 기본 조파 방법 외에 추가로 해석 영역 내부에서 조파하는 기법(Lin and Liu, 1999)을 구현하여 적용하였다. 원천함수(source function)를 s(t)라고 할 때 조파 영역에서 연속방정식은 다음과 같이 표시된다.

여기에서 C는 파 속도, η는 수면 높이, W는 조파 영역의 폭이며, l_x, l_y, l_z는 조파 영역의 x, y, z 방향의 길이를 각각 나타낸다.

또한 조파 영역의 크기와 높이는 Chen and Hsiao(2016)의 방법을 따라 선형파의 정규화된 속도분포에 근거하여 정하였다. 이 방법에 따르면 조파 영역의 윗면(z_s1)과 아랫면(z_s2)의 연직 높이 및 파 진행방향으로의 폭(w_s)은 각각 다음과 같이 정의된다.

여기에서 k는 파수, h는 수심, L은 파장을 각각 나타낸다. 조파하려는 파의 파장(주기)이 길어지게 되면 w_s도 길어지게 되지만 z_s1과 z_s2의 값은 큰 차이가 없다. 즉, 파장에 따라 조파 영역의 연직 두께에는 큰 차이가 없고 파 진행 방향으로의 폭만 유의미하게 달라진다.

한편 파 에너지의 소파를 위해서 스폰지층(sponge layer)을 사용하였다. 즉, 식 (2)의 운동량 방정식에 각 방향 성분별로 다음과 같은 감쇠항을 적용하여 에너지를 소산시켰다.

여기에서 x₀와 y₀는 스폰지층의 시작 위치를, N과 θ는 감쇠계수의 크기 및 분포를 결정하는 파라미터이다. 본 연구에서는 N = 2를 사용했고, θ의 값은 예비 해석 결과를 통해 x, y, z 방향에 대해 동일하게 θ = 0.6을 적용하였다.

4.1 2차원 내부 조파 테스트(S2)

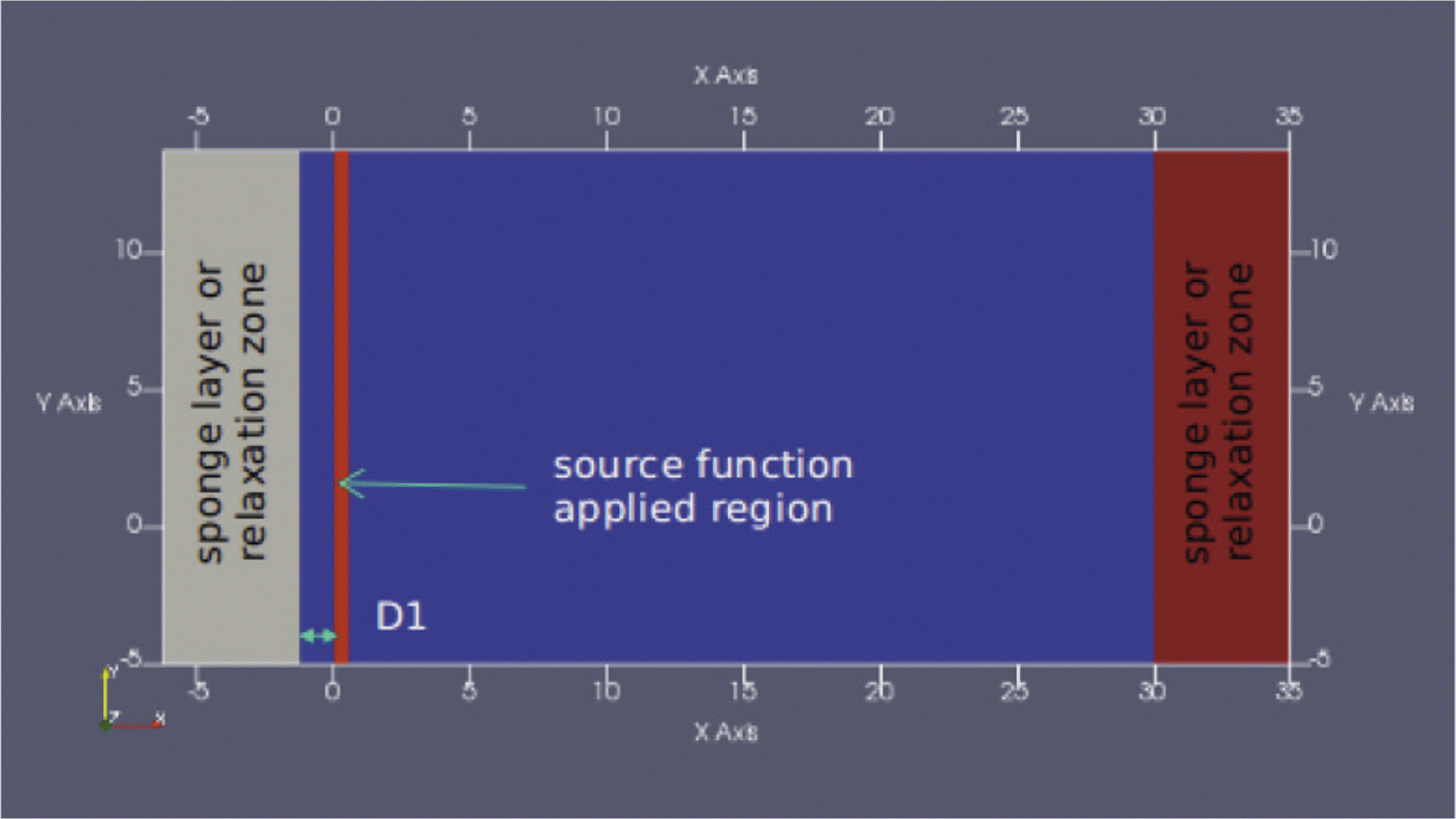
3차원 RIB 해석을 수행하기 전에 내부조파 및 스폰지층에서의 에너지 감쇠 성능을 평가하기 위한 2차원 수치모델링을 먼저 수행하였다. Fig. 2에 보인 것처럼 x = 0 위치에 조파 영역을 설정하였으며, 계산 영역 양 끝 쪽으로 스폰지층을 두었다. 스폰지층의 폭은 파장의 2배로, 스폰지층과 조파 영역 사이의 거리 D1은 파장의 0.5배로 설정하였다. 한편, 바닥 경계조건은 No-slip 조건을 적용하였다. Fig. 3에는 이러한 구성으로 Stokes 2차 이론을 따르는 규칙파 조파가 이루어졌을 때의 자유수면 분포 모습을 나타내었다. 이 그림으로부터 조파 영역을 중심으로 대칭적으로 파랑이 전파되며 스폰지 층에서 에너지가 잘 흡수됨을 확인할 수 있다.

Fig. 2.

Plan view of the computational domain for S2 setup.

Fig. 3.

A snapshot of water surface distribution for S2 setup.

4.2 3차원 RIB 해석(S3)

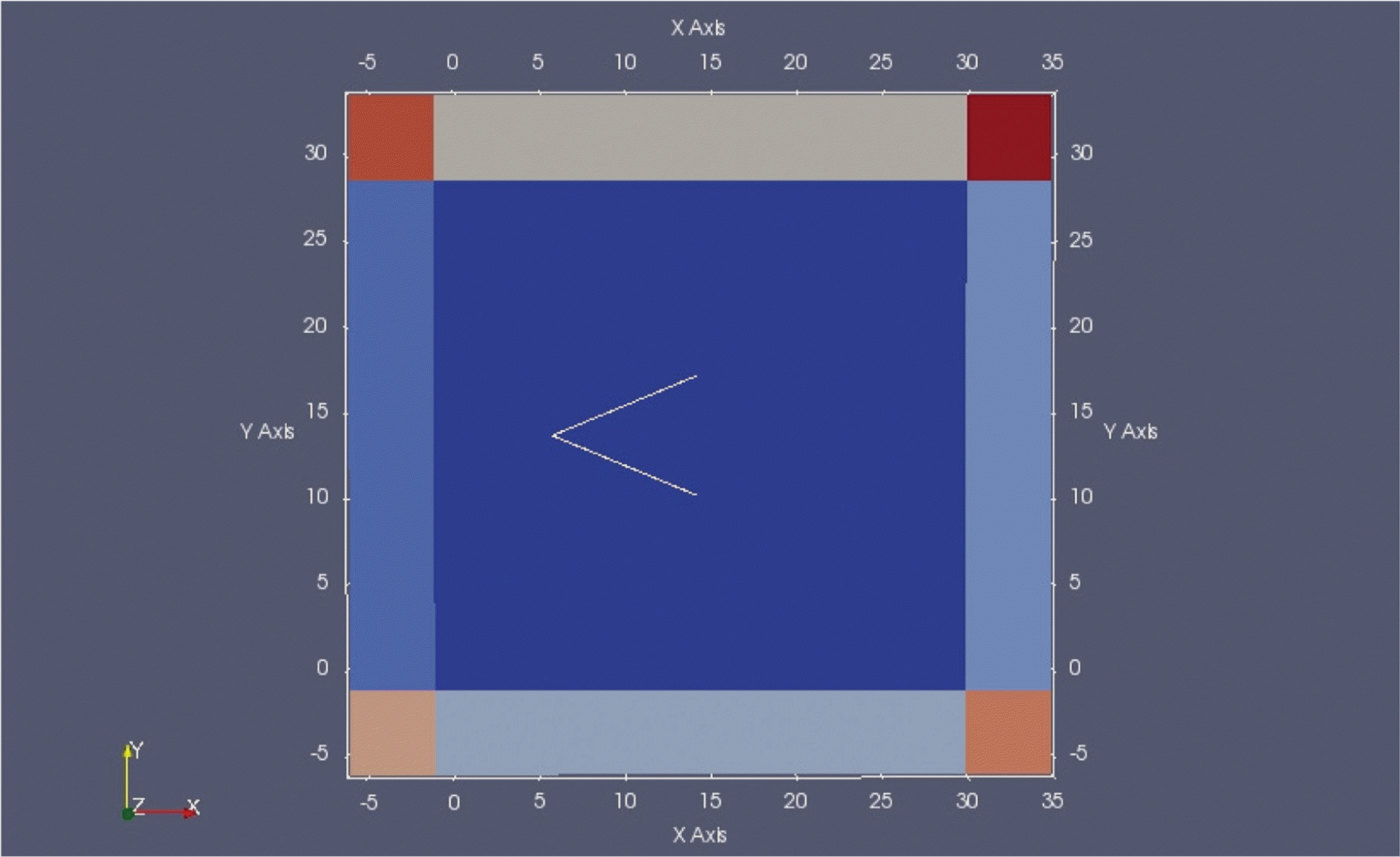
2차원 영역에서 내부조파 및 스폰지층의 성능평가를 마친 후 Briggs et al.(2001)의 수리실험(Fig. 1)을 재현하기 위한 수치모델링을 수행하였다. Fig. 4에 보인 것처럼 계산 영역을 둘러싼 네 면에 모두 스폰지층을 두어 반사파의 영향을 제거하였다. 바닥 경계조건은 마찬가지로 No-slip 조건을 적용하였다. 격자 간격은 파 진행방향(x) 및 측방향(y)으로 0.04 m의 균등격자를, 연직 방향(z)으로는 0.005~0.0575 m의 가변격자를 적용하였으며, 이에 따른 총 격자 수는 16,293,070개였다. 한편, RIB 구조물은 두께 없는 벽면으로 모델링하였다.

Fig. 4.

Plan view of the computational domain for S3 setup.

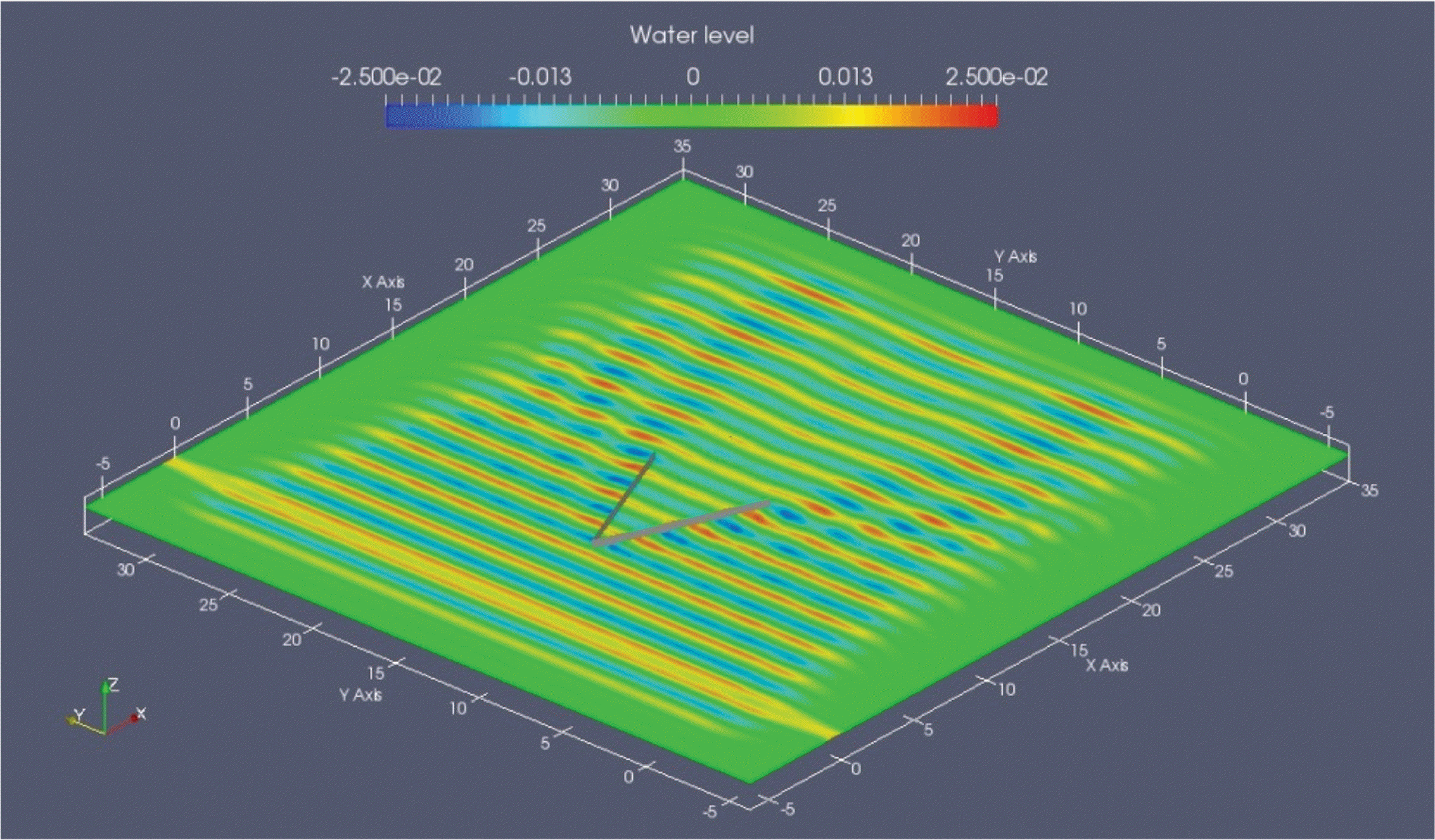
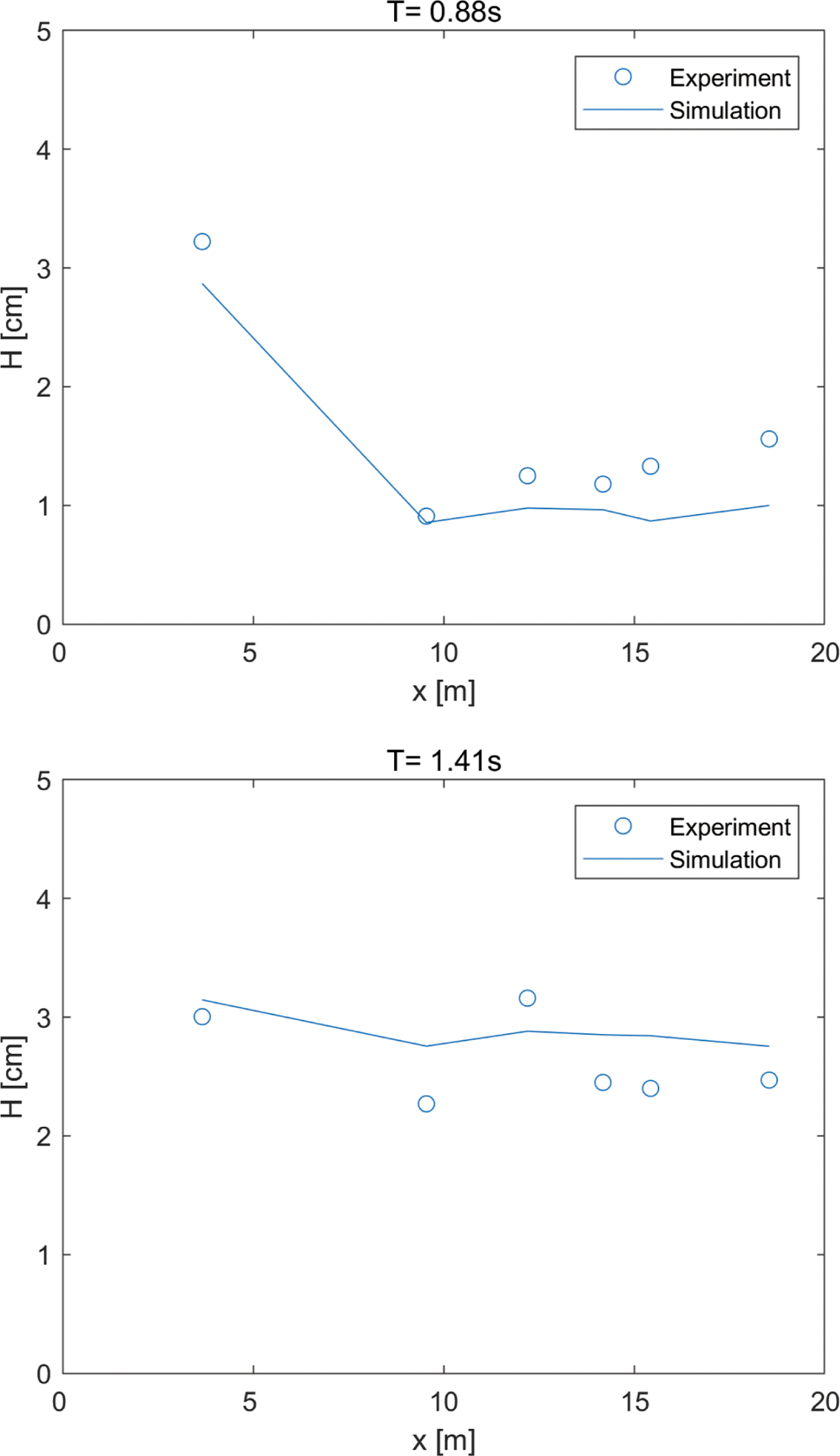
Table 2에 제시된 조건에 대하여 수치모델링을 수행하였고, Fig. 5에는 T = 1.41 s인 경우의 수면변위 모습을 제시하였다. 조파선에서 조파된 파가 계산 영역 내로 전파되며 네 면의 스폰지층에서 파랑 에너지가 잘 흡수됨을 확인할 수 있다. 또한 Fig. 6과 7에는 RIB 구조물 전면에서의 정압력과 동압력의 분포 그림을 제시하였다. 한편 파고 평가는 각 조건 별로 Table 1에 제시된 열 군데(Gauge 1~10)에서 조파 시작 후 40초에서 50초까지 10초 동안의 수면변위 자료를 추출하여 수행되었다. Fig. 8에는 Briggs et al.(2001)에서 제공하는 파고 관측 자료와 수치모델링 결과를 비교한 결과를 제시하였다. x = 3.66m의 값은 파고계 1번부터 5번까지 다섯 개 위치에서의 파고를 평균한 값이며, 나머지는 y = 13.72m 단면을 따라서 배치된 파고계 6번부터 10번까지에서의 값이다.

Fig. 5.

A snapshot of water surface distribution for S3 setup.

Fig. 6.

A snapshot of static pressure distribution for S3 setup.

Fig. 7.

A snapshot of dynamic pressure distribution for S3 setup.

Fig. 8.

Comparison of wave height simulation results with the experimental data.

T = 0.88 s의 경우 RIB에 의해 차폐된 파고계 6번 이후의 파고가 입사파고에 비해 훨씬 작아 RIB에 의한 파고 저감 효과가 확실하게 나타남을 알 수 있다. 반면 T = 1.41 s의 경우 파고계 6번 이후에서의 파고가 입사파고에 비해 그다지 작아지지 않음을 알 수 있다. 대체로 실험자료와 수치모델링 결과가 잘 일치함을 확인하였다.

한편, Fig. 9에는 두 가지 실험파 조건에 대한 수치해석 결과로부터 얻은 전달파고비(K_T)를 실험자료 및 WAMIT 수치모델 결과와 비교한 그림을 제시하였다. WAMIT은 경계적분법(Boundary integral equation method)으로 부유체의 운동 해석에 널리 활용되는 모델로 Briggs et al.(2001)에는 수리 Fig. 9에 보인 것처럼 T = 0.88 s 및 T = 1.41 s의 경우 WAMIT보다 본 연구에서 개발된 수치모델이 실험 자료에 더 근접한 결과를 제시하고 있다. Willmott et al.(2012)이 제안한 수정 일치지수(refined index of agreement)는 모델의 예측 정확도를 가장 합리적으로 평가하는 것으로 알려져 있다. Fig. 9의 결과에 대하여 수정 일치지수를 계산해보면 T = 0.88 s인 경우 WAMIT은 d_r = −0.51, 본 수치모델은 d_r = 0.32였고, T = 1.41 s인 경우 WAMIT은 d_r = 0.14, 본 수치모델은 d_r = 0.38로 나타났다. 수정 일치지수는 −1에서 1 사이에서 변하는 값으로 1에 가까울수록 예측 정확도가 더 높음을 의미한다. 따라서 본 연구에서 적용한 OpenFOAM 모델이 WAMIT에 비해 Briggs et al.(2001)의 수리실험 결과를 더 정확하게 예측함을 통계적 지표로도 확인할 수 있다.

Fig. 9.

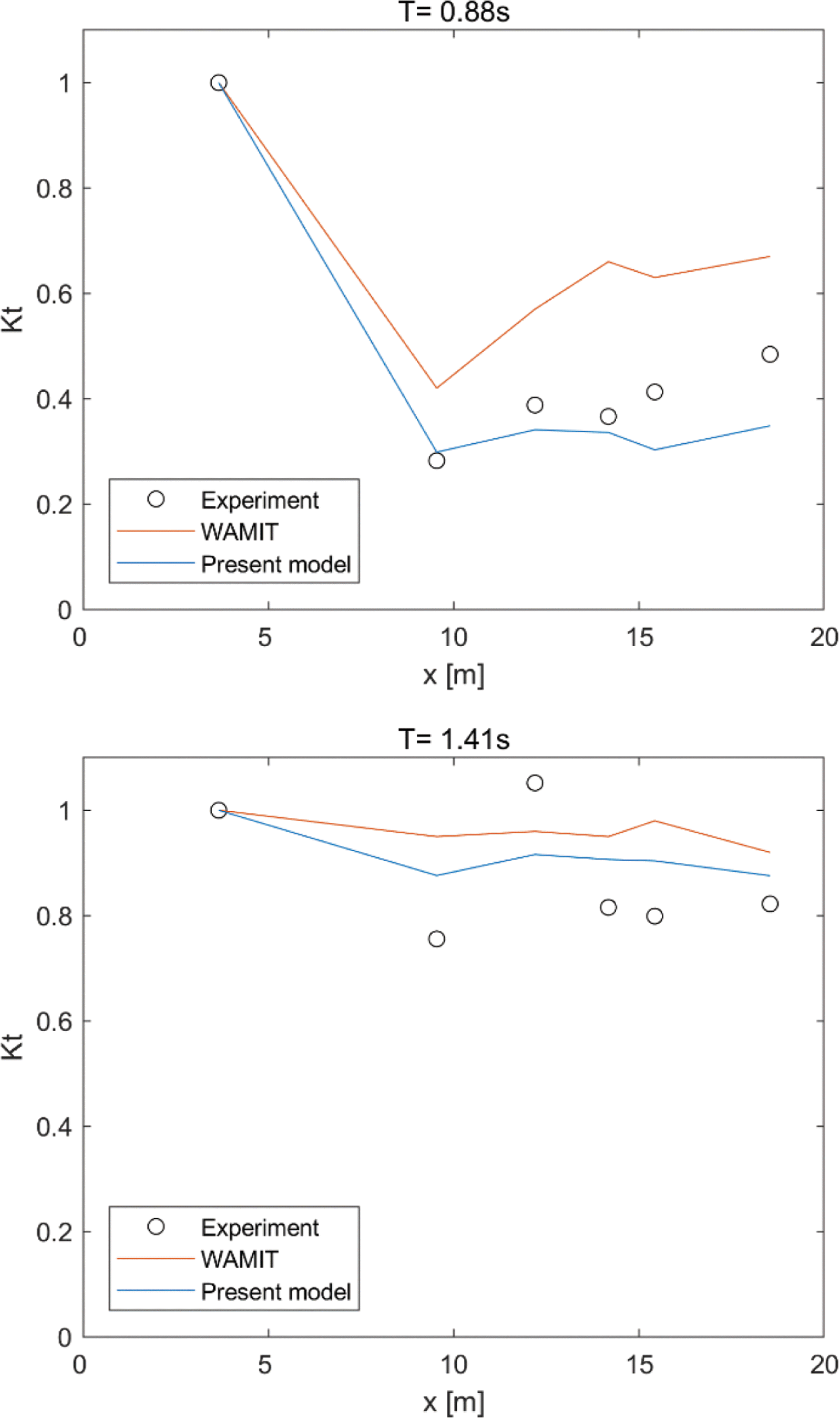
Comparison of wave transmission coefficients obtained by WAMIT (Briggs et al., 2001) and the present model with the experimental data.

WAMIT은 근본적으로 자유수면 및 구조물 주변에서의 선형 경계조건을 만족하는 라플라스 방정식의 속도 포텐셜을 구하며, 전달계수는 이 속도 포텐셜의 시간 미분항에 연계되어 구해진다. 따라서 부유식 연직판처럼 구조물 전후에서 속도장의 급격한 변화가 나타나는 물리 현상에 대한 모델링에는 어느 정도 한계를 가지게 될 것이라고 추론해 볼 수 있다. 반면에 본 연구에서 적용한 OpenFOAM의 경우 VOF 기법에 의해 보다 엄밀하게 자유수면을 모델링하며, 난류에 의한 에너지 소산도 수치적으로 고려되므로 WAMIT에 비해서 상대적으로 더 정확하게 부유식 연직판 앞뒤의 파고를 계산하게 된다. Fig. 9에서 WAMIT이 OpenFOAM 모델링에 비해서 전반적으로 전달계수를 더 크게 평가하는 것도 이러한 이유에서 비롯된다고 할 수 있다.

본 수치모델 결과로부터 파고계 6번부터 10번까지의 파고를 평균하여 입사파고로 나누어 전달파고비(K_T)를 계산한 값은 T = 0.88 s일 때 0.33, T = 1.41 s일 때 0.90이었다. 주기가 길어짐에 따라 전달파고비가 급속하게 증가함을 알 수 있다. Briggs et al.(2001)의 수리실험 축척이 1:32인 점을 고려하면 T = 0.88 s는 현장에서 T = 5 s에 해당하고, T = 1.41 s는 현장에서 T = 8 s에 해당한다. 이러한 점을 고려할 때 RIB 구조물에 의한 파랑 저감 효과는 주기 5초 내외의 단주기파에 대해서만 제한적으로 기대할 수 있다고 할 수 있다.