2.1 수치해석이론

본 연구에서 적용한 수치해석모델인 OLAFOAM은 비혼합 및 비압축성을 갖는 혼상유체(액체 및 기체)의 거동을 해석하기 위하여 식 (3)의 연속방정식과 식 (4)의 RANS(Reynolds-Averaged Navier-Stokes) 방정식을 유한체적법에 기초하여 이산화한다.

여기서, t는 시간, x_i는 공간벡터좌표, ρ는 유체밀도, u_i(i = x, y, z)는 유체속도의 Cartesian 성분, p^*는 Pseudo-dynamic 압력, X_j는 위치벡터, φ과 D₅₀은 해석영역 내에 위치하는 투과성구조물의 공극률과 중앙입경을 각각 나타내며, μ_eff는 μ + ν_turb로 μ는 점성계수이고, ν_turb는 난류동점성계수이며, [CT]는 투과성구조물에 의한 저항 항으로 다음의 식 (5)과 (6)으로 주어진다.

여기서, α와 β는 선형 및 비선형마찰계수로 본 연구에서는 Jensen et al.(2014)이 층류흐름, 층류와 난류가 혼합된 흐름 및 난류흐름에 대한 수치실험결과를 바탕으로 제시한 α = 500 과 β = 2.0을 각각 적용하였다. 또한, KC는 Keulegan-Carpenter 수로 T_ou_M/D₅₀φ를 나타내며, T_o은 진동주기이고, u_M은 유체입자의 최대진동속도이다.

액체와 기체의 경계면은 계산격자 내에서 유체가 점유하고 있는 체적을 나타내는 VOF 함수 F를 이용하는 VOF 법을 적용하며, VOF 법에서는 액체셀의 경우 F = 1, 기체셀의 경우 F = 0, 그리고 액체와 기체를 모두 포함하고 있는 경계셀의 경우 0 < F < 1의 값을 갖는다. VOF 함수 F는 식 (7)의 이류방정식에 의해 계산된다.

위의 식의 마지막 항에 나타낸 u_ic는 인공압축항으로 |u_ic| =min[c_α|u_i|, max(|u_i|)]와 같이 주어지며, 본 연구에서는 c_α= 1을 적용하였다. 또한, 각각의 계산셀에 있어서의 유체밀도와 점성계수는 VOF 함수를 가중치로 적용하여 다음과 같이 산정할 수 있다.

난류동점성계수 ν_turb는 LES 모델을 적용하여 산정하였으며, 그 밖의 OLAFOAM에 대한 상세한 수치해석기법은 Lee et al.(2016) 및 OLAFOAM 매뉴얼(https://gitgub.com/phicau/OLAFOAM/master/reference.zip)을 참조하기 바란다.

2.2 수치해석조건

본 연구의 수치시뮬레이션을 위해 Fig. 1에 나타낸 바와 같이 길이 12.5 m, 폭 10 m, 높이 0.4 m의 크기를 갖는 3차원 수치파동수조를 구성하고, 수심은 바닥의 경사를 고려하지 않는 일정수심 h = 25 cm를 적용하였으며, 수조의 끝단에는 1:20의 경사를 갖는 사빈을 설치하였다. 수치파동수조 내에 3차원투과성잠제를 설치하여 잠제 사이의 개구폭 및 잠제의 설치위치에 따른 수치시뮬레이션을 수행하였다.

Fig. 1.

Illustrative sketch of wave basin and submerged structure for numerical analysis.

이하에서는 Mizutani et al.(1998)과 같은 기존의 수리실험과 잠제 천단 상에서 강제쇄파의 유도 및 수치계산에서 소요되는 계산시간 등을 참조하여 잠제의 형상, 제체의 매질 및 사빈의 매질 등을 가정하였다. 먼저, Fig. 1에 보이는 바와 같이 해석대상의 잠제에서 천단고는 21 cm, 천단수심은 4 cm, 천단폭은 1.05 m의 크기를 각각 가지며, 사면경사는 2:1로 설정하였다. 그리고, 잠제의 제체는 공극율 φ = 0.33, 중앙입경 D₅₀ = 3.0 cm인 투과성매질로 구성되며, 잠제의 배후에 설치되는 사빈은 공극률이 φ = 0.3, 중앙입경이 D₅₀ = 0.2 cm인 모래로 각각 가정되었다. 잠제의 구성재료가 갖는 저항계수로 Jensen et al.(2014)이 제시한 α = 500, β = 2.0을 적용하였으며, 사빈의 경우는 모래 입경에 해당하는 D₅₀ = 0.2 cm의 다공성매질에 대한 Billstein et al.(1999)의 실험으로부터 산정된 α = 0.0, β = 3.0을 각각 적용하였다. 또한, Black and 평균유속의 공간분포 Fig. 2는 입사파고 H = 5 cm인 경우 개구폭의 변화에 따른 Andrews(2001)가 제시한 설상사주가 형성되는 조건인 L_s/S < 2.0의 범위를 고려하여 잠제의 설치위치를 선정하고, 각각의 조건에 따른 잠제 사이의 개구폭을 설정하였다. Table 1에 수치실험에 이용된 잠제의 배치와 입사파랑에 대한 조건을 나타낸다.

Fig. 2.

Spatial distribution of mean velocities at three vertical layers of horizontal plane.

Table 1.

Incident wave condition and 3-dimensional layout of submerged breakwater

한편, 계산영역의 격자는 수평방향으로 일정격자를 적용하고, 연직방향으로는 가변격자를 적용한 Δx = 3 cm, Δy = 3 cm, Δz = 0.7~1.4 cm로 구성하였으며, 구성된 격자에 대한 Courant 상수는 0.3 이하가 되도록 시간간격을 조정하면서 수치실험을 수행하였다. 경계조건으로는 계산영역의 모든 벽면에서 Neumann 조건인 ∂f/∂x_i = 0을 적용하였다.

3.1 개구폭의 변화에 따른 평균유속의 공간분포

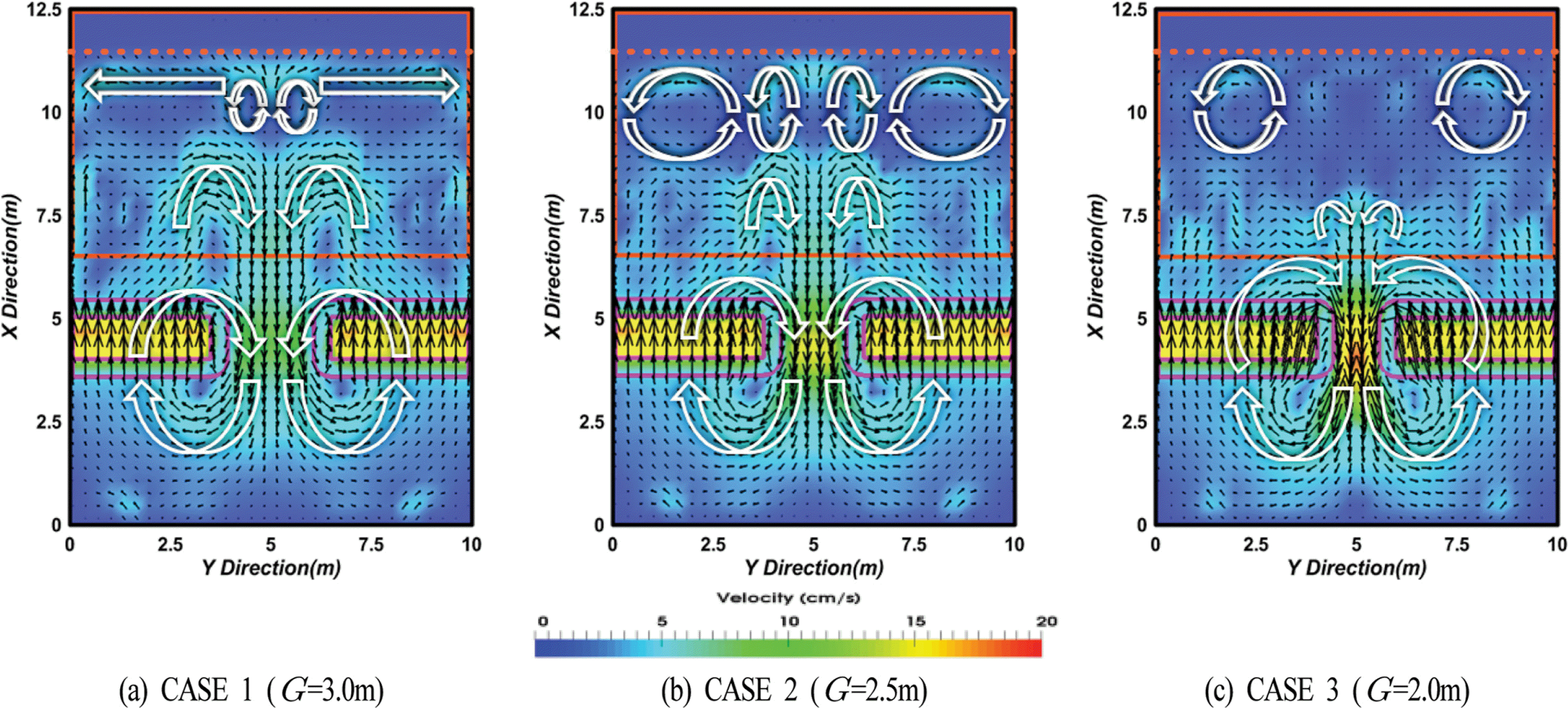
Fig. 2는 입사파고 H = 5 cm인 경우 개구폭의 변화에 따른 CASES 1~3에 대한 잠제 주변에서 시간평균유속을 나타낸 것이다. 각 그림에서 (i)는 바닥 근방에서 평균유속분포로 저면에서 z = 0.02m인 지점에서의 평균유속분포를 나타내며, (ii)는 수심의 중간위치에서 평균유속을 나타내고, (iii)는 정수면 상에서 평균유속분포를 각각 나타낸다. 먼저, 바닥 근방에서 평균유속을 살펴보면 잠제의 천단이 위치하는 곳에서는 육측(onshore side)으로, 개구부에서는 해측(offshore side)으로의 흐름이 탁월하게 발생하며, 특히 개구부에서 해측흐름은 개구폭이 좁을수록 보다 탁월하게 발생한다. 제두부에서 이러한 육측과 해측으로의 흐름에 의해 잠제 전면의 개구부 근방의 양측에서 순환류의 셀이 형성되는 것을 확인할 수 있다. 한편, 해안선 근방에서는 순환셀이 형성되지 않지만 개구폭이 넓은 경우에는 연안류성분이 탁월해지고, 반면에 개구폭이 좁은 경우에는 이안류성분이 탁월해지는 것을 확인할 수 있다. 수심의 중간위치의 경우를 살펴보면 바닥 근방에서와 유사하게 잠제 천단 상에서는 육측흐름이, 개구부에서는 해측흐름이 탁월하게 발생하며, 또한 개구폭이 좁을수록 해측흐름이 보다 탁월하게 발생한다. 그리고, 잠제 전면 및 개구부 제두부 근방에서는 바닥 근방에서와 같이 순환셀이 형성되고, 개구폭이 넓은 경우에는 개구부의 양측 제두부에서도 순환셀이 형성되며, 여기서도 해안선 근방에서는 개구폭이 넓은 경우에 연안류성분이 탁월해지고, 반면에 개구폭이 좁은 경우에 이안류성분이 탁월해지는 것을 확인할 수 있다. 수면에서는 개구부를 제외하면 전체적으로 육측흐름이 지배적으로 나타나며, 개구폭이 넓을수록 해안선 부근에서 연안류가 강하게 나타나고, 잠제 천단 상으로 유입되는 강한 육측흐름과의 상호간섭에 의해 양측벽 근방에서 순환셀이 형성된다.

Fig. 2는 입사파고 H = 5 cm인 경우 개구폭의 변화에 따른 CASES 1~3에 대한 잠제 주변에서 시간평균유속을 나타낸 것이다. 각 그림에서 (i)는 바닥 근방에서 평균유속분포로 저면에서 z = 0.02m인 지점에서의 평균유속분포를 나타내며, (ii)는 수심의 중간위치에서 평균유속을 나타내고, (iii)는 정수면 상에서 평균유속분포를 각각 나타낸다. 먼저, 바닥 근방에서 평균유속을 살펴보면 잠제의 천단이 위치하는 곳에서는 육측(onshore side)으로, 개구부에서는 해측(offshore side)으로의 흐름이 탁월하게 발생하며, 특히 개구부에서 해측흐름은 개구폭이 좁을수록 보다 탁월하게 발생한다. 제두부에서 이러한 육측과 해측으로의 흐름에 의해 잠제 전면의 개구부 근방의 양측에서 순환류의 셀이 형성되는 것을 확인할 수 있다. 한편, 해안선 근방에서는 순환셀이 형성되지 않지만 개구폭이 넓은 경우에는 연안류성분이 탁월해지고, 반면에 개구폭이 좁은 경우에는 이안류성분이 탁월해지는 것을 확인할 수 있다. 수심의 중간위치의 경우를 살펴보면 바닥 근방에서와 유사하게 잠제 천단 상에서는 육측흐름이, 개구부에서는 해측흐름이 탁월하게 발생하며, 또한 개구폭이 좁을수록 해측흐름이 보다 탁월하게 발생한다. 그리고, 잠제 전면 및 개구부 제두부 근방에서는 바닥 근방에서와 같이 순환셀이 형성되고, 개구폭이 넓은 경우에는 개구부의 양측 제두부에서도 순환셀이 형성되며, 여기서도 해안선 근방에서는 개구폭이 넓은 경우에 연안류성분이 탁월해지고, 반면에 개구폭이 좁은 경우에 이안류성분이 탁월해지는 것을 확인할 수 있다. 수면에서는 개구부를 제외하면 전체적으로 육측흐름이 지배적으로 나타나며, 개구폭이 넓을수록 해안선 부근에서 연안류가 강하게 나타나고, 잠제 천단 상으로 유입되는 강한 육측흐름과의 상호간섭에 의해 양측벽 근방에서 순환셀이 형성된다.

Fig. 3은 Fig. 2와 동일한 조건인 입사파고 H = 5 cm인 경우 산정된 유속성분을 저면에서 수면까지 수심방향으로 적분하고, 동시에 시간평균한 평균유속(해빈류)의 공간분포를 나타낸다. 그림으로부터 잠제 천단 상에서는 육측으로의 흐름이, 반면에 개구부에서는 해측으로 흐름이 나타나며, 이는 일반적으로 잠제에서 잘 알려진 플럭스수송현상과 일치한다. 개구부 근방에서 잠제 천단 상에서 육측으로, 그리고 개구부에서 해측으로 급변하는 이러한 흐름 특성으로 인하여 개구폭에 관계없이 개구부 근방의 잠제 전면에서 순환셀이 형성된다. 이는 다기이안제와 다기잠제 배후에서 순환셀의 방향을 실험적으로 검토한 Loveless and MacLeod(1999)의 결과와도 일치한다. 즉, 이안제의 경우 제두부에서 육측흐름이 발생하여 제간부로 향하는 순환류가 발생하는 반면, 잠제의 경우 제간부에서 육측흐름이 발생하여 제두부로 향하는 순환류가 발생한다는 것을 실험적으로 규명한 Loveless and MacLeod(1999)의 결과와 일치하며, 단일잠제에 대한 Nobuoka et al.(1996)에서도 유사한 순환패턴이 나타나는 것을 알 수 있다.

Fig. 3.

Spatial distribution of time- and depth-averaged mean velocities in horizontal plane.

또한, 해안선 부근에서는 개구폭에 관계없이 순환셀이 형성되지만 개구폭이 가장 좁은 CASE 3보다 개구폭이 넓은 CASE 2에서 순환셀의 크기가 해안선과 평행한 방향으로 보다 확장되고, 개구부 배후의 해안선 부근에서 순환셀이 형성된다. 한편, 개구폭이 가장 넓은 CASE 1에서는 순환셀의 크기가 작아지는 반면, 연안류가 형성되는 것을 확인할 수 있다. 이것은 개구부 배후 및 제간부 배후의 각각 해안선 부근에서 나타나는 평균수위(Lee et al., 2017)의 차이에 기인하는 연안류로 판단된다.

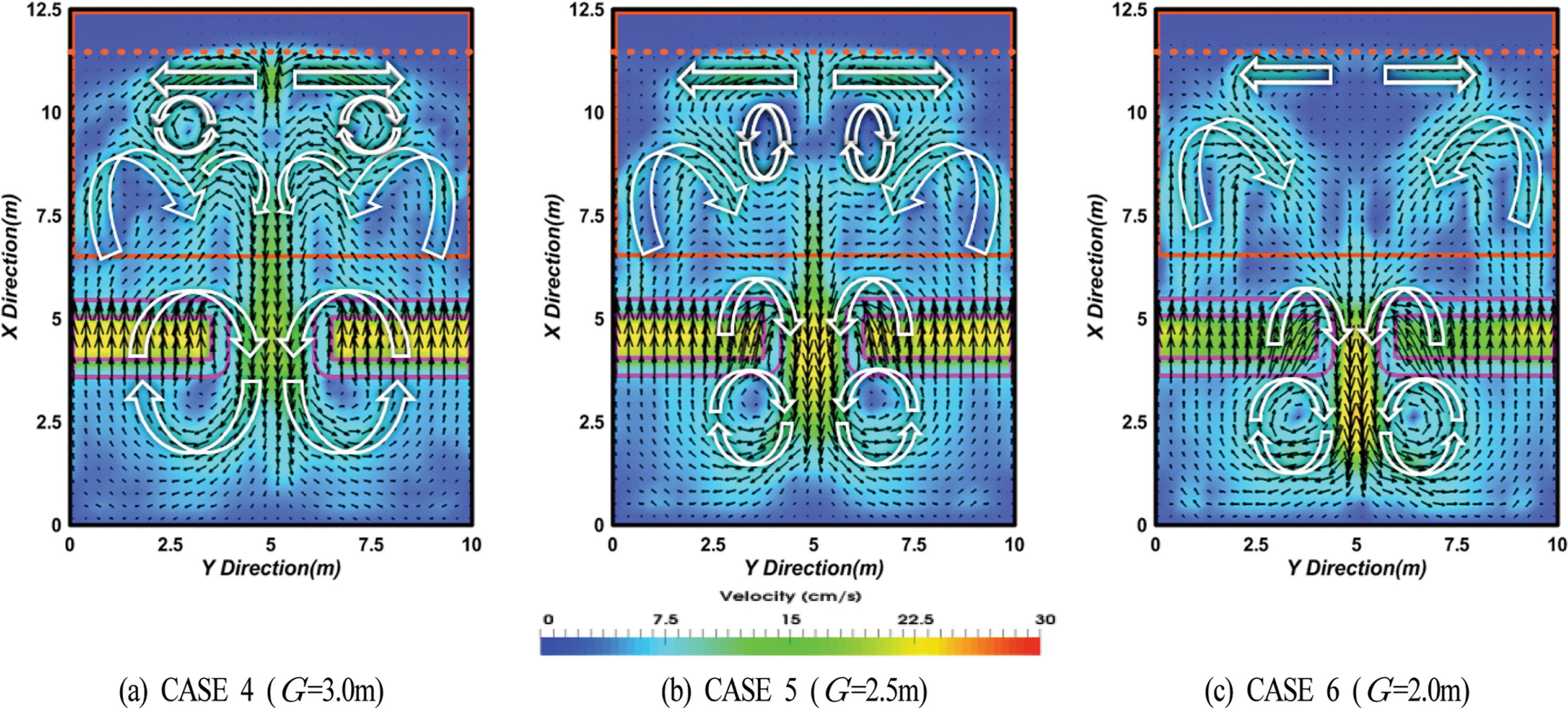
Fig. 4는 입사파고 H = 7 cm인 경우에 Fig. 3과 같이 수심적분 및 시간평균된 평균유속의 공간분포를 나타낸다. 입사파고 H = 5 cm의 경우와 동일하게 개구부 근방의 잠제 전면에서 순환셀이 형성되고, 이는 제두부 근방의 제간부에서 육측흐름과 개구부를 통한 해측흐름과의 간섭에 의해 발생한다. 전술한 입사파고 H = 5 cm인 Fig. 2의 경우와는 상이하게 개구폭에 관계없이 연안류가 형성되지만 개구폭이 넓을수록 보다 강한 연안류가 형성되며, 사빈 경사면 상에서 보다 명확한 순환셀이 형성된다.

Fig. 4.

Spatial distribution of time- and depth-averaged mean velocities in horizontal plane.

3.2 잠제의 설치위치에 따른 평균유속의 공간분포

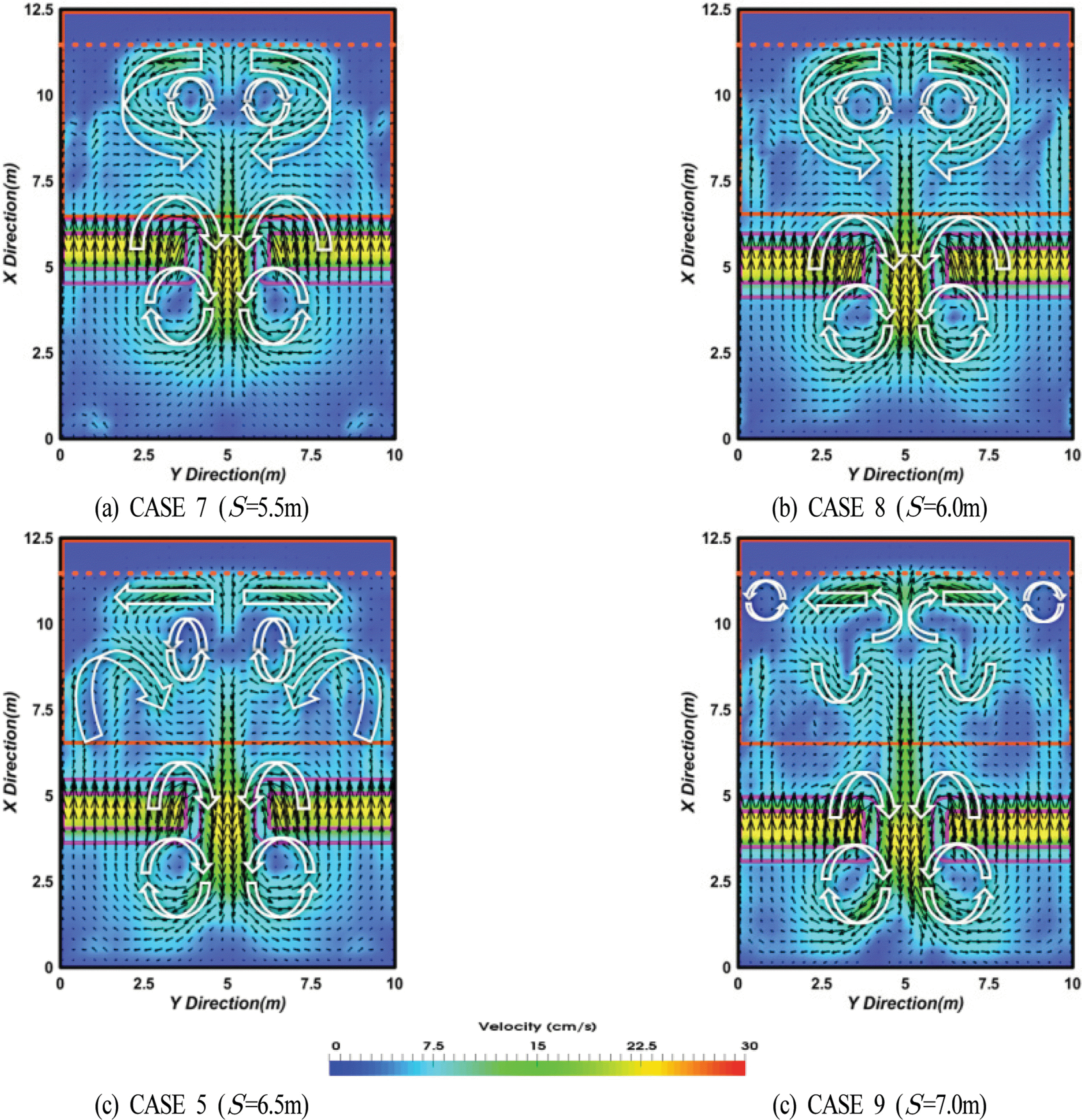
Fig. 5는 잠제 위치에 따른 수심적분 및 시간평균된 평균유속분포를 나타내며, 입사파고가 H = 7 cm, 개구폭이 G = 2.5 m인 경우에 잠제 위치 S = 6.5m를 중심(CASE 5)으로 해안선에서 1. 0m 더 가까운 S = 5.5m의 경우(CASE 7), 해안선에서 0.5 m 더 가까운 S = 6.0m의 경우(CASE 8)와 해안선에서 0.5 m 더 먼 S = 7.0m 경우(CASE 9)를 각각 제시한다. 결과를 살펴보면 개구부 근방의 잠제 전면에서는 모두 순환셀이 형성되며, 이는 Loveless and MacLeod(1999)에서도 지적되어 있는 바와 같이 제두부 부근에서 발생하는 제간부에서 육측흐름과 개구부에서 해측흐름과의 상호작용에 의해 발생된다. CASES 7과 8을 CASE 5와 비교하면 사빈 경사면 상에서 순환셀이 형성되는 현상은 동일하지만 CASE 5의 경우가 연안류의 형성이 보다 명확하다. 여기서, 잠제 위치가 해안선에 멀어질수록 CASE 5의 경우 사빈 경사면에서 종단방향으로 장축을 가진 타원형의 순환셀이 형성되고, 잠제 위치가 해안선에서 가장 멀리 떨어진 CASE 9의 경우 연안류성분이 강해지면서 순환셀의 형성은 불완전하게 되며, 최내측의 해안선 부근에서 순환셀이 형성되는 것을 알 수 있다.

Fig. 5.

Spatial distribution of time- and depth-averaged mean velocities in horizontal plane.

3.3 연안류분포

Ranasinghe and Turner(2006)의 결과에 의하면 해안선에 평행하게 설치된 단일잠제에 파가 직각방향으로 입사하는 경우 잠제 제간부 배후의 해안선 부근에서는 양측으로 발산하는 연안류가 발생하여 침식이 발생(Ranasinghe and Turner(2006)의 Fig. 11을 참조)하는 반면, 파가 해안선에 경사지게 입사하는 경우 파가 잠제를 통과한 후 해안선에서 연안류를 방해하여 연안류의 속도를 감소시키고, 이로 인하여 흐름이 정체되어 퇴적이 발생(Ranasinghe and Turner(2006)의 Fig. 12를 참조)한다. 또한, Ranasinghe et al.(2010)의 결과를 살펴보면 파가 해안선에 평행하게 입사하는 경우에도 잠제와 해안선과의 거리에 따라 해빈류 패턴이 달라지며, Ranasinghe and Turner(2006)와 동일하게 해안선 부근에서 양측으로 발산하는 연안류가 발생하는 경우에는 침식이 발생하고, 연안류가 수렴하는 지점에서 퇴적이 발생한다고 결론짓고 있다. 즉, 연안류는 해안선의 침 · 퇴적과 같은 지형변동에 큰 영향을 주며, 설상사주의 형성에 대한 예측에서 중요한 물리적 파라미터라고 할 수 있다.

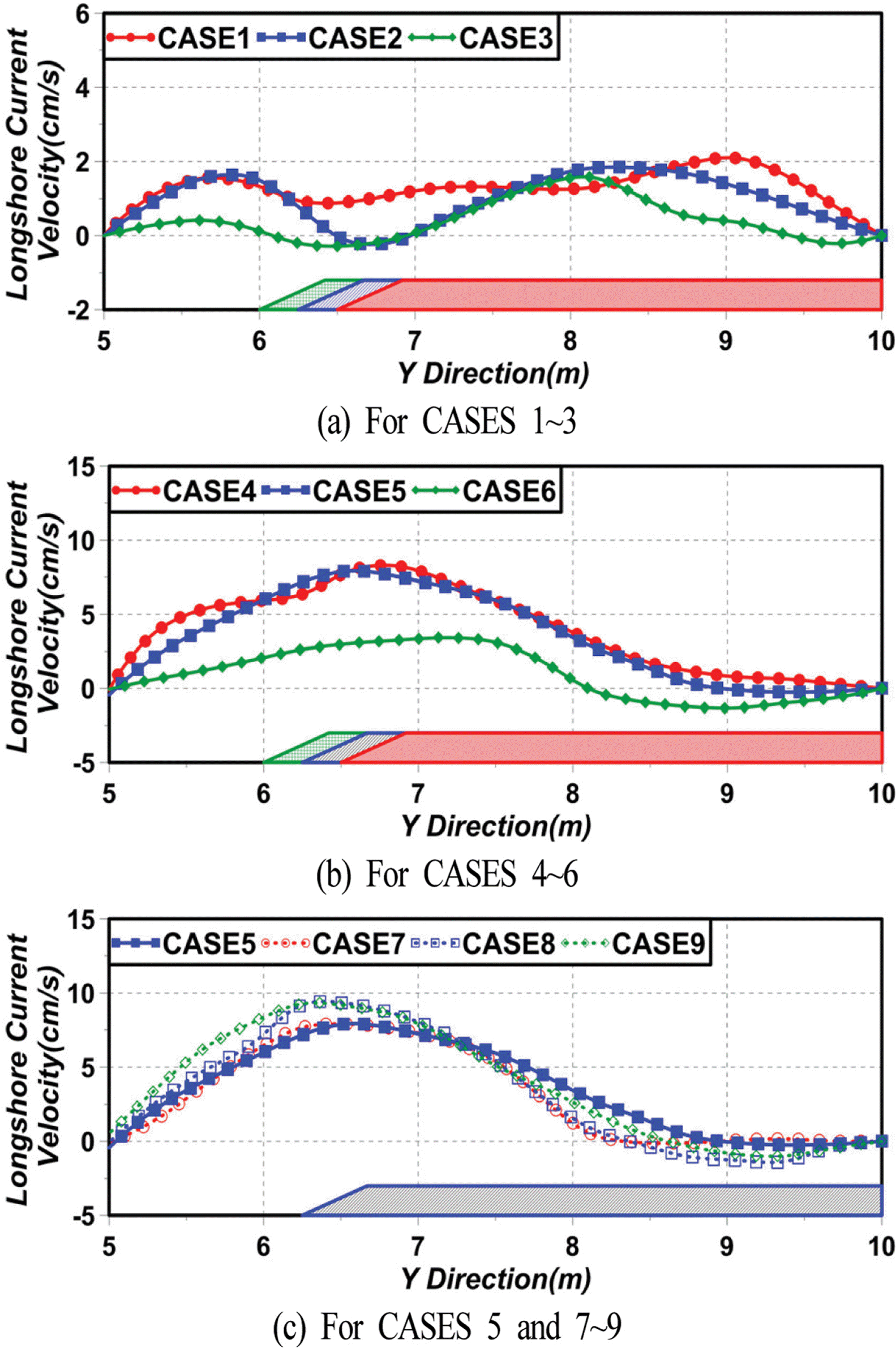
Fig. 6은 Figs. 3~5에서 조파지점으로부터 10.5~11.4 m 이 격된 부근에 형성된 연안류를 x방향으로 평균하여 y방향에 대해 나타낸 것이며, (+)는 제두부에서 제간부로 향하는 연안류를, (−)는 제간부에서 제두부로 향으로 연안류를 각각 나타낸다. 개구폭에 따른 연안류의 변동을 살펴보면 입사파고가 H = 5 cm인 경우 Fig. 6(a)에서 CASES 2와 3은 y축을 따라 연안류가 진동하는 것을 알 수 있고, 잠제의 제두부 근방에서 감소하는 경향을, 제간부에서 증가하는 경향을 각각 나타내며, 이러한 결과는 순환셀이 형성되기 때문이다. 반면, CASE 1은 전술한 바와 같은 약간의 진동은 있지만 제두부 및 제간부에서 연안류가 상대적으로 안정된 큰 값을 나타낸다. 입사파고가 H = 7 cm인 경우의 Fig. 6(b)에서는 개구폭이 넓은 CASES 4와 5에서 연안류가 보다 빠르게 나타나고, 이는 제두부에서 최대치를 나타낸 후 제간부로 갈수록 감소되는 경향을 나타낸다.

Fig. 6.

Spatial distribution of longshore current velocities.

잠제 위치에 따른 연안류의 차이를 나타낸 Fig. 6(c)는 Fig.5에서 언급한 바와 같이 CASE 9의 경우 사빈 경사면 상에서의 순환셀이 연안류 형성에 영향을 미쳐 연안류의 속도가 상대적으로 빠르게 나타나며, CASE 8의 경우는 CASE 5보다 사빈 경사면 상에서 형성된 순환셀이 연안류의 흐름방향으로 확장되어 연안류 속도의 증가에 영향을 준 것으로 판단된다. CASE 7의 경우도 CASE 8과 같이 CASE 5보다 사빈 경사면 상에서의 순환셀이 연안류의 흐름방향으로 확장되어 있지만 잠제 배후의 공간이 좁기 때문에 연안류가 다소 약하게 형성된 것으로 판단된다.

본 연구는 다기로 구성된 잠제로 단일잠제에 대한 Ranasinghe et al.(2006)과는 상이하게 파가 해안선에 직각으로 입사하는 경우 제간부 배후 해안선 부근에서 양측으로 발산하는 연안류가 발생하지 않으며, 개구부 배후 해안선 부근에서 상승된 평균수위에 의해 제간부측으로 이동하는 연안류가 발생하는 것을 확인할 수 있다.

여기서, 연안류가 수렴되는 지점에서 퇴적이 발생된다는 Ranasinghe et al.(2010)의 결과에 따라 Fig. 6에서 제시된 연안류의 속도가 (+)에서 (−)로 변하는 변곡점을 본 연구에서는 연안류가 수렴되는 지점으로 판단하고, 그 지점에서 각 방향(제두부에서 제간부측으로 향하는 방향과 제간부에서 제두부측으로 향하는 방향)으로 연안류에 의해 수송되는 유량을 산정하여 Table 2에 그 값을 제시한다.

Table 2.

A longshore current’s inflection point on shoreline and total transport flow discharge due to longshore current

Table 2에 제시한 수송유량은 연안류의 흐름속도와 x-z 평면에서 연안류가 형성된 면적을 곱하고 누적한 값으로 추정되었다. 그리고, CASES 2와 3의 경우 Fig. 3에 나타난 바와 같이 순환셀에 의해 연안류가 완전히 형성되지 않아 연안류가 수렴되는 지점을 선정하기 어려웠기 때문에 CASE 1과 동일하게 잠제 제간부 배후의 지점을 연안류가 수렴되는 지점으로 선정하였다. 결과를 살펴보면 CASES 1~6의 경우는 개구폭이 넓을수록 연안류에 의한 수송유량이 증가하는 것을 알 수 있고, 입사파고가 H = 7 cm인 경우의 CASES 4~6은 개구폭이 좁을수록 연안류의 변곡점이 제간부 중앙에서 제두부측으로 이동하는 것을 확인할 수 있다. 이러한 결과로부터 퇴적이 발생되는 지점이 이동된다는 것을 알 수 있고, 또한 이로부터 설상사주가 형성되는 지점을 예측할 수 있다. 한편, 잠제 위치에 따른 연안류의 수송유량은 잠제 위치에 상관없이 CASE 9, CASE 8, CASE 5, CASE 7의 순으로 크게 나타났으며, 연안류의 변곡점도 잠제 위치에 상관없이 CASE 7, CASE 5, CASE 9, CASE 8의 순으로 제간부에 근접하여 발생되었다.

3.4 개구폭의 변화에 따른 평균난류운동에너지분포

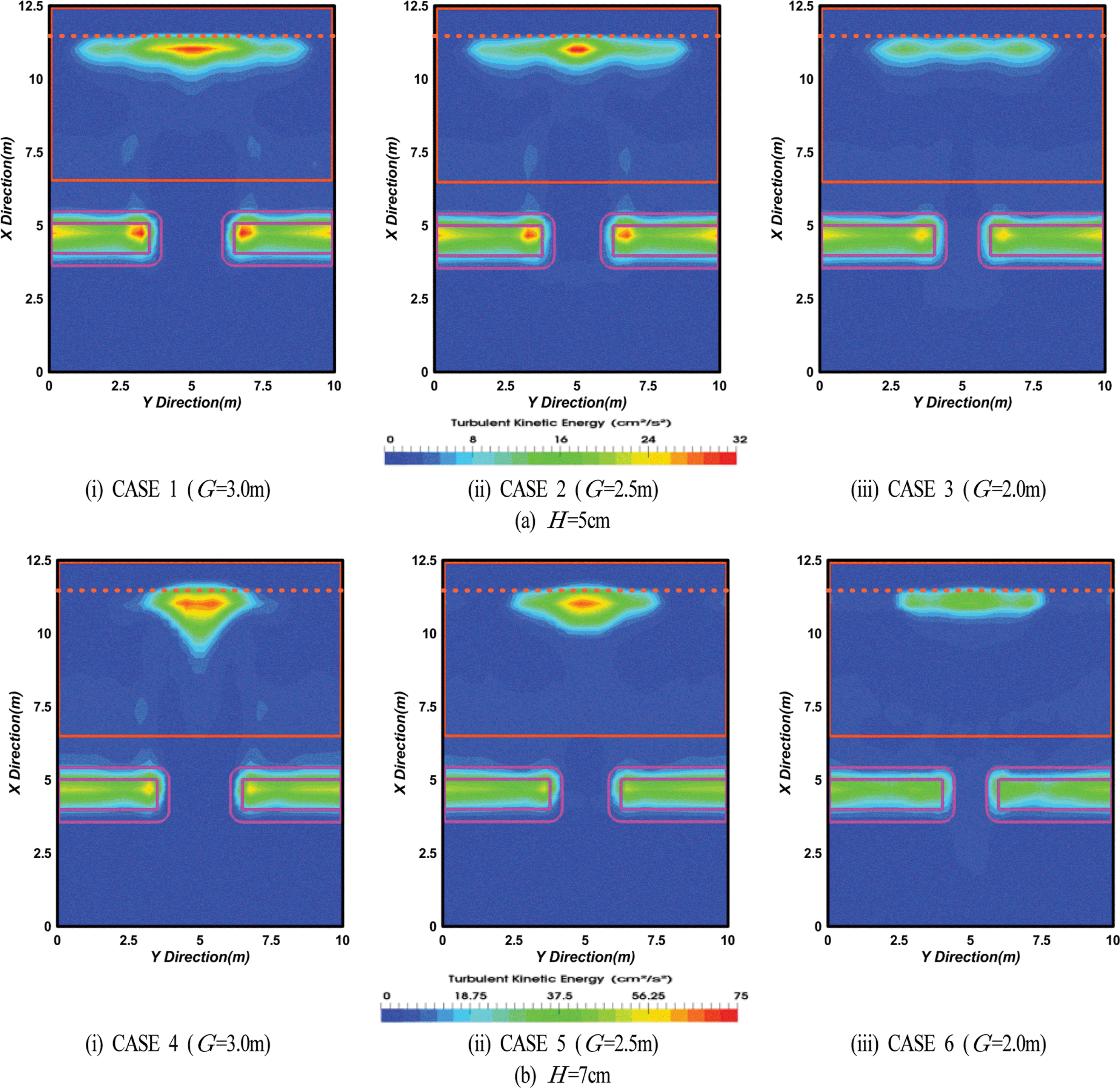
Fig. 7은 Figs. 3과 4에서와 같이 저면에서 수면까지 수심방향으로 적분한 유속을 적용하여 평균난류운동에너지를 나타낸 것이며, 이는 ux'2+uy'2+uz'2/2 으로 정의되는 난류에너지를 시간평균한 ux'2+uy'2+uz'2/2을 나타낸 것이다. 여기서, u^'_x, u^'_y, u^'_z는 각각 x, y, z방향으로 난류속도성분이다. 이러한 난류에너지는 난류성분의 크기와 그로 인한 파랑에너지의 소산 정도를 판정하는 중요한 요소로 전술한 바와 같이 파고의 변화 및 평균수위의 변화에 영향을 미친다. 여기서, Fig. 7(a)는 입사파고가 H = 5 cm인 경우를, Fig. 7(b)는 입사파고가 H = 7 cm인 경우를 각각 나타낸다. 그림으로부터 잠제 천단 상과 개구부 배후 해안선 부근에서 평균난류에너지가 전반적으로 집중 · 증가하고, 개구폭이 넓을수록 개구부 배후 해안선 부근에서 평균난류운동에너지가 상대적으로 크게 나타나며, 또한 종단방향으로 넓게 분포하는 것을 알 수 있다.

Fig. 7.

Spatial distribution of time- and depth-averaged turbulent kinetic energies in horizontal plane.

Fig. 8은 해안선과 평행한 방향으로 시 · 공간평균난류운동에너지분포를 나타내며, x = 10.2m에서 해안선 위치 x = 11.47 m 사이의 평균난류운동에너지의 공간분포를 평균한 결과이다. 시 · 공간평균난류운동에너지분포는 파랑에너지의 소산과 연관되어 있으므로 파고분포와 관계를 가진다. 또한, 파고의 자승에 비례하는 잉여응력(radiation stress)은 쇄파 시에는 증가하고, 쇄파 후에는 감소하므로 해안선 근방에서 평균수위 상승이 발생하여 이에 균형을 취하는 것으로 알려져 있다. 결과를 살펴보면 전술한 Fig. 7에서와 같이 개구부 배후의 해안선 근방에서 난류운동에너지가 증가하고, 더불어 개구폭이 넓을수록 이러한 경향이 증가하는 것을 확인할 수 있으며, 이는 해안선 부근에서 평균수위 상승의 결과로 작용한다.

Fig. 8.

Spatial distribution of time- and depth-averaged turbulent kinetic energies in longshore current region.

3.5 잠제의 설치위치에 따른 평균난류운동에너지분포

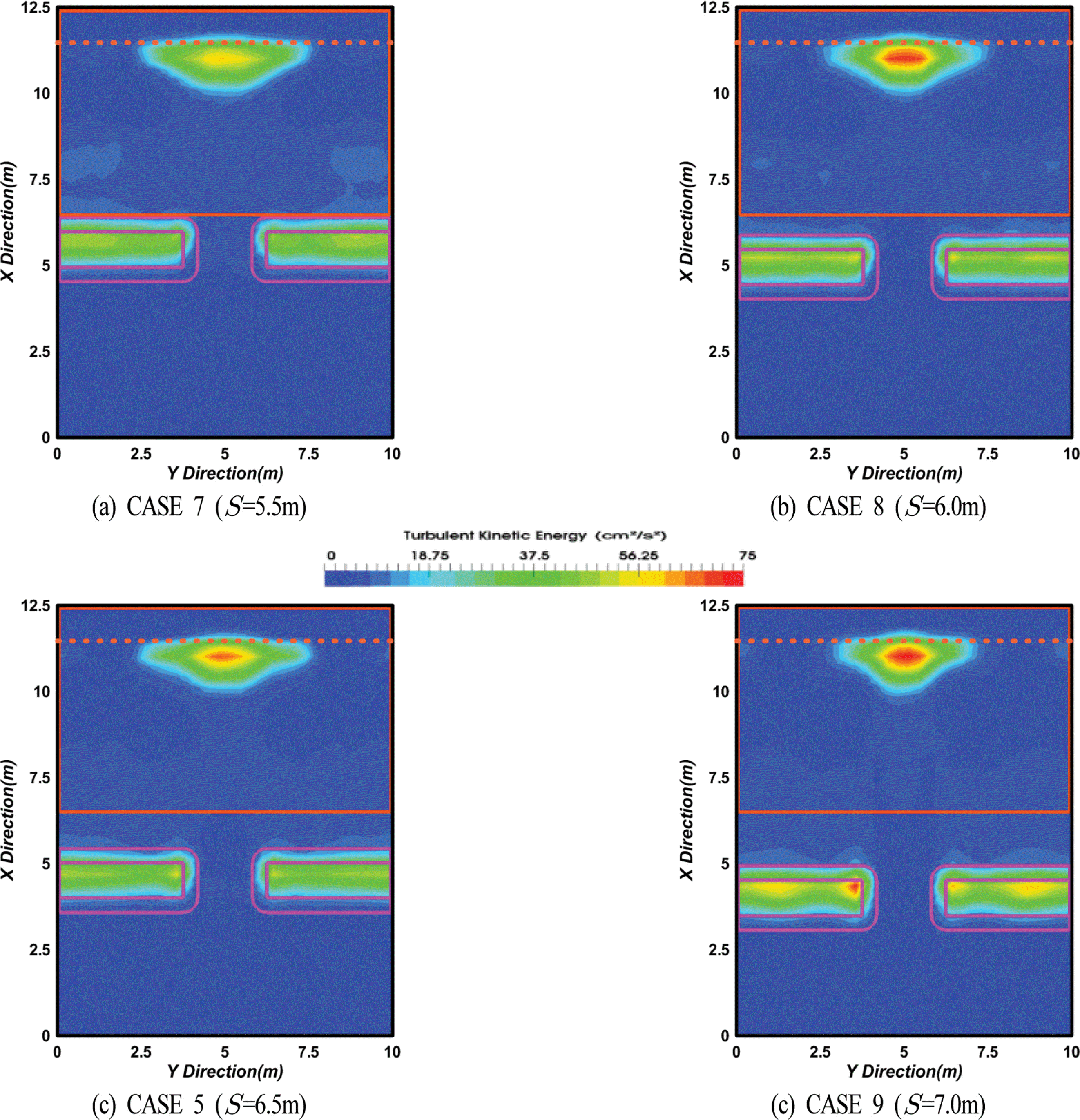
Fig. 9는 전술한 Fig. 7에서와 동일한 방법으로 잠제 위치에 따른 평균난류운동에너지분포를 나타낸 결과이다. 난류운동에너지의 분포 형상은 전술한 Fig. 7과 동일하게 잠제 천단 상 및 개구부 배후 해안선 부근에서 집중 · 증가되는 것을 알 수 있다. 반면, 해안선과 잠제 사이의 이격거리 S의 변화에 따른 뚜렷한 경향은 확인되지 않는다.

Fig. 9.

Spatial distribution of time- and depth-averaged turbulent kinetic energies in horizontal plane.

Fig. 10은 Fig. 8과 동일한 방법으로 해안선과 평행한 방향으로 시 · 공간평균난류운동에너지분포를 나타낸 것이다. 그림으로부터 개구부 배후 해안선 부근에서 CASES 8과 9의 경우 난류운동에너지가 다소 큰 값을 나타내지만 전제적으로는 제두부에서 제간부로 갈수록 난류운동에너지가 작아지는 변동양상을 보이고, 각각에서 값의 차이는 그다지 크기 않다.따라서, 이러한 변화는 전술한 파고분포나 평균수위 상승에서의 변화와 매우 유사하다는 것을 알 수 있다.

Fig. 10.

Spatial distribution of time- and depth-averaged turbulent kinetic energies in longshore current region.

이상으로부터 개구폭의 변화에 따른 개구부 배후의 평균수위변화 및 파고변화는 평균난류운동에너지와 크게 연관되어 있는 것을 확인할 수 있고, 평균난류운동에너지가 높을수록 개구부 배후에서 평균수위가 보다 상승하며, 이로 인하여 연안류의 속도에 간접적인 영향을 미치는 것으로 판단된다.