단면수리모형 및 해수유동모델링 결합기법에 의한 저마루 구조물 배후의 평균수위 상승 및 개구부 유출유속 예측
Prediction of Mean Water Level Rise Behind Low-Crested Structures and Outflow Velocity from Openings by Using a Hybrid Method Based on Two Dimensional Model Test and Hydrodynamic Numerical Modeling
Article information
Abstract
저마루구조물의 안정성 및 배후 호안의 월파량은 배후수역의 수위에 영향을 받음에도 단면 수리모형실험수행 시 수위상승량이 알려지지 않아 계측 결과가 왜곡될 수 있다. 본 연구에서는 저마루 구조물 제체 배후면의 평균수위 상승량을 예측하기 위해 단면수리모형실험과 해수유동수치모형실험을 수위-유량 관계식으로 결합하는 결합기법을 시도하였다. 이 기법을 사용함으로써 평균수위 상승량과 유속장을 단면수리모형실험과 동시간대에 얻을 수 있어 이러한 문제점들을 상당한 수준으로 해소할 수 있게 되었다. 또한 구조물의 개구부를 통한 유출유속의 강도에 관해서도 개략적인 정보를 얻을 수 있어 저마루구조물의 적정 평면배치안 선정에도 도움이 될 수 있다.
Trans Abstract
The stability of low-crested structure (LCS) and overtopping discharge over a seawall behind the LCS are influenced by the water level behind the structure. Hence, the experimental results can be distorted unless the increase of water level is known when two-dimensional experiment is carried out. In order to estimate increase of the mean water level behind the low-crested structure, this study applied a hybrid technique that combined results of two-dimensional model test and hydrodynamic numerical modeling based on the relationship between the water level and discharge. By using this technique, the mean water level increase and flow field can be obtained almost at the same time, which resolved the above problem considerably. In addition, this method can provide an approximate information about the outflow velocity from the openings of the structure, which is helpful for selecting appropriate planar configuration of the low-crested structure.
1. 서 론
해안에 내습하는 파고를 감소시킴으로써 해안침식을 억제하거나 호안의 월파량을 감소시키기 위해 해안선이나 호안과 나란하게 마루높이가 낮은 돌출제 또는 잠제형 이안구조물을 설치하는 사례가 많아지고 있다. 이러한 저마루구조물(Lowcrested structure: LCS)에서는 일반 방파제보다 월파량이 매우 많아 배후 수역에서 평균수위가 상승된다. 이러한 수위 상승은 구조물 주변에 세굴을 발생시키는, 구조물의 개구부를 통한 유출류를 형성하는 잠재적 에너지로 작용하기 때문에 비록 크기가 작더라도 그 크기를 개략적으로 예측하는 것이 구조물 설계 시 매우 중요하다.
Fig. 1 및 Fig. 2에는 미국 Florida 연안 Palm Beach항 입구 부근에서 해안침식을 억제하기 위해 설치된 PEP Reef의 위치도 및 단면도를 도시하였다. 잠제의 연장은 1,260 m로서 중앙에는 케이블 설치용으로 66 m 폭으로 개구부가 설치되었다. 잠제의 설치수심은 약 3.0 m, 주변해역의 파고는 0.26~0.81 m로 조사되었다. 설치 후 1992년 7월~1995년 6월 사이의 35개월 동안 침퇴적모니터링을 수행한 결과 116,000 m3의 모래가 유실되었는데, 이중 약 70%는 예상치 못하게 잠제의 배후에서 유실되었다. 이러한 모래 유실의 원인으로는 저조위 시 잠제의 배후에서 수위가 상승되어 흐름이 강하게 발생했을 것이기 때문이라고 추정되었다(Dean et al., 1997). 이 사례 이후 LCS 배후의 수위상승 예측에 관한 연구가 활성화되었다.
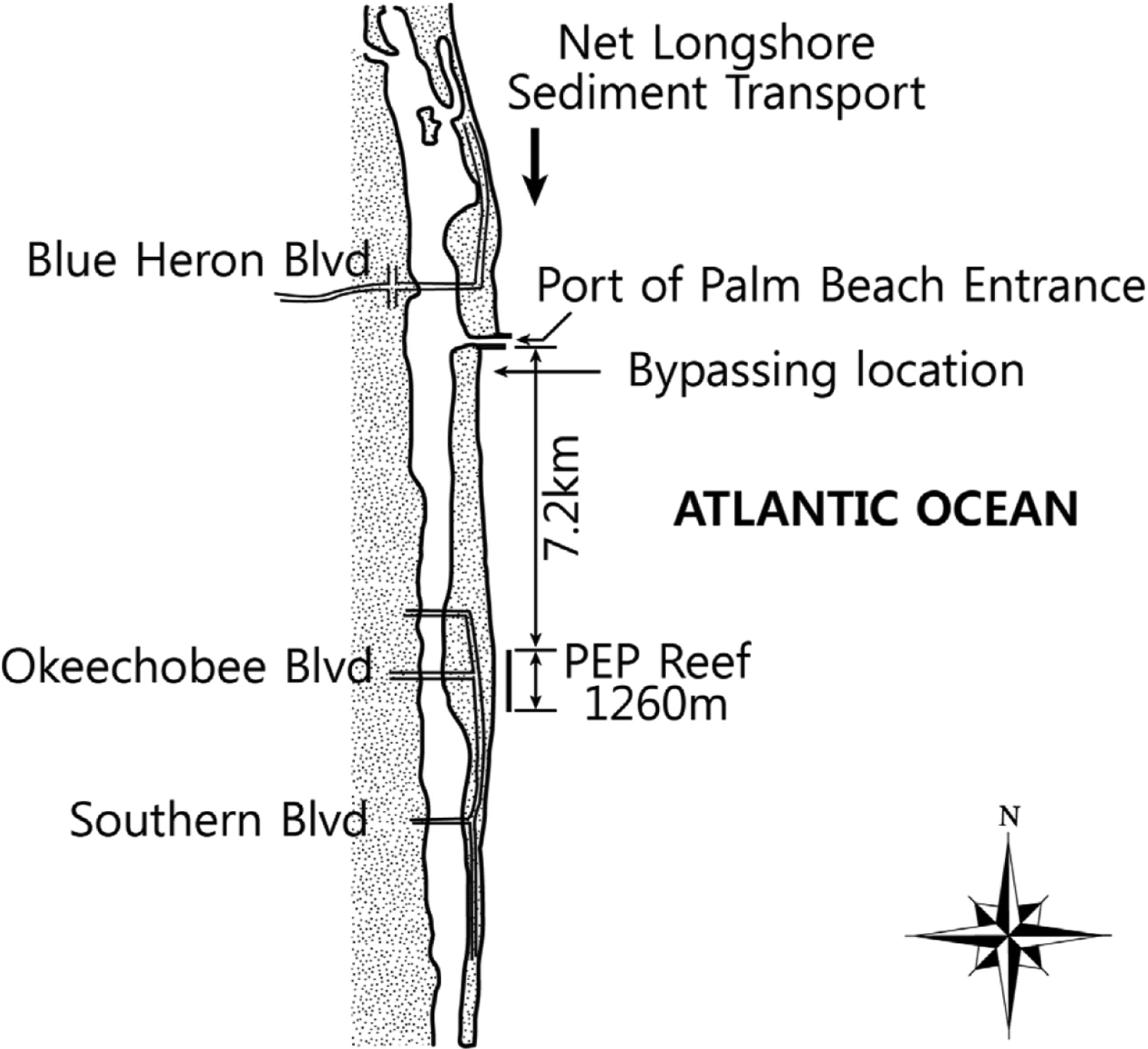
Location of PEP Reef (after Dean et al., 1997).

Schematic cross section of PEP Reef (after Dean et al., 1997).
통상의 LCS 설계에서는 단면수리모형실험에서 후보단면들을 대상으로 제체의 안정성과 전달파고를 예측하며, 필요시 최적단면안으로 평가된 단면들의 배치안에 대해 평면수리모형실험이나 파랑변형 수치모형실험을 수행함으로써 수위상승, 월파유량, LCS간의 개구부를 통한 유출흐름 등을 예측한다.
평면수리모형실험은 관심항목의 많은 부분을 현장과 유사하게 예측하는 장점은 있으나, 수행하는 데 시간과 비용이 많이 소요될 뿐 아니라 단면의 세부 제원을 반복적으로 변경해가며 많은 관심항목들을 계측하기에는 적합하지 않기 때문에, 통상 단면수리모형실험을 포함한 검토결과로 선정된 최적 후보단면안의 배치안에 대해 수행되고 있다. 특별히 단순한 경우가 아니라면 설계 초기의 후보단면을 도출하는 단계에서 단면수리모형실험을 생략한 채 평면수리모형실험을 수행하는 예는 드물다. 만일 단면수리모형실험으로 단면의 세부특성을 규명한 후에 평면수리모형실험을 수행했음에도 실험결과가 설계목표를 충족시키지 못해 단면의 세부제원을 변경하는 단면수리모형실험과 평면수리모형실험이 추가로 수행되어야 하는 경우가 발생한다면 설계 일정에 큰 차질을 빚을 수 있다. 이렇게 재실험을 수행해야 하는 경우는 평면 배치안에 따른 평균수위 상승의 크기, 또는 평균수위 상승에 따른 개구부들에서의 유출유속 규모를 설계 초기에 안정성 등을 검토하는 단면수리모형실험 단계에서부터 개략적으로라도 고려하지 못함에도 이유가 있을 수 있다.
최근에는 LCS 배후의 평균수위 상승과 개구부 유속을 예측하기 위해 평면수리모형실험보다 비용이나 시간이 적게 소요되는 수치모형실험이 수행되기도 한다. LCS 주변의 이러한 수리특성을 규명하기 위한 연구들은 단면 2차원 수치실험(Hur et al., 2003; Lee et al., 2016; Hur et al., 2017)이나 평면 2차원 연구(Zanuttigh et al., 2007)들이 대부분이다. 이러한 단면 2차원 수치실험은 균일한 단면이 아닌(법선상 수심이나 파고가 변하는) 입지에서는 적용이 어렵고, 평면 2차원 수치실험은 제체의 형상(돌출 또는 수중 잠제), 투수성(투과제 또는 불투과제), 제체에서의 난류 등과 같은 LCS의 수리특성을 재현하는 데 한계가 있다. Hur et al.(2012, 2013)는 개구부가 있는 3차원 잠제주변의 흐름특성과 2006년 태풍 에위니아 내습시 LCS가 설치된 송도해수욕장의 평균수위 상승, 개구부 유속 등을 3차원 수치모형실험을 통해 예측하였다. 그러나, 이러한 연구에도 불구하고 현재 LCS 주변의 흐름특성에 대한 연구는 아직 미흡한 실정이다(Hur et al., 2017).
LCS 배후의 수리특성을 비교적 잘 구현하는 3차원 수치모형시간의 계산시간은 실험영역 및 격자수에 따라 수~수십 시간이 소요되어, 많은 단면과 평면배치가 검토되는 설계의 초기단계에서 모든 계획안에 대해 실험을 수행하기는 어려운 실정이다. 그러나, 최근 많은 연구를 통해 수치기법의 발전 및 계산용 컴퓨터의 발달로 수치모형 실험의 정확도와 계산시간의 향상이 이루어지고 있다.
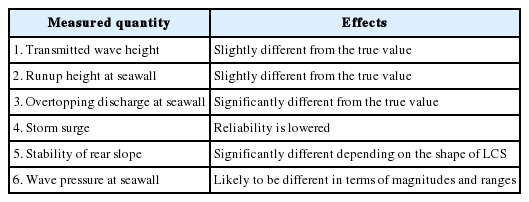
다른 한편, 단면수리모형실험에서는 배후수역의 평균수위상승량을 예측할 수 없는 조건에서 수행된 실험결과는 Table 1에 보인 바와 같이 여러 계측항목에서 현장과는 다르게 재현될 수 있다. 이러한 점을 고려하여 본 연구에서는 LCS 구간에서 설계를 위한 월파, 투과 및 쇄파를 잘 평가할 수 있는 단면수리모형실험의 장점과 LCS 배후 수역에서 개구부들을 통한 유출유량과 LCS 배후수역 수위의 관계를 빠르게 모의할 수 있는 해수유동수치모형의 장점을 결합하는 연구를 수행하였다. 즉, LCS 배후 수역의 평균수위 상승량을 단면수리모형실험과 동시간대에 개략적으로 예측함으로써 Table 1에 보인 단면수리모형실험 시의 문제점들을 상당 부분 해소시키며, 각 단면을 현장에 배치할 때 발생하게 될 개구부를 통한 흐름의 규모도 상대적으로 비교할 수 있는 결합 예측기법을 개발하였다.
2. 저마루구조물 주변의 수리현상
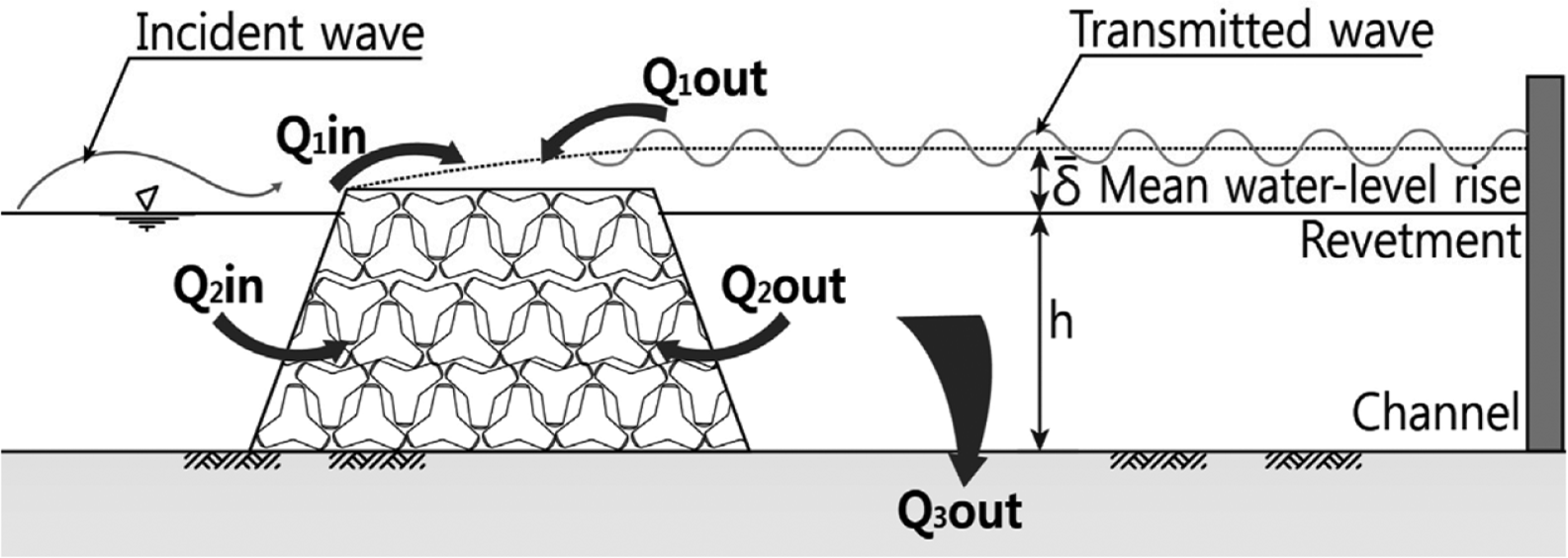
본 연구는 LCS 중에서 투과성 돌출제와 투과성 잠제를 대상으로 하고 있다. 그러나 이 장에서는 편의상 마루가 정지수면으로부터 약간 돌출된 투과성 LCS 주변의 수리현상에 중점을 두어 기술한다. Fig. 3에는 돌출형 LCS 단면의 주변에 형성되는 흐름의 종류를 모식도로 나타냈다. 이 그림에 보인 모든 종류의 흐름이 항상 동시에 발생되는 것은 아니다. LCS 전면에 파가 내습하면 한 주기 내에서 파봉이 형성되는 시간 동안에는 LCS를 육지쪽으로 월파하는 유입흐름(Q1in) 또는 제체를 투과하는 유입흐름(Q2in)이 발생하여 LCS의 배후로 외해수가 유입된다. 뒤이어 파곡이 형성되는 시간 동안에는 LCS의 상부를 역월파하는 유출흐름(Q1out) 또는 제체를 역투과하는 유출흐름(Q2out)이 외해측으로 발생한다.
LCS 배후에서 평균수위가 상승하는 이유로는 크게 다음의 두 가지 내재된 수리현상을 들 수 있다. 첫 번째로 LCS 배후로의 유입은 월파 및 투과로 이루어지는데 월파가 이의 대부분을 차지한다(Cappietti et al., 2006). 이 때 내습파는 파고가 크고 주기도 길기 때문에 월파하는 물의 두께가 커서 제체의 저항을 적게 받으며 유입된다. 그러나, LCS 배후에서는 파고가 작고 주기도 짧기 때문에 LCS를 가로지르는 역월파는 내습파의 경우에 비해 제체의 저항을 더 크게 받는다. 즉, LCS의 마루가 정지수면으로부터 위쪽으로 크게 돌출되어 있지 않는 한 역월파하는 물의 상당 부분은 제체의 마루 위를 끝까지 완전히 가로지르지 못하고, 마루 윗면에서부터 제체의 내부를 통해 외해로 나가므로 내습파의 월파 수괴에 비해 더 큰 저항을 받는다. 두 번째로는 내습파가 LCS를 월파하며 쇄파되는 경우에는 운동량을 방출하는데 이때 흐름의 속도는 배후수역 방향이므로 역월파 흐름에 추가적인 저항으로 작용한다.
이러한 이유로 LCS 배후 수역에서는 점차 해수가 쌓여 가며 이에 따라 수위가 점차 상승하게 된다. 배후의 수위가 상승하면 역월류나 역투과도 함께 강화된다. 그리고 유입량과 역류량이 균형을 이루면 수위 상승이 멈추고 안정된다. 이 때 수위 상승량의 시간평균을 평균수위 상승량(δ)이라 한다. 만일 배후 수로의 입구 또는 LCS간의 개구부가 있으면 이들 개구부들을 통해서는 외해로의 흐름(Q3out)이 지속적으로 발생하므로 평균수위 상승량은 대폭 감소하게 되며, 전달파는 이렇게 평균적으로 상승된 수위를 기준면으로 진행하게 된다. Fig. 4에는 LCS 주변에서의 평면적 흐름을 모식도로 나타냈다(Zanuttigh et al., 2008). 여기서,QIS와 QG는 각각 LCS를 가로질러 배후수역으로 유입되는 흐름과 개구부를 통해 유출되는 흐름을 의미한다.
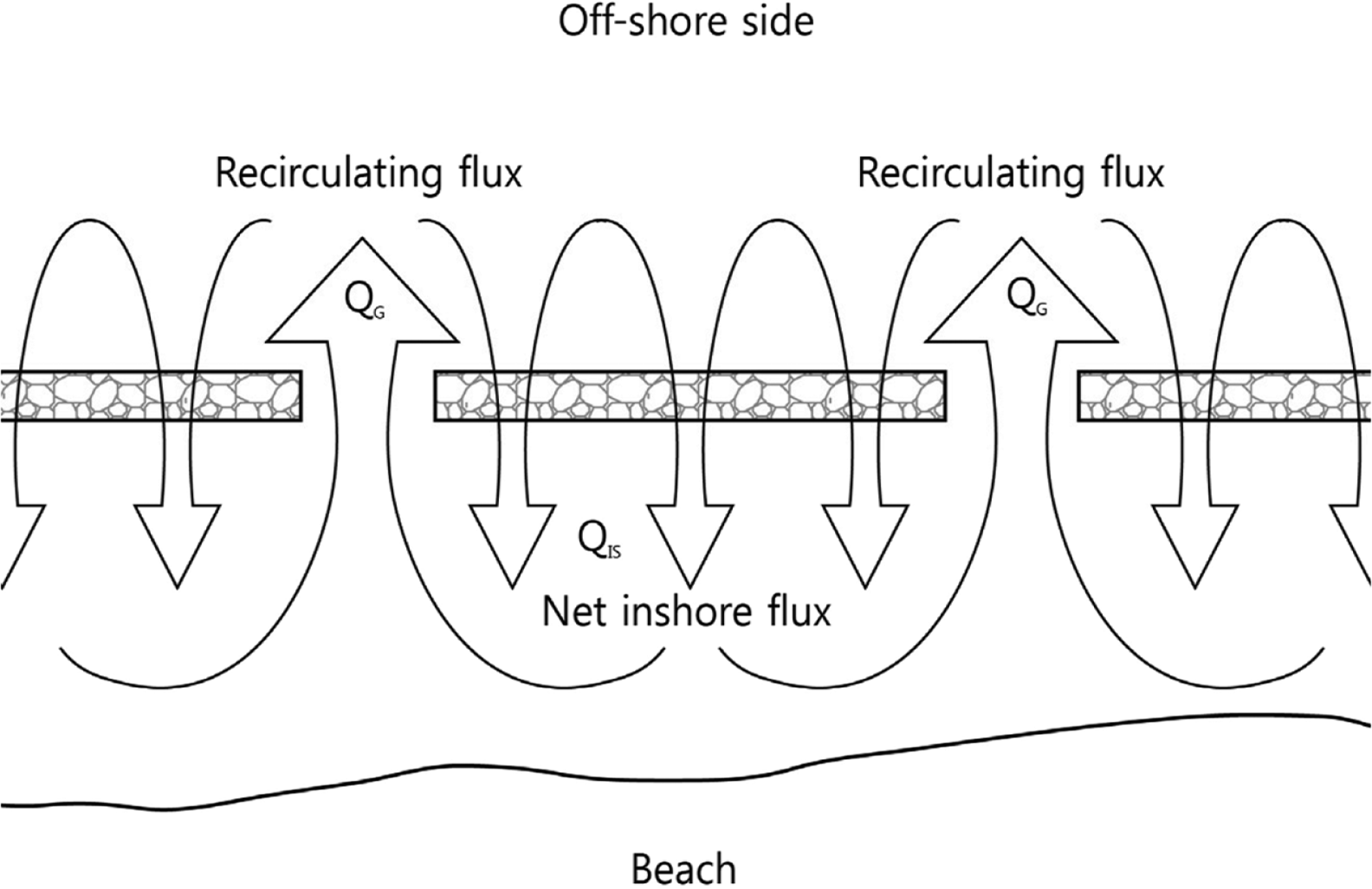
Diagram showing planar flow patterns around LCS (after Zanuttigh et al., 2008).
Fig. 5는 사석식 LCS를 대상으로 불규칙파를 사용한 단면수리모형실험의 결과로서 개구부들이 없을 때의 평균수위 상승량(δ0)을 입사파고(Hs)로 나누어 무차원한 값을 마루높이(R)를 입사파고로 나눈 상대마루높이의 함수로 표시한 것이다(Cappietti et al., 2006). 이 그림으로부터 평균수위 상승량은 제체의 마루가 정지수위보다 근소하게 높을 때 최대가 되며 제체를 구성하는 재료의 입경이 작을수록(투수성이 작을수록) 증가함을 볼 수 있다.
3. 단면수리실험과 해수유동수치모델링의 결합 기법
3.1 결합 기법 적용의 배경
본 연구에서 다루는 물리현상은 입사파가 LCS를 월파하거나 투과하는 과정에서 쇄파되어 배후수역으로 순유입유량이 발생함에 따라, 수역 내에서는 수위가 상승하며, 유입유량은 배후수역의 개구부들을 통해 외해로 유출됨에 있다. 이때 LCS 연장 상의 모든 위치에서 순유입유량은 LCS 제체 배후면의 평균수위에 따라서도 크게 달라지게 된다. 그런데 이 유입수가 배후수역을 통과하여 개구부들을 통해 유출되는 과정에서 수역의 형상 및 해저면에서의 마찰저항 등으로 인해 수두 손실이 발생하므로 배후수역 내에 손실수두의 크기에 해당하는 수두가 형성될 때까지 수위가 상승하게 된다. 그리고 LCS 제체 배후면의 수위가 상승함에 따라 LCS를 통한 순유입유량은 다시 변하게 된다. 따라서, LCS 연장상의 위치별 단위길이당 순유입유량과 LCS 제체 배후면의 평균수위 상승량을 구하기 위해서는 LCS 전장을 통한 총순유입유량과 개구부 전장을 통한 총순유출유량이 일치하며 평균수위의 공간분포가 안정되는 상태를 찾는 것이 필요하다.
이러한 물리현상에 관련된 연구 방법은 크게 파랑변형수치모형실험, 해수유동 수치모형실험, 단면수리모형실험,평면수리모형실험으로 구분할 수 있다. 이중 단면수리모형실험은 LCS 제체의 미세한 형상, 규모, 사용재료의 형상 및 크기(즉, 공극 및 투수성), 수심 및 상대마루높이에 따라 LCS에서의 월파, 쇄파 및 투과현상 등 파동장이 유동장으로 변형되는 과정을 잘 모의한다. 한편 검증된 해수유동 수치모형은 흐름장 내에서 수역의 형상 및 수심변화의 영향을 잘 반영하며, LCS 연장상의 순유입유량의 분포를 만족시키면서 총순유입량과 동일한 유량을 개구부들을 통해 순유출시킴과 동시에 평형상태에 이른 평균수위의 공간분포를 신속히 계산하는 장점이 있다.
따라서, 본 연구에서는 파랑과 구조물간의 상호작용을 효과적으로 재현하는 단면수리모형실험을 통해 LCS에 파가 내습할 때 LCS 제체 배후면에서 만족해야 하는 평균수위 상승량과 LCS 단위폭당 순유입유량과의 관계식을 도출하고, 수위와 유량의 관계 모델링에 특화된 해수유동 수치모형실험에서 이 관계식을 LCS 제체 배후면의 경계조건으로 사용하는 결합기법(hybrid method)을 적용하였다. 이하에서는 LCS 제체 배후면의 평균수위 상승량과 LCS 단위폭당 순유입유량 사이의 관계를 “수위-유량 관계”라고 지칭하였다.
3.2 수위-유량 관계식
수위-유량 관계는, 주어진 파와 수심 및 상대마루높이 조건에서 LCS 단면을 통해 LCS 단위폭당 순유입유량이 발생할 때, LCS 배후수역의 형상이나 규모와는 전혀 관계없이 이단위폭당 순유입유량과 LCS 제체 배후면의 평균수위 상승량만이 상호 의존적으로 변하는 관계로서, LCS 단면별 고유한 수리특성의 한 면을 나타낸다.
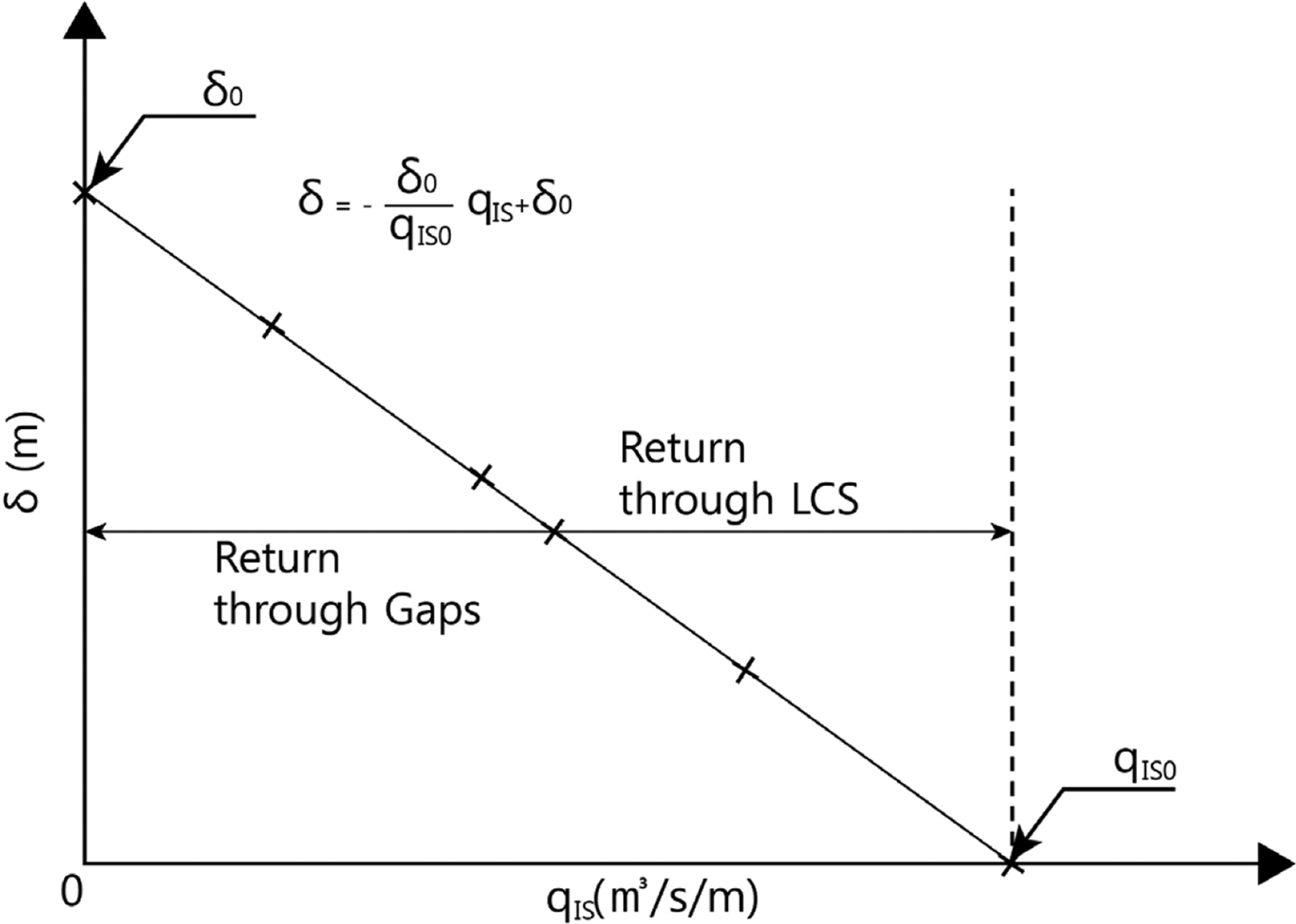
Fig. 6에는 Cappietti et al.(2006)에 제시된 그림을 참조하여 LCS 단면을 대상으로 수위-유량 관계식을 도출하는 방법을 보였다. 이는 투과성 LCS의 단면수리모형실험에서 펌프를 사용하여 LCS의 배후수역으로부터 일정한 유량을 조파수조의 상류쪽으로 회류시키면서 조파하는 작업을 반복함으로써 얻을 수 있다. 즉, 개구부들을 통해 외해로 돌아가는 3차원적인 유출유량을 단면 실험에서 펌프를 이용한 회류유량으로써 모의하는 것이다.
이 그림에서 수평축은 펌프를 가동해 LCS 단위길이당 회류시킨 유량, 즉 LCS 단위길이당 순유입유량(qIS)을, 연직축은 수위가 안정될 때의 평균수위 상승량(δ)을 나타낸다. × 로 표시된 계측값들은 LCS 단위길이당 회류량에 대응하는 평균수위 상승량을 의미한다. 단면수리모형실험에서 만일 배후 호안의 월파량을 LCS 배후수역으로 되돌려 보내지 않는 경우에는 그 월파량도 이 회류유량에 포함시켜야 한다. 만일 돌출형 LCS에서 폭풍해일고를 고려할 경우에는 단면수리모형실험은 정지수위를 그만큼 높인 상태에서 수행한다. 이 그림은 임의의 한 순간이 아니라 LCS 배후에서 평균수위가 안정된 평형상태에서 만들어지는 것이기 때문에 그림에서는 LCS를 통한 순유입유량과 개구부를 통한 순유출유량 그리고 펌프를 사용한 회류유량은 LCS 단위길이당의 값으로는 모두 동일한 크기를 가지게 된다. 여기서, δ0는 회류유량이 0일 때 발생하는 평균수위 상승량으로서 Fig. 6에 보인 수위 상승량 중 최고값이 되며 이는 Fig. 5에 보인 각 계측값들에 해당된다. 이는 현장에서는 LCS의 길이가 무한하여 LCS를 통한 유입량 전체가 다시 LCS를 가로질러 외해로 유출되고 있는 상태에 해당한다. 한편, qIS는 평균수위 상승량이 0인 경우의 LCS 단위길이당 회류유량으로서 순유입유량 모두가 개구부를 통해 유출되는 상태에 해당한다. 이 경우 LCS 단위길이당 순유입유량은 최대값이 된다. Ruol et al.(2004)에 의하면 이 두 점 사이를 연결하는 관계식은 거의 선형이다. 따라서, 이론적으로는 투과성 LCS의 단면수리모형실험에서 펌프를 작동하지 않을 때 구해지는 평균수위 상승량의 최고값(δ0)과 펌프를 작동하여 평균수위 상승량이 0이 되는 상태의 최대회류유량(qIS) 이렇게 2개의 값만 구하면 수위-유량 관계식을 작성할 수 있다. 이 관계식으로부터 LCS상의 임의의 한 소구간에서 단위길이당 순유입유량은 그 소구간 배후면의 평균수위에 영향을 받아 변함을 알 수 있다. 따라서, 수심과 파고가 동일하더라도 개구부가 최소 1개 이상 존재하는 현장 여건에서는 LCS의 위치별 단위길이당 순유입유량과 LCS 제체 배후면의 평균수위는 LCS 연장을 따라 동일하지 않고 변하게 된다. 한편, Fig. 6으로부터 LCS를 가로질러 외해로 유출되고 있는 유량은 qIS에서 회류유량(qIS)을 빼서 구할 수 있다.
4. 결합기법의 설계 적용 사례
4.1 단면수리모형실험
4.1.1 회류장치 및 모형 설치
단면수리모형실험에 사용한 장수로는 폭이 1.5 m로서 종방향으로 두께 0.15 m의 분리벽으로 양분되어 모형의 설치 및 수위계측은 폭이 0.675 m인 한 쪽 수로에서 이루어졌다.
Fig. 7은 회류장치와 모형 설치의 개략도이다. LCS와 호안의 모형은 수로의 하류부에 설치되었다. 펌프실을 호안의 배후에 두어 수중펌프를 설치하였으며, 이 펌프는 수조의 상류로 향하는 관수로에 연결되었다. LCS의 배후 해저면 아래에는 사각형 암거를 설치하고 암거의 덮개에는 작은 통수공들을 두었다. 암거의 하류측 벽과 펌프실은 수중파이프로 연결되었다. 따라서, 수중펌프를 가동하면 LCS 배후 수역으로부터 수로의 상류 방향으로 회류가 이루어진다. 회류량을 실시간으로 계측하기 위해 회류관에는 유량계를 설치하였다.
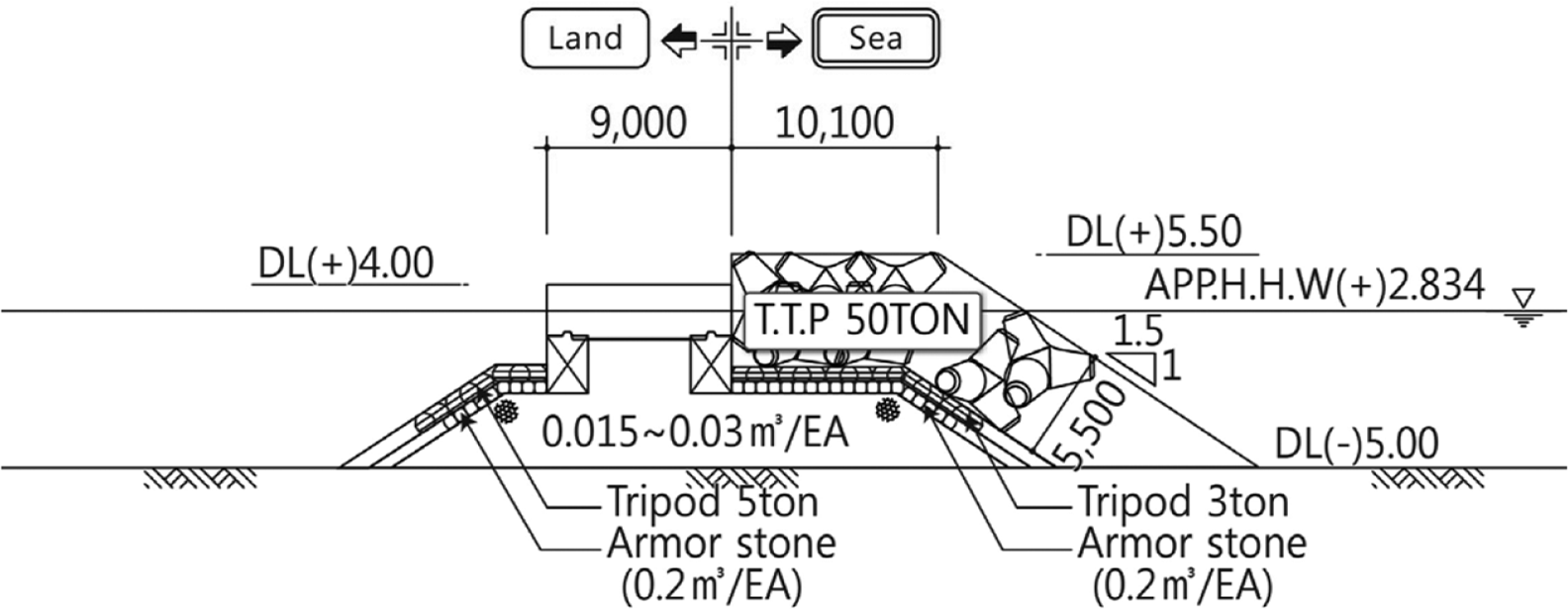
Fig. 8에는 LCS 실험단면의 제원을 원형(prototype)의 크기로 나타내었다. 모형은 Froude 상사법칙에 따라 축척 1/36로 제작되었고 모형 전면의 해저경사는 1/40이다. 실험파는 Bretschneider-Mitsuyasu 스펙트럼을 따르는 불규칙파로서 유의파고(Hs) 4.2 m, 유의파주기(Ts) 13.4 s이다. LCS 외해측 선단의 수심은 약최고고조위(App. H.H.W) 조건에서 7.83 m이다. 상치콘크리트 전면에 설치한 T.T.P. 상부의 높이(T.T.P.의 마루높이)는 정수면상 2.67 m로서 T.T.P. 마루의 입사파고에 대한 상대마루높이는 약 0.64이다.
수위 계측을 위해 용량식파고계를 사용하였으며, 입사파고는 모형의 외해측 선단의 위치에서 2점법으로 평가하였다. LCS 배후의 수위는 상치콘크리트 배후로부터 실험실 규모로 0.25 m 위치에서 계측하였고 이는 현장 조건으로는 9 m에 해당한다. 또한, 처오름높이는 호안의 전면벽에서, 그리고 중복전달파고는 LCS와 호안의 중간 위치에서 각각 계측하였다.
Fig. 9는 단면 전체가 투과성 재료들로만 구성된 LCS 배후의 전달율을 상대마루높이의 함수로 표시한 것이다(d’Angremond et al., 1997). 이에 의하면 전달율의 관점에서는 상대마루높이가 대략 1.0보다 작은 구조물을 LCS로 볼 수 있을 것이다. 이를 참고할 때 Fig. 8의 단면은 LCS 범주에는 속하겠지만, 적은 비용으로 전달파고를 소폭 감소시킬 목적으로 설치되는 통상의 LCS에 비해서는 T.T.P.의 마루높이가 높은 편이다. 따라서 상대적으로 월파량이 적어 배후 수역의 수위상승은 아주 크지는 않게 된다.
4.1.2 수위-유량 관계식의 도출
Fig. 10에는 유의파고 4.2 m(실험실 11.7 cm), 주기 13.4 s(실험실 2.23 s)의 실험파에 대한 수위-유량 관계를 현장값으로 나타냈다. 3.2절에 기술한 바와 같이 투과성 LCS에서 수위-유량 관계식은 선형이므로 최소 2점의 자료만 확보하면 관계식을 얻을 수 있다. 즉, 펌프를 가동하지 않은 상태인, qIS = 0일 때의 δ0와 펌프의 유량을 조절해서 δ≓0 부근에서 qIS를 구하면 된다.
회류는 조파로 인한 첫 파가 LCS에 도달한 10 s 후(실험실 기준)부터 펌프를 가동하여 600 s(현장 기준 60 min) 동안 일정한 유량으로 지속하였다. 평균수위 상승속도는 펌프 가동 후 약 30 s 이내에 현저히 둔화되었다. 한 번의 측정이 끝나면 펌프유량을 변경하며 재조파하였다. 평균수위 상승량은 600 s 동안의 수위 계측자료 중에서 150 s부터 600 s까지 450 s(약 200파, 현장시간 45 min) 동안의 자료를 산술평균하여 구하였다. 회류유량은 유량계로 계측한 시계열 자료로부터 평균수위 계산구간과 동일한 시간구간에 대하여 LCS 단위길이당 평균유량을 구하여 산정하였다. 이 후 계측값들을 현장값으로 환산하였다.
4.2 해수유동 수치모형 실험
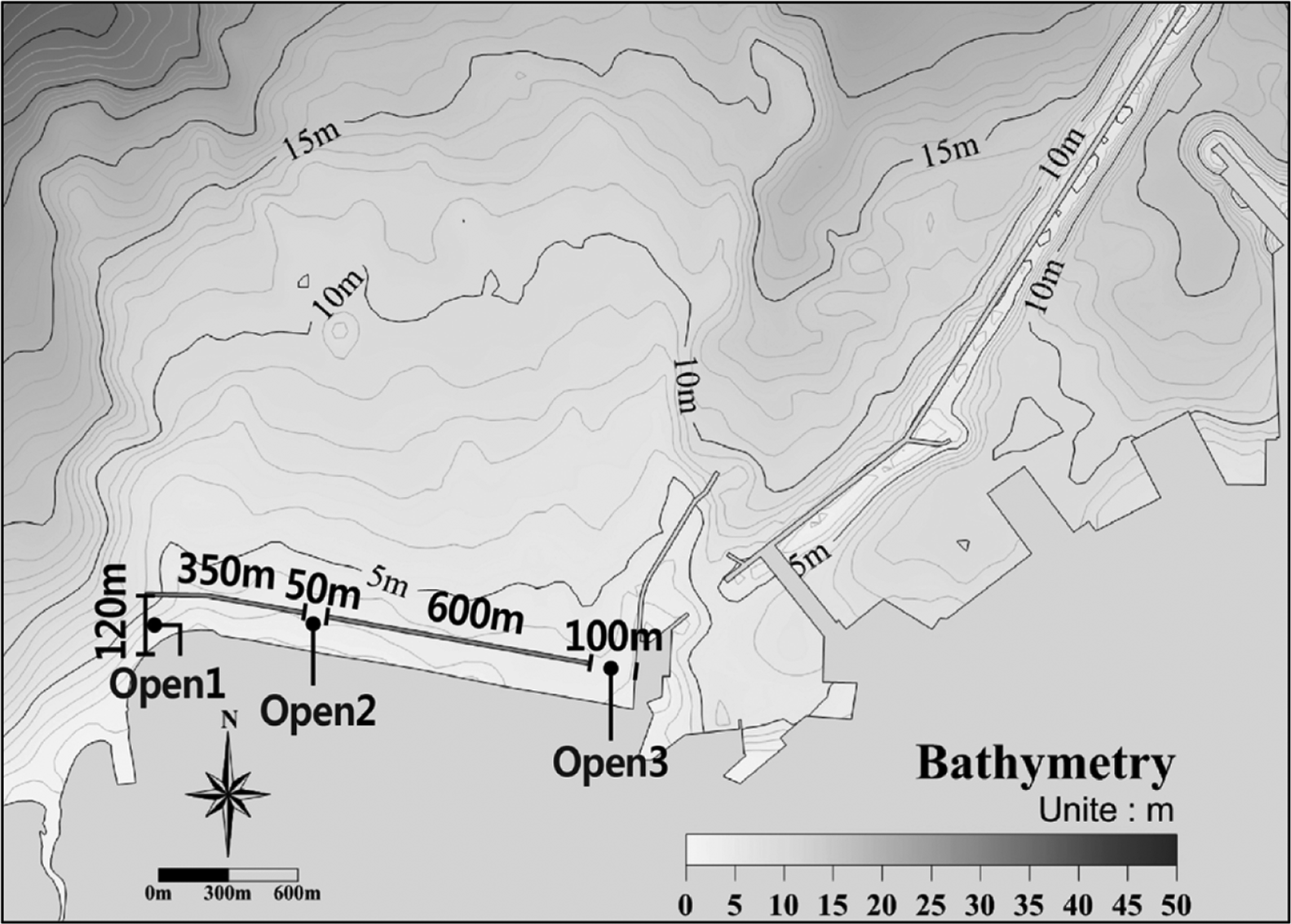
Fig. 11에는 본 연구에서 적용대상으로 한 제주도 탑동 LCS의 평면배치와 주변해역의 수심도를 나타냈다. LCS와 호안의 이격거리는 80 m이고, 두 개의 LCS의 길이는 서측으로부터 각각 350 m와 600 m이며, 개구부는 두 LCS 사이에 폭 50 m, 서측 두부에 폭 120 m 그리고 동측 기부측의 어항방파제와의 사이에 폭 100 m로 3개가 있다.
LCS 배후로의 유입유량에 따른 수위상승 및 흐름장을 계산하기 위한 해수유동수치모형으로는 EFDC 모형을 사용하였다. EFDC 모형은 해수유동, 수질, 부유사 이동, 독성물질의 4가지 모듈로 구성되어 있다. 이 가운데 해수유동 모듈을 이용하였으며, 지배방정식은 식 (1)의 연속방정식과 식 (2)와 식 (3)의 수평 및·수직방향에 대한 운동방정식이다.
여기서, ζ는 기준면 상 수심, u와 v는 각각 x와 y방향의 유속, mx, my는 곡선좌표계 임의거리
계산영역은 LCS 주변의 흐름 형성이 지장을 받지 않도록 충분히 넓게 동서방향으로 3.2 km× 2.6 km로 설정하였다. 격자는 간격 20 m의 정방격자로 구성하였고, 유효계산 격자수는 17,883개이다. LCS에서 유입된 순유입유량으로 인해 상승된 수위만을 예측하기 위해 개방경계에 분조, 코리올리 힘과 같은 외력조건을 ‘0’으로 입력하였다. 순유입유량은 단면수리모형실험을 통해 산정된 수위-유량 관계식(Fig. 10)을 활용하여 LCS 제체 배후면에 경계값으로 입력하였다.
수위-유량 관계는 상대마루높이에 따라 크게 변하므로 LCS 연장상 파고변화가 클 경우에는 LCS의 소구간별로 구분해 적용하는 것이 바람직하다. 그러나, 본 LCS의 경우 전 연장 1,100 m 중 간부가 1,000 m로 대부분을 차지하며, 상대적으로 두부의 길이는 짧기 때문에 간부 구간에 대하여 수위-유량 관계식을 구하여 LCS의 전구간에 적용하였다.
LCS 제체 배후면에 Fig. 10에 제시한 수위-유량 관계식에 따라 유입유량을 입력하여 해수유동수치모델링을 수행하고, 전체 해역에서 수렴되었을 때 검증 지점들에서의 평균수위 상승량과 입력된 유량에 따른 평균수위 상승량을 비교하여 이 두 개의 값이 거의 일치할 때까지 계산을 반복하였다.
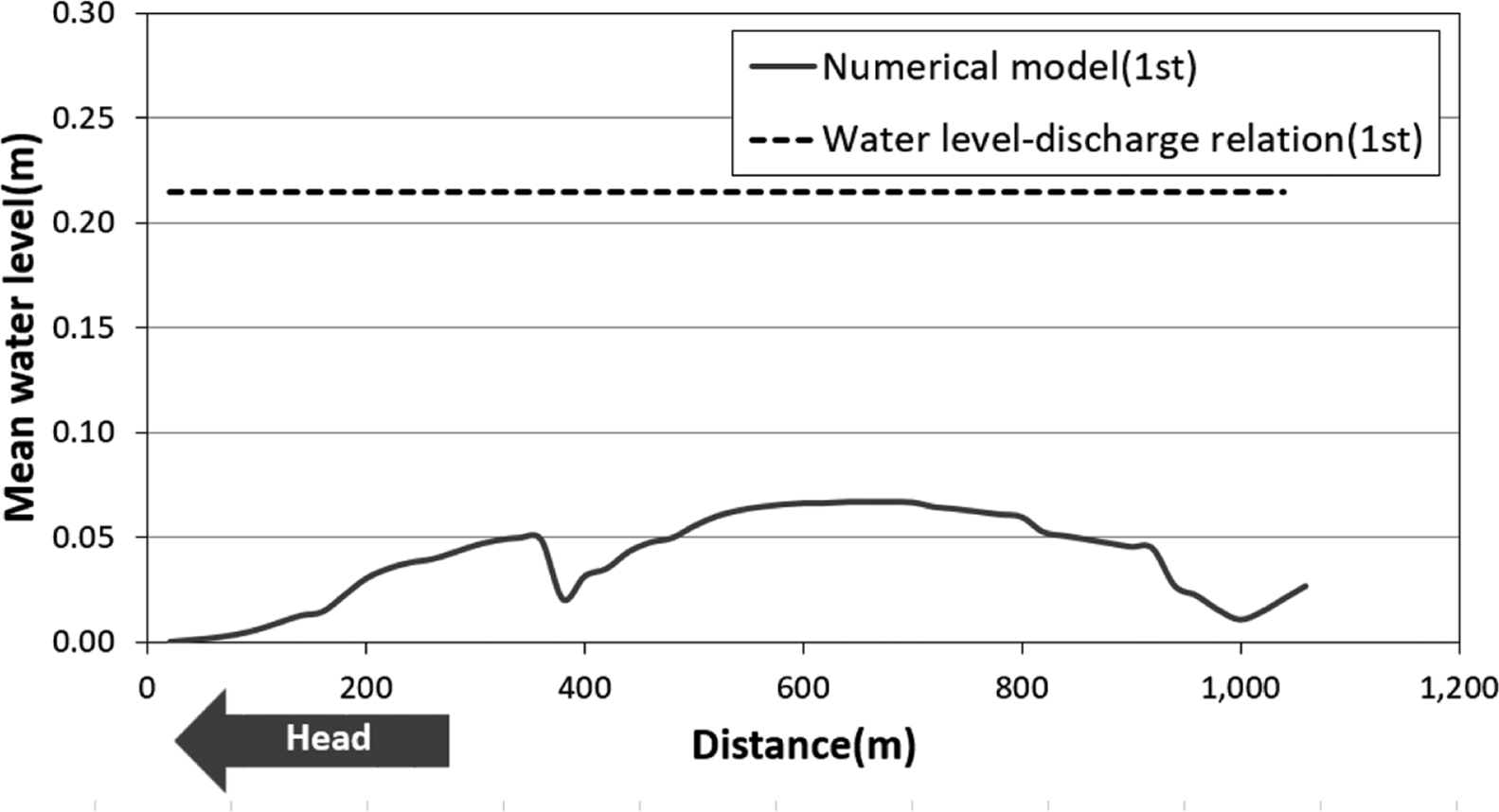
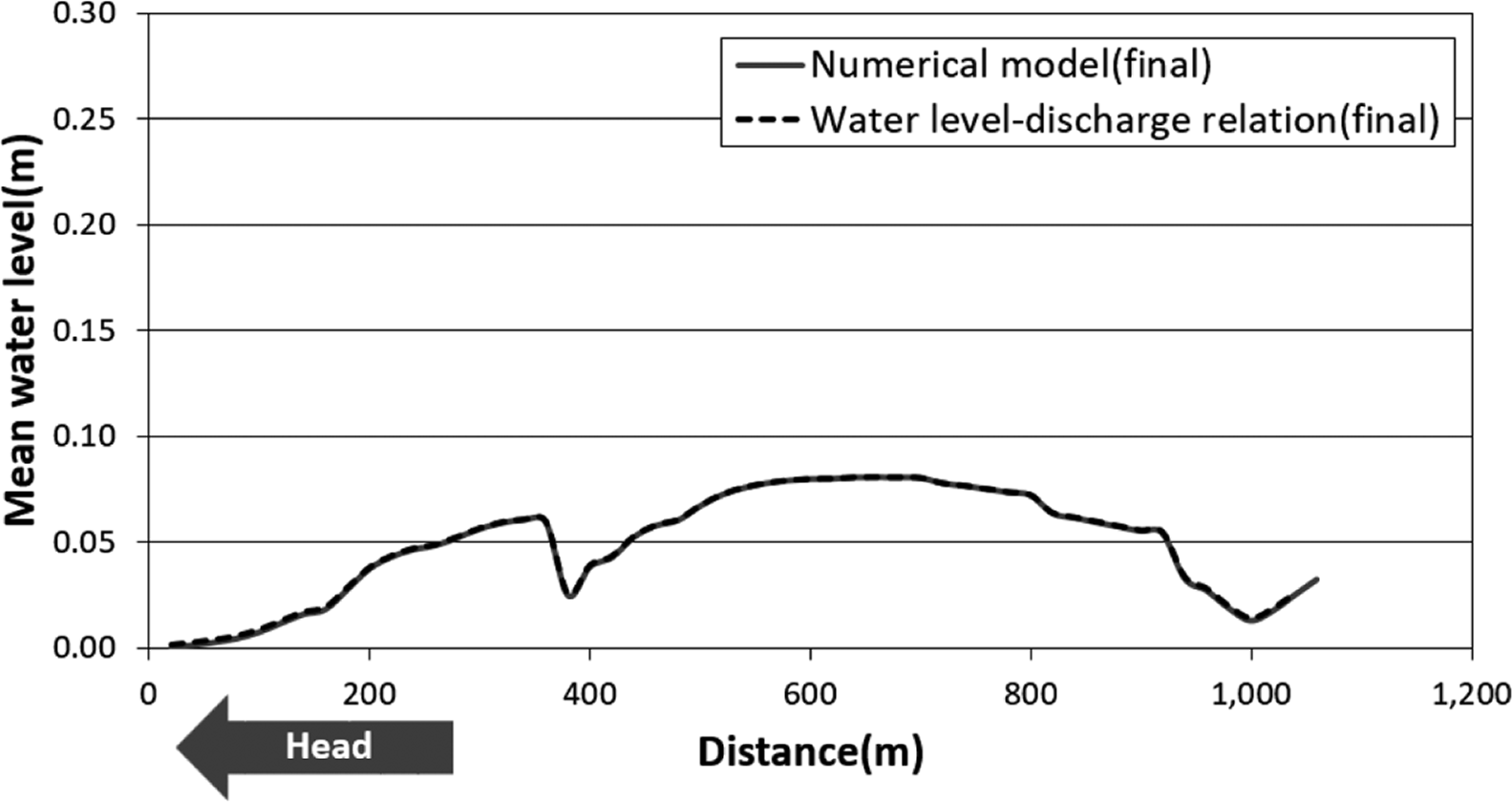
Fig. 12와 Fig. 13에는 검증점들에서의 초기 및 최종 수위계산 결과를 각각 도시하였다. 해수유동수치모형은 비교적 빠르게 수렴에 도달했으며, 최종결과를 얻기까지 총 4회 반복 수행이 이루어졌고 계산에 소요된 총시간은 9분이었다.
최대 평균수위 상승량은 LCS 의 두부측으로부터 약 650m 위치에서 0.08 m를 나타냈고, 개구부들이 위치한 곳에서는 외해로 유출되는 강한 유속의 영향으로 평균수위 상승량이 상대적으로 작았다. LCS 기부측에서는 평균수위가 다시 상승하였는데, 이는 기부측으로 흐르는 유량이 어항 방파제 인근수역에서 적체되어 수위가 다시 상승하기 때문이다.
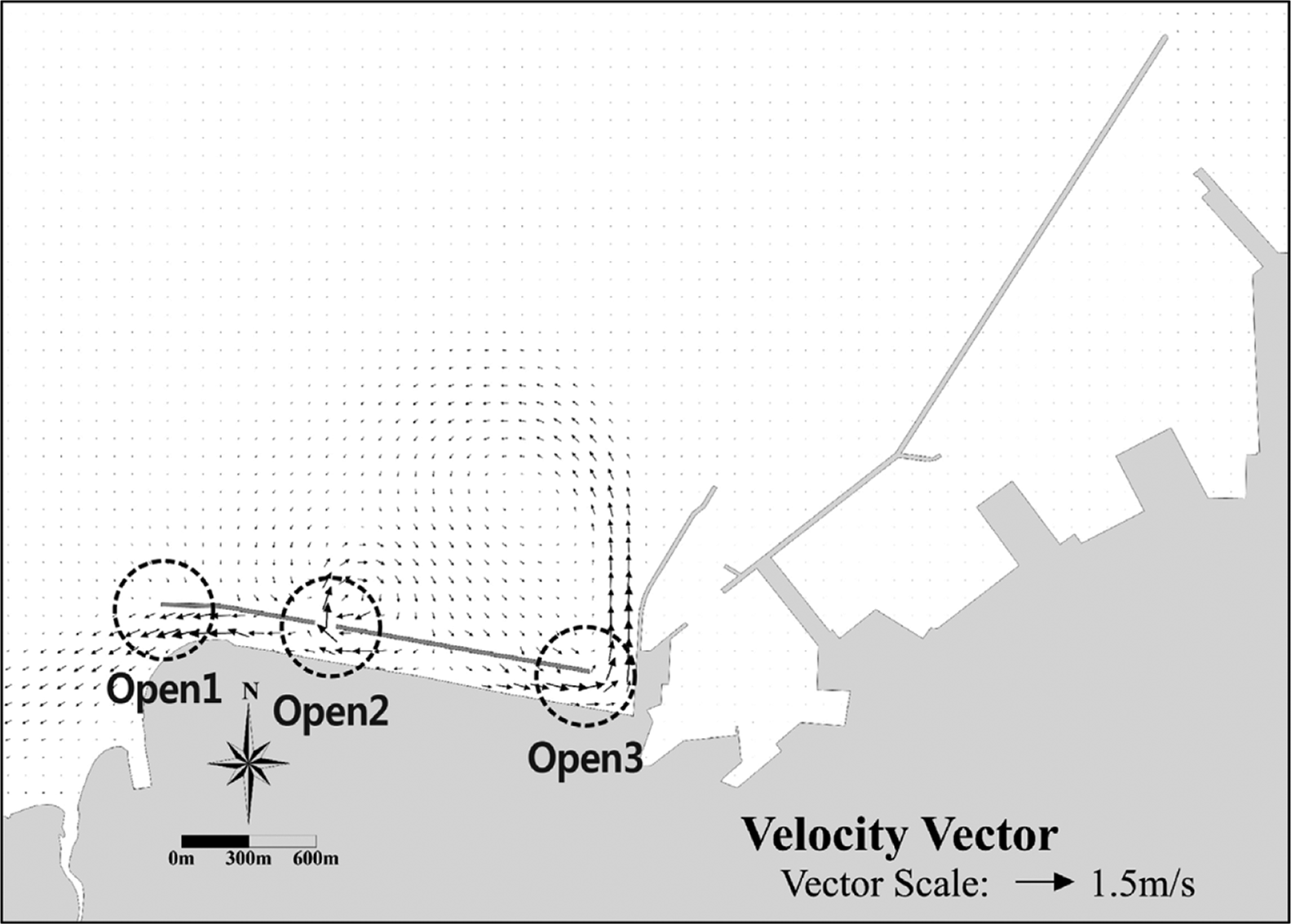
Fig. 14에는 최종 수위 계산 결과가 얻어졌을 때의 유속벡터도를 나타내었다. 개구부를 통한 유출흐름의 최대유속은 개구부1(서측)에서 0.58 m/s, 개구부2에서 0.70 m/s, 개구부3(기부측)에서 0.69 m/s로 나타났다. 한편, 평균유속은 위의 세 위치에서 각각 0.35 m/s, 0.65 m/s, 0.53 m/s로 나타났다. LCS 배후의 평균수위 상승량은 최대 0.08 m로 크지 않은 편이지만 LCS의 특성상 월파로 인한 유입유량 및 개구부를 통한 배출유량은 평균수위 상승량을 고려할 때 모두 많은 편이었다.
5. 토 의
5.1 결합기법 적용에 대한 평가
▪ 본 연구에서 제시한 결합기법은 평균수위와 유속이 급격히 변하는 개구부 부근에서도 실험단면의 수위-유량 관계를 잘 반영하는 것으로 확인되었다.
▪ 해수유동수치모형의 계산시간이 매우 짧아 수위-유량 관계식이 도출되면 개구부를 통해 외해로 빠져나가는 유속까지 신속하게 개략적으로 예측할 수 있었다.
▪ 수위-유량 관계식은 상대마루높이에 따라 크게 변하므로 LCS 연장상 파고나 수심의 변화가 클 경우에는 LCS를 몇 개의 소구간으로 나누어 도출하는 것이 필요하다. 본 연구에서는 수위-유량 관계식 작성을 위한 단면실험은 호안의 월파량실험과 함께 간부에서만 수행되었기에 길이가 가장 긴 간부에서 작성된 수위-유량 관계식을 LCS의 전구간에 적용하였다. 이러한 이유로 인해 수심이 깊고 파고가 큰 개구부1의 유속은 실제보다 과소평가되고 수심이 얕고 파고가 작은 개구부3에서의 유속은 실제보다 과대평가되었을 것으로 추정된다.
▪ 본 연구에서는 단면수리모형실험만 계획된 설계여건에 맞추어 수위-유량 관계식을 작성한 후 결합기법을 적용하여 해수유동수치모형실험을 수행하였다. 그런데, 해수유동수치모형실험에서 LCS 제체 배후면의 경계조건을 수위-유량 관계식으로 단순화했기 때문에 재현결과가 현장의 결과와는 차이가 있을 것으로 예상된다.
5.2 설계 시 결합기법의 활용 방안
본 연구에서 시도한 결합기법을 설계 실무에서 활용하는 방법의 예를 Fig. 15의 흐름도로 나타내었으며, 아래에 그에 대한 세부 설명을 제시하였다.
① 단면안, 대상파 및 평면배치안 선정: 기존 설계법으로 선정하되, 평면배치안에서 LCS간의 개구부폭은 결합기법 적용 결과로부터 얻은 개구부들에서의 유속강도를 감안하여 수정할 수 있다.
② 단면수리모형실험: 수위-유량 관계식을 작성한다. 이때 호안의 월파량, 호안의 처오름높이 및 전달파고도 동시에 관측함이 바람직하며, 평균수위가 변함에 따라 LCS의 안정성이 어떻게 변하는가를 주의 깊게 관찰할 필요가 있다.
③ 해수유동수치모형실험: 평균수위와 순유입유량이 LCS 제체의 배후면에서 상기 수위-유량 관계식을 만족시키는 상태를 재현해서 배후수역의 수위와 개구부들을 통한 유속을 예측한다.
④ 수리현상 비교 및 판단: 평균수위 상승, 유속, 호안 월파량, 전달파고 및 처오름높이 등이 허용기준 이내에 드는지를 평가한다. 개구부의 유속은 안별 상대비교를 위한 자료로 참조한다.
⑤ 만일 평균수위가 무시할 수 없을 크기로 상승하여 월파량 또는 처오름높이를 재평가해야 하는 경우에는 예측된 평균수위를 재현하며 재실험을 수행하거나 여의치 않은 경우에는 기존 실험에서 계측된 수위별 월파량 또는 처오름높이 자료들로부터 보간법으로 산정한다.
⑥ 수위-유량 관계식을 도출하는 단면수리모형실험 시 정지수위보다 근소하게 높은 수위에서 LCS의 안정성이 의심될 경우에는 결합기법으로 평균수위를 예측한 후 예측된 평균수위를 재현하며 안정성 평가를 수행하는 것이 권장된다.
⑦ 개선이 필요한 항목이 있을 경우에는 그 원인에 따라 단면을 변경할 것인지 아니면 평면상 LCS 사이의 개구부 위치 또는 간격 등을 조정할 것인지를 판단하여 필요한 변경을 수행한다.
⑧ 만일 수위 및 개구부의 유속 예측결과와는 무관하게 LCS 사이의 개구부 변경이 필요하지 않은 경우에는 단면실험 시 우선 수위-유량 관계식을 도출하여 결합 기법으로 평균수위를 예측한 후 이 예측된 배후수위를 재현하는 단면수리모형실험에서 안정성 검토와 모든 수리특성을 계측할 수도 있다. 이때, 안정성 평가실험은 통상적인 수리특성 평가 실험에 비해서 조파시간이 길기 때문에 실험이 수행되는 동안 평균수위가 무시할 수 없는 수준으로 벗어나지 않는지를 잘 살펴볼 필요가 있다.
⑨ 본 연구는 파가 LCS에 수직으로 입사하는 경우만을 다루었다. 그러나 만일 본 결합기법을 파가 사각으로 입사하는 경우에 적용하고자 할 경우에는, 수위상승의 대부분은 월파에 의해 발생하므로, 파의 사각 입사에 따른 월파량의 변화를 Fig. 16에 예로 보인 바와 같은 형식으로 LCS를 대상으로 제시한 국내 · 외의 연구결과를 참조하여 적용 여부를 판단하는 것이 필요하다.
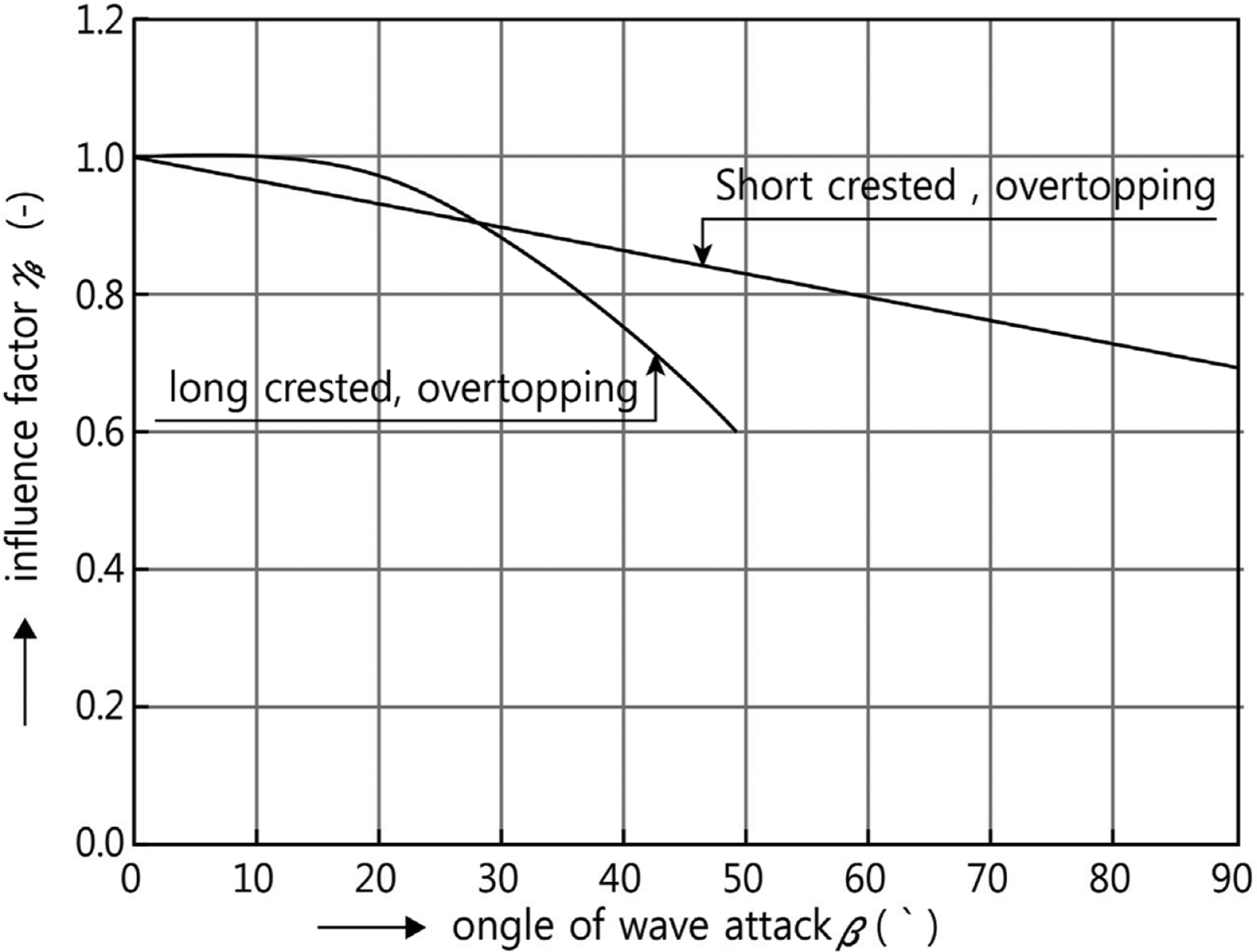
Recommended correction factor considering oblique wave incidence (after de Waal and van der Meer, 1993).
5.3 결합기법의 효과 및 한계점
LCS 설계 시 본 연구에서와 같이 결합기법을 적용할 때에는 다음과 같은 효과를 거둘 수 있을 것으로 예상된다.
▪ 해수유동수치모형실험으로 LCS 배후면의 평균수위를 짧은 시간 내에 예측할 수 있으므로 단면수리모형실험 시 발생하는 Table 1에 열거된 문제점들을 상당 부분 해소할 수 있다.
▪ LCS의 개구부 또는 배후수로 입구로부터의 유출유속의 규모를 단면수리모형실험 시부터 개략적으로라도 예측할 수 있어 안별 배치안의 상대적 비교에 활용할 수 있다.
▪ 평균수위 상승 및 개구부의 유출유속과 관련하여 개선안을 마련해야 할 경우 그 개선의 우선적인 대상이 LCS 단면인지 또는 LCS의 평면배치인지를 판단하는데 도움이 된다.
▪ 종합적으로 적정 단면안 및 평면배치안 선정결과의 신뢰성이 향상된다.
한편, 결합기법을 적용하는 데에는 다음과 같은 어려움 또는 제한점들이 있다.
▪ Fig. 5에 나타난 바와 같이 LCS의 투수성은 사용재료의 크기에 영향을 받아 평균수위 상승량에 영향을 미친다. 따라서, 모형의 축척효과를 감소시키기 위해서는 모형을 가능한한 크게 제작함이 필요하다. 이는 축소모형실험 자체가 안고 있는 문제이다.
▪ 수위-유량 관계식을 얻기 위한 실험을 계획할 때 많은 회류유량을 감당할 수 있는 대용량의 펌프와 유량계의 설치가 필요하다.
▪ 수위-유량 관계식을 얻기 위해서는 단면실험의 양이 크게 증가하므로 실험에 소요되는 시간도 이에 따라서 증가한다.
▪ 본 연구의 결합기법에서는 개구부로 내습하는 파랑의 쇄파로 인한 순유입유량은 고려되지 않았기에 현장의 실여건과는 차이가 있다.
▪ 본 연구의 결합기법에서는 해수유동수치모형실험 시 LCS 제체의 배후면에 경계조건으로 수위-유량 관계식이라는 매우 단순화된 관계식을 적용하므로 결과는 현장과 차이가 날 수 있다.
▪ 본 연구의 결합기법은 LCS 연장상 파고가 크게 변하거나 파가 큰 사각으로 입사할수록 평면수리모형실험이나 정밀 3차원수치모형실험 결과와의 차이는 증가할 것으로 예상된다.
▪ 본 연구의 결합기법의 정밀도는 평면수리모형실험으로 검증되지 않았으며, 평면수리모형실험이나 정밀한 3차원 수치모형실험을 수행하기 전단계의 예비정보를 얻을 수 있는 수준이라고 판단된다.
결 론
LCS 설계를 위한 단면수리모형실험 수행 시 배후의 평균수위 상승량이 알려지지 않아 LCS의 안정성 및 배후 호안의 월파량 계측 등에서 발생하는 문제점들을 빠르게 해소하기 위해 단면수리모형실험과 해수유동수치모형실험을 결합하는 결합기법이 시도되었다. 해수유동모형실험에서 수위와 유속장의 계산은 수렴속도가 매우 빨라 단면수리모형실험과 동시간대에 결과를 얻을 수 있어, 단면수리모형실험 또는 설계 수행 시에 배후수위가 알려지지 않아 발생하는 문제점들을 상당한 수준으로 해소할 수 있게 되었다. 동시에 LCS의 개구부를 통한 유출류의 규모에 관한 정보를 얻을 수 있어 적정한 평면배치안 선정을 위한 후보안들의 상대비교에 도움이 될 수 있다. 그러나 해수유동수치모형의 LCS 배후면에 단순화된 수위-유량 관계식을 사용함으로써 현장과 다른 결과를 얻을 수도 있으므로 향후 평면수리모형실험을 통한 예측 정확도 검증이 필요하다.
본 연구에서 제시한 결합기법은 설계 초기의 단면수리모형실험 단계에서 다양한 후보안들 중 유력한 후보안들을 신속히 압축 · 선정하기 위한 목적으로 개발되었기 때문에 LCS 주변에 내재된 일부 수리현상을 단순화하거나 고려하지 않았다. 따라서, 최종안을 결정하는 단계에서는 평면수리모형실험이나 정밀한 3차원수치모형실험의 수행이 필요하다.