준선형 수치모델을 이용한 투과성 소파장치의 반사율
Reflection of Porous Wave Absorber Using Quasi-linear Numerical Model
Article information
Abstract
본 연구에서는 투과성 판을 통과하면서 발생하는 에너지 손실효과를 나타내는 비선형 항력 항을 등가 선형화기법으로 선형화시킨 준선형 모델을 제안하였다. 이 모델을 경계요소법(Boundary Element Method)으로 풀어 2차원 조파수조의 투과성 소파장치를 개발에 활용하였다. 투과성 판에서의 항력계수는 수리 모형실험 결과와 비교를 통해 새롭게 구하였다. 공극률 0.1, 잠긴 깊이 d/h = 0.1, 경사각도 10º ≤ θ ≤ 20º 를 갖는 투과성 소파장치가 전반적으로 우수한 소파성능을 보였다. 개발된 준선형 수치모델은 앞으로 다양한 형태의 투과성 소파장치의 최적 설계에 활용될 것이다.
Trans Abstract
In present study, we suggested the quasi-linear model that linearizes the quadratic drag representing the energy loss across the porous plate. The quasi-linear model was solved by Boundary Element Method (BEM) for development of the porous wave absorber suitable for 2-D wave tank. The drag coefficient at the porous plate was newly obtained through comparison of experimental results. It is found that the porous wave absorber with porosity 0.1, submergence depth d/h = 0.1, and inclined angle 10º ≤ θ ≤ 20º shows the effective wave absorption. Using the developed quasi-linear numerical model, the optimal design of various types of a porous wave absorber will be applied.
1. 서 론
입사파와 투과성 구조물(Porous structure)의 상호작용 해석은 이론적인 측면과 실용적인 측면 모두를 고려하였을 때 흥미로운 주제이다. 항내 해수교환을 허용하여 쾌적한 항만을 조성하면서 항내 하역 활동에 지장을 주지 않도록 파의 일부분을 차단시키는 유공 방파제(Perforated breakwater)가 대표적인 투과성 구조물의 응용 분야이다. 또한 해양공학과 관련된 모형실험에서 폭 넓게 활용되는 조파수조(Wave flume) 내에서 발생되는 반사파를 줄여 파의 왜곡을 방지하고 수조의 효율성을 높이는 소파장치(Wave absorber)도 투과성 구조물의 한 예이다. 실험실내의 소파장치의 기능을 실해역으로 확장하면 항만 내 불투과성 안벽 전면에 투과성 구조물을 배치하면 안벽으로부터 발생하는 반사파 에너지를 줄일 수 있어 항만 내 정온도를 높일 수 있다. 또한 해양토목공사나 해양 구조물 설치 시 일시적으로 파랑 하중을 줄이기 위한 파 차단벽(Wave barrier)으로도 투과성 구조물을 이용할 수 있다.
입사파와 판 구조물 사이의 상호작용을 해석하는 논문들을 크게 분류하면 불투과성 판과 투과성 판으로 나눌 수 있다. 불투과성 수평 판이 수면 아래 일정 깊이 잠겨 있을 때 반사율과 투과율을 해석한 대표적인 논문들로는 McIver(1985), Patarapanich and Cheong(1989), Linton and Evans(1991), Siew and Hurley(1997)의 연구들을 들 수 있다. 불투과성 수평판이 수면에 놓여 있는 dock 문제에 대한 해석 해는 Linton (2001)에 의해 구해졌다. Neelamani and Gayathri(2006)는 이중 불투과성 판에 의한 반사율과 투과율을 규칙파와 불규칙파 실험을 통하여 살펴보았다. 이중 판 사이의 간격을 적절히 조절하면 단일 판보다 더욱 향상된 파 차단 성능을 보여줌을 밝혔다. 불투과성 판인 경우, 해석 모델 내에 에너지 손실 기구가 존재하지 않기 때문에 에너지 보존식(|Rf|2 + |Tr|2 = 1)을 만족한다. 따라서 투과율을 줄이기 위해서는 반사율을 높여야 한다.
Wu et al.(1998)는 수직 벽 앞에 놓인 투과성 수평 판에 의한 반사율을 고유함수전개법(Eigenfunction expansion method)을 사용하여 해석적으로 구하였다. 투과성 판의 공극률과 밀접한 관련이 있는 공극률 계수(Porous coefficient)를 도입하여 투과성 판의 공극률이 수직 벽에 작용하는 하중뿐만 아니라 반사율에 큰 영향을 미침을 밝혔다. Wu(1998)는 공극률뿐만 아니라 수평 판의 길이와 잠긴 깊이도 반사율에 큰 영향을 미침을 보였다. Cho and Hong(2004)은 경사형 투과성 판에 대한 모형실험을 수행하였다. 주요 설계변수(공극률, 경사각도, 입사파의 주기)들을 바꿔가면서 최적의 값을 도출하였다. 최적의 소파장치의 경사각도는 10도 전후이며, 공극률은 0.1임을 모형실험을 통하여 밝혔다. Liu et al.(2008)은 위판은 투과성 판으로 아래 판은 불투과성 판으로 구성된 이중 수평 판에 대한 동유체학적 성능을 연구하였다. 투과성 상판의 공극률을 적절히 조절한다면 이중 수평 판에 작용하는 수직 하중을 크게 줄일 수 있음을 보였다. Cho and Kim(2008)은 경사파(Oblique wave)와 수직 벽 앞에 놓인 투과성 판(수평판, 경사판, 이중판)과의 상호작용 문제를 고유함수전개법과 경계요소법(BEM, Boundary Element Method)을 사용하여 해석하였다. 투과성 판을 통한 에너지 손실효과를 나타내기 위하여 Darcy 법칙을 사용하였다. 그들은 최적 소파효율을 보이는 소파장치의 공극률은 0.1, 수평 판인 경우에는 잠긴 깊이는 수심의 10%, 경사판인 경우에는 경사 각도가 10도임을 밝혔다. 이를 토대로 제작된 소파장치를 KRISO(Korea Institute of Ships and Ocean Engineering)의 해양공학 수조에 설치하여 현재 운용 중에 있다. Yueh and Chuang(2009)은 투과성 방파제의 성능(반사율, 하중)을 평가하기 위하여 다중 영역 BEM 수치해석 방법을 사용하였다. Liu and Li (2011)는 투과성 수평 판의 성능을 나타내는 해석 해를 구하는 새로운 해석방법을 제시하여 반사율, 투과율, 수평판 작용 하중을 구하였다. Cho and Kim(2013)은 이중 투과성 수평판에 의한 파랑 제어에 대한 해석 해를 Liu and Li(2011)가 제시한 해석 방법을 사용하여 구하였다. Crowley and Porter (2012)는 파가 투과성 수직 판을 통과하면서 발생하는 에너지 손실효과를 비선형 항력 항으로 나타내는 해석모델을 제시하였다. Molin and Remy(2013)는 수평 운동하는 사각형 탱크내의 슬로싱 현상을 저감하는 목적으로 탱크 내에 설치한 투과성 배플(baffle)의 효과를 실험과 해석을 통하여 살펴보았다.
본 연구에서는 Cho and Kim(2008)이 사용한 투과성 판을 통과할 때 발생하는 에너지 손실효과를 구현하는 Darcy 법칙을 이용한 선형이론 대신에 Crowley and Porter(2012)가 제시한 비선형 항력 항을 선형화시킨 준선형 모델을 사용하였다. 이를 수치적으로 풀기 위하여 다중 영역 경계요소법을 이용하였다. 수치해석 결과를 검증하기 위하여 경사형 투과성 판에 대하여 수리실험을 실시하였다. 수치해석과 수리실험을 비교 분석한 결과, 두 결과는 서로 잘 일치함을 확인하였다. 개발된 준선형 수치해석 모델은 투과성 소파장치의 소파 성능을 수치적으로 잘 보여주므로 다양한 형태의 소파장치 개발에 폭 넓게 활용될 것이다.
2. 이 론
2.1 경계치 문제
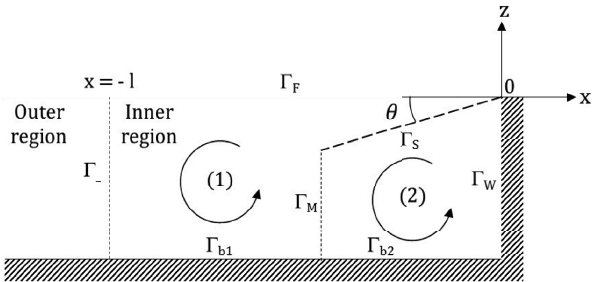
수심이 h인 조파수조 내에 진폭 A와 주파수 ω를 갖는 규칙파가 x축의 양의 방향으로 진행한다. 수조 끝단에 설치된 소파장치는 두께를 무시한 공극률 P를 갖는 투과성 판으로 이뤄졌으며 수면과 경사각도 θ을 갖고 설치된다. 유체를 비압축성, 비점성으로 유동을 비회전성이라 가정하면 속도포텐셜을 도입할 수 있으며, 속도포텐셜은 아래와 같은 경계치 문제의 해이다.
투과성 판이 유체 영역 내에 놓여 있다고 할 때 투과성 판에서의 경계조건식(Bennett et al., 1992; Crowley and Porter, 2012)은 다음과 같다.
여기서 위첨자 ±는 각각 투과성 판의 윗면과 아랫면을 뜻한다. α와 C은 각각 투과성 판을 통과하면서 발생하는 에너지 손실효과를 나타내는 항력계수(Drag coefficient)와 가속도에 비례하는 관성력 효과를 나타내며 투과성 판의 국부 형상과 밀접한 관련이 있는 차단계수(Blockage coefficient)이다.
Mei(1989)는 두께가 얇은 슬릿벽에서의 항력계수를
여기서 단면수축계수 Cc에 대하여 Mei(1989)는 예연 오리피스를 가정하여 다음의 경험식을 사용하였다.
파가 시간에 따라 주파수 ω를 갖고 조화운동을 한다고 가정하면 속도포텐셜을 시간과 공간의 함수로 분리할 수 있다.
여기서 φ는 속도포텐셜의 복소 공간함수이다. 주파수 ω와 파수(wavenumber) k는 선형분산식(ω2 = gktanhkh)을 만족한다.
식(6)을 경계치 문제(1)에 대입하면 속도포텐셜(φ)가 만족하는 경계치 문제를 얻을 수 있다.
여기서 φI는 입사파 포텐셜로 다음과 같다.
투과성 판에서의 경계조건식인 식(3) 안에 속도 제곱에 비례하는 비선형 항력 항으로 인해 입력 주파수 ω에 대해 여러 개의 주파수 성분(ω, 2ω, 3ω, …)들이 생성된다. 따라서 속도포텐셜을 주파수 ω의 배수로 나타내는 Fourier 급수 식으로 표현하고 첫 번째 항인 ω 성분만을 취하고 나머지 항(2ω, 3ω, …)들은 무시하였다. 이때 첫 번째 항의 Fourier 계수는 8/3π이다. 이러한 등가선형화(Equivalent linearization) 과정을 통하여 식(2)와 (3)을 다시 쓰면 다음과 같다.
여기서
2.2 경계요소법
위에 주어진 경계치 문제((7), (9), (10))를 풀기 위하여 다영역 경계요소법을 적용하였다. 유체영역을 Fig. 2에 나타나듯이 외부영역과 내부영역으로 나눈다. 내부영역은 투과성 판을 경계로 편의상 영역(1)과 영역(2)로 구분하고 각각 윗첨자(1), (2)로 나타낸다.
외부영역의 해는 Laplace 방정식과 자유표면, 바닥면, 방사 경계조건을 만족한다. 소멸파 모드(Evanescent mode) 성분들이 사라질 만큼의 거리(x = − l)에 외부영역의 경계를 위치시키면 외부영역에서의 속도포텐셜은 다음과 같이 진행파인 입사파와 반사파의 합으로 표현할 수 있다.
여기서 Rf는 소파장치로부터의 반사율을 나타낸다.
외부영역과 내부영역이 만나는 정합면 x = − l에서 유량이 서로 같다는 정합조건식으로부터 식(11)에 나타난 반사율을 내부영역(1)의 해로 나타낼 수 있다.
여기서
식(12)를 식(11)에 대입한 뒤, 정합면 x = − l에서 압력이 서로 같다는 두 번째 정합조건식을 적용하면 아래와 같이 x = − l에서 만족해야 할 경계조건식을 유도할 수 있다.
내부영역에 대한 해를 구하기 위한 모든 경계면에서의 경계조건식들이 준비되었다. 이를 풀기 위한 수치해석 기법으로 경계요소법(BEM)을 사용하였다. Green 정리를 사용하여 내부영역을 둘러싼 전 경계면을 여러 개의 요소들로 나누고 각 요소에서 속도포텐셜과 법선방향의 속도가 일정하다고 가정하면 아래와 같은 이산화 된 경계적분방정식을 유도할 수 있다.
여기서 G는 Laplace 방정식 ∇2G = − δ(x − ξ)δ(z − η)을 만족하는 기본해(Fundamental solution)로 다음과 같다.
여기서 (ξ, η)는 특이점(Source point)의 위치이다.
식(14) 내의 적분 항들은 아래 식과 같이 정의된다.
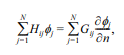
여기서
식(16)을 이용하면 내부영역(1)에 대한 적분방정식(14)는 아래와 같은 대수방정식으로 바뀐다.
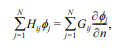
여기서
내부영역(1)과 (2)가 만나는 정합면(ΓM)에서 압력과 법선방향 속도는 서로 같다는 정합조건식은 다음과 같다.
여기서 윗첨자 —는 정합면(ΓM)에서 새롭게 정의된 값을 의미한다.
투과성 판이 위치한 경계면에서 내부영역(1)과 (2)의 법선방향 속도는 서로 같아야 하며
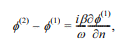
여기서
수치해석 모델로 투과성 판이 수조 끝단에서 경사각도 θ를 갖고 경사지게 설치된 경우를 다루겠다. 내부영역(1)을 둘러싼 경계면을 N개의 요소들로 나누고, 내부영역(2)을 둘러싼 경계면을 M개의 요소들로 분할하여 각 경계면에서 적용되는 경계조건식(7), (9), (19)를 적용한다.
먼저 내부영역(1)에 속한 경계면에서의 경계조건식들과 외부영역과 내부영역(2)와 만나는 정합면(Γ−, ΓM)에서의 정합조건식을 대입하면 내부영역(1)에서의 대수방정식을 유도할 수 있다.
같은 방법으로 내부영역(2)에 속한 경계조건식들과 내부영역(1)과의 정합면(ΓM)에서의 정합조건식을 적용하면 다음과 같다.
대수방정식인 식(20)과 식(21)을 행렬식으로 바꾸어 정리하면 다음과 같다.

여기서
위에 주어진 비선형 방정식을 풀기 위하여 본 논문에서는 축차법(Iteration method)을 사용하였다. (k)번째 반복 단계(Iteration step)에서의 미지수 [φ(1)], [φ(2)]을 얻기 위해서는 같은 단계에서의 [β](k)를 알아야 한다. 그러나 [β]((k)는 현 반복 단계의 해([φ(1)](k), [φ(2)](k))을 알아야 정의된다. 따라서 [β](k) 대신에 이전의 반복 단계에서의 [β](k−3/2)을 사용한다. 여기서 윗첨자(k − 3/2)는 반복 단계(k − 1)와 반복 단계(k − 2)에서의 값들의 평균값을 의미한다. 이러한 방법으로 각 반복 단계에서 해([φ(1)](k), [φ(2)](k))를 구하는데, 오차범위 |[φ](k+1) − [φ](k)| ≤ 10−4을 만족할 때까지 계산을 반복한다.
각 분할 요소에서 속도포텐셜 값이 구해지면 투과성 판에 작용하는 하중과 모멘트(Fk = Re{fke−iωt}, k = 1, 2, 3)은 Bernoulli 방정식을 사용하여 속도포텐셜을 적분하여 구해진다.
여기서 n1 = nx, n2 = nz, n3 = xn2 − zn1이다.
같은 방법으로 수조 벽에서의 수평 방향 유체력(Fx = Re{fke−iωt})은 아래와 같다.
3. 수리실험
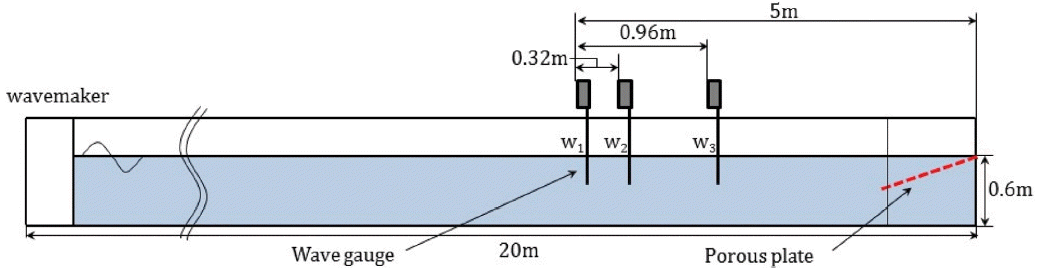
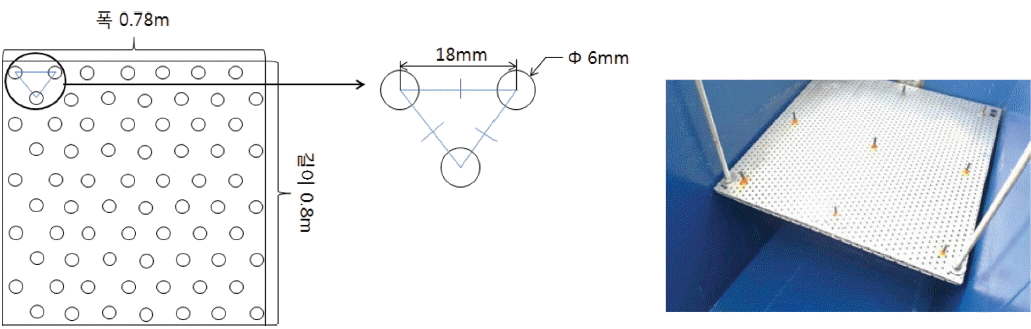
수리실험은 제주대학교 2차원 조파수조(길이 20 m, 폭 0.8 m, 깊이 1.0 m)에서 수행되었다. 수리실험에서 사용한 파고계와 투과성 판의 배치도는 Fig. 3과 같다. 조파수조 한 끝단에 놓인 피스톤 타입 조파장치를 가지고 파를 생성하였다. 생성된 입사파의 주기는 0.7 s, 0.8 s, 0.9 s, 1.0 s, 1.2 s, 1.4 s, 1.6 s, 1.8 s, 2.0 s로 총 9개이며 안정적으로 선형파 특성을 보이는 파 기울기(H/λ = 0.01)를 사용하였다. 수심은 0.6 m로 고정하였다. 정확도 ± 0.1 cm의 저항식 파고계를 통해 파고를 측정하였다. 수리실험에 사용한 투과성 판은 스테인리스 재질로 직경 6 mm의 작은 구멍이 일정한 간격(18 mm)을 갖고 배열된 형태이다(Fig. 4 참조). Cho and Kim(2008)에 의해 가장 소파 효율이 우수하다고 알려진 공극률 0.1인 투과성 판을 사용하였다. 투과성 판의 길이는 0.8 m이며 두께는 1.6 mm이다. 투과성 판은 수조 벽에 4개의 수직봉으로 고정된다. 조파실험중 투과성 판과 수직봉은 흔들림 없이 형태를 잘 유지하였다. 입사파와 반사파를 분리하기 위하여 Mansard and Funke(1980)가 제안한 최소자승법(least square method)을 사용하였다. 이 방법은 가정된 파형과 계측된 파형의 오차의 제곱의 합이 최소가 되도록 미지수를 구하는 방법으로 최소한 3개의 파고계(W1, W2, W3)가 필요하다. 입사파와 반사파를 정확히 분리하기 위하여 측정된 파의 분석 구간을 적절히 선정하여야 한다. 입사파가 소파제로부터 반사되어 파고계에 도달한 시간과 이후 조파장치로부터 재 반사되어 파고계에 도달되는 예측 시간내에서 파가 비교적 정상상태를 보이는 구간을 새로이 선정하여 입사파와 반사파를 분리하였다. 본 실험에 사용한 3개의 파고계의 설치 위치는 수조 벽으로부터 5.0 m, 4.68 m, 4.04 m이다. 파고계 W1과 W3 사이의 거리는 Shore Protection manual(1984)이 제안한 λ1−3 ≥ λmax/20을 만족해야 한다. 여기서 λmax는 실험에서 사용한 최대 파장이다. 현재 수리실험에서 최대 파장은 4.36 m이므로 W1과 W3 사이의 거리를 0.96 m로 하였다. W1과 W2 사이의 거리 λ1−2는 Shore Protection manual의 권고(λ1−2 = 0.3λ1−3)에 따라 0.32 m로 잡았다. 이와 같이 3개의 파고계의 간격을 정해진 규정을 따르는 이유는 입사파와 반사파 분리 시 발생하는 특이 거동을 피하기 위함이다(Goda and Suzuki, 1976). 수조벽 앞에 놓인 투과성 판의 경사 각도를 5o, 10o, 15o로 바꿔가면서 반사율을 측정하였다.
4. 결과 및 고찰
식(4)의 투과성 판에서의 항력계수를 구하기 위하여 식(4)의 γ 값을 바꿔가면서 계산된 반사율과 측정된 반사율의 오차(S)가 최소가 되는 γ 값을 선정하였다. 이를 수식으로 나타내면 다음과 같다.
여기서 ωi는 실험에서 사용한 주파수를 의미하며, M(= 9)은 주파수의 총 개수이다. Rf(ωi)는 측정된 반사율이며,
Fig. 5는 수리실험과 비교를 통하여 구한 항력계수를 가지고 계산한 수치계산결과와 수리실험 결과를 비교한 그림이다. 투과성 판의 경사 각도를 θ = 5o, 10o, 15o로 바꿔가면서 수치계산결과와 수리실험결과를 비교하였다. 수치계산에서 사용한 특이점의 총 개수는 320개이다. 전반적으로 수치계산결과와 실험결과는 서로 잘 일치하고 있음을 보여준다. 이러한 사실은 작은 구멍이 일정한 간격으로 배열된 얇은 투과성 판을 통한 에너지 손실을 나타내는 항력계수(α)가 적절함을 의미한다. 또한 본 논문에서 제시한 투과성 판을 통한 에너지 손실 효과를 나타내는 준선형 수치모델이 타당하다는 것을 뜻한다.
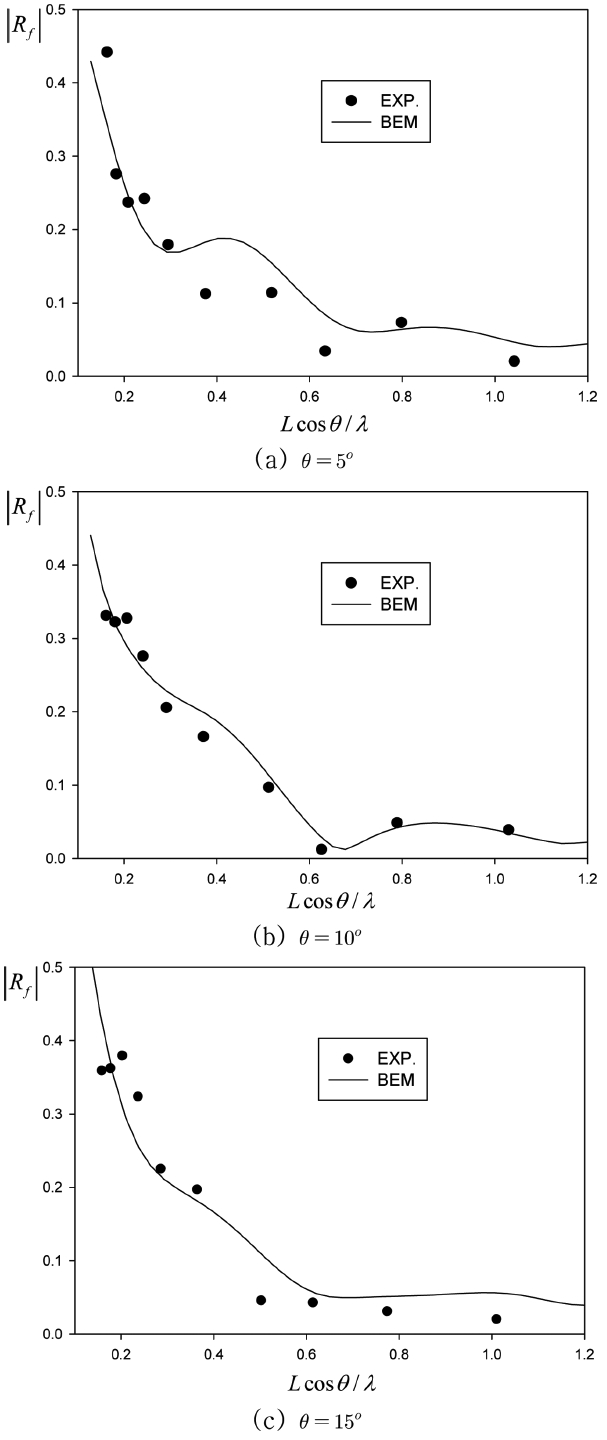
Comparison of numerical (BEM) and experimental results for a inclined porous plate with different angles for P = 0.1, H/λ = 0.01.
Fig. 6부터 9까지는 투과성 판이 수조 벽 앞에 수면과 평행하게 일정 깊이 잠겨있는 수치모델에 대하여 BEM을 사용한 수치계산 결과를 보여주고 있다. 투과성 판의 공극률은 0.1로 고정하였고, 무차원화된 잠긴 깊이는 d/h = 0.05, 0.1, 0.2이다. 투과성 판의 길이(= 1.0 m)와 수심의 비는 L/h = 1.0이며, 파 기울기(Wave steepness)는 H/λ = 0.01이다. 그림에서 x축은 투과성 판의 길이를 입사파의 파장으로 나눈 값(= L/λ)이며, y축은 반사율이다. 파랑에너지는 주로 수면 가까이에 분포하므로 투과성 판의 잠긴 깊이가 너무 깊으면 파랑에너지를 효과적으로 흡수할 수 없다. 따라서 잠긴 깊이가 깊을수록 반사율이 커질 것으로 예측할 수 있다. d/h = 0.2에 대한 계산 결과가 이러한 예측을 잘 뒷받침해 주고 있다. 그러나 잠긴 깊이가 필요 이상으로 너무 얕아도 오히려 반사율이 증가하는 경향이 단주기 영역에서 나타나고 있다. 투과성 판을 수평으로 설치하였을 때, 소파효율을 극대화하는 최적의 잠긴 깊이는 수심의 약 10%이다.

Reflection coefficients by a horizontal porous plate with different submerged depths for P = 0.1, H/λ = 0.01, L/h = 1.0.
Horizontal hydrodynamic force on a vertical wall with different porosities for d/h = 0.1, L/h = 1.0, H/λ = 0.01.
Fig. 7은 Fig. 6과 동일한 모델에 대하여 4개의 서로 다른 공극률 P = 0.05, 0.1, 0.2, 0.3을 갖는 투과성 판에 의한 반사율을 보여주고 있다. 여기서 투과성 판의 잠긴 깊이는 d/h = 0.1이다. 공극률이 0.1보다 클수록 투과성 판을 통과하면서 발생하는 에너지 손실 효과가 떨어져 반사율이 커짐을 보여주고 있다. 공극률이 상대적으로 작은 P = 0.05, 0.1를 갖는 투과성 판에 대한 반사율을 살펴보면 무차원화된 입사파의 파장(L/λ)에 따라 반사율의 변동성이 나타나지만 전반적으로 공극률 P = 0.1을 갖는 투과성 판의 소파 성능이 좀 더 우수하게 나타났다. 유지 보수 측면에서도 구멍의 크기가 너무 작은 P = 0.05보다 P = 0.1이 바람직하다. Fig. 6과 7로부터 P = 0.1, d/h = 0.1을 갖는 투과성 판을 이용한 수평형 소파장치는 비교적 짧은 설치 길이임에도 불구하고 우수한 소파성능을 보여 주었다.
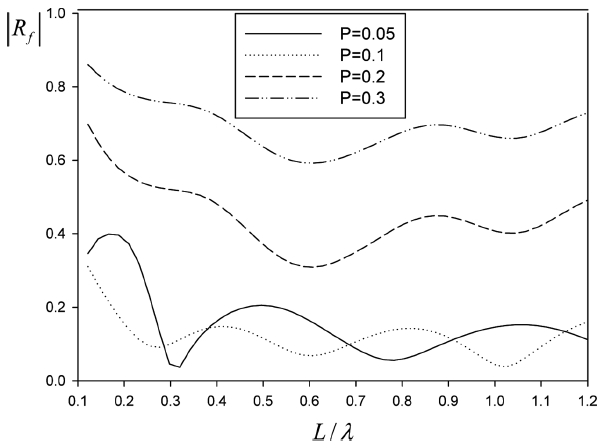
Reflection coefficient by a horizontal porous plate with different porosities for d/h = 0.1, L/h = 1.0, H/λ = 0.01.
Fig. 8과 9는 공극률 변화에 따른 수평형 투과성 판에 작용하는 수직 하중과 수조 벽에서의 수평 하중을 보여주고 있다. 수평형 투과성 판에 작용하는 수직 하중의 크기는 두 가지 요소에 의해 결정된다. 즉, 투과성 판을 통한 파랑에너지 손실률과 투과성 판 사이의 압력차이다. Fig. 7에 따르면 에너지 손실률은 공극률이 0.1일 때 가장 크므로 수직 하중이 가장 낮아야 한다. 그러나 공극률이 클수록 투과성 판 사이의 압력차는 줄어들기 때문에 이에 따라 수직 하중은 줄어든다. 이 두 가지 요소를 함께 고려한 Fig. 7은 투과성 판에 작용하는 수직 하중은 공극률이 커질수록 감소함을 보여주고 있다. 또한 본 논문에서 고려치 않은 공극률에 따른 작용면적의 변화를 추가한다면 이런 경향은 더욱 두드러지게 나타날 것이다. Fig. 9에 나타난 수조 벽에서의 수평 하중은 투과성 판의 소파 효율과 밀접한 관련이 있어 소파 성능이 가장 우수한 P = 0.1에서의 하중이 가장 낮게 나타났다. 입사파의 파장 변화에 따른 하중 곡선의 특징은 장주기 영역에서 단주기 영역으로 진행함에 따라 주기적으로 변동하면서 줄어드는 경향을 보인다. 그러나 공극률이 가장 작은 P = 0.05 곡선은 나머지 곡선과 다른 패턴을 보여주고 있다. 수평형 투과성 판의 설치로 인해 수조 벽과 투과성 판에 작용하는 하중을 크게 줄일 수 있으며 하중의 감소율은 투과성 판의 공극률과 밀접한 관련이 있다.
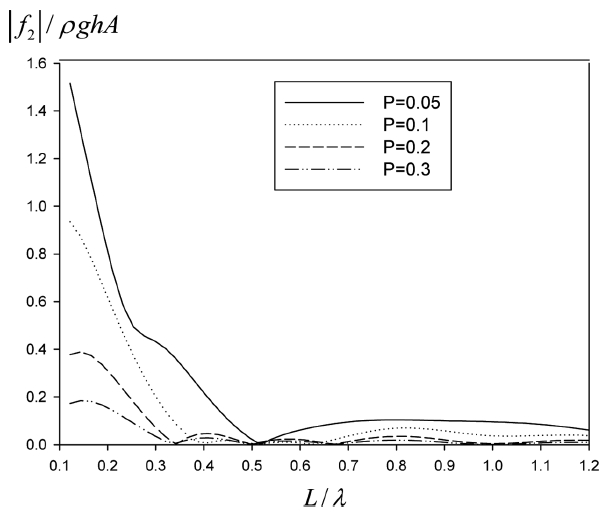
Vertical hydrodynamic force on a horizontal porous plate with different porosities for d/h = 0.1, L/h = 1.0, H/λ = 0.01.
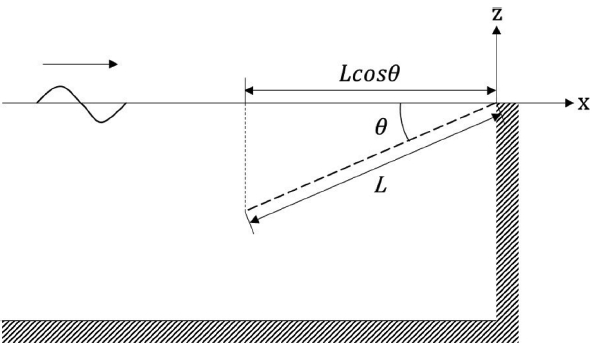
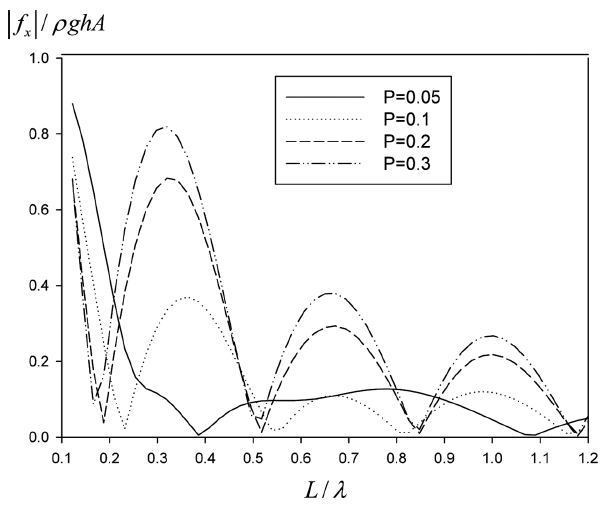
Fig. 10부터 12는 투과성 판이 수조 벽 앞에 일정 각도로 경사지게 놓여있을 때(θ = 5o, 10o, 15o, 20o, 25o)의 반사율의 특성을 살펴보았다. 투과성 판의 길이(= 1.0 m)와 수심의 비는 L/h = 1.0이며, P = 0.1, H/λ = 0.01이다. x축은 투과성 판의 수평 길이를 입사파의 파장으로 나눈 값(= Lcosθ/λ)이다. 경사형 투과성 판이 수평으로 놓인 투과성 판에 비해 단주기 영역에서 상대적으로 우수한 소파성능을 보인다. 또한 투과성 판의 경사 각도가 적정 범위 내에 놓여 있으면 반사율에 큰 영향을 미치지 않음을 알 수 있다. 적정 경사 각도는 10o ≤ θ ≤ 20o이다. Fig. 11은 같은 계산조건에서 수직 벽에 작용하는 수평 하중을 그렸다. Lcosθ/λ > 0.2인 단주기 영역에서는 투과성 판의 경사 각도가 증가할수록 수평 하중은 증가하나 Lcosθ/λ < 0.2인 장주기 영역에서는 반대의 경향이 나타남을 볼 수 있다.
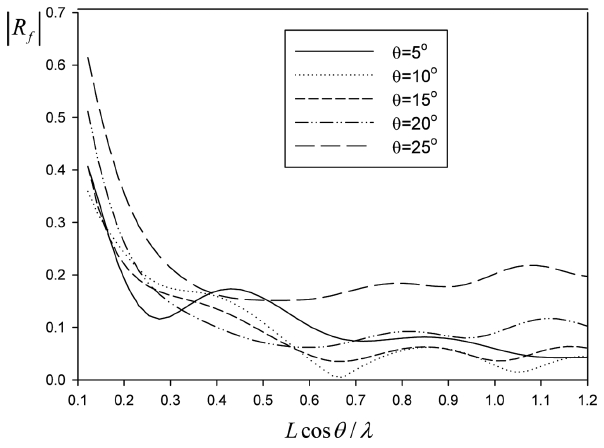
Reflection coefficient by a inclined porous plate with different angles for P = 0.1, H/λ = 0.01, L/h = 1.0.
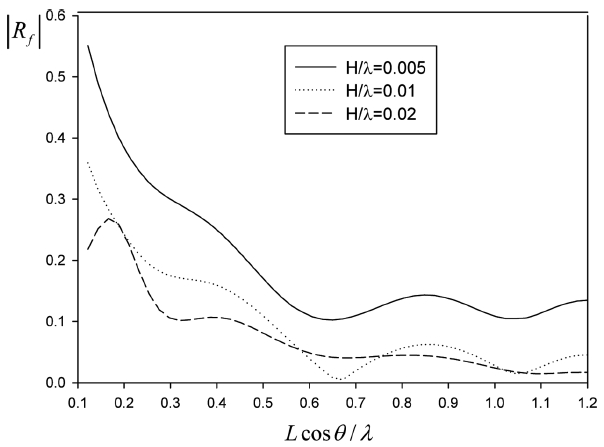
Reflection coefficient by a inclined porous plate with wave steepness for P = 0.1, θ = 10°, L/h = 1.0.
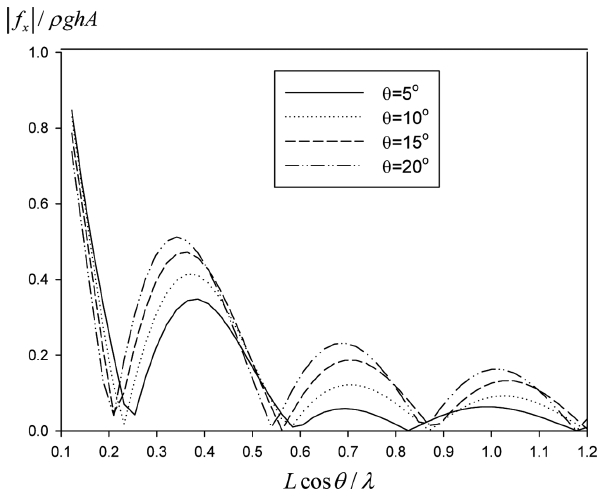
Horizontal hydrodynamic force on a vertical wall with different angles for P = 0.1, H/λ = 0.01, L/h = 1.0.
Fig. 12는 파 기울기(H/λ)가 변할 때 반사율의 변화를 보여주고 있다. 파 기울기가 크다는 것은 비선형성이 강함을 뜻하며 선형이론의 결과와는 차이를 보일 것으로 예측된다. 본 논문에서 다룬 수치모델은 비록 등가 선형화 과정을 통하여 유도한 준선형(Quasi-linear) 모델이므로 비선형 효과를 일부분 담고 있어 Fig. 12와 같이 파 기울기 변화에 따른 반사율의 특성을 파악하는데 도움이 된다. 입사파의 주기에 따라 달라질 수도 있지만 전반적으로 파의 기울기가 클수록 비선형 효과로 인해 투과성 판을 통한 에너지 손실이 더욱 커져 반사율이 줄어드는 경향을 보여주고 있다. 그러나 비선형성이 너무 강한 문제에서는 다른 결과를 줄 수도 있다.
5. 결 론
이상의 수치계산과 수리실험의 결과로부터 다음과 같은 결론을 내릴 수 있다.
1) 일정한 구멍이 일정한 간격으로 배열된 투과성 판에 대한 항력계수를 경사형 투과성 판의 수리실험 결과와 비교하여
2) 투과성 판을 수평으로 설치하였을 때, 소파효율을 극대화하는 최적의 잠긴 깊이는 수심의 약 10%이며, 최적의 공극률은 0.1이다. 수평형 투과성 판의 설치로 인해 수조 벽과 투과성 판에 작용하는 하중이 크게 줄어들었다. 이때 하중의 크기는 투과성 판의 공극률과 밀접한 관련이 있다.
3) 경사각도 변화에 따른 소파성능을 검토한 결과 최적의 소파효율을 주는 경사 각도의 적정 범위는 10o ≤ θ ≤ 20o이다. 투과성 판의 경사 각도가 증가할수록 단주기 영역에서는 수직 벽에 작용하는 수평 하중은 증가하나 장주기 영역에서는 반대의 경향이 나타났다.
4) 파의 기울기가 증가할수록 비선형 효과로 인해 투과성 판을 통한 에너지 손실이 커져 반사율이 줄어드는 경향을 보여주었다. 현재 개발된 준선형 수치모델은 파 기울기가 H/λ = 0.01일 때 수리실험 결과와 비교를 통하여 검증되었다. 그러나 비선형성 더욱 강한 문제에 대해서는 추가적인 검증이 필요하다.
5) 투과성 판 사이의 압력차를 유체 속도의 제곱으로 표현하는 비선형 항력항을 등가 선형화시켜 해를 구하는 Crowley and Porter(2012)의 준선형 모델을 경계요소법으로 푼 수치계산결과는 수리실험결과와 정성적으로 잘 일치하였다. 좀 더 개선된 수치모델 개발을 위해서는 다양한 조건(형상, 파 기울기, 공극률, 입사파)에서의 수리실험 결과와의 비교가 요구된다.
Acknowledgements
이 논문은 2017년도 정부(교육부)의 재원으로 한국연구재 단의 지원을 받아 수행된 이공분야기초연구지원사업임(No. 035231). 본 연구는 2016년도 산업통상자원부의 재원으로 한 국에너지기술평가원(KETEP)의 에너지인력양성사업「풍력 O&M 기술 고급트랙」으로 지원받아 수행한 인력양성 성과 입니다(No. 20164030201230).