진동 수주형 축대칭 부유식 파력발전장치의 성능평가

Performance Evaluation of an Axisymmetric Floating Wave Power Device with an Oscillating Water Column in the Vertical Cylinder

Article information

J Korean Soc Coast Ocean Eng. 2018;30(1):29-38

Publication date (electronic) : 2018 February 28

doi : https://doi.org/10.9765/KSCOE.2018.30.1.29

Woo-Sun Park ^*, Shin Taek Jeong^,^**, Hyukjin Choi ^**, Uk Jae Lee ^**

^*Coastal Engineering Division, Korea Institute of Ocean Science & Technology

^**Department of Civil and Environmental Engineering, Wonkwang University, Iksandae-ro 460, Iksan, Jeonbuk 54538, Korea

박우선^*, 정신택^,^**, 최혁진^**, 이욱재^**

^*한국해양과학기술원 연안공학연구본부

^**원광대학교 토목환경공학과

Corresponding author: Shin Taek Jeong, Department of Civil and Environmental Engineering, Wonkwang University, Iksandae-ro 460, Iksan, Jeonbuk 54538, Korea, Tel: +82-63-850-6714, Fax: +82-63-857-7204, stjeong@wku.ac.kr

Received 2017 December 12; Revised 2018 February 23; Accepted 2018 February 23.

Abstract

축대칭 진동수주형 부유식 파력발전의 성능을 평가하기 위하여 PTO를 고려한 선형화된 자유수면경계조건을 유도하여 유한요소 수치모델을 수립하였다. 발전효율에 영향을 미칠 것으로 판단되는 동력인출장치(PTO)가 설치되는 실린더내 수주의 공진현상과 부유체의 heave 공진현상에 직접적으로 영양을 줄 수 있는 설계변수인 실린더 및 스커트 길이, 그리고, 수심을 변화시키며 수치실험을 실시하여 발전시스템의 최적설계에 필요한 기초 자료를 확보하였다. 연구결과, 발전시스템의 효율은 실린더내 진동수주의 공진보다는 부유체의 heave 운동 공진에 지배되며, 부이 외측에 스커트를 부착함으로써 효율적으로 공진조건을 변화시킬 수 있음을 확인하였다.

Trans Abstract

In order to evaluate the performance of the floating wave power, which is an axisymmetric oscillating water column type, linearized free surface boundary condition considering the influence of PTO (power takeoff) was derived and a finite element numerical model was established. Numerical experiments were carried out by varying cylinder length, skirt length, and depth of water, which are design parameters that can change the resonance of water column in cylinder and heave resonance of the float, which is considered to affect the power generation efficiency. Finally, the basic data necessary for the optimum design of the power generation system were obtained. As a result, the efficiency of the power generation system is dominated by the heave motion resonance of the float rather than the water column resonance in the cylinder, and the resonance condition for the heave motion can be changed efficiently by attaching the skirt to the outside of the buoy.

Keywords: 부유식 파력발전; 동력인출장치; 진동수주; heave; 공진; 유한요소법

Keywords: floating wave power; PTO; oscillating water column; heave; resonance; finite element method

1. 서 론

미래의 불투명한 에너지 정세에 대처하기 위해서는 기존 에너지자원의 효율적인 이용은 물론, 새로운 에너지 개발 또는 자연에너지를 활용하는 등 에너지원의 다양화 및 절대량을 확보할 필요가 있다. 특히 전 세계적으로 기후변화협약에 따라 지구온난화를 유발하는 온실가스에 대한 배출 규제가 점차 강화됨에 따라 공해문제가 없는 청정에너지원 확보의 필요성이 커지고 있어, 기존의 화석연료를 대체할 수 있는 무공해 에너지원으로 태양열, 지열, 바람, 해양의 조석, 조류, 파랑 등 같은 천연 에너지 분야가 연구 · 검토되고 있다(KORDI, 2001; Koo et al., 2010; Douglas-Westwood, 2011; Oh et al., 2015).

파랑에너지는 조석에너지 및 조류에너지와 함께 대표적인 해양에너지원 중의 하나로 꼽힌다. 파랑에너지를 이용하는 파력발전은 파랑의 운동 및 위치에너지를 이용하여 터빈을 구동하거나 기계장치의 운동으로 변환하여 전기를 생산하는 기술로써 파고가 높고 파주기가 긴 해역이 적지이다. 발전 방식은 작동 원리에 따라 가동물체형, 진동수주형, 월파형으로, 설치형태에 따라서는 착저식과 부유식으로 구분된다(Ryu et al., 2006; JODCA, 2006; Joao, 2008; Lee, 2014). 본 연구에서는 Fig. 1과 같이 일본에서 등부표에 활발히 실용화를 추진하고 있는 부유식 진동수주형을 대상으로 하였다.

Fig. 1.

Axisymmetric floating wave power device with an oscillating water column in the cylinder (Source: Ryokusei).

진동수주형은 파랑에너지를 공기의 유동에너지로 1차 변환하고, 이를 공기 터빈을 사용하여 기계적인 회전 에너지로 2차 변환한다. 2차 변환장치인 공기터빈은 웰스(Wells)터빈, 임펄스(Impulse)터빈 등이 사용되며, 이 같은 진동 수주 방식의 발전 모델은 Masuda and Miyazaki(1979)에 의해 처음 제안된 이후 많은 연구자들이 효율 향상을 위한 다양한 연구를 수행하였다. 최근, Koo et al.(2010)은 고정식 진동수주형 파력발전장치의 챔버 유동 및 파에너지 변환효율 연구를 수행한 바 있으며, Koo et al.(2012)은 수리 실험을 통하여 기본적인 형상 인자들의 영향을 파악하였다. Kim et al.(2012)은 부유식 진동수주형 파력발전기(BBDB)의 유체 동역학적 성능 실험 연구를 수행하였다. 수치적 성능해석에는 경계요소법(Koo et al., 2010, 2012; Kim et al., 2012)과 유한요소법이 주로 사용되는데(Kyoung et al., 2006; Seo et al., 2016), 본 연구에서는 구조해석과 직접적으로 연계가 가능한 유한요소법을 채택하였다.

유한요소법을 이용하여 진동수주형 축대칭 부유식 파력발전 장치의 성능평가를 효율적으로 수행하기 위하여 선형포텐셜 이론을 적용하였으며, PTO의 영향을 고려하기 위하여 추출 에너지를 고려한 자유수면 경계조건을 도출하여 적용하였다. 유동장은 등매개변수 요소로 이산화하였으며, 무한원방에서의 방사경계조건은 무한요소로 모델링하였다. 구조물의 축대칭성을 이용하여 속도포텐셜을 Fourier 급수로 표시함으로써 3차원 문제를 2차원문제로 변환하여 수치해석을 간편화하였다(Park et al., 1989).

2. 문제의 정식화

2.1 지배방정식 및 경계조건

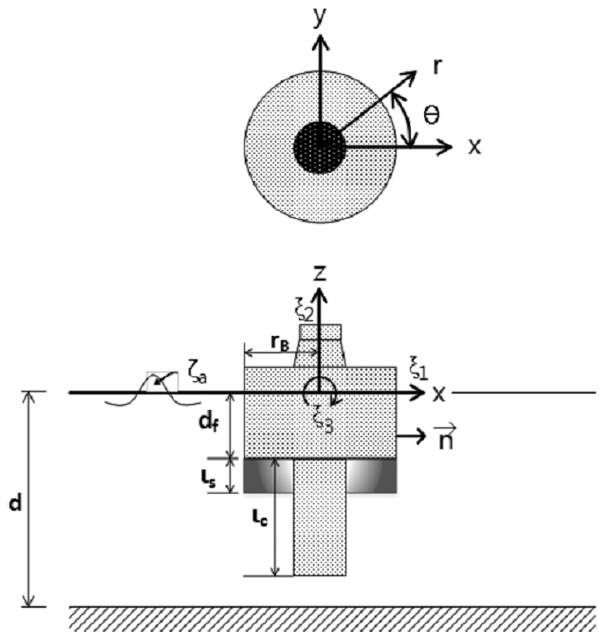
파고가 ζ_a이고 진동수가 ω인 정현파가 수심 d에 위치한 연직 축대칭 진동수주형 부유식 파력발전 구조물에 입사할 경우를 검토하였다. Fig. 2에서 r_B는 부이 반지름, d_f는 부이 흘수, l_s는 스커트 길이, l_c는 실린더 길이를 나타낸다. 에너지 변환효율을 해석하기 위하여, 유체를 비압축성, 비점성임을 가정하고, 비회전류이며, 입사파고가 충분히 작다는 가정을 하는 선형포텐셜이론을 채택하였다. 즉, 유동장은 다음과 같이 Laplace 방정식을 만족하는 속도포텐셜, Φ로 나타낼 수 있으며,

Fig. 2.

Definition sketch.

(1) ∇2Φ(r,θ,z;t)=0

자유수면(S_f), 유동장의 바닥면(S_d), 물체의 표면(S_b)에서 경계 조건은 다음과 같이 선형으로 주어진다.

(2)

(3)

(4)

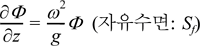
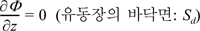
여기서, V_n은 물체표면에서의 유체영역으로 향하는 수입자의 수직속도 성분을 의미하며, ω는 입사파의 진동수를, g는 중력가속도를 나타낸다.

전체 포텐셜에서 입사파를 제외한 방사파 및 회절파의 포텐셜, Φ_s는 무한원방에서 다음의 방사경계조건을 만족하여야 한다.

(5)

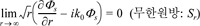
여기서, k₀는 입사파의 파수를 의미하며, i는 -1 을 나타낸다.

발전터빈이 설치되는 부유체 중앙의 실린더 내의 자유수면 조건은 부유체 외부의 자유수면 조건과 다르다. 즉, PTO에 의해 자유수면 활동이 제약을 받게 되고, 실린더 하단의 유입구에서의 유체 점성에 의한 감쇠가 발생하게 된다. 특히, 실린더내 공진조건 부근에서 점성에 의한 감쇠가 중요한 영향을 미치기 때문에 이의 영향을 적절히 고려해야 한다. 이러한 현상을 효율적으로 고려하기 위하여 Koo et al.(2010)이 제시한 비선형 운동학적 조건과 동역학적 조건을 다음과 같이 선형화하여 적용하였다.

(6) ∂Φ∂z=ω2g−iωρ(Cdm+v)Φ−ω2ρCdmg−iωρ(Cdm+v)ξ2

여기서, C_dm은 PTO에 의한 에너지 추출에 관련된 추출계수이며, ν는 유체의 점성에 관련된 계수이다.

식(1)~(6)의 경계치 문제는 선형이기 때문에, 입사파가 고정된 부유체에 부딪혀 발생한 회절파가 관련되는 회절문제(diffraction problem)와 부유체의 각 방향 운동에 의해 발생되는 방사파에 관련된 방사문제(radiation problem)로 분리할 수 있고, 전체 포텐셜, Φ는 각 성분파에 관한 포텐셜의 합으로 표시할 수 있다. 즉,

(7) Φ=(ϕ0+ϕ4+∑j=13ϕj⋅ξj)e−iωt

로 표현되며, φ₀는 입사파에 의한 성분, φ₄는 회절파에 의한 성분, φj는 j-방향운동에 관련된 방사파에 의한 성분을 나타낸다.

2.2 파력

유체의 동압력, p(r, θ z; t)는 선형화된 Bernoulli 방정식으로부터 다음과 같이 구할 수 있다.

(8) p=Re[−ρ∂Φ∂t]=Re[iρω(ϕ0+ϕ4+∑j=13ϕjξj)e−iωt]

여기서, Re(·)는 괄호안 복소수의 실수부를 나타낸다. 수평, 수직하중 및 원점에 대한 모멘트 등의 각 방향하중은 압력을 물체표면에 대해서 적분함으로써 구할 수 있다.

(9) Fj=−∫sbpnjdSb=Re[(Fje+∑k=13Fjkrξk)e−iωt](j=1,2,3)

여기서, Fje 는 φ₀ + φ₄에 관련된 파랑기진력을 의미하며, Fjkr 는 방사포텐셜, φ_k에 관련된 힘으로 부가질량계수, a_jk와 파랑감쇠계수, b_jk로 나타낼 수 있다.

(10a) Fje=−iωρ∫sb(ϕ0+ϕ4)njdSb

(10b) Fjkr=−iωρ∫sbϕknjdSb =−ω2ajk−iω⋅bjk

(11a)

(11b) bjk=−1ωIm[Fjkr]

Im(·)는 각각 괄호안 복소수의 허수부를 의미한다.

한편, 부유체에 작용하는 파력은 동수압에 의한 파력 외에, 실린더내 PTO를 통하여 부유체에 전달되는 파력이 있다. 이 파력은 다음과 같이 표현되는 실린더내의 공기압(Koo et al., 2010)을 적분함으로써 구할 수 있다.

(12) pa=Cdm{∂ϕ0∂z+∂ϕ4∂z+∑j=13∂ϕj∂zξj+iωξ2}

2.3 부유체 동적 응답

부유체의 동적응답은 다음의 운동방정식으로부터 구할 수 있다.

(13) ∑j=13−ω2(mij+aij)ξj−iω(cij+bij)ξj+kijξj=Fie

여기서, m_ij, c_ij, k_ij는 부유체의 질량, 감쇠 및 강성 행렬 계수이며, ξ_j는 부유체의 각 방향 운동 진폭을 나타낸다.

2.4 실린더내 수면 변위 및 속도

실린더내 수면 변위 진폭, ηa는 동역학적 경계조건과 식(6)을 이용하면 다음과 같이 표현된다.

(14) ηa=iωg−iωρ(Cdm+ν)(ϕ0+ϕ4+∑j=13ϕiξj) −iωρCdmg−iωρ(Cdm+ν)ξ2

수면 변동 속도 진폭, η_av는

(15) ηav=−iωηa

2.5 에너지 추출효율

실린더내 설치된 PTO에 의한 에너지 추출효율, η_e는 입사파 에너지와 식(12)의 공기압에 의한 에너지 추출된 에너지의 비로 나타낼 수 있다(Koo et al., 2010). 즉,

(16a) ηe=EAPEW

(16b) EW=12ρgζa2Cg

(16c) EAP=12CdmAcω2|ηa−ξ2|2

C_g는 입사파의 그룹속도이며, A_c는 실린더 단면적을 나타낸다.

3. 수치해석 및 결과분석

3.1 수치해석

파력발전시스템은 공진효과를 이용하면 발전효율을 높일 수 있다. 즉, 파 에너지가 많이 모여 있는 주기대에 발전시스템의 공진조건을 맞추면 고효율로 에너지 추출이 가능하다. 대상으로 하고 있는 축대칭 진동수주형 부유식 발전시스템은 두가지 공진조건이 있다. 하나는 실린더 내 수주의 공진이고, 다른 하나는 부유체의 공진(특히, heave 운동 공진)이다. 이 두 공진조건을 적절히 조화하여 설계한다면 발전효율을 극대화할 수 있다. 따라서, 본 연구에서는 형상변화를 통화여 이 두 공진조건이 어떻게 변하는지와 발전효율에는 어떤 영향을 주는지를 알아 보기위하여 Table 1에 보인 바와 같은 다양한 구조형상에 대하여 수치해석을 실시하였다. Case 1은 PTO 공기터빈이 설치되는 실린더의 길이(흘수심)를 변화시켜 진동 수주의 공진조건을 변화시킨 것이고, Case 2는 부유체 하단에 스커트를 둠으로써 부유체의 공진조건을 변화시킨 것이고, Case 3은 이 둘을 병합한 것이다. Case 4는 수심의 영향을 살펴보기 위한 것이다. 본 수치해석에서는 계류시스템의 영향을 배제한 자유부유(free floating)된 경우를 대상으로 하였다.

Table 1.

Cases for numerical experiments

식(1)~(6)으로 주어지는 경계치 문제를 풀기 위하여 유한요소법을 이용하였다. 구조물의 축대칭성을 이용하여 3차원 문제를 2차원 문제로 단순화하여 푸는 Park et al.(1989)이 개발한 수치모델을 이용하였다. 식(6)의 실린더 내의 자유수면 경계조건을 고려할 수도 있도록 기존 모델을 확장하여 적용하였다.

Fig. 3에 수치실험에 사용한 유한요소망도를 제시하였다. 부유체 주변의 유체영역은 8절점 등매개변수 요소로 모형화하였으며, 외해 영역은 산란파의 거동을 효율적으로 모의할 수 있는 무한요소로 이산화하였다.

Fig. 3.

Finite element mesh for Case1 (c-3-0-10).

PTO가 실린더 내에 설치되면 없는 경우에 비하여 수주의 공진에 의한 수위증폭이 대폭 제한되며, 부유체 운동도 크게 영향을 받는다. 특히, heave 방향의 부가질량이 증대되어 heave 공진조건이 변화를 일으킨다. 이러한 현상을 살펴보고 발전시스템의 최적설계를 위하여 PTO가 없는 경우와 있는 경우로 구분하여 수치실험을 실시하였다.

3.2 결과분석

공진시 응답이 적정 수준으로 제한시키기 위하여 부유체 운동 및 실린더내 수위의 변동에 인위적으로 감쇠를 부가하였다. 부유체의 surge 및 heave 운동 감쇠는 heave 운동의 임계감쇠의 10%를, pitch 운동은 pitch 임계감쇠의 25%를 적용하였다. 실린더내 수위 감쇠를 위해서 유체의 점성계수 ν를 300으로 설정하였다(Case 1에서 실린더 길이 3 m일 때 실린더내 수위증폭을 입사파고의 4배 이내로 제한). 수치해석은 무차원 주파수(ω²r_B/g)를 0.02~1.2까지 변화시켜가며 실시하였다. PTO가 공진에 미치는 영향에 대하여 살펴보기 위하여 PTO가 설치되지 않은 경우(C_dm = 0)에 대한 해석도 병행하였다.

3.2.1 PTO가 없는 경우

① 실린더 길이(l_c) 변화 영향: Case 1

단면이 일정한 수로내의 진동수주의 공진은 수주의 길이와 직접적으로 관계된다. 즉, 공진주기, T_n은 다음과 같이 표현된다.

(17) Tn=2πlc+dfg

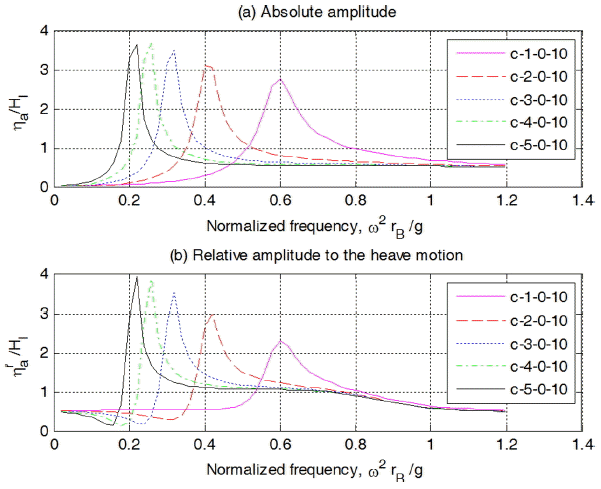
여기서, l_c는 실린더 길이, d_f는 흘수심이며, g는 중력가속도이다. 따라서, 수치해석을 수행한 Case 1의 경우, 실린더 1 m인 경우는 공진주기가 2.8초, 2 m인 경우는 3.5초, 3 m인 경우는 4.0초, 4 m인 경우는 4.5초, 5 m인 경우는 4.9초가 된다.

Fig. 4에 나타낸 실린더내 수위변화를 보면, 수주 공진조건 부근(긴 주기 방향으로 약간 치우침)에서 증폭 현상이 발생함을 알 수 있다. 부유체 운동(heave)에 대한 상대 수위변화도 살펴보면 같은 경향을 볼 수 있다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 5를 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다. 그림에서 H_I = 2ζ_a이다.

Fig. 4.

Amplitudes of the free surface fluctuation in the cylinder for Case 1 without PTO.

Fig. 5.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 1 without PTO.

② 부유체 하단 부착 스커트 길이 변화 영향: Case 2

부유체의 공진주기 특히, heave 공진주기, T_n2은 다음과 같이 표현된다.

(18) Tn2=2πmB+a22k22

여기서, m_B는 부유체의 질량이며, a₂₂는 공진조건에서의 연직방향 부가질량이고, k₂₂는 부유체의 연직방향 강성계수를 나타낸다. 일반적으로 스커트의 길이, l_s가 길어지면 부가질량이 크게 발현된다.

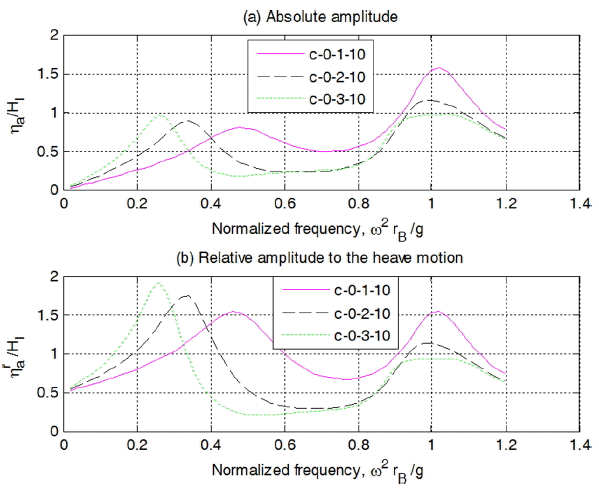
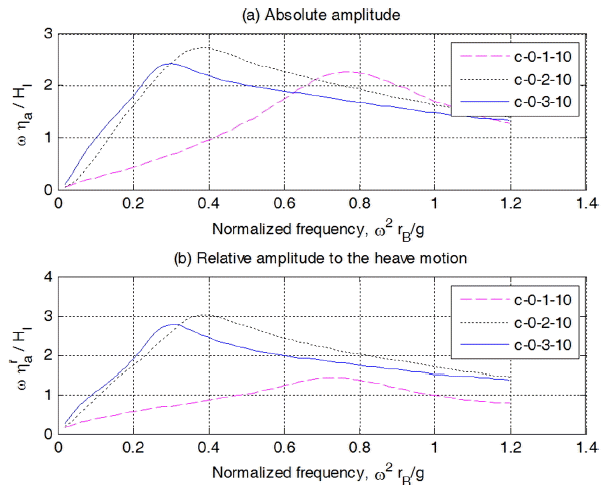
Fig. 6에 나타낸 실린더내 수위변화를 보면, 무차원 주파수 1.0 부근에 피크가 있고, l_s가 1 m인 경우는 0.44, 2 m인 경우는 0.32, 3 m인 경우는 0.26 부근에서 낮은 피크가 발생함을 알 수 있다. 이는 부유체의 heave 운동 공진에 기인된 것으로, l_s가 길어질수록 부가질량이 증가하여 공진조건이 긴 주기쪽으로 이동함을 알 수 있다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 7을 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 6.

Amplitudes of the free surface fluctuation in the cylinder for Case 2 without PTO.

Fig. 7.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 2 without PTO.

③ 스커트 길이 3 m일 때 실린더 길이 변화 영향: Case 3

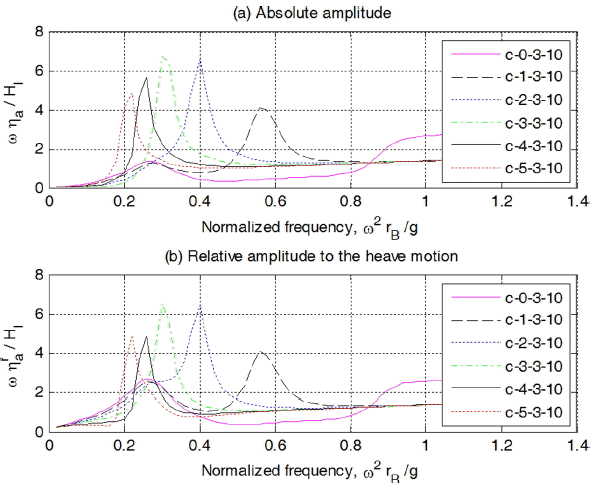
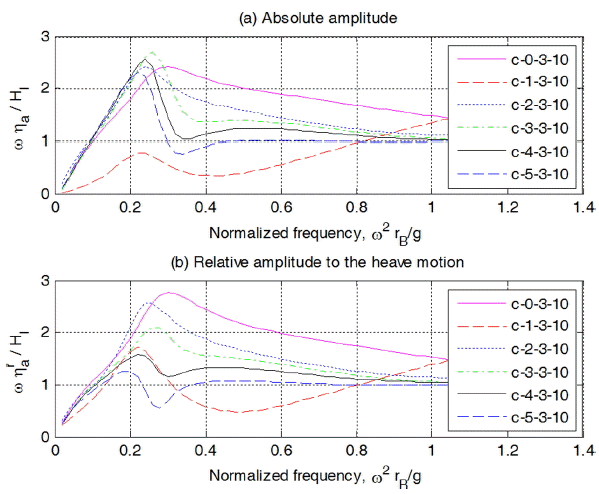
스커트 길이가 3 m일 때 실린더의 길이 변화에 대한 해석결과를 Fig. 8에 나타내었다. l_c가 1 m인 경우는 무차원 주파수 0.56, 2 m인 경우는 0.4, 3 m인 경우는 0.3, 4 m인 경우는 0.26, 5 m인 경우는 0.22에서 낮은 피크가 발생함을 알 수 있다. 이는 부유체의 heave 방향 공진에 기인된 것이다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 9를 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 8.

Amplitudes of the free surface fluctuation in the cylinder for Case 3 without PTO.

Fig. 9.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 3 without PTO.

④ 수심변화 영향

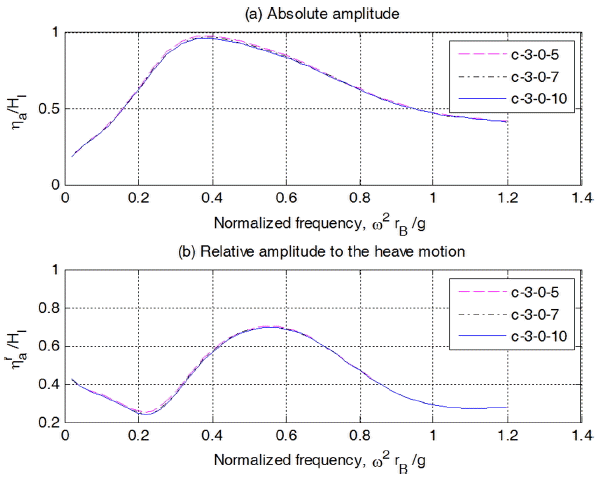
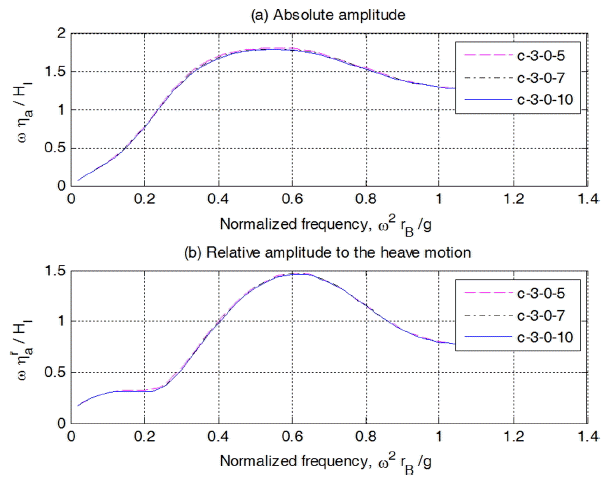
실린더 길이 3 m, Case 1의 경우, 수심을 5 m, 7 m, 10m로 변화시켰을 경우의 해석결과를 Fig. 10에 제시하였다. 그림을 보면 수심의 영향은 거의 없음을 알 수 있다. 특히, 현재 대상으로 하고 있는 파조건이 주기가 짧아 수심의 영향은 극히 미미한 것으로 제시되었다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 11을 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 10.

Amplitudes of the free surface fluctuation in the cylinder for Case 4 without PTO.

Fig. 11.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 4 without PTO.

3.3.2 PTO가 있는 경우

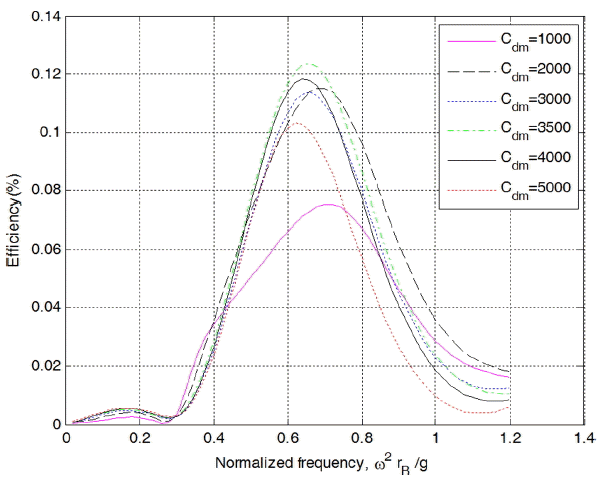
최고의 효율을 주는 PTO를 고려하여 수치실험을 하기 위하여, 실린더 길이 3 m의 Case 1을 대상으로 하여 C_dm을 변화시키며 해석한 결과, 최적의 C_dm을 도출하였다(Cdm = 3,500일 때 최대 효율 12.4%, Fig. 12 참조). 다른 케이스의 경우도 같은 결과를 주는지는 여부는 확인해 보아야 하지만, 유사할 것으로 판단되어 최적의 Cdm은 3,500으로 설정하고 수치실험을 수행하였다.

Fig. 12.

Efficiency of energy extraction for Case 1 with 3 m of cylinder length.

① 실린더 길이(l_c) 변화 영향: Case 1

Fig. 13에 실린더내 수위변화를 제시하였다. Fig. 4의 PTO가 없는 경우에 비하면 수위증폭이 상당히 제한되었음을 알 수 있으며, 고주파수 영역에서 진동수주의 공진과는 벗어나는 새로운 피크가 나타남을 알 수 있다. 이 피크는 PTO에 의해 발생된 부가질량에 기인한 것으로 부유체의 heave 공진조건이 이동하여 발생된 것이다. PTO와의 상호작용이 중요함을 나타내는 결과이다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 14를 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 13.

Amplitudes of the free surface fluctuation in the cylinder for Case 1 with PTO.

Fig. 14.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 1 with PTO.

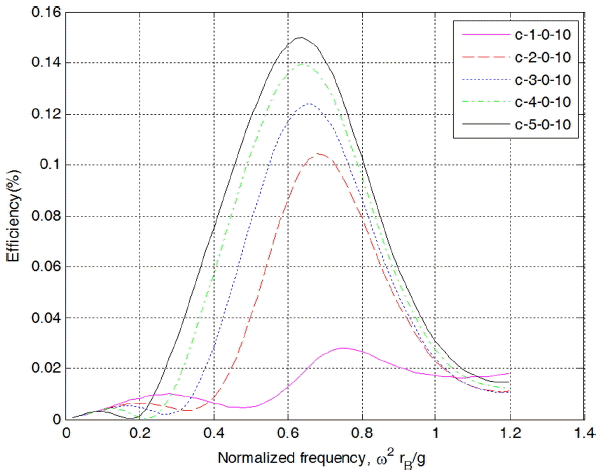
Fig. 15에 나타낸 것은 에너지 추출효율(식(16))로, 실린더 길이가 길어질수록 효율이 높아짐을 나타내고 있고, 모든 경우 무차원 주파수 0.68 근처에서 최대치가 발생하는 특징을 확인할 수 있다.

Fig. 15.

Efficiency of energy extraction for Case 1.

② 부유체 하단 부착 스커트 길이 변화 영향: Case 2

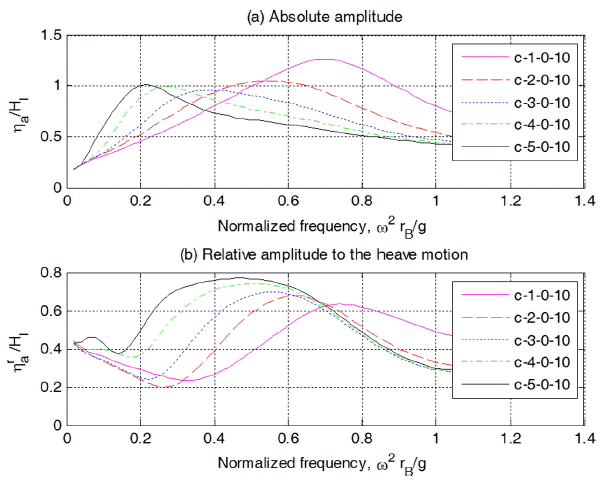
Fig. 16에 나타낸 실린더내 수위변화를 보면, PTO가 없을 때 무차원 주파수 1.0 부근에 발생한 피크는 사라지고, l_s가 1 m인 경우는 0.74, 2 m인 경우는 0.34, 3 m인 경우는 0.28 부근에서 낮은 피크가 PTO가 없을 때와 유사하게 발생함을 알 수 있다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 17을 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 16.

Amplitudes of the free surface fluctuation in the cylinder for Case 2 with PTO.

Fig. 17.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 2 with PTO.

③ 스커트 길이 3 m일 때 실린더 길이 변화 영향: Case 3

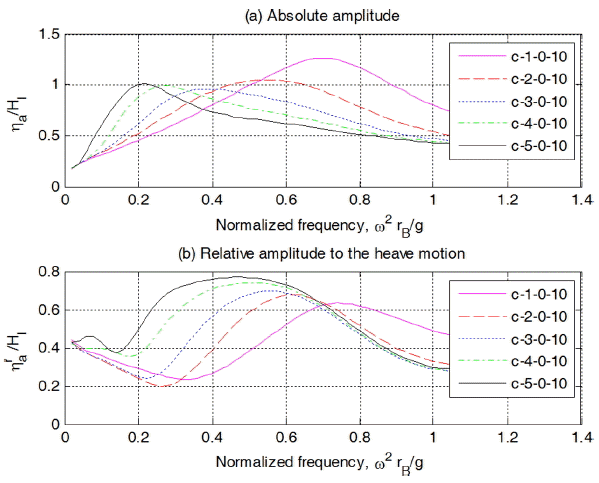
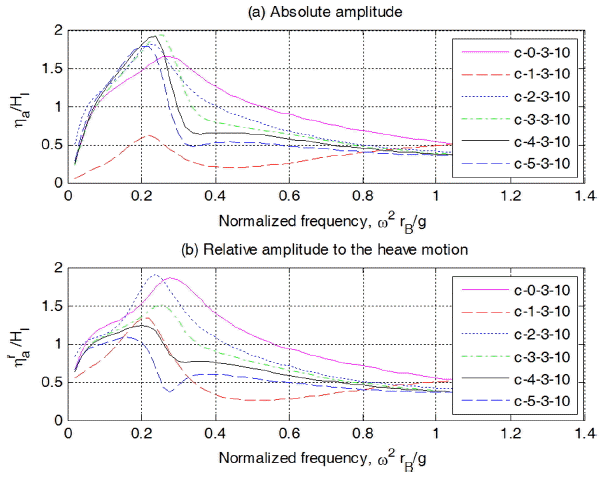
스커트 길이가 3 m일 때 실린더의 길이 변화에 대한 해석결과를 Fig. 18에 나타내었다. l_c가 1 m인 경우는 무차원 주파수 0.22, 2 m인 경우는 0.22 3 m인 경우는 0.24, 4 m인 경우는 0.22, 5 m인 경우는 0.22에서 피크가 발생함을 알 수 있다. 이는 부유체의 heave 방향 공진에 기인된 것이다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 19를 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 18.

Amplitudes of the free surface fluctuation in the cylinder for Case 3 with PTO.

Fig. 19.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 3 with PTO.

④ 수심변화 영향

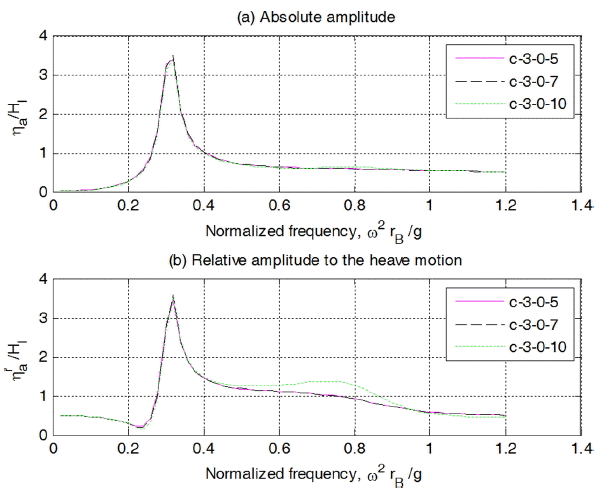
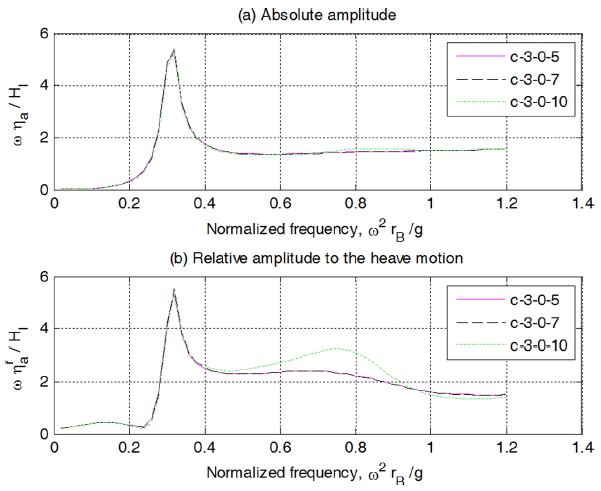
실린더 길이 3 m, Case 1의 경우, 수심을 5 m, 7 m, 10 m로 변화시켰을 경우의 해석결과를 Fig. 20에 제시하였다. 그림을 보면 수심의 영향은 거의 없음을 알 수 있다. 특히, 현재 대상으로 하고 있는 파조건이 주기가 짧아 수심의 영향은 극히 미미한 것으로 제시되었다. 실린더내 수위 속도 및 상대속도 변화를 나타낸 Fig. 21을 보면 수위의 경우와 같은 경향을 나타냄을 알 수 있다.

Fig. 20.

Amplitudes of the free surface fluctuation in the cylinder for Case 4 with PTO.

Fig. 21.

Velocity amplitudes of the free surface fluctuation in the cylinder for Case 4 with PTO.

4. 결론 및 토의

축대칭 진동수주형 부유식 발전시스템의 성능을 평가하기 위하여 PTO 영향을 고려한 선형화된 자유수면경계조건을 유도하였으며, 이를 Park et al.(1989)이 개발한 유한요소모델에 반영하여 수치모델을 수립하였다. 발전시스템의 최적설계에 필요한 기초 자료를 확보하기 위하여 발전효율에 영향을 미칠 것으로 판단되는 PTO가 설치되는 실린더내 수주의 공진현상과 부유체의 heave 공진현상에 변화를 줄 수 있는 설계변수를 변화시키며 수치실험을 실시하였다. 수치실험을 통하여 도출된 주요결과를 요약하면 다음과 같다.

- 실린더내의 진동수주의 공진조건은 실린더 길이(l_c)와 흘수심(d_f) 조정을 통하여 변화시킬 수 있으며, 단면이 일정한 실린더내 진동수주의 공진주기, T_n은 2πlc + df/g로 추정할 수 있다.

- 부유체의 하단에 스커트 길이 조정을 통하여 부유체의 heave 운동 공진조건을 변화시킬 수 있다. 스커트 길이를 길게 하면 부가질량이 증가하여 공진주기가 길어진다.

- 축대칭 진동수주형 부유식 발전시스템의 효율은 실린더 내 진동수주의 공진보다는 부유체의 heave 운동 공진이 지배적인 역할을 한다.

- 본 연구에서는 수심을 5, 7, 10 m로 변경하여 발전량 변화를 파악하였으나, 그 효과는 나타나지 않았다. 이는 현재 대상으로 하는 파의 주기가 짧아 수심 변화에 따른 파의 변화가 미미한 결과로 이해될 수 있다. 다만, 더욱 얕은 수심에 발전구조물을 설치하여 입사파의 천수효과를 부각시킨다면 발전 성능 증대 효과를 기대할 수 있다. 또, 발전구조물을 크게 하여 천해조건의 파랑주기에 맞게 공진조건을 설정하는 경우에는 수심효과 영항이 다소 증대될 수 있다.

- 발전량을 극대화하기 위해서는 유체 점성에 의한 감쇠와 부유체의 구조적 감쇠를 최소화할 필요가 있으며, 수치적으로 발전효율을 평가할 때는 이 감쇠를 적절히 고려할 필요가 있다.

본 논문에서 도출한 결과는 향후 고정도의 수치해석 결과와의 비교 등을 통해 검증할 예정이다.

Acknowledgements

본 연구는 해양수산부 해양청정에너지기술 개발 사업인 “항로표지 등부표용 파력발전시스템 형상 최적화에 관한 연구(과제번호: 20170323)”와 한국해양과학기술진흥원 미래해양산업기술개발 해양중소벤처지원사업인 “콘크리트 쉬라우드를 이용한 조류발전시스템 연구(과제번호: 20170122)”의 지원으로 수행되었습니다. 연구지원에 감사드립니다.

References

Douglas-Westwood. 2011;The World Wave & Tidal Report 2011–2015.

Hong K, Shin S-H, Hong D-C. 2007;Wave energy absorption efficiency of pneumatic chamber of OWC wave energy converter. J. of the Korean Society for Marine Environmental Engineers 10(3):173–180. (in Korean).

Hong K-Y, Ryu H-J, Shin S-H, Hong S-W. 2004;Wave energy distribution at Jeju Sea and investigation of optimal sites for wave power generation. J. of Korean Society of Ocean Engineers 18(6):8–15. (in Korean).

Japan Ocean Development Construction Association. 2006. Ocean energy development technology in the 21st century (in Japanese).

Cruz Joao. 2008. Ocean Wave Energy: Current Status and Future Prespectives Springer.

Kim S-J, Kwon J, Kim J-D, Koo W, Shin S, Kim K. 2012;Experimental study of hydrodynamic performance of backward bent duct buoy (BBDB) floating wave energy converter. J. of Ocean Engineering and Technology 26(6):53–58. (in Korean).

Koo W-C, Kim M-H, Choi Y-R. 2010;Numerical analysis of chamber flow and wave energy conversion efficiency of a bottom-mounted oscillating water column wave power device. J. of the Society of Naval Architects of Korea 47(3):388–397. (in Korean).

Koo W-C, Kwon J-S, Kim J-D, Kim S-J, Kim M-W, Choi M-K. 2012;Experimental study of shape parameter of land-based OWC wave energy converter. J. of Korean Society of Ocean Engineers 26(3):33–38. (in Korean).

KORDI (Korea Ocean Research and Development Institute). 2001. Coastal Development (in Korean).

Kyoung J-H, Hong S-Y, Hong D-C. 2006;Numerical analysis on wave energy absorption of OWC-type wave power generation. J. of Korean Society of Ocean Engineers 20(4):64–69.

Lee M. 2014. Renewable and Ocean Energy Engineering (in Korean).

Nam BW, Hong SY, Kim K-B, Park J, Shin S-H. 2011;Numerical analysis of wave-induced motion of floating pendulor wave energy convertor. J. of Korean Society of Ocean Engineers 25(4):28–35. (in Korean).

Oh NS, Jeong ST, Ko DH. 2015;Experimental study for wave energy convertor using floating light buoy. Journal of Korean Society of Coastal and Ocean Engineers 27(1):50–55. (in Korean).

Park JY, Shin SH, Hong KY. 2011;Experimental study for overtopping performance and control system of overtopping wave energy convertor. J. of the Korean Society for Marine Environmental Engineering 14(1):11–18. (in Korean).

Park WS, Yun CB, Pyun CK. 1989;Infinite elements for the evaluation of wave forces. Journal of Korean Society of Coastal and Ocean Engineers 1(1):71–80. (in Korean).

Ryu CR, Hong S-W, Kim H-J, Kang Y-K. 2006. Ocean Energy Engineering (in Korean).

Ryu H-J, Shin S-H, Hong K-Y, Hong S-W, Kim D-Y. 2007;A simulation of directional irregular waves at Chagui-Do Sea area in Jeju using the Boussinesq wave model. J. of Korean Society of Ocean Engineers 21(1):7–17.

Shin S-H, Hong K. 2005;Experimental study on wave overtopping rate of wave overtopping control structure for wave energy conversion. J. of Korean Society of Ocean Engineers 19(6):8–15. (in Korean).

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Case	Cylinder length, l_c (unit : m)	Skirt length, l_s (unit : m)	Water depth, d (unit : m)	Notation	Remarks
1	1, 2, 3, 4, 5	0	10	c − 1 − 0 − 10	5 cases
				c − 2 − 0 − 10
				c − 3 − 0 − 10
				c − 4 − 0 − 10
				c − 5 − 0 − 10

2	0	1, 2, 3	10	c − 0 − 1 − 10	3 cases
				c − 0 − 2 − 10
				c − 0 − 3 − 10

3	0, 1, 2, 3, 4, 5	3	10	c − 0 − 3 − 10	6 cases
				c − 1 − 3 − 10
				c − 2 − 3 − 10
				c − 3 − 3 − 10
				c − 4 − 3 − 10
				c − 5 − 3 − 10

4	3	0	5, 7, 10	c − 3 − 0 − 5	3 cases
				c − 3 − 0 − 7
				c − 3 − 0 − 10