비정수압 수치모형을 이용한 다공성 구조물의 유동에 관한 수치적 연구

A Numerical Study on Flow in Porous Structure using Non-Hydrostatic Model

Article information

J Korean Soc Coast Ocean Eng. 2018;30(3):114-122

Publication date (electronic) : 2018 June 30

doi : https://doi.org/10.9765/KSCOE.2018.30.3.114

Choong Hun Shin ^*, Sung Bum Yoon^,^**

^*Industry-University Cooperation Foundation, ERICA Campus, Hanyang University

^**Dept. of Civil and Env. Engrg., ERICA Campus, Hanyang University

신충훈^*, 윤성범^,^**

^*한양대학교 ERICA 산학협력단

^**한양대학교 건설환경공학과

Corresponding author: Sung Bum Yoon, Dept. of Civil and Env. Engrg., ERICA Campus, Hanyang University, 55 Hanyangdaehak-ro, Sangnok-gu, Ansan, Gyeonggi-do 15588, Korea, Tel: +82-31-400-5144, Fax: +82-31-436-8147, sbyoon@hanyang.ac.kr

Received 2018 May 4; Revised 2018 June 7; Accepted 2018 June 19.

Abstract

본 연구는 다공성 구조물과의 파랑의 상호 작용을 수치모의하기 위한 비정수압 수치모형인 SWASH를 소개한다. 이 수치모형은 σ-좌표계에 Volume Averaged Reynolds Averaged Navier-Stokes(VARANS)을 지배방정식으로 다공성 매체에서의 유동을 계산한다. 다공성 매체에서의 유동을 고려하기 위해 사용된 경험적 저항 계수는 보정 작업이 필요하다. 본 연구에서는 수치모형에 사용된 경험적 저항 계수를 다공성 매체를 통과하는 댐 붕괴 실험과 다공성 구조물과 고립파의 상호 작용에 대한 실험을 이용하여 보정 및 검증하였다. 실험 결과와 수치실험 결과는 비교적 잘 일치하는 것으로 나타났다. 또한 비정수압 수치모형인 SWASH가 VOF 접근법을 기반으로 하는 3차원 다공성 유동 모델보다 계산상 훨씬 더 효율적이라는 것이 확인되었다.

Trans Abstract

This paper introduces a non-hydrostatic wave model SWASH for simulating wave interactions with porous structures. This model calculates the flow in porous media based on volume-averaged Reynolds-averaged Navier-Stokes equations (VARANS) in σ-coordinate. The empirical coefficients of resistance used to account for the flow in a porous media often need to be measured or calibrated. In this study, the empirical resistance coefficients used in the model are calibrated and validated using laboratory experiments, involving dam-break flow through porous media, and solitary wave interactions with a porous structure. It is shown that the agreement between experimental and numerical results is generally satisfactory. It is also confirmed that non-hydrodynamic model, SWASH, is computationally much more efficient than the three-dimensional porous flow models based on VOF approach.

Keywords: 다공성 구조물; 다공성 유동; 비정수압 수치모형; SWASH

Keywords: porous structure; porous flow; non-hydrostatic model; SWASH

1. 서 론

다공성 구조물(porous structure)은 외해로부터 내습하는 파랑의 영향을 줄이고, 파랑 및 조류에 의한 표사 이동의 방지를 목적으로 폭넓게 활용되는 구조물이다. 특히 연안 및 해안지역의 경사식 방파제는 소파블록, 쇄석 등을 활용한 대표적인 다공성 구조물로 외해로부터 내습하는 파랑의 에너지를 소산시키기 위해 자주 사용된다.

다공성 구조물을 통과하는 파의 전파에 대한 Madsen(1974)의 연구 이후 지난 수십 년 동안 다공성 구조물과 파랑의 상호작용에 대한 많은 연구가 수행되었다. 그 과정에서 다공성 구조물과 파랑의 상호작용을 시뮬레이션하기 위해 많은 수치모형이 개발되었다. 다공성 물질과 관련된 매개변수에 대한 근본적인 연구는 van Gent(1994)에 의해 수행되었다. 이후 van Gent(1995)는 비선형 천수방정식에 다공성 항력 모델(porous drag model)을 추가하여 1개의 투수층 위를 전파하는 경우에 대해 해석 가능한 비선형 천수방정식을 유도하였다. 이후 다공성 항력 모델은 완경사 방정식(Losada et al., 1996a, b) 및 Boussinesq 방정식(Cruz et al., 1997; Hsiao et al., 2002, 2010; Lynett et al., 2000; Lee et al., 2014; Vu and Lee, 2015; Huynh et al., 2017)과 결합되어 다양한 지배방정식을 활용하는 수치모형들이 개발되었다.

Nam et al.(2002)은 투과성 구조물의 사면상의 처오름 특성에 대한 수리모형실험을 수행하고 Kobayashi and Wurjanto (1992)에 의해 개발된 천수방정식 기반의 수치모형을 이용해 결과를 비교하였다. 천수방정식 기반의 수치모형의 경우 투과성 구조물의 사면상의 처오름 높이를 과소평가하는 경향이 있는 것으로 나타났다. Yoon et al.(2005)은 Navier-Stokes 방정식을 Porous body model에 근거하여 확장한 CADMAS-SURF를 이용해 투과성 구조물의 사면상의 처오름 특성에 대해 연구를 수행하였고 이를 통해 CADMAS-SURF의 적용성을 확인하였다.

Lee et al.(2014)은 투수층이 있는 경우의 확장형 Boussinesq 방정식을 유도하고, 고립파를 이용한 수리모형 실험 결과와 비교적 잘 일치함을 보였다. 최근 Huynh et al.(2017)은 투수층을 전파하는 2개층 Boussinesq 방정식을 유도하고 이를 Navier-Stokes 방정식(CADMAS-SURF)을 이용한 결과와 비교하여 유도된 2개층 Boussinesq 방정식이 투수성 매질을 통과하는 파랑 변형을 잘 해석하고 있음을 보였다.

최근에는 Volume of Fluid(VOF) 기법을 도입한 Volume Averaged Reynolds Averaged Navier-Stokes(VARANS) 방정식의 수치모형(Liu et al., 1999; Hsu et al., 2002; Hu et al., 2012; Lara et al., 2012; del Jesus et al., 2012; Higuera et al., 2014; Jensen et al., 2014)을 통해 다공성 구조물 내에서의 흐름을 분석하고 예측하는 연구가 다수의 연구자들에 의해 수행되었다. 국내의 경우 Jung(2014)은 VARANS 방정식의 수치모형을 이용해 다공성 구조물을 통과하는 댐 붕괴파의 전파특성에 대한 연구를 수행하였다. VARANS 방정식의 수치모형의 경우 다공성 구조물 내부 및 외부에서의 수심분포가 수리모형 실험 결과와 잘 일치하는 것으로 나타났다. 또한 Lee et al.(2016), Lee et al.(2018)은 VARANS 방정식을 이용한 오픈소스 기반의 CFD 코드인 OLAFOAM(Higuera et al., 2015)을 활용해 규칙파 및 불규칙파 조건하의 투과성 잠제가 설치된 해역을 대상으로 흐름 및 구조물의 상호작용에 따른 파동장의 특성을 수치해석적으로 분석하였다.

VARANS 방정식을 이용한 수치모형은 다공성 해안 구조물 내부 및 외부에서의 파랑 변형 및 흐름 등의 해석에 있어 비선형 천수방정식과 Boussinesq 방정식에 내재하는 제약을 극복하기 위해 적용될 수 있음이 많은 연구들에 의해 검증되었다. 그러나 정확도 높은 계산 결과를 얻기 위해서는 매우 조밀한 계산 격자를 필요로 하고 그로 인한 계산 시간의 증가로 인해 넓은 공간으로 확장하지 못하는 한계가 있다. 이러한 한계를 극복하고자 최근 계산시간을 단축시키며 정확도 높은 계산을 위해 비정수압(non-hydrostatic) 가정을 이용한 수치모형들이 개발되었으며 그 활용 범위가 넓어지고 있다. 본 연구에서는 다공성 매체 내부를 통과하는 흐름에 대한 비정수압 수치모형인 SWASH 모형의 정확도를 확인하고 다공성 구조물과 파랑의 상호작용에 대해 적용성을 검토하였다.

2. 수치모형

2.1 지배방정식

다공성 매체 내부를 통과하는 흐름은 VARANS 방정식으로 나타낼 수 있다. VARANS 방정식에 대한 자세한 설명은 del Jesus et al.(2012), Jensen et al.(2014), Higuera et al. (2014)를 참조할 수 있으며, del Jesus et al.(2012)가 유도한 VARANS 방정식을 다공성 매체 내부의 저항력을 모아 정리하면 다음과 같이 나타낼 수 있다.

(1) ∂∂xj*uin=0

(2) ∂∂t*uin+ujn∂∂xj*uin=-1ρ∂p∂xi*+gi+∂∂xj*[(ν+νt)∂∂xi*uin]+Ruin

여기서 (i, j) = 1, 2, 3, xi*는 직교 좌표계의 x 방향, u_i는 xi* 방향의 유속, n은 공극률, ρ는 물의 밀도, p는 전압력, g_i는 중력가속도, ν와 ν_t는 층류와 난류 동점성계수이다. 위 식(2)의 마지막 항은 다공성 매체 내부의 저항력을 의미하며 다음과 같다.

(3) R=-ap-bp|u|-cp∂∂t

여기서 a_p는 층류 저항계수, b_p는 난류 저항 계수, c_p는 부가질량의 현상을 포함하는 관성 저항계수이다. u는 유속의 크기로 u=∑iui2와 같다. 여러 연구자들에 의해 저항계수에 대한 다양한 관계식이 제안되었다. 본 연구에서는 van Gent (1994)가 제안한 식을 이용하였으며 각 계수는 다음과 같이 산정된다.

(4) ap=α(1-n)2n2νD502

(5) bp=β(1+7.5KC)1-nn21D50

(6) cp=γ1-nn

여기서 항력 계수(α, β)는 많은 연구자들에 의해 제안된 경험상수로 수치실험이나 수리모형실험을 통해 산정되었으며 다양한 값들이 존재한다(Losada et al., 2016). γ는 경험상수로 0.34를 사용하고(Liu et al., 1999), D₅₀은 다공성 물질의 평균 입경, KC는 Keulegan-Carpenter number로 다공성 매질 내에서의 유체 입자 운동의 특성 길이 규모 비율(characteristic length scale)을 나타내며 KC=uT/(nD50)과 같이 나타낸다. 여기서 T는 파의 주기이다.

VARANS 방정식에서 공극률(n)이 1인 경우 지배방정식은 RANS 방정식으로 변환되고 이는 기존의 SWASH 수치모형의 지배방정식과 동일하다. RANS 방정식을 지배방정식으로 하는 SWASH 수치모형은 불규칙한 수심 변화 고려와 자유수면 변위의 정확한 계산을 위해 연직 방향으로 총 수심에 대한 각 층의 상대적인 비로 층을 나누는 σ-좌표계(Phillips, 1957)를 적용해 RANS 방정식을 계산한다.

(7) t=t*,x=x*,y=y*,σ=z*+hD

여기서 D(x, y, t) = h(x, y) + ζ(x, y, t)는 총 수심, h는 정수위, ζ는 자유수면변위이다. σ-좌표계의 도입으로 인해 매핑 된 계산 영역은 고정 된 직사각형 영역이며 0과 1 사이의 σ 범위에 따라 각각 바닥에서 부터 자유수면을 표현한다. SWASH 모형에 자세한 내용은 Stelling and Zijlema(2003), Stelling and Duinmeijer(2003), Zijlema and Stelling(2005, 2008), Smit et al.(2013), Zijlema et al.(2011) 등의 문헌들을 참조할 수 있다.

2.2 난류 모델

본 연구에서는 k-ε 난류 모형을 이용하여 난류흐름을 해석하였다. 체적 평균 접근법은 k-ε 방정식에도 적용할 수 있으며, Darcy의 체적 평균된 와동점성(Darcy’s volume-averaged eddy viscosity)은 다음과 같이 계산할 수 있다(Hsu et al., 2002).

(8) νt=Cμk2nε

체적 평균된 k-ε 방정식은 보존식의 형태(conservative form)로 다음과 같이 표현할 수 있다(del Jesus et al., 2012).

(9) ∂∂t(Dkn)+∇⋅(Dukn2)∇⋅[D(υ+νtσk)∇kn]+D(Pk-εn)+Dε∞

(10) ∂∂t(Dεn)+∇⋅(Duεn2)∇⋅[D(υ+νtσε)∇εn]+εkD(C1εPk-C2εεn)+DC2εε∞2k∞

여기서 σ_k, σ_ε, C_1ε, C_2ε, C_μ는 경험상수이며, 각 상수의 값은 다음과 같다(Rodi, 1987).

(11) σk=1.0, σε=1.3, C1ε=1.44, C2ε=1.92, Cμ=0.09

여기서 k와 ε는 각각 Darcy의 체적 평균된 난류운동에너지(turbulent kinetic energy)와 난류운동에너지의 소산율이다. k_∞와 ε_∞는 다공성 매질 흐름 내부를 의미하며, k_∞와 ε_∞는 Nakayama and Kuwahara(1999), Hsu et al.(2002)에 따라 다음과 같이 계산할 수 있다.

(12) ε∞=39.0(1-n)2.5n(∑iui2)3/21D50

(13) k∞=3.7(1-n)n∑iui2

P_k는 평균 전단(mean shear)에 의한 난류 에너지(turbulent energy)의 생성으로 점성력에 의해 발생되는 것으로 다음과 같은 식으로 표현한다.

(14) Pk=νt[(∂u∂z)2+(∂υ∂z)2]

3. 수치실험

3.1 수치모형의 검증

본 연구에서 적용된 수치모형의 검증을 위해 Liu et al. (1999)에 의해 수행된 다공성 구조물을 통과하는 댐 붕괴 흐름에 대한 수리모형실험을 재현하였다. 다음 Fig. 1은 Liu et al.(1999)이 수행한 수리모형실험의 제원을 보여준다. 수조의 길이와 폭은 각각 0.892 m와 0.44 m이고 길이 0.29 m 그리고 높이 0.37 m의 다공성 구조물은 수조의 중앙, x = 0.3m에 위치하고 물을 가두어 놓기 위해 사용된 수문은 다공성 구조물로부터 0.02 m 떨어져있다. Liu et al.(1999)은 유리구슬(grass bead)과 쇄석(crushed stone)으로 이루어진 다공성 구조물에 대해 수리모형실험을 수행하였으나 본 연구에서는 쇄석으로 구성된 다공성 구조물에 대해서만 고려하였다. 쇄석으로 구성된 다공성 구조물은 공극률 0.49, 평균입경(D₅₀ = 0.0159 m)이다. 수문 상류에는 수심 0.25 m 그리고 하류에는 0.0025 m로 물이 채워져 있고 수조의 양 측면과 바닥은 물이 통과할 수 없는 불투과 조건이다.

Fig. 1.

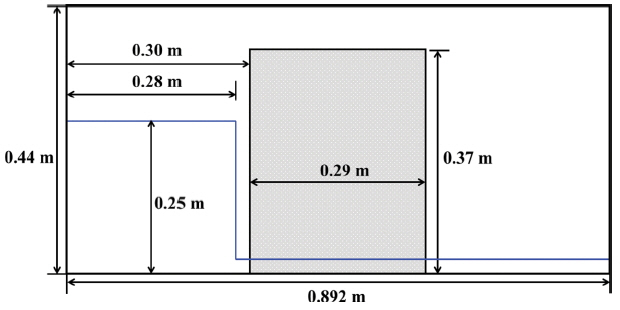
Definition sketch of porous dam break (Liu et al., 1999).

최근 Jensen et al.(2014)은 VOF 기법을 기반으로 VARANS 방정식을 지배방정식으로 하는 3차원 수치모형에 van Gent (1994)의 다공성 항력 모델을 이용해 모든 흐름 조건에 적용가능한 α = 500, β = 2.0 값을 도출하였다. 본 연구에서는 Jensen et al.(2014)이 제안한 α, β 값을 이용하여 수치실험을 수행하였다. 전체 계산 영역에 대해 Δx = Δy = 0.004m의 조밀한 격자망을 구성하고 연직방향으로는 10개의 층으로 나누어 수치실험을 수행하였다. 또한 실험은 흐름이 안정적이거나 주기에 따라 진동하지 않기 때문에 KC 값을 산정하기 어렵다. 따라서 본 연구에서는 Liu et al.(1999)이 제안한 시간 스케일 1.0초(다공성 구조물을 물이 통과하는 시간)를 사용해 KC 값을 산정하였다.

Fig. 2는 SWASH 모형을 이용한 수치실험 결과로 총 수치실험 수행시간 2.2초를 0.2초 간격으로 전체 영역에 대해 수심 분포를 보여준다. 댐 붕괴 초기 단계에서 다공성 구조물이 저항체 역할을 하여 물의 흐름이 지체되어 다공성 구조물 우측면에서 수면이 상승하게 되고 이후 상승된 수면은 흐름의 역방향으로 진행하면서 수조벽 근처의 수면을 증가시킨다. 이후 다공성 구조물을 통과한 흐름의 수면 감소와 함께 도수현상이 발생된다. 이는 다공성 구조물과의 경계면에서의 나타나는 수두차이에 의해 발생되는 것으로 판단된다. 또한 시간이 지나감에 따라 수두차이가 감소하게 되어 도수현상은 점차 사라지는 것을 볼 수 있다. 수리모형실험 결과와 유사하나 다공성 구조물 내부의 흐름과 다공성 구조물 통과 이후에 나타나는 수심의 급격한 감소와 함께 발생되는 도수현상을 잘 재현하지 못하는 것으로 보인다. 이는 다공성 구조물 내부를 통과하며 발생되는 운동량 손실이 적절하게 고려되지 못한 것으로 Jensen et al.(2014)이 제안한 항력계수(α = 500, β = 2.0)는 SWASH 수치모형에는 적합하지 않다고 판단된다.

Fig. 2.

Comparisons of free surface profiles for porous dam break flow. Circles: measurements presented in Liu et al. (1999); Solid lines: numerical results with α = 500, β = 2.0.

3.2 항력계수 보정

본 연구에서는 SWASH 수치모형에 적합한 항력 계수(α, β)를 찾기 위해 Liu et al.(1999)의 수리모형실험을 이용하여 항력계수에 따른 오차 범위를 산정하였다. 항력계수는 α = 100, 200, 400, 800, 1000, 1500, 2000, 2500, 3000], β = 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0]의 조합을 이용하였으며, 항력계수의 조합에 따른 수치실험과 수리모형실험 사이의 오차를 식(15)에 따라 계산하였다. 식(15)는 0.2초 간격의 수치실험결과와 수리모형실험결과 사이의 위치에 따른 평균제곱오차(Mean Square Error, MSE)를 계산하고 이를 전체 시간 간격으로 평균한 값을 의미한다.

(15) error=1M∑j=1M(1N∑i=1N(ζexp,i−ζvm,i)2)

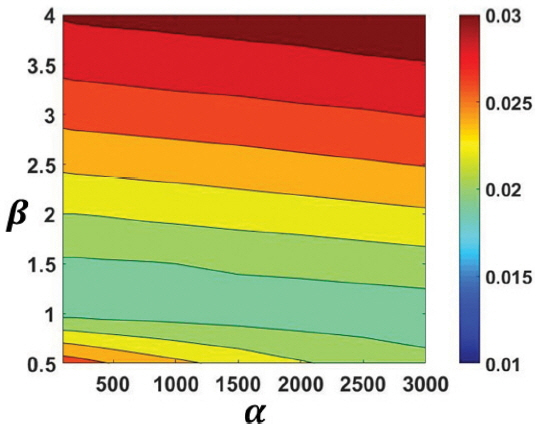
여기서 M은 전체 시간 간격의 수, N은 x 방향을 따르는 전체 셀의 개수이다. 항력 계수 α와 β의 조합에 따른 수치실험과 수리모형실험 사이의 오차를 등고선으로 다음 Fig. 3에 표현하였다. 항력 계수 β에 따라 오차가 크게 변화하는 것을 볼 수 있다. 이는 Liu et al.(1999)에 의해 보고된 바와 같이 다공성 구조물 내부의 저항력은 항력 계수 β에 대해 의존성이 크다는 것을 보여주는 결과이다. 그러나 반면 윤곽선이 대부분 항력 계수 α를 나타내는 축을 따라 정렬되어있는 것으로 볼 수 있다. 이는 항력 계수 α의 효과가 거의 없음을 의미한다. 또한 항력 계수 α와 β의 유일한 한가지의 조합이 최소 오차를 주지 않는다는 것을 확인할 수 있다. 오히려 항력계수 α와 β의 조합에 따른 특정 대역(band)이 낮은 오차를 주는 것으로 나타났다. 낮은 오차를 나타내고 있는 특정 대역은 정량적으로 1.0 ≤ β ≤ 1.5인 구간으로 항력 계수 α의 값이 증가함에 0.75 ≤ β ≤ 1.25으로 변동되는 것을 확인하였다.

Fig. 3.

Contour of error between numerical results and measurements for porous dam break flow.

앞서 언급한 낮은 오차를 주는 특정 대역에서 한가지의 α = 2500, β = 1.0를 선택해 수치실험을 수행하고 그 결과를 수리모형실험과 비교하였다. 항력계수를 제외한 나머지 조건들은 앞서 수행한 수치실험조건과 모두 동일하다. 다음 Fig. 4는 0.2초 간격으로 전체 영역에 대해 수심 분포를 보여준다. 수치실험과 수리모형실험 사이에 차이는 존재하지만, 전반적으로 수리모형실험 결과와 유사하며 α = 500, β = 2.0인 경우와는 다르게 흐름이 강하게 발생하는 초기 단계(0.8초 이전) 이후 다공성 구조물 내부의 흐름과 다공성 구조물 통과 이후에 나타나는 도수현상을 잘 재현하는 것을 확인할 수 있다. 반면 댐 붕괴 초기 단계(0.8초 이전)에서의 차이는 크게 개선되지 않은 것으로 보인다. 이는 비정수압 수치모형의 한계인 것으로 보여지며, Jung(2014)의 연구결과에서 VARANS 방정식의 3차원 수치모형이 댐 붕괴 초기 단계의 다공성 구조물 내부의 흐름과 다공성 구조물 통과 이후에 나타나는 도수현상을 잘 재현하는 것을 확인할 수 있다. 그러나 시간에 따른 전체 영역에 대한 수심 분포가 수리모형실험 결과와 유사한 것을 확인할 수 있다. 따라서 보정작업을 통해 도출한 항력 계수 α와 β는 적절한 것으로 판단된다.

Fig. 4.

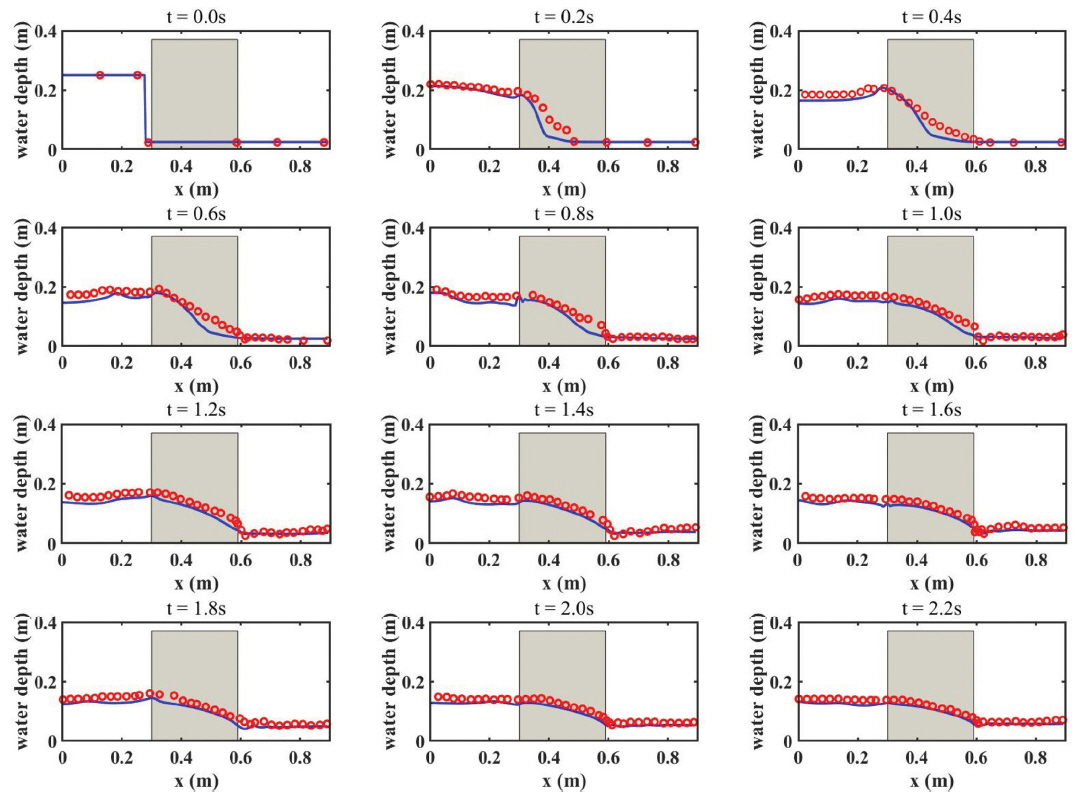
Calibration results for porous dam break flow. Circles: measurements presented in Liu et al. (1999); Solid lines: numerical results with α = 2500, β = 1.0.

3.3 다공성 구조물과 파랑의 상호작용

다공성 구조물과 파랑의 상호작용에 대한 적용성을 검토를 위해 Lara et al.(2012)에 의해 수행된 고립파(solitary wave)를 이용한 수리모형실험을 재현하였다. 다음 Fig. 5는 Lara et al.(2012)이 수행한 수리모형실험의 제원을 보여준다. 수조의 길이와 폭은 각각 17.8 m와 8.6 m이고 길이 4.0 m, 폭 0.5 m, 높이 0.6 m의 다공성 구조물은 수조로부터 x = 10.5 m만큼 떨어져있다. 다공성 구조물은 공극률 0.51이고 평균입경은 D₅₀ = 0.015 m이다. 입사파의 조건은 수심 0.4 m, 파고 0.09 m의 고립파를 이용하였다. 또한 수조 전체에 15개의 위치에서 시간에 따른 수면변위를 관측하였으며 관측 위치는 다음 Table 1과 같다.

Fig. 5.

Wave gauges and porous structure position (Lara et al., 2012).

Table 1.

Wave gauge positions

SWASH 수치모형을 이용한 계산격자의 구성은 Δx = Δy = 0.04 m로 고립파의 파형을 충분히 재현할 수 있도록 하였으며 연직방향으로 10개 층, 항력 계수(α, β)는 앞서 수행한 댐붕괴 흐름에서 사용한 α = 2500, β = 1.0로 동일하다. 본 연구에서는 Shin and Yoon(2017)의 Relaxation 조파기법을 이용해 고립파를 조파하였으며 이완영역 내에 부가되는 매 시간 단계의 수면변위는 Wang(1993)의 식을 이용하였다. 고립파의 파형은 다음과 같다.

(16) ζ=a1+ah[sech2K(x−ct−x0)+ahsech4K(x−ct−x0)]

여기서 a는 고립파의 파고, t는 시간, x₀는 고립파 파봉의 초기 위치,

(17) K=1h3ah4(1+ah),c=g(h+a)

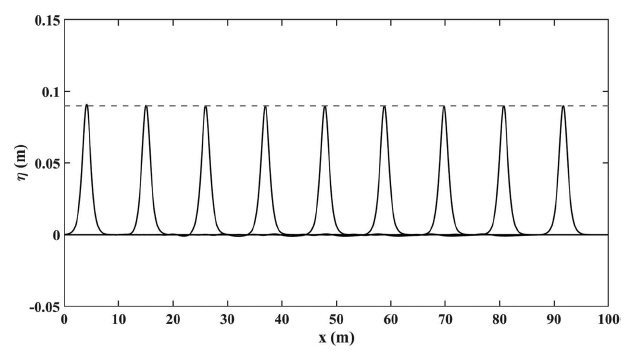
이다. 고립파가 계산 영역 내로 잘 전파되는지 확인하고자 동일한 계산격자를 이용해 다공성 구조물이 없는 상태로 수치실험을 수행하였다. 다음 Fig. 6은 시간에 따른 수면변위를 전체 계산 영역에 대해 나타낸 결과이다. 먼 거리를 전파 한 이후에도 고립파의 파형이 잘 유지되는 것을 확인할 수 있다. 이 결과로부터 Relaxation 조파기법을 이용한 고립파의 조파 방법은 고립파의 파형을 재현하기에 충분하다고 판단된다.

Fig. 6.

Propagation of solitary wave.

Lara et al.(2012)의 수리모형실험과 동일한 조건을 재현하기 위해 고립파가 계산영역 내로 전파 된 이후 Relaxation 영역 내의 이완계수를 조절하여 조파영역으로 반사파가 전파되지 못하도록 하였다.

다음 Fig. 7은 각 위치에서의 시간에 따른 수면변위를 비교한 결과이다. Higuera et al.(2014)이 수행한 수치실험(3차원 전산유체해석 프로그램인 OPENFOAM을 이용; VOF 기법을 적용한 VARANS 방정식에 k-ε 난류 모형 사용) 결과도 함께 비교하였다. 여기서 붉은색 점선은 Lara et al.(2012)이 수행한 수리모형실험 결과, 파랑색 실선은 Higuera et al. (2014)이 수행한 수치실험 결과, 검정색 실선은 SWASH 수치모형을 이용한 계산결과이다.

Fig. 7.

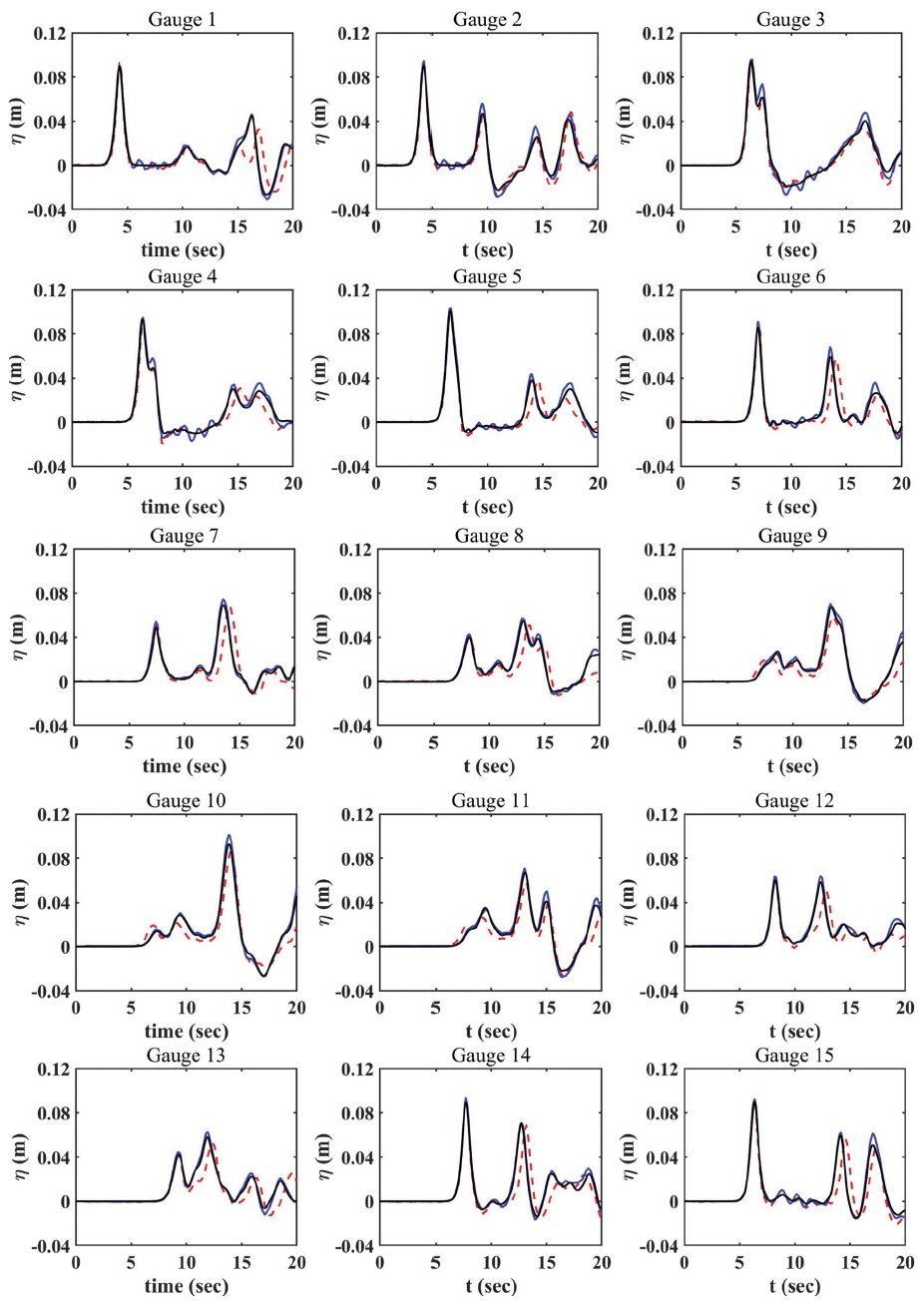
Comparisons of free surface elevations at different wave gauges. Red dashed lines: measurements; Solid blue lines: numerical results of OPENFOAM; Solid black lines: numerical results of SWASH.

SWASH 수치모형의 계산결과는 전반적으로 수리모형 실험과 잘 일치하는 것으로 보인다. 다공성 구조물과 조파 영역 사이에 위치한 관측점 1과 2를 보면 수치실험을 통해 재현한 고립파의 파형과 파고가 수리모형 실험 결과와 잘 일치하는 것을 확인할 수 있다. 또한 다공성 구조물에 가까운 위치의 관측점 3과 4를 보면 수치실험이 다공성 구조물 전면에서의 고립파의 입사 및 반사를 잘 재현하는 것을 확인할 수 있다. 관측점 6, 7, 8, 12를 보면 다공성 구조물을 통과하는 투과 및 회절파를 확인할 수 있다. 수치실험 결과 투과 및 회절파의 크기는 수리모형 실험결과와 비교적 잘 일치하고 있으나 투과 및 회절파의 도착시간에서는 조금 차이가 있는 것으로 보인다. 파의 도착시간 지연은 재 반사로 인한 반사파의 경우 더 크게 나타나고 있으나 반사파의 크기나 파형은 수리실험 결과와 비교적 잘 일치하는 것으로 확인된다. 앞서 언급한 수리모형실험 결과와의 차이는 Higuera et al.(2014)이 수행한 수치실험 결과에서도 동일하게 확인된다. Lara et al. (2012)와 Higuera et al.(2014)는 이러한 차이의 주요한 요인으로 조파장치에 대한 재 반사 문제를 언급하였다. 고립파를 안정적으로 조파한 뒤 조파판은 정확한 위치에 정지되어 있어야 하나 다공성 구조물로부터 전파되는 반사파에 의해 조파판이 뒤로 이동하게 되면서 전체 실험 영역이 변하게 되는 상황을 예상할 수 있다. 이러한 요인으로 재 반사로 인한 반사파의 도착시간이 지연 된 것으로 예상된다.

SWASH 수치모형의 계산결과는 전반적으로 OPENFOAM을 이용한 Higuera et al.(2014)의 수치실험 결과와 비슷한 정확도를 보여주고 있다. 그러나 두 수치모형은 효율성에서 큰 차이를 보여준다. Higuera et al.(2014)에 따르면 OPENFOAM을 이용한 수치실험의 경우 20초를 계산하는 데 있어 2.6 GHZ 프로세스 128개를 이용해 약 2176 h(CPU time)이 소요되었다고 보고되었다(Ma et al., 2014). 반면 SWASH 수치모형을 이용한 계산은 인텔 코어 i7-3770 CPU(3.4 GHZ) 프로세스 28개를 병렬처리로 구성해 약 120 h(CPU time)이 소요되었다. CPU 타임(CPU time)은 한 컴퓨터 프로그램이 CPU를 차지하여 일을 한 시간의 양을 의미한다. 따라서 이러한 비교로부터 VARANS 방정식을 계산하는데 있어 SWASH 수치모형이 3차원 다공성 유동 모델(OPENFOAM)보다 효율적이라는 것을 확인할 수 있다.

4. 결 론

본 연구는 VARANS 방정식을 지배방정식으로 하는 비정수압 수치모형인 SWASH를 이용하여, 다공성 구조물을 통과하는 댐 붕괴 흐름에 대해 검증하고, 수치모형에 적합한 항력 계수를 산정하였다. 또한 본 연구에서 산정한 항력 계수를 이용해 다공성 구조물과 파랑의 상호작용을 확인하였다. 그 결과 다공성 구조물 전면에서 파의 입사 및 반사를 잘 재현하는 것을 확인할 수 있다. 다공성 구조물을 통과하는 투과 및 회절파의 경우 그 크기는 수리모형 실험결과와 비교적 잘 일치하고 있으나 도착시간에서는 차이가 있는 것으로 확인되었다. 또한 SWASH 수치모형이 기존의 VOF 기법을 이용한 방법과 유사한 정확도를 가지며 계산시간의 이점이 있다는 것을 확인할 수 있다. 그러나 SWASH 수치모형은 σ-좌표계의 도입으로 인한 근본적인 제약이 있어 구조물 전면부에서의 급격한 쇄파나 자유수면의 불연속 등을 정확하게 고려하기 어렵다. 또한 SWASH 수치모형을 폭 넓게 활용하기 위해서는 Jensen et al.(2014)이 수행한 연구와 같이 모든 흐름 조건(층류, 천이류, 난류)에 대해 적용 가능한 항력계수 산정을 위한 연구가 추가로 필요하다고 판단된다.

Acknowledgements

본 논문은 행정안전부 극한 재난대응 기반기술 개발사업의 일환인 “해안가 복합재난 위험지역 피해저감 기술개발(연구과제번호: 2018-MOIS31-008)”의 지원으로 수행되었습니다.

References

Cruz EC, Isobe M, Watanabe A. 1997;Boussinesq equations for wave transformation on porous beds. Coastal Engineering 30(1–2):125–156.

del Jesus M, Lara JL, Losada IJ. 2012;Three-dimensional interaction of waves and porous coastal structures: Part I: Numerical model formulation. Coastal Engineering 64:57–72.

Higuera P, Lara JL, Losada IJ. 2014;Three-dimensional interaction of waves and porous coastal structures using Open-FOAM®. Part I: Formulation and validation. Coastal Engineering 83:243–258.

Higuera P, Losada IJ, Lara JL. 2015;Three-dimensional numerical wave generation with moving boundaries. Coastal Engineering 101:35–47.

Hsiao S-C, Liu PLF, Chen Y. 2002;Nonlinear water waves propagating over a permeable bed. In Proceedings of the Royal Society of London A: Mathematical. Physical and Engineering Sciences 458(2022):1291–1322.

Hsiao S-C, Hu KC, Hwung HH. 2010;Extended Boussinesq equations for water-wave propagation in porous media. Journal of Engineering Mechanics 136(5):625–640.

Hsu TJ, Sakakiyama T, Liu PLF. 2002;A numerical model for wave motions and turbulence flows in front of a composite breakwater. Coastal Engineering 46(1):25–50.

Hu KC, Hsiao S-C, Hwung HH, Wu TR. 2012;Three-dimensional numerical modeling of the interaction of dam-break waves and porous media. Advances in Water Resources 47:14–30.

Huynh TT, Lee C, Ahn SJ. 2017;Numerical simulation of wave overtopping on a porous breakwater using Boussinesq equations. Journal of Korean Society of Coastal and Ocean Engineers 29(6):326–334. (in Korean).

Jensen B, Jacobsen NG, Christensen ED. 2014;Investigations on the porous media equations and resistance coefficients for coastal structures. Coastal Engineering 84:56–72.

Jung W. 2014;A numerical study on propagation characteristics of dam-break wave through a porous structure. Journal of Korea Water Resources Association 47(1):11–24. (in Korean).

Kobayasi N, Wurjanto A. 1992. Numerical model for random waves on permeable coastal structures. Technical Report. CACR-92-02.

Lara JL, del Jesus M, Losada IJ. 2012;Three-dimensional interaction of waves and porous coastal structures: Part II: Experimental validation. Coastal Engineering 64:26–46.

Lee C, Vu VN, Jung TH. 2014;Extended Boussinesq equations for waves in porous media: Derivation of governing equations and generation of waves internally. Coastal Engineering Proceedings 1(34):57.

Lee KH, Bae JH, An SW, Kim DS, Bae KS. 2016;Numerical analysis on wave characteristics around submerged breakwater in wave and current coexisting field by OLAFOAM. Journal of Korean Society of Coastal and Ocean Engineers 28(6):332–349. (in Korean).

Lee KH, Bae JH, An SW, Kim DS. 2018;Nonlinear irregular waves-current interaction on flow fields with wave breaking around permeable submerged breakwater. Journal of Korean Society of Coastal and Ocean Engineers 30(2):39–50. (in Korean).

Liu PLF, Lin P, Chang KA, Sakakiyama T. 1999;Numerical modeling of wave interaction with porous structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 125(6):322–330.

Losada IJ, Silva R, Losada MA. 1996a;3-D non-breaking regular wave interaction with submerged breakwaters. Coastal Engineering 28(1–4):229–248.

Losada IJ, Silva R, Losada MA. 1996b;Interaction of non-breaking directional random waves with submerged breakwaters. Coastal Engineering 28(1–4):249–266.

Losada IJ, Lara JL, del Jesus M. 2016;Modeling the interaction of water waves with porous coastal structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 142(6)

Lynett PJ, Liu PLF, Losada IJ, Vidal C. 2000;Solitary wave interaction with porous breakwaters. Journal of Waterway, Port, Coastal, and Ocean Engineering 126(6):314–322.

Ma G, Shi F, Hsiao S-C, Wu Y-T. 2014;Non-hydrostatic modeling of wave interactions with porous structures. Coastal Engineering 91:84–98.

Madsen OS. 1974;Wave transmission through porous structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 100(3):169–188.

Nakayama A, Kuwahara F. 1999;A macroscopic turbulence model for flow in a porous medium. Journal of Fluids Engineering 121(2):427–433.

Nam IS, Yoon HS, Kim JW, Ryu CR. 2002;Numerical modeling of wave run-up and internal set-up on and in permeable coastal structures. Journal of Ocean Engineering and Technology 16(5):34–40. (in Korean).

Phillips NA. 1957;A coordinate system having some special advantages for numerical forecasting. Journal of Meteorology 14(2):184–185.

Rodi W. 1987;Examples of calculation methods for flow and mixing in stratified flows. Journal of Geophysical Research 92(5):5305–5328.

Shin CH, Yoon SB. 2017;Improvement of wave generation for SWASH model using relaxation method. Journal of Korean Society of Coastal and Ocean Engineers 29(4):169–179. (in Korean).

Smit P, Zijlema M, Stelling G. 2013;Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coastal Engineering 76:1–16.

Stelling G, Zijlema M. 2003;An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. International Journal for Numerical Methods in Fluids 43(1):1–23.

Stelling GS, Duinmeijer SPA. 2003;A staggered conservative scheme for every froude number in rapidly varied shallow water flows. International Journal for Numerical Methods in Fluids 43:1329–1354.

van Gent MRA. 1994;The modelling of wave action on and in coastal structures. Coastal Engineering 22(3–4):311–339.

van Gent MRA. 1995;Wave interaction with berm breakwaters. Journal of Waterway, Port, Coastal, and Ocean Engineering 121(5):229–238.

Vu VN, Lee C. 2015;Solitary wave interaction with porous structures. Procedia Engineering 116:834–841.

Wang KH. 1993;Diffraction of solitary waves by breakwaters. Journal of Waterway, Port, Coastal, and Ocean Engineering 119(1):49–69.

Yoon HS, Cha JH, Kang YK. 2005;An application of CADMAS-SURF to the wave run-up in permeable coastal structures. Journal of Ocean Engineering and Technology 19(4):49–55. (in Korean).

Zijlema M, Stelling GS. 2005;Further experiences with computing non-hydrostatic free-surface flows involving water waves. International Journal for Numerical Methods in Fluids 48:169–197.

Zijlema M, Stelling GS. 2008;Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure. Coastal Engineering 55:780–790.

Zijlema M, Stelling G, Smit P. 2011;SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coastal Engineering 58:992–1012.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Wave gauge	x (m)	y (m)
①	5	7
②	5	1
③	9.5	1
④	9.5	3
⑤	10	4
⑥	11	4.5
⑦	11.5	3.5
⑧	12.5	2.5
⑨	12	1.5
⑩	11.5	0.5
⑪	13	0.5
⑫	13.5	4
⑬	15	2
⑭	12.5	7
⑮	9.5	7.5