쉬라우드 조류 발전 시스템 상부 두께 변화에 따른 유속 변화에 관한 연구
Numerical Analysis for the Optimum Design of Shroud Tidal Stream Generation System
Article information
Abstract
쉬라우드 조류 발전 시스템 상부 두께 변화에 따른 유동장 내 유속 변화 연구를 위해 수치 모의실험을 통하여 분석하였다. 본 연구는 일정한 조류 속도 조건에서 수행하였으며, 같은 조건으로 쉬라우드의 성능 분석을 추가 수행하였다. 상부 높이가 증가할수록 유속 변화율은 점차 증가하는 양상을 보였으며, 일정 높이에서 재차 감소하는 경향을 보였다. 또한, 쉬라우드의 성능 평가를 위해 블레이드를 단독 설치한 경우와 쉬라우드와 결합한 형상을 분석한 결과, 쉬라우드 시스템에 의한 유속 증가로 블레이드의 회전력은 증가하였다. 본 연구를 통해 얻은 구조물의 형상과 유동장 내의 유속 분포에 대한 분석 결과는 효율적인 쉬라우드 조류 발전 시스템 개발에 필요한 자료를 제시할 수 있을 것으로 기대된다.
Trans Abstract
Numerical simulations were carried out to investigate the flow velocity changes in the flow field due to the variation in the thickness of the upper part of the shroud tidal power generation system. In this study, it was performed under constant flow velocity condition. In addition, performance analysis of shroud was performed under the same conditions. As the height of the upper part increases, the flow velocity rate gradually increases, and it tends to decrease at a certain height. As a result of analyzing the shape of the blade and the shape of the blade combined with the shroud, the torque of the blade increased due to the increase of the flow rate by the shroud system. It is expected that the shape of the structure obtained by this study and the analysis of the flow velocity distribution in the flow field can provide the data necessary for the development of an efficient shroud tidal power generation system.
1. 서 론
전 세계적으로 지구온난화에 따른 환경 변화에 대처하기 위해 탄소 배출 규제가 강화되고 있으며 우리나라도 파리기후협정을 통해 2030년까지 온실 가스를 배출 전망치(BAU) 대비 37%까지 감축할 것을 국제사회에 약속하고 이를 이행하기 위한 전략을 수립하고 있다(산업통상자원부, 2017). 재생 에너지원 중 해양 에너지는 지속 개발이 가능하고 무공해 청정 에너지원 이라는 장점을 가지고 있다(Oh et al., 2015). 특히 조류 발전은 해양 에너지원 중 가장 상용화에 근접한 기술로써 조류의 운동에너지를 이용하여 수차발전기를 가동, 전기에너지로 변환하는 발전 방식으로 계절 및 기상 환경의 영향을 받지 않으며 안정적인 출력이 가능하다(Kim et al., 2012). 또한 국내 서 · 남해안은 좁은 수로 사이에 강한 흐름이 발생하고 있어 조류 발전 후보지로 손꼽히고 있다. 따라서 초기 유입 에너지 손실을 최소화하고 전기에너지로의 변환을 높일 수 있는 상용 조류 발전 시스템 개발이 가능하다면 국내 조류 발전 산업은 빠른 시일 내에 급성장할 것으로 기대된다.
이러한 조류 발전은 본래 자연이 가진 에너지를 전기에너지로 변환 시키는 기술이 중요하기 때문에 TRL 8(준상용화 단계) 이상 수준의 상용 조류 발전 시스템 개발이 필요하다. 이에 Zhou et al.(2015)는 대형 해저 조류 터빈 기술의 최신 검토를 통해 조류 발전 구조물에 대한 최적 형상화 연구를 진행하였으며, Kim et al.(2012)은 광역의 채널을 활용한 조류의 효율 개선 연구를 수행한 바 있다. 또한 Kim et al.(2012)은 조류 발전 시스템용 쉬라우드의 형상 각도별 일정 도류 속도장 내 해수 유동 특성에 대한 연구를 수행하였고, Jo et al.(2016)는 일점 계류식 조류 발전 덕트의 디퓨져 각도에 따른 내부 유동 분석을 통해 연구를 수행하였다.
본 연구에서는 조류발전용 쉬라우드 시스템의 상부 두께에 따른 내부 유속 증가율을 검토하기 위해 3차원 CFD 모델인 FLOW-3D 모델을 이용하여 쉬라우드 내·외부의 유동 해석을 수행하였다.
2. 수치해석 모형
본 연구에서는 Dassault system의 Solidworks 프로그램을 이용하여 쉬라우드 형상을 제작하였으며, 수치해석은 Flow science에서 개발한 3차원 범용 유동 해석 프로그램인 Flow-3D(ver.11.1)을 사용하였다. 좌표계는 직교좌표계를 사용하였으며 쉬라우드의 정확한 형상화를 위하여 FAVOR(Fractional Area/Volume Obstacle Representation Method) 기법을 각 방정식에 적용하고 있다. 또한 직교좌표계 x, y, z에서 3차원 비압축성 흐름을 해석하기 위해 연속방정식과 운동방정식이 사용되었다. Flow-3D에서 제공하는 난류 모델은 k−ε, RNG k−ε, LES(Large Eddy Simulation) 모델이며, 본 연구에서 사용한 난류 모델은 등방성 스칼라 값으로 속도의 변동을 처리하여 시간에 따라 이를 감쇠시킬 수 있는 RNG(renormalized Group) k−ε 모델을 사용하였다.
2.1 지배방정식
2.1.1 연속방정식
직교좌표계 x, y, z에서 비압축성 유체의 3차원 흐름을 해석하기 위한 지배 방정식인 연속방정식은 다음과 같다.
여기서, u, v, w는 x, y, z 방향별 유체 속도, Ax, Ay, Az는 각 방향별 유체 흐름을 위해 확보된 면적 비(Area fraction), ρ는 유체 밀도, RSOR은 질량 생성/소멸(Mass source/sink)항이다.
2.1.2 운동방정식
본 연구에서는 3차원 난류 모형인 RNG(renormalized Group) k−ε 모델을 사용하며, 난류 확산을 적용한 난류 운동방정식은 다음과 같다.
여기서, RSOR은 질량 생성/소멸(Mass source/sink)항, VF는 체적비(Volume fraction), p는 압력, Gx, Gy, Gz는 방향별 체적력항, fx, fy, fz는 방향별 점성력항, bx, by, bz는 다공질 매체에서 방향별 흐름 손실이다.
2.2 모델 및 형상 구성
2.2.1 형상 구성
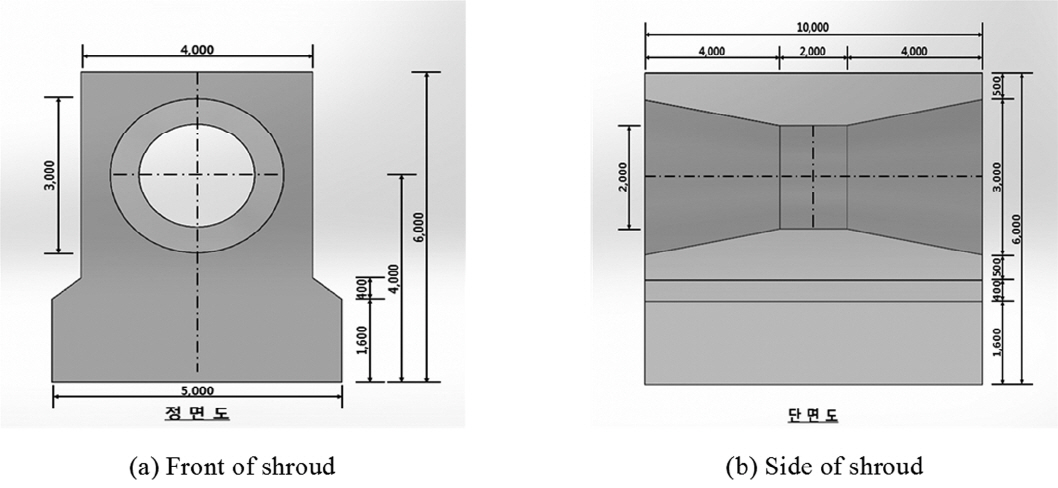
본 연구에서 사용한 쉬라우드 시스템은 저 유속에서도 유속이 증폭될 수 있도록 쉬라우드 형식의 내부형상을 가지고 있다. 또한, 활동과 전도에 대한 수중 구조물 안정 검토를 통해 쉬라우드 형상을 설계하였으며, 시스템의 다양한 변수를 변화하여 분석한 후 선정하였다. 이에 대한 제원은 다음 Fig. 1과 같다.
Concrete shroud geometry (mm).
2.2.2 모델 구성
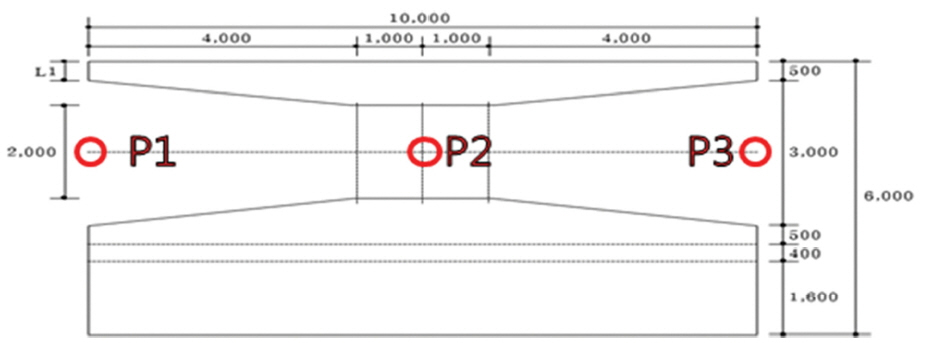
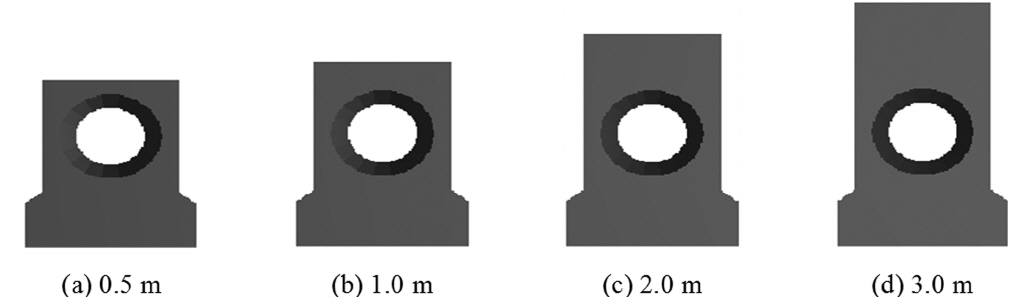
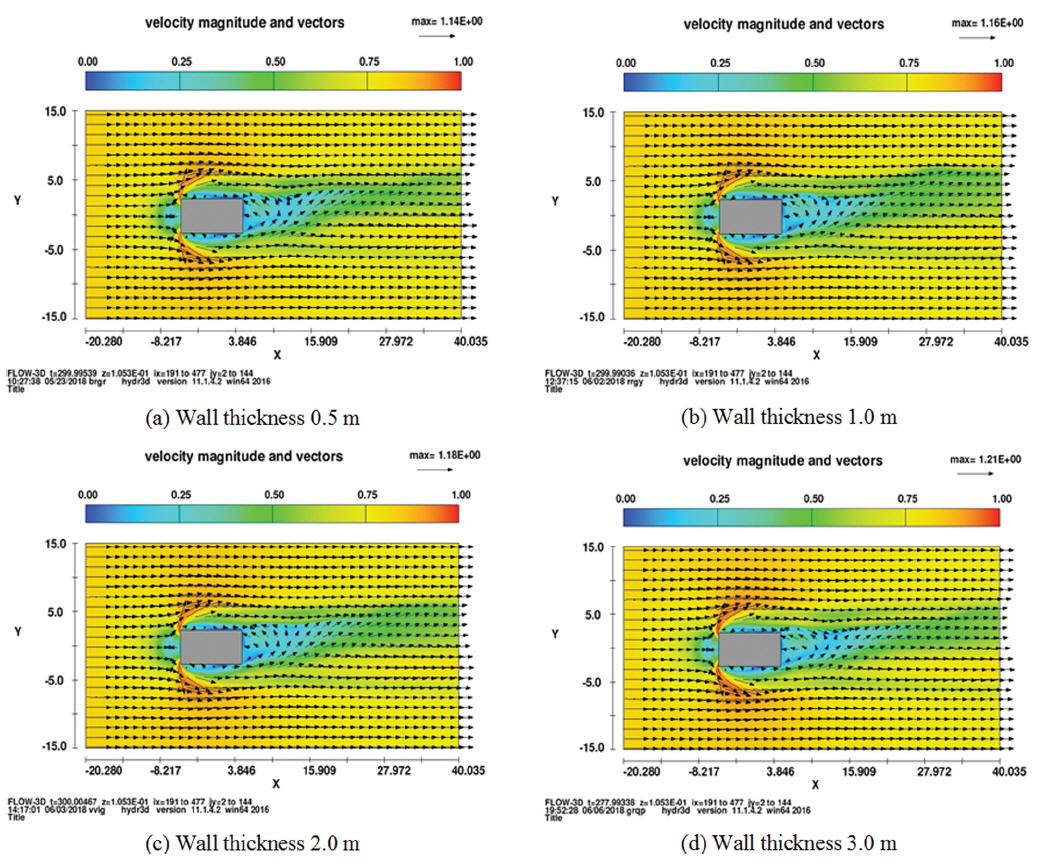
쉬라우드 상부 두께의 변화에 따라 유동장 내부에서의 유속 변화를 파악하기 위하여 4 가지 형상에 대하여 해석하였다. 상부 두께는 0.5 m, 1.0 m, 2.0 m, 3.0 m로 구성하였으며, 변화 조건에 대한 제원 정보는 Fig. 2와 Table 1에 정리하였다. 또한 형상이 변화 되었을 때의 기하학적 형상은 Fig. 3에 나타냈다. 본 연구에서는 Fig. 2에 표시된 P1, P2, P3에 대한 유속 분포를 분석하였다.
Concrete shroud geometry (mm).
Shroud thickness (L1) variation
Design of shroud for thickness.
2.3 계산 조건 및 격자
2.3.1 격자 구성
Flow-3D에서 사용하는 격자는 직교 가변 격자 체계를 사용했다. 본 연구에서 사용된 격자 정보는 다음 Table 2에 제시했으며, 총 15,514,070개의 직교 가변 격자를 구성하였다.
Modeling information
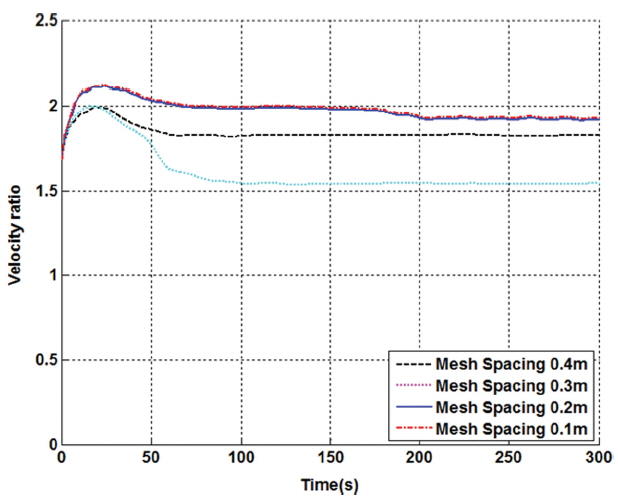
또한, 격자 의존도를 파악하기 위하여 격자 간격 0.4 m, 0.3 m, 0.2 m, 0.1 m로 같은 해석을 수행한 결과 격자 간격 0.1 m와 0.2 m의 해석 결과의 차이는 약 0.2%로 나타났으며, 해석 결과는 초기 유속(v0) 대비 P2 지점 유속(v)으로서 무차원화로 표현하여 다음 Fig. 4에 제시하였다. 이에 해석 시간을 고려하여 격자 간격 0.2 m를 선택하여 해석을 수행하였으며, 해석 영역의 격자 형상은 다음 Fig. 5와 같다.
Velocity change with mesh spacing.
Shroud 3 dimensional grid.
2.3.2 계산 조건
쉬라우드 형상의 상부 두께 변화에 따른 유동장 내 유동 분석을 위한 경계 조건으로 유입부(V,velocity)에 1.0 m/s의 조건을 주었다. 그리고 흐름이 나가는 유출부(O, outflow) 조건을 적용했으며, 하부는 지반 조건의 특성을 가진 벽(W, wall) 조건을 적용하였다. 양 측면 및 상부는 대칭면에 수직한 방향의 에너지와 질량의 유출입이 없고, 대칭면에 평행한 방향의 유동 저항이 없는 대칭(S, symmetry) 조건을 적용하였으며, 경계조건에 대한 형상은 다음 Fig. 6과 같다.
Shroud boundary condition.
한편, 유속의 초기 흐름은 난류 상태의 비정상흐름이 되므로 정상상태의 해석을 위해 충분한 해석시간을 수행하였다.
2.4 쉬라우드의 성능 분석
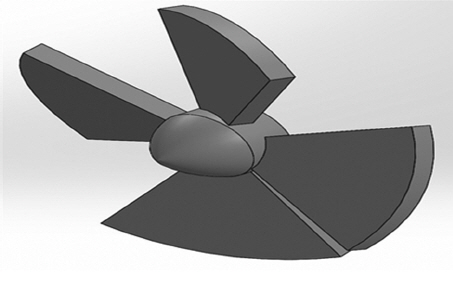
일정한 해수 흐름 상태의 터빈이 회전하는 조건에서 쉬라우드의 영향을 추정하기 위하여 쉬라우드와 블레이드가 있는 경우, 블레이드 단독으로 있는 경우에 대한 성능 분석을 수행하였다. 수치해석에 사용된 모든 조건은 상부 두께 분석에 사용된 조건과 동일하며, 고정 RPM 조건을 사용하여 분석을 수행하였다. 또한 블레이드에 대한 제원 및 기하학적 형상은 다음 Table 3 및 Fig. 7과 같다. 분석을 통해 얻은 토크 값으로 쉬라우드의 성능 분석을 실시하였다.
General design parameter
Turbine blade.
3. 실험 결과
3.1 상부 두께 변화에 대한 실험 결과
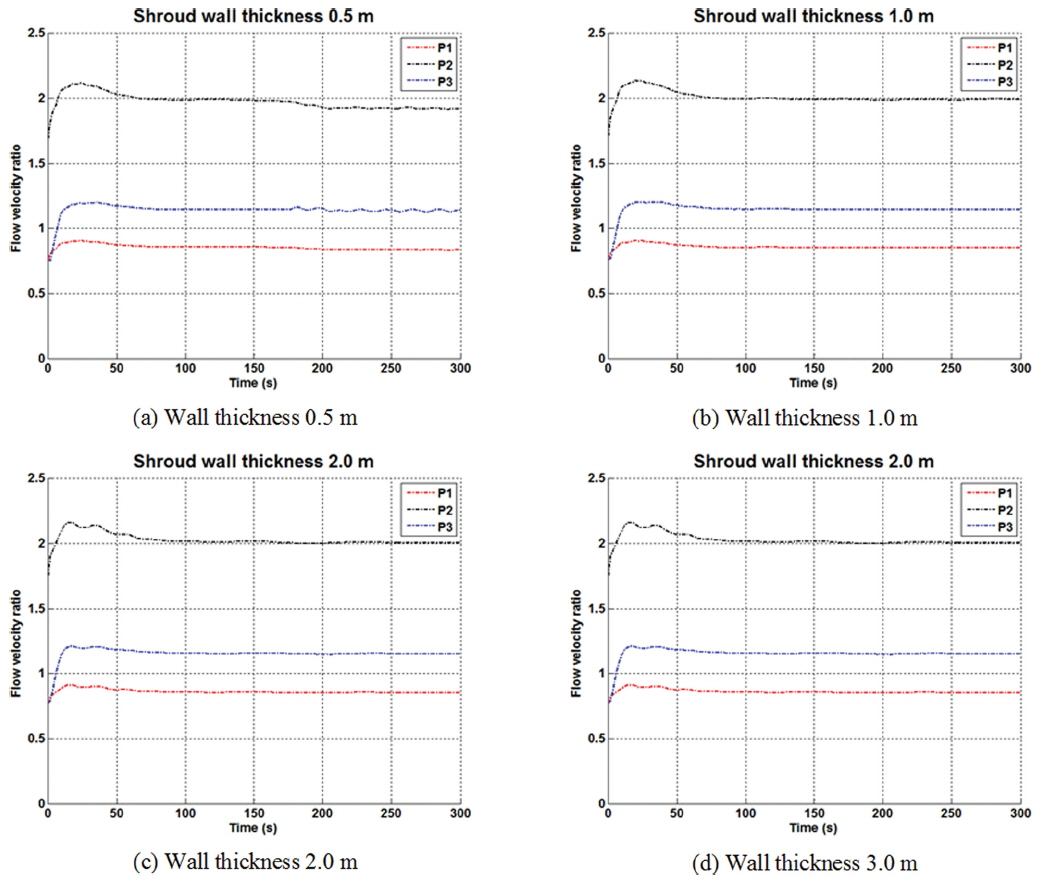
Fig. 8은 상부 두께에 따른 각 위치별 유속 분포 경향을 보이고 있으며, 유속비는 초기 유속(v0) 대비 각 지점에서의 유속(v)을 무차원화로 표현하였다. 쉬라우드 상부 두께를 변화시키며 분석한 결과 P1, P2, P3에서 유속은 점차 증가한 뒤, 일정 유속비에서 감소하는 경향을 보였다. 유속 증가율은 P1으로 유입되는 유속 대비 P2 지점에서의 유속으로 판단할 수 있으며, 이때 압력차의 경향은 유속비의 경향과 유사하고, 상부 두께 2.0 m와 3.0 m의 압력차의 비는 약 23%로 나타났다. 이때, 유속 증가율은 약 4.0% 나타났다.
Velocity variation in the flow field.
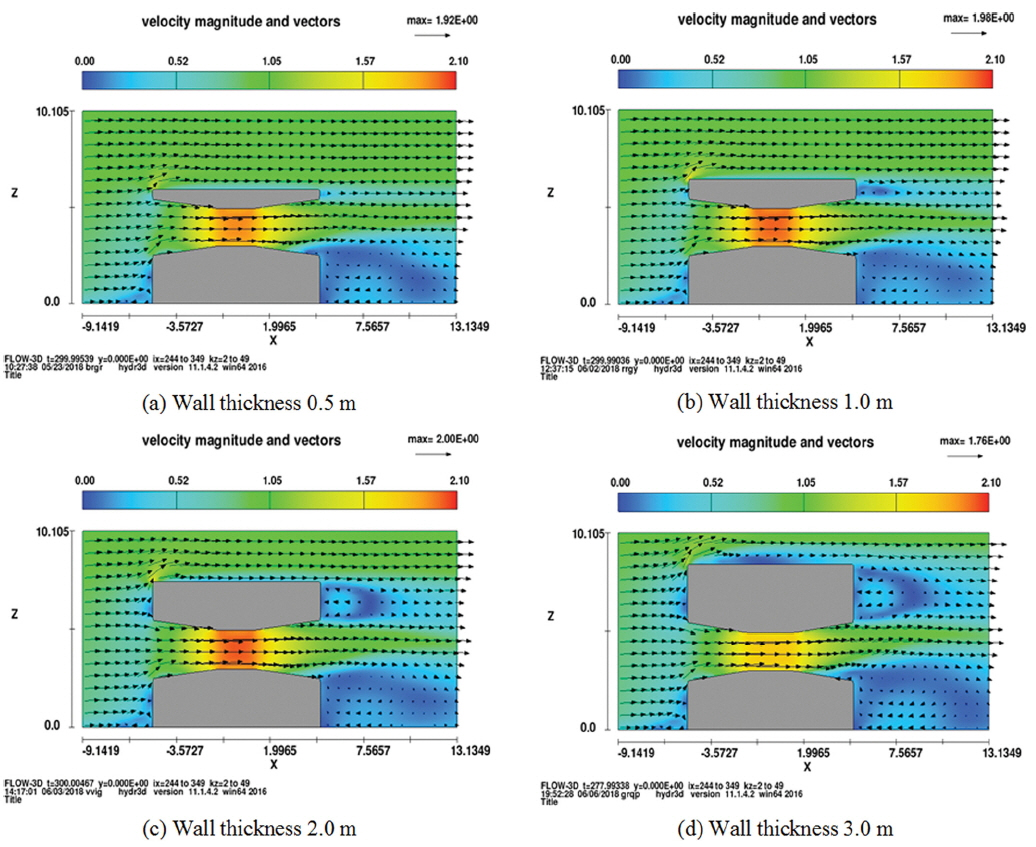
한편, 상부 두께에 따른 벡터 분포도를 측면과 위에서 본 결과를 다음 Fig. 9과 Fig. 10에 제시하였다. 분석한 네 가지 경우 모두 초기 유속 대비 40% 이상 증가함을 보였으며, 두께 2.0 m인 경우 유속 증가율은 약 50%로 나타났다. 또한 P3를 지난 흐름은 쉬라우드 상부 벽면 및 하부 벽면 뒤에서 와류가 발생하였다.
Vector distribution in flow field (side view, m/s).
Vector distribution in flow field (top view, m/s).
3.2 쉬라우드 영향 분석 결과
3.2.1 블레이드 단독 분석
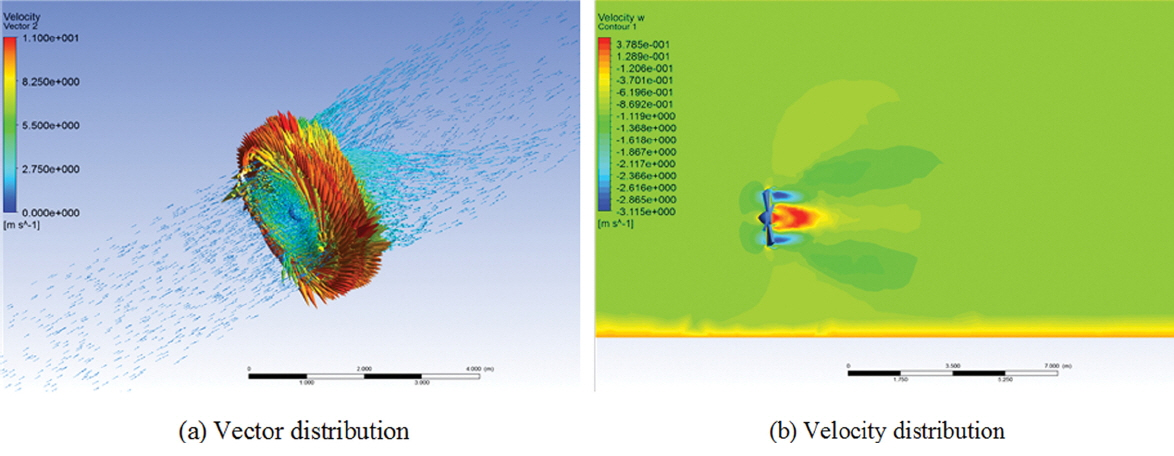
상부 두께를 분석하기 위한 경계조건 및 계산 조건을 동일하게 하여 블레이드를 단독으로 구성하여 회전력을 추정한 결과, 앞부분에서 입구 유속보다 낮은 속도로 블레이드에 접하게 되며, 블레이드 끝 부분에서 회전에 따른 유속과 토크가 발생하는 것을 확인하였다. 또한 블레이드의 후면은 회전에 의하여 선회 유동이 발생하였으며, 후류의 영향은 블레이드 직경(D)에 비해 약 3D로 나타났다. 또한 블레이드 뒤쪽에서 강한 와류가 발생함을 보이고 있었다. 블레이드만 단독으로 구성된 유동장의 벡터 및 유속 분포에 대한 결과는 다음 Fig. 11에 제시하였다. 또한 분석된 블레이드의 회전력은 약 6800 N · m로 나타났다.
Vector and streamline distribution in flow field (only blade).
3.2.2 쉬라우드와 블레이드 결합 후 분석
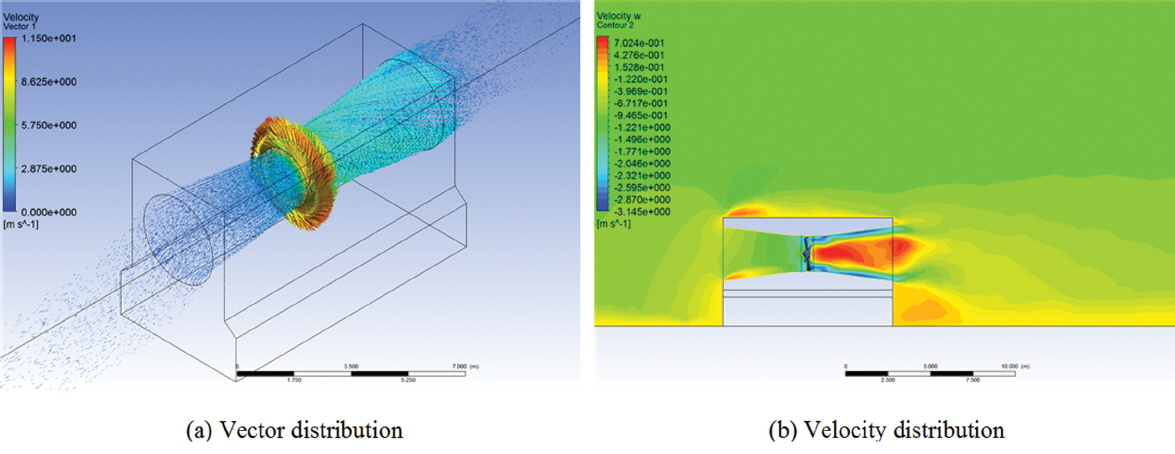
쉬라우드의 성능을 파악하기 위하여, 블레이드가 포함된 쉬라우드 형상체에 대한 유속 및 회전력을 추정하였다. 안정화된 흐름이 쉬라우드 시스템 내부로 유입되면서, 급격히 줄어드는 단면적에 의해 강한 유속을 발생시킨다. 이에 블레이드에 작용하는 힘의 크기는 블레이드 단독으로 있는 경우보다 커지며, 회전력을 증가시킨다. 이 때, 측정되는 회전력은 블레이드 단독 조건에 비해 약 3% 이상 증가하는 효과가 나타났으며, 이는 블레이드가 흐름에 저항체로 작용하여 회전력이 낮은 증폭율을 보인 것으로 기인된다. 추후 블레이드의 다양한 변수를 통해 적정 블레이드를 모색하는 것이 중요하다고 판단된다. 또한, 후류의 영향은 약 6D로 나타났으며, 이는 블레이드를 통과한 흐름에 회전력을 미쳐 쉬라우드 뒷부분에서 와류를 발생시키는 것으로 기인된다. 이에 따른, 벡터 및 유속 분포를 Fig. 12에 제시하였다.
Vector and streamline distribution in flow field (shroud and blade).
4. 결 론
본 연구에서는 조류 발전용 쉬라우드 시스템의 기하학적 형상 변화에 따른 내부 유동장에서의 유속 증가율을 확인하기 위하여 수치해석을 실시하였으며, 이러한 쉬라우드 시스템이 실제 터빈 설치가 된다면 어느 정도의 영향을 주는지에 대한 분석까지 수행하였다. 우선, 상부 두께가 증가함에 따라 P1, P2, P3 모든 지점에서의 유속은 소폭 증가하였다. 하지만 일정 높이 조건에서 재차 감소하는 경향을 보였으며, 쉬라우드 주변 유동장의 흐름은 크게 변화하지 않았다. 쉬라우드 내부 유속의 변화는 P1 지점과 P2 지점의 압력차로 인하여 발생하는 것으로 판단된다. 쉬라우드 출구부에서 불안정한 흐름을 보이며 난류를 형성하였으며, 초기 유속 대비 블레이드가 설치되는 P2 지점에서의 유속은 최대 50%까지 상승하였다.
블레이드와 쉬라우드 + 블레이드 분석을 통해 쉬라우드의 성능을 분석한 결과 쉬라우드가 있을 때 더 높은 토크값을 얻었으며, 이는 쉬라우드를 통해 유속이 충분히 증폭하는 현상에 의해 발생하는 것으로 판단된다. 또한, 초기 유속 대비 강한 유속이 발생되어 블레이드를 돌리는 힘 즉, 회전력을 증가시켜 최종적으로 더 나은 발전 효율을 보일 수 있을 것으로 사료된다.
추후 블레이드의 다양한 분석을 통해 더 높은 성능을 얻을 수 있는 블레이드를 선정하는 연구가 필요하며, 본 연구의 결과는 효율적인 쉬라우드 조류발전 시스템 개발에 필요한 자료를 제시할 수 있을 것으로 기대된다.
Acknowledgements
본 연구는 해양수산부 해양청정에너지기술 개발 사업인 “항로표지 등부표용 파력발전시스템 형상 최적화에 관한 연구(과제 번호: 20170323)”와 한국해양과학기술진흥원 미래해양산업기술개발 해양중소벤처지원사업인 “콘크리트 쉬라우드를 이용한 조류 발전 시스템 연구(과제 번호: 20170122)”의 지원으로 수행되었습니다. 연구 지원에 감사드립니다.