Article information

Abstract

Trans Abstract

1. 서 론

Boussinesq 파랑 수치모형은 연안에서 파랑의 전파 및 변형을 정확히 모의할 수 있어 많은 연구가 진행 중에 있다. 장파 및 단파의 모의가 가능하며, 불규칙파 모의에 대한 적용이 가능하다. 또한 운동방정식으로부터 유속을 계산함으로써 파랑과 흐름의 상호작용을 고려할 수 있으며, 파랑 쇄파로 인하여 발생하는 연안류의 모의가 가능하다(Shi et al., 2012; Yoon et al., 2014; Choi et al., 2015). Spectral 파랑 모형에서 재현하기 어려운 파랑회절 현상을 보다 정확하게 모의할 수 있으며(Shi et al., 2001; Choi et al., 2018), 파랑의 천수, 굴절 및 반사 현상 등 파랑의 전반적인 현상을 모의할 수 있는 장점이 있다.

초기의 Boussinesq 파랑모형은 직교좌표계의 일정한 격자 크기를 사용하는 유한차분모형이 주로 개발되었다(Kirby et al., 1998; Nwogu and Demirbilek, 2001; Lynett and Liu, 2004). 이후 복잡한 해안선과 같이 굴곡진 경계를 처리할 수 있는 곡선좌표계를 이용한 유한차분모형(Shi et al., 2001)과 비구조 삼각형 격자를 사용할 수 있는 유한요소모형(Walkley and Berzins, 2002; Woo and Liu, 2004)이 개발되었다. 하지만, 초기에 개발된 이들 모형에서는 고주파 성분의 수치 진동으로 인하여 수치해가 발산하는 문제가 많이 제기되어 왔다(Liu, 1995; Kirby et al., 1998; Walkley and Berzins, 2002). 이러한 수치적인 불안정성(numerical instability)은 쇄파 모의와 같은 비선형성이 큰 문제를 모의할 때 많이 나타나며, 초기의 유한차분방법이나 유한요소방법으로 개발된 모형에서는 수치적인 불안정성을 완화시키기 위하여 수치 필터를 사용해왔다(Kirby et al., 1998; Walkley and Berzins, 2002; Woo and Liu, 2004). 하지만 수치 필터를 사용하여도 급변하는 수심을 통과하는 파랑의 모의나 비선형성이 크게 작용하는 파랑 모의의 경우에서는 수치적인 불안정성이 여전히 나타났다.

Toro(1999, 2001), Zhou et al.(2001)의 결과에서 찾아볼 수 있듯이 최근 들어 Euler 방정식이나 천수방정식에 HLL(Harten et al., 1983)이나 HLLC(Toro et al., 1994) 기법과 같은 근사 Riemann solver와 TVD(Total Variation Diminishing) 기법이 안정적인 수치결과를 제시함에 따라 Boussinesq 방정식에도 이러한 기법들이 적용된 수치모형이 개발되었다(Erduran et al., 2005; Kim et al., 2009; Shi et al., 2012; Roeber and Cheung, 2012). 개발된 Boussinesq 수치모형의 경우 대부분 Erduran et al.이 제안한 방법에 따라 지배방정식의 flux항까지는 근사 Riemann solver와 TVD 기법을 적용하였으며, 분산항에 대해서는 유한차분방법으로 수치이산화를 하였다.

Shi et al.(2012)에 의해 개발된 FUNWAVE-TVD 수치모형은 Chen(2006)의 완전 비선형 Boussinesq 방정식을 지배방정식으로 사용하고 있으며, flux항을 풀기 위하여 HLL 기법과 TVD 기법이 적용되어 있다. FUNWAVE-TVD 모형 버전 2.1(Shi et al., 2013)까지는 Yamamoto and Daiguji(1993)가 제안한 4차 정확도의 MUSCL-TVD 기법(TVD4-YD)과 Zhou et al.(2001)이 제안한 2차 정확도의 MUSCL-TVD 기법(TVD2)이 적용되어 있어 두 기법 중에서 선택하여 모의할 수 있도록 되어있다. 최근, Abadie et al.(2012)은 FUNWAVETVD 수치모형을 이용하여 쯔나미의 수치모의를 실험하였는데, TVD4-YD에서 나타난 수치적인 불안정성으로 인하여 TVD2를 사용하여 결과를 제시하였다. Choi et al.(2018)은 TVD4-YD 대신 Erduran et al.(2005)이 제안한 4차 정확도의 MUSCL-TVD 기법(TVD4-E)을 FUNWAVE-TVD 모형에 적용하여 부산항의 파랑 전파 변형 실험을 수행하였으며, 수치적인 불안정성 없이 관측치를 잘 재현하는 결과를 보였다. 이러한 결과에 따라 FUNWAVE-TVD 수치모형 버전 3.0(Shi et al., 2016)에서는 TVD4-YD 대신 TVD4-E 기법이 적용되었다.

본 연구에서는 FUNWAVE-TVD 모형 버전 3.0을 대상으로 하였으며, 적용된 TVD 기법들의 수렴도와 안정성을 비교하기 위하여 수리실험 관측치가 제시되어 있는 Vincent and Briggs(1989)의 불규칙 파랑실험에 적용하였다. Vincent and Briggs의 실험에 대한 수치모의 결과는 이미 많은 연구(Suh et al., 1993; Yoon et al., 2004; Choi et al., 2009)에서 제시된 바 있지만, 본 연구에서는 공간 격자를 줄여가며 각 TVD 기법의 수렴도를 비교하였다. 또한, 기법에 의한 numerical dissipation 현상을 최대한 줄이기 위하여 공간격자간격을 충분히 작게 한 상태에서 결과를 제시하였으며, 수리실험 관측치와의 비교 및 각 기법간의 수치적인 안정성을 비교하였다. 본 연구에서는 FUNWAVE-TVD 수치모형에서 TVD4-YD(Yamamoto and Daiguji, 1993), TVD4-E(Erduran et al., 2005), TVD2(Zhou et al., 2001)를 사용한 수치실험의 결과를 비교하였다.

2. FUNWAVE-TVD 모형의 지배방정식

파랑의 특성은 진폭(a), 파장(l), 수심(h) 등의 인자로 나타낼 수 있는데, ε = a/h와 μ = h/l는 각각 파랑의 비선형성과 분산성을 나타내는 무차원 계수를 의미한다. FUNWAVE-TVD 수치모형의 지배방정식은 Chen(2006)의 Boussinesq 방정식을 사용하고 있으며, 이 방정식은 완전 비선형, 약분산성의 파랑 전파 모의를 위하여 ε = O(1), O(μ²) << 1라는 가정을 하였다. Chen의 Boussinesq 방정식에서는 특정 수심(z = z_α)에서의 유속을 사용하고 있으며, O(μ²)의 수직 와도(vertical voticity)항이 운동방정식에 포함되어 있다. Shi et al.(2012)은 이 방정식을 conservative 형태의 방정식으로 변환하여 TVD 기법과 함께 HLL Riemann solver 기법을 이용하여 수치이산화하였다. FUNWAVE-TVD 수치모형의 conservative 형태의 Boussinesq 방정식은 다음과 같이 나타낼 수 있다.

여기서, H = η + h이며, η는 수면변위를 의미한다. 식(2)에 제시되어 있는 각 항들은 식(3)-(6)과 같다.

식(3)-(6)에서 u→a는 z = z_α = − 0.53h에서 정의된 유속을 의미하며, 식(5)와 (6)의 하첨자 x, y, t는 각각 x, y, t에 대한 미분을 의미한다. 식(3)-(6)의 (U1', V1'), (U1", V1"), (U₂, V₂), (U₄, V₄)는 분산항을 의미하며, (U₃, V₃)는 수직 와도항을 나타낸다. (U1', V1'), (U1", V1"), (U₂, V₂), (U₃, V₃), (U₄, V₄) 항들의 자세한 전개는 Choi and Seo(2015), Shi et al.(2016)에 제시되어 있다. 식(2)의 (R^x, R^y)는 바닥마찰항을 의미하며, (R^bx, R^by)는 C_brk1, C_brk2를 계수로 사용하는 eddy viscosity 형태의 쇄파 방법에 의하여 모의되는 쇄파항을 의미한다. 쇄파방법에 대한 자세한 설명은 Kennedy et al.(2000)과 Shi et al.(2016, 2018)에 제시되어 있다.

FUNWAVE-TVD 수치모형에서는 flux항(F, G)을 풀 때 MUSCL-TVD 기법에 따라 각 격자점 경계의 좌, 우측값을 계산한 뒤 HLL 기법(Zhou et al., 2001)을 이용하여 numerical flux를 계산한다. FUNWAVE-TVD 수치모형 버전 2.1까지는 Yamamoto and Daiguji(1993)가 제안한 4차 정확도의 MUSCL-TVD 기법과 van-Leer limiter를 이용한 2차 정확도의 MUSCL-TVD 기법을 선택하여 사용할 수 있도록 되어있으며, 최근 Choi et al.(2018)은 Erduran et al.(2005)이 제안한 4차 정확도의 MUSCL-TVD 기법을 적용하여 부산항의 실제 해역에 대한 파랑모의를 수행하였다. 본 연구에서는 위의 세가지 MUSCL-TVD 기법을 사용하여 FUNWAVE-TVD 수치모형에서의 각각의 수치해를 비교하였다.

3. MUSCL-TVD 수치기법

4. 수치실험 결과

Vincent and Briggs(1989)는 타원형 수중천퇴를 통과하는 규칙파 및 불규칙파의 굴절, 회절, 천수 및 쇄파를 모의하기 위한 수리실험을 수행하였다. 다방향 조파기를 사용하여 일방향 주파수 스펙트럼 불규칙파, 협폭 다방향 불규칙파, 광폭 다방향 불규칙파의 파랑 전파, 변형 실험을 하였으며, 입사파고를 다르게 하여 비쇄파 및 쇄파 조건의 실험을 수행하였다.

본 연구의 수치실험에 사용된 타원형 수중천퇴가 있는 수심 지형을 Fig. 1에 제시한다. 수중천퇴의 중심은 x = 6.1m, y = 12.5m이며, 수중천퇴를 제외한 영역은 0.4572 m로 일정하다. FUNWAVE-TVD 모형에서는 파를 조파하기 위하여 내부조파 방법을 사용하는데, x = 0m에 내부조파기를 설치하였다. Fig. 1에 제시되어 있지 않지만, 모의영역 경계에서 반사파의 생성을 방지하기 위하여 x 방향의 실험영역 왼쪽과 오른쪽 경계에 파랑 흡수층(sponge layer)을 설치하였다.

Fig. 1.

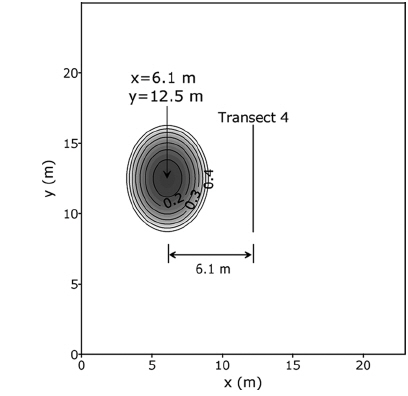
Bottom topography for Vincent and Briggs (1989) experiment.

Vincent and Briggs의 수리실험에 대한 수치실험 결과는 Yoon et al.(2004)과 Choi et al.(2009)에 의하여 제시된 바 있으며, 특히 Yoon et al.은 REFDIF S 모형과 천수방정식모형을 결합시켜 파랑이 쇄파될 때 수중천퇴 후면에서 파고가 낮아지는 역학구조를 설명하였다. Choi et al.은 TVD 기법이 사용되기 이전 버전의 FUNWAVE 모형과 REF/DIFSHORECIRC 결합모형, SWAN-SHORECIRC 결합모형을 이용하여 수치모형 실험결과와 수리실험 관측치를 비교한 바 있다.

본 연구에서는 FUNWAVE-TVD 모형에서 MUSCL-TVD 기법에 따른 수치실험 결과와 관측치를 비교하여 모형의 정확성을 검토하였다. TVD4-YD, TVD4-E, TVD2를 사용하여 비교하였으며, TVD4-YD 기법의 경우 식(9)-(12)에서 b = 1.1, 2, 3, 4일 때를 함께 비교하였다. 각 기법에서 나타나는 numerical dissipation 차이를 비교하기 위하여 bottom friction은 사용하지 않았다. 또한, 공간 격자 간격을 줄여가며 기법에 따른 모형의 수렴도 및 안정도를 비교하였으며, 쇄파 실험의 경우 numerical dissipation에 의한 오차를 최대한 줄이기 위하여 공간 격자 간격을 충분히 줄였을 때의 wave-induced current를 모의하였다.

Vincent and Briggs는 각 실험에 대하여 Fig. 1의 Transect 4에서 무차원화된 파고 관측값을 제시하였는데, 규칙파 실험의 경우 36.4초(= 28 주기) 동안 기록된 수면변위를 이용한 파고를 제시하였으며, 불규칙파 실험의 경우는 260초(= 200주기) 동안 기록된 수면변위를 이용하여 무차원화된 파고값을 제시하였다. FUNWAVE-TVD 모형을 이용한 규칙파의 실험 결과는 Choi and Seo(2015)에 제시되어 있으며, 본 연구에서는 비교적 긴 시간을 모의하였을 때의 수치실험 결과와 관측치를 비교하기 위하여 Vincent and Briggs의 수리실험 중 불규칙파의 비쇄파 및 쇄파 현상에 대한 모의를 수행하였다. 실험조건은 Table 1에 제시한다.

Table 1.

Test cases in Vincent and Briggs (1989) experiments

Transect 4에서 관측치와 비교하기 위한 수치실험 결과의 파고값은 불규칙 파랑이 계산영역을 충분히 통과한 시간인 27.3초(= 21 주기) 이후부터 260초(= 200 주기) 동안 계산된 수면변위를 이용하여 유의파고(H_mo)를 산정하였다. 산정된 유의파고를 무차원화할 때는 기존의 연구(Yoon et al., 2004; Choi et al., 2009)에서 제시된 바와 같이 입사파고로 무차원화하였으며, Choi et al.(2009)에 제시된 Vincent and Briggs의 수리실험 관측값을 사용하여 수치실험 결과와 비교하였다.

4.1 비쇄파 실험

비쇄파 실험 조건에 해당하는 N3, N4 실험의 파랑 스펙트럼을 이용하여 수중천퇴를 통과하는 불규칙 파랑의 전파, 변형 실험을 수행하였다. 내부조파 방법에 의하여 조파된 불규칙 파랑은 수중천퇴를 통과하면서 수심의 변화로 인하여 굴절 현상이 나타나며, 천퇴 후면 중앙부근에서 파랑의 집중현상으로 파고가 커지게 된다. 이 때 천퇴 후면에서는 파랑이 집중되는 구간과 집중되지 않는 구간의 파고 차이로 인하여 파랑의 회절 현상도 함께 나타난다.

N3와 N4 실험의 입사파랑 제원은 유의파고 0.0254 m, 첨두주기 1.3 s이다. TMA 주파수 스펙트럼은 각각 폭이 넓은 광대역 주파수 스펙트럼(γ = 2)과 폭이 좁은 협대역 주파수 스펙트럼(γ = 20)을 사용하였으며, 방향분포(wrapped normal spreading, Borgman(1984)) 함수는 두 실험 모두 σ = 10을 사용하였다.

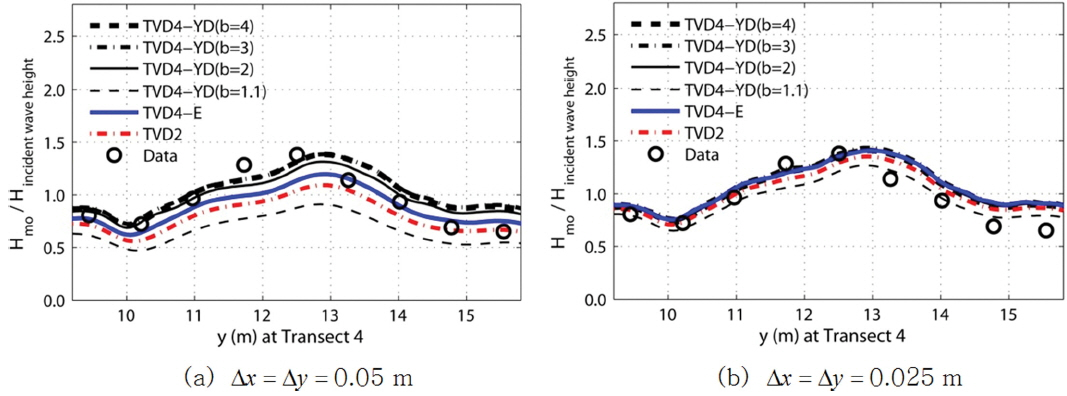
수중천퇴 후면의 Transect 4에서 계산된 N3 실험의 수치실험 결과와 Vincent and Briggs의 수리실험 관측치와 비교한 결과를 Fig. 2에 제시하였다. Kim et al.(2009)은 완전 비선형 Boussinesq 모형을 이용하여 TVD4-YD의 b값에 따른 고립파 전파 실험을 수행한 바 있는데, 고립파의 이동거리를 비교하여 b = 1.1일 때 numerical dissipation이 가장 크다는 결과를 보였다. 본 연구에서도 식(9)-(12)에서 TVD4-YD의 b를 조절한 결과를 같이 제시하였다. 또한 수치모형의 수렴도를 보기 위하여 공간격자간격 Δx = Δy = 0.05 m(Fig. 2(a)), 0.025 m(Fig. 2(b))를 사용하여 결과를 비교하였다.

Fig. 2.

Comparison between normalized wave height by FUNWAVE-TVD and experimental data for N3 case.

Fig. 2(a)의 Δx = Δy = 0.05 m를 사용한 결과에서는 각 기법의 numerical dissipation에 의하여 파고 분포가 다르게 나타나는 결과가 명확히 나타난다. Δx = Δy = 0.025m를 사용한 결과와 비교했을 때 TVD4-YD(b = 4)를 사용한 결과에서 numerical dissipation 현상이 가장 작게 나타났으며, 낮은 b를 사용할수록 numerical dissipation이 크게 나타났다. Fig. 2(b)의 Δx = Δy = 0.025 m를 사용한 결과에서 TVD2와 TVD4-YD(b = 1.1)을 제외한 TVD4에서는 상당히 유사한 파고 분포로 수렴하는 결과를 보였다.

FUNWAVE-TVD 모형에서 Δt는 식 (28)과 같이 계산되는데, 각각의 time-step마다 CFL, u_{i, j}, v_{i, j}, H_{i, j}에 따라서 Δt가 달라지게 된다. N3 실험을 수행하기 위하여 사용한 최대 CFL을 Table 2에 제시하였다(실험은 CFL ≤ 0.5 범위에서 수행하였다).

Table 2.

Maximum CFL condition for N3 case

(28) Δt=CFLmin(minΔx|ui,j+gHi,j|,minΔy|vi,j+gHi,j|)

TVD4-YD(b = 4)는 안정적인 모의를 위해서 Δx = Δy = 0.05m 격자에서 CFL = 0.4, Δx = Δy = 0.025m 격자에서는 CFL = 0.2를 사용하였다. 반면에, TVD4-E와 TVD2에서는 Δx = Δy = 0.05, 0.025 m에서 모두 CFL = 0.5를 사용하여도 안정적인 모의가 가능하였다. 따라서 TVD4-YD(b = 4)는 TVD4-E에서 요구하는 격자의 크기만큼 세밀한 격자를 요구하지는 않지만, 더 낮은 CFL을 사용해야 안정적인 모의가 가능하며, 반면에 TVD4-E는 TVD4-YD(b = 4)에 비하여 numerical dissipation을 줄이기 위하여 세밀한 격자를 요구하지만 비교적 높은 CFL을 사용할 수 있는 것으로 나타났다.

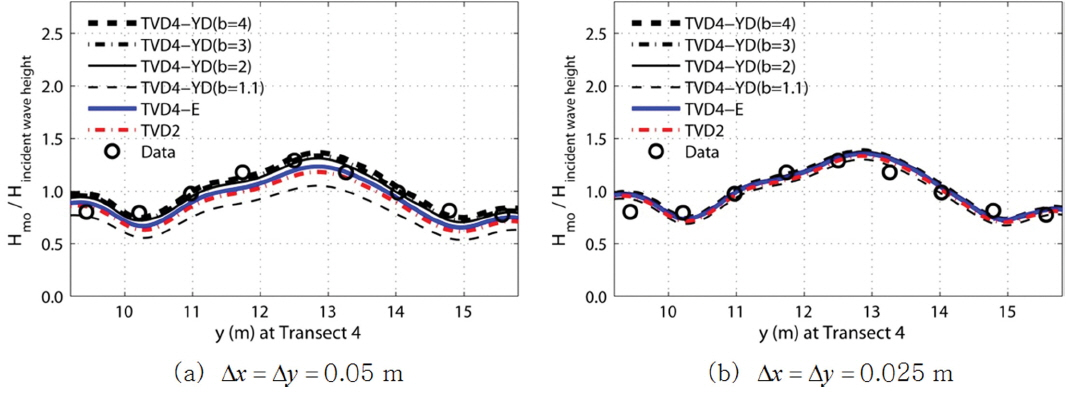
수중천퇴 후면의 Transect 4에서 계산된 N4 실험의 무차원화 파고를 Fig. 3에 제시하였다. N4 실험 결과에서 나타난 각 기법에 대한 차이는 N3 실험 결과와 유사하다. N4 실험의 안정적인 모의를 위하여 사용된 CFL 또한 N3 실험에서 사용된 CFL과 유사하다. 하지만, Δx = Δy = 0.05m의 격자를 사용했을 때 N3 실험 결과(Fig. 2(a))에 비하여 N4 실험 결과(Fig. 3(a))에서 각 기법에 의한 numerical dissipation 현상이 더 작게 나타난다. N3 실험에서는 폭이 넓은 광대역 주파수 스펙트럼을 사용하였기 때문에 폭이 좁은 협대역 주파수 스펙트럼에 비하여 단파 성분의 주파수 스펙트럼을 더 많이 포함한다. 따라서 N3 실험에서는 이러한 단파의 적절한 재현을 위해서 N4 실험에서 사용되는 격자보다 더욱 세밀한 격자를 요구하며, 충분히 줄여지지 않은 같은 공간격자 상에서 모의할 경우 N3 실험 결과에서 numerical dissipation 현상이 더 나타나게 된다.

Fig. 3.

Comparison between normalized wave heights by FUNWAVE-TVD and experimental data for N4 case.

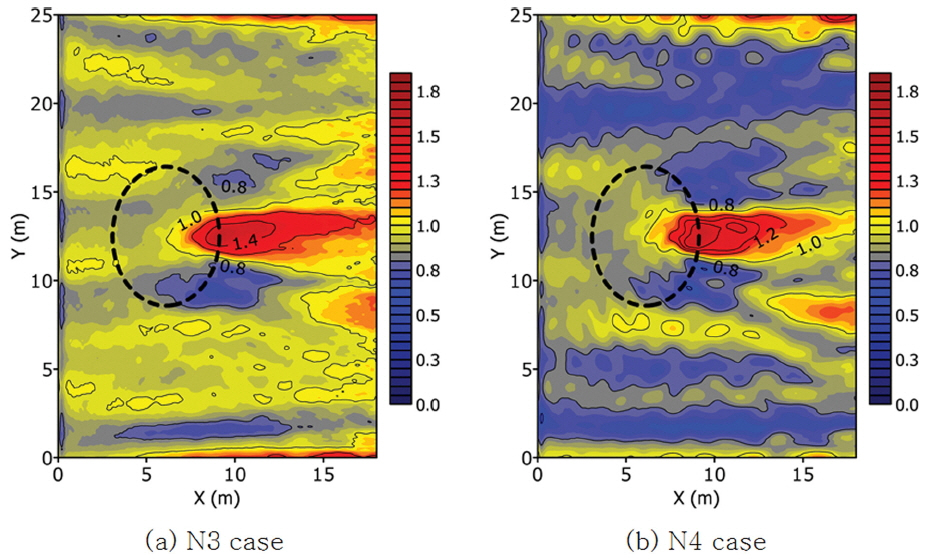
Fig. 4에 N3, N4 실험에 대한 x-y 평면상의 무차원화 파고 분포를 나타내었다. Δx = Δy = 0.025m를 사용한 결과이며, TVD4-YD와 수렴되는 결과를 보인 TVD4-E의 결과를 제시하였다. 수중천퇴 후면에서 불규칙파랑의 굴절-회절로 인하여 나타난 파고의 공간적 변화가 잘 나타나 있다. 또한 수중천퇴의 중심선 y = 12.5m를 기준으로 파고의 비대칭 분포가 나타나는 것을 알 수 있는데, Choi et al.(2009)에 의해 제시된 바와 같이 불규칙파랑이 내부조파 방법에 의해 조파될 때 내부조파선을 따라 일정한 파고로 조파되지 않았기 때문일 수 있으며, 다른 한편으로는 다방향 불규칙 파랑을 조파함에 있어서 실험시간이 충분하지 않았기 때문에 한 방향으로 파향이 우세한 결과가 나올 수 있었기 때문인 것으로 추정된다. 실제로 이러한 비대칭성은 Fig. 2와 Fig. 3의 관측치에서도 잘 나타난다.

Fig. 4.

Horizontal normalized wave height distributions using TVD4-E with Δx = Δy = 0.025 m.

4.2 쇄파 실험

쇄파 실험은 비쇄파 실험에 비하여 높은 입사파고를 사용하며, 비선형성이 상대적으로 증대된 실험에 해당한다. Boussinesq 모형에서 비선형성이 큰 문제를 모의하는 경우 수치모형 내에서 수치적인 불안정성이 많이 나타나는데, 이러한 Boussinesq 모형의 수치적인 불안정성에 대한 문제는 선행 연구에도 많이 제시되어 왔다(Liu, 1995; Kirby et al., 1998; Walkley and Berzins, 2002). 4.2절에서는 FUNWAVE-TVD 모형을 이용하여 불규칙 파랑의 쇄파 실험을 수행하였으며, 본 연구에서 고려된 각각의 TVD 기법으로 안정적으로 모의되는지 검토하였다. 불규칙 파랑의 비쇄파 실험 결과에서 TVD4-YD(b = 1.1)는 TVD2보다 numerical dissipation 현상이 과하게 나타났기 때문에 쇄파 실험 결과에서는 생략하였다.

Table 1에 제시된 실험안 중 Vincent and Briggs의 불규칙 파랑의 쇄파 실험(N5, B5 case)에 해당하는 결과를 제시한다. N5, B5 실험의 입사파랑 제원은 유의파고 0.190 m, 첨두주기 1.3 s이다. TMA 주파수 스펙트럼은 각각 폭이 좁은 협대역 주파수 스펙트럼(γ = 20)과 폭이 넓은 광대역 스펙트럼(γ = 2)을 사용하였으며, 방향분포 함수는 각각 폭이 좁은 분포(σ = 10)와 폭이 넓은 분포(σ = 30)를 사용하였다. Vincent and Briggs의 관측치와 비교하기 위하여 관측치와 동일한 시간간격인 260초(= 200 주기) 동안 계산된 수면변위를 이용하여 무차원화 파고를 산정하였으며, 총 290초를 모의하였다.

Fig. 5에 N5 실험의 Δx = Δy = 0.05m를 사용한 결과를 제시한다. 비쇄파 실험결과에서 Δx = Δy = 0.05m를 사용하였을 때 모든 기법의 결과에서 numerical dissipation 현상이 나타났지만, 여기서는 격자를 충분히 줄인 Δx = Δy = 0.025m의 결과와 비교하기 위하여 Δx = Δy = 0.05m 격자를 사용했을 때의 결과를 함께 제시한다. 쇄파계수와 관련하여 Shi et al.(2016, 2018)에 제시된 바와 같이 낮은 값의 C_brk1과 C_brk2를 사용하면 쇄파 작용이 많이 발생하는데, 관측치와 비교했을 때 쇄파가 과하게 발생하지 않도록 본 연구에서는 C_brk1 = 0.45로 고정하고, C_brk2를 조절하여 관측치를 재현하였다. Fig. 5에 쇄파계수 C_brk1 = 0.45, C_brk2 = 0.35를 사용한 결과를 제시한다.

Fig. 5.

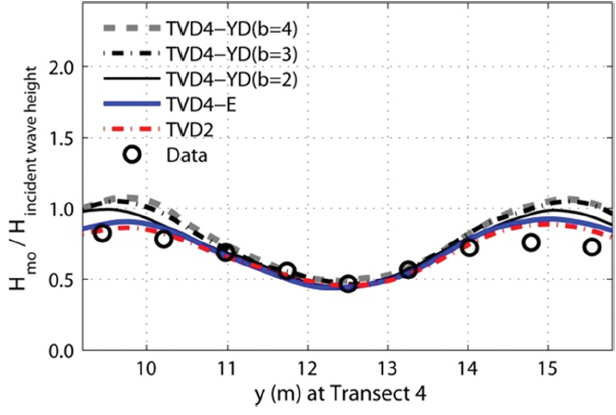
Comparison between normalized wave heights by FUN-WAVE-TVD and experimental data for N5 case using Δx = Δy =0.05 m.

Yoon et al.(2004)은 수중천퇴 위를 전파하는 파랑이 쇄파되면 wave-induced current가 발생하고, 이 흐름이 수중천퇴 후면 중앙부에서 나타나는 파랑의 집중을 방해하여 쇄파 현상이 발생하지 않는 실험에 비하여 파고가 낮아지게 된다는 역학구조를 제시한 바 있다. Fig. 5에 제시된 결과에서는 각 기법에 따라 약간의 차이는 있지만 수중천퇴 후면의 중앙부에서 파고가 낮은 분포를 확인할 수 있다. 또한 본 연구에서 고려한 모든 TVD 기법은 Δx = Δy = 0.05m를 사용했을 때 numerical dissipation의 영향으로 수치해의 발산 현상 없이 모의완료되었다. Fig. 5의 결과는 각 기법의 numerical dissipation의 영향을 줄이지 않은 상태에서 쇄파 계수를 사용하여 관측치를 재현한 결과이기 때문에 x-y 평면상에서의 파고 분포는 생략한다.

다음은 numerical dissipation의 영향을 가능한 줄이기 위하여 공간격자간격을 충분히 줄인 Δx = Δy = 0.025m를 사용한 결과를 제시한다. 총 290초의 모의시간 동안 Δx = Δy = 0.025 m를 사용한 N5, B5 실험에서는 각 기법의 특성이 보다 명확히 나타나는데, 0.05 ≤ CFL ≤ 0.5 범위 안에서 b = 2, 3, 4를 사용한 TVD4-YD는 모두 수치해가 발산하였으며, TVD4-E와 TVD2를 사용한 모형에서만 모의 완료되었다. 쇄파계수 C_brk1은 0.45로 고정하고, C_brk2는 0.20, 0.35를 사용하여 모의하였으며, 관측치와 비교하였다.

Fig. 6과 7에 N5, B5 실험의 결과를 제시한다. Fig. 6에는 수중천퇴 후면의 Transect 4에서 관측치와 각 기법을 이용하여 모의된 무차원화 파고를 비교하였다. 또한 Fig. 6(a)의 N5 실험 결과에서는 쇄파계수 C_brk1은 0.45로 고정하고, C_brk2는 0.20, 0.35를 사용하여 비교하였으며, C_brk2 = 0.35를 사용했을 때보다 C_brk2 = 0.20을 사용했을 때 관측치와 비교적 잘 일치하는 결과를 보였다. B5 실험에서도 C_brk1 = 0.45, C_brk2 = 0.20을 사용했을 때 관측치와 잘 일치하는 결과를 보였다.

Fig. 6.

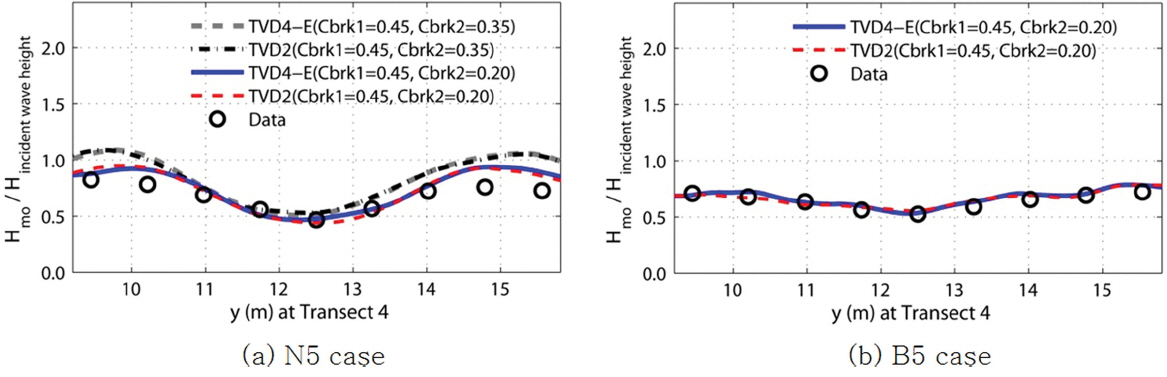
Comparison between normalized wave heights by FUNWAVE-TVD and experimental data for (a) N5 and (b) B5 cases using Δx = Δy = 0.025 m.

Fig. 7.

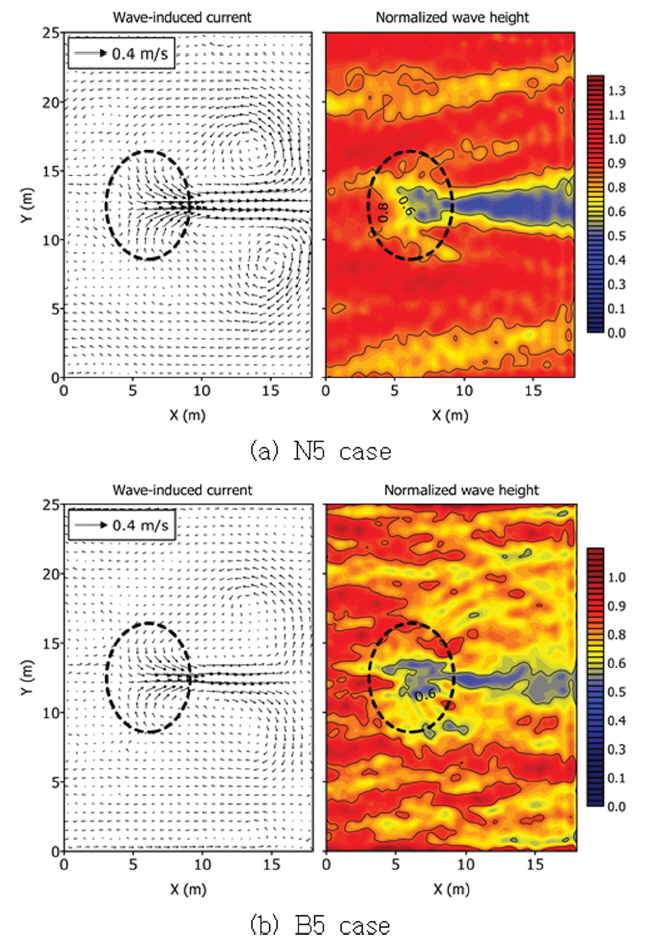
Normalized wave heights and wave-induced currents by FUNWAVE-TVD using TVD4-E for (a) N5 and (b) B5 cases.

Fig. 7에 N5, B5 실험의 x-y 평면상에서의 wave-induced current와 무차원화 파고 분포를 제시하였다. Fig. 6에 제시된 결과와 동일하게 27.3초 이후 260초 동안 계산된 결과이며, 쇄파계수 C_brk1 = 0.45, C_brk2 = 0.20와 TVD4-E를 사용한 결과를 제시하였다. 쇄파 실험은 비쇄파 실험에 비하여 수치적인 불안정성을 완화시키기 위하여 상대적으로 낮은 CFL을 필요로 하였으며, Fig. 7에는 모의 가능한 최대 CFL을 사용한 결과를 제시하였다. Fig. 7(a)에 제시된 N5 실험 결과는 CFL = 0.1, Fig. 7(b)의 B5 실험 결과는 CFL = 0.08을 사용하였다. TVD2의 경우 Fig. 2와 3의 비쇄파 실험에서 Δx = Δy= 0.025m 격자를 사용함에도 약간의 numerical dissipation 현상을 보였기 때문에 x-y 평면상에서의 결과는 생략한다.

Fig. 7에 수중천퇴 위를 전파하는 파랑의 쇄파로 인하여 발달된 wave-induced current가 명확히 나타나 있으며, wave-induced current가 생성된 구간의 파고가 낮은 분포를 보이고 있다. N5 실험의 wave-induced current 결과의 경우 current를 중심으로 위, 아래의 와류 분포가 명확히 나타난다. 하지만, 비쇄파 실험 결과에서도 언급한 바와 같이 N5, B5의 쇄파 실험결과에서도 모두 y = 12.5 m를 기준으로 비대칭 구조의 current 결과와 파고 결과가 나타나는 것을 확인할 수 있다.

5. 결 론

기존의 많은 연구(Liu, 1995; Kirby et al., 1998; Walkley and Berzins, 2002)에서 Boussinesq 파랑모형의 수치적인 불안정 문제는 제시되어 왔다. 초기의 Boussinesq 파랑모형에서는 고주파 성분의 수치진동으로 야기되는 수치적인 불안정 문제를 완화시키기 위하여 수치 필터를 사용하였다(Kirby et al., 1998; Woo and Liu, 2004). 하지만 수치 필터를 사용하여 수치적인 불안정 문제를 완화시키는 것은 모의하는 문제에 따라 상당히 제한적이었으며, 특히 급변하는 수심을 통과하는 파랑의 모의나 비선형성이 크게 작용하는 모의에서 수치해가 발산하는 현상은 여전히 나타났다.

최근 들어 Boussinesq 파랑모형의 수치적인 불안정 문제를 완화시키고자 TVD 기법을 사용한 Boussinesq 파랑모형이 개발된 바 있으며, FUNWAVE-TVD 수치모형도 그 중의 하나에 해당한다. 최근 Abadie et al.(2012)은 FUNWAVE-TVD 모형에서 TVD4-YD를 사용했을 때 수치적인 불안정이 나타난다는 결과를 제시한 바 있으며, Choi et al.(2018)은 FUNWAVE-TVD 모형을 이용하여 TVD4-YD 대신 TVD4-E를 사용하여 총 7200초의 모의시간 동안 부산항에서의 파랑 전파 변형실험을 수행했으며, 관측치를 잘 재현하는 결과를 보였다.

본 연구에서는 FUNWAVE-TVD 모형을 이용하여 적용되어 온 TVD 기법들의 수렴도와 수치적인 안정성을 비교하기 위하여 수리실험 관측치가 제시되어 있는 Vincent and Briggs(1989)의 불규칙 파랑실험에 적용하였다. 비쇄파 실험에 적용한 결과에서 b = 4를 사용한 TVD4-YD는 TVD4-E에서 요구하는 격자의 크기만큼 세밀한 격자를 요구하지는 않지만, 더 낮은 CFL을 사용해야 안정적인 모의가 가능하였으며, 반면에 TVD4-E는 numerical dissipation을 줄이기 위하여 TVD4-YD에 비하여 세밀한 격자를 요구하지만 비교적 높은 CFL을 사용할 수 있는 것으로 나타났다.

불규칙 파랑의 쇄파 실험에서는 numerical dissipation의 영향을 가능한 줄이기 위하여 공간격자간격 Δx = Δy= 0.025m를 사용했는데, 이 경우 각 TVD 기법들의 특성이 보다 명확히 나타났다. 관측치와 비교하기 위한 총 290초의 모의시간동안 TVD4-E와 TVD2에서 안정적인 수치결과가 계산되었으며, TVD4-YD를 사용한 결과에서는 Abadie et al.(2012)이 제시한 결과처럼 수치해가 발산하는 현상을 보였다. 또한 TVD4-E와 TVD2는 비쇄파 실험에 비하여 낮은 CFL을 사용해야만 쇄파 실험에 대한 모의가 가능하였다.

본 연구에서 수행된 실험만으로 특정 TVD 기법이 가장 정확하고 안정적인 기법인 것으로 결론 내리기는 어렵지만, 쇄파 실험과 같이 비선형성이 크게 작용하는 모의에서는 TVD4-E나 TVD2와 같이 numerical dissipation이 허용범위 내에 존재하는 기법을 사용하여 격자를 충분히 작게 나누는 방법이 안정적으로 모의되는 것으로 나타났다. 또한 본 연구에서 고려한 TVD 기법 외에도 Boussinesq 파랑모형 내에서 수치적인 불안정을 완화시킬 수 있는 수치해석 방법이 개발된다면 Boussinesq 파랑모형이 보다 광범위하게 사용될 수 있을 것으로 판단된다.

Article information Continued