2.1 파랑 모형 및 물리적 계수 설정

동해안에서 발생하는 너울성 장주기파랑을 모의하기 위해, 본 연구에서는 네덜란드 Delft 공과대학에서 개발된 3차원 풍파모형인 SWAN(Simulating WAves Nearshore) 을 이용하여 수치모의를 수행하였다. 이 모형은 파랑 작용을 파향 에너지 스펙트럼의 형태로 표현하고, 2차원 수평공간에 대해 파랑 에너지 스펙트럼의 변화를 에너지 평형방정식인 식(1)과 같이 에너지 평형 방정식에 의해 계산한다.

식(1)에서 θ는 방향, σ는 상대 각주파수, N은 작용 밀도 스펙트럼이며 c_x, c_y, c_σ 및 c_θ는 각각 x, y, σ 및 θ 방향에 대한 파랑 에너지의 전파 속도를 의미한다. 그리고, 파랑 작용 밀도 스펙트럼 N(σ, θ)는 파랑 에너지 밀도 스펙트럼 E(σ, θ)을 파랑 주파수로 나눈 N(σ, θ) = E(σ, θ)/σ의 관계를 가지며, S는 파랑에너지의 생성 및 감쇠 그리고 비선형 상호작용을 나타내는 원천항으로 식(2)와 같이 표현된다.

여기서 S_in은 바람에 의한 파랑 에너지 성장, S_{nl, 3}과 S_{nl, 4}는 3방향 또는 4방향 파랑 비선형 상호작용에 의한 에너지 전이, S_{ds, w}, S_{ds, bed} 및 S_{ds, br}는 백파, 바닥 마찰 및 수심으로 인한 파랑에너지 소실을 나타낸다. 본 연구에서는 너울성 파랑의 예측 정확도를 개선하기 위해 식(2)에서 백파에 의한 파랑에너지 감쇠항 S_{ds, w}를 Rogers et al.(2003)가 제시한 기법을 사용하였다. 이를 간단히 설명하면, 백파에 의하여 발생하는 파랑에너지 소산은 강한 비선형성으로 인해 수식화가 쉽지 않아 대부분 경험식에 의존하고 있다. Hasselmann(1974)는 백파에 의한 파랑 에너지 소산을 다음과 같은 경험식을 통해 표현하였다.

여기서, C_ds는 백파에 의해 발생하는 에너지 감쇠비 계수, m는 Pierson-Moskowitz 스펙트럼으로 정규화한 값의 멱수이며, n은 상대 파수(Relative wave number)의 가중치를 의미하는 경험상수이다. SWAN 모델에서는 C_ds = 2.36 × 10⁻⁵, m = 4, n = 1을 기본값(Default Parameter)로 사용하고 있다. Rogers et al.(2003)에서는 장주기 너울성 파랑의 재현성을 높이기 위해 상대파수의 가중치 n은 2.0의 값을 사용하였으며, C_ds와 m은 기본값을 사용하였다. 그리고 장주기 파랑에서 발생하는 파랑에너지 소산을 감소시키기 위해 식(4)와 같이 백파 에너지 소산항을 개선하였다.

여기서 C_{σ, ψ, ζ}(σ, θ)는 파랑의 주기(σ), 기상 조건(ψ) 및 파형 경사(ζ)에 의해 결정되는 계수로, 파랑의 주파수별로 다른 특성을 가지는 에너지 소산을 표현하여 너울성 파랑의 예측 정확도를 높이는 데 기여하는 경험 상수이다. 본 연구에서는 너울성 장주기 파랑의 모의하기 위해 SWAN version 40.72을 사용하였으며, 수치모의 시 사용한 계수는 Table 1에서 제시한 값들을 제외하고는 모델의 Default 값을 사용하였다.

Table 1.

Numerical and physics parameters except for default setting

2.2 격자 구축 및 수심

본 연구에서는 바람에 의한 파랑의 성장과 전파, 그리고 연안지역에서 수심 변화에 의한 파랑 변형을 예측하기 위해 1단계 네스팅(nesting) 기법을 적용하였다(Fig. 1(a)). 광역 모델은 동해 북쪽의 오호츠크해를 포함하도록 격자 체계를 정방 격자로 구성하였으며, 격자의 해상도는 약 5 km× 5 km(총 45,000개의 격자)이며 수심자료는 ETOPO5 수심자료(https://www.ngdc.noaa.gov/mgg/global/etopo5.HTML)와 KorBathy30s 자료(Seo, 2008)를 이용하여 구축하였다. 그리고 본 연구에서는 수심의 변화에 따른 파랑 변형을 고려하기 위해 약 300 m × 300 m(총 250,000개의 격자) 해상도의 연안모델을 우리나라 동해안에 구축하였다. 연안 모델의 외해 경계에서는 광역 모델 결과를 2차원 파랑 에너지 스펙트럼의 형태로 저장한 후, 입력 조건으로 사용하였으며 광역 모델과 동일하게 바람에 의한 파랑 변형도 고려하였다. Fig. 1(b)는 본 연구에서 구축한 연안 모델 격자의 범위 및 수심을 보여주고 있다. 연안 모델의 수심자료는 광역 모델에서 사용한 KorBathy30s 자료와 국립해양조사원에서 관측한 150 m 간격의 해상도 자료를 이용하여 생성하여 연안역에서의 수심을 정밀하게 표현하였다.

Fig. 1.

(a) Model domains of the numerical model for two-stage nesting procedure: (white) overall model and (red) Coastal model domains (b) bottom topography of coastal model.

2.3 해상풍자료

수치모델을 통해 동해안에서 발생하는 너울성 파랑을 정확하기 예측하기 위해서는, 먼저 시공간적으로 변화하는 해상풍에 대한 자료가 필수적이며 이는 대부분 수치 기상 모델 결과를 이용한다. 연안공학분야에서 널리 사용된 수치 기상모델자료는 중규모 유럽 기상예보센터(ECMWF, The European Centre for Medium-Range Weather Forecasts)에서 제공하는 ECMWF ERA-interim(Berrisford et al., 2011) 자료이며, 파랑 후측 모의 및 장기간 유의파고 추세 분석 등에 많이 이용되었다(Lee and Jun, 2006; Kang et al., 2015; Ko et al., 2017). 이 자료는 지역 기상 데이터 통신 네트워크(RMDCN, the Regional Meteorological Data Communication Network)를 이용하여 수치모델에 자료동화를 적용하여 기상 예측도가 높다고 알려져 있다(Berrisford et al., 2011). ECMWF ERAinterim 자료는 1979년부터 현재까지 0.125° 해상도로 기상자료를 제공하고 있으며, 시간 간격은 6시간이다. 하지만 6시간 간격의 해상풍 자료로는 동해안에서 발생하는 너울성 고파랑을 예측하기에는 한계가 있어, NOAA에서 제공하는 1시간 간격의 NCEP(National Centers Environmental Prediction) 자료, 일본 기상청의 바람 예보자료 등이 활용되고 있다(Eum et al., 2016; Chun et al., 2014; Yuk et al., 2016).

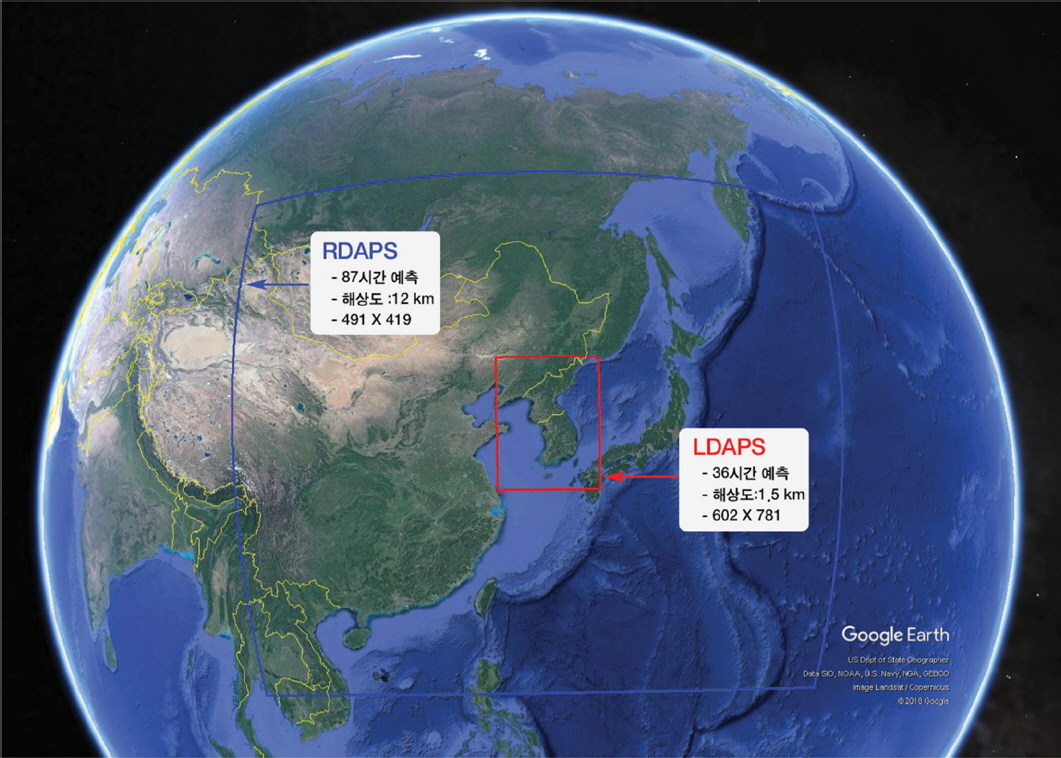
본 연구에서는 기상청 현업기상예보모델에서 생산되는 시공간 바람장을 수치모델의 해상풍 입력자료로 이용하였다. 기상청에서는 우리나라 주변의 기상을 지역예보모델(RDAPS, Regional Data Assimilation and Prediction System)과 국지예보모델(LDAPS, Local Data Assimilation and Prediction System)을 이용하여 현업 예보하고 있다. 지역예보모델은 기상청에서 운용 중인 전지구예보모델(GDAPS, Global Data Assimilation and Prediction System)로부터 초기 및 경계 기상조건을 제공받아 운영되며, 4차원 변분자료 동화 기법을 이용하여 1일 4회, 3시간 간격으로(00, 06, 12, 18 UTC) 분석-순환체계 기상예보를 수행하고 있다. 지역예보모델은 공간 해상도는 12 km를 가진 87시간 동안의 기본 단기예측자료를 생성하며 이는 현재 기상청에서 구축중인 파랑 및 폭풍해일모델의 입력 자료로 이용되고 있다. 국지예보모델의 공간 해상도는 1.5 km이며, 지역예보모델로부터 필요한 입력자료를 제공받아 1일 8회, 1시간 간격의(00, 06, 12, 18 UTC: 36시간 예측, 03, 09, 15, 18 UTC: 3시간 예측) 기상자료를 예보하고 있다. 국지예보모델은 3차원 변분자료 동화기법이 적용되어 예측 정확도를 높이는데 활용되고 있다. Fig. 2는 국지예보모델과 지역예보모델의 운영 범위를 보여주고 있다.

Fig. 2.

Outline of the domains of the LDAPS and RDAPS models.

모의된 파랑의 예측 정확도를 비교 · 평가하기 위하여 ECMWF ERA-interim 재분석 자료 및 한국해양과학기술원 해양예보시스템 WRF 예측 자료(Park et al., 2015) 또한 수치모델의 해상풍 입력자료로 사용하여 모의하여 그 결과를 상호 비교하였다. 사용된 WRF는 1시간 및 20 km의 시공간 해상도를 갖는다.

3.1 수치모의 시나리오 및 파랑관측자료

동해지역에서 발생하는 너울성 고파랑은 계절성 기후에 의해 생성되는 기압배치로 인한 강한 바람과 취송거리에 의해 발생하며, 주로 가을 및 겨울철에 집중되어 발생하여 연안역에 많은 피해를 주고 있다(Oh and Jeong, 2014; Chun et al., 2014). 특히, 2015년 겨울철에는 강원도 동해안에서 발생한 너울성 고파랑으로 인하여 정동진 레일바이크 선로 파괴, 속초 해변의 모래와 나무 데크 유실 및 연안 시설물 파손 등 2015년 11월부터 2016년 1월동안 약 51억 7400만원의 재산피해가 발생된 것으로 조사되었다(자료: 강원도 동해안권 상생발전협의회). 이에 본 연구에서는 2015년 11월 15일부터 12월 20일을 수치모의 기간으로 선정하였으며, 겨울철 동해안에서 발생하는 너울성 파랑을 모의하였다. 이 기간은 유의파고 3미터 이상, 첨두주기 8초 이상의 폭풍파가 최소 4차례 이상 지역별로 발생하여 본 연구에서 구축한 수치모델의 재현 정도를 살펴보는 데 적합하다.

본 연구에서는 각 기관별로 제공하는 바람자료에 따른 파랑모델의 정확도를 분석하기 위해 2.3절에서 기술한 각기 다른 기관에서 생산하는 4가지 시공간 바람자료(RDAPS, LDAPS, ERA-interim, WRF)를 입력 외력으로 사용하여 동해안 너울성 고파랑을 수치모의 하였으며, 이를 SWAN-RDAPS, SWANLDAPS, SWAN-ECMWF, SWAN-WRF로 표기하기로 한다. 이 때, 기상청에서 생산하고 있는 LDAPS 모델 자료는 그 영역이 한반도 주변만을 대상으로 하고 있어 동해안에서 발생하는 장주기 너울성 파랑을 예측하기에는 공간적으로는 충분하지 않다. 그러므로 본 연구에서는 LDAPS 모델이 포함하고 있지 않은 동해 북동부 및 일본 연안 지역에서의 해상풍 자료는 기상청에서 제공하는 RDAPS 모델의 결과를 이용하여 바람장을 생성하였다. 이때 입력 바람장은 ECMWF ERAinterim는 재분석자료이고, WRF는 예측자료이며, RDAPS 및 LDAPS는 현업 예보자료라는 차이점이 있다.

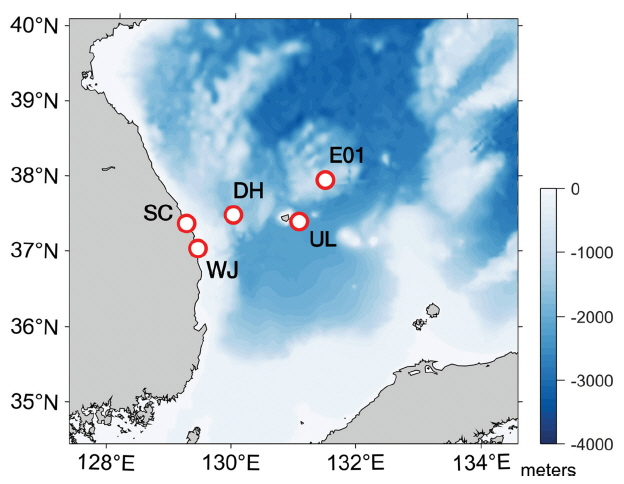
파랑 모델의 재현정도를 비교하기 위해 본 연구에서는 기상청에서 협업 예보 중인 파랑모델 및 동해에서 관측된 파랑 및 바람자료를 이용하였다. 파랑 관측자료로는 국립해양조사원 울릉도북동 해양관측부이(E01), 외해 기상청 동해 부이(DH), 그리고 한국해양과학기술원에서 삼척(SC) 및 울진(WJ) 연안에서 관측한 파랑자료를 이용하였다. 연안 정점의 경우에는 AWAC(Acoustic Wave And Current profiler) 장비를 해당 기간 동안 계류하여 취득한 자료이며(Caires et al., 2018), 본 연구에서는 해당 정점에서의 유의파고, 첨두주기 및 평균파향 자료를 이용하여 수치모델의 정확도를 분석하였다. Fig. 3은 본 연구에서 사용한 파랑 및 바람 관측자료의 정점 위치를 보여주고 있으며, 각 정점의 위치 및 수심에 대한 정보는 Table 2에 나타내었다.

Fig. 3.

Location of wave and wind measurement sites.

Table 2.

Coordinates and water depth of the wave and wind measurement site

3.2 수치모의 결과 검증

본 연구에서는 각 기관별로 제공하는 바람자료에 따른 파랑 모델의 정확도를 분석하기 위해, 입력 바람자료로 사용된 ECMWF, WRF, RDAP 및 LDAPS에 대해 외해 3개 정점에서 관측된 풍속 및 풍향자료와의 비교하였으며 이를 시계열 그래프로 나타내었다(Fig. 4). 그리고, Root-Mean-Square-Error(RMSE) 통계값을 산출하여 Table 3에 나타내었다. 하지만, DH 정점에서는 모의 기간 중 상당 기간 결측이 발생하여(2015.11.28.~2015.12.10.), RMSE 비교 시 표본의 개수가 적어 기상청 울릉도 관측 정점(UL, 131.100oE, 37.450oN)의 바람 자료를 사용하여 그 값을 제시하였다. 또한 이를 입력 바람장으로한 파랑모델 재현도에 대한 성능평가를 위하여 Fig. 5에 SWAN-ECMWF, SWAN-WRF, SWAN-RDAPS의 유의파고 및 첨두주기를 관측자료와 함께 시계열 그래프로 표현하였다. 연안에서 너울성 고파랑이 발생한 11월 27일(11/26~28)과 12월 11일(12/10~13)의 모델링 결과를 살펴보면, 삼척(SC)과 울릉도북동(E01) 정점에서는 SWAN-WRF와 SWAN-RDAPS는 비교적 관측치와 유사한 값을 보이지만, SWAN-ECMWF는 다소 과소 추정한다. 이는 ECMWF 모델에서 제공하는 바람장의 시공간 해상도가 다른 두 자료에 비해 낮아서 발생하는 오차로 보인다. 동일 기간 울진(WJ) 및 동해(DH) 정점의 경우에도 SWAN-WRF 및 SWAN-RDAPS의 정확도가 높지만, 관측치보다는 유의파고를 과소추정하고 있다. 상대적으로 유의파고가 낮은 기간(12/4~6)에서는 SWANWRF는 모의 기간 전반에 걸쳐 유의파고를 다소 크게 추정하는 것으로 보여지며, 특히 2015년 12월 4~5일에는 연안 및 외해 정점의 유의파고는 3가지 모의 케이스 중에 가장 큰 차이(과대추정)를 보인다. 첨두주기의 경우에는 상대적으로 파랑에너지가 높은 기간에서는 관측자료와 유사한 결과를 보이고 있지만, 유의파고가 낮게 관측된 12월 3일부터 8일 기간에는 첨두주기를 관측치보다 다소 과대하게 추정하고 있다.

Fig. 4.

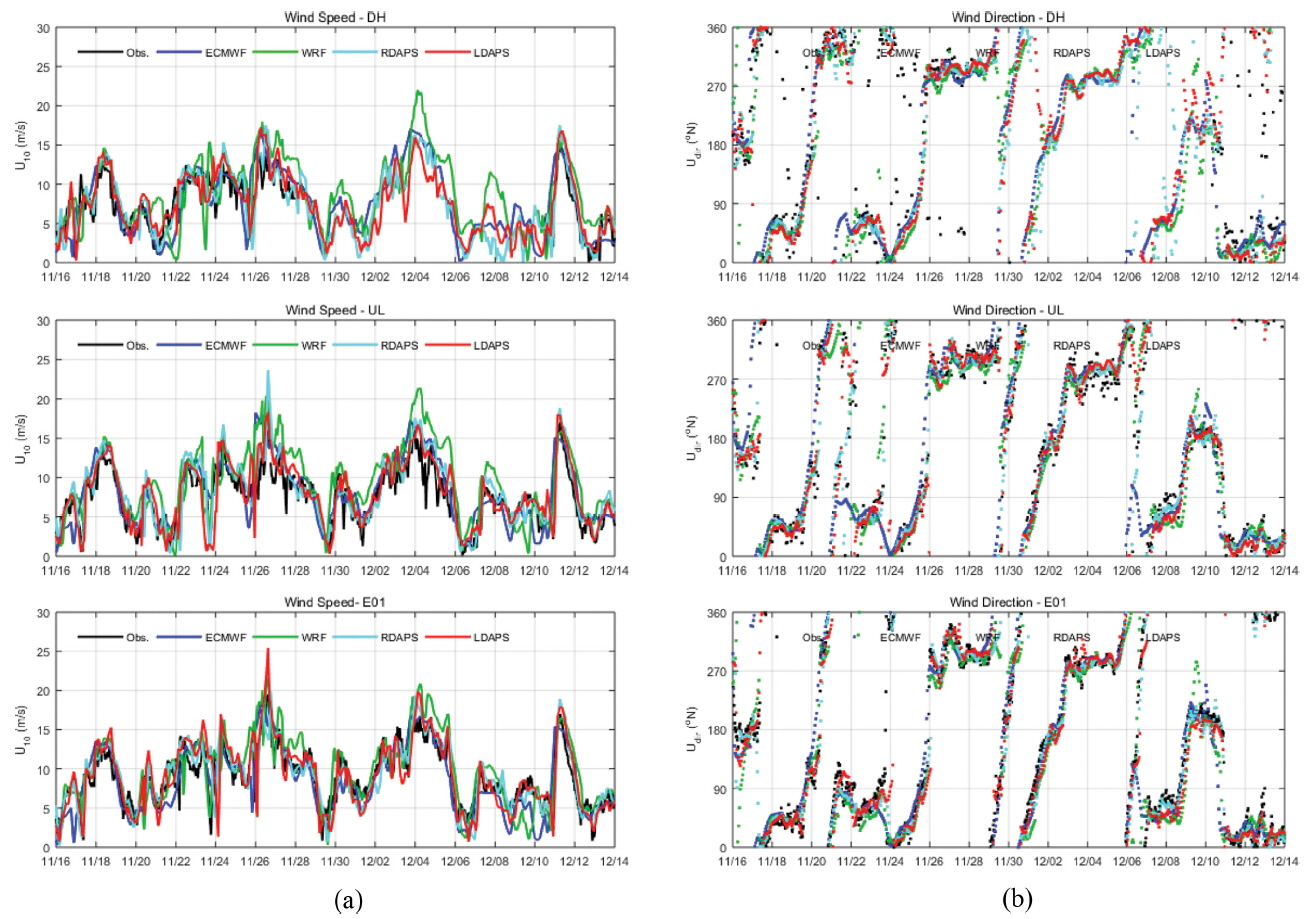
Comparisons between the observed and the modeled of (a) wind speed (u₁₀) and (b) wind direction (u_dir) of the ECWMF, WRF, RDAPS and LDAPS model prediction at DH, UL and E01.

Table 3.

Root-Mean-Square-Error (RMSE) of wind speed and wind direction for the ECMWF, WRF, RDAPS and LDAPS wind predictions at UL and E01 observation stations

Fig. 5.

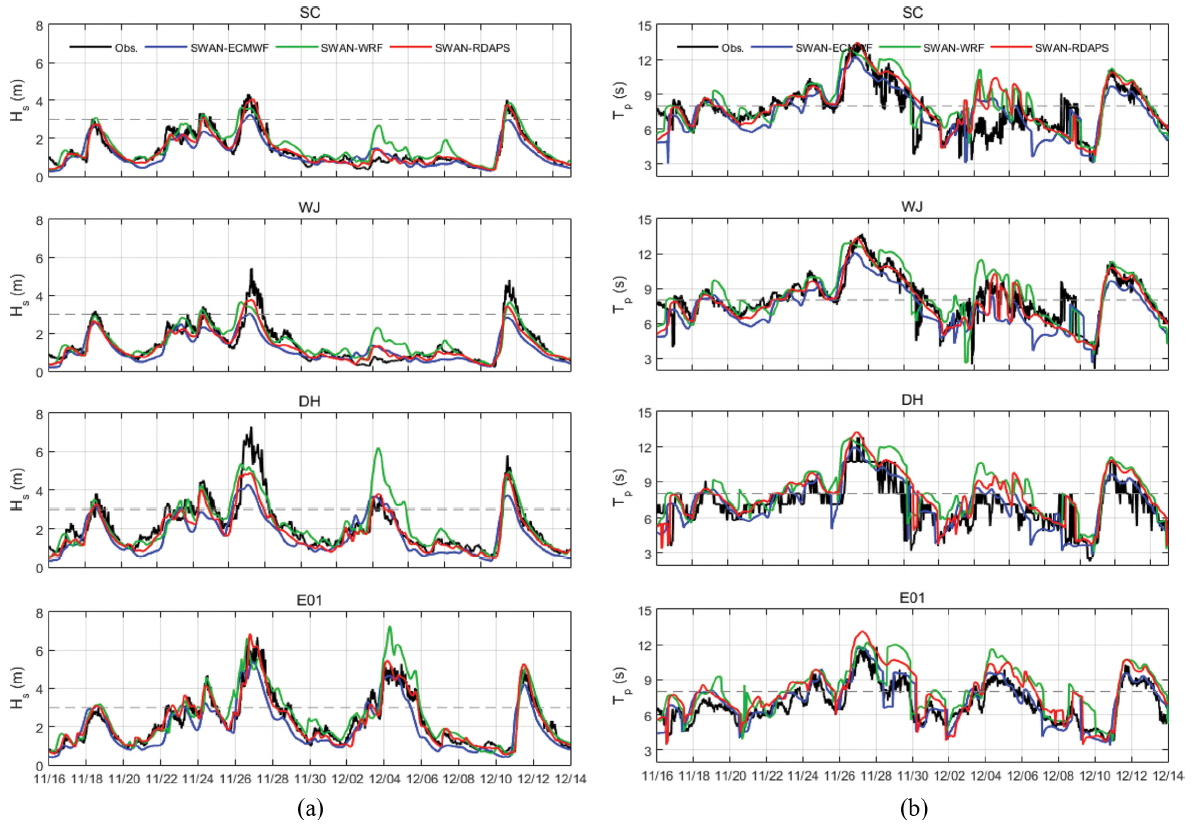
Comparisons between the observed and the modeled of (a) significant wave height (Hs) and (b) peak wave periods (Tp) of the SWAN-ECWMF, SWAN-WRF and SWAN-RDAPS model prediction at SC, WJ, DH and E01.

Fig. 6는 본 연구에서 기상청 현업 예보모델의 바람자료를 입력자료로 구축한 SWAN-RDAPS 및 SWAN-LDAPS와 기상청 현업 연안 파랑모델에 대한 유의파고 및 첨두주기 관측자료와 비교한 시계열 자료이다. 이를 분석해 보면, 기상청 현업예보 기상자료인 RDAPS의 시공간 해상도가 12 km, 3시간인 것에 비해 LDAPS는 1.5 km, 1시간으로 시공간 해상도가 높음에도 불구하고 두 입력자료에 따른 파랑모의 결과는 그리 크지 않다. 그리고 세 모델의 결과는 비교적 유사한 시계열 그래프의 형태를 보이며, 기상청 파랑 모델 결과가 11월에 유의파고를 조금 과대 추정한 것으로 보여진다. 그러나 이들 역시 11월 26~28일 사이에 발생한 너울성 고파랑을 관측치에 비해 약 2 m 정도 과소 추정하고 있다. 첨두주기의 경우에는 RDAPS와 LDAPS 모두 관측치와 유사한 값을 보이고 있지만, 기상청 파랑 모델은 삼척(SC), 울진(WJ), 동해(DH) 정점에서 너울성 고파랑이 발생한 시점(11월 27일과 12월 11일)에 파랑의 첨두주기를 약 3초 이내로 과소 추정하고 있다. 이러한 주기의 차이는 2.1 절에서 설명한 바와 같이 장주기 파랑에서 발생하는 에너지 소산을 감소하기 위해 Rogers et al.(2003)이 제안한 방법으로 인한 효과로 너울성 고파랑의 주기를 예측하는 데 효율적임을 보여주고 있다.

Fig. 6.

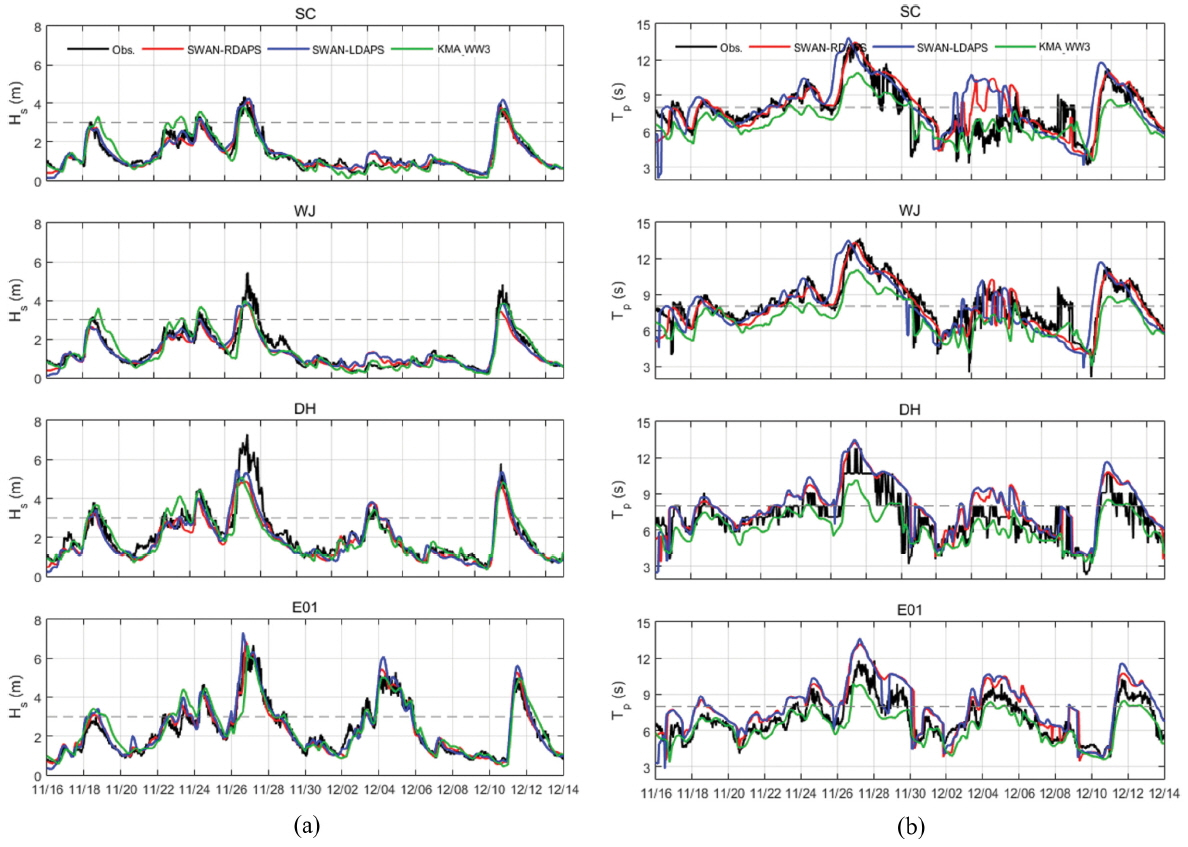
Comparisons between the observed and the modeled of (a) significant wave height (Hs) and (b) peak wave periods (Tp) of the SWAN-RDAPS, SWAN-LDAPS and KMA-WW3 model prediction at SC, WJ, DH and E01.

본 연구에서는 각각의 파랑 모의 케이스에 대한 정확도를 정량적으로 비교 및 분석하기 위해 유의파고, 첨두주기 및 평균파향에 대한 관측 정점별로 통계 분석을 수행하였으며, 그 결과를 Table 4에 나타내었다. 여기서, 통계 분석은 관측치를 기준으로 유의파고 1 m 이상이 관측되었을 경우를 대상으로 하였으며, 이는 파랑에너지가 적을 경우에 발생하는 수치모델의 오차를 통계분석에서 제외하여, 너울성 고파랑시 파랑 모의결과를 보다 엄격하게 비교 · 분석하기 위함이다. 본 연구에서 사용한 에러 통계량은 편차(bias), 평균 제곱근 오차(RMSE, Root-Mean-Square-Error), 산란 지수(SI, Scatter Index, SI), 대칭 경사(R, Symmetric Slope) 및 상관계수(ρ, Correlation Coefficient)이며, 각각의 계산식은 다음과 같다.

Table 4.

Error statistics of the SWAN-RDAPS, SWAN-LDAPS, SWAN-WRF, SWAN-ECMWF and KMA-WW3 wave predictions for SC, WJ, DH and E01’s observation stations that the measured significant wave height is greater than or equal to 1 meter

여기서, n은 에러 통계값 산출에 이용된 관측자료의 개수(샘플 개수)를 의미하며, x_i는 관측값, y_i는 모델의 결과값을 의미한다. Fig. 7은 에러통계량 중 정점별 유의파고 및 첨두주기의 RMSE를 바 그래프로 가시화한 그림이다. Table 4과 Fig. 7의 각 모의 케이스에 따른 정점별 RMSE와 상관계수를 살펴보면, 유의파고의 경우에는 모든 관측 정점에 대해 SWAN-RDAPS 및 SWAN-LDAPS의 경우가 가장 작은 RMSE 및 가장 높은 상관계수를 가지며, 이는 모의 결과의 정확도가 가장 높은 것을 의미한다. 특히, 이 두 모델의 결과는 연안에 위치한 2개 정점(SC 및 WJ)에서 RMSE가 0.3 이하, 상관계수가 0.94 이상으로 관측치와 매우 유사하게 유의파고를 예측하고 있다. 파랑의 첨두주기는 연안에서는 SWAN-RDAPS 및 SWAN-LDAPS의 RMSE가 가장 낮으나, 외해의 두 개 정점에서는 SWAN-ECMWF와 KMA-WW3의 RMSE가 조금 낮다. 그러나 특이한 것은 상관계수는 SWANRDAPS 및 SWAN-LDAPS가 더 높은 값을 갖는다. 이는 첨두주기의 관측값과 예측값의 차이는 조금 더 크나, 두 값의 경향성은 더 좋다고 볼 수 있다. 하지만, Fig. 5(b)에서 외해 두 개 정점에서 관측된 파랑의 첨두주기를 살펴보면, 연안 정점에 비해 그 시간적 변동성이 매우 크며 불규칙한 패턴을 보인다. 수치모델의 경우 이러한 불규칙한 패턴의 주기를 재현하지 못하여 모든 정점에서 ± 1.3초 및 0.8 이상의 RMSE가 발생하였으며, 외해의 경우에는 관측자료의 한계로 인해 각 모델의 정확도를 상대적으로 비교 · 평가하는 것이 쉽지 않다.

Fig. 7.

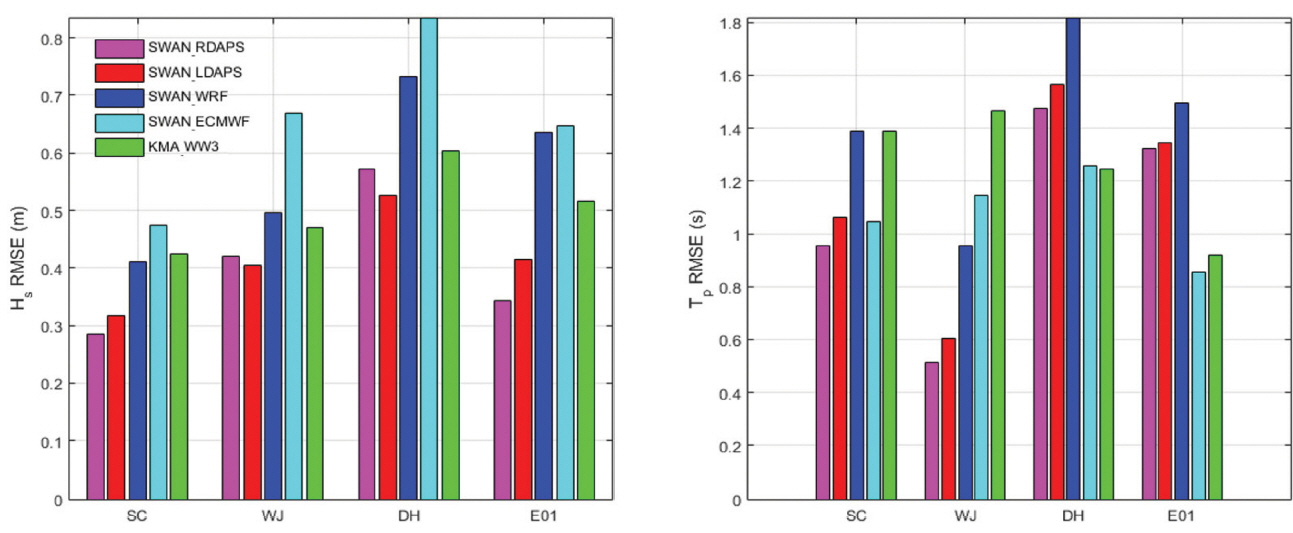
Bar graph of the root-mean-square-error (RMSE) of the wave model results (Hs and Tp) that the measured significant wave height is greater than or equal to 1 meter during simulated period (2015.11.16∼2015.12.15).

마지막으로 수치모델에서 생산하는 파향에 대한 정확도를 분석하기 위해 Fig. 8에서는 관측자료와 각각의 모델링 케이스에서 계산된 평균파향에 대한 시계열 자료 및 RMSE를 바 그래프로 나타내었다. 평균 파향 역시, 첨두주기와 마찬가지로 연안에 위치한 2개 정점에서는 모든 모델링 케이스에 대해 RMSE가 10~13도 내외로 그 정확도가 매우 높지만 외해의 경우에는 상대적으로 오차가 크다. Fig. 8(a)에서 보여주는 시계열 자료를 분석해보면, 외해 두 개 정점에서 관측된 파향은 주기와 마찬가지로 연안 정점에 비해 시간적 변동성이 매우 크며, 불규칙한 패턴을 보인다. 특히, 이러한 불규칙한 패턴으로 인하여 RMSE가 크게 발생된 것으로 보이며 모델의 정확도를 평가하기에는 외해에서 관측된 울릉도북동 해양관측부이(E01)와 기상청 동해 부이(DH)에서 생산하는 평균파향의 신뢰도가 낮아 한계가 있다. 하지만, 안정적으로 파향을 관측한 연안 정점의 경우에는 수치모델의 정확도가 매우 높으므로 너울성 고파랑의 파향 재현도가 높다고 판단된다.

Fig. 8.

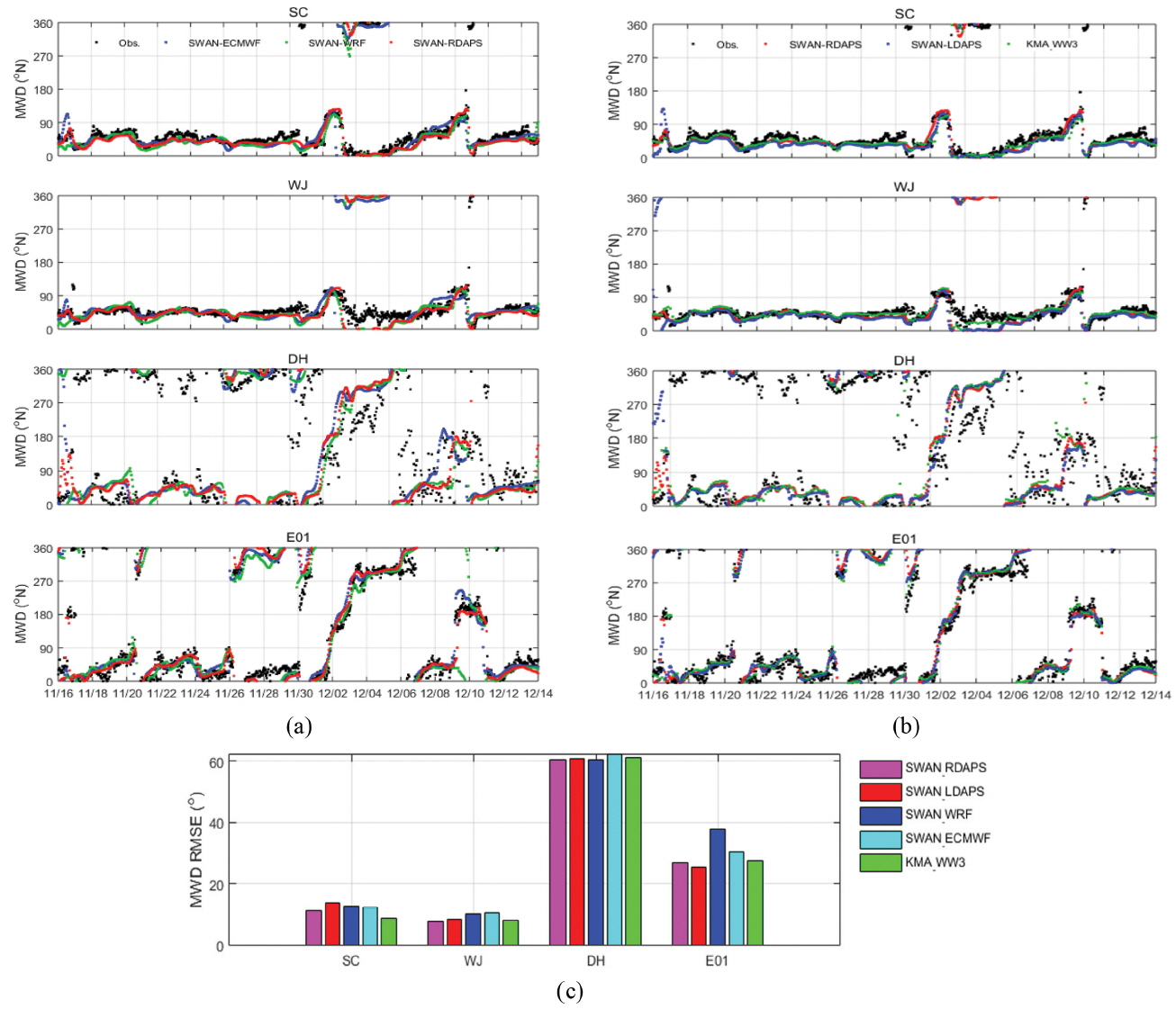
Time series of the wave observations and mean wave direction of the (a) SWAN-ECMWF, SWAN-WRF and SWAN-RDAPS, (b) SWAN-RDAPS, SWAN-LDAPS and KMA-WW3 model prediction at SC, WJ, DH and E01 and (c) Bar graph of the root-mean-square-error (RMSE) of the wave model results (MWD) that the measured wave height is greater than or equal to 1 meter during simulated period (2015.11.16∼2015.12.15).