Article information

Abstract

Trans Abstract

1. 서 론

해저에서의 지각변동 또는 산사태는 수심의 변동을 야기하며 이러한 수심의 변화는 자유수면으로 전달되어 지진해일이라고 일컫는 수면변화를 일으킨다. 상승된 수면은 천수 및 굴절 현상 등을 겪으면서 해안으로 전파하고 이에 의해 증가된 파고는 연안 지역에 막대한 피해를 야기한다.

지진해일의 발생과 그로 인한 피해는 역사적으로 오랜기간 동안 관측 및 기록되어 왔다(Braynt, 2014; Gusiakov, 2009). 한 연구를 통해 보고된 바에 따르면 지구상 20여개국의 100여개 도시가 지진해일의 위험성에 심각하게 노출되어 있다고 한다(Wilson et al., 2013). 2000년대에 발생한 지진해일의 대표적 사례를 소개하면 다음과 같다. 우선 2004년 12월 26일 인도네시아 수마트라 섬 서부 해안의 40 km 지점에서 발생한 규모 9.3의 인도양 수마트라 지진에 의해 약 33 m에 이르는 지진해일고가 해안에 전파되었으며, 이로 인해 약 23만명이 목숨을 잃고 5만 명 이상이 실종, 169만 명 이상의 난민이 발생하는 등의 인명피해를 입었다. 이는 역사상 3번째로 큰 규모의 대지진으로 기록되기도 하였다(Grilli et al., 2007). 한편, 2011년 3월 11일에 일본 동북부 태평양 연안에서 발생한 규모 9.0 도호쿠-오키 지진해일은 38.9 m의 최대 지진해일고를 기록함에 따라 막대한 인명 및 재산피해를 야기했다(Bryant, 2014). 약 2만 명의 사망 및 실종자와 6천 여명 부상자가 발생하였으며 총 피해액이 330조 원에 이르는 등 그 피해가 천문학적이었다. 가장 최근인 2018년 9월 28일에 인도네시아 팔루시에서 약 77 km 떨어진 곳에서 일어난 규모 7.5의 술라웨시 지진은 약 2100명의 사망피해를 낳기도 하였다. 한 가지 주목할 만한 점은 술라웨시 지진의 경우 섭입대(subduction zone)에서 주로 발생하는 지진과 달리 지진해일이 발생하기 힘들다고 알려진 주향이동단층(strike-slip, 수평 이동하는 단층)이었음에도 불구하고 약 4~7 m의 지진해일고를 기록하였다는 점이다. 그 원인에 대해서는 만의 형태를 지닌 피해지역의 지형, 해저산사태의 연쇄작용 등 현재 과학계에서 다양한 주장이 제기되고 있는 실정이며 정확한 원인규명을 위한 후속연구가 진행 중이다.

이처럼 지진해일의 피해는 불의 고리라고 일컫는 환태평양 조산대를 중심으로 하여 여러 나라에서 지속적으로 발생하고 있으며, 그 피해 역시 엄청난 규모를 나타내기에 정확한 예측모형개발과 방재시스템 구축에 많은 노력을 기울이고 있다. 지진해일을 모의 할 때, 통상적으로 장파이론에 기반을 둔선형 혹은 비선형의 비분산성 천수방정식을 사용하게 되고, 이에 따라 다양한 모형들이 구축되어 왔다. 몇 가지 예를 들면, Titov and Synolakis(1998)가 개발한 MOST(Method Of Splitting Tsunami), Wang(2009)이 개발한 COMCOT(COrnell Multi-grid COupled Tsunami model), Kowalik et al.(2005)가 개발한 GTM(Global Tsunami Model), George and LeVeque(2006)이 만든 TsunamiClaw(Conservation Laws) 등이 있다. 한편 지진해일 등의 장파해석에 Boussinesq 방정식 혹은 Navier-Stokes 방정식을 이용하는 등 파랑의 분산성과 동수압을 고려함으로써 정확도 높은 해석결과를 얻으려는 노력도 병행되고 있다(Son et al., 2011; Grilli et al., 2007; Saito and Furumura, 2009; Pringle et al., 2018).

이상에서 소개한 지진해일과 관련된 지금까지의 연구는 해저 수심의 변화가 자유 수면에 즉시적이고 동일하게 전달된다는 가정하에 초기파형을 결정하고 파랑의 전파양상을 수치모의하는 방식이 대부분이다. 하지만 최근 관측장비의 발전과 분석기법의 개발을 통해 지진발생의 세밀한 과정이 규명됨에 따라 지진시 해저지반의 운동이 시간이력과 공간분포 특성을 지니고 있음이 알려졌고, 이에 따라 지진해일 또한 이를 반영하여 생성된다고 밝혀졌다. Suppasri et al.(2010)과 Ohmachi et al.(2001)은 파열 속도(rupture velocity)가 느리고 단층에 가까운 지역일수록 시간이력을 고려함에 따른 지진해일의 차이가 증가함을 확인하였다. 또한 Imai et al.(2010)은 수분의 시간차를 두고 발생하는 대규모 지진의 경우 단층운동의 시간이력에 따라 지진해일이 해안에서 증폭될 수 있음을 보였다. Ishii et al.(2005) 및 Suzuki et al.(2011)은 각각 2004년 수마트라지진 및 2011년 동일본 대지진에 대하여 단층파괴과정의 시간이력을 실제적으로 확인하였으며 이에 따라 시간이력의 중요성을 강조하기도 하였다. 더군다나 기존의 접근법은 상대수심(파장에 대한 수심비)이 매우 작은 경우에만 성립하며 지진해일의 파장이 짧거나 수심변화의 지속시간이 긴 경우에는 적용할 수 없다(Lee et al., 2015; Saito and Furumura, 2009).

수심변화에 의한 초기 수면변위를 예측하는 연구는 주로 해석적인 방법을 통해 이루어졌다. Kajiura(1963)는 Green 함수를 이용하여 바닥의 변화가 근거리 및 원거리에서의 수면변위에 끼치는 영향을 검토하였으며, Hammack(1973)은 속도 포텐셜을 이용하여 수심변화가 자유수면에 끼치는 영향을 해석적으로 연구하였다. 이후 Dutykh et al.(2006), Dutykh and Dias(2007), Kervella et al.(2007) 및 Dutykh et al.(2013) 등은 Hammack(1973)의 접근법을 응용하여 다양한 수심변위 조건에서 수면변위를 계산하였다.

이상의 논문들을 통해서 다양한 수심변화에 의해서 발생하는 수면변화 및 기타 수반되는 여러가지 물리량들에 대해서는 연구가 수행되었으나 바닥수심의 변화가 시간차를 가지고 발생하는 경우에 대해서는 아직까지 연구된 바가 없다. 따라서 본 연구에서는 Hammack(1973)의 해석해를 확장하여 영역별로 시간차를 가지고 바닥수심이 변하는 경우에 대해 해석해를 제시하여 수면변위를 계산하였다. 본 연구에서는 2개의 영역에서 대해서만 다루었으나 이를 다수의 영역으로 확장할 수 있으며 또한 수심변화가 발생하는 시간 또한 다수로 나누어 계산할 수 있다. 이와 같은 접근법은 공간 및 시간 영역을 세밀하게 나누어 계산할 경우, 실제에서 발생하는 바닥 수심의 변화를 좀 더 정확하게 모의할 수 있다는 장점이 있다.

2. 해석해 유도

비압축성 유체의 비회전 흐름을 가정하면, 속도포텐셜을 이용하여 지배방정식을 다음과 같이 표현할 수 있다.

여기서 φ는 속도포텐셜을 의미하며 D는 해석 영역을 의미한다. 선형화된 자유수면 경계조건은 다음과 같이 표현이 가능하며,

이를 합쳐 다음과 같은 단일화된 자유수면 경계조건식을 구할 수 있다. 여기서 η는 자유수면, g는 중력가속도, h는 정수면으로부터 측정된 수심을 의미한다.

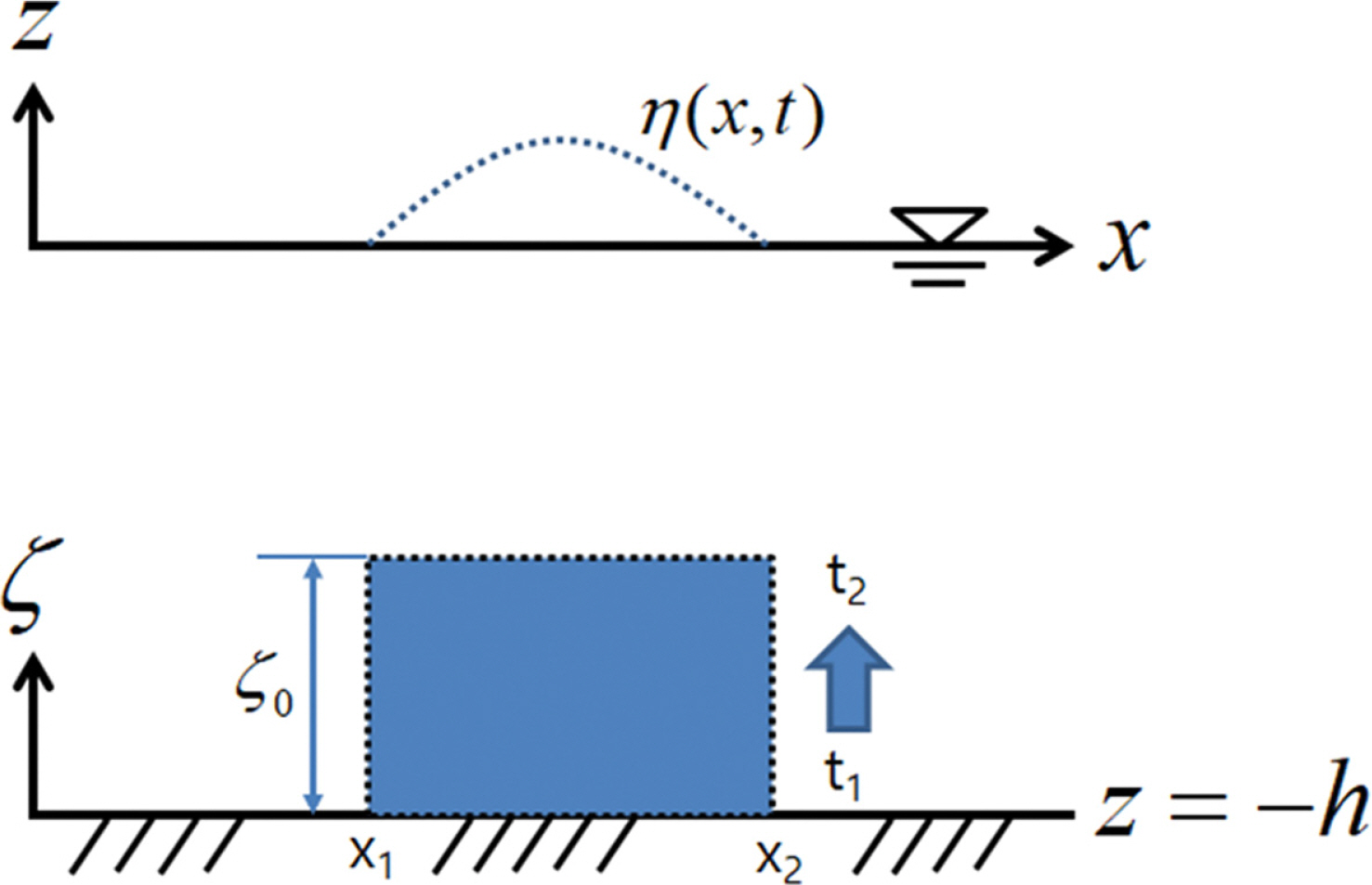
Fig. 1과 같이 시간에 따른 수심의 변화를 고려하면 선형화된 바닥경계조건은 다음과 같이 된다.

Fig. 1.

Definition sketch of bottom variation with time.

식(1), (4) 및 (5)에 대하여, 시간에 관해서는 Laplace 변환을 적용하고 공간에 대해서 Fourier 변환을 적용하면, 각각 다음과 같이 나타낼 수 있다.

여기서 f는 다음과 같이 정의된다.

식(6)~(8)을 이용하여 ϕ를 구한후, Fourier 및 Laplace 역변환을 취하면 수심변화에 의한 자유수면을 다음과 같이 계산할 수 있다(Hammack, 1973; Dutykh and Dias, 2007).

Hammack(1973)은 원점을 중심으로 대칭인 직사각형 형태의 지형이 바닥에서 상승하거나 하강하는 경우에 대한 선형파의 해석해를 제시한 바가 있다. 이를 좀 더 일반화하여, Fig. 1과 같이 특정시간(t₁ →t₂) 동안 특정범위(x₁ ≤ x ≤ x₂)에서 최대변위(ζ₀)가 발생한다고 하면 ζ는 다음과 같이 나타낼 수 있다.

또는

여기서 H는 단위 계단함수를 의미한다. 식(12)를 식(9)에 대입하여 ζ를 구하면 다음과 같이 되며,

이를 다시 식(10)에 대입하면 최종적으로 Fig. 1과 같이 주어진 조건에서 바닥지형변화에 따른 수면변위를 구할 수 있다.

여기서 A 및 B는 식(13)에서 공간과 시간에 해당하는 부분으로 실수값으로 각각 다음과 같이 주어진다.

식(14)의 적분값은 해석적으로 구하는 것이 힘들기 때문에 수치적분을 통해 구할 수 있다. 이 경우 Filon(1930)이 제안한 구적법(quadrature formula)를 사용하면 효율적으로 계산할 수 있다.

2.1 Hammack(1973)의 해와의 연관성

Hammack(1973)은 |x| ≤ b에서 수심변화가 발생하는 경우에 대하여 다음과 같은 해석해를 제안하였다.

(17) ηHammack(x,t)=ζ0π∫0∞[2coskxsinkbkcoshkh]{(α2α2+ω2)(−e−at+cosωt+ωαsinωt)}dk

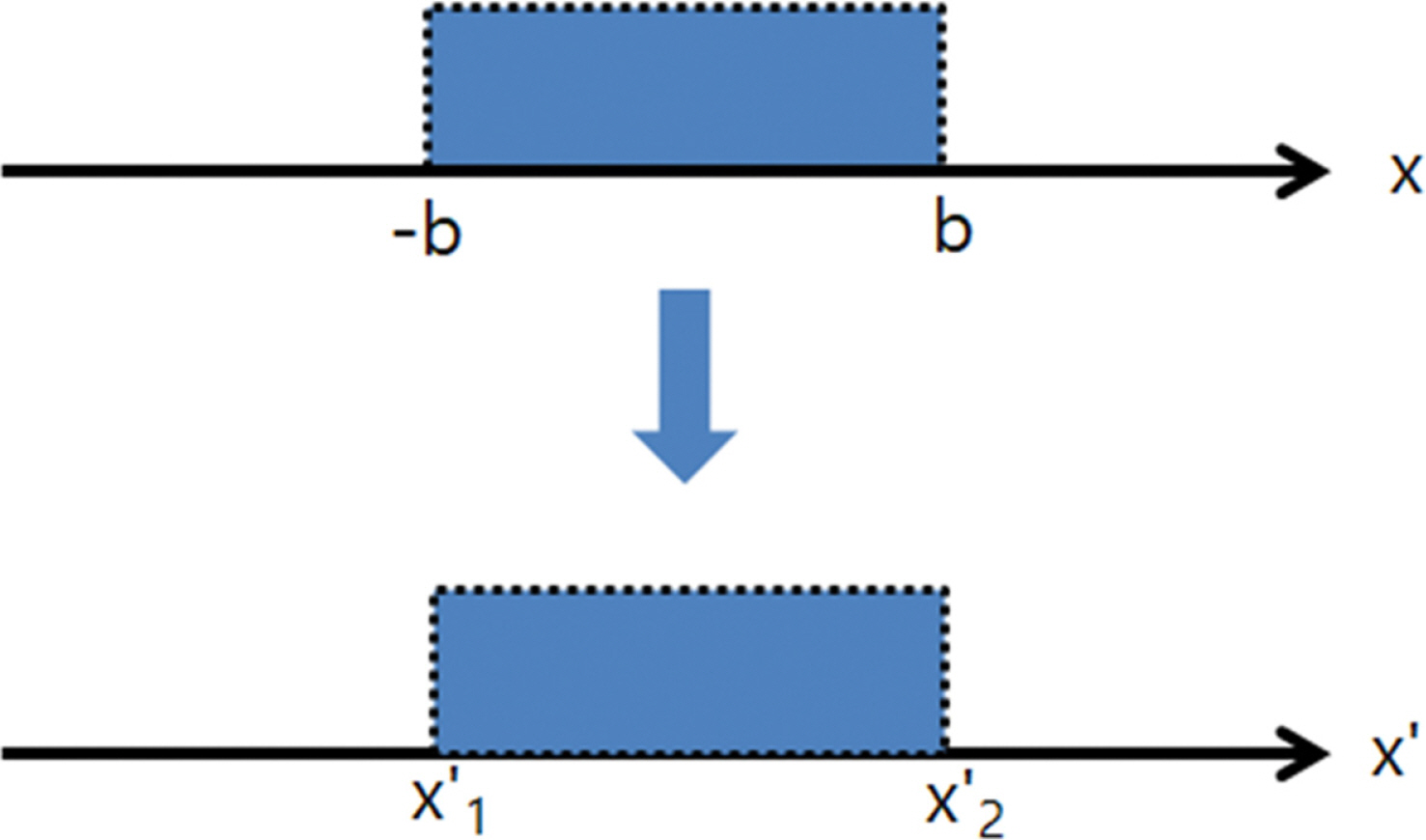
여기서 [ ]에 해당하는 부분이 식(14)의 A와 대응되는 부분이다. x₂ = b 및 x₁ = − b로 놓으면 식(15)는 Hammack(1973)의 해와 동일하게 된다. 반대로 Hammack(1973)의 해석해로부터 식(15)를 유도할 수 있다. Hammack(1973)은 수심변화 구간의 중심을 원점으로 설정하였다. 따라서, 본 연구에서의 좌표체계를 Fig. 2와 같이 x'로 가정하면 다음과 같은 관계식이 성립한다.

Fig. 2.

Relation between Hammack’s paper and present study.

(18) x = x' − (x2' +  x1')/2  및  b =(x2' +  x1')/2

식(18)을 식(17)의 [ ]에 대입하여 정리하면,

(19) 2coskxsinkbkcoshkh=2kcoskhcos(kx′−k(x2'+x1')2)sin(k(x2'−x1')2)

삼각함수에 대한 합과 곱의 공식을 사용하면

(20) cos(kx′−k(x2'+x1')2)sin(k(x2'−x1')2)=coskx′(sinkx2'−sinkx1')2−sinkx′(coskx2'−coskx1')2

이 되어 식(19)는 식(15)와 동일하게 된다. 식(14)의 시간에 해당하는 B 부분은 Dutykh and Dias(2007)의 결과와 비교하여 검증할 수 있다. Dutykh and Dias는 초기부터 해저 지형이 움직이는 경우인 경우에 대한 시간항의 해석해를 제시한 바가 있다. 이는 B의 t₁이 0이 되는 경우로서, t₁ =0으로 놓으면 본 연구의 시간항은 그들의 결과와 동일하게 된다.

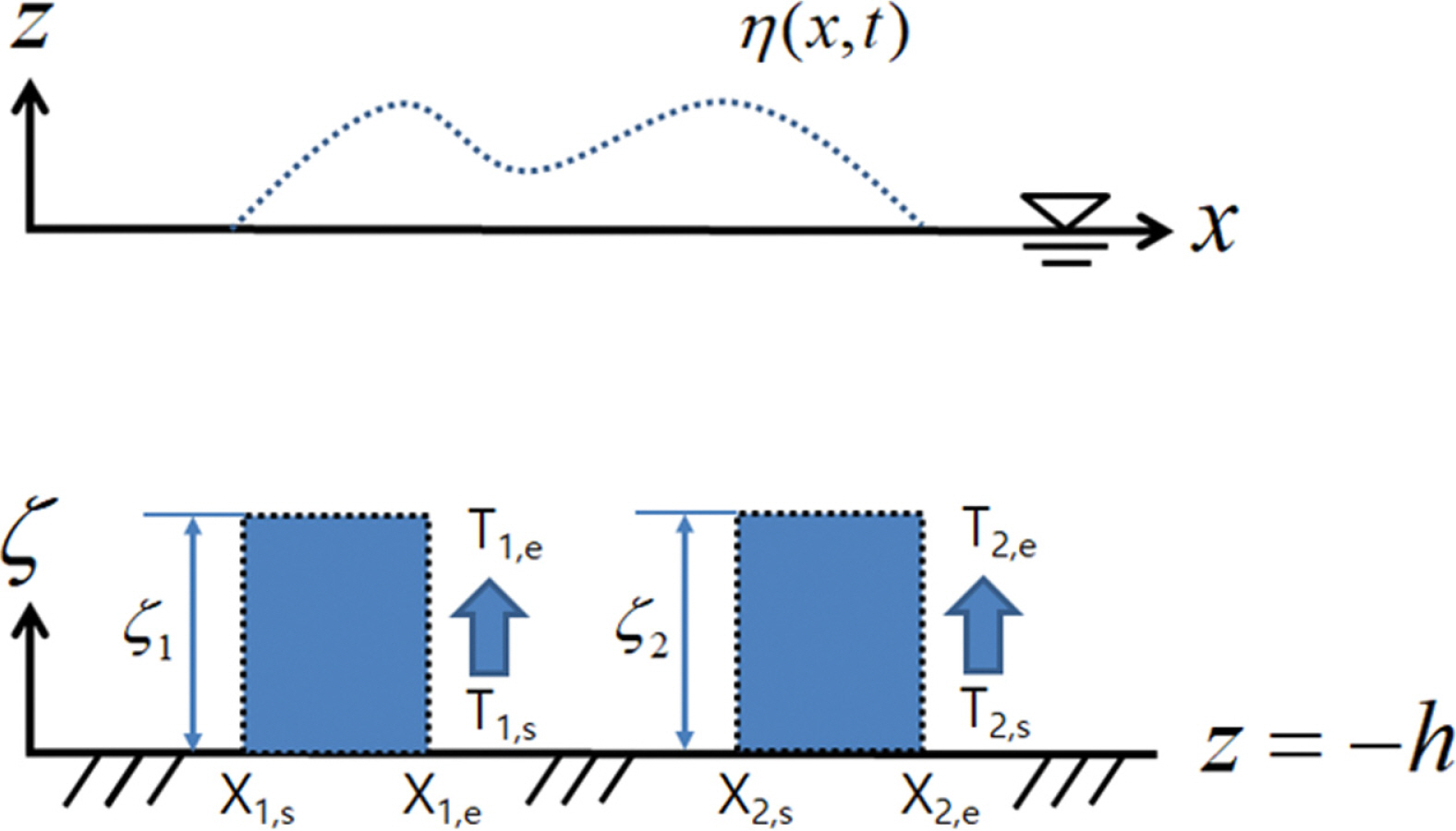
2.2 두 영역에서 수심변화가 있는 경우

Fig. 3과 같이 두 영역에서 시간차를 가지고 수심변화가 발생하는 경우 수심은 다음과 같이 표현할 수 있다.

Fig. 3.

Definition sketch of bottom variaon with time in two regions.

(21) ζ(x,t)=ζ1{H(t−t1,e)(1−t−t1,st1,e−t1,s)                    +H(t−t1,s)t−t1,st1,e−t1,s}[H(x−x1,s)−H(x−x1,e)]                 +ζ2{H(t−t2)(1−t−t2,st2,e−t2,s)                  +H(t−t2)t−t2,st2,e−t2,s}[H(x−x2,s)−H(x−x2,e)]

앞선 과정을 반복하며 주어진 수심변화로 인한 수면변화를 구해보면 다음과 같다.

(22) η(x,t)=ζ1π(t1,e−t1,s)∫0∞A1B1dk+ζ2π(t2,e−t2,s)∫0∞A2B2dk

여기서 A₁, B₁, A₂ 및 B₂는 각각 다음과 같다.

(23) A1=1kcoshkh{coskx(sinkx1,e−sinkx1,s)−sinkx(coskx1,e−coskx1,s)}

(24) B1=H(t−t1,s)sinω(t−t1,s)−H(t−t1,e)sinω(t−t1,e)ω

(25) A2=1kcoshkh{coskx(sinkx2,e−sinkx2,s)−sinkx(coskx2,e−coskx2,s)}

(26) B2=H(t−t2,s)sinω(t−t2,s)−H(t−t2,e)sinω(t−t2,e)ω

식(22)는 동일한 방법을 사용하여 n개 영역에서 수심변화가 발생하는 경우로 확장할 수도 있다.

3. 결과 분석

본 연구의 접근법에 대한 검증은 Hammack(1973)이 실험값과 비교함으로써 증명하였기 때문에 생략하였다. 먼저, Fig. 1과 같이 하나의 영역에서 바닥수심이 변하는 경우에 대하여 자유수면 변화를 모의하였다. 계산 조건은 Hammack(1973)과 동일하게 수심(h) 0.5 m, 원점에서 영역의 우측경계까지의 거리(b) 0.61 m 및 바닥수심의 최대 변동폭(ζ₀)은 0.05 m로 설정하였다.

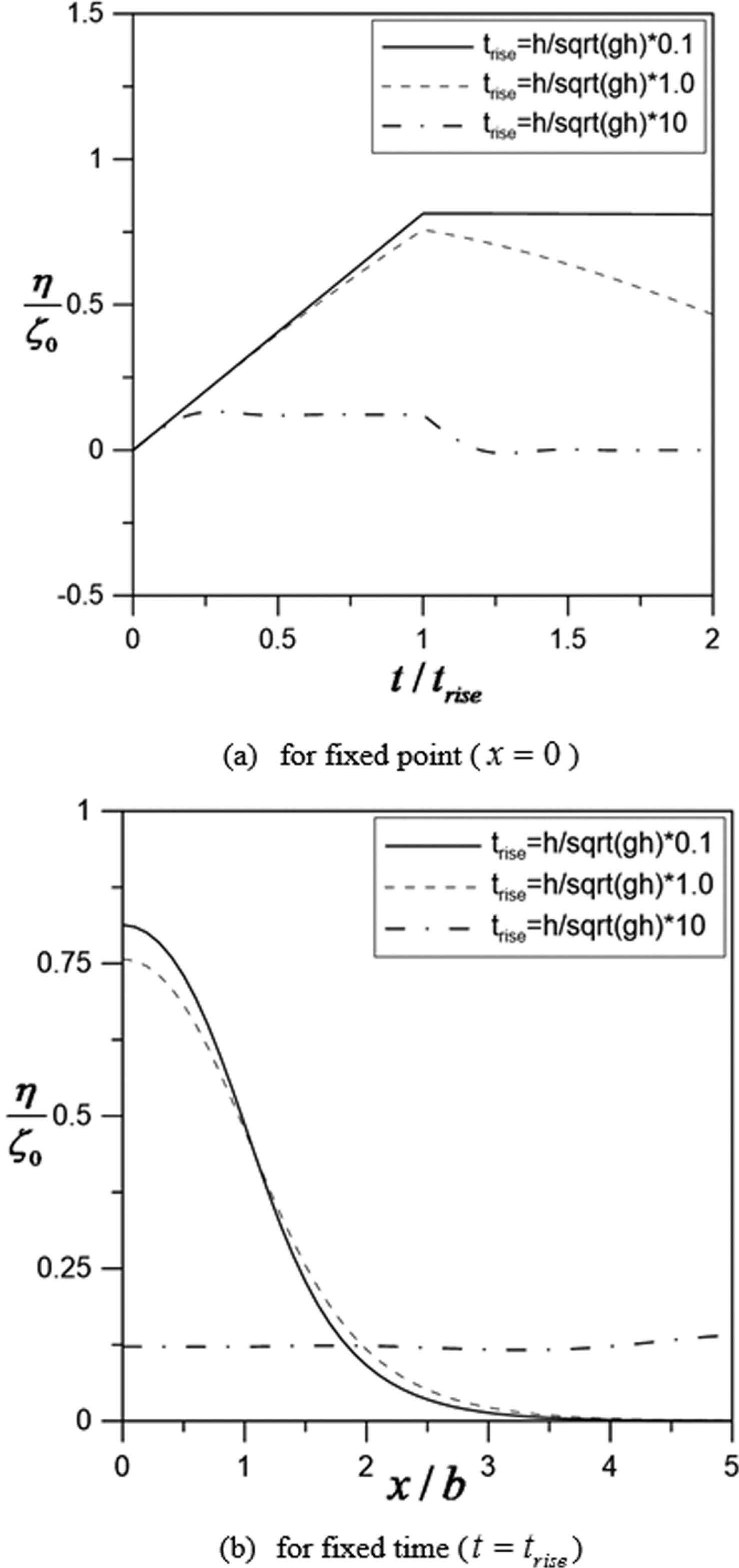
Fig. 4는 주어진 조건에서 바닥이 상승하는 시간(t_rise)에 변화를 주면서 특정지점에서의 수면변위와 특정 시간대에서의 수면분포를 도시한 그림이다. 무차원화된 바닥상승시간(t'=trise·gh/h)의 값은 0.1, 1.0 및 10.0을 사용하였으며 Fig. 4(a)는 원점(x = 0)에서 시간에 따른 수면변위를 계산한 값이며 Fig. 4(b)는 t = t_rise에서 위치에 따른 수면분포를 계산한 결과이다. 수심변화가 비교적 짧은 시간에 발생하는 경우, 수위는 수심이 증가하는 동안 꾸준히 상승하다가 수심 변화가 멈춘 뒤 점진적으로 감소하는 모습을 보였다. 그러나 수심 변화가 느리게 발생하는 경우에는 수심이 상승하는 동안 상승된 수면이 좌우로 이동하면서 0.2~1.0 의 시간대에서는 거의 수면변화가 발생하지 않았다. 이는 Fig. 4(b)를 통해서도 확인할 수 있다. t'의 값이 증가할수록 수면의 진행이 크게 발생하여 10.0인 경우에는 이미 많이 진행을 하여 거의 전 영역에서 비슷한 수면 변위를 보이는 것을 알 수 있다.

Fig. 4.

Normalized free surface elevation for different up-rising time; (a) x =0; (b) t = t_rise.

다음으로 Fig. 3과 같이 두 개의 영역에서 시간차를 가지고 수심 변화가 발생하는 경우에 대하여 수면변위를 계산해보았다. 계산 조건은 Fig. 4의 경우와 유사하게 설정하였다. 수심은 0.5 m로 설정하였으며, ζ₁ = ζ₂ = ζ₀ = 0.05 m 그리고 x_{1, e} − x_{1, s} = x_{2, e} − x_{2, s} = b = 0.61m로 설정하였다.

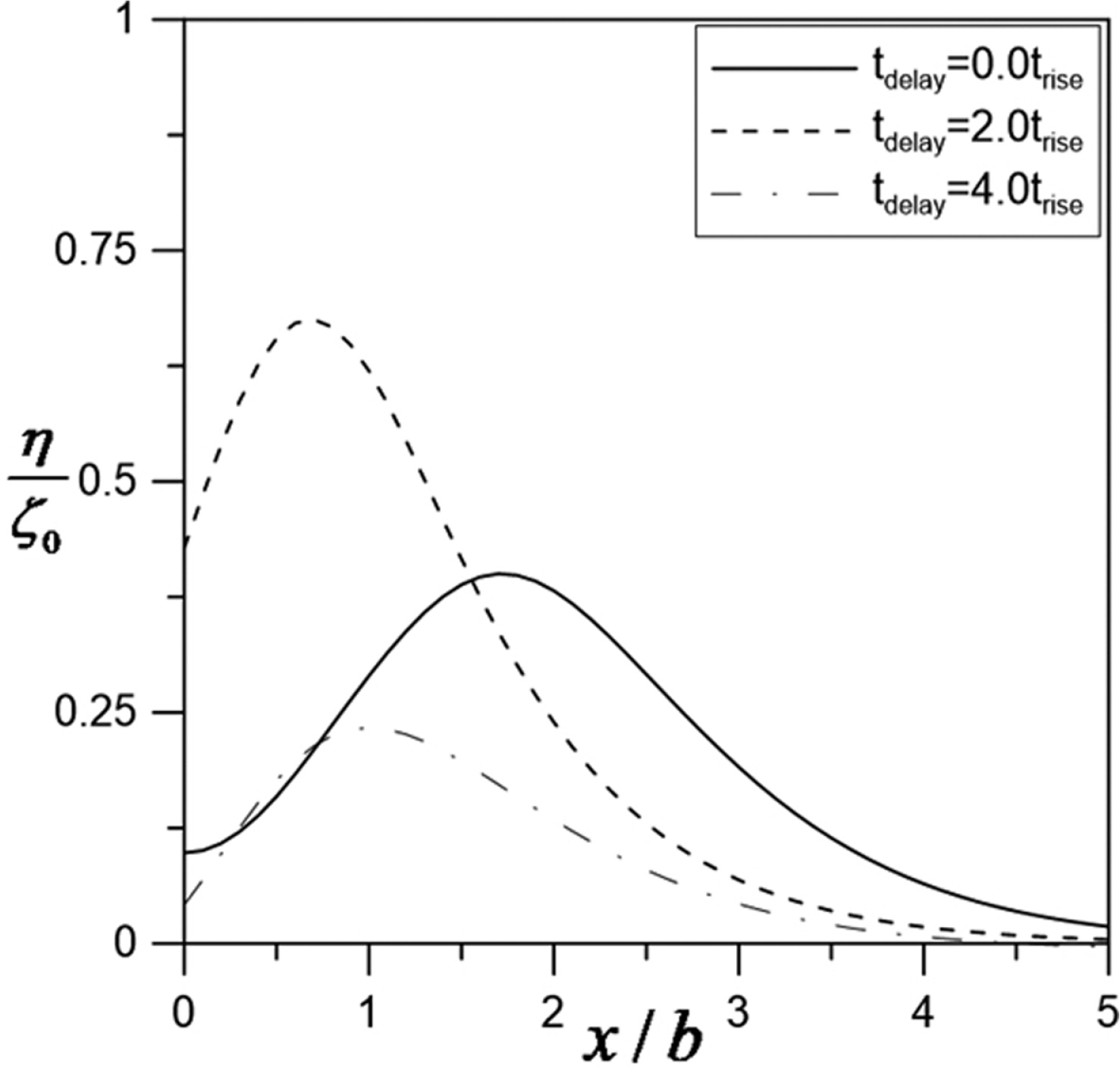
Fig. 5는 두 영역이 이웃한 상황 (즉, x_{2, s} = x_{1, e})에서 시간차를 가지고 상승하는 경우에 수면분포를 모의한 결과이다. 수심의 상승시간은 두 영역 모두 t' = 1.0으로 하였으며, 파가 어느 정도 진행을 한 t = 3t_rise인 순간에 위치에 따른 수면변위를 계산하였다. 시간차가 없는 경우(실선)와 비교해보면, t_delay = 2.0t_rise인 경우에는 최대수면변위는 상승하였으며 t_delay = 4.0t_rise인 경우에는 최대수면변위가 오히려 감소하였다. 아울러 최대값이 발생하는 지점 역시 모두 달랐다.

Fig. 5.

Normalized free surface elevation for different time-delayed bottom variation.

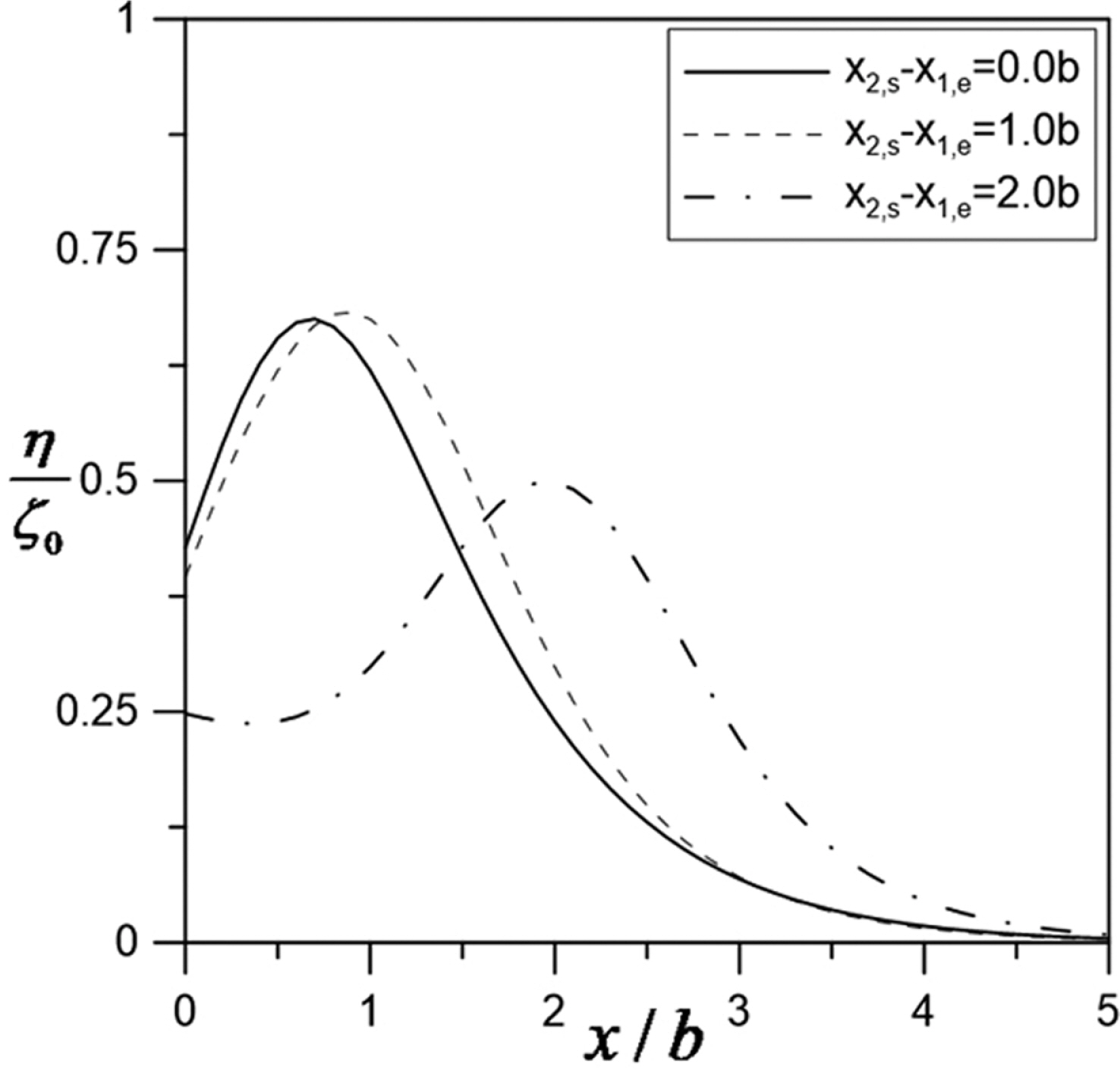
Fig. 6은 다른 조건 등을 동일하게 두고 두 영역의 거리에 변화를 주면서 수면변위를 계산한 결과이다. t' = 1.0 및 t_delay = 2.0t_rise인 상황에서 두 영역 사이의 거리(x_{2, s} − x_{1, e})를 0, 1b 및 2b로 변화를 주면서 값을 계산하였다. Fig. 5의 결과와 유사하게 거리에 따라 최대수면변위의 값과 최대변위가 발생하는 지점이 달라지는 것을 확인할 수 있다.

Fig. 6.

Normalized free surface elevation for different gaps between two bottom variation regions.

4. 결 론

본 연구에서는 Hammack(1973)의 해석해를 응용하여 수심 변화가 발생하는 경우에 초기 수면변위의 생성 및 전파 특성을 검토하였다. 수심이 상승하는 시간이 짧으면 수심변화에 의해 상승된 수면이 이동하기 전에 수심 상승이 발생하여 수심의 상승과 수면의 상승이 비례하면서 거의 동시에 발생하였다. 그러나 수심이 상승하는 시간이 긴 경우에는 수심이 상승하기 전에 이미 상승된 수면이 좌우로 이동하여 수심이 상승하는 동안에 더 이상의 수면상승이 발생하지 않았다.

두 개의 영역에서 시간차를 가지며 수심변화가 발생하는 경우에는 두 영역간의 거리차 및 수심이 변하는 시간차에 따라서 최대 수면변위의 값이랑 위치가 달라지는 것을 확인할 수 있다. 이는 먼저 상승한 수심으로 인해 발생한 수면이 이동하면서 두 번째로 상승한 수심으로 인한 수면변위와 중첩하여 발생하는 것으로 경우에 따라 증가하거나 감소하였다.

실제 해역에서 지진해일이 발생하는 경우, 대부분의 지진해일 수치모형은 바닥의 변화를 자유수면의 초기파형으로 가정하기 때문에 이러한 시간차에 의해 발생하는 효과를 고려하지 못하고 있다. 본 연구를 확장하여 바닥변화와 자유수면과의 인과관계 및 상승된 자유수면의 이동속도 등을 규명한다면 향후 지진해일 수치모형연구에 도움이 될 것으로 기대한다.

Article information Continued