2.1 파랑

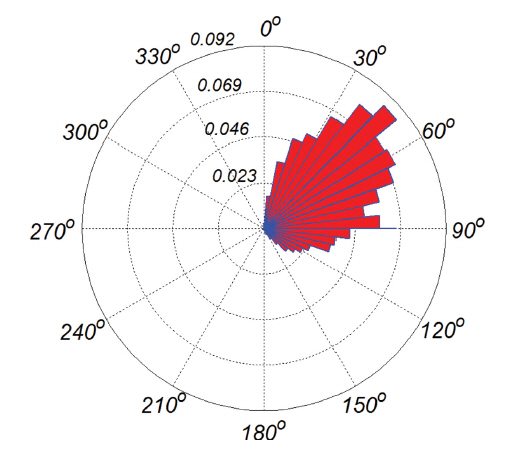
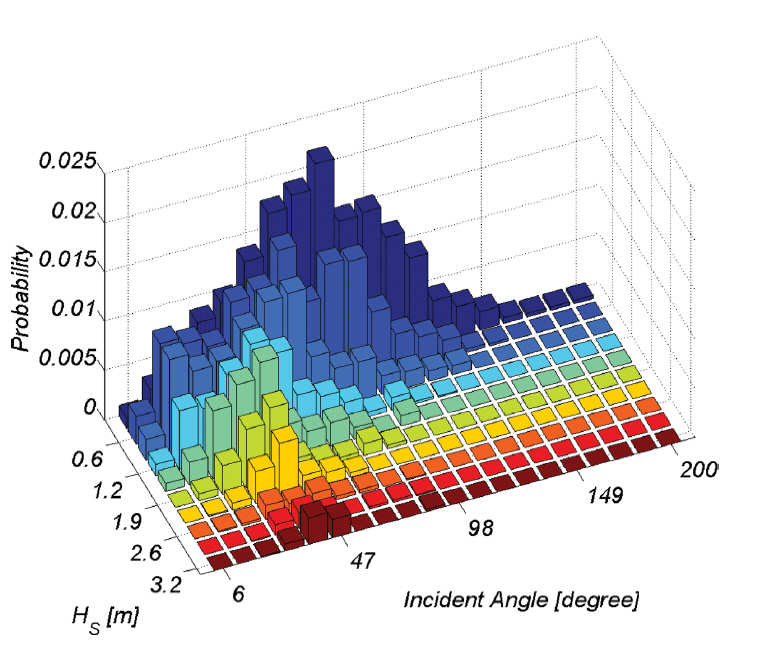
강원도 맹방해변에 직접적인 영향을 미치는 동해는 SW에서 NE 방향으로 길게 늘어선 모양을 띤다(Fig. 1, 2 참조). 이로 인해 NE 방향의 취송거리가 상대적으로 길어, NE 방향으로 파랑이 충분히 발달할 수 있는 가능성이 가장 높다. 이러한 동해의 지형적 특성을 고려하면 맹방해변으로 직각으로 입사되는 NE 계열 파랑의 출현 빈도율이 상대적으로 우월한 것은 자연스러워 보인다(Fig. 3 참조). 본고에서 사용한 좌표계는 Fig. 3, 파고 확률분포와 누적확률분포는 Fig. 4, 입사각도별 파고 확률분포는 Fig. 5에 각각 도시하였다. Fig. 6에는 일년에 걸친 파랑과 주기 벡터도를 도시하였다. 여기서 벡터 크기는 파고와 주기를 각각 나타내며, 방향은 파향을 나타낸다.

Fig. 1.

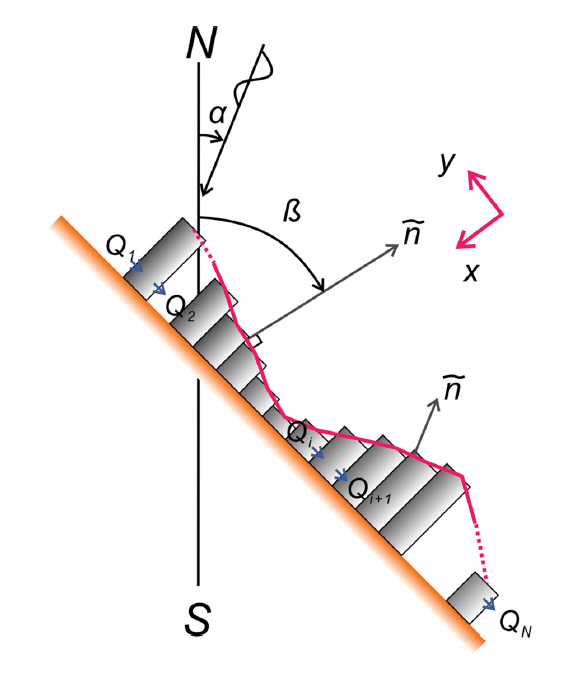
Definition sketch of global coordinate system, local coordinate system, and outward normal vector ñ.

Fig. 3.

Wave rose.

Fig. 4.

Probability distribution of wave height and its cumulative distribution.

Fig. 5.

Joint probability distributions of wave height and its associated incident angle.

Fig. 6.

Yearly vector plot of wave height and period with its corresponding wave ray.

3 m 이상의 고파랑은 주로 10월과 3월에 걸쳐 NE 계열에서 발생하며, 0.8 m 내외의 너울은 3월부터 9월에 걸쳐 ESE 계열에서 주로 발생하였다. 3월부터 9월에 발생하는 너울은 파고는 그리 크지 않으나 주기가 크게는 십초에 이르는 장파로 상대적으로 긴 여정에서 성분 파랑간의 비선형 간섭에 의해 생성된 외중력파로 판단된다. 이와 더불어 년 중 303일 동안 파고가 1.3 m 미만의 파랑이 지배적이며(Fig. 4 참조), 해변에 직각으로 입사되는 파랑이 우월한 해양환경을 고려하는 경우 고파랑에 의해 일시적으로 침식되어 원역으로 이송된 표사가 장기간에 걸쳐 파랑에 의해 다시 해안으로 회귀될 수 있다는 가능성이 상당하다. 따라서 침식 저감을 위해 해안과 나란히 거치된 이안제, artificial reef 혹은 잠제는 해안으로 회귀되는 표사를 일정부분 차폐할 수 있어 적용에 신중할 필요가 있어 보인다.

2.2 파고와 주기 결합 확률분포

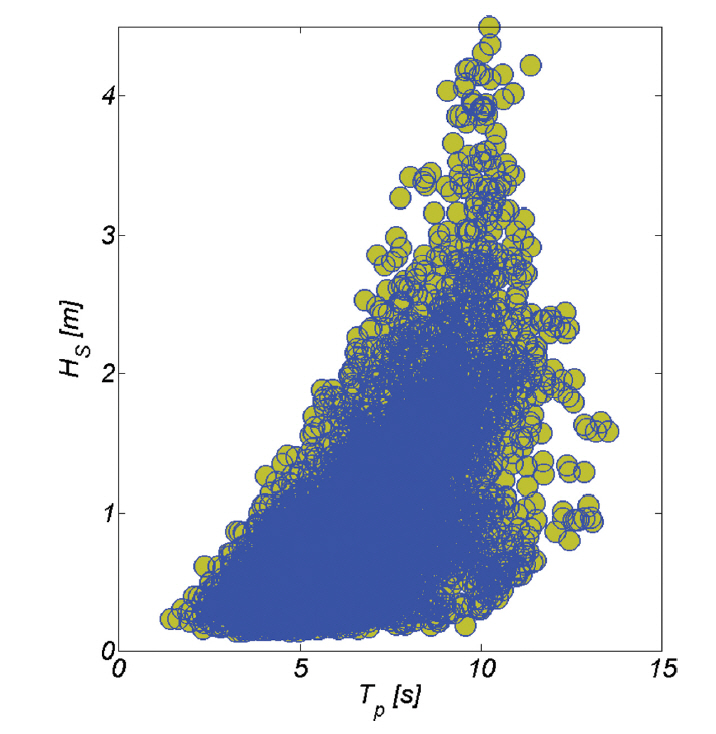
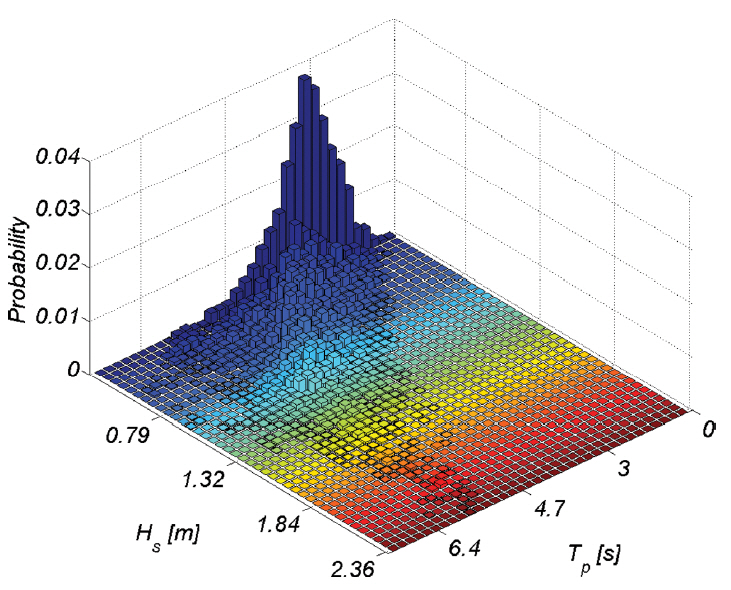
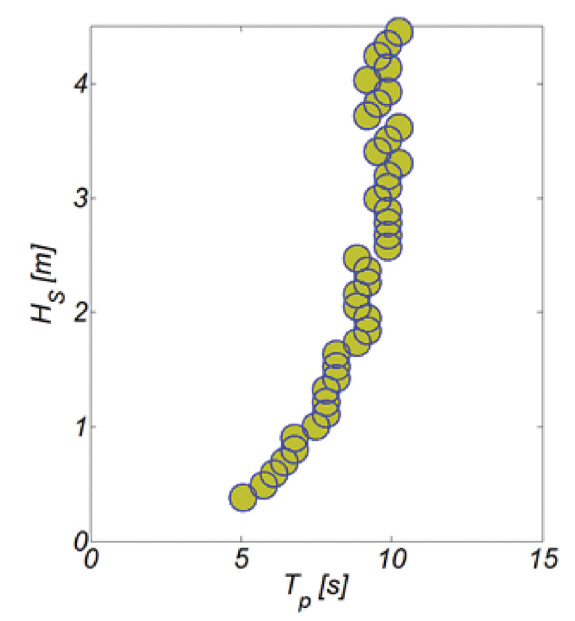
횡단 표사량은 Irribaren NO.와 인과 관계를 이룬다는 그동안의 해안 공학계 정설을 고려하는 경우, 파랑 주기는 해빈 표사에 미치는 영향이 결코 작지 않으나, 그 동안의 해빈 표사 해석에서 소홀히 다루어진 듯하다. 본고에서는 파랑 주기가 해빈 표사에 미치는 영향을 해석하기 위해 파랑과 주기 결합 확률분포를 파랑관측 자료로부터 유도하였으며, Fig. 7에는 관측된 파랑과 주기 복합사상을, Fig. 8에는 파랑과 주기 복합 확률분포를 각각 도시하였다.

Fig. 7.

Trajectories of wave height and its associated period.

Fig. 8.

Joint probability distribution of wave height and its associated period.

여기서 특기할만한 현상은 파고가 1.2 m 내외의 너울에서 주기가 14초 내외의 장파가 관측되어(Fig. 6 참조) 파랑간의 공진성 비선형상호작용에 의한 Bound mode의 외중력파 출현 가능성이 상당히 높아 보인다, 이에 비해 고 파랑의 경우 외중력파의 발생가능성은 상대적으로 낮아 보인다.

파고 2.5 m 이상의 고파랑의 경우 파고가 증가해도 주기는 10초 내외에서 성장을 멈추었다. 이러한 현상은 고파랑의 경우에도 파고가 증가하는 경우 주기를 선형 비례하는 것으로 해석해온 그 동안의 강성 구조물 설계 관행에서는 해빈 표사량 산출에 오류가 있을 수 있음을 시사하는 것으로 시정이 필요해 보인다. Fig. 9에는 이해를 돕기 위해 파고별 발생 확률이 가장 높은 최빈 주기(modal period)를 도시하였다.

Fig. 9.

Trajectories of modal wave period corresponding to specific wave heights.

3.1 연안 표사

연안 표사량 Q은 각 해안에서 가용한 파랑에너지 유입률 EC_GB와 인과관계를 형성하는 것으로 인식되어왔으며, 이러한 인과 관계는 오래기간 여러 검증과정을 통해 이제는 해안공학계의 정설로 굳어진 듯하다(Komar and Inman, 1970; Kraus et al., 1982; Dean et al., 1982; Dean and Dalrymple, 2002). 본고에서는 이러한 사실에 기초하여 연안 표사량 Q은 가용한 파랑에너지 유입률 EC_GB에 결과 되는 것으로 해석하였으며, 사용된 Energy flux 모형을 기술하면 다음과 같다.

여기서, K는 계수, H_o는 심해 입사파고, g는 중력 가속도, T는 주기, θ_o는 심해 입사각도, S는 표사 비중, P는 공극율, κ = 0.79, θ_b는 쇄파역에서의 입사각도를 각각 나타내며(Fig. 10 참조), 식(1)의 유도과정에는 Snell’s Law가 활용되었다(Dean and Dalrymple, 2002).

Fig. 10.

Schematic sketch of mechanics underlying the Energy flux model for longshore sediment transport.

3.2 횡단 표사

먼저 논의의 전개를 위해 Bailard(1981)의 횡단표사모형 유도과정을 정리하면 다음과 같다.

소류사 이송을 해석하려는 노력은 Bagnold(1963)에 의해 처음 시도되었다. Bagnold(1963)는 저면 표사가 이송되기 위해서는 저층 표사간의 구속이 이완되는 과정이 선행되어야 하며 이러한 팽창 혹은 확장(dilatation)에 필요한 수직응력은 유동에 의한 전단력에 의해 발생한다고 추정하였다. 이어 이러한 가설을 일련의 정교히 설계된 실험을 통해서 입증한 바 있다. 이 연구에서 Bagnold(1963)는 유동에 의한 전단력 τ_G은 수직응력 σ_G과 다음과 같은 관계식을 충족하며

, 유동에 의해 야기된 수직응력 σ_G는 sheet layer의 무게와 균형을 이룬다는 사실에 기초하여 식(2)으로부터 다음과 같은 관계식을 유도한 바 있다.

식(2), (3)에서 Φ는 마찰 각도를 나타내며, 자연 해빈처럼 저면이 경사진 경우(β ≠ 0) 사면을 따라 작용하는 중력 성분을 이겨내야 하므로, 이 경우 상기 식은 다음과 같이 수정된다.

식(4)를 소류사 이송에 소요되는 에너지로 기술하는 경우 다음과 같이 전환된다.

식(5)에서 여기서 U는 소류사 이송속도를 나타낸다.

여기서, 가용한 파랑에너지 W 중 일부분 εW 이 소류사 이송에 소요된다는 점에서 다음과 같은 관계식을 생각해 볼 수 있다.

식(5)와 (6)으로부터 소류사 이송률 I은 다음과 같이 기술될 수 있다.

이 후 Bailard(1981)는 표사를 부유사와 소류사로 분류하여 전술한 Bagnold(1963)의 Energy 모형을 다음과 같이 확장한 바 있다.

여기서, 〈 〉는 주기평균 연산자, C_f는 마찰계수, ε_b와 ε_s는 각각 가용한 파랑에너지 중 소류사와 부유사 이송에 소요되는 비율, ρ는 밀도, u는 유속 벡터, i는 표사 이송량 벡터, w는 표사 침강속도, j는 해안방향을 가리키는 단위 벡터를 각각 나타낸다.

이 연구에서 Bailard(1981)는 모형의 적용성을 높이기 위해 유동계 u를 파동계 n~와 평균류 n¯의 중첩으로 해석하여 다음과 같은 간략식을 제안한 바 있다.

여기서, δ_u, Ψ₁, Ψ₂, u₃*, u₅*는 각각 저류, 왜도, 정규화된 평균유속을 나타내며 다음과 같이 기술될 수 있다.

현재로서는 δ_u, Ψ₁, Ψ₂에 대한 해석해는 가용하지 않으며, 이를 해결하기 위해 Bailard(1981)는 일 개월에 걸친 관측 자료로부터 전술한 통계량을 유추하고 미 California Torrey Pines 해변을 대상으로 모형의 적용성을 검증한 바 있다.

본 연구에서는 가용한 맹방 해변 유동 관측자료의 부재로 인한 어려움을 해결하기 위해 쇄파역에서의 비선형 천수과정을 수치 모의하였다. 수치모의에는 주파수 영역 Boussinesq Eq.(Frelich and Guza, 1984)을 활용하였으며, 이를 기술하면 다음과 같다.

여기서, ζ는 해수면 변위, u는 유속, A_n은 비선형 파동계를 구성하는 n번째 성분파의 진폭, i=-1는 단위 복소수, c.c.는 공액 복소수, k는 파수, ω는 각 주파수, h는 수심, 아래첨자 x는 연안방향으로의 미분 연산자를 각각 나타낸다. 식(16)의 우변 항은 쇄파로 인한 에너지 소산을 의미하며 에너지 소산계수 α_n은 Mase와 Kirby(1992), Cho와 Lee(2003)에 따르면 다음과 같이 기술될 수 있다.

여기서, ω_p는 첨두 주파수, ω_n는 n번째 성분파의 각 주파수, F는 가중계수로 F = 1인 경우 쇄파로 인한 에너지 소산은 주파수와 무관하나 F < 1인 경우 쇄파로 인한 에너지 소산은 주파수에 종속하며 F = 0.1인 경우 쇄파역에서 관측되는 왜도된 파동계를 모의할 수 있는 것으로 보고된 바 있다. 계수 Λ(x)는 다음과 같이 정의되며

여기서, H_rms는 root mean square 파고, D와 γ는 각각 1과 0.6의 값을 지니는 계수를 나타낸다. 저면 마찰로 인한 감쇄는 다음 항을 추가하는 경우 기술이 가능하다.

식(20)에서 ν는 동점성계수, b는 수로폭을 각각 나타낸다.

4.1 수치 모의

이안 표사량 산출에 필요한 저류, 왜도, 정규화된 평균유속을 구하기 위해 비선형 파랑의 천수과정을 수치모의하였다. 수치모의에 사용된 계산영역은 Fig. 11에 도시하였으며 해변경사는 맹방 해변의 지형 특성을 반영하여 1:30으로 선정하였다. 수치모의에 사용될 파랑조건을 도출하기 위해, 먼저 맹방해변 전면 해역에서 관측된 파고[0.25~4.5 m]와 주기[1.25~15 s]를 0.15 m와 0.1 s 간격으로 등 분할하고 출현빈도가 상대적으로 높은 총 71개의 파고 및 주기 조합을 선정하였다(Fig. 7 참조). 수치모의는 이렇게 선정된 파랑 주기 복합사상에 대해 수행하였다. 수치모의에 사용된 파랑조건이 단파에서부터 외중력파까지를 아우르고 있어 쇄파역 폭이 상당하다는 사실을 고려하여 천수구간은 342.5 m로 선정하였으며, 입사파랑은 강 비선형 천수과정을 정확히 모의하기 위해 20개의 성분파로 구성된 Cnoidal 파형으로 조파하였다. Cnoidal 파형을 구성하는 각 성분파랑의 진폭 An은 다음과 같이 산정하였다(Cayley, 1895; Frick et al., 1981).

Fig. 11.

Numerical wave flume.

식(21)에서 k는 첫 번째 성분파랑의 파수, q는 다음과 같이 정의되는 방정식의 해를 의미하며

여기서, 변량 m은 파고로부터 다음과 같이 산출될 수 있다.

식(21), (23)에서 K(m)은 제 일종 complete elliptic integral을 나타낸다.

4.2 수치 결과

4.2.1 유동 적률(moment)

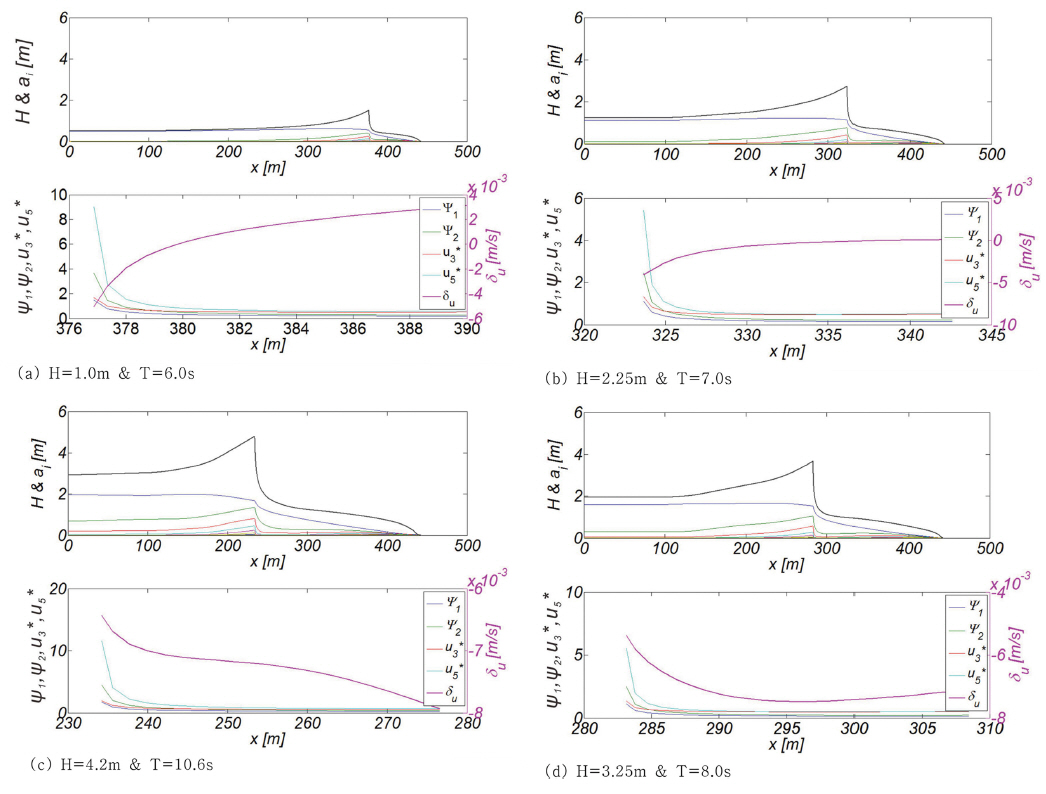
Fig. 12에는 수치모의된 쇄파점 인근에서의 수면형과 저면 유속분포를 도시하였다. 쇄파역에서 흔히 관측되는 왜도된 파동계가 상당히 근접하게 모의된 것을 알 수 있다. Fig. 13에는 수치모의된 비선형 천수 과정에서 관측된 파고 H, 성분파랑 진폭 a_n, δ_u, Ψ₁, Ψ₂, u₃*, u₅*를 도시하였다. 우리의 예측대로 쇄파가 시작되는 지점이 x_b = 403.5m에서 x_b = 236.01 m까지 상당히 넓게 포진하는 것을 알 수 있다. 또한 유속분포의 왜도 정도를 나타내는 Ψ₁과 Ψ₂, 정규화된 평균유속 u₃*와 u₅*는 쇄파가 시작되는 지점에서 그 정점을 이루다 해안으로 갈수록 급속히 감소하였다. 또한, 천수과정에서 첫 번째 조화성분의 진폭 감소는 고차 조화성분 진폭 증가를 수반하는 것을 알 수 있으며 이는 유속분포의 왜도 증가로 귀결되며, 이러한 거동은 그 동안에 해안 공학계에 잘 알려진 인식과 부합한다.

Fig. 12.

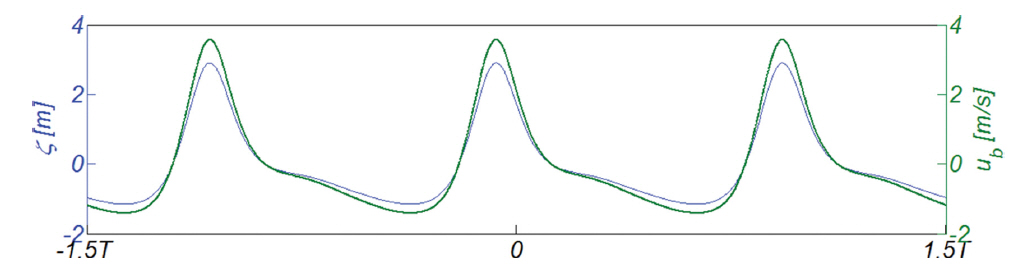
Numerically simulated water surface profile and its corresponding velocity profile near the bottom when wave breaking commences (H = 4.2 m and T = 9.5 s).

Fig. 13.

Numerically simulated wave height, δ_u, Ψ₁, Ψ₂, u3* and u5* across the surf zone.

그러나 일견하면 Bailard(1981)의 연구와는 달리 δ_u, Ψ₁, Ψ₂, u₃*, u₅*와 입사파고 간의 단순한 선형 인과관계는 쉽게 찾아볼 수 없다. 이러한 차이는, 먼저 본 연구는 일개월에 걸친 관측결과를 다룬 Bailard(1981)의 연구와는 달리 맹방해안의 년 표사수지를 다룬다는 점에서 찾을 수 있다. 따라서 사계를 포함한 파랑관측결과에는 보다 광범위한 파랑주기가 출현할 수밖에 없어 Bailard(1981)의 모형을 우리나라 해안의 년 표사수지 해석에 단순 적용하는 것은 무리라 판단된다. 두 번째는 미 California 해변에 영향을 미치는 태평양과 맹방해안에 영향을 미치는 동해의 규모에서 찾아야 할 것으로 보인다. 동해의 경우 취송거리가 우월한 특정한 방향이 있으나, 태평양의 경우 그 규모가 광활하여 풍성파가 충분히 발달하는데 필요한 취송거리가 다양한 방향에서 확보된다. 따라서 그 긴 여정에서 풍성파는 너울로 전환되며 이 과정에서 수반되는 성분 파랑간의 상호작용으로 인해 북반구 너울(Northern Hemisphere Swell)과 남반구 너울(Southern Hemisphere Swell)은 10초와 14초 사이의 비슷한 주기 분포를 지닌다. 이러한 주기 특성으로 인해 Bailard(1981)는 파랑 관측결과 해석에서 주기 변화를 간과하였으나, 그 해석 결과는 미 California 해변에 국한해서 적용되어야 할 것으로 판단된다.

전술한 사실에 기초하여, 본고에서는 맹방해안을 대상으로 한 δ_u, Ψ₁, Ψ₂, u₃*, u₅*와 입사파랑 간의 회귀분석과정에 파고와 주기의 복합사상을 고려하였다. 전술한 통계량과 파고와 주기간의 인과관계에서 Bailard(1981)가 간과한 주기의 영향을 보다 극명하게 드러내기 위해 수치모의한 각 파고와 주기 복합사상에 해당하는 Irribaren NO. ξ를 산출하고 이를 Fig. 14에 정리하였으며, Irribaren NO.는 다음과 같이 정의된다.

Fig. 14.

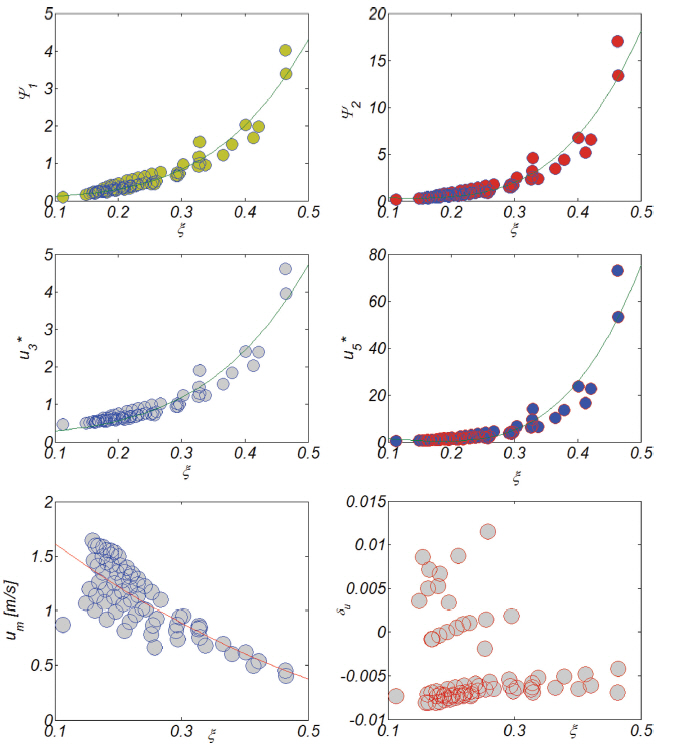
Variation of numerically simulated δ_u, Ψ₁, Ψ₂, u3* and u5* with respect to Irribaren NO. and its corresponding regression results.

(24) ξ=tanβHoLo

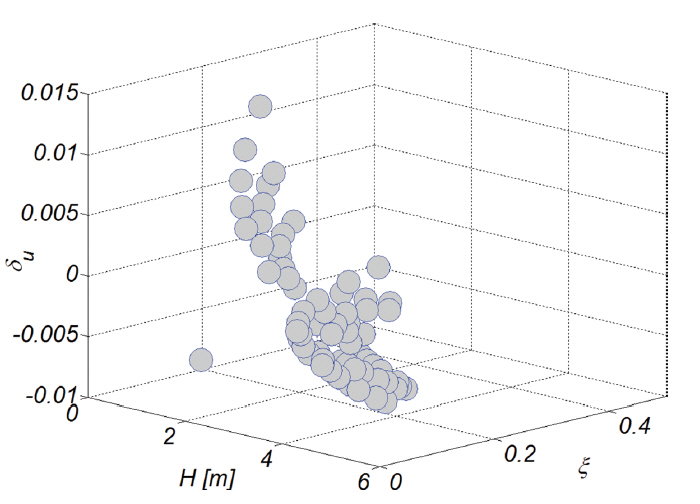
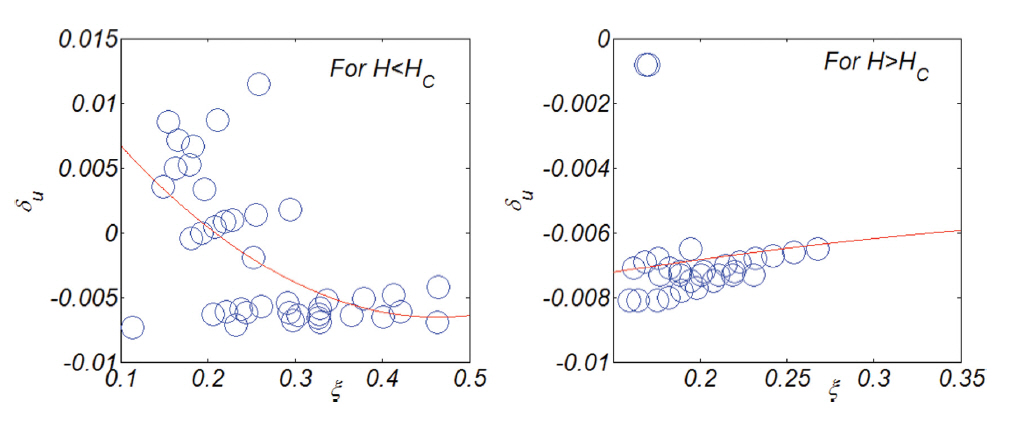
우리의 추론대로 u_m, Ψ₁, Ψ₂, u₃*, u₅*와 Irribaren NO. ξ와의 인과관계가 확연히 드러나, 전술한 유동 적률(moment)은 Irribaren NO. ξ가 증가하면 급격히 증가하는 것을 알 수 있으나(Fig. 14 참조), δ_u의 경우 서로 다른 두 가지 경향이 혼재하는 것으로 보인다(Fig. 15 참조). δ_u에 영향을 미치는 물리량을 보다 확연히 드러내기 위해 수치모의 과정에서 관측된 δ_u를 [H, ξ] 공간에 도시하였다(Fig. 15 참조). 동일한 Irribaren NO. ξ 대역에서 파고가 임계 파고 H_c보다 작은 경우 δ_u는 해안을 향하나, 임계 파고 H_c보다 큰 경우, 이러한 경향은 역전되는 것을 알 수 있다(Fig. 16 참조). 이러한 사실에 기초하여 먼저 수치모의 과정에서 관측된 δ_u를 임계 파고 H_c보다 작은 경우와 큰 경우로 분류하고, 각각의 경우에 대하여 회귀분석을 수행하였으며 회귀분석 결과를 정리하면 다음과 같다.

Fig. 15.

Trajectories of numerically simulated δ_u in the spatial domain of Irribaren NO. and wave height.

Fig. 16.

Strikingly different variation of δ_u under swell and energetic wind waves.

(25) Ψ1=53.62ξ4−3.52ξ2+0.0854

(26) Ψ2=337ξ4−13.17ξ2+0.43

(27) u3*=45.62ξ4−6.57ξ2+0.22

(28) u5*=1631.5ξ4−115.6ξ2+2.3

(29) um=2.699(ξ−0.874)2

(30.1) δu=0.1002(ξ−0.464)2−0.00652     if H<Hc

(30.2) δu=−0.01001(ξ−0.576)2−0.005406     if H≥Hc

4.2.2 표사수지

전절에서 다룬 유동적률에 관한 회귀분석 결과와 Bailard(1981)의 횡단표사모형, Energy flux 연안표사 모형에 준거하여 맹방해변의 년 표사수지를 수치모의 하였으며 그 결과는 Fig. 17에 도시하였다(K = 0.2, P = 0.3, ε_s = 0.025, ε_b = 0.21, C_f = 0.005). 수치모의에 사용된 표사 물성치는 맹방 표사분포를 고려하여 d₅₀ = 0.017 m, S = 2.6, w = 0.04 m/s, β = 1/30로 선정하였다(Oh et al., 2007).

Fig. 17.

Time series of longshore sediment and its accumulation, time series of cross shore sediment and its accumulation with wave height and period for β = 41.6°.

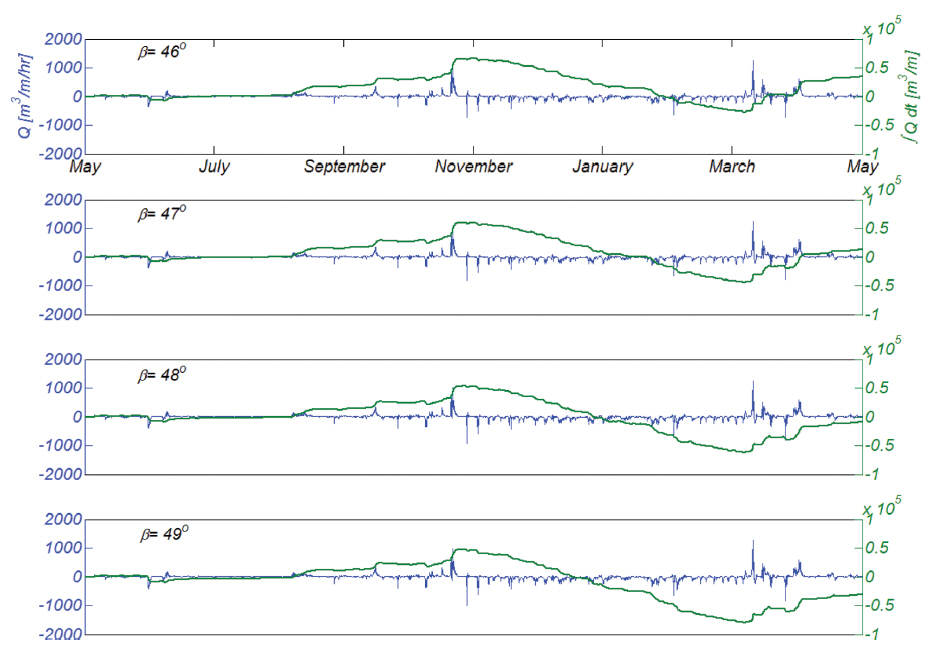
Fig. 17은 맹방해변의 평균 방위 β = 41.6o을 대상으로 수행된 것으로 연안표사의 경우 북서진하는 연안표사가 우월하며 그 양은 년 125,000 m³/m에 달하는 것으로 모의 되었다. 횡단표사의 경우 4월부터 10월 중순까지는 연안방향으로의 퇴적이 점진적으로 진행되나, 10월말과 3월 중순에 단발적으로 발생한 고파랑에 의해 대규모의 침식이 진행된 것을 알 수 있다. 그러나 11월과 1월 말 사이, 2월과 3월 초순사이, 4월 초순 이후에는 연안방향으로의 표사 이송이 다시 복원되어 자연 해빈이 지니는 자기 복원능력을 부분적으로 확인할 수 있다. 북서진하는 연안표사와 남동진하는 연안표사와가 균형을 이루는 null point을 확인하기 위해 β = 46°, 47°, 48°, 49°에 대해 맹방해변의 년 표사수지를 수치모의 하였으며, 그 결과는 Fig. 18에 도시하였다. 맹방해변의 null point는 β = 47o에 위치하는 것을 확인할 수 있다. 5월부터 10월 하순까지는 북서진하는 연안표사가 우월하며, 10월 하순부터 예외적인 고파랑이 간헐적으로 발생한 3월 중순 사이에는 남동진하는 연안표사가 우월하며 남동진한 누적 연안 표사량은 50,000 m³/m에 달한다. 또한 남동진한 연안 표사량의 대부분은 3월 중순에 발생한 고파랑에 의해 다시 북서방향으로 회귀되는 것을 알 수 있다.

Fig. 18.

Time series of longshore sediment and its accumulation for β =46°, 47°, 48° and 49°.

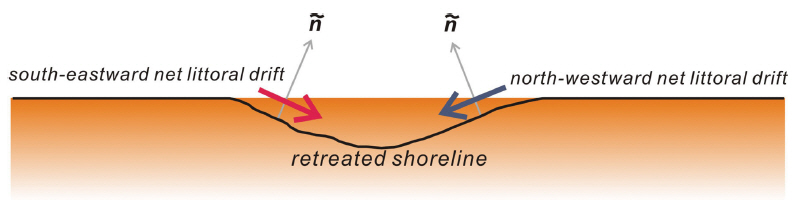
또한 맹방해변 외향법선벡터 n~과 진북방향이 이루는 각도 β에 따른 순 연안 표사량 변화를 살펴보기 위해 연안표사 장미도(littoral drift rose)를 산출하였으며(Fig. 1 참조), 산출된 연안표사 장미도는 Fig. 19에 도시하였다(Walton and Dean, 1973; Walton and Dean, 2010). 여기서 빨간 실선은 남동진하는 연안표사를 나타내며, 파란 실선은 북서진하는 연안표사를 나타낸다. 따라서 해안선이 Fig. 20처럼 일시적으로 퇴각하더라도, 침식된 해변의 전반부에서는 β > β_{null point}가 되며, 이 경우 순 연안표사는 남동방향으로 향한다(Fig. 20 참조). 이에 반해 침식된 해변의 후반부에서는 β_{null point} 가 되며, 이 경우 순 연안표사는 북서 방향을 향하게 되므로 침식된 해안은 점차 복원되는 것을 알 수 있다(Fig. 20 참조). 이를 종합하면 맹방해변은 일시적으로 침식되더라도 스스로 복원될 수 있는 능력을 지닌 안정적인 해변임을 의미한다.

Fig. 19.

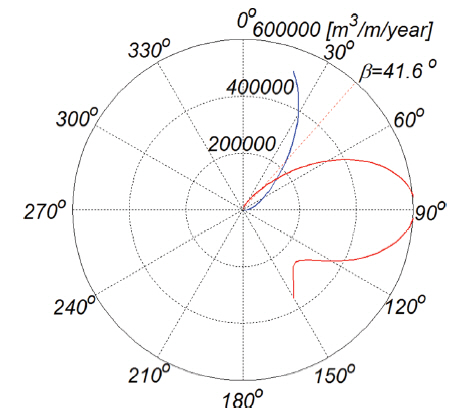
Longshore sediment drift rose (blue line: north-westwardly moving longshore sediment, red line: south-eastwardly moving longshore sediment).

Fig. 20.

Illustrative sketch of self restoring process of the Mang-Bang beach after a shoreline is temporarily retreated following the Longshore sediment drift rose presented in this study.