추계학적 감마 확률과정을 이용한 경사제의 기대 잔류유효수명 예측
Prediction of Expected Residual Useful Life of Rubble-Mound Breakwaters Using Stochastic Gamma Process
Article information
Abstract
추계학적 확률과정의 하나인 감마 확률과정을 이용하여 구조물의 잔류유효수명을 확률론적으로 예측할 수 있는 수학적 모형을 수립하였다. 수립된 모형은 과거부터 현재 시점까지 관측된 피해자료와 관련된 표본의 불확실성과 장래 시간 진행에 따른 누적피해의 불확실성을 올바로 고려할 수 있다. 또한 최소자승법과 모멘트법을 함께 사용하여 경사제의 재령, 운용환경 그리고 피해이력을 고려할 수 있는 모수 추정법을 제시하였다. 먼저 현재 재령의 단일 피해 자료를 갖는 임의의 조건에서 모수에 대한 민감도 분석을 수행하여, 잔류유효수명과 관련된 여러가지 거동 특성들을 분석하였다. 또한 잔류유효수명 예측모형을 경사제에 적용하였다. 경사제 피복재의 피해 이력에 대한 실험자료를 이용하여 감마 확률과정의 모수를 추정하였는데 실험자료와 매우 잘 일치하였다. 해석 결과에 의하면 현재 시점으로부터 상당히 오랜 시간이 경과하면 파괴한계를 초과할 확률이 일정한 값으로 수렴해야 하는 제약 조건을 잘 만족하였다. 한편 기대 잔류유효수명은 피해 이력의 거동 특성에 따라 각기 다르게 산정되었다. 특히 피해의 변동계수가 크면 추계학적으로 산정된 기대 잔류유효수명은 결정론적 회기모형의 해석 결과와 큰 차이를 보인다. 이는 해석과정에 포함된 불확실성의 영향으로 판단된다. 변동계수가 크면 파괴한계에 도달하는 시간의 분포가 넓게 퍼지기 때문이다. 따라서 본 연구에서 수립된 추계학적 잔류유효수명 예측모형은 현재 재령에서 경사제의 피해에 대한 확률적 평가를 수행할 수 있을 뿐만 아니라 장래 시간의 진행에 따른 누적피해의 불확실성을 올바로 고려할 수 있다.
Trans Abstract
A probabilistic model that can predict the residual useful lifetime of structure is formulated by using the gamma process which is one of the stochastic processes. The formulated stochastic model can take into account both the sampling uncertainty associated with damages measured up to now and the temporal uncertainty of cumulative damage over time. A method estimating several parameters of stochastic model is additionally proposed by introducing of the least square method and the method of moments, so that the age of a structure, the operational environment, and the evolution of damage with time can be considered. Some features related to the residual useful lifetime are firstly investigated into through the sensitivity analysis on parameters under a simple setting of single damage data measured at the current age. The stochastic model are then applied to the rubblemound breakwater straightforwardly. The parameters of gamma process can be estimated for several experimental data on the damage processes of armor rocks of rubble-mound breakwater. The expected damage levels over time, which are numerically simulated with the estimated parameters, are in very good agreement with those from the flume testing. It has been found from various numerical calculations that the probabilities exceeding the failure limit are converged to the constraint that the model must be satisfied after lasting for a long time from now. Meanwhile, the expected residual useful lifetimes evaluated from the failure probabilities are seen to be different with respect to the behavior of damage history. As the coefficient of variation of cumulative damage is becoming large, in particular, it has been shown that the expected residual useful lifetimes have significant discrepancies from those of the deterministic regression model. This is mainly due to the effect of sampling and temporal uncertainties associated with damage, by which the first time to failure tends to be widely distributed. Therefore, the stochastic model presented in this paper for predicting the residual useful lifetime of structure can properly implement the probabilistic assessment on current damage state of structure as well as take account of the temporal uncertainty of future cumulative damage.
1. 서 론
국내 사회기반시설물들은 국가재건과 산업화 기반 마련의 일환으로 1960, 70년대부터 경제개발 5개년 계획에 따라 건설되기 시작하여 최근까지 도로 146조원, 철도 및 도시철도 86.5조원, 항만 약 36.8조원이라는 막대한 비용이 투입되었다. 이와 같은 성장기에 건설된 대부분의 구조물들은 보통 내구년수 50년으로 설계되었다. 현재 시점을 기준으로 많은 구조물들의 사용년수가 30년 이상 경과하였으며, 여러 가지 원인에 의해 해당 구조물의 노후화가 상당히 진행된 상태이다. 2014년을 기준으로 전체 사회기반시설물 중 준공 후 30년이 지난 노후 시설물은 전체의 9.6% 수준이며, 향후 10년 내에 21.5%로 2배 이상 급증할 것으로 전망되고 있다. 특히 기후 변화에 따른 해양환경이 점점 더 불확실해지고 시설물의 안전성에 미치는 외력이 증대되고 있어 방파제나 안벽 등과 같은 항만 시설물의 노후화는 다른 육상 시설물 보다 빠르게 가속화될 수 있다. 따라서 높아지는 요구수준을 만족시키면서 유지관리 예산을 효율적으로 사용하기 위해서는 시설물 별로 최적의 예방적 유지관리를 수행해야 한다. 항만 구조물의 경우 외력 증대에 따른 성능보완 뿐만 아니라 노후화된 항만 구조물의 예방적 보수보강이 동시에 최적으로 수행되어야 한다. 미국에서도 1920, 30년대 건설된 사회기반시설을 올바로 유지관리하기 위하여 1980년대에 연구를 시작하여 1990년대에 현재까지 적용되는 유지관리 체계를 수립하였다. 향후 10년간 4.59조 달러라는 막대한 비용이 유지관리를 위해 필요할 것으로 추산되고 있다. 일본의 경우도 1940, 50년대 고도성장기에 건설된 사회기반시설물에 대한 유지관리 연구가 1990년대부터 시작되어 2000년대 적용되기 시작하였다. 미국과 일본 등 선진국들이 이와 같은 노력을 경주하는 이유는 사회기반시설물의 올바른 유지관리가 국가발전의 원동력이기 때문이다(Choate and Walter, 1983). 특히 저성장 시대가 도래하고 저출산, 고령화 사회가 가속화됨에 따라 국가 예산의 총액대비 사회기반시설에 신규로 투입되는 재원의 규모가 시간이 갈수록 줄어들 수밖에 없다. 또한 사회가 발전함에 따라 사회기반시설물에 요구되는 성능도 점점 높아지는 추세이다. 이와 같이 건설 예산에서 신규 사업이 차지하는 비중은 시간이 갈수록 줄어들게 되고 기존 구조물의 유지관리 예산은 더 커질 수밖에 없다. 일반적으로 유지관리는 예방적 유지관리(PM: Preventive Maintenance)와 사후 유지관리(CM: Corrective Maintenance)로 구분되는데 사후 유지관리는 복구의 개념이다. 따라서 최소의 비용으로 최적의 성능을 달성하기 위해서는 예방적 유지관리 개념이 도입되어야 한다(Cui et al., 2004; Wang, 2007a, b; Wang and Zhang, 2008; Lee, 2013, 2016a). 최적의 예방적 유지관리를 수행하기 위해서는 재령 기반 유지관리(ABM: Age-Based Maintenance) 모형이나 조건기반 유지관리(CBM: Condition-Based Maintenance) 모형이 개발되어야 하는데 이때 가장 핵심적인 요소가 잔류유효수명을 올바르게 예측하는 것이다(Jia and Christer, 2002; Wang, 2002; Lee, 2016b; Lee and Park, 2017).
공학적 관점에서 잔류유효수명(RUL: Residual Useful Lifetime)이란 구조물의 현재 피해상태를 기준으로 미래 임의 시점까지 유용하게 사용할 수 있는 구조물의 수명으로 정의된다(Si et al., 2011). 잔류유효수명은 구조물의 현재까지의 피해상태와 미래에 발생될 피해진행에 따라 변하기 때문에 확률변수로 고려되어야 한다. 일반적으로 잔류유효수명은 구조물의 재령, 운용환경 그리고 현재까지의 피해 이력에 의존한다고 알려져 있다. 이 세 가지 요인 중 가장 중요한 것이 피해이력인데 이는 점검을 통한 관측에 의하여만 얻을 수 있다. 이를 CM(Condition Monitoring)이라 하며, 이를 통해 잔류유효수명 추정에 사용될 수 있는 임의 형식의 자료를 얻을 수 있다. CM에 의해 얻어지는 자료는 일반적으로 사건자료(event data)와 피해자료(damage data)로 구분되는데, 피해자료는 또 직접적인 피해자료와 간접적인 피해자료로 구분된다(Wang and Christer, 2000). 사건자료는 구성방정식을 통해 간접적인 피해자료로부터 직접적인 피해자료를 추출하는 것을 의미한다. Jardine et al.(2006, 2008), Heng et al.(2009), Pecht and Jaai(2010), Gorjian et al.(2009), Dragomir et al. (2009), Peng et al.(2010) 등이 잔류유효수명 추정에 대하여 연구를 수행하였다. 먼저 기계장치 등에서는 주로 파괴에 대한 사건자료를 기반으로 하는 파괴율 함수(failure rate function) 모형이 일반적으로 사용되었다(Kalbfleisch and Prentice, 2002; Lawless, 2002). 그러나 항만 구조물과 같이 파괴가 발생하면 막대한 손실을 유발하는 중요한 구조물에서는 파괴에 대한 사건자료가 거의 없기 때문에 이와 같은 모형을 적용할 수 없다. 따라서 피해자료를 기반으로 하는 모형들이 연구되기 시작하였는데, 대부분은 직접적인 피해자료를 사용하는 모형이다. 각각의 연구들은 점검의 불완전성으로 피해자료에 내포되는 표본의 불확실성(sampling uncertainty)과 미래의 피해진행 상황을 추정하는 과정에 발생하는 시간에 따른 불확실성(temporal uncertainty)을 어떻게 고려하느냐에 따라 다르다. 먼저 수학적으로 가장 간단한 모형이 피해의 진행을 멱함수(power function) 형태로 가정하는 회기기반모형(regressionbased model)인데, 표본의 불확실성을 고려할 수 있지만 시간에 따른 불확실성은 고려할 수 없다는 단점을 가지고 있다(Pandey et al., 2009). 이와 같은 문제점을 해결하기 위하여 제안된 방법이 위너 확률과정(WP: Wiener Process)이나 감마 확률과정(GP: Gamma Process) 등과 같이 추계학적 확률과정을 이용하는 모형이다(van Noortwijk, 2009). WP는 피해 진행이 단조 증가하는 경우에는 그 적용에 한계성을 가지기 때문에, 항만 구조물과 같이 피해진행이 단조 증가하는 경우에는 GP를 사용하는 것이 바람직하다(Lee, 2015). 따라서 본 연구에서는 GP를 이용하여 항만 구조물 방파제의 대표적 구조형식인 경사제에 대한 잔류유효수명을 해석하고자 한다. 특히 경사제는 제체의 안전성이 파랑과 직접적으로 만나는 피복재의 안전성에 의하여 의존하기 때문에 본 연구에서는 피복재의 피해를 기준으로 다양한 조건에 대한 경사제의 잔류유효수명을 추정하였다.
본 논문의 구성은 다음과 같다. 먼저 제 2절에 GP를 이용하여 구조물의 잔류유효수명을 해석할 수 있는 수학적 모형을 수립하였고, 제 3절에서는 GP 모형에 포함된 매개변수를 추정할 수 있는 방법을 제시하였다. 최소자승법과 모멘트법을 함께 사용하는 방법이다. 제 4절에서는 임의 조건에 대한 민감도 분석을 수행하였고, 제 5절에 경사제 피복재의 피해에 적용하여, 잔류유효수명을 예측한 결과를 제시하였다. 마지막으로 제 6절에 결론을 제시하였다.
2. 잔류유효수명 예측모형의 개발
구조물의 피해는 시간의 진행에 따라 누적되기 때문에 잔류유효수명을 올바르게 예측하기 위해서는 현재까지 누적된 피해 상태를 먼저 확인한 후 미래의 누적 피해 진행을 예측할 수 있어야 한다. Fig. 1에 나타낸 바와 같이 임의의 시간 ti에서 누적피해 Z(ti)는 그 시간 동안 발생하는 피해 증분 Yn(n = 1, 2, …, i)의 합으로 정의된다. 따라서 현재 상태의 피해를 관측하는 과정과 미래의 피해를 예측하는 과정에 불가피하게 여러 불확실성이 포함된다. 전 절의 공학적 정의에 따라 수학적으로 잔류유효수명을 임의로 설정된 사용한계 또는 파괴한계까지 도달하는데 걸리는 시간으로 정의할 수 있다. 따라서 본 연구에서는 이들을 각각 구분하여 현재 시점을 기준으로 누적피해 Z(t)가 사용한계 δ까지 도달하는데 걸리는 시간을 사용한계 잔류유효수명, Tδ로 정의하고, 파괴한계 ζ까지 도달하는데 걸리는 시간을 파괴한계 잔류유효수명, Tζ로 구분하였다. Tδ는 파괴가 발생하기 전에 점검이나 예방적 유지관리를 하기 위한 기준으로 활용할 수 있으며, Tζ는 파괴 발생시점의 예측에 활용할 수 있다. 두 가지 잔류유효수명은 조건기반 유지관리 모형 개발에 활용될 수 있다.
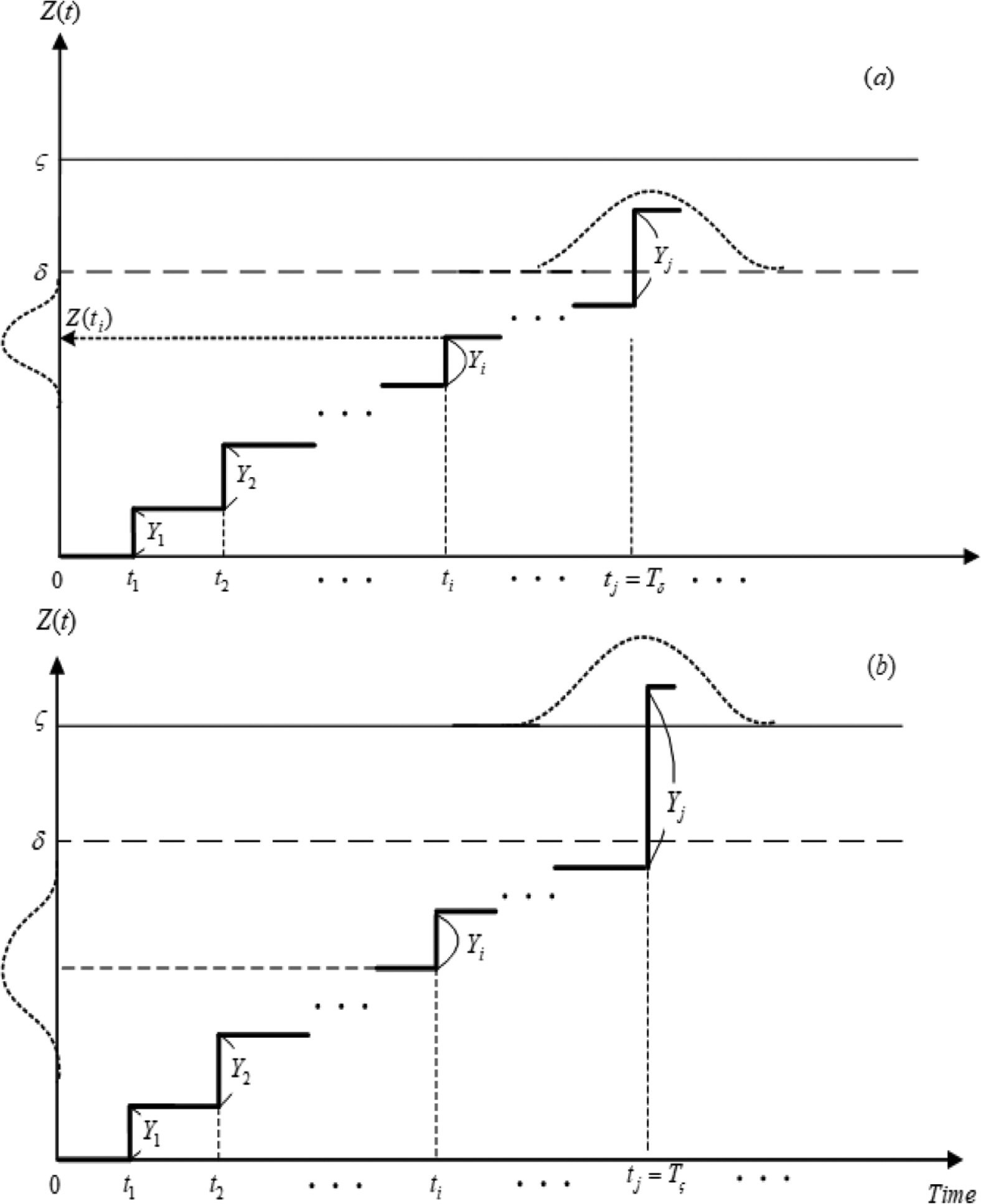
Definition of residual useful lifetime for (a) serviceability threshold, Tδ and (b) failure threshold, Tζ.
물리적으로 현재의 피해상태 뿐만 아니라 미래의 피해진행도 불확실하기 때문에 사용한계나 파괴한계를 초과하는 시점인 잔류유효수명은 확률변수이다. 따라서 불확실성을 고려하면서 미래의 피해진행을 예측할 수 있는 모형이 필요하다. 이를 위해 본 연구에서는 감마 확률과정, GP에 기반한 추계학적 모형을 이용하였다.
수학적으로 감마 확률과정은 시간에 따른 누적피해를 나타내는 임의의 확률변수, Z(t)가 형상함수 v(t) > 0와 축척모수 u > 0를 갖는 다음 식(1)과 같이 정의되는 감마분포함수를 따른다고 정의한다.
시간에 따른 피해진행의 단조증가 성질을 반영하기 위하여 형상함수 v(t)는 반드시 v(0) = 0을 만족하면서 우연속이고 실수값을 갖는 증가함수(right-continuous, real-valued, non-decreasing function)라는 것과 축척모수 u가 시간에 따라 일정하다는 것이다. 이와 같은 조건을 만족시키면 감마 확률과정은 다음과 같은 특성을 갖게 된다. Z(0) = 0이고, 임의의 시간 ti − ti−1 사이에 발생하는 피해의 증분, Yi = Z(ti) − Z(ti−1)~Ga[Yi|v(ti) − v(ti−1), u]이며 Z(t)는 Yi와 독립이다(Abdel- Hameed, 1975; van Noortwijk, 2009). 따라서 감마 확률과정은 임의 시간에서의 피해는 그 시간 동안 아주 작은 피해의 증분들이 독립적으로 누적되어 발생한다는 개념이다.
감마 확률과정을 이용하여 잔류유효수명을 예측하는 방법은 현재의 피해정도에 따라 두 가지로 구분된다. 하나는 현재 시점에서 피해가 전혀 없는 구조물에 대한 것이다. 피해가 전혀 발생하지 않은 신규 구조물이나 피해가 있어도 현재 시점에서 완벽한 보수보강이 이루어진 경우이다. 이 경우는 간단하게 다음 식(2)를 이용하여 구조물의 잔류유효수명을 예측할 수 있다.
여기서 w는 임의의 한계(threshold level)로 사용한계나 파괴한계를 의미한다. Tw는 피해가 w를 초과하는 최초시간(FHT: First Hitting Time) 이다. 따라서 w = ζ인 경우에 식(2)는 파괴한계를 최초로 통과하는 내구수명(lifetime)의 분포함수가 된다. 현재 신규 구조물 설계에서는 일반적으로 활용되고 있는 설계공용수명(design working life)에 해당된다. ISO 2394(1998)에서는 신규 구조물을 설계할 때 구조물의 중요도를 4단계의 계급별로 구분하여 설계공용수명을 결정론적으로 결정하도록 권고하고 있다. 따라서 식(2)를 이용하면 설계공용수명도 확률론적으로 결정할 수 있다.
두 번째는 현재 시점에서 구조물이 일정한 피해를 가지고 있는 경우이다. 본 연구에서 이에 대한 잔류유효수명을 확률적으로 예측할 수 있는 모형을 개발하고자 한다. 모형을 개발하기 위해서는 먼저 현재 피해상태 Z(ti)에 대한 확률적인 평가가 있어야 한다. 현재 시점을 ti라고 하면 Z(ti)가 가질 수 있는 경우는 Fig. 1에 나타낸 바와 같이 모두 세 가지이다. 첫 번째가 사용한계 δ 미만인 경우, 두 번째가 사용한계 이상이면서 파괴한계 ζ 미만인 경우 그리고 마지막 세 번째가 파괴한계 이상인 경우로 각각 Z(ti) < δ, δ ≤ Z(ti) < ζ 그리고 Z(ti) ≥ ζ이다. 이중 P[Z(ti) ≥ ζ]는 물리적으로 현재 피해상태가 파괴될 확률을 나타내기 때문에 잔류유효수명의 정의에 의하여 고려 대상이 아니다. 잔류유효수명을 예측한다는 것은 현재의 피해상태가 파괴한계보다 작다 라는 조건을 만족해야 한다.
먼저 현재의 피해상태 Z(ti) < δ인 조건에서 미래의 임의의 시점에서 누적피해 Z(tj)가 가질 수 있는 경우는 Z(tj) < δ, δ ≤ Z(tj) < ζ 그리고 Z(tj) ≥ ζ이기 때문에 다음 식(3)~식(5)를 정의할 수 있다.
앞에서 정의된 바에 따라 P11은 현재 피해상태가 사용한계 미만이면서 미래 임의의 시점에서 누적피해도 사용한계 미만일 확률로 정의된다. 따라서 식(3)~(5)를 이용하면 현재 시점에서 피해가 사용한계보다 작으면서 임의 시간 Δt 후에 피해가 나타날 확률들을 구할 수 있다. 수학적으로 P11 + P12 + P13 = P[Z(ti) < δ] = FZ(ti)(δ)을 만족하여야 한다. 여기서 FZ(ti)(δ)는 현재의 누적피해가 사용한계 δ보다 작을 확률이다. 다음으로는 현재의 피해상태 δ ≤ Z(ti) < ζ인 조건에서 미래의 임의의 시점에서 누적피해 Z(tj)가 가질 수 있는 경우는 δ ≤ Z(tj) < ζ와 Z(tj) ≥ ζ이다. 따라서 다음 식(6)과 식(7)을 정의할 수 있다.
앞의 경우와 동일하게 P22 + P23 = P[δ ≤ Z(ti) < ζ] = FZ(ti)(ζ) − FZ(ti)(δ)를 만족하여야 한다.
따라서 현재 피해상태 Z(ti)에 대한 분포함수와 미래 누적피해 Z(tj = ti+ Δt)에 대한 분포함수를 알면 각각의 사건에 대한 발생확률을 수치적으로 산정할 수 있다. 이를 위해 본 연구에서는 감마 확률과정을 사용하였다. 식(1)에 정의된 감마분포함수와 수학적 convolution을 이용하면 식(3)을 다음 식(8)과 같이 나타낼 수 있다.
여기서 Yj는 Δt 시간 동안 발생하는 피해의 증가량, Z(tj = ti + Δt) − Z(ti) = Yj로 분포함수 gYj(y)~Ga[y|v(tj) − v(ti), u]를 따른다. 또한 식(4)와 (5)도 다음 식(9)와 (10)처럼 나타낼 수 있다.
동일한 전개과정을 거치면 식(6)과 (7)의 경우도 다음 식(11)과 (12)처럼 나타낼 수 있다.
따라서 Δt를 변화시키면서 사용한계와 파괴한계를 초과하는 확률을 수치적으로 계산할 수 있다.
식(2)가 피해가 없는 초기 상태를 기준으로 해석하는 것이라면 본 연구에서 제시한 식(3)~식(12)는 실무에서 자주 만날 수 있는 임의 재령에서 일정 크기의 피해가 있는 구조물에 적용이 가능하다. 따라서 서론에서 언급하였듯이 잔류유효수명이 구조물의 재령, 운용환경, 그리고 현재의 피해상태에 의존한다는 특성들을 잘 반영할 수 있다. 즉, 일정 시간이 경과하여 임의 크기의 피해가 존재하는 구조물의 잔류유효수명을 올바로 해석할 수 있다.
3. 감마 확률과정의 모수 추정
추계학적 확률과정의 하나인 감마 확률과정을 이용하여 구조물에 대한 잔류유효수명을 확률적으로 올바로 해석하기 위해서는 관련 모수에 대한 정확한 추정이 필요하다. 모수에 대한 추정은 관련 피해 점검 관측자료의 통계적 해석에 의해서만 가능하다. 피해자료는 임의의 시점에서 관측된 단일 피해자료와 시간의 진행에 따른 피해이력에 대한 자료로 구분된다. CM의 어려움 때문에 전자의 경우가 대부분이지만 일부 중요 구조물에서는 후자의 경우도 존재한다. 전자의 경우가 잘 관리되면서 일정 시간 간격으로 반복되면 피해이력에 대한 자료를 얻을 수 있기 때문이다.
식(1)에 의하면 임의 시간까지 누적된 피해, Z(t)의 평균과 분산은 형상함수 v(t)와 축척모수 u에 의존하고 다음 식(13)과 같이 정의된다.
식(1)에 언급된 바에 의하면 감마 확률과정에서 형상함수 v(t)는 v(0) = 0을 만족하면서 우연속이고 실수값을 갖는 증가함수여야만 한다. 이와 같은 조건을 만족하기 위하여 많은 연구자들이 형상함수를 다음 식(14)와 같이 정의되는 멱함수를 사용하였다(van Noortwijk and Klatter, 1999; Ellingwood and Mori, 1993; Hoffmans and Pilarczyk, 1995).
여기서 α와 β는 시간에 따른 피해 진행과 관련된 물리적 모수이며, 특히 α는 축척모수 u와 함께 임의 시간에서 피해의 크기와 직접적으로 연관되고, β는 시간에 따른 피해 진행 형태를 결정하는 역할을 한다. 철근 부식에 따른 콘크리트의 강도 저하 등 여러 가지 물리적 현상에 대한 실험을 통하여 매개변수 β를 결정하여 그 적용성을 확인한 바 있다. 특히 β = 1이 되면 수학적으로 선형 모형이 되고 이를 정상 확률과정(stationary process)이라 한다. 한편 β ≠ 1인 경우를 비선형 모형이라 하는데 β < 1인 포화모형(saturated model)과 β > 1인 가속모형(accelerated model)으로 구분된다. 이를 모두 비정상 확률과정(non-stationary process)이라 한다. 따라서 추정해야 할 모수는 α, β 그리고 u이다.
현재까지 가장 일반적으로 사용되는 방법이 β와 임의 시점 ti에서 변동계수 VZ(ti)를 가정하고 그 시점에서 누적피해에 대한 평균값을 이용하는 추정방법이다. 이와 같은 모멘트법을 이용하면
그러나 이 방법은 β와 VZ(ti)를 가정하였기 때문에 시간에 따른 피해 진행 형태를 미리 결정하고 현재의 불확실성만 고려한다는 단점을 가지고 있다. 따라서 본 연구에서는 이와 같은 제약성을 해결하는 방법을 아래에 제시하였다. 먼저 현재를 기준으로 ti 시간 동안 n개의 누적피해에 대한 관측 평균치 Z(tj)(j = 1, 2, …, n)가 있다고 하고 약간의 수학적 과정을 거치면 다음 식(16)이 정의된다.
따라서 최소자승법에 의하여 관측치와 추정치의 오차의 제곱의 합이 최소라는 조건을 이용하면
다음으로 임의 시간에서 피해의 크기와 직접적으로 연관된 αˆ와 uˆ를 추정하여야 한다. 본 연구에서는 Cinlar et al. (1977)이 제안한 방법을 사용하였다. 식(14)에
구조물의 피해를 관측할 때 피해의 증분보다는 시간에 따른 누적피해 Z(t)를 측정하는게 일반적이다. 따라서 식(18)은 마지막 시간 tn에서 관측된 누적피해 Z(tn)를 이용한다는 의미이다. 이는 지난 과거의 피해이력이 가장 최근의 자료에 모두 포함되기 때문이다. 추정해야 할 모수가
약간의 복잡한 수학적 전개과정을 거쳐 식(19)의 우변을 정리하면 다음 식(20)을 얻을 수 있다.
따라서 식(17)과 식(20)을 이용하여 모수 βˆ와 uˆ를 직접 추정한 후, 그 결과를 식 (18)에 대입하면 모수 αˆ를 추정할 수 있다.
이상과 같이 감마 확률과정의 모수를 추정할 수 있는 식을 제시하였다. 따라서 추정식의 정확성을 수학적으로 검증하기 위하여 다른 모수 추정방법인 최우도법(maximum likelihood method)에 의한 결과와 비교하였다. 먼저 피해 증분에 대한 우도함수(likelihood function)는 다음 식(21)과 같이 정의된다.
그러므로 다음 식(22)와 같이 정의된 피해 증분에 대한 우도함수가 최대가 된다는 조건을 이용하면 최우도법에 의해 모수 αˆ와 uˆ를 추정할 수 있다.
따라서 우도함수인 식(21)을 식(22)에 대입하여 정리하면 다음 식(23)을 얻을 수 있다. 이때 우도함수 양변을 대수를 취함으로써 수학적 전개를 쉽게 하였다.
여기서 ψ(x) = ∂[lnΓ(x)]/∂x = Γ'(x)/Γ(x)로 정의되는 디감마함수(digamma function)이다. 쉽게 알 수 있듯이 식(23a)는 식(18)과 수학적으로 정확히 일치한다. 따라서 감마 확률과정의 모수 추정식이 올바르게 수립되었다는 것을 알 수 있다. 식(23)은 디감마함수를 포함하는 음함수이기 때문에 수치적으로 반복계산을 수행해야 하는 어려움이 있지만 차이는 크지 않다. 따라서 본 연구에서는 수치적 편의를 위해 양함수인 식(17), (18) 그리고 (20)을 이용하여 감마 확률과정의 모수를 추정하였다.
4. 민감도 분석
추계학적 확률과정의 하나인 감마 확률과정을 이용한 잔류유효수명 예측 모형과 모수 추정 방법을 제시하였다. 따라서 개발된 모형을 실제 구조물에 직접 적용하기 전에 모형을 구성하는 주요한 모수, 형상모수 v(t) = αtβ와 축척모수, u에 따른 거동특성을 먼저 살펴보았다. Pandey et al.(2009)이 사용한 조건을 이용하였는데, 재령이 20년인 임의 구조물에 대하여 점검을 실시하여 현재 시점의 누적피해 Z(20) = 40인 경우이다. 이들은 현재 시점에서 관측된 자료를 평균E[Z(20)] = 40으로 고려한 후, β = 1과 누적피해의 변동계수 VZ(20) = 0.4를 가정하여 모멘트법인 식(15)를 이용하여 간편하게 모수 α와 u를 추정하였다. 사용한계 δ = 70, 파괴한계 ζ = 100이라는 조건에서 누적피해 진행 과정에 영향을 주는 β를 고정시킨 후 현재 시점의 표본에 대한 불확실성, 즉, 변동계수를 변화시키면서 그에 따른 영향을 해석하였다. 그러나 잔류유효수명 뿐만 아니라 β의 변화에 따른 해석을 수행하지 않았다. 본 연구에서는 동일한 조건에 대하여 민감도 분석을 수행하고자 한다. 이는 본 연구에서 개발한 잔류유효수명 예측 모형에서 β가 미래 누적피해를 예측하는 과정에 어떤 영향을 주는지 살펴보기 위함이다. 즉, 현재 시점에서 표본의 불확실성 뿐만 아니라 누적피해의 장래 진행에 따른 불확실성의 거동특성을 해석하기 위함이다.
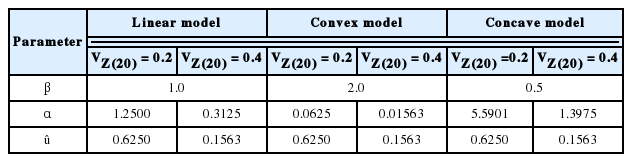
따라서 본 연구에서는 정상 및 비정상 확률과정을 고려하기 위하여 β를 1.0, 2.0 그리고 0.5로 구분하여 주어진 조건에 대하여 식(15)를 이용하여 모수들을 추정하였다. 추정된 결과들을 Table 1에 제시하였는데 현재 시점의 변동계수, VZ(20) 변화에 따른 결과도 함께 나타냈다. 현재 시점의 누적피해에 대한 통계량만을 가지고 해석하는 경우이다. 추정된 결과에 의하면 축척모수 uˆ는 β에 상관없이 일정하고 변동계수에만 의존하는 것을 알 수 있다. 그러나 αˆ는 두 가지 모두에 의존한다.
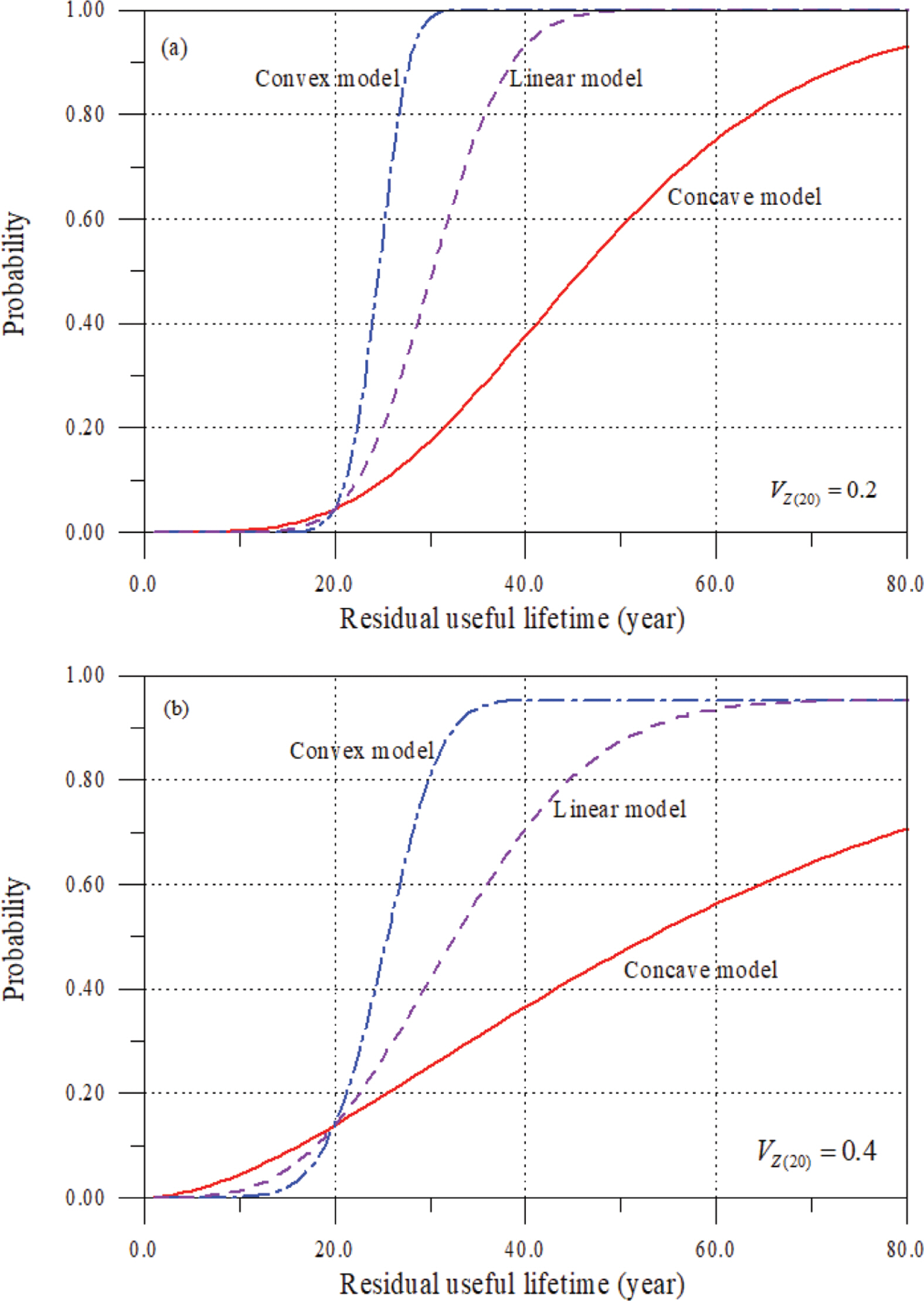
Table 1의 모수와 식(10)을 이용하여 시간의 경과에 따라 누적피해가 파괴한계를 초과할 확률을 계산하여 Fig. 2에 제시하였다. 현재 시점에서 누적피해의 평균 E[Z(20)] = 40이기 때문에 파괴한계, ζ = 100까지 남은 피해의 여유는 60이다. 따라서 Fig. 2는 현재 시점의 누적피해를 기준으로 앞으로의 시간 진행에 따라 나타나는 장래 누적피해가 피해의 여유에 도달하는 과정을 확률적으로 해석한 것이다.
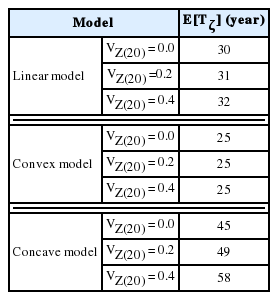
그림에서 알 수 있듯이 동일한 잔류유효수명에서 가속모형의 확률이 가장 크고 포화모형이 제일 작다. 이는 시간의 진행에 따른 미래 피해가 가속모형에서 제일 크게 나타난다는 의미이다. 또한 변동계수가 클수록 확률이 작다는 것을 알 수 있다. 변동계수가 크다는 것은 현재 시점에서의 피해가 넓게 분포한다는 의미로 변동계수가 작은 경우보다 상대적으로 P[Z(ti) < δ] = FZ(ti)(δ)가 작아지게 된다. 한편 Fig. 2로 부터 산정된 각각의 경우에 대한 기대 잔류유효수명을 산정하여 Table 2에 제시하였다. VZ(20) = 0.0인 결정론적 회기모형(deterministic regression model)으로 산정한 결과도 함께 제시하였다. 쉽게 알 수 있듯이 누적피해의 진행에 빠를수록, 즉, β가 클수록 기대 잔류유효수명이 짧다. 또한 변동계수가 작을수록 동일한 거동특성을 보인다. 이는 Pandey et al.(2009)의 해석과 일치하는 결과이며 불확실성에 따른 영향이다. 변동계수가 클수록 누적피해가 파괴한계에 도달하는 시간의 분포가 넓게 퍼지기 때문이다. 그러나 β = 2인 가속모형에서는 기대 잔류유효수명이 모두 25년인데 이는 시간에 따른 누적 피해의 불확실성에 따른 영향이 다른 피해진행 모형보다 상대적으로 작게 나타나기 때문이다. 즉, 가속모형의 단위 시간당 누적피해인 피해증가율이 선형모형의 두 배, 포화모형의 네 배이기 때문이다.
5. 경사제 피복재에 대한 해석
민감도 분석에서 감마 확률과정을 이용한 잔류유효수명 예측 모형에 포함된 각 모수의 변화에 따른 해석결과의 거동 특성을 자세히 살펴보았다. 따라서 본 절에서는 경사제 피복재의 피해에 적용하고자 한다. CEM(2006)에 의하면 경사제의 파괴는 파랑과 직접적으로 만나는 전면에 거치된 피복재의 연속적인 피해에 의하여 발생된다.
본 절에서는 전 절의 민감도 분석에서 접근한 방법, 한 시점에서 통계적 특성을 가정하는 방법과는 다르게 시간에 따라 경사제 피복재의 피해 진행과정에 대한 자료를 해석하는 방법을 사용하였다. Melby(1999)는 모형실험을 통하여 실제 해상에서 처럼 시간에 따라 파랑조건 및 수심조건을 변화시키면서 Series A에서 Series G까지 모두 7가지 조건에 대하여 경사제 피복석의 누적된 평균 피해수준을 측정하였다. 피복석의 피해는 van der Meer(1988)가 제안한 S = Ae/D2 n50의 피해수준을 사용하였다. 여기서 Ae와 Dn50은 각각 피복재의 피해면적과 대표입경이다. Series A에서 Series C까지는 피해가 크게 발생하는 조건에 대한 실험이고 나머지는 상대적으로 피해가 작게 나타나는 경우에 대한 실험이다. 식(17), (18) 그리고 식(20)을 사용하여 7가지 모든 경우에 대하여 감마 확률과정의 모수를 추정하였으나 대표적으로 Series A, B, C, D, E와 Series G에 대한 결과를 Fig. 3에 제시하였다. 그림에는 파선으로 평균 피해 수준으로부터 표준편차의 합 또는 차이에 해당하는 결과도 함께 제시하였다. 그림에서 볼 수 있듯이 전반적으로 포화모형을 따르면서 추정된 결과가 실험자료와 매우 잘 일치하고 있다. 특히 과거 이력에 대한 자료의 변동성이 큰 경우에도 시간의 진행에 따라 그 영향이 잘 반영되는 것을 알 수 있다. 따라서 경사제 피복재 피해에 대한 감마 확률과정의 모수 추정이 올바로 수행되었다. Table 3에 Series F를 포함한 모든 실험 자료에 대한 모수 추정 결과를 제시하였다. 쉽게 알 수 있듯이 모든 경우에서 β < 1.0인 포화모형을 따르고 있다.
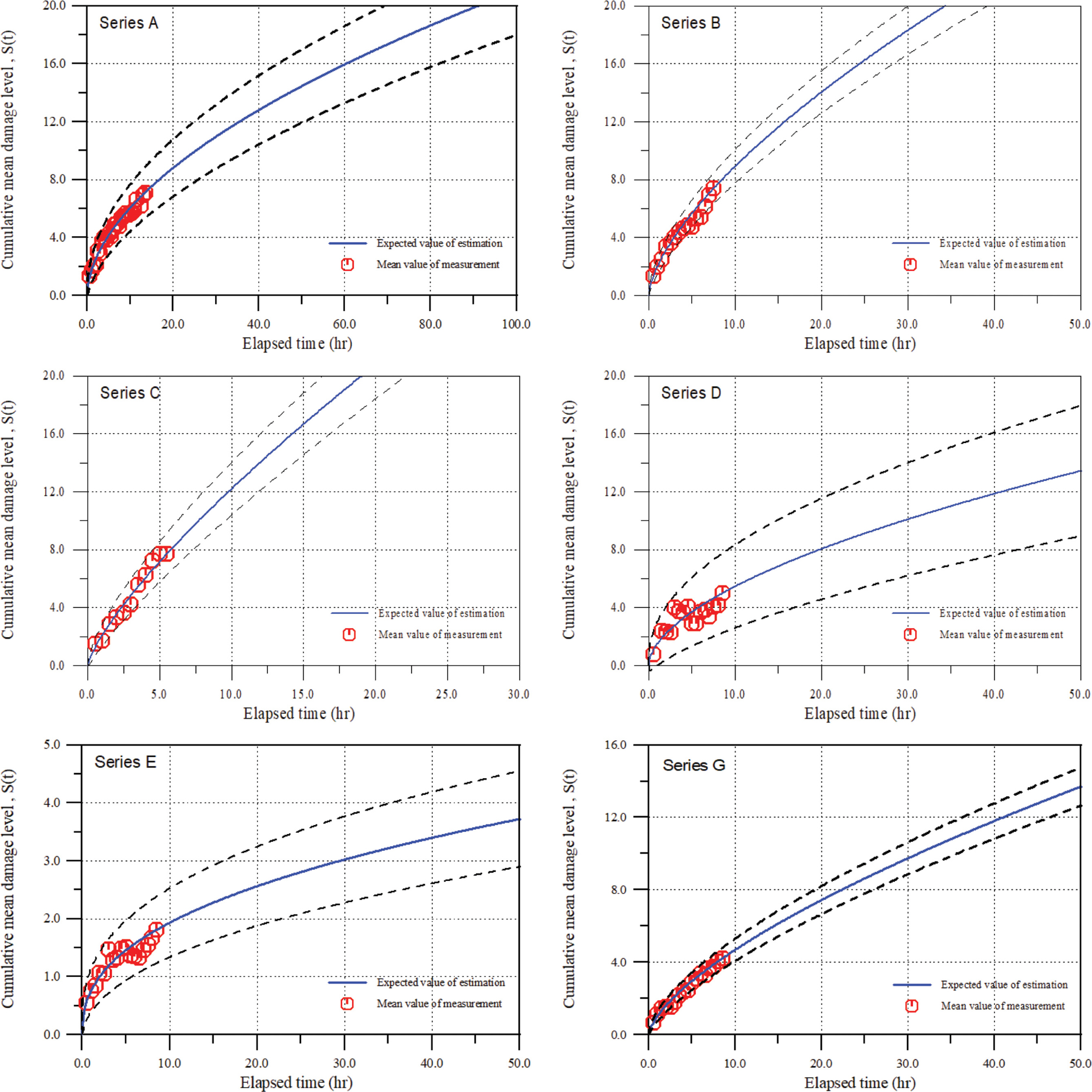
Comparison of cumulative mean damage level estimated in this paper with experimental data measured by Melby (1999) for test Series A, B, C, D, E and Series G.
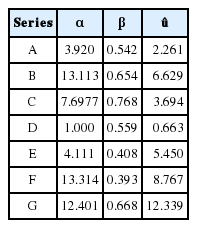
Estimated values of parameter of gamma process for armor rock of rubble-mound breakwater testing experimentally by Melby (1999)
따라서 이하에서는 제 2절에서 제시한 잔류유효수명 예측모형을 이용하여 피복석의 피해에 따른 경사제의 잔류유효수명을 해석하였다. 해석을 수행하기 위하여 먼저 사용한계, δ와 파괴한계, ζ를 정의하였다. 본 연구에서는 CEM(2006)과 PIANC(1992)에서 제시한 δ = 8, ζ = 14를 사용하였다.
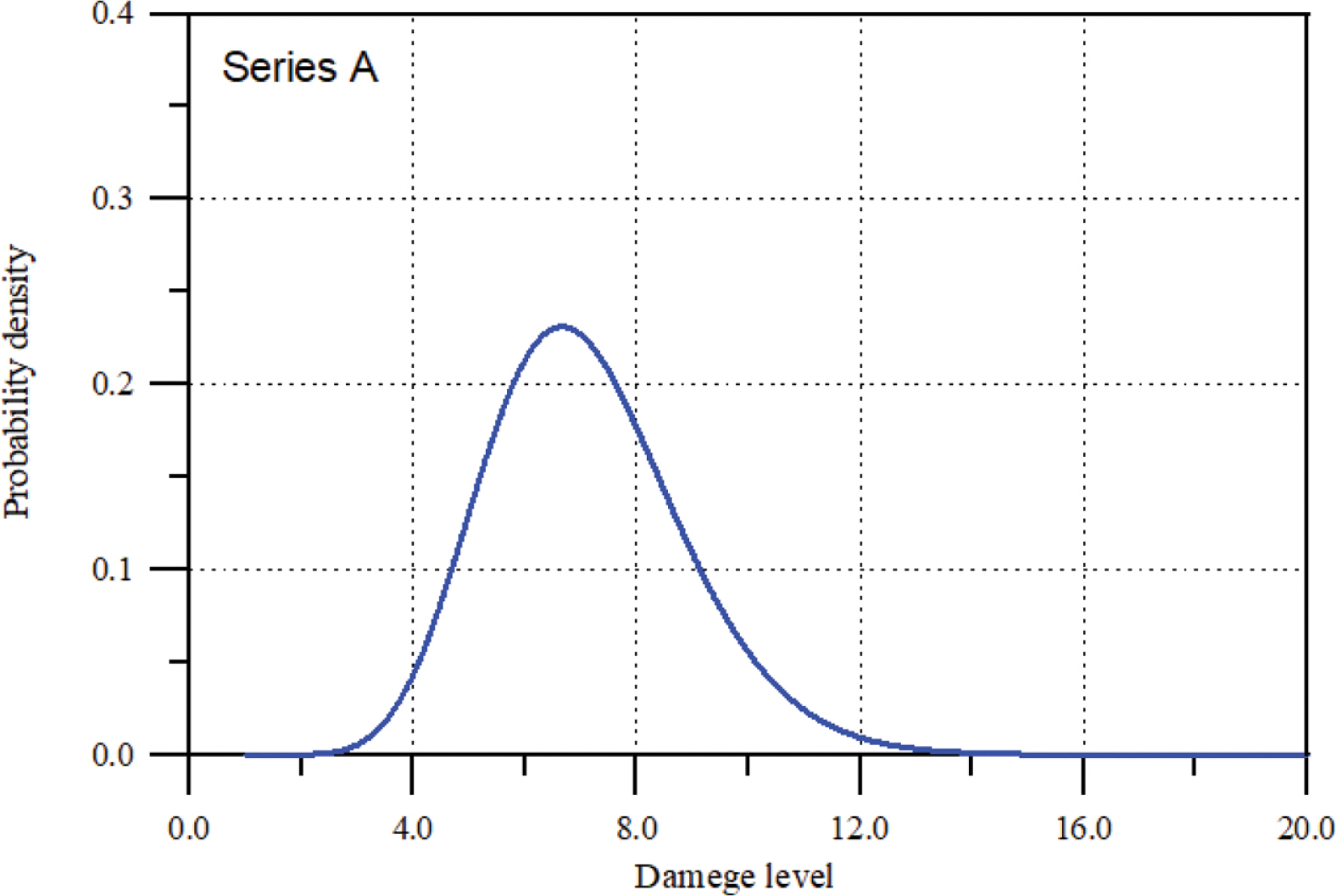
먼저 Series A에 대한 해석이다. 피복석의 누적피해에 대한 관측자료가 13.5시간까지 존재한다. 이는 식(13-1)에 의하여 현재 시점의 평균 피해수준이 7.107이기 때문에 피해의 여유는 파괴한계 ζ = 14에서 현시점의 누적피해를 뺀 6.893이다. 따라서 현재 시점 13.5시간부터 6.893까지 도달하는데 걸리는 시간을 확률적으로 예측하는 문제가 된다. 이를 위해서는 먼저 현재 시점의 피해수준에 대한 평가가 확률적으로 수행되어야 한다. 현재 시점의 피해수준에 대한 분포함수를 산정하여 Fig. 4에 제시하였다. 평균 피해수준 E[Z(13.5)] = 7.107, 변동계수 VZ(13.5) = 0.25의 통계적 특성을 갖는다. 또한 현재 시점 13.5시간에서 누적피해가 사용한계보다 작을 확률, FZ(13.5)(8) = 0.715이고, 파괴한계와 사용한계 사이에 있을 확률, FZ(13.5)(14) − FZ(13.5)(8) = 0.285라는 것을 쉽게 확인할 수 있다.
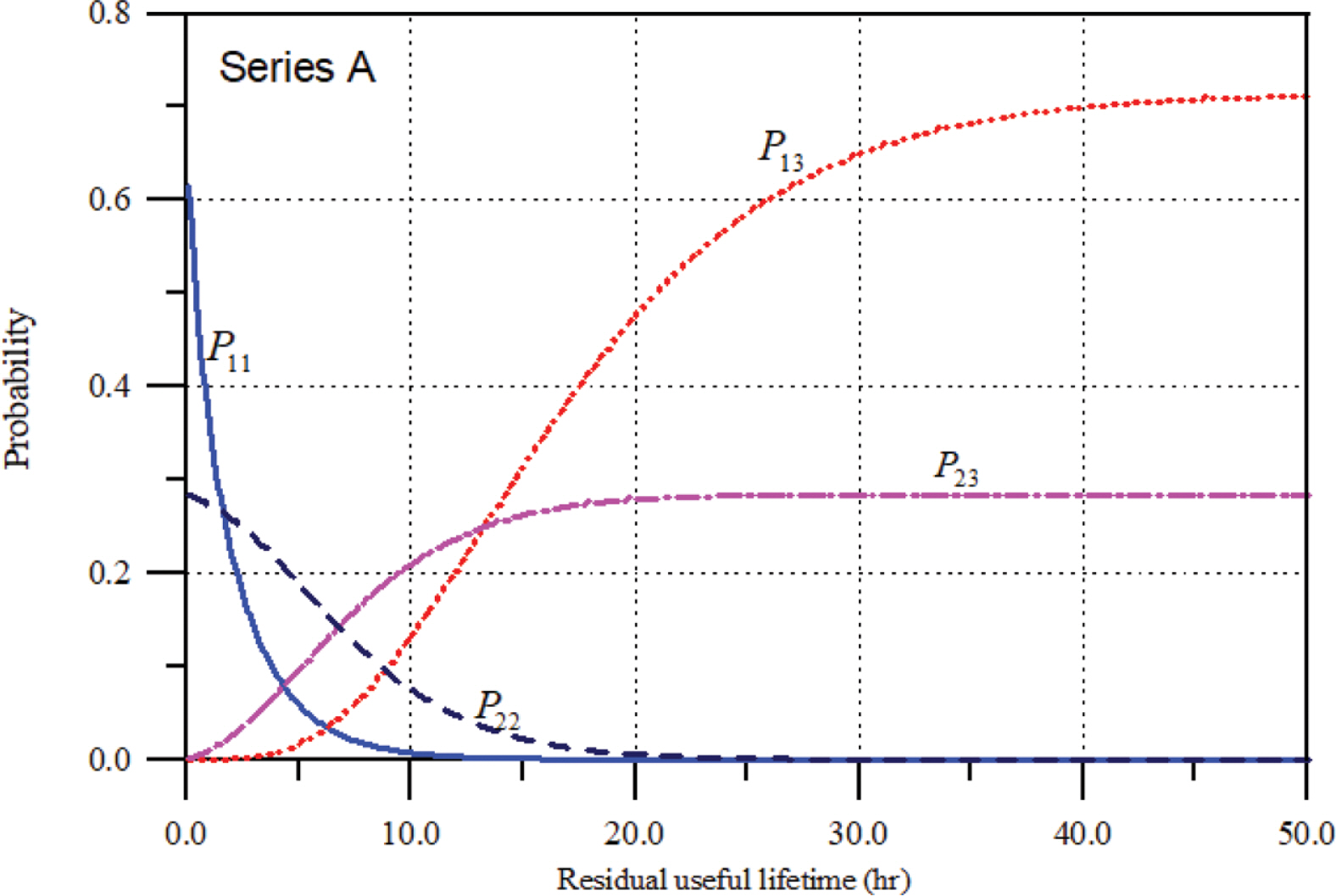
따라서 Fig. 4와 식(8)~식(12)를 이용하여 산정된 확률론적 해석 결과를 Fig. 5에 제시하였다. 먼저 현재 시점의 누적피해가 사용한계보다 작은 쪽에서 시작해 그 상태를 유지할 확률 P11은 시간이 진행해 감에 따라 지수함수적으로 감소하는 것을 쉽게 볼 수 있다. 반면 파괴한계를 초과할 확률 P13는 시간이 진행해 감에 따라 점진적으로 증가한다. 또한 사용한계를 초과한 상태에서 파괴한계보다 작을 확률 P22는 상대적으로 P11보다 오래 지속되지만 파괴한계를 초과할 확률 P23는 P22와 유사한 시간대에서 발생된다. 그림을 보면 현재 시점으로부터 상당히 오랜 시간이 경과하면 P13 = 0.715로 수렴하고, P23 = 0.285로 수렴함을 알 수 있다. 이는 Fig. 4에서 제시한 결과와 일치하는 것이다. 따라서 수치해석이 올바로 수행되었음을 알 수 있다.
한편 정량적인 해석을 위하여 Fig. 5로 부터 평균 잔류유효시간을 산정하였다. 먼저 결정론적 해석에 의하면 현재 시점 ti에서 평균 누적피해가 E[Z(ti)]인 구조물의 잔류유효수명은 다음 식(24)를 이용하여 산정할 수 있다.
따라서 Series A의 경우는 결정론적 해석에 의하면 잔류유효수명은 Tζ = 12.8시간이 된다. 확률론적 해석에 의하여 산정된 P13의 평균 잔류유효수명, E[Tζ] = 12.7로 유사한 결과를 나타내고 있다. 그러나 결정론적 해석에서는 구할 수 없는 P23의 평균 잔류유효수명, E[Tζ] = 2.2시간으로 산정되었다.
따라서 본 연구에서 수립된 잔류유효수명 예측 모형을 이용하면 결정론적 해석에서는 고려할 수 없는 누적 피해 관측자료인 표본의 불확실성에 따른 영향과 시간의 진행에 따른 불확실성의 영향을 모두 고려하여 해석할 수 있다.
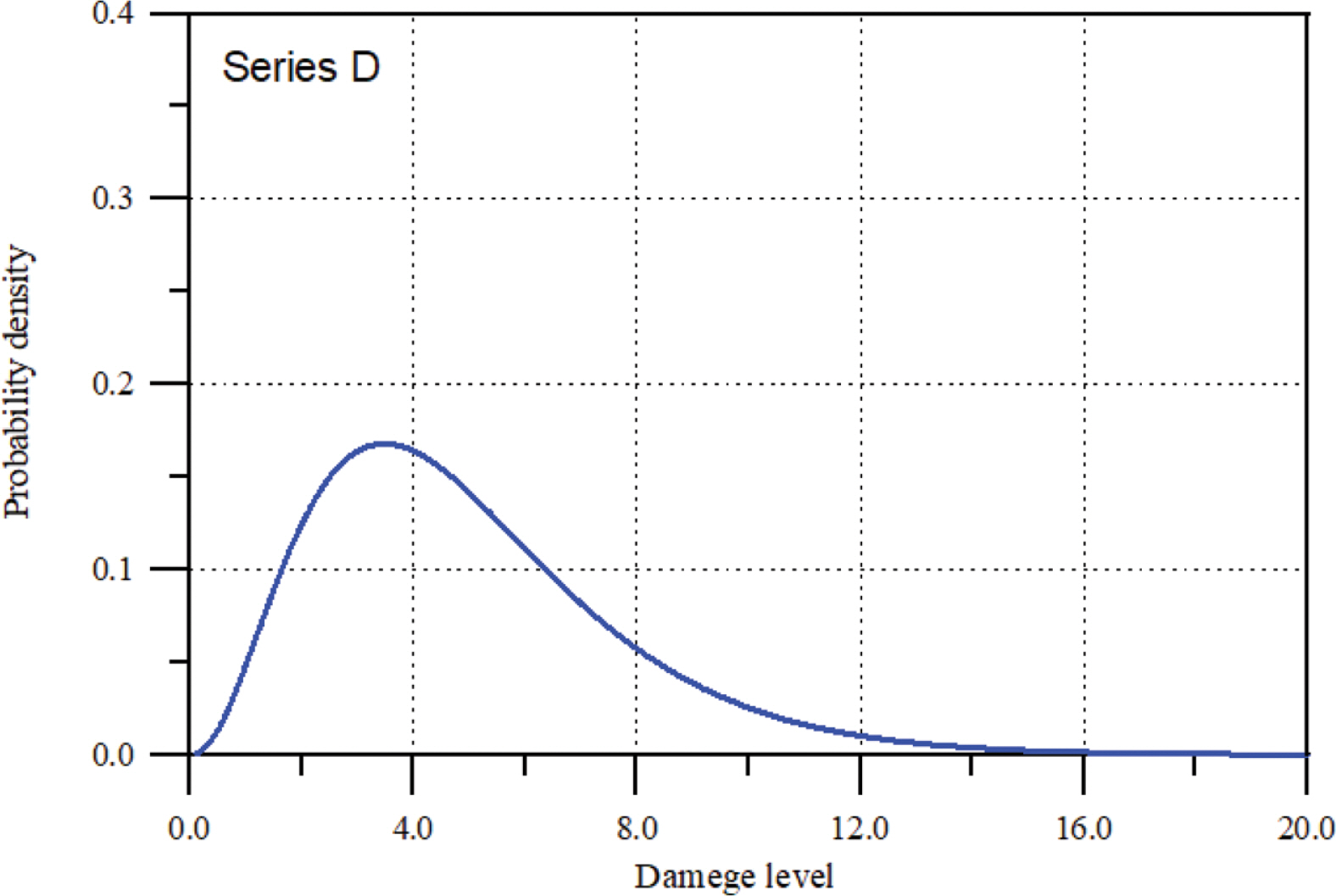
다음으로 Series A 보다 상대적으로 관측자료의 변동성이 큰 경우인 Series D를 해석하였다. 8.5시간까지 존재하는 피복석의 누적피해에 대한 관측자료를 이용하여 앞의 경우와 동일하게 현재 시점의 피해수준에 대한 분포함수를 산정하여 Fig. 6에 제시하였다. 현재 시점의 평균 피해수준 E[Z(8.5)] = 4.988, 변동계수 VZ(8.5) = 0.550의 통계적 특성을 갖는다. Series A에 대한 Fig. 4와 비교하면 불확실성이 2배 이상 크다. 이는 Fig. 3에서 알 수 있듯이 과거 자료의 변동성에서 기인한다. 또한 현재 시점 8.5시간에서 누적피해가 사용한계보다 작을 확률, FZ(13.5)(8) = 0.866이고 파괴한계와 사용한계 사이에 있을 확률, FZ(13.5)(14) − FZ(13.5)(8) = 0.126이다. 현재 시점에서 파괴한계를 초과할 확률도 0.008로 비록 작지만 가능성이 존재한다.
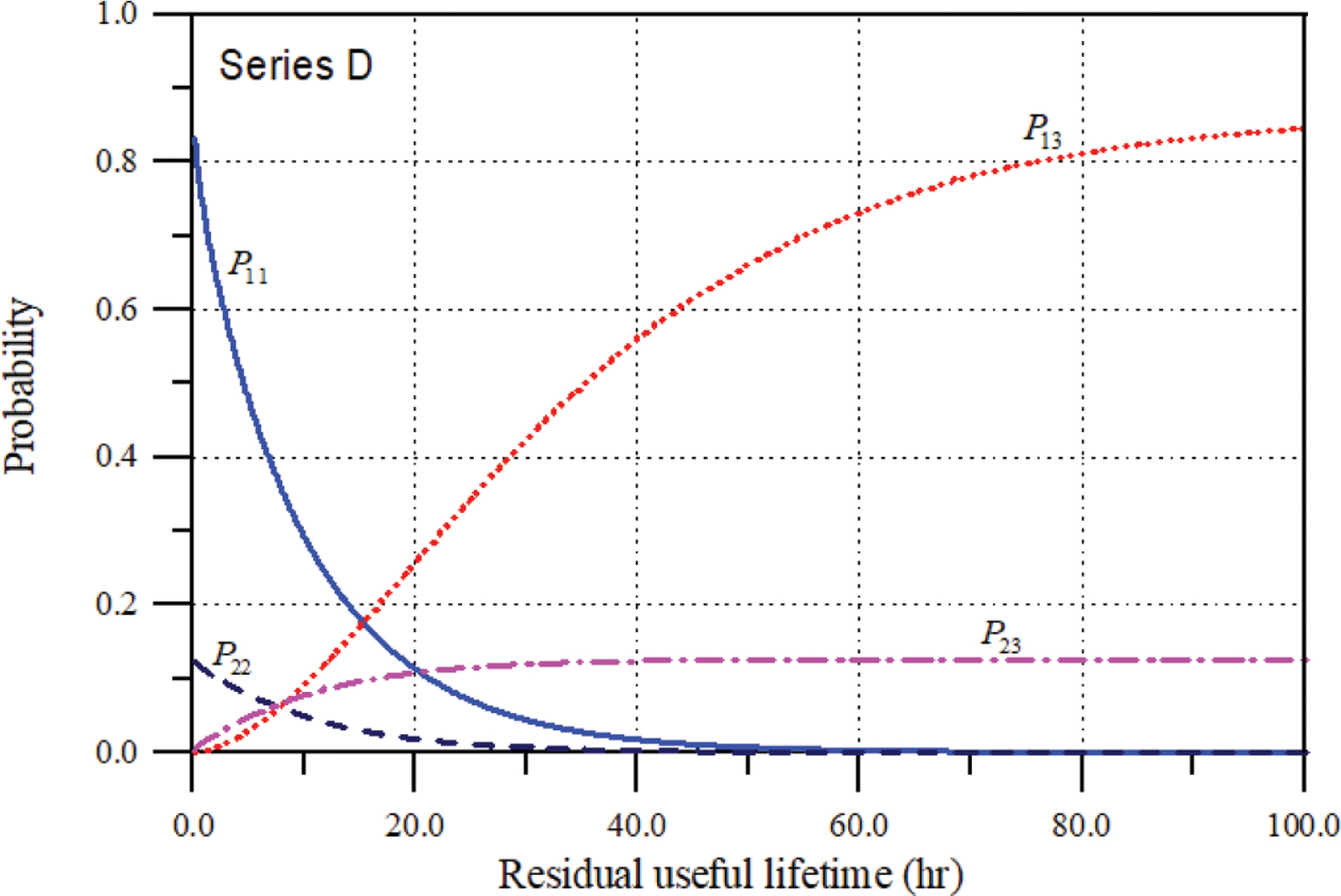
현재 시점의 평균 피해수준이 4.988이기 때문에 피해의 여유는 9.012라는 의미이다. 현재 시점부터 피해의 여유까지 도달하는데 걸리는 잔류유효수명을 확률적으로 예측하는 문제가 된다. 동일하게 Fig. 6과 식(8)~식(12)를 이용하여 산정된 확률론적 해석 결과를 Fig. 7에 제시하였다. 먼저 현재 시점의 누적피해가 사용한계보다 작은 쪽에서 시작해 그 상태를 유지할 확률 P11은 시간이 진행해 감에 따라 지수함수적으로 감소하는 것을 쉽게 볼 수 있다. 그러나 Series A보다 상당히 오랜 기간 동안 유지한다. 이는 현재 시점의 누적피해가 Series A 보다 작기 때문이다. 또한 파괴한계를 초과할 확률 P13는 시간이 진행해 감에 따라 점진적으로 증가한다. 반면 사용한계를 초과한 상태에서 파괴한계보다 작을 확률 P22는 상대적으로 P11보다 짧게 지속되며 파괴한계를 초과할 확률 P23도 P22와 유사한 시간대에서 발생된다. 마지막으로 그림을 보면 현재 시점으로부터 상당히 오랜 시간이 경과하면 P13 = 0.866로 수렴하고, P23 = 0.126으로 수렴함을 알 수 있다.
정량적인 해석을 위하여 Fig. 7로부터 잔류유효시간의 평균을 산정하였다. 먼저 식(24)를 이용하여 결정론적 해석으로 산정된 Series D의 잔류유효수명은 Tζ = 24.5시간이다. 확률론적 해석에 의하여 산정된 P13의 평균 잔류유효수명, E[Tζ] = 31.3로 결정론적 해석의 결과와 큰 차이를 보이고 있다. 이는 해석과정에 포함된 불확실성의 영향으로 판단된다. 전 절의 민감도 분석에서 살펴본 바와 같이 변동계수가 크면 파괴한계를 도달하는 시간의 분포가 넓게 퍼지기 때문이다. 또한 P23의 평균 잔류유효수명, E[Tζ] = 1.3시간으로 산정되었다.
앞에서 설명한 Series A와 Series D와 동일한 과정을 거쳐 확률론적 해석에 의하여 산정된 P13, 즉, 사용한계 δ보다 작은 피해수준에서 시작하여 파괴한계 ζ에 도달하는데 걸리는 시간의 평균으로 정의되는 평균 잔류유효수명의 결과를 Table 4에 제시하였다. 식(24)에 의하여 산정된 결정론적 해석의 결과도 함께 제시하였다.
Table 4에서 볼 수 있듯이 평균 잔류유효수명은 과거의 피해 이력의 거동에 직접적으로 의존하는 것을 알 수 있다. 서론에서 언급하였듯이 일반적으로 잔류유효수명은 구조물의 재령, 운용환경 그리고 현재까지의 피해 이력에 의존한다. 이를 복합적으로 해석하면 현재의 재령만이 아니라 운용에 따른 피해상태가 함께 작용한다. Series A와 Series B, C를 비교하면 재령이 짧아도 현재 시점에서 피해가 크면 잔류유효수명은 짧아진다. 동일한 재령을 갖는 Series D와 Series G의 비교에서도 동일한 경향을 보이고 있다. 따라서 단순히 재령보다는 현재 시점의 피해의 여유가 장래 잔류유효수명에 가장 큰 영향을 미친다. 현재 시점의 피해는 과거의 운용환경에 따른 피해이력과 직접적으로 관련된다. 예로 Table 3을 보면 Series A보다 Series B의 β가 크고 Series C가 더 크다. β가 크다는 것은 피해가 더 급격하게 발생한다는 것을 의미한다. 한편 현재 시점의 불확실성을 나타내는 변동계수 VZ(ti)를 보면 Series D가 제일 크다. 따라서 상대적으로 다른 경우보다 기대 잔류유효수명이 결정론적인 해석의 결과와 큰 차이를 보인다. 변동계수는 피해에 대한 과거이력의 변동성을 반영하는 것이다.
따라서 기대 잔류유효수명을 해석하기 위해서는 현재 시점의 피해수준에 대한 분포함수를 산정하여 현재 시점의 피해에 대한 정확한 평가가 확률적으로 수행되어야 한다. 이는 현재 시점까지 관측된 누적피해 자료로부터 추계학적 감마 확률과정의 모수를 올바로 추정하는 것을 의미한다. 즉, 현재 시점까지 관측된 누적피해 자료와 관련된 표본의 불확실성과 장래 누적피해의 시간의 진행에 따른 불확실성을 올바로 고려할 수 있을 때 기대 잔류유효수명을 올바로 추정할 수 있다.
6. 결 론
잔류유효수명이란 구조물의 현재 피해상태로부터 미래 임의 시점까지 사용 가능한 유용한 구조물의 수명으로 정의된다. 잔류유효수명은 구조물의 현재까지의 피해상태와 미래에 발생될 피해진행에 따라 변하기 때문에 확률변수로 고려되어야 한다. 본 연구에서는 감마 확률과정을 이용하여 구조물의 잔류유효수명을 확률론적으로 예측할 수 있는 수학적 모형을 수립하였다. 수립된 모형은 현재 시점까지 관측된 누적피해자료와 관련된 표본의 불확실성과 장래 누적피해의 시간의 진행에 따른 불확실성을 올바로 고려할 수 있다.
일반적으로 잔류유효수명은 구조물의 재령, 운용환경 그리고 현재까지의 피해 이력에 의존한다고 알려져 있다. 이를 고려하기 위하여 감마 확률과정에 의해 수립된 모형에 포함된 매개변수를 추정할 수 있는 방법을 제시하였다. 최소자승법과 모멘트법을 함께 사용하여 두 가지 방법이 제시되었다. 하나는 현재 시점의 자료만을 이용하는 방법이고, 다른 하나는 과거의 복수의 시간에서 누적피해의 이력을 알고 있는 경우이다. 전자의 방법을 적용하여 임의의 조건에 대해 민감도 분석을 수행하였다. 해석 결과에 의하면 동일한 잔류유효수명에서 가속모형의 확률이 가장 크고 포화모형이 제일 작다. 또한 변동계수가 클수록 확률이 작다. 한편 기대 잔류유효수명을 정량적으로 산정한 결과에 의하면 누적피해의 진행이 빠를수록 기대 잔류유효수명이 짧다. 또한 변동계수가 작을수록 동일한 거동특성을 보인다. 이는 불확실성에 따른 영향으로 변동계수가 클수록 누적피해가 파괴한계에 도달하는 시간의 분포가 넓게 퍼지기 때문이다. 가속모형에서는 시간에 따른 누적피해의 불확실성에 따른 영향이 다른 피해진행 모형보다 상대적으로 작게 나타난다. 이는 가속모형의 단위 시간당 누적피해인 피해증가율이 선형모형이나 포화모형보다 크기 때문이다.
마지막으로 본 연구에서 제시한 잔류유효수명 예측 모형을 경사제 피복재의 피해에 적용하였다. 일반적으로 경사제의 파괴는 파랑과 직접적으로 만나는 전면에 거치된 피복재의 연속적인 피해에 의하여 발생된다는 개념을 이용하였다. 시간에 따라 경사제 피복재의 피해 진행과정에 대한 실험 관측자료를 이용하여 감마 확률과정의 모수를 추정하였는데, 전반적으로 포화모형을 따르면서 추정된 결과가 실험자료와 매우 잘 일치하고 있다. 한편 해석 결과에 의하면 현재 시점으로부터 상당히 오랜 시간이 경과하면 파괴한계를 초과할 확률이 일정한 조건으로 수렴하여 수치해석이 올바로 수행되었음을 확인 할 수 있었다. 특히 현재 시점의 누적피해가 사용한계보다 작은 쪽에서 시작해 그 상태를 유지할 확률은 시간이 진행해 감에 따라 지수함수적으로 감소하는 것을 확인할 수 있었다. 그러나 파괴한계를 초과할 확률은 시간이 진행해 감에 따라 점진적으로 증가한다. 반면 사용한계를 초과한 상태에서 파괴한계보다 작을 확률은 과거의 피해 이력에 따라 다르게 거동하였다. 한편 정량적으로 산정된 기대 잔류유효수명은 피해 이력의 거동특성에 따라 각기 다르게 산정되었다. 특히 변동계수가 크면 본 연구에서 수립된 모형을 이용하여 확률론적으로 산정된 기대 잔류유효수명은 결정론적 해석의 결과와 큰 차이를 보이고 있다. 이는 해석과정에 포함된 불확실성의 영향으로 판단된다. 변동계수가 크면 파괴한계에 도달하는 시간의 분포가 넓게 퍼지기 때문이다. 따라서 기대 잔류유효수명을 해석하기 위해서는 현재 시점의 피해수준에 대한 분포함수를 산정하여 현재 시점의 피해에 대한 정확한 평가가 확률적으로 수행되어야 한다. 즉, 현재 시점까지 관측된 누적피해 자료와 관련된 표본의 불확실성과 장래 누적피해의 시간의 진행에 따른 불확실성을 올바로 고려할 수 있을 때 기대 잔류유효수명을 올바로 추정할 수 있다.
본 연구에서는 임의의 조건에 대한 민감도 분석과 실험자료에 기반한 경사제 피복재 피해에 대하여만 해석하였다. 따라서 장래 실제 경사제 피복재 피해에 대한 실측자료를 확보할 수 있다면 이에 대한 해석이 추가적으로 수행되어야 한다.
Acknowledgements
본연구는해양수산과학기술진흥원의지원(과제번호 20180323)으로 수행되었으며 지원에 감사드립니다.