3차원저천단구조물(LCS) 주변에서 파동장의 변동특성
Variation Characteristics of Wave Field around Three-Dimensional Low-Crested Structure
Article information
Abstract
최근, 유럽이나 일본 등은 해빈유실방지대책공법의 하나이며, 잠제의 대안으로 여겨지는 저천단구조물(LCS)에 관한 많은 연구를 수행하였고, 그의 결과들을 집약하여 설계매뉴얼까지 편찬하였다. 지금까지 LCS에 관한 연구는 2차원적인 파랑전달율과 피복재의 안정중량산정에 치우쳐 있으며, 이들은 주로 실험에 기초하여 검토·논의되었다. 본 연구에서는 투과성의 LCS를 대상으로 3차원수치해석을 수행한다. 수치해석에 Navier-Stokes 운동방정식에 기반한 오픈소스 CFD Code인 olaFlow를 적용하였으며, 이는 쇄파와 난류해석까지도 가능한 강비선형해석법이다. 이로부터 수위, 흐름 및 난류운동에너지 등의 분포특성을 검토·논의하였으며, 동시에 잠제의 경우와도 비교·검토하였다. 이로부터 해안선 근방에서 연안류의 흐름패턴과 평균난류운동에너지의 연안방향 및 종단방향의 공간분포에 관해 잠제와 LCS의 경우에 각각 차이가 발생하는 것을 알 수 있었다. 이러한 결과의 차이는 모래이동에서의 차이로 이어질 것으로 판단된다.
Trans Abstract
In recent years, countries like Europe and Japan have been involved in many researches on the Low-Crested Structure (LCS) which is the method to protect beach erosion and it is regarded as an alternative to the submerged breakwaters, and compiled its results and released the design manual. In the past, studies on LCS have focused on two-dimensional wave transmission and calculating required weight of armor units, and these were mainly examined and discussed based on experiments. In this study, three-dimensional numerical analysis is performed on permeable LCS. The open-source CFD code olaFlow based on the Navier-Stokes momentum equations is applied to the numerical analysis, which is a strongly nonlinear analysis method that enables breaking and turbulence analysis. As a result, the distribution characteristics of the LCS such as water level, water flow, and turbulent kinetic energy were examined and discussed, then they were carefully compared and examined in the case of submerged breakwaters. The study results indicate that there is a difference between the flow patterns of longshore current near the shoreline, the spatial distribution of longshore and on-offshore directions of mean turbulent kinetic energy in case of submerged breakwaters and LCS. It is predicted that the difference in these results leads to the difference in sand movement.
1. 서 론
수중에 설치되는 잠제(submerged breakwater)는 연안의 자연경관을 살릴 수 있고, 천단상으로 원활한 해수교환에 따른 생태환경을 포함한 친환경적인 효과도 기대할 수 있다. 공학적으로는 잠제 배후에 양빈된 저질의 침식을 방지하거나 침식성 해빈에서 저질이동을 방지하여 해빈의 현상유지·회복을 도모할 수 있고, 자연발생적인 형태와 유사한 해빈을 조성할 수 있는 것으로도 알려져 있다.
그러나, 우리나라 동해안을 비롯한 다수의 해역에 침식방지대책으로 잠제를 계획·설치하여 왔지만, 의도한 침식방지 역할이 충실히 수행되는 현장은 그다지 많지 않은 것으로 판단된다. 이러한 이유로는 잠제의 천단폭, 개구폭, 길이 및 해안선에서 이격거리 등이 현장조건에 부합되지 않게 설치된 것, 그리고 평상파랑과 이상파랑의 두 파랑조건에 동시에는 부합되지 않게 설치된 것 등을 들 수 있을 것이다.
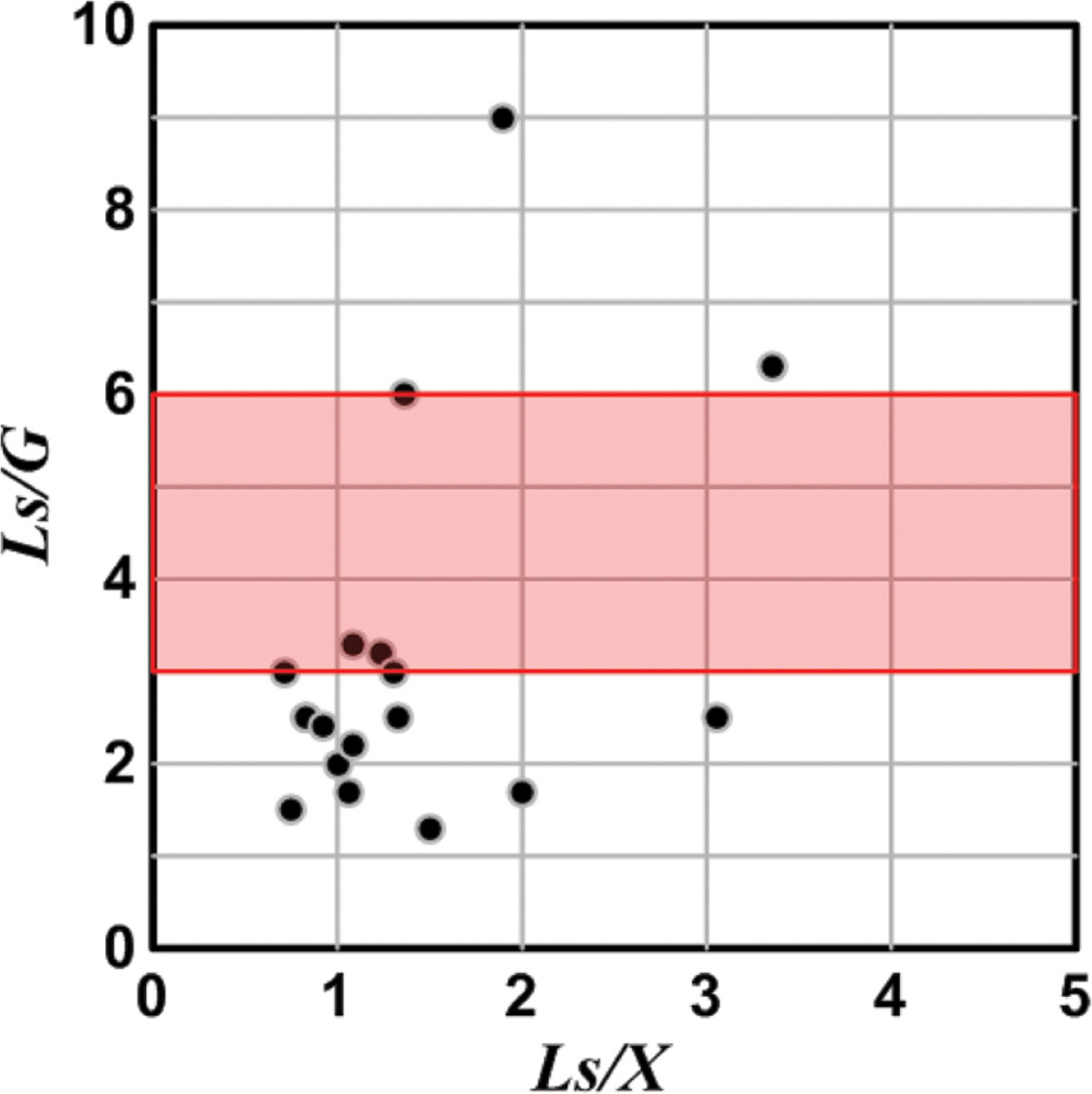
다음의 Fig. 1은 국내현장에 설치된 잠제의 배치조건을 분석하여 그의 무차원제원를 도시한 결과(Shim, 2017)이다(그림에서 G는 개구폭, X는 해안선에서 잠제까지의 이격거리, Ls는 잠제의 길이이며, 여기서 Ls는 후술하는 본 연구에서 Ls의 2배에 해당함). 분석에 따르면 무차원연직축 Ls/G의 변동폭이 매우 크게 나타나는 연직축의 값은 신중히 결정될 필요가 있고, Sim은 이 영역에 대한 3차원이동상수리실험으로부터 침식방지의 목적상 무차원연직축의 값으로 3.0~6.0을 제시하였다.
Layout condition of submerged breakwaters installed in Korea.
여기서, 침식방지대책으로 설치되어 성공적인 역할을 수행하는 것으로 알려진 Photo 1의 부산 송도해수욕장 전면 해역에서 잠제를 예로 나타낸다. 한편, 전술한 바와 같이 잠제가 경관 및 해양환경의 측면 등에서 우수한 요소가 고려되지만, 해빈의 미흡한 침식방지대책과 광폭이라는 비경제적인 관점이 또한 많이 지적되고 있는 것이 현실이다.
Submerged breakwaters to protect beach erosion of Songdo, Busan (https://www.crowdpic.net).
이러한 측면에서 일본 및 유럽에서는 Photo 2에서 제시하는 저천단구조물(LCS; low-crested structures)이 오래 전부터 관심을 받아왔다(DELOS project, 2003). 여기서, LCS는 일반적으로 해빈을 보호하기 위해 해안에 평행한 낮은 천단의 구조물로 전술한 잠제와 이안제(detached breakwater)의 중간적인 역할을 수행하는 것으로 알려져 있으며, LCS의 형상은 잠제나 이안제와 동일하지만, 천단고가 이안제보다 상대적으로 낮은 저천단이므로 고파랑의 경우는 월파가 허용되는 구조이고, 따라서 종래의 이안제보다 작용수평파력이 적어진다. 그리고, 광폭에 의한 마찰저항을 향상시키고 천단수심을 적게 하여 천단상에서 강제쇄파를 유도하는 잠제의 파랑제어기구와는 달리, LCS는 잠제에 비해 천단폭이 좁고, 천단이 공기중으로 돌출되어 천단고가 높기 때문에 반사와 월파 및 마찰저항에 의한 파랑제어기능이 우수하므로 잠제보다는 훨씬 경제적이다. LCS와 잠제 모두는 해빈에 작용되는 파에너지를 소멸시키지 않고 어느 정도로 줄이지만, LCS의 경우가 더 많은 전달파에너지를 감소시킨다. 이상과 같은 LCS의 장점에 주목하여 유럽에서는 많은 이론연구와 실험을 수행하여왔고, 결과의 현장적용으로 설계기술이 많이 향상되었으며, 집대성되었다. 이에 대한 경우로 Lamberti and Martinelli(1999)는 유럽에서 연안관리를 위한 LCS의 적용사례를 종합하였고, Hawkins et al.(2007)은 LCS에 대한 설계지침서를 발표하였다.
DELOS (www.delos.unibo.it).
이상의 LCS에 대한 초기연구는 2차원적인 파랑전달과 소요안정중량에 상대적으로 많이 집중되었다. 파랑전달과 관련해서는 Iwasaki and Numata(1969), Hattori(1975), Tominaga and Sakamoto(1971), Katayama et al.(1973), Goda and Ahrens(2008), Tanaka(1976) 등과 같은 일본의 많은 연구사례를 예로 들 수 있고, 유럽의 경우는 상대적으로 최근이며, 대표적으로 Allsop and Channel(1989), Calabrese et al.(2002), Buccino and Calabrese(2007), D’Angremond et al.(1996), Seabrook et al.(1998), Van der Meer et al.(2005), Melito and Melby(2002), Van der Meer et al.(2000) 및 Van der Meer and Daemen(1994)와 같은 연구사례가 보고되어 있다. LCS의 파랑전달에 대해서는 비월파시와 월파시를 구분하여 구조물의 투과층을 통한 파랑에너지과 월파시 천단상을 통한 파랑에너지의 합으로 전달율을 평가하였다. 그리고, LCS의 안정중량에 대한 연구로는 Van der Meer and Pilarczyk(1990), Vidal et al.(1995), Burcharth et al.(2006), Kramer et al. (2005), Kramer and Burcharth(2003), Kudale and Kobayashi (1996), Van der Meer et al.(1996) 등과 같은 주로 유럽의 연구사례를 들 수 있다.
한편, 우리나라에서 LCS에 대한 연구는 매우 미진한 수준이며, 최근의 사례로 Lee et al.(2017c)의 연구를 들 수 있을 것이다. 한편, LCS에 대한 3차원연구는 대부분이 수리실험에 의해 수행되었으며, 대표적으로 Kramer et al.(2005), Vicinanza et al.(2009) 및 Burcharth et al.(2006) 등을 들 수 있다. 여기서, 3차원수치시뮬레이션에 의한 연구는 매우 미흡한 수준이고, 일부 기존의 연구(Zanuttigh and Lamberti, 2006; Ryu et al., 2007)는 평면파랑이론을 적용하여 파고분포 등의 일부 수리특성을 규명한 수준에 머물고 있으며, 본 연구와 같은 강비선형의 3차원시뮬레이션을 수행한 연구는 거의 없는 것으로 판단된다.
여기서, Lee et al.(2017a, b; 2018a, b)은 3차원수치파동수조에서 규칙파랑 및 불규칙파랑 작용시 설상사주의 형성조건하에 투과성잠제를 대상으로 잠제 주변에서 형성되는 파고분포, 평균수위분포 및 유속의 변동특성 등을 Navier-Stokes solver에 기초한 유한체적법의 수치기법으로 3차원혼상류를 해석하는 공개된 CFD Code인 olaFlow(Higuera et al., 2018)로부터 면밀히 평가한 바 있다. 본 연구는 이에 대한 후속연구이며, 잠제 대신에 LCS를 적용한 경우에 해당한다. LCS의 배치를 잠제의 경우와 동일하게 하여 LCS 주변에서 파고와 유속변화 및 난류운동에너지 등을 도출하고, 구조물의 개구폭, 천단수심과 같은 배치형상의 변화 및 입사파고와 주기와 같은 입사파랑조건의 변화에 따른 결과를 잠제의 경우와 비교·검토하여 LCS와 잠제의 각각에 대한 특성의 차이 등을 면밀히 분석·논의한다.
2. 수치해석이론
본 연구에서 적용한 olaFlow모델(Higuera et al., 2018)은 기본적으로 비압축성의 혼상유체에 적용이 가능하며, 다음의 식(1)과 (2)에 나타내는 연속방정식과 운동량보존방정식을 유한체적법으로 이산화한다.
여기서, t는 시간, xi는 공간벡터좌표, ρ는 후술하는 액체와 기체상태를 고려한 혼상유체의 밀도로 ρ = ρwaterF + ρair(1 − F)로 산정되며, F는 계산격자내에서 유체의 점유율을 나타내는 VOF 함수이다. 또한, ui와 uj는 속도벡터, p*는 Pseudo-dynamic 압력, Xj는 위치벡터, ϕ과 D50은 해석영역내에 위치하는 투과성구조물의 공극률과 중앙입경을 각각 나타내며, μeff는 μ + νturb로 μ는 점성계수이고, νturb는 난류동점성계수이며, [CT]는 투과성구조물에 의한 저항 항으로 다음의 식(3)과 (4)로 주어진다.
여기서, α, β는 선형 및 비선형마찰계수이며, 본 연구에서는 Jensen et al.(2014)이 층류흐름, 층류와 난류가 혼합된 흐름 및 난류흐름에 대한 수치실험결과를 바탕으로 제시한 α = 500, β = 2.0을 각각 적용하였다. 또한, KC는 Keulegan-Carpenter수로 TouM/D50ϕ를 나타내며, To은 진동주기이고, uM은 유체입자의 최대진동속도이다. 또한, C는 Del Jesus(2011)가 제시하고 있는 C = 0.34를 취하는 계수이다.
이상과 같은 olaFlow 모델(Higuera et al., 2018)의 기초방정식으로부터 시간발전에 따른 유속과 압력에 대한 물리량의 계산이 가능하고, 이러한 물리량을 바탕으로 Kissling et al. (2010)이 제안한 VOF 법을 이용하여 자유수면을 추적한다. olaFlow 모델의 수치해석기법에 대한 보다 자세한 사항은 Lee et al.(2016) 및 olaFlow 매뉴얼(https://gitgub.com/phicau/OLAFOAM/master/reference.zip)을 참조하기 바란다.
3. 수치해석결과의 검증
3.1 3차원투과성직립벽 주변에서 수위 및 파압
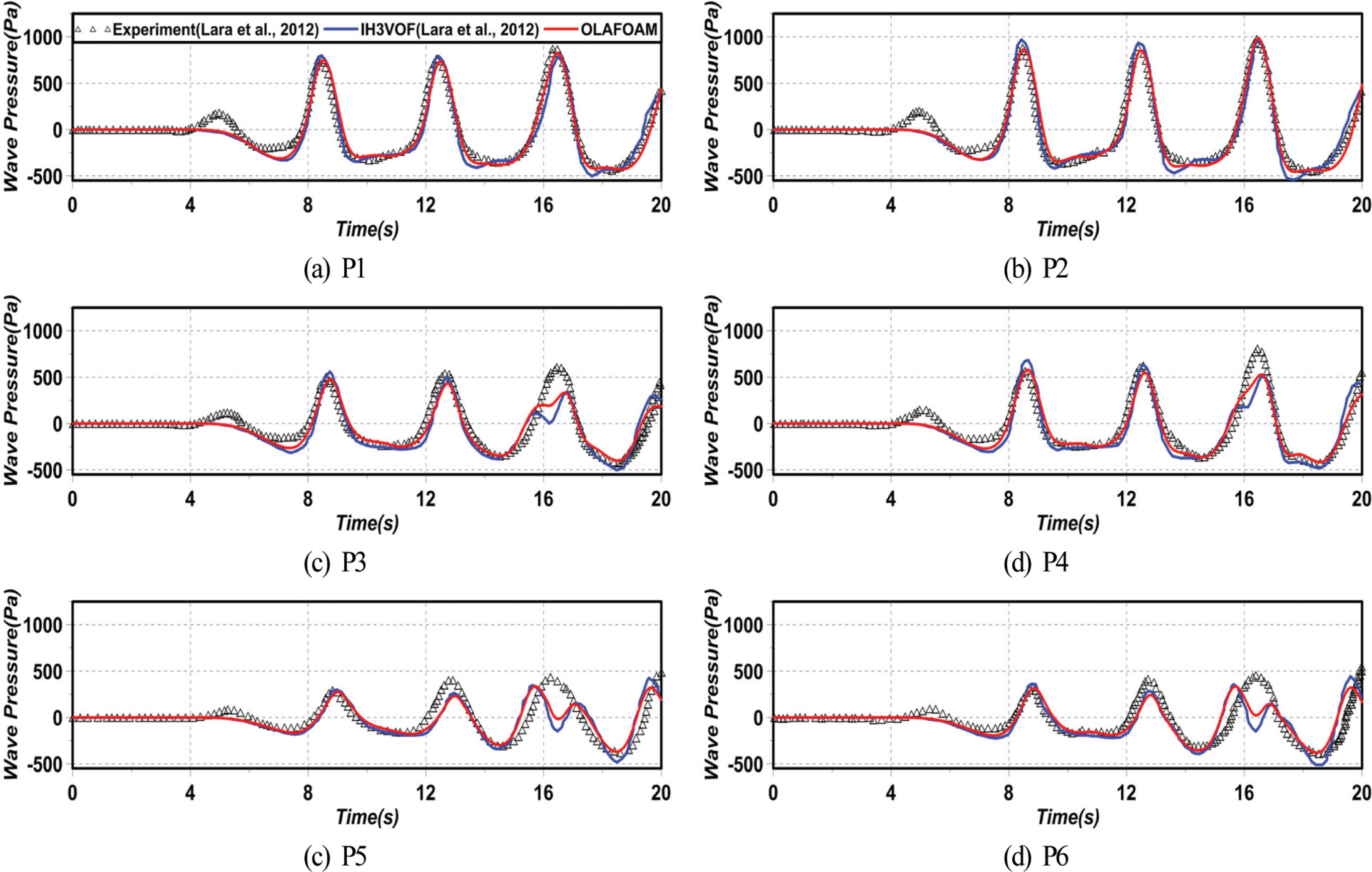
본 연구에서 적용하는 olaFlow 모델(Higuera et al., 2018)의 이안제 혹은 LCS로 적용성을 검토할 목적으로 Lara et al.(2012)이 수리실험 및 수치해석을 수행한 투과성직립이안제를 대상으로 수치해석을 수행하여 도출된 수치결과를 Lara et al.(2012)에 의한 수위 및 파압에 관한 실험결과와 IH3VOF 모델에 의한 수치해석결과를 각각 비교·검토한다.
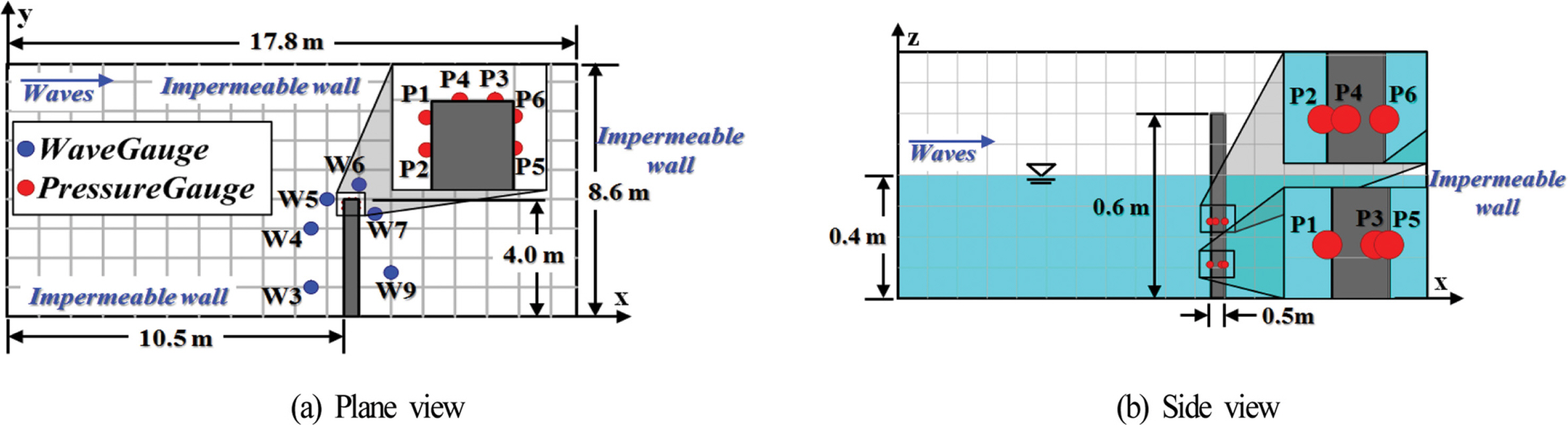
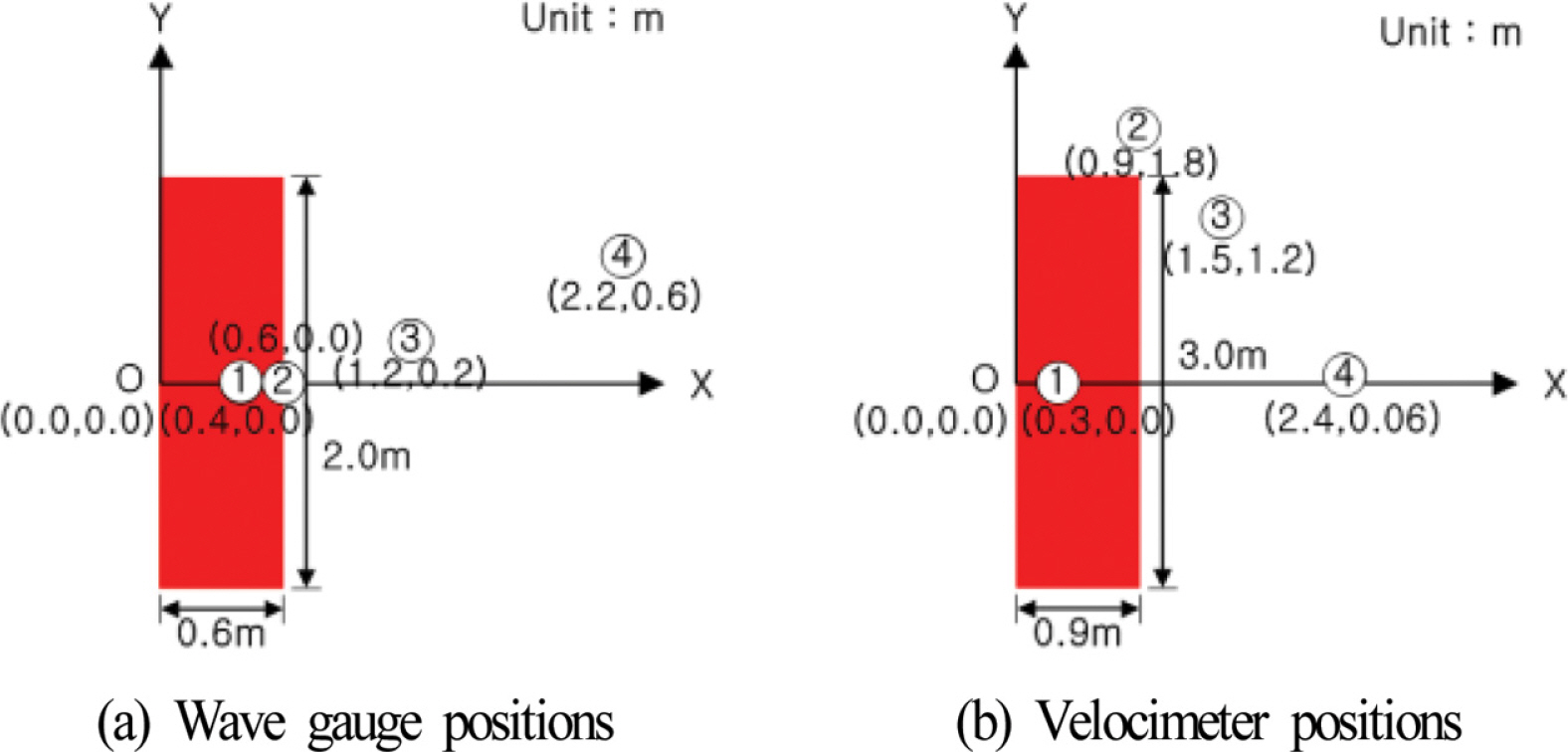
Lara et al.(2012)은 Fig. 2과 같이 수심 h = 0.4m를 갖는 3차원파동장에 설치된 높이 0.6 m, 길이 4.0 m, 폭 0.5 m의 투과성직립이안제에 규칙파를 작용시켜 직립벽 주변에서 수위변동과 파압변화를 각각 측정하였다. 수리실험에 사용된 조파수조는 길이 17.8 m, 폭 8.6 m, 높이 1.0 m이며, 투과성직립벽은 조파판에서 10.5 m로 이격되어 있고, 우측벽에 접해 있다. 양측벽과 수조 끝단은 완전반사가 발생되도록 불투과 성직립벽으로 구성되었다. 이 때, 투과성직립벽의 공극률은 ϕ = 0.51, 중앙입경은 D50 = 1.5 cm, 입사파고는 H = 9 cm, 주기는 T = 4 s이다.
Illustrative sketch for layout of three-dimensional basin and permeable vertical structure.
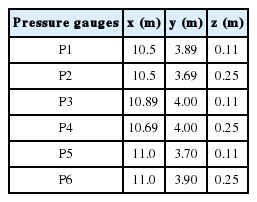
수치해석에 사용된 수치파동수조의 크기는 전술한 수리실험수조의 경우와 동일하지만, 구조물의 천단상으로 월파가 발생되지 않으므로 계산효율상 계산결과에 영향이 없는 것으로 판단되는 수조 높이를 투과성직립벽의 경우와 동일한 0.6 m로 구성하였다. 격자크기에서 수조 길이방향의 경우 조파지점에서부터 8 m까지는 Δx = 5~2.5 cm의 가변격자로, 8~12.5 m의 범위에서는 Δx = 2.5 cm로, 12.5~17.8 m의 범위에서는 Δx = 5~2.5cm의 가변격자로 각각 구성하였고, 수조 폭방향의 크기는 Δy = 2.5 cm, 연직방향의 크기는 Δz = 1.25 cm로 각각 일정한 격자로 구성하였으며, 따라서 적용된 격자의 총 개수는 대략 880만개에 달한다. 수치조파에 Cnoidal 파이론을, 난류모델에 LES 모델(Ghosal et al., 1995)을 각각 적용하였으며, 조파 개시 후 20 s 동안 파랑의 전파과정을 시뮬레이션하였다. 투과성직립이안제에 대한 저항계수 식(4)의 α와 β는 전술한 바와 같이 Jensen et al.(2014)이 제시한 α = 500과 β = 2.0을 적용하였다. 여기서, Fig. 2는 수위 및 파압변동에 관한 수리실험 및 수치해석결과의 산정위치로, Fig. 2(a)가 수위변동의 경우를, Fig. 2(b)가 파압변동의 경우를 각각 나타내며, Table 1에 수위계의 설치위치를, Table 2에 파압계의 설치위치를 각각 제시한다. 수리실험에서 수위변동 및 파압 변화는 총 15개 지점에서 각각 측정되었지만, 이 중에 6개 지점(W3~W7 지점, W9 지점)에서 산정된 수위와 6개 지점(P1~P6 지점)에서 파압에 대한 각 실험결과를 olaFlow에 의한 수치해석결과와 이하에서 상호 비교·검토한다.
Wave gauge positions
Pressure gauge positions
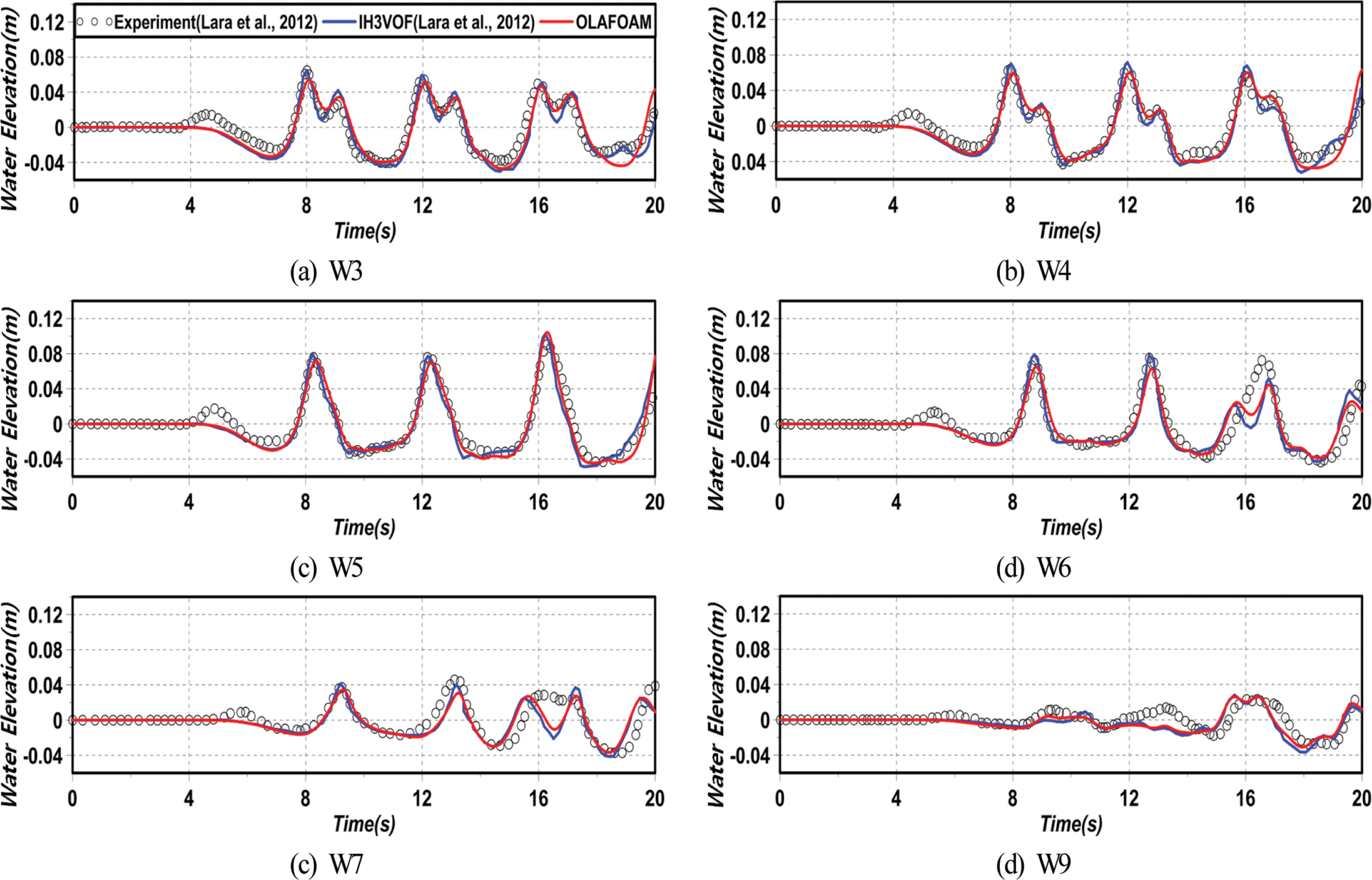
Fig. 3은 수치해석결과와 실험결과를 비교한 투과성직립이 안제 주변에서 수위변동을 나타낸 것으로, 그림에서는 IH3VOF 모델에 의한 Lara et al.(2012)의 수치해석결과도 같이 병기되어 있다. 그림을 살펴보면 W3과 W4 지점은 투과성직립이 안제 전면에서 수위변동을 나타낸 것으로, 8 s 이후에 쌍봉형의 수위변동이 나타나며, 앞의 파봉은 입사파에 의한 것이고, 뒤는 투과성직립이안제로부터의 반사파에 의한 것이다. W5와 W6 지점에서의 수위변동은 투과성직립이안제와 후면 불투과벽체로부터의 회절파 및 반사파의 영향을 동시에 받는 경우로, W6 지점의 16 s 근방에서 발생되는 쌍봉형의 수위변동은 후면 불투과벽체에 의한 반사파의 영향이다. 다음의 W7지점은 투과성직립이안제에 의한 회절파가, W9 지점은 후면 불투과벽체에 의한 반사파가 각각 영향을 크게 미치는 지점이다. 수리실험 및 수치해석결과의 대응성은 W6과 W7 지점의 16 s 이후 쌍봉형 수위변동에서 약간이 차이가 나타나지만, 전반적으로 매우 잘 구현되는 것으로 판단되며, 특히 이러한 결과는 W3, W4, W5, W9 지점에서 확인할 수 있고, 또한 Lara et al.(2012)의 수치해석결과와 본 수치해석결과는 거의 동일한 값을 나타내는 것을 알 수 있다.
Comparison between simulated and measured water surface elevations.
Fig. 4는 투과성직립이안제 주변에서 파압변동에 관한 수치해석결과와 실험결과를 비교한 것으로, Fig. 3과 동일하게 IH3VOF 모델에 의한 Lara et al.(2012)의 수치해석결과도 병기하였다. 그림을 살펴보면 투과성직립이안제 전면에서 파압 변동을 나타낸 P1과 P2 지점의 경우는 실험치와 거의 동일한 값을 나타내는 것을 확인할 수 있다. 또한, 투과성직립이 안제과 후면 불투과벽체로부터의 회절파 및 반사파의 영향을 동시에 받는 P3~P6 지점에서 파압변동은 전반적으로 실험치를 잘 재현하고 있지만, 수위변동에서와 같이 P3, P5, P6 지점의 16 s 근방에서 후면 불투과벽체에 의한 반사파의 영향에 의해 생성되는 쌍봉형의 파압변동에서 약간의 차이가 인정된다. 그러나, 전체적으로 실험치를 잘 재현하고 있는 것을 알 수 있다. 따라서, olaFlow 모델(Higuera et al., 2018)에 의한 본 연구의 수치해석결과는 투과성직립이안제에 의한 파랑변형과 작용파압의 변동과정에서 실험치를 잘 재현하고 있으므로 LCS와 같은 투과성구조물로의 적용성이 높은 것으로 판단된다.
Comparison between simulated and measured wave pressures.
3.2 3차원불투과성잠제 주변에서 수위 및 유속
구조물의 천단상에서 유수심을 갖는 3차원잠제로 olaFlow(Higuera et al., 2018)의 적용·타당성을 검토하기 위해 Kawasaki and Iwata(1999)의 수리실험을 재현하였다. Kawasaki and Iwata(1999)은 Fig. 5와 같이 h = 0.4m를 갖는 3차원파동장에 설치된 높이 0.24 m의 직사각형불투과잠제에 규칙파를 작용시켜 잠제 주변에서 수위변동과 유속변화를 수리실험으로부터 측정하였다. 수리실험에 사용된 조파수조는 길이 28 m, 폭 8 m, 높이 0.8 m이며, 조파판에서 7 m의 이격지점에 직사각형불투과잠제를 설치하였다. 그리고, 조파판 반대쪽의 수조 끝단에는 반사파의 제어를 위해 경사 1:10의 감쇠영역을 설치하였다. 입사파랑은 수위 측정에서는 파고 H = 0.1m, 주기 T = 1.2 s의 규칙파를, 유속 측정에서는 파고 H = 0.087m, 주기 T = 1.68 s의 규칙파를 각각 적용하였으며, 불투과잠제의 제원과 수위계 및 유속계의 설치위치를 Fig. 6에 각각 나타낸다.
Illustrative sketch for layout of three-dimensional basin and impermeable vertical structure.
Dimension of submerged breakwater and measuring positions of water surface elevation and velocity.
수치해석에 사용된 수치조파수조의 크기는 수치계산의 계산효율을 위하여 길이 3L(L은 파장)과 폭 2L로 적용되었고, 불투과잠제는 조파판으로부터 1.5L의 이격지점에 설치되었다. 여기서, 수위 측정시는 L≒ 2.0 m이고, 유속 측정시는 L≒ 3.0 m의 값을 가진다. 바닥경계조건은 Slip 조건을, 배후면과 양측면은 모두 감쇠영역으로 적용되었으며, 격자크기는 Δx = 2 cm, Δy = 2 cm, Δz = 1 cm이고, 격자의 총 개수는 수위 측정의 경우에 대략 310만개에, 유속 측정의 경우에 대략 702만개에 달한다. 수치조파에는 Stokes 5차파이론을 적용하였으며, 난류모델에는 LES 모델(Ghosal et al., 1995)을 적용하였다.
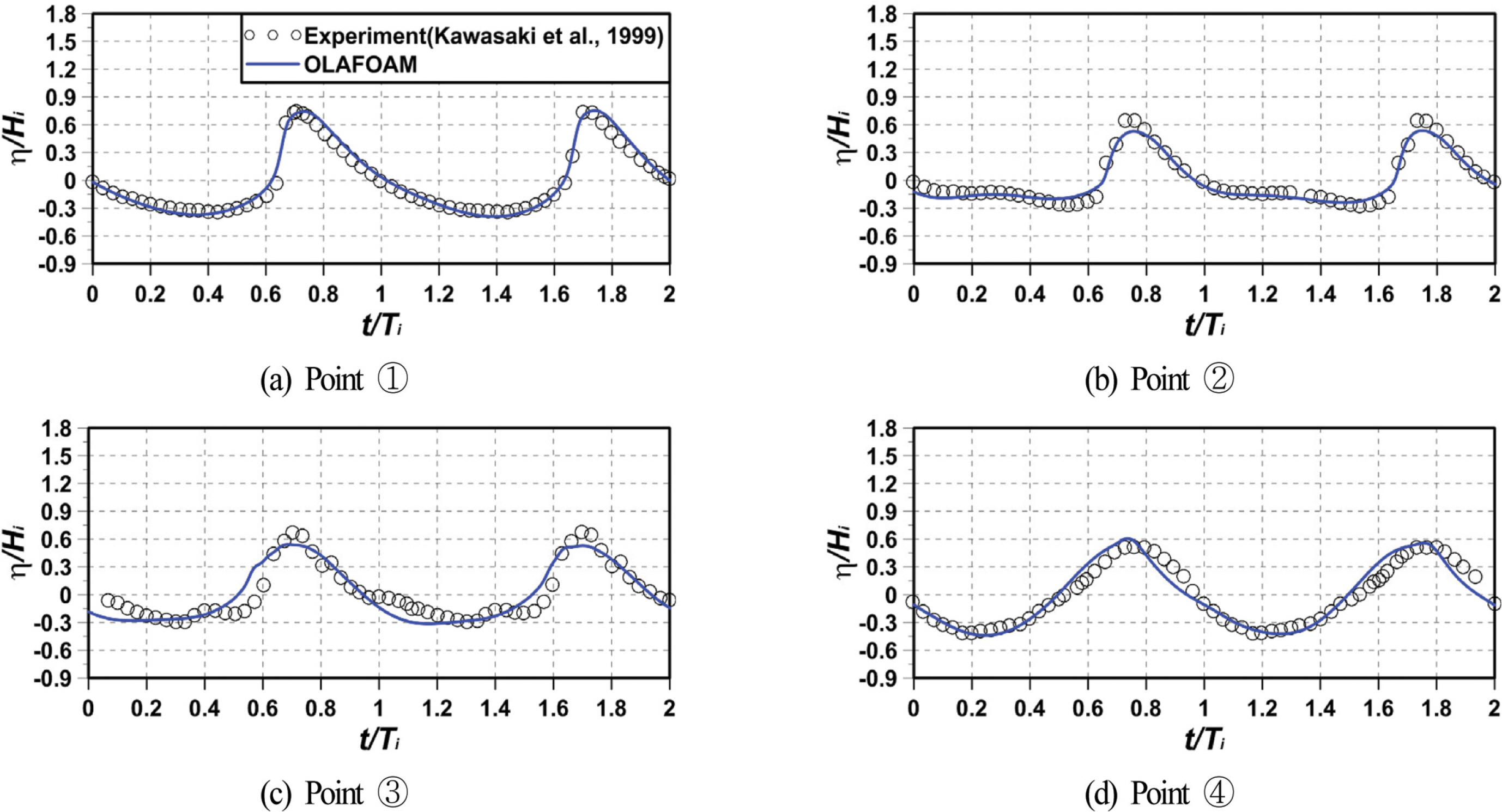
Fig. 7은 Figs. 5와 6의 조건으로부터 산정된 Fig. 4(a)의 불투과잠제 주변에서 무차원수위변동에 관한 수치해석결과와 실험결과를 나타낸 것이다. 잠제 천단상인 ①과 ② 지점에서는 급격한 비선형파의 발생·발달로 인하여 파형에서 대칭성이 붕괴되기 시작하고, 잠제 배후인 ③과 ④ 지점에서는 파의 재형성과정을 통하여 다시 대칭성을 갖는 파형이 재형성되는 것을 알 수 있다. ③ 지점의 실험파형에 포함된 작은 변동은 잠제로부터 짧은 이격거리 때문에 잠제 천단상에서 형성된 산란파(evanescent mode waves)가 직접적인 영향을 미친 결과이며, 이격거리가 보다 긴 ④ 지점에서는 그의 영향이 감소된 것을 알 수 있다. 이러한 시간변동과정에서 수치해석결과와 실험결과를 비교하면 상호간에 일치성이 매우 양호한 것으로 판단되며, 따라서 본 수치해석의 타당성이 충분히 확인된다.
Comparison between simulated and measured water surface elevations.
Fig. 8은 Figs. 5와 6의 조건으로부터 산정된 Fig. 6(b)의 불투과잠제 주변에서 수치해석결과와 실험결과를 비교한 불투과잠제 주변에서 x 방향과 y 방향의 무차원수평유속변화를 나타낸 것이며, 측정 높이는 모두 바닥으로부터(① 지점은 잠제 천단상으로부터) z = 0.28m인 지점이다. ① 지점은 천단상이고, ②와 ③ 지점은 회절파의 영향을 직접적으로 받는 곳이며, ④ 지점은 잠제의 배후이다. 잠제 천단상에서는 x 방향의 유속이, 나머지 지점에서는 y 방향의 유속이 탁월한 것을 알 수 있고, 시간변동과정에서 수평유속에 관한 수치해석결과와 실험결과를 비교하면 상호 대응성이 탁월한 것으로 판단되며, 따라서 olaFlow(Higuera et al., 2018)에 의한 3차원 투과성잠제의 파동장 해석결과에 대한 타당성이 충분히 검증된다.
Comparison between simulated and measured X- and Y-direction velocities.
4. 수치해석
4.1 수치해석 조건
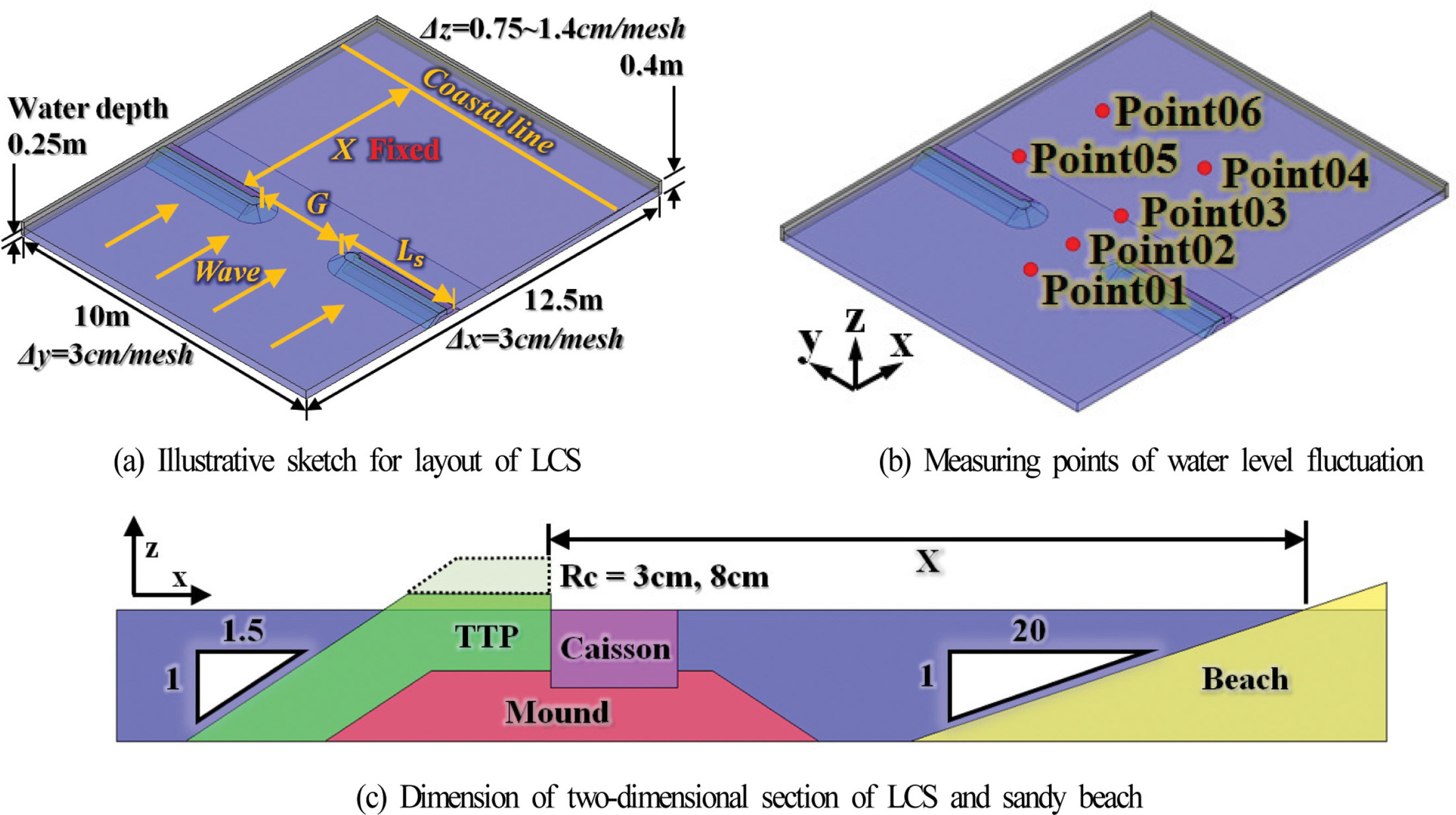
본 수치해석의 3차원수치파동수조는 Fig. 9(a)와 같은 길이 12.5 m, 폭 10 m, 높이 0.4 m의 수조에 0.25 m의 일정수심으로 구성되었고, 그 내부에 본 수치해석의 대상구조물인 LCS과 해빈이 설치되었다. 바닥경계는 Slip 조건으로 구성되었고, 양측벽경계조건에도 y축방향으로 LCS가 반복적으로 설치되는 것으로 가정하여 Slip 조건을 적용하였다. 격자크기는 Δx = 3 cm와 Δy = 3 cm이며, 계산효율상 수조바닥에서 수면까지는 Δz = 1.4~0.75 cm의 가변격자로, 수면에서 수조상부경계까지는 Δz = 0.75~1.4 cm의 가변격자로 각각 구성하였으며, 조파시에 z축으로 5개 이상의 격자가 포함되도록 하였다. 여기서, G는 정수위에서 구조물 사이의 개구폭을, Ls는 정수위에서 구조물의 길이를, X는 정수위에 대해 해안선에서 구조물까지의 이격거리를 각각 의미한다. 여기서, 본 논문에서 설상사주의 형성조건하라는 것에 대해 검토한다. Black and Andrews(2001)가 제시한 조건에 따르면 설상사주의 형성조건은 Ls/X < 1.0로 주어지며, 본 연구에서 LCS의 배치조건은 이 조건의 범위에 속하므로 설상사주가 형성되는 조건을 만족한다.
Definition sketch for layout of LCS, measuring points of water level and cross section.
Fig. 9(b)는 파랑의 정상상태를 파악하기 위한 수위측정위치의 좌표점을 나타낸다. Fig. 9(c)는 본 연구에 작용한 LCS의 형상에 대한 상세도이며, 이는 Lee et al.(2017c)에서 적용된 LCS를 참조하여 도출하였다. 여기서, TTP 층은 1:1.5의 경사와 0.1967 m의 두께를 갖고 월파를 허용할 때와 허용하지 않을 때를 상정하여 천단고를 Rc = 3 cm와 8 cm로 각각 구축하였으며, 공극률 ϕ = 0.5, 중앙입경 D50 = 5 cm, 그리고 다공성매질에 대한 Madsen and White(1975)의 실험으로부터 산정된 α = 1200과 β = 1.7을 적용하였다. 마운드부분은 1:1.5의 경사와 0.1333 m의 높이를 가지며, 공극률 ϕ = 0.33, 중앙입경 D50 = 3 cm, 그리고 Jensen et al.(2014)의 실험으로부터 산정된 α = 500과 β = 2.0을 적용하였다. 케이슨의 높이는 0.1467 m이고, 불투과성으로 적용하였다. 해빈은 1:20의 경사를 가지며, 공극률 ϕ = 0.3, 중앙입경 D50 = 0.2 cm, 그리고 Billstein et al.(1999)의 실험으로부터 산정된 α = 0과 β = 3.0을 적용하였다.
Table 3은 수치해석에 적용된 규칙파랑의 제원, 구조물의 개구폭, 구조물의 길이, 구조물의 천단고 및 해안선으로부터 이격거리에 대한 각각의 수치를 나타낸다. 계산은 LES에 의한 난류모델(Ghosal et al., 1995)을 적용하고, 계산의 안정을 위해 Courant 상수를 0.1 이하가 되도록 설정하여 수치해석을 수행하였다.
Incident wave condition and 3-dimensional layout of LCS
4.2 정상상태의 판단
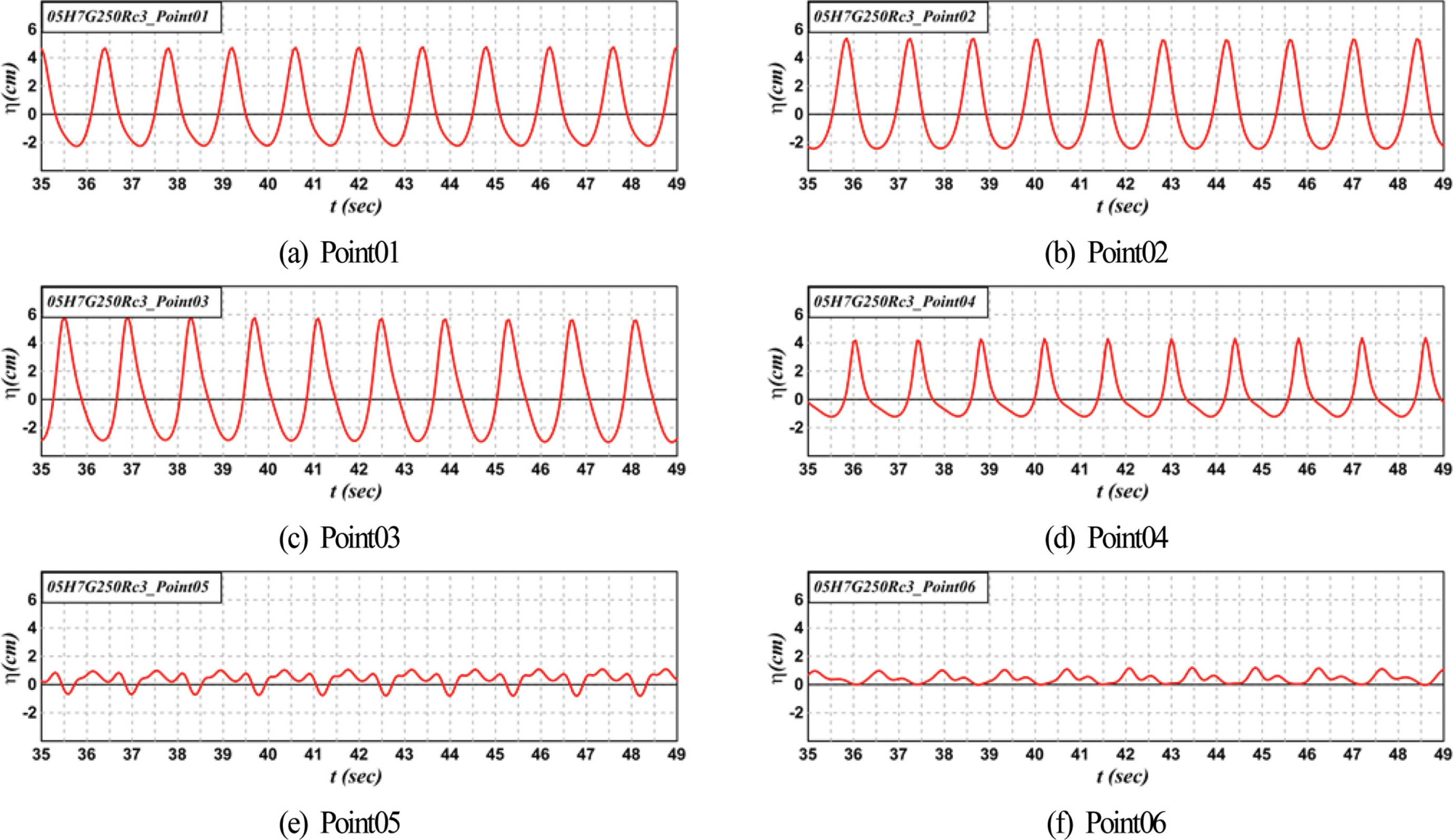
본 수치해석에 사용되는 olaFlow 모델(Higuera et al., 2018)에 의한 3차원강비선형수치해석은 혼상류해석법이며, 유한체적법에 기초하여 3차원 Navier-Stokes 운동방정식, LES에 의한 난류모델 및 VOF 법에 의한 수면추적 등을 시간경과에 따라 반복계산과 수렴계산이 수행되기 때문에 많은 계산시간이 소요되고, 또한 많은 데이터의 양을 발생시킨다. 본 3차원 수치해석에서는 대략 528만개의 격자로 구성되고, 문제가 발생하지 않는 경우 1케이스의 계산에 Workstation(Intel® Xeon(R) CPU E5-2630 v3 @2.40GHz x16)의 16개 Processor로 병렬계산을 수행한 경우 49 s의 파전파에 대해 대략 192 h이 소요되며, 데이터량은 600 GB에 달한다. 따라서, 본 수치계산의 물리량에 대해 정상상태의 데이터를 취하여야 하는 시간을 알기 위하여, 그리고 물리량에 대한 평균치를 산정하기 위한 파의 수 등을 결정하기 위하여 파가 정상상태에 도달하는 시간을 사전에 파악·인지할 필요가 있다. 여기서, Table 3의 05H7G250Rc3의 케이스에 대해 대략 정상상태에 도달한 것으로 추정되는 t = 35 s 이후의 파의 시간변동을 나타낸 것이 Fig. 10이다.
Time variation of water level.
그림을 살펴보면 Fig. 10(a)~(d)는 Fig. 9(b)에 그의 위치를 나타내는 바와 같이 수조 중앙의 개구부에 위치한 지점에서 파의 시간변동을 나타낸 것이다. 여기서, Fig. 10(a)→(b)→(c)→(d)로 진행할수록 육측의 정선에 가까운 위치를 나타내며, Fig. 10(d)는 수심이 얕아진 경우이다. Fig. 10(a)→(b)→(c)로 갈수록 파고가 점차로 커져 파봉부분이 뾰족해지지만, 파의 비선형성은 크게 나타나지 않는 것으로 보인다. Fig. 10(d)의 경우는 회절의 영향으로 일부의 파가 LCS의 배후로 회절되어 전술한 경우보다 파고가 감소되고, 파곡부분에 비선형파가 발달되는 것을 볼 수 있다. Fig. 10(e)와 (f)는 LCS의 배후지점에서 파의 시간변동을 나타낸 것으로, Fig. 10(f)가 보다 수심이 얕은 경우이다. Fig. 10(e)의 경우는 천단상을 월파한 파와 개구부를 통하여 구조물 배후로 회절된 파가 중첩된 결과로 파고가 적고, 파봉부분에 매우 큰 비선형파가 포함된 것을 알 수 있다. Fig. 10(f)는 파의 시간변동 전체가 정수위 위에서 나타나므로 이 지점에서는 평균수위상승(wave set-up)이 발생된다는 것을 알 수 있다. 이상으로부터 비록 Fig. 10(f)의 경우 t < 36 s에서 완전한 정상상태에 도달하지 않았지만, 전반적으로 t > 35 s 이후에는 정상상태의 시간파형을 나타낸다는 것을 확인할 수 있다. 이로부터 파고, 유속 및 그의 평균치 등은 t > 36 s 이후의 파를 대상으로 하였고, 평균치는 t > 36 s 이후 5개의 파를 평균하였다.
4.3 파고분포와 파의 전파
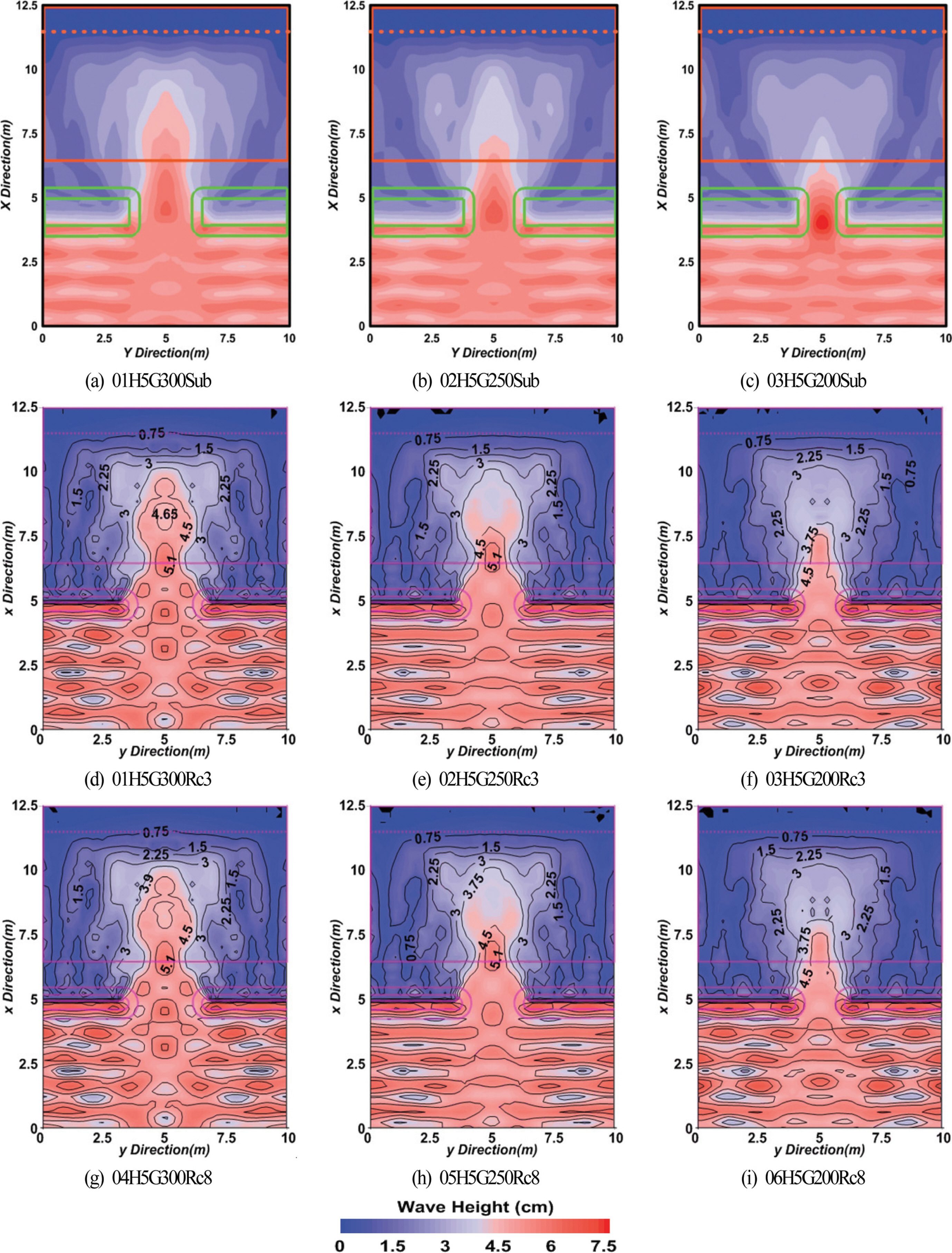
Fig. 11은 Table 3에 제시된 케이스 중에 입사파고가 H = 5 cm인 경우에 LCS 주변, 특히 그의 배후에서 파고분포를 나타낸 것이며, 잠제에 관한 선행 연구(Lee et al., 2017b)의 결과도 비교·검토를 위하여 병기한다. 여기서, LCS(저면폭이 1.20 m; 천단고가 3 cm, 8 cm)와 잠제(저면폭이 1.89 m; 천단수심이 4 cm)의 평면배치에서 개구폭 G과 구조물의 길이 Ls 및 해안선에서 구조물까지의 이격거리 X는 동일하다. 하지만, 잠제는 천단이 잠수되어 있으므로 천단수심을 가지는 반면, LCS는 정수면상으로 돌출되어 있으므로 천단고를 가지는 관계로 단면형상이 상이하며, 잠제와 LCS의 구성재료 또한 상이하다.
Spatial distribution of simulated wave heights according to the change of gap width (H = 5 cm).
먼저, 잠제와 LCS에 대한 각각의 파고분포를 비교·검토한다. Figs. 11(a)~(c)는 잠제의 경우를, Figs. 11(d)~(i)는 LCS의 경우를 각각 나타낸다. 잠제의 경우는 투과성재료로 구성되고, 천단상에 천단수심을 가지는 관계로 천단상과 제체 내부를 통한 파에너지의 전달이 발생하기 때문에 잠제 바로 배후에서 어느 정도의 크기를 갖는 파고를 확인할 수 있다. 개구폭이 줄어드는 경우(Figs. 11(a)→(b)→(c))에도 잠제 바로 배후의 파고변화에 거의 차이가 주어지지 않기 때문에 전술한 천단상과 제체 내부를 통한 파에너지의 전달이 많은 부분을 차지하는 것으로 여겨지며, 따라서 잠제의 바로 배후에서는 개구부를 통한 회절의 영향이 상대적으로 적다는 것을 확인할 수 있다. 그리고, 잠제의 경우 개구폭이 좁아질수록 개구부의 중앙에 파 집중과 파고 증폭으로 배후로 전달되는 파에너지는 줄어들어 배후역에서 파고가 작아지는 결과를 나타낸다.
다음에, LCS에서 천단고가 Rc = 3 cm인 Figs. 11(d)~(f)의 경우를 살펴보면 역시 구조물 바로 배후에 작은 파고를 확인할 수 있다. Table 2에서 나타낸 바와 같이 천단고가 3 cm인 경우는 월파가 발생하므로 잠제와 같이 천단상과 TTP 내부를 통한 파에너지의 전달로 인하여 바로 배후에서 약간의 파고가 발생되는 것으로 판단된다. 개구폭이 좁아짐에 따라 구조물 배후역에서 전체적으로 파고가 줄어들는 현상은 개구부를 통하여 배후로 전달되는 파에너지가 줄어들기 때문이다. 구조물 바로 배후에서 파고의 변화에 큰 차이를 나타내지 않는 것은 잠제와 같이 월파와 제체 내부를 통한 파에너지 전달이 커고, 반면에 구조물 바로 배후에서는 회절의 영향이 적다는 것을 나타낸다. 한편, 개구부 배후에서 파고가 줄어드는 경향은 잠제의 경우와 동일하지만, 개구폭이 좁아짐에 따라 잠제의 경우와는 달리 LCS의 경우는 개구부 중앙에서 파 집중과 파고 증폭이 줄어든다. 한편, 항외측인 구조물 전면에서는 전반적으로 잠제의 경우보다 다소 큰 부분중복파동장이 형성되는 것을 알 수 있으며, 이는 LCS에 적용된 불투과성의 케이슨에 의한 큰 반사의 영향으로 판단된다.
Figs. 11(g)~(i)는 천단고가 Rc = 8 cm로 구조물의 천단상으로 월파가 발생하지 않는 경우이다. 구조물 바로 배후에서 회절파의 영향과 개구폭이 좁아질수록 구조물 배후에서 파고분포의 변화, 개구부에서 파 집중 및 파고 증폭과 같은 변동양상은 월파가 발생하는 Figs. 11(d)~(f)의 경우와 대체적으로 동일하다. 여기서, 월파시 Figs. 11(d)~(f)의 경우와 비월파시 Figs. 11(g)~(i)의 경우가 구조물 배후에서 거의 동일한 파고 변동과 파고분포를 나타내는 것은 비월파시 Figs. 11(g)~(i)의 경우는 케이슨을 전체적으로 피복하는 TTP 부분의 천단고가 높아 월파되지 않아 제체 내부를 통한 파에너지 전달이 많아지는 반면, 월파시 Figs. 11(d)~(f)의 경우는 TTP의 천단고가 낮아 내부를 통한 파에너지 전달은 상대적으로 적어지고 천단상 월파로 인한 파에너지 전달이 상대적으로 많이 발생하기 때문이다. 따라서, 본 수치해석에서 적용한 파랑조건과 구조물의 형상조건에 대해 비월파시 내부를 통해 전달되는 파에너지는 월파시 내부를 통한 파에너지와 천단을 통한 파에너지의 합과 거의 동일하다는 것이 추정될 수 있다.
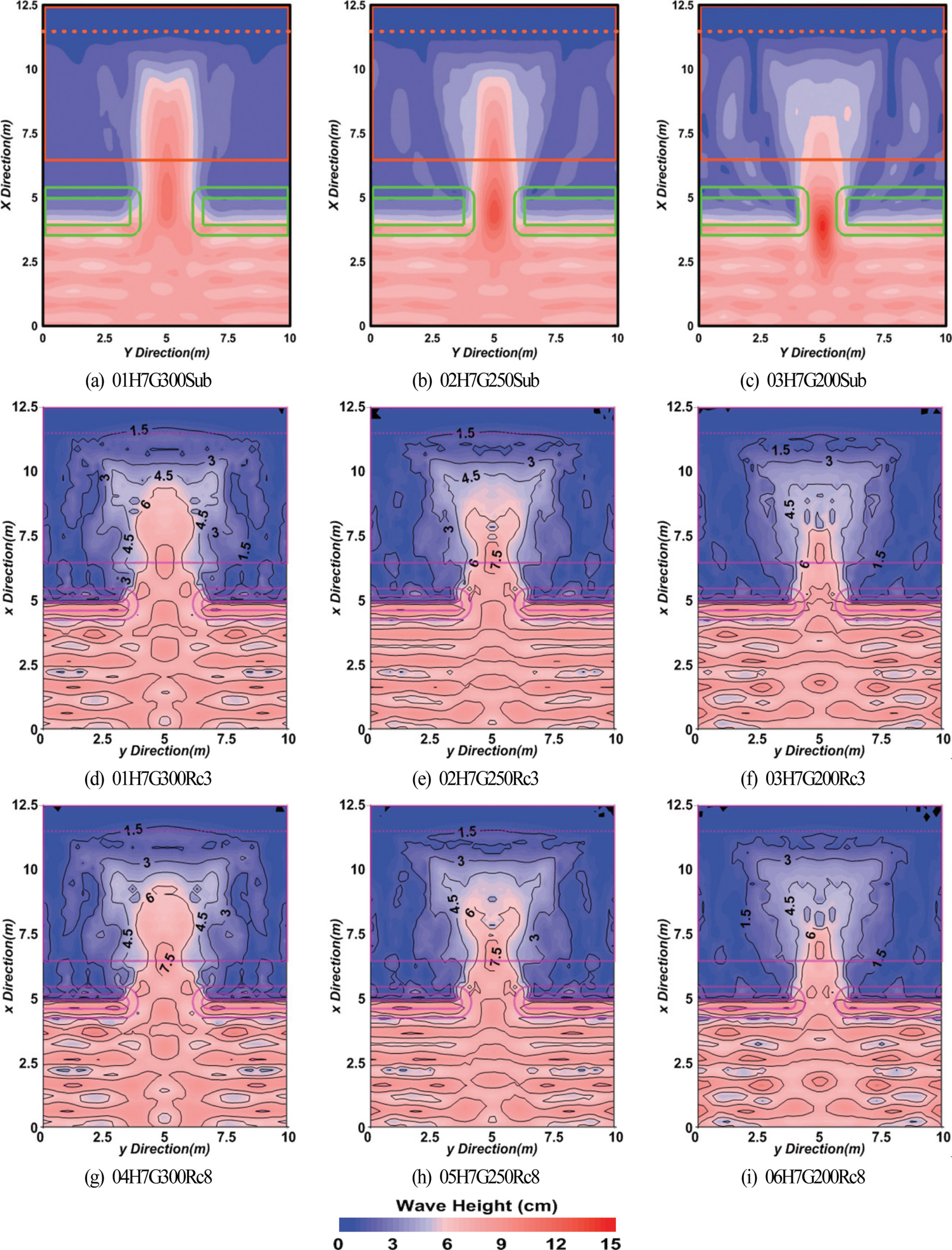
Fig. 12(Figs. 11과 12에서 범례의 크기가 다르다는 것에 유의바란다)는 Table 3에서 입사파고가 H = 7 cm인 경우 LCS 주변에서 파고분포를 나타낸 것이며, 또한 조건에 대응하는 잠제에 관한 선행 연구(Lee et al., 2017b)의 결과도 비교·검토를 위하여 병기한다. 전술한 Fig. 11의 경우와 비교하면 입사주기는 동일한 T = 1.4 s이지만, 입사파고가 H = 7 cm증가되었기 때문에 전체적으로 구조물 배후역에서 파고는 상대적으로 큰 값을 나타내고, 두부에서 회절이 적게 발생되어 해안선 근방까지 큰 파가 유입된다. 잠제에 대한 Figs. 12(a)~(c)의 경우는 전술한 Figs. 11(a)~(c)와 동일하게 개구폭이 좁아짐에 따라 배후역에서 파고가 전체 공간에 대해서는 다소 줄어들고, 개구부에서 파 집중과 파고 증폭이 나타난다. 반면에 잠제 바로 배후에서 파고가 커지는 것은 두부에서 회절의 영향이 상대적으로 커지기 때문인 것으로 판단된다. 다음으로, 잠제와 LCS의 경우를 비교하면 전체적으로 LCS의 경우가 다소 적은 파고를 나타내고, 두부에서 회절현상이 상대적으로 약간 큰 경향을 나타낸다. LCS에서 개구폭의 감소에 따른 차이는 배후에서 파고가 줄어드는 것은 Fig. 11의 경우와 동일하지만, 회절의 영향이 감소하는 것은 Fig. 11의 경우와 약간 상이하다.
Spatial distribution of simulated wave heights according to the change of gap width (H = 7 cm).
Figs. 12(g)~(i)는 천단고가 Rc = 8 cm로 구조물의 천단상으로 월파가 발생하지 않는 경우이며, 월파가 발생하는 Figs. 12(d)~(f)의 경우와 구조물 바로 배후에서 회절파의 영향과 개구폭이 줄어듬에 따라 구조물 배후에서 파고분포의 변화 , 개구부에서 파 집중 및 파고 증폭과 같은 변동양상이 대체적으로 동일하다.
Fig. 13는 Table 3에서 제시된 05H7G250Rc3의 케이스에 대해 파의 전파과정을 시·공간적으로 나타낸 결과이다. LCS의 전면에서 부분중복파가 형성되어 파봉선이 구조물의 길이 방향과 평행하게 나타나고, LCS의 천단상을 월파하며, 개구부를 통하여 파에너지가 유입되고, 두부에서 구조물에 의해 차폐된 배후역으로 파가 회절되어 유입되며, 해안선 근방에서 파고가 크게 줄어든 상태로 정선에 거의 직각으로 입사되는 과정을 시각적으로 명확하게 파악할 수 있을 것이다.
Snapshots of wave diffraction behind LCS (05H7G250Rc3).
4.4 평균유속
Figs. 14와 15(두 그림에서 범례의 크기가 다르다는 것에 유의바란다)는 전술한 Figs. 11과 12와 동일한 케이스에 대해 LCS 주변, 특히 그의 개구부와 배후에서 유속을 시간평균하고, 그리고 연직방향으로 평균한 유속을 나타낸 것이며, 잠제에 관한 선행 연구(Lee et al., 2017b)의 결과도 비교·검토를 위하여 병기한다. 여기서, LCS와 잠제는 4.3절에서 기술한 것과 동일한 단면, 평면배치 및 구성재료를 갖는다.
Spatial distribution of time- and depth-averaged mean velocities in horizontal plane (H = 5 cm).
Spatial distribution of time- and depth-averaged mean velocities in horizontal plane (H = 7 cm).
먼저, 잠제의 경우를 살펴보면 개구부에서 항내측에서 항외측으로의 강한 평균유속(흐름)이 발생하고, 이는 개구폭이 좁을수록 강해진다. 잠제의 천단상에서는 월류에 의한 강한 항내측 흐름이 발생하고, 개구폭이 넓을수록 해안선 근방에서 좌우측으로 발산하는 연안류 및 순환류가 발생한다. 잠제와 LCS의 경우를 비교하면 전체적으로 LCS에 의한 차폐역인 배후 5 m < x < 8.2m 구간에서 흐름양상이 잠제의 경우보다 상당히 복잡한 패턴을 나타내고, 개구부에서 항외측으로 흐르는 이안류의 크기가 상대적으로 적다는 것을 알 수 있다. 그리고, 해안선 근방에서 해빈류 패턴에 대해 LCS의 경우는 수렴하는 연안류가, 잠제의 경우는 발산하는 연안류가 각각 발생하는 것이 큰 차이이며, 이로 인하여 궁극적으로 해안선 근방에서 후술하는 난류운동에너지 및 모래이동에서의 차이로 나타날 것으로 판단된다.
LCS의 경우 월파시의 Figs. 14(d)~(f)와 비월파시의 Figs. 14(g)~(i)를 비교하면 동일한 입사파고에 대해 천단고 차이에 따른 해빈류의 차이는 거의 나타나지 않는다는 것을 알 수 있다. 이것은 4.3절의 파고분포에서 서술한 바와 같이 비월파 시 Figs. 11(g)~(i)의 경우는 제체 내부를 통한 흐름이 많아지는 반면, 월파조건인 Figs. 11(d)~(f)의 경우는 제체 내부를 통한 흐름은 상대적으로 적고, 천단상 월류로 인한 흐름이 상대적으로 크게 발생하여 비월파시와 월파시 LCS 전체를 통한 유입흐름의 차이는 거의 없기 때문인 것으로 판단된다. 단지, 본 수치계산조건하에서는 개구폭의 너비에 따른 차이가 강하게 나타나며, 즉 개구폭이 넓어질수록 개구부에서 항외측으로 흐르는 이안류는 약해지고, 해안선 근방에서 연안류는 수렴되는 경향이 보다 강하게 나타나는 것을 알 수 있다. 여기서, LCS 배후 5 m < x < 8.2m 구간에서 복잡한 흐름패턴을 나타내는 것은 LCS 천단상을 통한 월류와 제체 내부를 통한 흐름이 구조물의 길이방향으로 일정하지 않고, 그리고 두부에서 회절파에 의한 흐름과 상호간섭이 발생되기 때문인 것으로 판단된다.
다음으로, 입사파고가 H = 7 cm로 증가된 Fig. 15를 살펴보면 잠제의 경우 해안선 근방에서 연안류가 상대적으로 명확히 나타나고, 또한 발산하는 경향을 나타낸다. 그리고, 개구부에서 항외측으로의 이안류가 보다 강하게 되는 것을 알 수 있다. LCS의 경우는 전술한 H = 5 cm의 경우보다 개구부에서 이안류 및 해안선 근방에서 수렴하는 연안류의 강도가 보다 강해지지만, 비월파시와 월파시에 대한 차이는 전술한 경우와 동일하게 거의 나타나지 않는다.
4.5 평균난류운동에너지
Figs. 16과 17(두 그림에서 범례의 크기가 다르다는 것에 유의바란다)은 전술한 Figs. 14와 15와 동일한 케이스에 대해 시간평균난류에너지를 연직방향으로 평균한 평균난운동에너지의 공간분포를 나타낸 결과이다. 입사파고 H = 5 cm인 Fig. 16을 살펴보면 잠제의 경우는 개구부를 향해 열려있는 해안선 근방의 중앙부에서 큰 값을 나타내고, 이를 중심으로 해안선에 평행한 좌·우측으로 감소하는 값의 변화를 나타낸다. 그리고, 잠제의 천단상에서도 평균난류에너지가 큰 값이 분포하는 것을 알 수 있다. 이러한 값의 공간분포는 개구폭이 좁아질수록 연안방향으로 다소 좁아지지만, 거의 동등한 분포양상을 나타내고, 값의 크기는 줄어든다는 것을 확인할 수 있다.
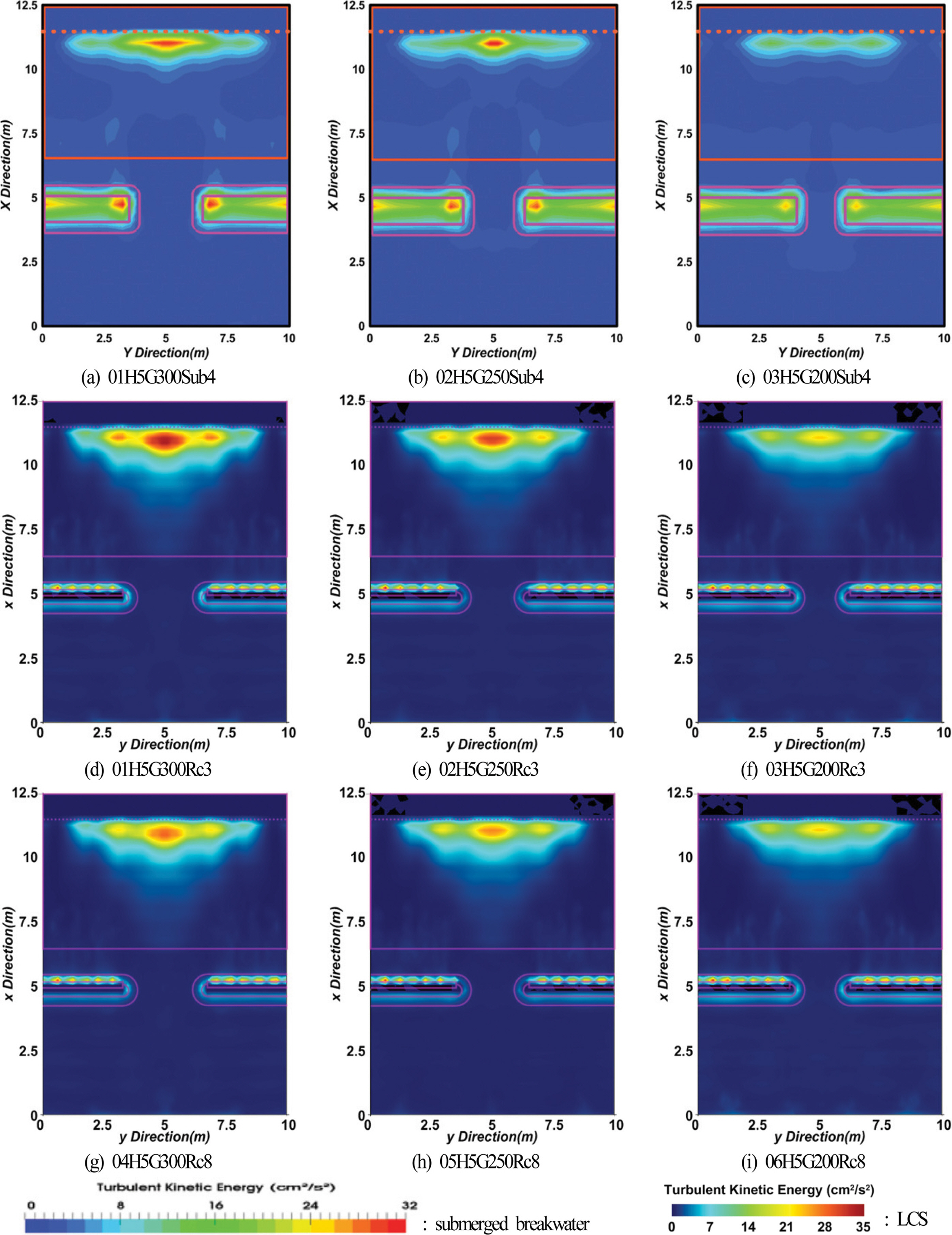
Spatial distribution of time- and depth-averaged turbulent kinetic energies in horizontal plane (H = 5 cm).
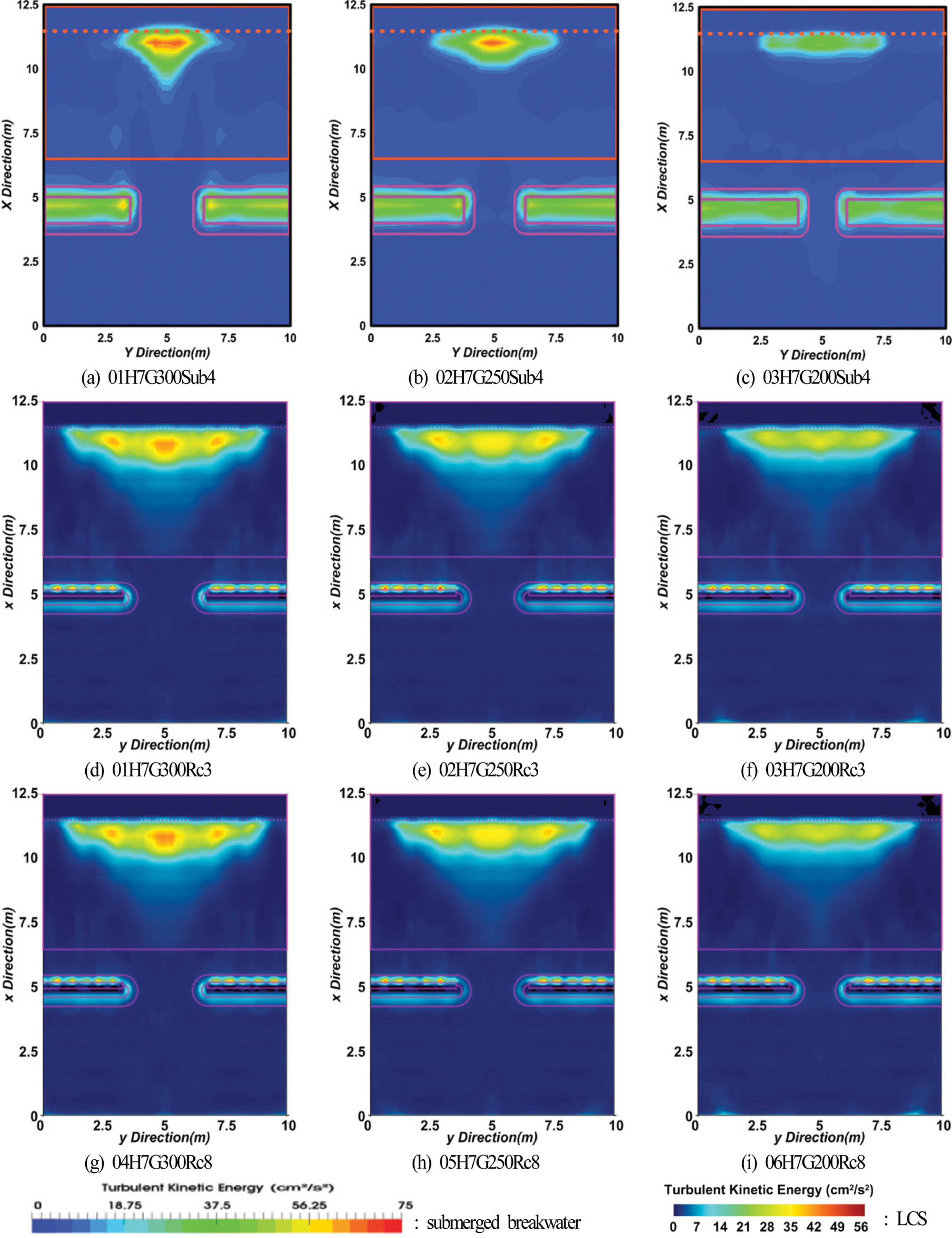
Spatial distribution of time- and depth-averaged turbulent kinetic energies in horizontal plane (H = 7 cm).
LCS의 경우 천단고가 Rc = 3 cm의 경우 평균난류에너지의 전반적인 공간분포양상은 잠제의 경우와 대체로 유사하지만, 해안선 근방에서는 잠제의 경우보다 종단방향의 분포폭이 넓어지고, 극대치 3개가 거의 동일한 위치에 명확히 나타나는 것은 잠제와 다르다. 또한, 이러한 값의 크기는 잠제의 경우와 동일하게 개구폭이 좁아질수록 줄어드는 것을 볼 수 있다. 여기서, LCS의 항내측 천단상에서 평균난류에너지의 값이 크게 나타나는 것은 천단상에서의 월류에 따른 난류강도가 강하게 나타나기 때문인 것으로 판단된다. 다음으로, 비월파인천단고가 Rc = 8 cm인 경우 평균난류에너지의 전반적인 공간분포양상은 전술한 잠제나 월파가 발생하는 Rc = 3 cm의 경우와 유사한 분포양상을 나타낸다. 그러나, 월파가 발생하는 LCS에 대한 케이스의 경우보다 전반적으로 분포값이 적어진다는 것을 알 수 있다.
입사파고가 H = 7 cm로 증가된 Fig. 17로부터 다음을 확인할 수 있다. 잠제의 경우는 개구부를 향해 열려있는 해안선 근방의 중앙부에서 큰 값을 나타내고, 이를 중심으로 해안선에 평행한 좌·우측으로 감소하는 것은 전술한 Fig. 16의 경우와 유사한 결과이다. 그러나, 공간분포는 개구폭이 좁아질수록 연안방향으로 분포폭이 넓어지는 반면, 종단방향으로 다소 많이 좁아지는 경향을 나타내는 것은 전술한 Fig. 16의 경우와 상이한 결과이다. 그리고, 잠제의 천단상에서도 평균난류에너지가 큰 값이 분포하는 것을 Fig. 16의 경우와 동일하다.
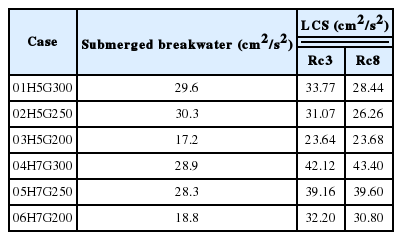
LCS의 경우 천단고가 Rc = 3 cm의 경우 평균난류에너지의 전반적인 공간분포양상은 잠제의 경우와는 달리 해안선 근방에서 연안방향으로 분포폭이 넓고, 극대치 3개가 거의 동일한 위치에 명확히 나타나는 것을 볼 수 있다. LCS에서 값의 크기는 잠제의 경우와 동일하게 개구폭이 좁아질수록 줄어든다. 비월파인 천단고가 Rc = 8 cm인 경우 평균난류에너지의 전반적인 공간분포양상은 전술한 잠제나 월파가 발생하는 Rc = 3 cm의 경우와 유사한 분포양상을 나타낸다. 그러나, 월파가 발생하는 LCS에 대한 케이스의 경우보다 값이 약간 적어진다는 것을 알 수 있다. Figs. 16과 17에서 해안선 근방에서 평균난류에너지의 최대치를 다음의 Table 4에 제시한다. 표로부터 H = 7 cm의 경우는 LCS가 잠제의 경우보다 전체적으로 큰 값을 나타내는 반면, H = 5 cm의 경우는 개구폭과 천단고에 따라 LCS가 큰 경우 혹은 잠제가 큰 경우가 각각 나타나므로 일률적인 경향을 나타내지 않는다.
Maximum depth-averaged turbulent kinetic energy around coastal line
이상과 같이 잠제와 LCS에서 나타나는 평균난류에너지에 대한 공간분포의 차이는 전술한 파고 및 흐름에서의 차이와 중첩되어 최종적으로 모래이동에서의 차이로 이어질 것으로 판단된다.
5. 결 론
본 연구에서는 Navier-Stokes solver에 기초한 3차원혼상류의 해석법인 공개된 CFD Code인 olaFlow를 이용하여 규칙파동장하 3차원투과성구조물인 LCS에 의한 파고, 평균유속(흐름) 및 평균난류운동에너지 등을 수치해석하였으며, 기존의 실험해석 및 수치해석에 대한 결과와의 비교ㆍ검토로부터 LCS로의 타당성을 검증하였다. 실제 수치해석에서는 LCS에 관해 월파 여부가 중요한 차이를 나타낼 것으로 판단하여 파고와 천단고를 변화시켰고, 또 다른 해빈유실대책공법으로 적용되는 잠제와의 역학적인 차이점을 규명한다는 차원에서 동일한 파랑조건과 개구부폭에 대해 잠제의 경우와 비교·분석하였다. 이로부터 도출된 중요한 사항을 다음에 요약·서술한다.
(1) 파고의 공간분포: LCS의 경우, 항외측에서는 구조물에 의한 반사파의 영향으로 큰 파고의 부분반사파동장이 형성된다. 항내측에서는 항외측보다 정온한 해역이 형성되며, 개구폭이 좁을수록 입사파고가 작을수록 항내측의 파고가 줄어든다. 이러한 항내측의 파고에는 천단상으로 월파 및 제체내를 통한 파랑에너지의 전달 및 두부에서 회절파의 영향을 크게 받을 수 있지만, 본 수치계산에 따르면 동일한 입사파고에 대해 천단고의 차이에 따른 월파 여부는 항내측의 파고분포와 그의 크기에 거의 영향을 미치지 않는다. 잠제와 LCS의 차이는 잠제의 경우 개구폭이 좁아질수록 개구부의 중앙에 파집중과 파고 증폭의 현상이 보다 강해지고, 배후로 전달되는 파에너지는 줄어드는 반면, LCS의 경우 개구폭이 좁아짐에 따라 개구부 중앙에서 파 집중과 파고 증폭의 현상이 미미해지고, 배후로 전달되는 파에너지가 줄어든다.
(2) 평균유속의 공간분포: LCS의 경우, 해안선 근방에서는 개구부를 향해 열린 중앙지점으로 수렴하는 연안류가 발생하며, 이는 개구폭이 넓을수록 강해진다. 개구부에서는 이안류가 발생하며, 이러한 경향은 개구폭이 좁을수록 강해진다. 연안류와 이안류의 크기는 전체적으로 입사파고가 클수록 커진다. 한편, 동일한 입사파고에 대해 천단고의 차이에 따른 월류 여부가 평균유속에 미치는 영향은 거의 나타나지 않는다. 여기서, 잠제의 경우는 해안선 근방에서는 개구부를 향해 열린 중앙지점에서 좌·우측으로 발산하는 연안류가 발생하고, 해안선 근방의 항내측과 잠제 개구부와 개구부 근방의 천단상에 걸쳐 순환류가 형성되며, 이것이 평균유속의 공간분포에서 LCS와의 차이로 판단된다.
(3) 평균난류운동에너지의 공간분포: LCS의 경우, 해안선 근방에서는 개구부를 향해 열린 중앙지점에서 가장 큰 값이 주어지고, 이를 중심으로 좌·우측의 연안방향으로 갈수록 값이 감소한다. 이러한 경향은 개구폭이 좁을수록 분포값이 줄어드는 반면, 입사파고가 커지면 보다 커진다. 한편, 동일한 입사파고에 대해 천단고의 차이에 따른 월류 여부에 대해서는 비월파의 경우에 평균난류운동에너지에 미치는 영향이 줄어든다. 여기서, 잠제의 경우는 해안선 근방에서는 개구부를 향해 열린 중앙지점에서 좌·우측으로 갈수록 감소하고, 개구폭이 좁을수록 값의 크기가 또한 감소하는 경향은 LCS와 동일한 현상이지만, 입사파고가 커지면 LCS의 경우보다 해안선 근방에서 종단방향으로 분포폭이 보다 넓어지는 것이 LCS와의 차이로 판단된다.