Article information

Abstract

Trans Abstract

1. 서 론

기후변화와 난개발로 인해 기존에 유지되던 준 평형 상태가 훼손된 우리나라의 각 해안에서는 현재 상당한 침식이 진행되고 있다. 현재 이안제, 돌제, 인공 곶(head land), 광폭 잠제(artificial reef) 등으로 침식을 저감하려는 노력이 수행되고 있으나, 해빈 안정화 효과가 기대에 미치지 못하는 경우도 상당하며, 거치지역의 인근해안에 추가적인 침식 혹은 퇴적, 항매몰 등과 같은 역기능을 야기한 경우도 보고된 바 있다(Cho and Kim, 2019). 최근 이러한 인식을 반영하여 연성공법인 양빈을 통하여 해안침식을 저감하려는 시도가 미국 Florida 연안과 일본, 부산 송도, 해운대 등에서 이루어져 부분적인 성공을 거둔 것으로 보인다(Dean and Dalrymple, 2002).

최적의 해빈침식 대응방안을 마련하기 위해서는 해양환경에 따라 침퇴적을 반복하는 해빈 대순환 과정에 대한 이해가 필요하며, 이를 계절별로 정리하면 다음과 같다(Cho et al., 2008).

기상악화로 고파랑이 우세한 수 환경에서는 성분파랑간의 공진성 비선형 상호작용 등으로 인해 성격이 상이한 여러 파랑이 혼재한다. 이 경우 전술한 기작 중 상쇄 간섭으로 인해 파랑 마루 사이의 이격 시간은 너울에 비해 상당히 짧아지며 평균해면 위로 드러나는 파형의 체적은 증가한다.

이러한 특성의 고파랑이 내습하는 경우 내습 파랑 누적에 따라 쇄파대역의 지하수위는 급격히 상승하여 곧 포화상태에 도달한다. 지하대수층의 포화로 전빈의 사면을 통해 처올려진 수주의 대부분은 저면을 통해 침투되지 못하고 해빈단구[berm] 인근의 정점에서 중력에 의해 방향을 바꾸어 먼바다를 향하는 흐름[down rush]이 형성되며 이는 너울에 의해 형성된 해빈 단구의 급속한 침식으로 이어진다. 풍속의 3.5% 정도인 바람에 의해 밀려온 자유수면 인근의 표류가 더해져 외해방향의 흐름[undertow]은 너울의 경우와는 달리 상당한 크기로 침식된 표사와 저면에서 강한 소류력에 의해 부유된 표사를 먼 바다방향으로 이송하는 주요한 기작으로 작용한다.

전빈에서 파곡이 형성되는 경우 해수위보다 높아진 지하수 수위로 인해 지하수는 해안선 인근에서 용출되며 이때 상당량의 표사가 부유된다. 이러한 현상은 Longuet Higgins(1983)에 의해 처음 관측되었으며 이 후 quick sand 혹은 액상화라 불리며, 전술한 부유로 인해 전빈의 선단은 급속히 침식되며 전빈은 내륙 쪽으로 후퇴한다. 이렇게 수심이 증가되면 전술한 먼 바다 방향의 흐름은 그 세력이 감소되고 이송되어온 표사는 퇴적되기 시작하며 비교적 굵은 표사는 해안선 가까이에, 고운 표사는 더 먼 곳에 쌓이며 연안사주가 형성된다.

이렇게 형성된 연안사주는 후행하여 내습하는 파랑에 대해 일종의 잠제로 기능하며, 사주 형성 이후 해빈에 내습하는 파랑의 파고와 수반되는 downrush는 상대적으로 약해진다(Fig. 1 참조). 폭풍이 잦아들고 다시 너울이 우세한 해양환경이 복원되면 연안사주에 쌓여있던 표사는 경계층 streaming에 의해 점진적으로 해빈으로 회귀된다. 전빈 사면을 통해 쳐올려진 수주의 대부분은 낮아진 지하대수층의 수위로 인해 침투되며 이 과정에서 퇴적되는 표사로 해안단구는 순차적으로 복원된다.

Fig. 1.

Schematic sketch of the mechanisms underlying the formation of sand bar at the surf zone.

이처럼 자연 해빈은 일시적으로 침식되더라도 스스로 복원할 수 있는 능력을 지니며, 따라서 해빈 안정화를 목적으로 거치되는 강성 구조물의 형태와 규모는 전술한 해빈 대순환 과정이 훼손되지 않는 범위에서 결정되어야 하나, 최근 지나치게 대형화 되어 광폭 잠제도 빈번하게 차용되고 있는 실정이다.

Irie et al.(1994)가 제안한 왜도 된 연흔모양 매트는 규모가 크지 않다는 점에서 현재 선호되는 광폭잠제의 대안이 될 수 있을 것으로 보이며, Irie et al.(1994)가 제안한 왜도 된 연흔모양 매트는 down-wave side 쪽으로 높이가 감소되는 비대칭 구조물로 해빈 안정화 효과를 지니는 것으로 보고된 바 있다. 전술한 왜도 된 연흔모양 매트의 해빈 안정화 효과가 구현되기 위해서는 먼저, 매트의 유수 단면 축소부에서 강제되는 와류가 run-down 시 외해방향으로 이송되는 표사를 효과적으로 포획할 수 있어야 하며, 둘째, 와류에 포획된 표사를 적절히 부유 상태로 유지하여 후행하는 파랑에 의해 포획된 표사가 연안으로 회귀될 수 있어야 한다(Fig. 2 참조).

Fig. 2.

Schematic sketch of the beach stabilization effect of an asymmetric ripple mat by Irie et al. (1994).

본 논문에서는 이러한 인식에 기초하여 먼저 왜도 된 연흔모양 매트의 해빈 안정화 효과가 극대화 되도록 변화를 주어, Run-down 시 매트의 유수 단면 축소부에서 강제되는 와류 강도가 최대가 될 수 있도록 매트 형상을 조정하였다. 유수 단면 축소부에서 강제된 와류에 의해 포획된 표사가 충분히 부유 상태를 유지할 수 있도록 조절하여, 후행하는 파랑에 의해 연안으로 회귀되는 표사의 회귀율이 증가될 수 있도록 하였다. 이어 최종 선정된 왜도 된 연흔모양 매트의 해빈 안정화 효과를 검증하기 위해 Navier-Stokes 식과 물리기반 지형모형에 기초한 수치모의가 수행된다.

2. 왜도 된 연흔모양 매트의 설계요소

왜도 된 연흔모양 매트의 해빈 안정화 효과에 영향을 미치는 설계요소로는 매트 길이 λ 높이 η 등으로 보인다(Fig. 3 참조). Irie et al.(1994)에 의하면 매트 정점에서 해안으로 회귀되는 유량은 d_o/λ = 1.7에서 정점에 이르며(Fig. 3 참조) 여기서 d_o는 파랑으로 인해 경계층 인근에서 수입자가 그리는 궤적의 크기로 현재 해안공학 계에서 Excursion amplitude로 불리는 진폭 A_o의 두 배에 해당한다. 그러나 전술한 결과는 일정 수심부에서 수행된 수리모형실험 결과로부터 도출된 것으로 쇄파역 적용 여부에 대해서는 좀 더 많은 논의가 필요해 보인다.

Fig. 3.

Schematic sketch of an asymmetric ripple mat and vertical distribution of time mean velocity.

Excursion amplitude A_o는 다음과 같이 기술될 수 있으며

여기서 H는 파고, k는 파수, h는 수심을 각각 나타내며, 쇄파역에서 파고의 성장은 수심에 의해 제한된다는 경험적 인식으로부터 Ao은 다음과 같이 근사될 수 있으며,

여기서 κ_b = H_b/h는 수심대비 쇄파파고 H_b의 크기를 나타내며 0.78~0.8의 값을 지닌다.

전절에서 다루었듯 해빈 침식의 대부분은 년 출현 빈도가 20일 이내인 고파랑에 의해 진행된다. 따라서 왜도 된 연흔모양 매트는 고파랑 내습 시 해빈 안정화 효과가 발현될 수 있도록 설계되어야 하며, 우리나라 동해안의 경우 파고가 상대적으로 큰 경우 파고와 주기의 상관성은 소멸되며 주기는 성장을 멈추어 T = 12~15 s 사이에 분포 한다(Cho et al., 2019). 주기를 T = 14 s, 쇄파 지점을 h = 4m라 가정하는 경우 do와 Irie et al.(1994)이 권하는 매트 길이는 각각 do = 11.0.9 m, λ = 6.48m로 산출된다.

3. 수치모형

3.2 표사이송 및 지형모형(Morphology Model)

현재 가용한 물리기반 표사이송모형의 대부분은 Shields Diagram에 기반 한다. Shields는 표사 초기 이송 여부는 저면에 작용하는 유체력과 표사 수중무게의 비인 Shields parameter에 의해 결정되며, Shields parameter가 θc' = 0.05를 상회하는 경우 이송이 시작되는 것으로 보았다. Shields parameter θ'는 다음과 같이 기술할 수 있으며,

(6) θ′=τbρ(s−1)gd

여기서 s는 표사 비중, ρ는 해수 밀도, g와 d는 각각 중력 가속도, 표사직경, τ_b는 저면전단응력을 나타내며 다음과 같이 기술될 수 있다.

(7) τb=ρ(ν+νturb)(∂u∂z+∂w∂x)

사면 각도가 β인 경사부에서 임계 Shields parameter θ'c는 사면을 따라 작용하는 중력 성분 Wτ으로 인해 다음과 같이 수정되며(Fig. 4 참조),

Fig. 4.

Definition sketch of agitating and stabilizing forces acting on a sand grain on a sloping bed [modified from Roulund et al. (2005)].

(8) θ′c=θ′co(cosβ1−sin2αtan2βμs2−cosαsinβμs)

여기서 α는 접선 방향 저면 유속 u_τ과 W_τ가 이루는 각도, μs는 정적 마찰계수로 0.65의 값을 지닌다(Fig. 4 참조).

3.2.1 부유사

부유사 농도 c는 이송-확산 방정식에 기반 하여 산출되며, 이를 기술하면 다음과 같다.

(9) ∂c∂t+∇⋅[(γu+wf)c]=∇⋅[γ(ν+νt)∇c]

여기서 c는 단위체적당 부유사 농도, wf와 u는 각각 표사 침강속도벡터와 유속벡터를 나타낸다. γ는 VOF 법에서 자유수면을 추적하기 위해 도입된 VOF 계수를 나타내며, 식(9)에서 ν와 νt는 각각 동점성계수와 와동점성계수를 나타내며, 표사가 공기 중으로 부유되었을 때 바로 회귀할 수 있도록 침강속도 wf로 인한 질량 이송 항에는 VOF 계수 γ를 생략하였다.

이송-확산 방정식 해석에 필요한 부유사 농도 저면 경계 값 cb는 Shields parameter에 종속하며, Fredsoe와 Deigaard(1992)에 준거하면, 순간 저면 체적 표사농도 c_b(θ')는 다음과 같이 기술될 수 있다.

(10) cb=co(1+1λb)3

여기서 c_o는 최대 부유사 농도를 나타내며 본고에서는 0.35의 값을 취하였다. λ_b는 저면에서의 순간 선형 표사농도를 나타내며 다음과 같이 정의된다.

(11) λb2=κ2α120.013sθ′(θ′−θ′c−π6μdpEF)

식(11)에서 θ'c는 임계 Shields parameter, μd는 동 마찰계수, κ와 α1는 계수를 각각 나타내며, pEF는 표사가 부유사 형태로 이송되는 확률을 의미하며 다음과 같이 기술될 수 있다(Fredsoe and Deigaard, 1992).

(12) pEF=[1+(16πμdθ′−θ′c)4]−1/4

3.2.2 지형모형(Morphology Model)

소류사 순 이송량과 부유사 형태의 침·퇴적량 사이에 균형을 이루지 못하는 경우 저면에는 변화가 발생하며, Fig. 6에 도시된 통제용적에 표사수지 개념을 적용하는 경우 지형모형(morphology model)을 유도 할 수 있으며, 이렇게 얻은 지형모형을 기술하면 다음과 같다.

Fig. 6.

Layout of numerical wave flume.

(13) ∂h∂t=−11−ed[∇⋅qb+E+D]

상기식은 Exner 방정식 형태로, 여기서 e_d는 공극률, q_b는 소류사 이송률, E와 D는 각각 부유사에 의한 침식률과 침강속도로 저면으로 회귀하는 퇴적률을 각각 나타낸다. 식(13)에서 소류사 이송량 qb는 다음과 같이 산출될 수 있으며(Fredsoe and Deigaard, 1992),

(14) qb=16πdpEFub

여기서 d는 표사직경, ub는 소류사 이송속도, pEF는 표사이송확률을 나타내며 식(12)에 기 정의된 바 있다.

식(13)에서 E는 van Rijn(1986)의 pick up function을 활용하는 경우 다음과 같이 기술될 수 있으나,

(15) E(t)=0.00033(θ′−θcθc)1.5(s−1)0.6g0.6d0.8ν0.2,θ′>θc=0,θ′<θc

전술한 van Rijn(1986)의 pick up function은 정상상태의 파동계를 대상으로 유도되어 쇄파역으로 확대 적용하는 것에 대해서는 좀 더 많은 논의가 필요해 보인다.

따라서 본 논문에서는 보다 일반적인 Fick’s Law에 준거 다음과 같이 산출하였다.

(16) E=−(ν+νt)∂c∂n|N|

여기서 ν와 νt는 기 정의된 점성계수와 와점성계수를 나타내며, 음의 부호는 본고에서 사용한 외향법선 벡터와 침식이 진행되는 방향의 차이를 보정하기 위해 도입하였다. n은 저면에서의 단위 외향 법선벡터를 나타내며, 따라서 외향 법선벡터 N은 다음과 같이 정의된다(Fig. 5 참조).

Fig. 5.

Schematic sketch of morphology change of the sea bed of slope α due to the erosion, and deposition process of suspended load, and the net flux of bed load.

(17) N=|N|n

여기서 |N|은 경계 인근 육면체로 구성된 셀에서 저면과 접하는 면의 면적을 나타낸다.

식(13)에서 D는 표사 침강속도 wf와 유속 u의 합을 저면법선벡터 N에 투영하여 산출되며 이를 내적을 활용하여 기술하면 다음과 같다.

(18) D=cb|(wf+u)⋅N|

여기서 c_b는 식(10)에 기 정의된 저면에서의 표사농도를 나타낸다.

q_b에 의한 Δt 동안의 연직방향으로의 저면높이의 변화 Δhb는 다음과 같이 기술된다.

(19) Δhb=−11−ed∇⋅qbn⋅egΔt

여기서 n과 e_g는 각각 저면의 바깥쪽으로 향하는 단위법선벡터와 아랫방향으로 향하는 연직방향 단위벡터이다. Δt는 시간 격자의 사이시간을 나타낸다. Δt 동안 경사진 저면을 따라 이송되는 소류사의 순 이송량은 ∇·qbΔt/1 − ed이므로 이 식을 |n·eg|로 나누면 연직방향으로의 높이변화 Δhb로 전환될 수 있다.

4. 수치모의

본 논문에서 사용된 지형 모형을 검증하기 위해, 경사가 1/m인 단조 해안에서의 천수과정, plunging 형태의 쇄파, 처오름, 처내림 과정을 수치 모의하였다.

파형은 거친 해역을 고려하여 Korteweg-de Vries 식의 해석해로 정의되는 Cnoidal wave로 취하였으며, Cnoidal waves는 다음과 같이 정의되며,

여기서 ζ는 해수면 변위, H는 파고, Cn은 Jacobi elliptic function, c는 파속, L은 파장, T는 주기, M은 0과 1 사이의 값을 지니는 elliptic parameter를 각각 나타낸다. K_M은 제1종 타원적분, E_M은 제2종 타원적분을 각각 나타내며, K_M과 EM은 M 값에 종속한다. Cnoidal wave 파형은 M이 0에 수렴하면 Stokes I 파형에, M이 1에 수렴하면 Solitary wave 파형에 수렴하며, Cnoidal wave의 유속은 다음과 같이 기술될 수 있다.

식(24), (25)에서 ζ_x, ζ_xx, ζ_xxx는 x에 대한 자유수면의 1차, 2차, 3차 derivatives이고, 는 주기 평균을 나타낸다.

표사 물성치는 우리나라 해빈 특성을 고려하여 s = 2.4와 d = 0.02mm로 취하였다. Fig. 6에 도시한 계산영역은 250,000여개의 격자를 이용하여 이산화 하였다. Breaker type이 표사이송에 미치는 영향을 파악하기 위해 파고와 주기에 변화를 주어 가장 역동적인 plunging breaker 뿐만 아니라 spilling breaker를 대상으로 총 7번의 수치모의를 수행하였으며, Table 1에는 수치모의에 사용된 해빈 경사, 파랑조건, Iribarren NO. ξ를 정리하였다.

Table 1.

List of wave conditions used in the numerical simulation

5. 수치결과

5.1 유속분포

Fig. 7에는 수치모의 과정에서 관측된 자유수면 snapshot을 도시하였다. 목표했던 파랑이 조파되어 정연하게 단조 해안으로 접근하는 것을 알 수 있으며, 전빈에서 진행되는 plunging 형태와 spilling 형태의 쇄파가 진행되는 것을 알 수 있다.

Fig. 7.

Snapshot of numerically simulated free water surface in RUN 1, 2, and 3.

Fig. 8, 9에는 Gauge No. 1, 2, 3에서 관측된 유속 연직분포를 도시하였다(Fig. 6 참조). 한 주기를 총 일곱 개의 frame으로 나누어 위상별 유속 변화가 확연하게 드러나도록 구성하였으며, 저류특성을 파악하기 위해 주기 평균 유속도 함께 도시하였다. 또한 비교를 위해 왜도 된 연흔모양 매트가 미거치 된 단조 해안에서의 유속분포와 주기 평균 유속[undertow]도 함께 도시하였다. 왜도 된 연흔모양 매트로 인해 유동계에는 미세한 변화가 야기되는 것으로 보이며, 변화 양상을 정리하면 다음과 같다.

Fig. 8.

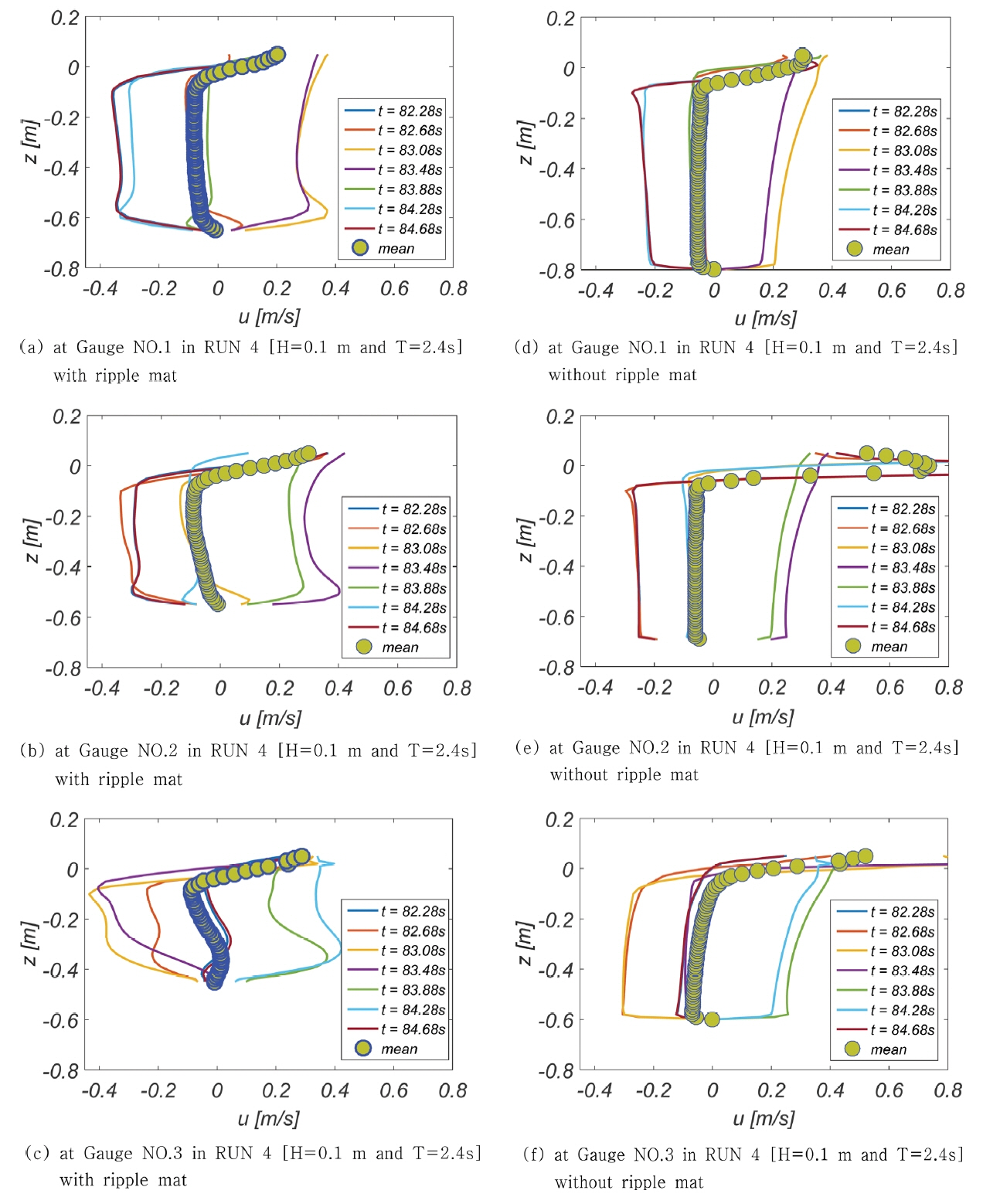
Variation of the vertical profiles of horizontal velocity at Gauge No. 1, 2, and 3 over a wave period in RUN 4 [H = 0.1m and T = 2.4 s].

Fig. 9.

Variation of the vertical profiles of horizontal velocity at Gauge No. 1, 2, and 3 over a wave period in RUN 1 [H = 0.1 m and T = 2.1 s].

A 왜도 된 연흔모양 매트 거치 시 under-tow는 수면 인근까지 확대되며, Gauge NO. 3에서는 under-tow의 진행방향이 저면 인근에서 연안방향으로 역전되어, 기대했던 왜도 된 연흔모양 매트의 해빈 안정화 효과를 확인할 수 있다. 그러나 이러한 경향은 단파의 경우[RUN 5, 6]에는 발생하지 않았다.

B 왜도 된 연흔모양 매트 거치 시 수면 인근에서 진행되는 Stokes drift 최대치는 감소하나 발생하는 영역은 확대되었으며, 이러한 경향은 주기가 길수록 보다 확연하게 드러난다.

5.2 왜도 된 연흔모양 매트의 높이가 유속분포에 미치는 영향

왜도된 연흔모양 매트의 높이가 해빈 안정화 효과에 미치는 영향을 살펴보기 위해 매트 높이를 η = 0.15m에서 η = 0.17 m(Fig. 3 참조)로 상향 조정하여 수치모의를 수행하였으며, Fig. 10에는 첫 번째, 두 번째, 세 번째 매트 정점에서 관측된 주기 평균 유속의 연직분포를 도시하였다.

Fig. 10.

Comparison of vertical distribution of mean velocity at 1^st, 2^nd, 3^rd crest of asymmetric ripple mat of different height in RUN2 [H = 0.2 m and T = 2.1 s].

첫 번째 정점에서는 저류는 여전히 먼 바다 방향으로 향하나 그 크기는 매트 높이가 증가할수록 감소하는 것을 알 수 있다. 두 번째, 세 번째 매트 정점에서는 저류는 방향을 바꾸어 해안으로 향하며, 이러한 경향은 매트 높이가 증가할수록 더욱 확연해지는 것으로 보이며, 이는 고파랑 내습 시 매트의 높이가 클수록 해빈 안정화 효과는 증가한다는 것을 시사한다. 그러나 왜도 된 연흔모양 매트는 거치 후 생애주기의 대부분을 고 파랑과는 성격이 상이한 너울에 노출되며, 이 과정에서 자연 해빈이 지니는 자기 치유능력이 발현된다는 사실을 상기하면 해빈 대순환 과정에 대한 인위적 간섭은 최소화되어야 한다고 판단되며, 따라서 매트 높이를 임계치 이상으로 높이는 것은 지양되어야 할 것으로 보인다.

5.3 왜도 된 연흔모양 매트의 해빈 안정화 효과

Fig. 11에는 RUN 7에서 관측된 x-z 평면에서의 와도를 나타내는 w_y 분포를 순차적으로 도시하였다[Fig. 6 참조]. 강한 와도는 전빈에서의 쇄파과정에서 관측되나 왜도 된 연흔모양 매트의 up-wave side와 down-wave side에서 강제되는 와류의 순차적 이송과정을 확인할 수 있으며, 이는 강제 와류에 포획된 표사가 연안으로 회귀됨을 의미한다.

Fig. 11.

Contour plot of numerically simulated vorticity field under breaking waves of plunging type in RUN 7 [H = 0.1 m and T = 3.0 s].

Fig. 12에는 89초 동안 파랑에 노출된 이후 저면 형상을 도시하였으며[RUN 1, 2, 3], 비교를 위해 왜도 된 연흔모양 매트가 거치되지 않은 자연 해빈의 저면 형상도 함께 수록하였다. Dean NO.로 침·퇴적 여부를 가늠하는 경우 RUN 1과 RUN 2는 퇴적이 우세하며, RUN 3는 침식이 우세한 해양환경에 해당된다. 이해를 돕기 위해 Dean NO. D를 기술하면 다음과 같으며(Dean and Dalrymple, 2002)

Fig. 12.

Comparison of the bed morphology of protected beach with a ripple mat with the one of unprotected beach after exposed to waves for 89 s.

(26) D=HbwoT

D > 6인 경우 침식이, D < 1인 경우 퇴적이 우세한 것으로 전해진다(Dean and Dalrymple, 2002). 식(26)에서 Hb는 쇄파파고, T는 주기, wo는 침강속도를 각각 나타내며 wo는 다음과 같이 산출될 수 있다(Nielsen, 1979, 1992).

(27) wo=(s−1)gd218ν

먼저, RUN 1의 경우에는 일정 수심부에서 연흔이 형성되지 않으나, 파고가 상대적으로 큰 RUN 2, RUN 3의 경우 sand wave가 형성되는 것을 알 수 있다. 왜도 된 연흔모양 매트 거치 시 일정 수심부에서 관측되는 sand wave의 진폭과 형태는 왜도 된 연흔모양 매트 거치 전과 동일하게 유지되나 위상에는 미세한 변화가 관측된다. 이는 왜도 된 연흔모양 매트로 인한 반사율 증가로 정상파동계 배와 절점의 형성 위치에 생성되는 미세한 변화에 기인하는 것으로 판단된다.

왜도 된 연흔모양 매트 거치 시 퇴적이 우세한 수환경의 경우[RUN 1, 2], 연안사주[sand bar]는 해안으로 전진하며, 이로 인해 후빈에서의 퇴적량은 왜도 된 연흔모양 매트 거치 전보다 미세하게 감소하였다. 이에 반해 침식이 우세한 수환경의 경우[RUN 3], 연안사주는 소멸하나, 후빈에서의 퇴적량은 증가하여 왜도 된 연흔모양 매트의 해빈 안정화 효과가 상당부분 검증된 것으로 판단된다.

6. Irie et al.(1994)이 수행한 수리모형실험

본 논문에서 수행한 수치모의의 검증과정에 활용하기 위해 Irie et al.(1994)가 수행한 수리모형실험 결과를 살펴보았다.

6.1 표사 수리모형실험 제작 기법 검토

표사 이송 문제를 수리모형실험으로 다루는 경우 표사 직경을 모형 제작을 위해 선정된 축적(scale) 대로 선정하는 경우 표사에 작용하는 소류력이 지나치게 비대해지는 왜곡문제가 발생한다. 전술한 왜곡문제를 해결하기 위해 모형에서의 침강속도가 Froude 상사법칙이 충족되도록 표사 직경이 조정되며, 이 과정에서 대개의 경우 밀도는 가벼워지며 표사 직경은 축적이 가리키는 것보다는 커진다.

이와 더불어 무차원 표사 이송률 q*도 모형과 원형에서 동일하도록 조정되어야 하며 이 과정은 Vanoni(1975)의 관측결과(Fig. 13 참조)를 토대로 모형과 원형에서의 경계층 Reynolds NO. [u*d/ν]와 Shield’s parameter[τo/(s − 1)ρd]가 임계 Shield’s parameter가 그리는 궤적과 나란한 궤적에 떨어지도록 미세조정하는 것으로 구현될 수 있다.

Fig. 13.

Plot showing the critical Shields values along with Shield’s values for constant-value segments of Taylor’s function data [from Vanoni 1975].

무차원화 된 표사 이송률 q*는 Taylor’s function이라 불리며 다음과 같이 기술될 수 있으며,

(28) q*=qu*d

여기서 u*는 해저면 마찰속도를 나타내며, 전술한 조정과정에서 모형에서의 해저면 경사는 대부분의 경우 원형보다 급하게 조정된다.

6.2 Irie et al.(1994)가 수행한 수리모형실험 관측결과 검토

Irie et al.(1994)은 왜도 된 연흔모양 매트의 해빈 안정화 효과를 확인하기 위해 길이가 4 m, 폭이 15 cm, 높이가 20 cm, 해빈 경사가 1/20인 수조에서 수리모형 실험을 수행한 바 있다.

이 연구에서 Irie et al.(1994)은 표사 이송의 상사를 이루어내기 위해 자연에서 관측할 수 있는 모래가 아닌 비중이 2.4, 직경이 0.08 mm인 grass beads를 사용하였으며, 해빈 경사는 자연해빈의 경우보다 급하도록 1/20으로 조정한 것으로 보인다. Irie et al.(1994)의 수리실험에서 표사는 왜도 된 연흔모양 매트의 down-wave 쪽에서 일정하게 공급된다. 또한 수조제원에서 알 수 있듯 지나치게 작은 규모에서 수행된 것으로 보인다.

전술한 조건은 천수과정에서 쇄파되는 파랑에 의해 자연 표사가 부유되고 재분배되는 과정에서 왜도 된 연흔모양 매트의 해빈 안정화 효과를 다루는 본 논문의 목적과는 다소 거리가 있어, Irie et al.(1994)가 수행한 수리모형실험 관측결과는 본고에서 제시된 수치모형의 정량적 검증과정에 활용되기는 어려울 것으로 판단된다.

그러나 현재 가용한 유일한 수리모형실험 결과라는 점에서 본 논문에서 수행된 수치모의의 정성적 검증을 위해 왜도 된 연흔모양 매트로 인한 해빈 변화추이를 살펴보았다.

Fig. 14에는 Irie et al.(1994)가 수행한 수리실험에서 관측된 해빈 변화를 수록하였다. 두 번의 실험 중 비교적 큰 규모에 해당되는 I1에서 관측되는 왜도 된 연흔모양 매트 up-wave side에서의 침식과 down-wave side에서 진행되는 퇴적 양상이 RUN 3에서도 유사하게 관측되는 것을 알 수 있다[Fig. 12(c) 참조].

Fig. 14.

Variation of beach profile following the beach fill by dumping (I1, medium scale experiments) [modified from Irie et al. (1994)].

7. 결 론

기후변화와 난개발 등으로 인해 기존에 유지되던 준 평형상태가 훼손된 우리나라의 각 해안에서는 현재 상당한 침식이 진행되고 있다. 최근 해안 침식에 대응하기 위해 이안제, 돌제, 인공 곶(headland), 광폭잠제(artificial reef), 양빈(beach nourishment) 등이 거치 혹은 시행되고 있으나, 기대와는 달리 해빈 안정화 효과가 미미한 경우도 상당하다(Cho et al., 2019). 또한 해빈 안정화를 위해 거치되는 구조물의 규모는 해빈의 자기 치유 능력이 발현되는 해빈 대순환 과정이 훼손되지 않는 범위에서 결정되어야 하나 최근 지나치게 대형화되어 해빈의 자기 치유 능력이 상당부분 훼손된 것으로 보인다. 이러한 예는 해안침식이 외중력파에 기인되며 따라서 장주기파인 외중력파를 감쇄하는 경우 해빈 안정화를 이룰 수 있다는 시각에서 최근 빈번히 차용되는 광폭 잠제에서 찾아 볼 수 있다.

해안 침식에 대응하기 위한 구조물은 해당 수역에서의 횡단 표사량에 대한 정량적 평가에 기초하여 그 형식과 성격이 결정되고 시공되어야 하나, 현재 국내에서 거치된 광폭 잠제의 상당부분은 전술한 최적화 과정을 거친 것으로 보기 어렵다. 그러나 횡단표사는 해빈의 자기 치유 능력의 상당부분을 설명한다는 점에서 개선이 시급해 보인다. 전술한 최적화 과정이 생략되어온 관행은 표사이송 문제에 내재한 난해함과 계측상의 어려움에 기인하나 최근 3D 물리기반 지형모형(3D morphology model)이 개발되어 사주(sand bar)의 형성과정과 계절별 이행과정이 모의되는 등 상당한 성과가 이루어진 것으로 보인다(Jacobsen et al., 2012, 2014; Cho, 2019).

이러한 시각에서 본 논문에서는 규모는 크지 않으나 장기간에 걸친 해빈 안정화 효과를 지니는 Irie et al.(1994)의 왜도 된 연흔모양 매트 거치 시 결과되는 해빈변화를 Navier-Stokes 식과 물리기반 지형 모형에 기초하여 수치모의 하였다. 수치모의결과 왜도 된 연흔모양 매트 거치 시 유동계에는 미세한 변화가 야기되며 이는 상당한 해빈 지형변화로 이어지는 것을 확인할 수 있었으며, 관측된 변화 양상을 정리하면 다음과 같다.

A. 왜도 된 연흔모양 매트 거치 시 under-tow는 수면 인근으로 확대되며, 저면 인근에서 under-tow의 진행방향이 연안방향으로 역전되어, 기대했던 왜도 된 연흔모양 매트의 해빈 안정화 효과를 확인할 수 있다.

B. 왜도 된 연흔모양 매트 거치 시 수면 인근에서 진행되는 Stokes drift 최대치는 감소하나 발생하는 영역은 확대되었으며, 이러한 경향은 주기가 길수록 보다 확연하게 드러난다.

C. 수치 모의된 와도분포에서 왜도 된 연흔모양 매트의 upwave side와 down-wave side에서 강제되는 와류의 순차적 이송과정을 통해 단면 수축부에서 강제된 와류에 의해 포획된 표사의 연안 회귀가 왜도 된 연흔모양 매트의 해빈 안정화 효과를 구성하는 주요 기작이라는 추론은 상당한 설득력을 지니는 것으로 보인다.

D. 매트 높이가 증가할수록 저류는 방향을 바꾸어 해안으로 향하는 경향이 보다 뚜렷해졌으며, 이는 고파랑 내습 시 매트의 높이가 클수록 해빈 안정화 효과는 증가한다는 것을 시사한다.

E. 그러나 왜도 된 연흔모양 매트는 생애 주기의 대부분을 고 파랑과는 성격이 상이한 완만한 파랑에 노출되며, 이 과정에서 자연 해빈이 지니는 자기 치유능력이 발현된다는 사실을 상기하면 해빈 대순환 과정에 대한 인위적 간섭은 최소화 되어야 하며, 따라서 매트 높이를 임계 치 이상으로 높이는 것은 지양 되어야 할 것으로 보인다.

F. 정밀한 물리기반 지형 모형에 기초한 수치모의를 통해 침식이 우세한 수환경의 경우, 연안사주(sand bar)는 소멸하나, 후빈에서의 퇴적량은 증가하여 왜도 된 연흔모양 매트의 해빈 안정화 효과를 확인 할 수 있었다.

또한 본 논문에서 수행된 수치모의의 정성적 검증을 위해 Irie et al.(1994)가 수행한 수리실험에서 관측된 왜도 된 연흔모양 매트 거치 시 결과 되는 해빈 변화추이를 살펴보았다. Irie et al.(1994)가 수행한 두 번의 실험 중 비교적 큰 규모의 실험에서 관측되는 연흔모양 매트 up-wave side에서의 침식과 down-wave side에서 진행되는 퇴적 양상이 수치모의에서도 유사하게 관측되는 것을 확인할 수 있었다.

Article information Continued