2.1 지배방정식

수치해석을 위한 지배방정식은 연속방정식, 운동량방정식과 난류 해석을 위한 난류운동에너지 및 소산율 방정식이 적용됐으며, 식(1)~(6)과 같이 표현된다.

연속방정식

운동량 방정식

난류운동에너지 및 소산율 방정식

여기서 x는 좌표축상의 거리, ρ는 유체의 밀도, u는 축방향의 속도, p는 압력, g는 중력가속도, k는 난류운동에너지, μ_t는 난류점도, ε은 난류 소산율, 하첨자 i, j, k는 각각 1, 2, 3으로 x, y, z 방향을 나타낸다.

2.2 조류발전 시스템 및 블레이드 형상

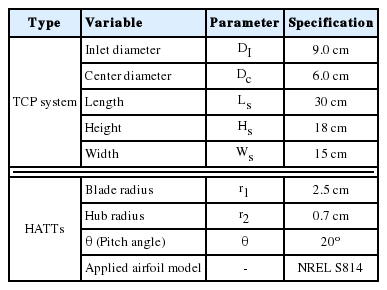
유속 및 회전수 변화에 따른 시스템 효율을 추정하기 위해 Lee et al.(2019)에서 사용한 조류발전 시스템 및 터빈 블레이드 형상을 이용했으며, 유입 유속 대비 중심부에서의 유속 증폭을 통해 발전하는 쉬라우드 시스템 내 직경비(D_C:D_I)는 1:1.5, 블레이드의 회전각은 20°이다. Fig. 1의 (a), (c)는 시스템 및 블레이드의 정면, (b), (d)는 각각의 측면에 해당하는 기하학적 형상 모습이며, 이에 대한 제원은 다음 Table 1에 제시했다.

Fig. 1.

Three Dimension model for the TCP system and HATTs.

Table 1.

Specification of TCP system and HATTs

2.2 해석 조건 및 격자 구성

변화하는 유속 및 회전수에 대해 쉬라우드 시스템 내 효율 분석을 위한 경계 조건으로, 유입부와 유출부에 유속 조건 및 유출 조건을, 그 외 모든 면은 벽 조건으로 설정했다. 이에 대한 해석 조건 정보를 다음 Fig. 2에 제시했다. 해석 유동장의 크기는 추후 수행할 모형실험 수조와 동일 크기로서 구성했으며, 본 해석에서는 0.35 m/s, 0.5 m/s, 0.75 m/s, 1.0 m/s에 대한 유속변화와 50 rpm, 100 rpm, 150 rpm, 200 rpm, 250 rpm, 300 rpm의 회전수 변화에 대해 효율 특성을 분석했다.

Fig. 2.

Flow field boundary condition and specification.

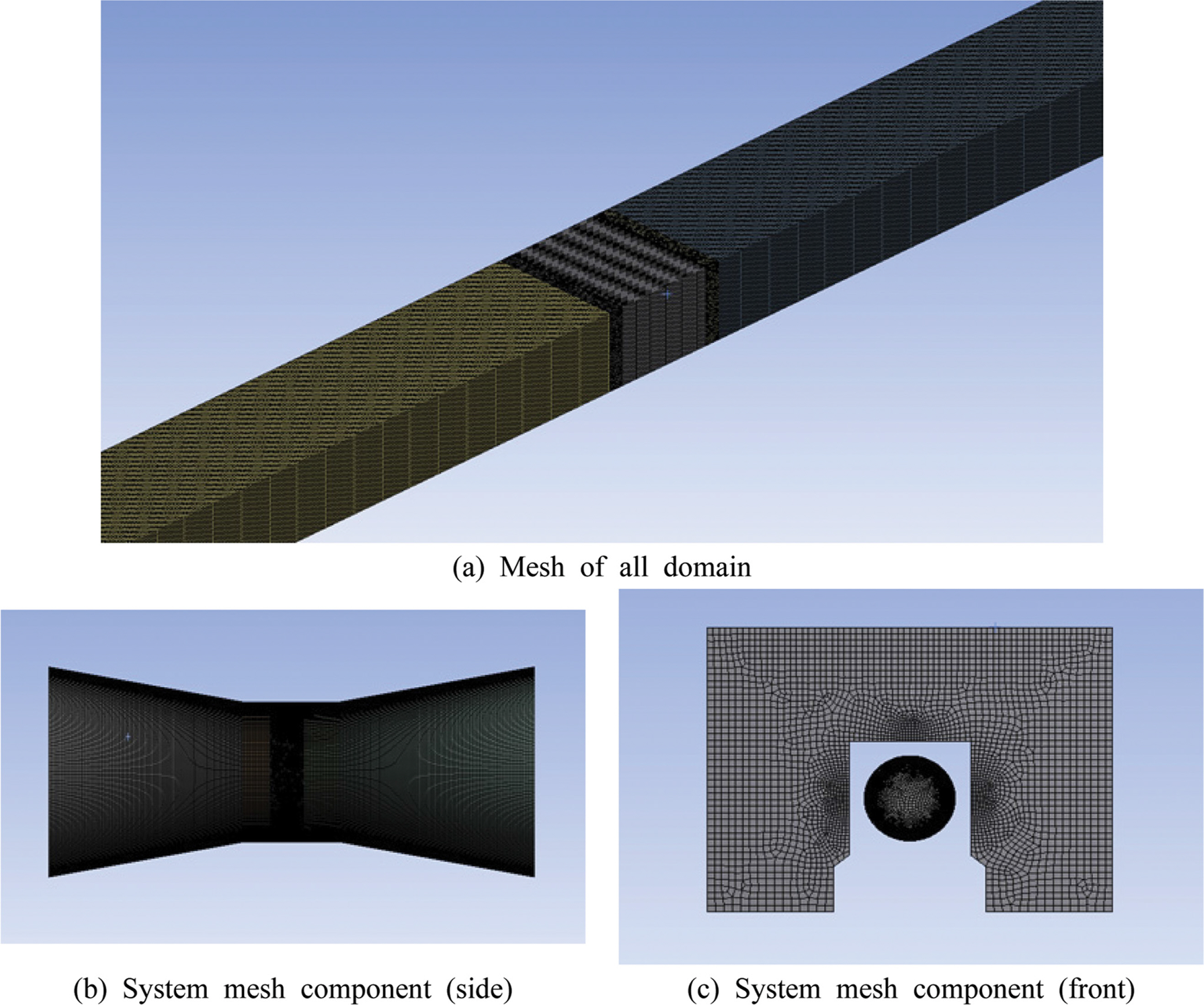
본 연구에서는 수치 해석적 기법을 사용했으며, 다음 Fig. 3에 해석에 사용된 격자 구성을 제시했다. 해석에 사용된 격자는 약 100만개이며, 격자에 따른 해석 결과의 오차를 추정하기 위해 격자수를 조정하여 65만개, 80만개, 120만개에 대하여 해석한 결과 100만개와 120만개의 결과 오차율은 0.21%로서 두 경우에 대해서 결과의 경향이 유사하게 분석됐다. 이에 해석에서 사용된 격자는 계산 시간을 고려하여 약 100만개로 구성했다. 또한 헥사 격자를 효율적으로 구성하기 위해 관심 부분의 전·후방에 테트라 격자를 사용하여 결과의 정확도를 높였다.

Fig. 3.

Three dimensional mesh component.

3.1 시스템 내 유속 변화 분석

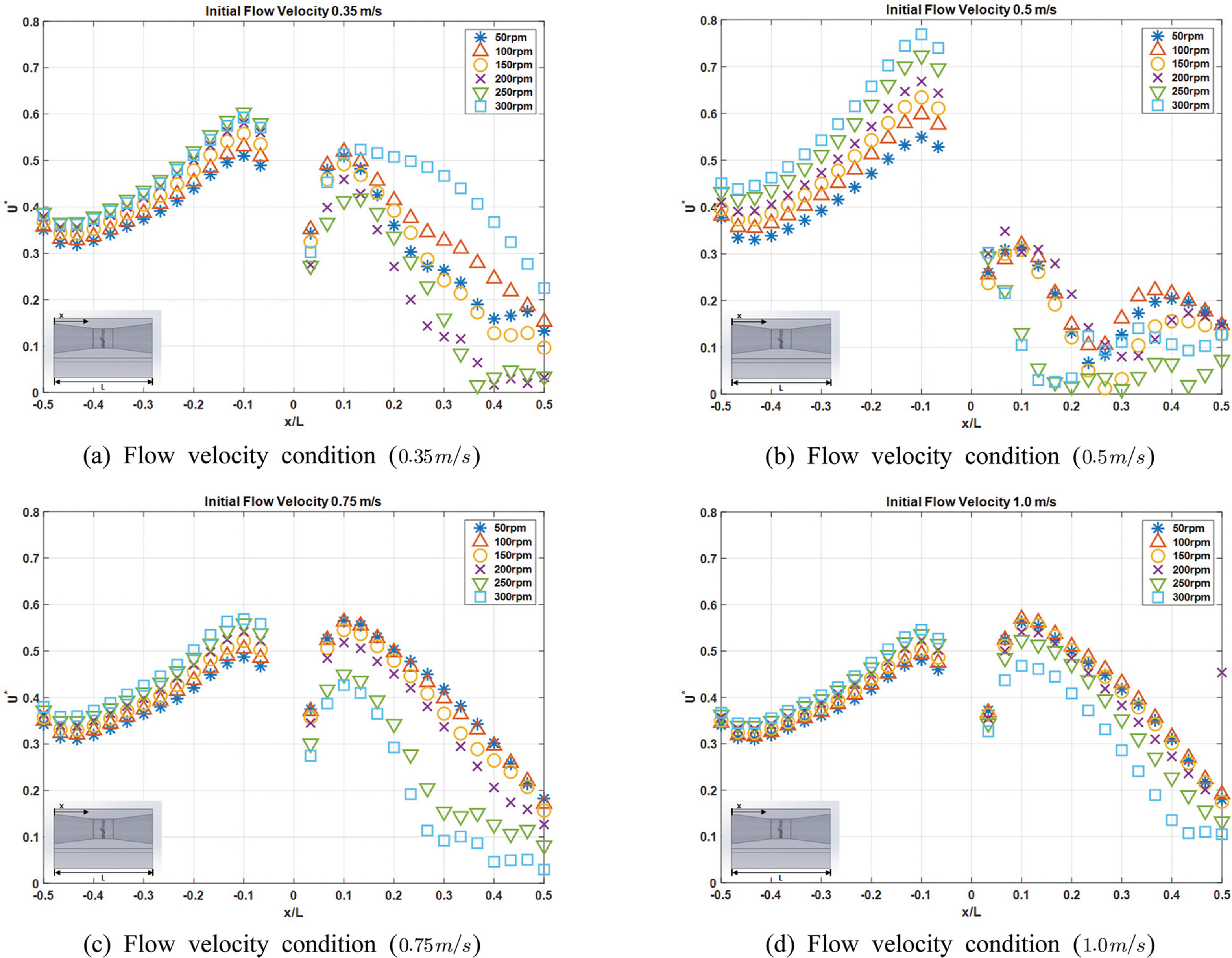
단면적 차이를 이용해 발전하는 쉬라우드 시스템 내 유속증가율을 분석하기 위해 시스템 내 유입부에서 유출부까지 유속 변화를 분석했으며, 초기유속 대비 중심부의 유속비를 다음 식(7)을 이용해 무차원화로 표현했다. 이에 대한 결과는 다음 Fig. 4에 제시했다.

Fig. 4.

Flow velocity distribution characteristics in shroud system expressed dimensionally.

여기서, U_x[m/s]는 유입부에서의 유속이며, U_∞[m/s]는 쉬라우드 중심부에서의 유속이다.

초기 흐름이 쉬라우드 시스템 내부로 유입되는 유입부에서 블레이드 앞까지의 유속은 점차 증가하는 경향을 보이고 있으며, 블레이드를 통과한 흐름은 일정하지 않은 유속 분포를 보였다. 이는 회전하고 있는 블레이드에 의해 흐름이 급격히 변화하며, 난류를 형성하는 것으로 판단된다. 또한 초기 유속이 증가할수록 유속 변화율이 증가하다가 0.75 m/s에서 유속 변화율이 약 1.3배 감소하고, 이는 해석 유동장의 크기로 인해 발생하는 현상으로 사료되며, 유속 증가율 경향은 Lee et al.(2019)의 연구결과와 유사하게 나타났다. 한편, 각각의 경우 동일하게 블레이드의 회전수가 빠를수록 유속변화가 크게 나타나는 경향을 보였으며, 이에 대한 수치해석 결과를 Fig. 5에 제시했다.

Fig. 5.

Comparison of distribution of flow velocity variation around shroud (for 4 flow velocity).

3.2 시스템 내 효율 특성 분석

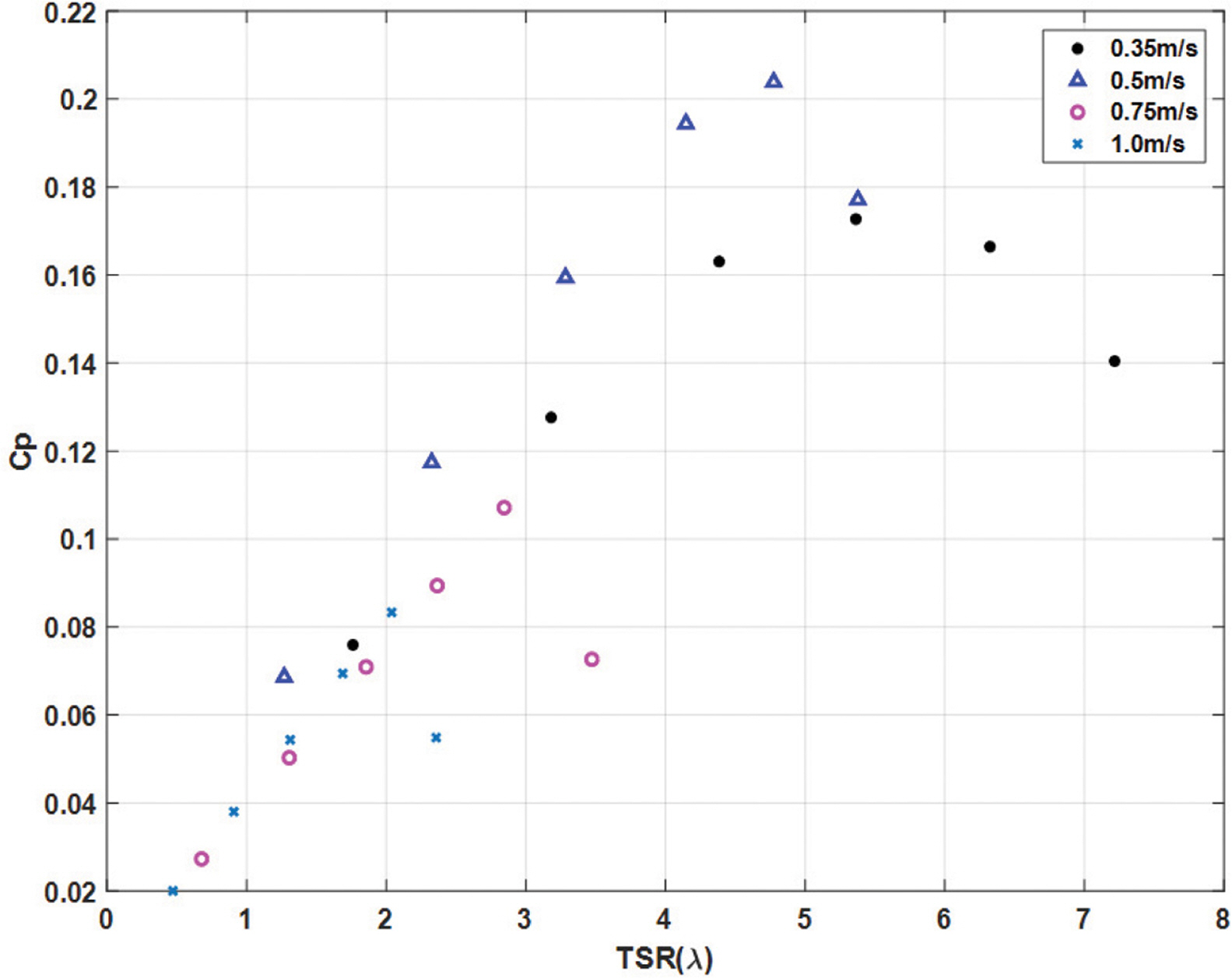
쉬라우드 시스템 내 효율 변화 특성을 분석했으며, 회전수의 무차원화 표현을 위해 다음 식(8)를 이용했다. 다음 Fig. 6은 해석을 통해 분석된 결과이다. 선 끝단 속도를 나타내는 주속비(Tip Speed Ratio, TSR, λ)는 변화하는 유속 및 블레이드의 회전수, 반경 조건에 대해 무차원화를 함으로서 다양한 형태의 블레이드 성능 특성을 비교할 수 있다.

Fig. 6.

Tip speed ratio (λ) - power efficiency (C_p) distribution characteristic.

여기서, U_∞[m/s]는 시스템 중심부 유속, w[rad/s]는 블레이드의 회전수, 은 블레이드의 반경이며, 본 연구에서 분석하고자 하는 시스템 내 기계적 효율은 다음 식(9)를 이용해 산정했으며, 이에 대한 결과를 다음 Fig. 6에 제시했다.

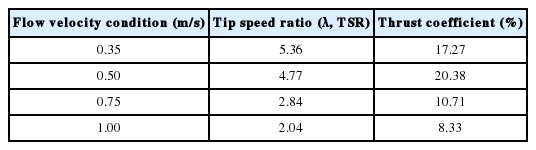
여기서, ρ[kg/m³]는 유체의 밀도이며, A_I[m²]는 중심부에서의 단면적, T[N/m]는 블레이드의 토크를 의미하며, 해석을 통해 블레이드의 토크를 구할 수 있다. 산정된 토크와 입력조건에 사용된 회전수를 이용하여 효율을 평가했으며, 이를 통해 주속비와 기계적 효율 관계 곡선을 도시했다. 덕트 형태를 지닌 쉬라우드 시스템은 모든 경우에서 주속비가 증가할수록 효율이 급격히 증가한 후, 특정 지점에서 재차 감소하는 경향을 보였으며 각 경우에 대한 효율 곡선의 첨두 부분을 다음 Table 2에 정리하여 제시했다.

Table 2.

TSR-C_p analysis result

본 해석결과의 간략한 검증을 위해 모형실험을 수행한 Han et al.(2019)와 비교한 결과 TSR-C_p 관계 곡선의 경향성은 대체적으로 유사하게 나타났으며, 유사한 유속 및 주속비와의 결과를 비교했을 때 약 10%의 오차가 발생했다. 이는 실험의 경우 기계적 출력에서 전기적 출력으로 변화될 때, 수심 밖으로 연결된 출력장치에서 효율 손실이 발생하는 오차로 판단된다. 한편, 주속비-효율 관계 곡선의 경향은 초기 유속이 증가함에 따라 블레이드의 회전수가 증가하고, 이때 효율이 증가함을 Han et al.(2019)와 Yi et al.(2013)의 연구 결과를 통해 증명됐다. 그러나 본 연구는 초기 유속과 블레이드 회전수에 따른 최적 효율을 추정하는 연구이며, 0.75 m/s부터 저유속에 비해 효율이 감소하는 것은 유체의 힘을 통해 발생하는 블레이드의 회전수가 아닌 6가지의 회전수 고정조건을 통해 분석이 수행되어 발생한 것으로 사료되며, 또한 부여된 유속에 비해 유동장의 크기가 작아 효율의 한계성을 보인 것으로 판단된다.