해역별 최적 해빈 안정화 공법 선정 Platform 개발을 위한 기초연구 II - 양빈 된 해빈 침식률 산정을 위한 물리기반 해빈 지형모형 개발을 중심으로
Preliminary Study on the Development of a Platform for the Optimization of Beach Stabilization Measures against Beach Erosion II - Centering on the Development of Physics-Based Morphology Model for the Estimation of an Erosion Rate of Nourished Beach
Article information
Abstract
양빈이 수행된 해빈의 침식률 산정을 위한 물리기반 해빈 지형모형이 제시되었다. 동수역학 모형은 OpenFOAM에 기반 한 tool box인 IHFOAM으로 구성되며, Morphology 모형은 부유사를 대상으로 한 이송확산방정식, 소류사 이송을 포함한 표사 수지 개념으로부터 유도된 Exner 식으로 구성하였다. 표사 이송여부, 부유사 농도 저면 경계치, 소류사 이송률 산출과정에는 Shields Diagram, 삼차원 수치 모의된 유동계 정보로부터 직접 산출된 저면 전단응력이 활용된다. 본 논문에서 제시된 지형 모형을 검증하기 위해, 경사가 1/6인 단조 해안에서의 천수과정, 쇄파과정, 이에 따른 저면 변화를 수치 모의하였다. 모의결과 비선형 천수과정에서 예상되는 왜곡되고 왜도된 저면 전단응력이 비교적 정확히 모의되었다. 또한 전빈에서 진행되는 쇄파로 인해 부유되고 침식된 표사가 up-rush에 의해 후빈으로 이동되어 형성되는 swash bar와 up-rush 정점에서 방향을 바꾸어 먼 바다 방향으로 진행되는 back-wash에 의해 쓸려간 표사가 수심증가에 따라 back-wash 흐름 강도가 약해지면서 퇴적하여 형성되는 breaker bar가 성공적으로 모의되는 것을 확인할 수 있었다.
Trans Abstract
In this study, a physics-based 3D morphology model for the estimation of an erosion rate of nourished beach is newly proposed. As a hydrodynamic module, IHFOAM toolbox having its roots on the OpenFoam is used. On the other hand, the morphology model comprised a transport equation for suspended sediment, and Exner type equation derived from the viewpoint of sediment budget with the bed load being taken to accounted. In doing so, the incipient motion of sediment is determined based on the Shields Diagram, while the bottom suspended sediment concentration, the bed load transport rate is figured out using the bottom shearing stress directly calculated from the numerically simulated flow field rather than the conventional quadratic law and frictional coefficient. In order to verify the proposed morphology model, we numerically simulate the nonlinear shoaling, breaking over the uniform beach of 1/m slope, and its ensuing morphology change. Numerical results show that the partially skewed, and asymmetric bottom shearing stresses can be successfully simulated. It was shown that sediments suspended and eroded at the foreshore by wave breaking are gradually drifted toward a shore and accumulated in the process of up-rush, which eventually leads to the formation of swash bar. It is also worth mentioning that the breaker bar formed by the sediments dragged by the back-wash flow which commences at the pinnacle of up-rush as the back-wash flow gets weakened due to the increased depth was successfully duplicated in the numerical simulation.
1. 서 론
기후변화와 난개발 등으로 인해 기존에 유지되던 준 평형 상태가 훼손된 우리나라의 각 해안에서는 현재 상당한 침식이 진행되고 있다. 현재 이안제, 돌제, 인공 곶[head land], 혹은 저 천단 방파제[artificial reef] 등으로 침식을 저감하려는 노력이 수행되고 있으나, 해빈 안정화 효과가 기대에 미치지 못하는 경우도 상당하며, 거치지역의 인근해안에 추가적인 침식 혹은 퇴적, 항 매몰 등과 같은 역기능을 야기한 경우도 적지 않다(Cho and Kim, 2019; Cho, 2019). 최근 이러한 인식을 반영하여 연성공법인 양빈을 통하여 해안침식을 저감하려는 시도가 미국 Florida 연안과 일본, 부산 송도, 해운대 등에서 이루어져 부분적인 성공을 거둔 것으로 보인다(Dean and Dalrymple, 2002; Cho, 2019). 그러나 양빈으로 침식이 우세한 연안 수환경이 준 평형상태로 복원되는 것은 아니며 주기적인 양빈을 필요로 하며, 따라서 자연 해빈에 가까운 수려한 해빈을 유지하기 위해서는 양빈 수행 전 해빈 침식률에 대한 정량적 평가가 선행되어야 할 것이다.
현재 해빈 변화에 대한 정량적 평가를 위해 가용한 해석방법으로는 준 경험모형에서부터 물리기반 지형모형까지 다양하게 존재한다.
경험기반 장기 해안선 거동 모형으로는 Plant et al.(1999, 2001)의 모형이 대표적이다. 이 연구에서 Plant et al.(1999, 2001)은 해저 지형은 일시적으로 교란된 경우 다시 특정한 형태로 회귀하며 이를 equilibrium profile이라 명하였으며 쇄파역 사주의 위치는 해양환경에 종속하는 것으로 해석하였다. 해양환경이 거친 경우 생성된 쇄파역 사주는 장기간에 걸쳐 다시 equilibrium profile로 이행되며 equilibrium profile은 출현빈도가 우월한 파고에 의해, 쇄파역 사주의 위치는 경험식을 사용하여 결정된다. 전술한 해석방법은 미 노스캐롤라이나, Duck에서 진행된 장기관측결과에 기초하나, 해양환경이나 표사분포에 따라 상이한 결과가 도출될 수 있어 범용성에 대해서는 추가적인 검증이 필요해 보인다.
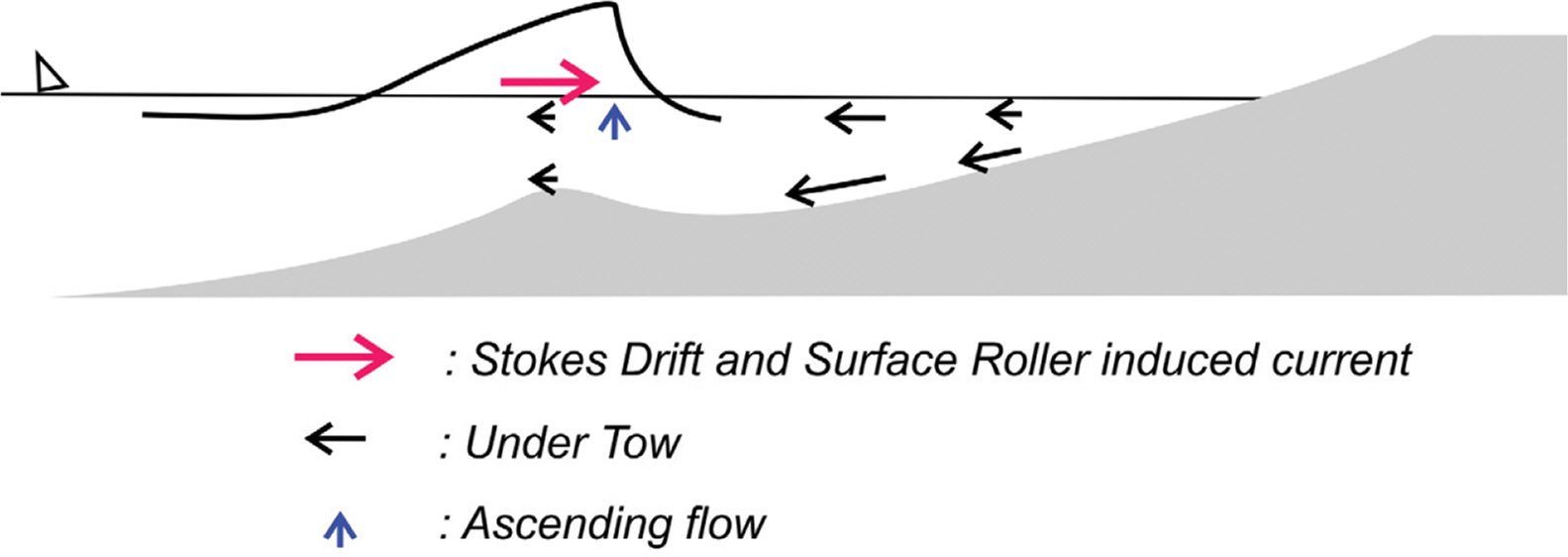
물리기반 지형모형으로는 일차원 수심적분 모형으로부터, 이차원 수심적분 모형, 정수압 분포라는 가정에 기초한 의사 삼차원 모형까지 다양하게 존재하나, 수심적분 모형에서 연직 방향에서의 유속분포는 (z + h)2로 가정되므로 저류[undertow]로 인해 쇄파역 해저면 인근에서 표사가 외해방향으로 회귀하는 현상은 모의할 수 없다. 전술한 오류를 시정하기 위해 유사 삼차원 모형이 제시된 바 있으며, 유사 삼차원 모형에서 저류가 표사 이송에 미치는 영향은 매개변수로 모의된다. 해빈표사 거동을 정확히 모의하기 위해서는 쇄파역 사주 인근에서의 Stokes drift, Surface Roller에 의해 질량 이송, 저류 간의 국지적 균형을 기술할 수 있는 능력을 지녀야 하나, 이는 전술한 이차원 수심적분 모형과 유사 삼차원 모형으로는 불가능하다. Stokes drift, Surface Roller에 의해 질량 이송이 저류와 조우하는 경우, 원역 방향으로 점점 약해지는 저류로 인해 쇄파역 언저리에 생성되는 연직방향 흐름으로 인해 표사 이송형태에는 급격한 변화가 야기된다[Fig. 1 참조]. 전술한 이차원 수심적분 모형과 유사 삼차원 모형에서는 이러한 변화를 설명하기 위해 천수과정이 지배적인 해역으로부터 쇄파가 지배적인 해역으로의 천이구간에 연화과정 혹은 지체과정을 자의적으로 도입하였으나 전술한 연화과정 혹은 지체과정의 해양환경과의 함수관계는 아직 밝혀진 바 없다.
최근 OpenFoam이 개발된 이래, RANS[Reynolds Averaged Navier-Stokes equation]을 직접 해석함으로써 swash zone에서의 흐름에 대한 우리의 이해를 넓히려는 다수의 시도가 이루어진 바 있다(Jacobsen et al., 2014; Jacobsen et al., 2012). 전술한 연구 중 Jacobsen et al.(2014)의 모형은 swash 대역에서의 충분히 발단된 경계층 형성 여부와 이로부터 파생되는 유효 전단력 산출과 관련된 논란으로부터 자유롭다는 점에서 가장 포괄적이고 범용성을 지니는 것으로 보이며, 이 연구에서 Jacobsen et al.(2014)은 사주의 형성과정과 계절적 이동을 성공적으로 모의한 바 있다. 그러나 수치모형의 불안정성을 단위 계산과정이 종료되는 시점에 filtering 과정을 인위적으로 적용하여 해결하였으나, 이로 인해 도입되는 수치적 소산이 지형변화에 미치는 영향을 가늠할 수 없다는 점과, 차용된 filtering 과정을 뒷받침 할 수 있는 물리적 근거를 찾기 힘들다는 점에서 전술한 filtering의 과다한 사용은 지양되어야 할 것으로 판단된다.
이상의 논의를 토대로 본 논문에서는 쇄파역에서의 표사 이송을 부유사와 소류사로 분류하고 가장 강건한 파랑모형인 Navier-Stokes 식, 부유사 해석을 위한 이송확산 방정식, 유동계와 연계된 소류사 이송을 포함한 물리기반 해빈 지형모형을 개발하고자 하며 이 과정에서 filtering은 배제된다. 2장에서는 본 논문에서 다루는 삼차원 물리기반 해빈 지형모형을 기존의 연구와 차별화하기 위해 해빈 지형모형의 유도과정을 부유사, 소류사, 지형모형으로 나누어 정리하였으며, 이 과정에서 비교를 위해 현재 문헌에서 가장 빈번하게 언급되는 소류사 모형의 근간을 구성하는 Meyer-Peter and Müller(1948), Luque(1974), Wilson(1987), Hanes and Bowen(1985) 등의 소류사 모형 유도과정도 함께 살펴보며, 3장에서는 파랑모형을 정리하였으며, 4장에서는 수치결과를 다룬다.
2. 표사이송 모형
현재 가용한 물리기반 표사이송 모형의 대부분은 Shields Diagram에 기반 한다. Shields는 표사 초기 이송 여부는 저면에 작용하는 유체력과 표사 수중무게의 비인 Shields parameter에 의해 결정되며, Shields parameter가 0.05를 상회하는 경우 이송이 시작되는 것으로 보았다. Shields parameter θ를 기술하면 다음과 같다.
여기서 τb는 저면 전단응력, s는 표사의 비중, ρ는 해수 밀도, g와 d는 중력 가속도와 표사직경을 각각 나타낸다.
2.1 부유사
부유사 이송농도는 이송-확산 방정식에 기반 하여 산출되며, 이를 기술하면 다음과 같다.
여기서 c는 단위체적당 부유사 농도, wf와 u는 각각 표사 침강속도와 유속 벡터를 나타낸다. γ는 VOF 법에서 자유수면을 추적하기 위해 도입된 지표로, 1에 가까울수록 액체 상태, 0에 가까울수록 기체 상태를 나타내며 본 논문에서는 자유수면의 위치를 γ = 0.5로 정의하였다. 식(2)에서 ν와 νt는 각각 동점성계수와 와동점성계수를 나타내며, 표사가 공기 중으로 부유되었을 때 바로 회귀할 수 있도록 침강속도 wf에 의한 질량 이송항에는 VOF 계수 γ를 생략하였다.
2.1 부유사 저면 경계 값 cb
표사이송에 관한 첫 이론적 성과는 Einstein(1950)에 의해 이루어졌으며, 이 연구에서 Einstein(1950)은 표사 이송에 내재된 불확정성을 인지하고 확률을 활용하여 자연계에서 관측되는 표사 거동과 부분적으로 일치하는 성과를 이루어 낸 바 있다. 이 후 Bagnold(1954)는 Shields parameter가 임계치를 상회하는 경우에는 저면에 있는 전 표사 층이 쇄굴 되는 것으로 해석하는 Einstein(1950) 모형의 모순을 지적하고, 임계치를 상회하는 경우에도 저면에 작용하는 전단응력 중 일 부분은 표사간의 충돌로 부동 표사층으로 전달되는 것으로 이해하였다. 이어 이러한 가설을 일련의 정교한 실험을 통해 확인한 바 있다[Fig. 2 참조].
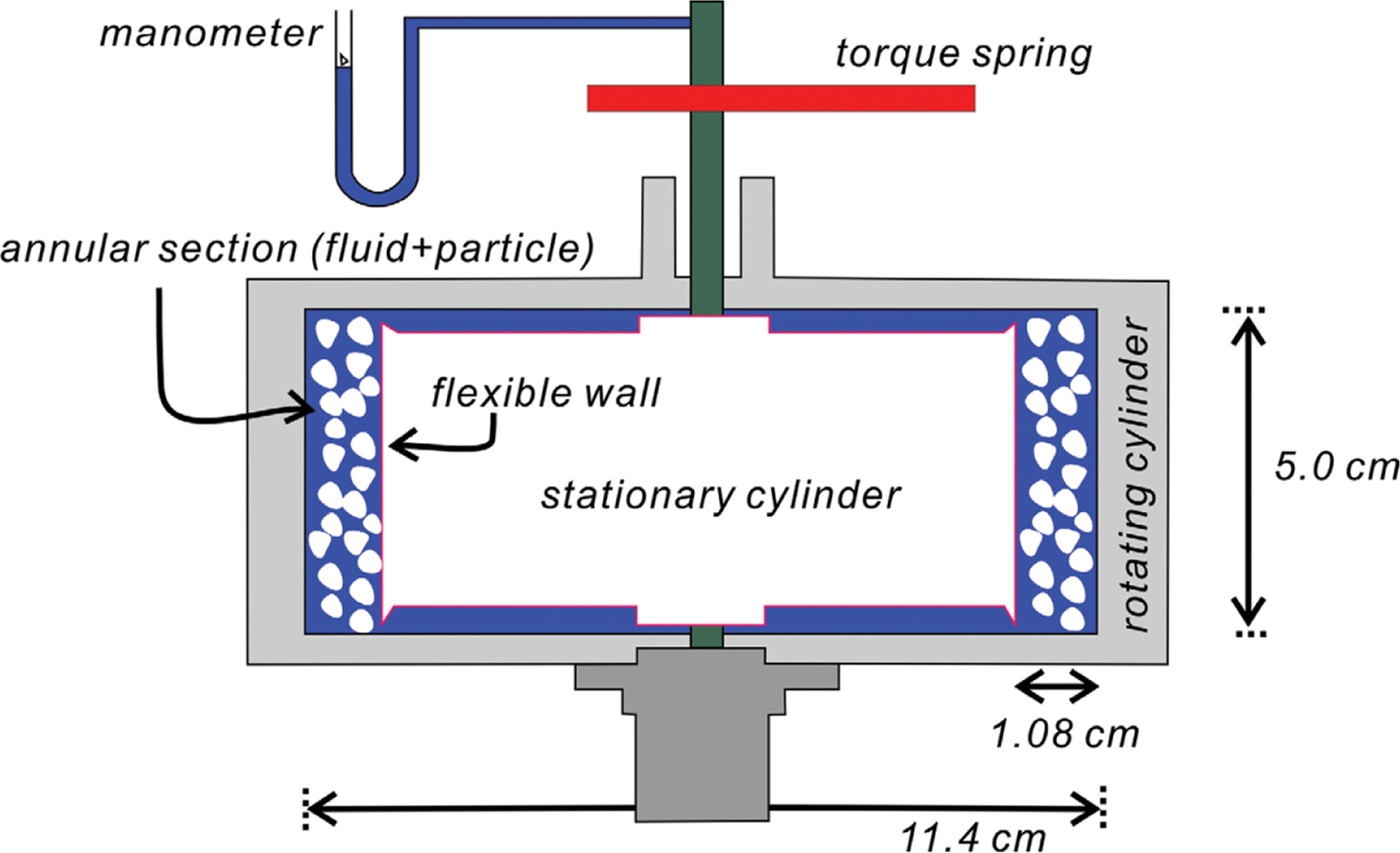
Experimental apparatus used by Bagnold (1954) to measure the shear and normal forces in a sheared suspension.
Bagnold(1954)가 실험 과정에서 관측한 저면 표사층으로 전달되는 전단응력 τG과 수직응력 σG은 다음과 같이 정의되는 무차원 수인 NB과 G로 기술될 수 있으며,
여기서 λ는 Bagnold(1954)가 소개한 저면에서의 선형 표사농도를 나타내며 표사 농도가 증가하면 표사간의 이격거리는 감소하므로 농도는 이격거리의 역에 비례하는 편의성을 취하기 위해 도입된 물리량이다.
유체력에 의해 n개의 표사입자가 소류사 형태로 이송된다면 저면에 작용하는 순간 전단응력 τ'는 다음과 같이 기술될 수 있으며[Fig. 3 참조],
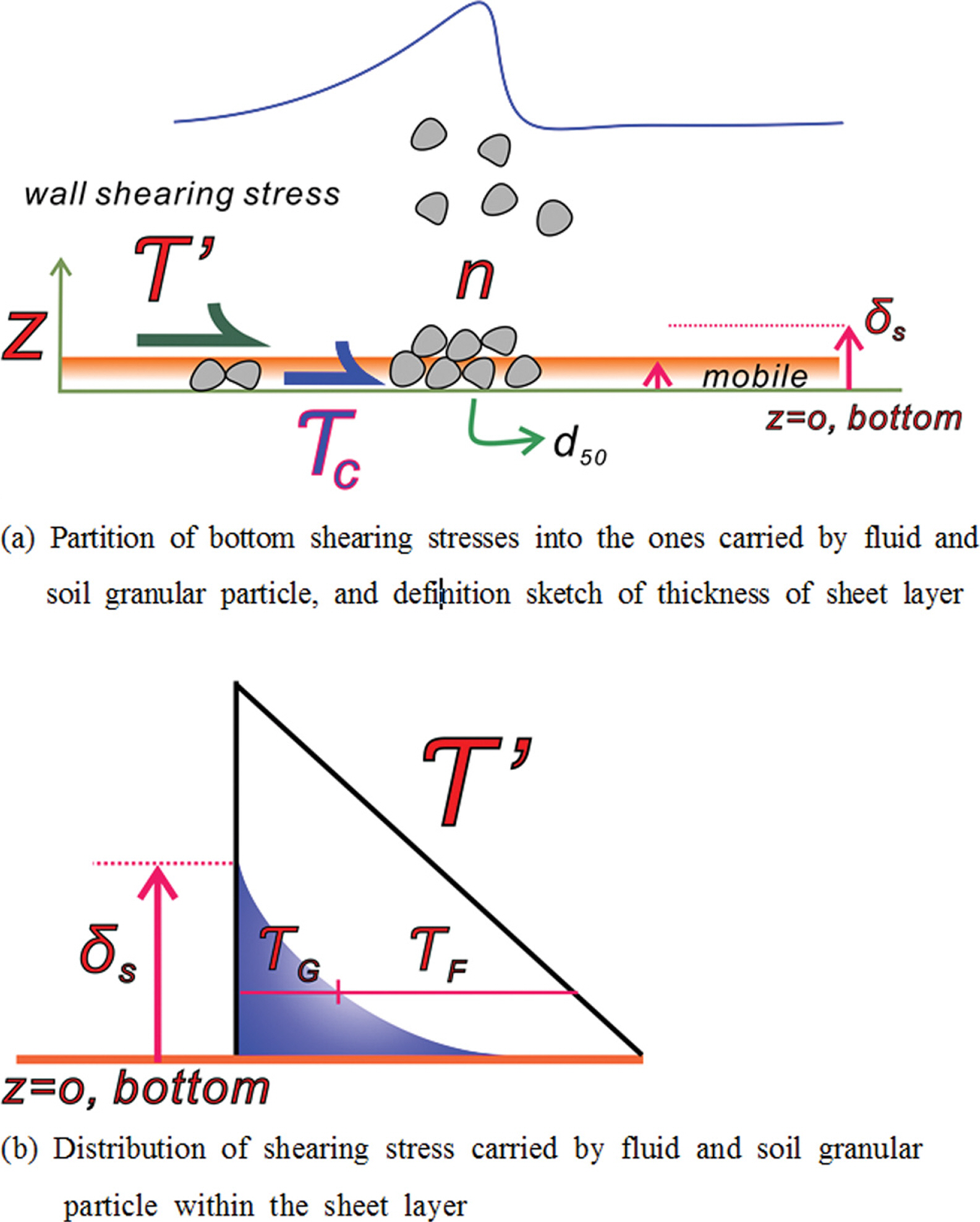
Partition of bottom shearing stresses into the ones carried by fluid and soil granular particle, respectively, and a distribution of shearing stress.
여기서 τF는 유체를 통해 부동 표사층에 작용하는 전단응력, FD는 소류사 형태로 이송되는 표사에 작용하는 유체 항력으로 다음과 같이 기술될 수 있다.
수중무게에 비례하는 저면 마찰력을 중심으로 기술하는 경우, FD는 다음과 같이 정의될 수 있다.
식(6), (7)에서 CD는 유체 항력계수를 나타내며, μd는 운동마찰계수를 나타내며 0.6의 값을 지닌다.
유체를 통해 부동 표사층으로 전달되는 전단응력 τF는 소류사로부터의 반력으로 임계 전단응력을 상회할 수는 없음으로 임계 전단응력 τc으로 근사할 수 있다[Luque, 1974]. 이 경우 저면 전단응력 관계식은 다음과 같이 전환된다[Fig. 3 참조].
식(8)의 양변을 ρg(s − 1)d로 나누어 정규화하면 다음과 같은 관계식을 얻을 수 있으며,
단위면적당 표사 수는 1/d2라는 것을 상기하면 nd2는 저면 표사가 부유사 형태로 이송되는 확률 pEF을 의미하므로 다음과 같은 관계식을 얻을 수 있다.
전단응력이 비교적 큰 경우 pEF가 over shooting하는 문제를 해결하기 위해 미세한 조정을 거쳐 저면 표사가 부유사 형태로 이송되는 확률 pEF는 다음과 같이 정의 될 수 있다.
빠른 유속으로 유체력이 증가하는 경우 표사는 소류사외에 부유된 상태로 이송되는 표사가 출현하며, 이 경우 저면 전단응력 τ'은 다음과 같이 수정되며
여기서 τG는 저면표사가 부유하는 과정에 사용된 전단응력을 의미하며 Bagnold(1954) 모형을 차용하는 경우 다음과 같이 기술될 수 있다.
저면 인근 경계층에서 유속이 대수분포를 추종하다고 가정하면 유속 구배는 다음과 같이 근사할 수 있으며
여기서 κ는 von Karman의 우주상수를 나타내며 0.4의 값을 지닌다. 대수분포를 추종하는 영역은 제한적이므로 식(14)에서 저면으로부터의 이격거리 z는 다음과 같이 근사할 수 있으며
α1는 O(1)의 값을 지닌다. 식(13), (14), (15)을 식(12)에 대입하고 정리하면 다음과 같은 관계식을 얻을 수 있다.
상기 식으로부터 저면에서의 순간 선형 표사농도 λb는 다음과 같이 정의되며
, 식(17)으로부터 본 논문에서 사용되는 순간 저면 체적 표사농도 cb(θ')는 다음과 같이 기술될 수 있으며[Fredsoe and Deigaard, 1992],
여기서 co는 최대 부유사 농도를 나타내며 본 논문에서는 0.35의 값을 취하였다.
그러나 식(18)로부터 산출된 cb 값은 흐름이 감소하는 경우 빠르게 0으로 수렴된다. 이처럼 저면 부유사 농도가 상층부에서의 값보다 작은 경우 일종의 확산 과정[E = − (ν + νt)∂c/∂n]으로 해석되는 부유사 도약방향이 역전되어 침강되는 양이 과다하게 평가될 수 있다[Fig. 4 참조]. 이러한 오류를 방지하기 위해 다음과 같이 강제하였다.
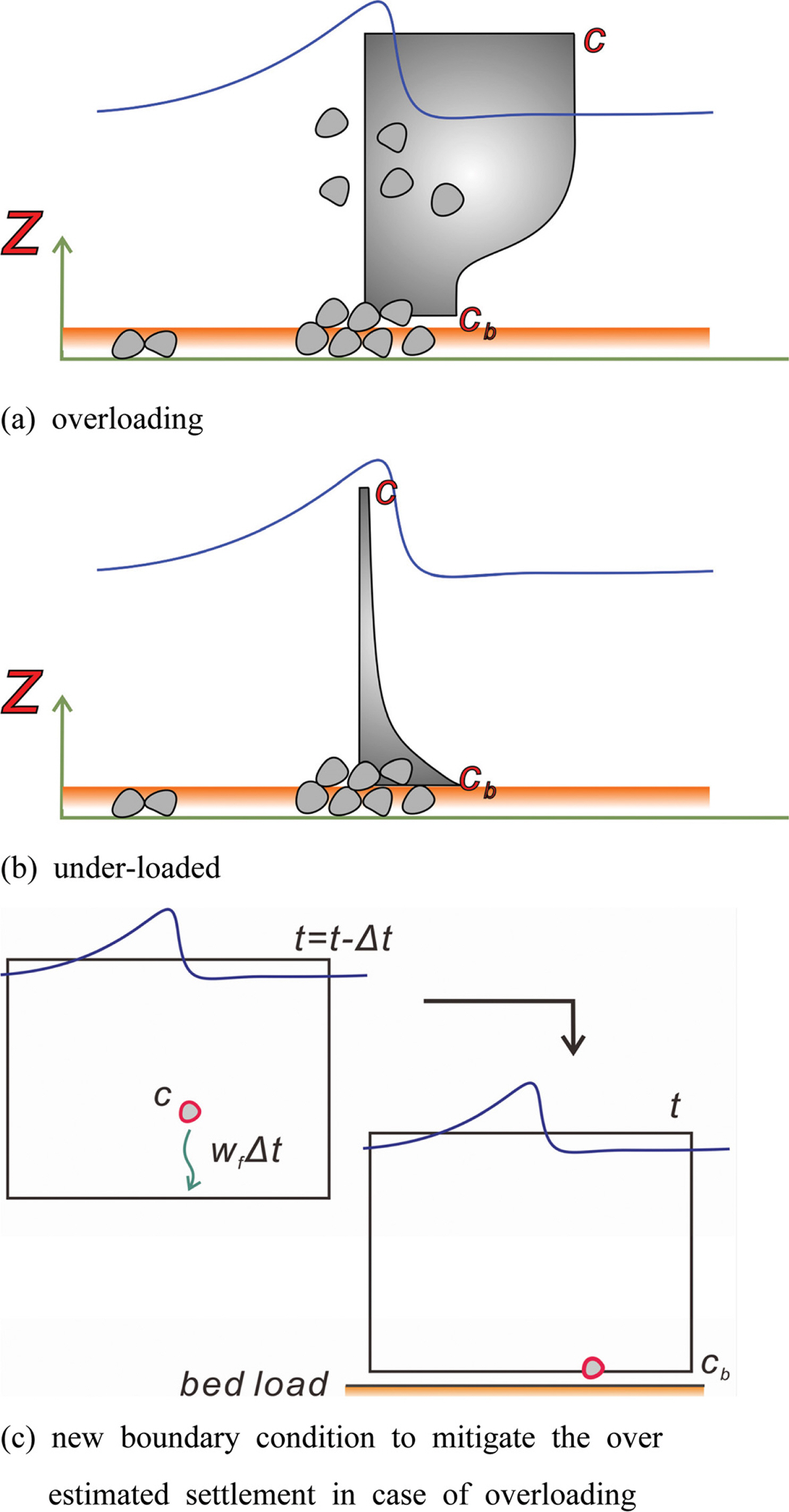
Definition sketch of boundary condition for suspended sediment concentration [modified from Jacobsen et al. (2014)].
여기서 cb(θ')는 식(18)로 정의되며, c(wfΔt, t − Δt)는 한 단계 이전에 모의된 수치결과에서 저면과 마주하고 있는 상층부 격자점에서의 부유사 농도를 나타낸다[Fig. 4 참조]. 따라서 식(19)는 cb 값이 0으로 수렴하는 경우[overloading, Fig. 4(a) 참조], cb 값을 이전 구간[t − Δt] 수치결과에서 저면 바로 윗부분 격자에서의 부유사농도로 치환시켜주는 역할을 한다. 이렇게 함으로써 흐름이 느린 경우 저면에서 도약하는 부유사량은 영으로 치환되어 과다하게 평가되기 마련인 침강되는 양을 제어할 수 있다. 그러나 상층부에서의 cb 값이 저면 보다 큰 경우[under loaded, Fig. 4(b) 참조], 물리기반 모형인 식(18)로 산출된 cb 값이 경계치로 활용되어 보다 설득력 있는 부유사 거동 기술이 가능하다.
2.2 소류사
본 논문에서 다루는 삼차원 물리기반 해빈 지형모형을 기존의 연구와 차별화하기 위해서는 현제 문헌에서 가장 빈번하게 언급되는 소류사 모형의 근간을 구성하는 Meyer-Peter and Müller(1948), Luque(1974), Wilson(1987), Hanes and Bowen(1985) 등의 소류사 모형 유도과정을 살펴볼 필요가 있으며 본 절에서는 이를 정리하였다. 또한 비교를 위해 본 논문에서 다루는 삼차원 물리기반 해빈 지형모형의 유도과정을 소류사 이송속도와 이송률로 구분하여 함께 다룬다.
2.2.1 소류사에 관한 기존의 연구
A. Luque(1974), Meyer-Peter and Müller(1948)
소류사 해석에서 가장 큰 어려움은 sheet layer에서의 소류사 이송속도와 농도 산출 과정에서 발생한다. 이러한 어려움을 비껴가기 위해 기존의 연구에서는 난류특성상 실시간으로 요동하는 유속 대신 시간 평균 유속에 기대어 표사에 작용하는 항력을 산출하여 왔다. 이와 유사한 해석방법은 소류사 이송률 산출과정과 저면 대표유속으로 마찰속도의 정수배[αU'f]로 취하려는 연구에서도 찾아볼 수 있다.
표사 초기 이동시 유체 항력과 마찰력이 균형을 이룬다는 가정을 수행하면 다음과 같은 관계식을 얻을 수 있다.
상기 식으로부터 소류사 이송속도 UB는 다음과 같이 기술될 수 있다.
여기서
Luque(1974)는 그가 수행한 일련의 실험에서 θo는 θo/2의 값을 지닌다는 것을 확인하고 소류사 이송속도를 다음과 같이 근사하고,
이어 소류사 이송률 qb를 다음과 같이 정의한 바 있다.
식(24)에서 pEF는 표사가 부유사 형태로 이송되는 확률로 식(11)에 기 정의된 바 있다. 식(11)을 식(24)에 대입하고 정규화하면 무차원 부유사 이송률 ΦB는 다음과 같이 기술될 수 있다.
동적 마찰계수 μd를 1.0으로 취하는 경우, 전술한 부유사 이송률 ΦB는 현재 가장 선호되는 Meyer-Peter and Müller(1948) 식에 근접하며, 비교를 위해 Meyer-Peter and Müller(1948) 식을 이기하면 다음과 같다.
B. Wilson(1987), Hanes and Bowen (1985)
Wilson(1987), Hanes and Bowen(1985)은 먼저 sheet layer 내에서 표사농도 c는 다음과 같이 선형 분포한다고 가정하고
이어 sheet layer 내에서 표사 무게는 표사충돌 등으로 부동표사층으로 전달된 힘 중 수직 성분에 의해 지탱되며, 따라서 이로부터 다음과 같은 관계식을 도출한 바 있다.
적분을 수행하면 상기 식은 다음과 같이 전환되며
, 이어 sheet layer 상단 δs[Fig. 3 참조]에서 표사층에 전달되는 수직응력은 미미하다는 가정[σG, δ ≈ 0]을 수행하고, 다음과 같이 정의되는 Bagnold(1954) 관계식을 활용하여
Sheet layer 내 전단응력으로 기술하는 경우 식(29)은 다음과 같이 전환된다.
식(30), (31)에서 φ는 마찰 각도를 나타내며, 상기 식에 선형 표사 농도분포를 대입하고 정리하면 sheet layer 내 유체력 τF는 다음과 같이 포물형 분포를 추종한다는 것을 알 수 있다.
또한 sheet layer 내에 혼합거리 l 난류모형을 사용하면 sheet layer내 유체 전단력은 다음과 같이 기술될 수 있으며,
식(32)과 (33)로부터 sheet layer 내 유속을 기술하는 상미분방정식을 얻을 수 있으며 이를 기술하면 다음과 같다.
전술한 상미분방정식에 대한 근사해로부터 sheet layer 내 소류사 이송속도 U와 이송률 qb는 각각 다음과 같이 기술될 수 있다.
비교를 위해 무차원화하는 경우 무차원 소류사 이송률 ΦB는 다음과 같이 기술될 수 있다.
C. 기존 소류사 모형의 한계와 새로운 소류사 모형의 제안
이상의 논의에서 알 수 있듯, 기존의 소류사 이송률 ΦB 모형 중 Luque(1974), Meyer-Peter and Müller(1948) 식은 초기 소류사 이송, Wilson(2012) 식은 sheet layer를 대상으로 한다. 따라서 각 소류사 이송률 모형은 적용할 수 있는 Flow regime이 특정되며, sheet layer 내에서의 역동적인 유동계를 모의하기에는 차용된 난류모형이 상당히 부족하다는 것을 알 수 있다. 또한 표사 이송이 가장 활발한 쇄파역에서 파랑은 saw tooth처럼 왜도된 파형을 지니며, 따라서 이로 인해 결과 되는 왜곡 혹은 왜도된 저면 전단응력의 정확한 모의 여부는 표사이송모형의 정확성을 가름하는 인자로 판단된다. 그러나 기존 소류사 모형에서는 예외 없이 마찰계수 f, quadratic friction Law, 수심방향으로 평균된 유동계 정보를 활용하여 저면 전단응력이 산출되어 왔으며(Cho and Kang, 2017), 전술한 quadratic friction Law를 기술하면 다음과 같다.
저면 조도와 wave Reynolds NO.에 종속하는 것으로 추정되는 마찰 계수 f에 대한 정보는 Lab scale에서 수행된 수리모형실험에서 측적된 자료를 중심으로 추정되어 왔으며, 이 과정에서 활용된 대부분의 수리모형실험은 flat bottom, 정상 상태의 파동계를 대상으로 수행되었다. 그러나 쇄파역에서 관측되는 왜도 혹은 왜곡된 파동계의 경우 연안방향으로의 흐름 지속시간이 먼 바다 방향의 흐름보다 짧은 지속시간으로 인해 경계층이 충분히 발달되지 못한다. 따라서 전술한 사실을 상기하면 기존 소류사 모형으로 쇄파역에서 진행되는 표사이송을 기술하기에는 한계가 있다는 것을 알 수 있다.
본 논문에서 다루는 삼차원 유동 수치모의에서는 저면 인근 경계층에서의 유속이 정밀하게 모의될 수 있으며, 이렇게 수치모의된 유동계 정보로부터 저면 전단응력은 다음과 같이 산출될 수 있다.
이는 기존에 사용되던 마찰계수 f로부터 자유로우며 왜도 혹은 왜곡된 저면 전단응력의 모의가 가능하며, 식(39)에서 νt는 와점성계수로 본 논문에서는 k-ε 모형을 차용하여 산출된다.
2.2.2 새로운 소류사 모형
A. 소류사 이송속도
본 논문에서 다루는 삼차원 유동 수치모의에서는 저면 인근 경계층에서의 유속이 정밀하게 모의될 수 있다. 따라서 모의된 유속으로부터 소류사 이송속도는 간단한 평형방정식으로부터 산출이 가능하며 이해를 돕기 위해 평형방정식의 유도과정을 살펴보면 다음과 같다.
소류사 이송 속도 ub는 저면 인근 접선방향 유속성분 unw, τ에 의해 결정되며, unw, τ는 저면 인근 유속 unw와 저면 외향 법선벡터 N과의 외적에 의해 다음과 같이 정의된다[Fig. 4 참조].
표사입자에 작용하는 외력으로는 중력 w, 항력 FD, 마찰력 ff 등이 있으며, ub는 전술한 외력이 균형을 이루고 있다고 추정하면 해석이 가능하다. 표사에 작용하는 중력은 기술하면 다음과 같고
, 저면과 나란한 방향으로 작용하는 접선방향 성분 wτ은 식(40)와 유사하게 외적으로 기술이 가능하며 이를 기술하면 다음과 같다[Fig. 5 참조].
표사가 ub라는 속도로 이송하면 이와 반대방향으로 작용하는 마찰력이 형성되며, 이를 운동마찰계수와 수직반력으로 기술하면 다음과 같다.
여기서 − ub/|ub|는 마찰력의 작용방향이 ub의 방향과 반대라는 것을 나타낸다.
마지막으로 표사입자에 대한 항력 fD은 다음과 같이 기술될 수 있으며,
여기서 ur은 상대속도를 나타내며 unw, τ − ub로 정의된다. cs는 항력과 물에 잠긴 표사입자의 부력에 의한 중량감소를 설명해 주는 계수이며 Luque(1974)에 의한 실험에 의해 다음과 같이 기술될 수 있다.
식(42), (43), (44), (45)로부터 소류사 평균 이송속도 ub는 다음과 같이 기술되는 평형방정식에 의해 산출될 수 있다.
B. 소류사 이송률
수치 모의된 유속계 정보로부터 저면전단응력 τb가, 식(46)에 기술된 평형방정식으로부터 소류사 이송속도 ub가 산출된 경우 소류사 이송량 qb는 다음과 같이 산출될 수 있으며
여기서 d는 표사직경, pEF는 표사이송확률을 나타내며 식(11)에 기 정의된 바 있다.
2.3 Morphology Model
소류사 순 이송량과 부유사 형태의 침·퇴적량 사이에 균형을 이루지 못하는 경우 저면에는 변화가 발생하며, Fig. 6에 도시된 단위 통제용적에 표사수지 개념을 적용하는 경우 Morphology Model을 유도 할 수 있다. 표사 수지 개념을 적용하여 얻은 Morphology Model를 기술하면 다음과 같다.
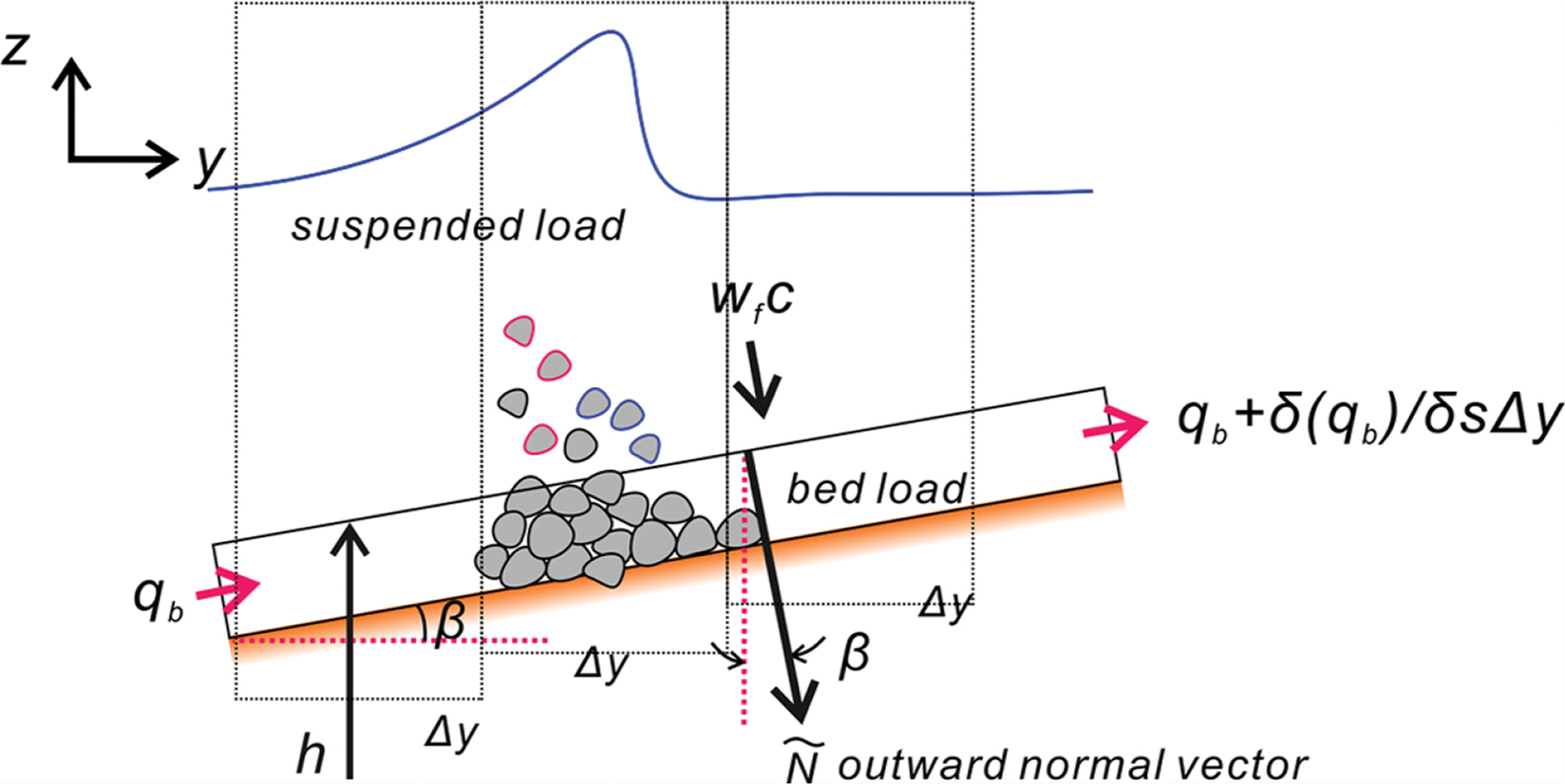
Schematic sketch of morphology change of the sea bed of slope α due to the erosion, and deposition process of suspended load, and the net flux of bed load [modified from Jacobsen et al. (2014)].
상기 식은 Exner 방정식 형태로, 여기서 ed는 공극률, qb는 2.2절에서 소개한 소류사 이송률, E와 D는 각각 부유사에 의한 침식과 침강속도로 저면으로 회귀하는 퇴적량을 각각 나타낸다.
식(48)에서 E는 다음과 같이 산출될 수 있으며
여기서 ν와 νt는 기 정의된 점성계수와 와점성계수를 각각 나타내며, 음의 부호는 본 논문에서 사용한 외향법선 벡터와 침식이 진행되는 방향의 차이를 보정하기 위해 도입하였다. n은 저면에서의 단위 외향 법선벡터를 나타내며, 따라서 외향법선벡터 N은 다음과 같이 정의된다.
여기서 |N|은 경계 인근 육면체로 구성된 셀에서 저면과 접하는 면의 면적을 나타낸다. 식(49)에서 D는 표사 침강속도 wf와 유속 u의 합을 저면법선벡터 N에 투영하여 산출되며 이를 내적을 활용하여 기술하면 다음과 같으며,
여기서 cb는 기 정의된 저면에서의 표사농도이다.
qb에 의한 Δt 동안의 연직방향으로의 저면높이의 변화 Δhb는 다음과 같이 기술될 수 있으며,
여기서 n과 eg는 각각 저면의 바깥쪽으로 향하는 단위법선벡터와 아랫방향으로 향하는 연직방향 단위벡터이다. Δt는 시간격자의 사이시간을 나타낸다. Δt 동안 경사진 저면을 따라 이송되는 소류사의 순 이송량은 ∇ · qbΔt/1 − ed이므로 이 식을 |n · eg|로 나눠주는 경우 연직방향에서의 높이변화 Δhb로 전환된다.
3. 수치모형
수치모의는 OpenFoam 기반 Tool box인 IHFoam을 사용하여 수행되며(Losada et al., 2008), IHFoam에서 파랑모형은 RANS(Reynolds Averaged Navier-Stokes equation)와 질량 보존식으로 구성되며, 자유수면은 VOF[Volume Of Fraction] 법을 활용하여 추적된다. 난류모형으로는 k-ε 모델을 차용하였다.
IHFoam(Losada et al., 2008) 에서 사용되는 파랑모형인 RANS, 연속 방정식을 기술하면 다음과 같다.
식(53), (54)에서 U는 속도벡터, g는 중력가속도벡터, X는 위치벡터를 각각 나타낸다. μeff는 μ + ρνturb로서 동점성계수, p*는 유사 동압력을 각각 나타낸다.
이상 유체를 해석하기 위한 VOF 식을 기술하면 다음과 같으며,
여기서 γ는 단위격자 체적에서 물이 차지하는 비율을 나타내는 VOF 계수로 2절에서 기 설명한 바 있다.
4. 수치결과
본 논문에서 제시된 지형 모형을 검증하기 위해, 경사가 1/m인 단조 해안에서의 천수과정, plunging 형태의 쇄파, 처오름, 처내림 과정을 수치 모의하였다. 파형은 거친 해역을 고려하여 Korteweg-de Vries 식의 해석해로 정의되는 Cnoidal wave로 취하였으며, Cnoidal wave를 기술하면 다음과 같다.
여기서 ζ는 해수면 변위, H는 파고, Cn은 Jacobi elliptic function, c는 파속, L은 파장, T는 주기, M은 0과 1 사이의 값을 지니는 elliptic parameter를 각각 나타낸다. KM은 제1종 타원적분, EM은 제2종 타원적분을 각각 나타내며, KM과 EM은 M 값에 종속한다. Cnoidal wave 파형은 M이 0에 수렴하면 Stokes I 파형에, M이 1에 수렴하면 solitary wave 파형에 수렴한다. Cnoidal wave에서의 유속은 다음과 같이 기술될 수 있으며
여기서 ζx, ζxx, ζxxx는 x에 대한 자유수면의 1차, 2차, 3차 도함수,
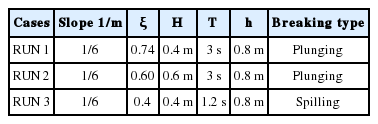
표사 물성치는 우리나라 해빈 특성을 고려하여 s = 1.4와 d = 0.02mm로 취하였다. Fig. 7에 도시한 계산영역은 250,000여개의 격자를 이용하여 이산화하였다. Breaker type이 표사이송에 미치는 영향을 파악하기 위해 파고와 주기에 변화를 주어 가장 역동적인 Plunging breaker뿐만 아니라 Spilling breaker를 대상으로 총 세 번의 수치모의를 수행하였으며, Table 1에는 수치모의에 사용된 해빈 경사, 파랑조건, Iribarren NO. ξ를 수록하였다.
Fig. 8에는 수치 모의시 Gauge No. 2에서 관측된 수면변위와 저면 전단응력을 도시하였다. 우리의 예상대로 비선형 천수과정에서의 wave-wave interaction으로 생성된 고차 조화성분으로 인해 왜곡되고 왜도된 파형이 관측되는 것을 알 수 있다. Fig. 9에는 Gauge No. 1, 2, 3에서 관측된 진행방향 유속의 연직분포를 도시하였다. 한 주기를 총 아홉 개의 frame으로 나누어 위상별 유속 변화가 드러나도록 구성하였으며, 비교를 위해 주기 평균 유속도 함께 도시하였다. Gauge No. 1, 2, 3에서 모두 외해 방향 유속[undertow]이 우세하나, 천수 초기단계인 Gauge No. 1, 2의 경우 수면인근에서는 해안 방향 흐름인 Stokes drift가 우월하다는 것을 확인할 수 있다. 최대 저류 유속은 Gauge No. 3의 경우 0.05 m/s, Gauge No. 2의 경우 0.072 m/s로 증가하나, Gauge No. 1의 경우 0.05 m/s로 다시 감소하며 최대 저류의 발생위치는 수심이 증가함에 따라 점차 저면 인근에서 수면 인근으로 이동되는 것을 알 수 있다.
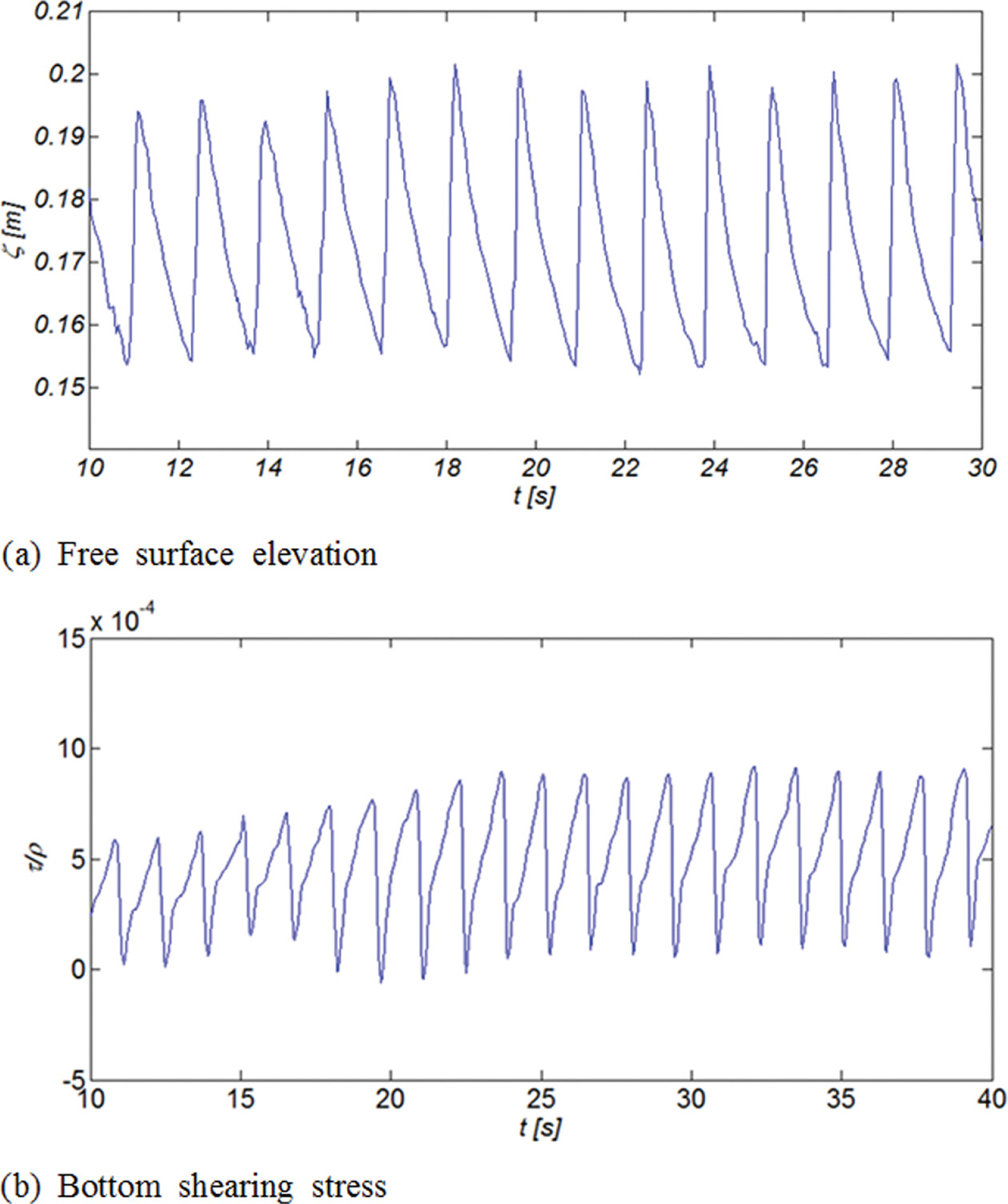
Sampled time series of the numerically simulated free surface elevation and the bottom shearing stress at Gauge No. 1 [RUN 2].
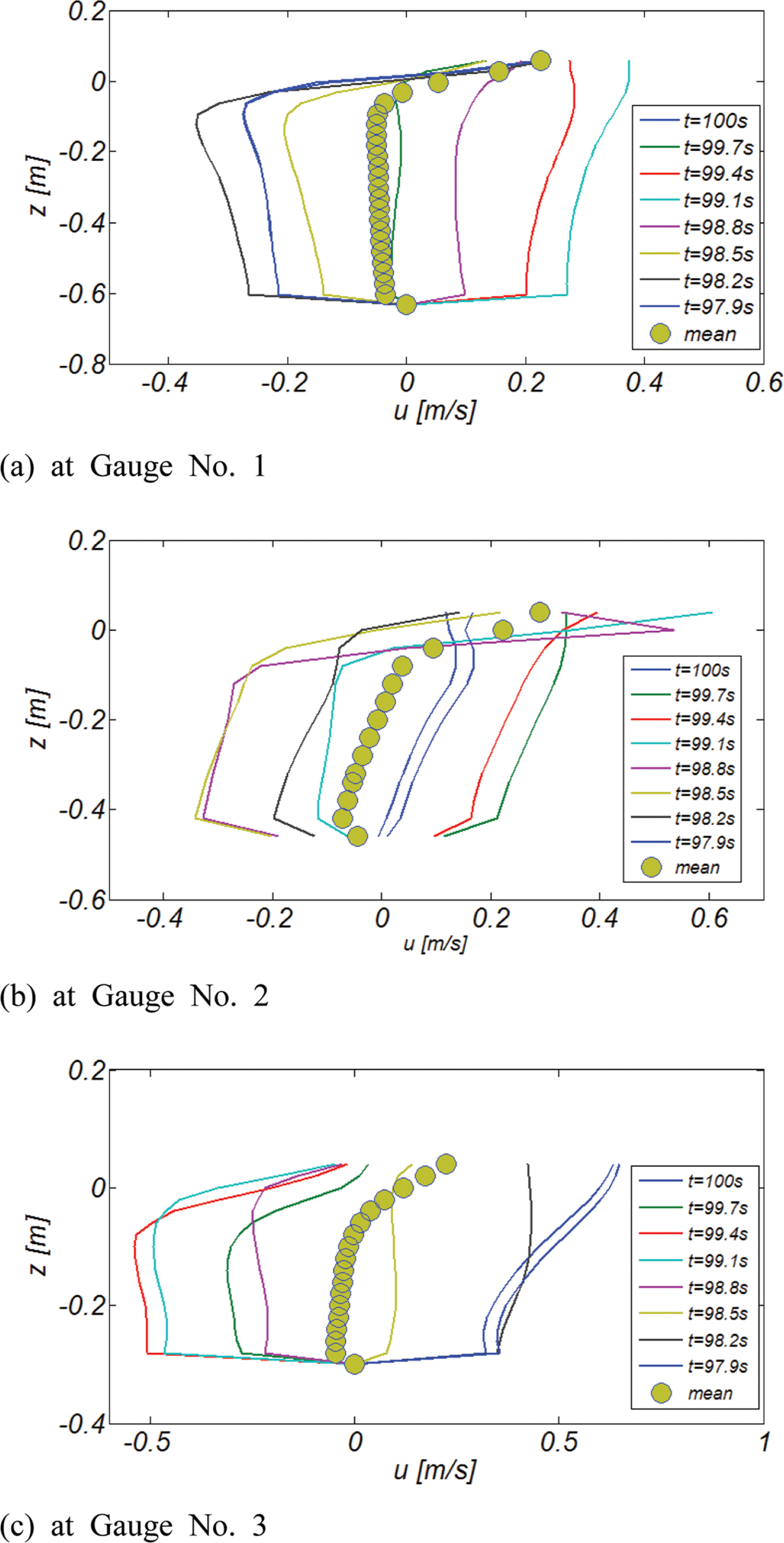
Temporal variation of the vertical profiles of horizontal velocity at Gauge No. 1, 2, and 3 [RUN 2].
쇄파선 인근에 거치된 Gauge No. 3의 경우, 저면 인근 경계층에서는 해안 방향의 흐름인 boundary layer streaming이, 중간 수역에서는 저류가, 자유수면 인근에서는 해안 방향 흐름인 Stokes drift가 여전히 지배적이나, 저면 경계층에서의 boundary layer streaming의 영향으로 저면 흐름과 중간 수역에서의 흐름 사이에 적지 않은 위상차가 존재 하는 것을 알 수 있다.
이상의 논의를 정리하면, 쇄파역 전까지의 초기 천수과정에서 표사이송과 관련된 가장 지배적인 기작은 저류와 파형의 왜도라는 것을 확인할 수 있으며, 이러한 시각은 현재 문헌에서 가장 빈번하게 언급되는 횡단 표사량 모형 중의 하나인 Bailard(1981) 모형에서도 공유된다.
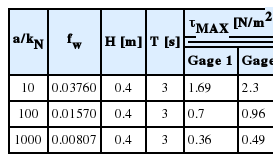
Fig. 10에는 수치 모의된 부유사 농도, 난류 운동에너지 snapshot과 저면 전단응력을 순차적으로 도시하였다. t = 30 s와 t = 100 s에서의 부유사 농도를 비교하면 t = 100 s에서의 부유사 농도가 전 수역에서 증가한 것을 알 수 있으며 [Fig. 10(h) 참조], 이러한 현상은 일차 쇄파와 후행하는 이차 쇄파로 인해 저면에서 부유된 표사가 저류에 의해 먼 바다 방향으로 이송, 확산되어 발생하는 것으로 판단된다. 최대전단응력은 이차 쇄파 시 발생하며 그 최대치는 τmax = 40 N/m2에 이르며, 쇄파 후 진행되는 up-rush 과정에서도 전단응력은 상대적으로 큰 값을 지니는 것으로 모의되었다[Fig. 10(e) 참조]. 이러한 수치는 saw tooth profile처럼 왜도 된 파형의 경우, 연안 방향 유속은 외해 방향 유속보다 큰 값을 지니며, 또한 상대적으로 짧은 시간에 급격히 가속되어 경계층이 충분히 숙성될 만한 시간이 부족하고, 따라서 경계층의 두께는 상대적으로 얇으며 저면 전단응력은 큰 값을 지닌다는 Fredsoe and Deigaard(1992)의 연구를 상기하면 수용 가능해 보인다. Table 2에는 비교를 위해 Quadratic Friction Law와 마찰계수 f를 사용하여 산출된 저면 전단응력을 수록하였으며 산출과정은 Appendix A에 정리하였다. Table 2에서 알 수 있듯 Quadratic Friction Law와 마찰계수 f에 기초하여 산출된 저면 전단응력은 일정 수심부에서는 수치모의 결과에 상당히 근접하나 연안에서 가용한 해빈표사의 대부분이 공급되는 swash 대역에서는 과소하게 평가되는 것을 알 수 있다[Fig. 10 참조]. 최대 난류 운동에너지는 쇄파가 시작되는 파마루 인근 수역과 이차쇄파를 수반하는 처오름 과정에서 관측되었다[Fig. 10(e) 참조].
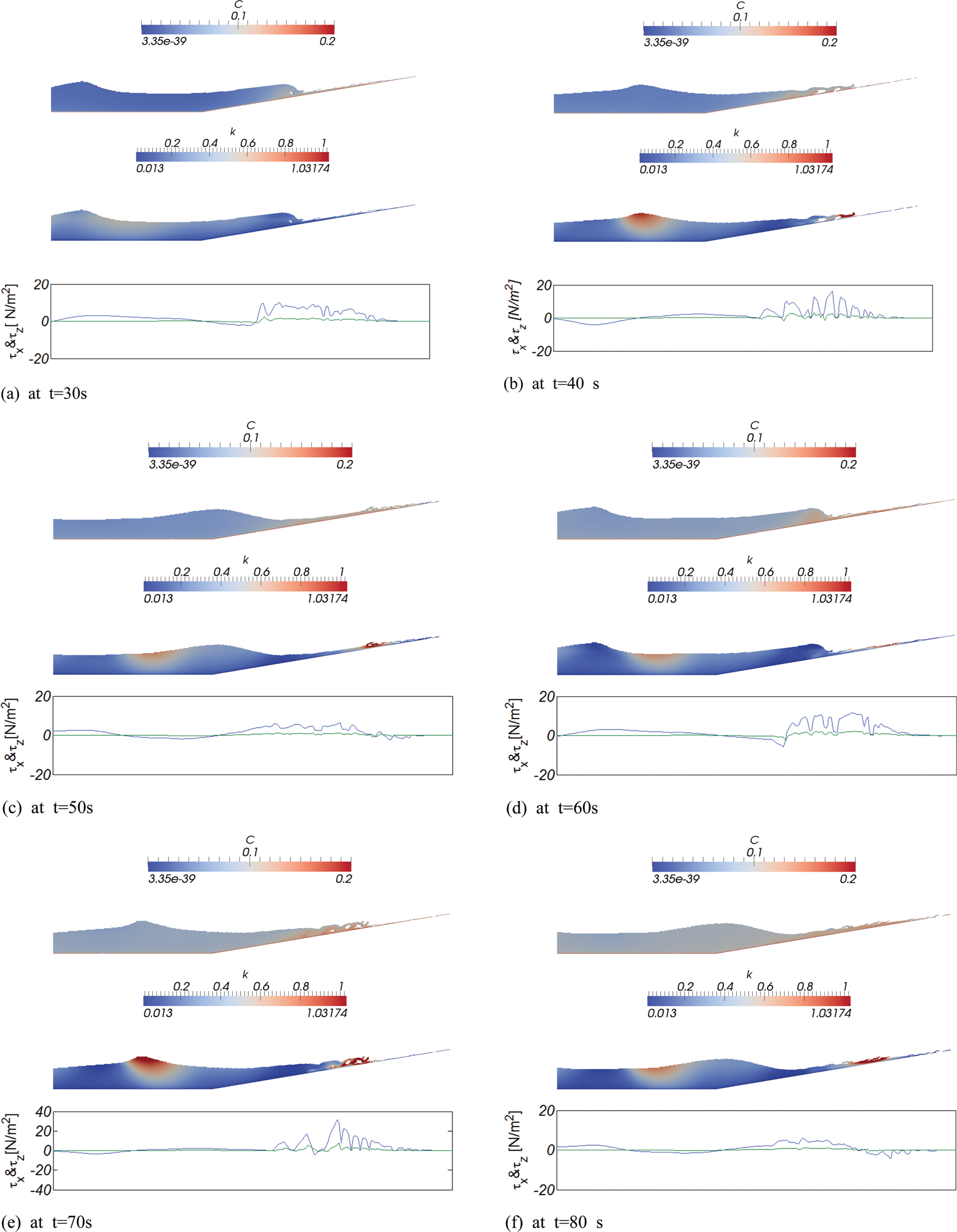
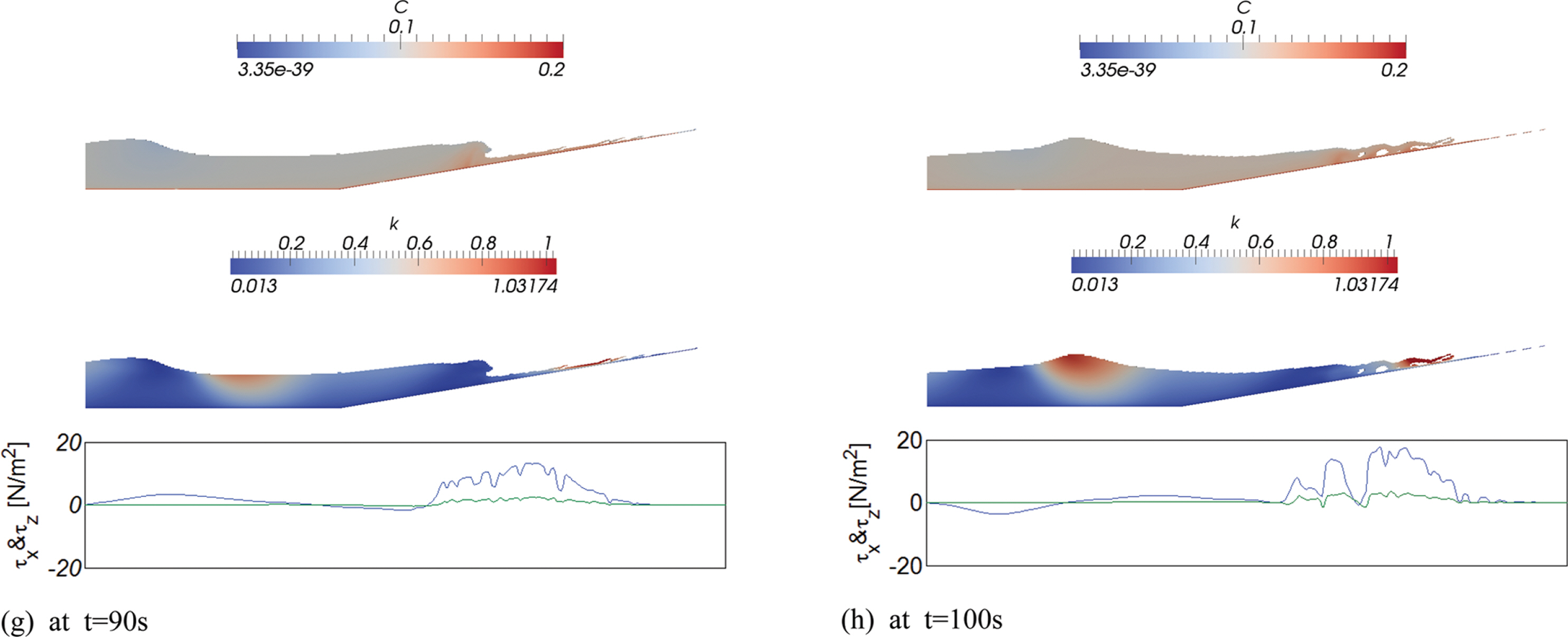
Sequential snapshots of numerically simulated suspended sediment concentration, turbulence kinetic energy [unit: m2s−2], bottom shearing stress as the plunging breaker proceeds toward the shore [Run 2] [
 : τx,
: τx,
 : τz].
: τz].
Fig. 11에는 해안이 파랑에 100초 동안 노출된 이 후 RUN 1, 2에서 수치 모의된 부유사 농도 분포를 도시하였다. Run 1의 경우보다 보다 역동적인 쇄파가 진행되는 Run 2에서 표사 이송이 활발하며, Run 2의 경우에서 부유사 농도가 전 수역에서 상대적으로 큰 값을 지니는 것을 알 수 있다.
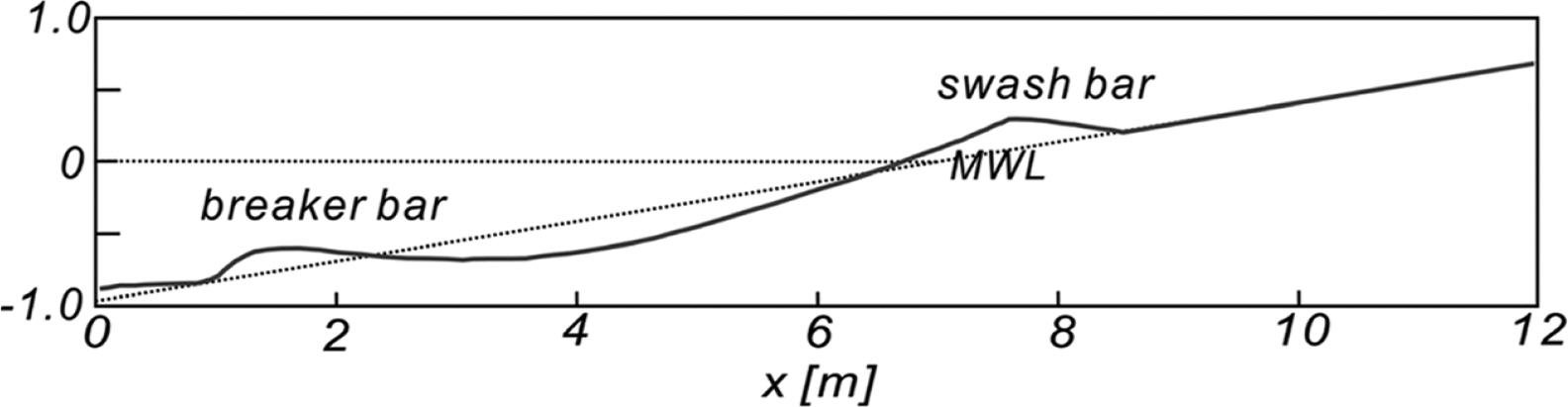
Fig. 12에는 파랑에 100초 동안 노출된 이후 지형을 도시하였다. Run 1, 2, 3에서 전빈에서 진행되는 쇄파로 부유되고 침식된 표사가 up-rush에 의해 후빈으로 이동되어 형성되는 swash bar와 up-rush 정점에서 방향을 바꾸어 먼 바다 방향으로 진행되는 back-wash에 의해 쓸려간 표사가 backwash 흐름 강도가 약해지면서 퇴적하여 형성되는 breaker bar가 성공적으로 모의되는 것을 확인할 수 있다. 또한 우리의 예상대로 spilling breaker[RUN3]보다 plunging breaker[Run 1, 2]에서 전빈에서의 침식이 활발하게 진행되는 것을 알 수 있다. Breaker bar의 생성위치는 파고가 클수록 먼 바다 방향으로 이동하는 것을 확인할 수 있으며, Fig. 13에는 비교를 위해 Dodd et al.(2008)이 수행한 실험에서 관측된 지형 변화를 수록하였다. 본 논문에서 관측되는 swash bar와 breaker bar와 유사한 지형변화를 관측할 수 있다.
Morphology change after being exposed to wave attack of T = 5 s and Ho = 0.25 m for 5,000 s [from Dodd et al., (2008)].
여기서 한 가지 흥미로운 현상은 수치모의 시 재현이 상당히 어려운 것으로 알려진 sand wave가 Run 1, 2의 일정 수심부에서 관측되는 것으로 이는 상당한 논의가 필요해 보이며 논의를 전개 위해 수치모의 과정에서 관측되는 sand wave의 특징과 연관된 생성기작을 정리하면 다음과 같다:
A. Run 1, 2에서 주기는 동일하게 유지되나, 결과 된 sand wave의 파장은 파고가 상대적으로 큰 Run 2에서 다소 짧아졌으며, 먼 바다 방향으로 미세하게 이동하는 것을 알 수 있다.
B. 파고가 가장 큰 Run 2의 경우 sand wave의 먼 바다 방향으로의 왜도는 증가하며, breaker bar의 규모는 감소하나 swash bar의 규모는 증가한다.
C. 전술한 sand wave의 왜도 증가는 상대적으로 큰 값을 지니는 연안 방향 유속이 짧은 시간 안에 급격히 가속되는 가속도의 횡단 방향으로의 비대칭성에 기인하는 것으로 추정되며 이를 단계별로 정리하면 다음과 같다.
D. 본 논문에서 사용한 Cnoidal wave의 경우 고차 성분은 bound mode로 해석되며 이 경우 파형의 왜도는 상당한 값을 지닌다.
E. 전술한 왜도로 인해, 파고가 증가한 Run 2의 경우, 연안 방향으로의 유속은 먼 바다 방향으로의 유속보다 크며, 흐름이 지속되는 기간은 먼 바다 방향이 상대적으로 길다.
F. 따라서 상대적으로 큰 연안 방향 유속은 짧은 시간 안에 급격히 가속되는 반면 먼 바다 방향으로의 흐름은 느리게 가속된다.
G. 전술한 한 가속도의 횡단 방향으로의 비대칭성은 표사에 작용하는 유체력에도 그대로 반영되며 이는 sand wave의 down-wave side는 침식성 해빈의 경우처럼 구배가 완만하나, sand wave의 up-wave side는 퇴적성 해빈의 경우처럼 구배가 급하다는 사실에서 확인할 수 있다.
H. 파고가 가장 약한 Run 3의 경우 sand wave는 관측할 수 없다
I. 이러한 현상은 파고가 상대적으로 큰 Run 1, 2의 경우 bound mode의 Cnoidal wave의 고차 조화 성분으로 인해 증가한 파형 왜도와 boundary layer streaming에 의해 상당한 표사가 해안 방향으로 이송되나, 파고가 제일 작은 Run 3의 경우 전술한 표사 이송은 상대적으로 작아 발생하는 것으로 판단된다.
J. 이러한 추론의 근거는 파고가 가장 큰 Run 3의 경우 Run 3에 비해 일정 수심부 전 영역에서 침식이 균일하게 증가한다는 사실과, Run 3에서 swash bar의 규모가 가장 크다는 관측결과에서 찾을 수 있다.
K. Run 3의 경우 상당한 규모의 swash bar가 형성되며, 이로 인해 급해진 전빈경사로 반사율은 증가하는 것으로 보인다. 이는 전빈 전면 수역에 형성되는 정상파 배 [antinode]가 생성되는 위치의 미세한 변화로 이어지며, 이러한 변화로 인해 sand wave의 파장은 다소 짧아졌으며, 먼 바다 방향으로 미세하게 이동하는 것으로 보인다.
5. 결 론
기후변화와 난개발로 인해 준 평형 상태의 수환경이 훼손된 우리나라의 각 해안은 현재 상당한 침식이 진행되고 있다. 현재 이러한 기후변화에 대응하기 위해 이안제, 돌제, 인공곶, artificial reef, 잠제 등과 같은 강성구조물, 양빈과 같은 연성공법이 독자적으로 혹은 혼용되어 해안침식을 저감하려는 노력이 시도되고 있는 것으로 보인다. 그러나 양빈으로 침식이 우세한 연안 수환경이 준 평형상태로 복원되는 것은 아니며 주기적인 양빈을 필요로 한다. 따라서 자연 해빈에 가까운 수려한 해빈을 유지하기 위해서는 양빈 수행 전 해빈 침식율에 대한 정량적 평가가 선행되어야 할 것이다. 현재 우리나라에서는 전술한 해안선 변화에 대한 정량적 평가는 간단한 표사 수지 식과 Dean(2002)이 이야기 하는 equilibrium profile에 기초한 one-line model이 주류를 이루나, 전술한 모형은 쇄파역 사주 같은 지형 특성, 구조물 축조로 인해 발생하는 수환경 변화를 설명할 수 있는 물리적 장치가 결여되어 상당한 오류를 내포할 수 있다.
이러한 시각에서 본 논문에서는 쇄파역 사주 해역에서 진행되는 Stokes drift, Surface Roller에 의해 질량 이송, 저류 간의 국지적 균형과 구조물로 인한 수환경 변화를 기술할 수 있는 물리기반 해빈 지형모형이 제시되었다. 이 과정에서 현재 가용한 소류사 이송률 모형(Meyer-Peter and Müller, 1948; Wilson, 2012)의 유도과정을 살펴보았다. 그 결과 현재 가장 선호되는 Meyer-Peter and Müller(1948) 모형은 초기 소류사 이송, Wilson(2012) 모형은 sheet layer를 대상으로 유도되어, 각 소류사 이송률 모형은 적용할 수 있는 flow regime이 특정되며, sheet layer 내에서의 역동적인 유동계를 모의하기에는 차용된 난류모형이 상당히 부족하다는 것을 알 수 있었다.
또한 표사 이송이 가장 활발한 쇄파역에서 상당히 왜곡되고 왜도된 파형과 이로 인해 결과 되는 왜도된 저면 전단응력의 정확한 모의 여부가 표사이송모형의 정확성을 가름하는 인자로 판단하였다. 이러한 인식에 기초하여 동수역학 모형으로는 OpenFOAM에 기반한 wave tool box인 IHFOAM과 k-ε 난류모형에 기반하여 구성하였다. 이어 저면 전단응력은 기존에 선호되던 Quadratic Friction Law대신 와점성계수와 구배모형을 활용하여 산출하였다. Morphology 모형은 부유사를 대상으로 한 이송확산방정식, 소류사 이송이 반영된 표사 수지 개념으로부터 유도된 Exner 식으로 구성하였다. 표사 이송여부, 부유사 농도 저면 경계치, 소류사 이송률은 Shields Diagram, 삼차원 수치 모의된 유동계 정보로부터 직접 구한 저면 전단응력을 활용하여 결정하였다(Fredsoe and Deigaard, 1992).
이어 본 논문에서 제시된 지형 모형을 검증하기 위해, 경사가 1/6인 단조 해안에서의 천수과정, 쇄파과정, 이에 따른 저면 변화를 수치 모의하였다. 모의결과 비선형 천수과정에서 예상되는 왜곡되고 왜도된 저면 전단응력이 비교적 정확히 모의되었으며, 전빈에서 진행되는 쇄파로 부유되고 침식된 표사가 up-rush에 의해 후빈으로 이동되어 형성되는 swash bar와 up-rush 정점에서 방향을 바꾸어 먼 바다 방향으로 진행되는 back-wash에 의해 쓸려간 표사가 back-wash 흐름 강도가 약해지면서 퇴적하여 형성되는 breaker bar가 성공적으로 모의되는 것을 확인할 수 있었다. 또한 수치모의 시 재현이 상당히 어려운 것으로 알려진 sand wave가 일정 수심부에서 관측되는 상당히 고무적인 결과도 얻을 수 있었다. 전술한 sand wave는 파고가 증가하는 경우 먼 바다방향으로의 왜도가 증가하는 경향을 보였으며, 이러한 거동은 비선형 파동계의 경우 상대적으로 큰 값을 지니는 연안방향 유속이 짧은 시간 안에 급격히 가속되는 가속도의 횡단 방향으로의 비대칭성에 기인하는 것으로 추정된다. 이러한 추정은 sand wave의 down-wave side는 침식성 해빈의 경우처럼 구배가 완만하나, sand wave의 up-wave side는 퇴적성 해빈의 경우처럼 구배가 급하다는 사실에 근거한다. 이와 더불어 우리의 예상대로 spilling breaker보다 plunging breaker에서 침식이 활발하게 진행되는 것을 확인할 수 있었다.
References
Appendices
Quadratic Friction Law와 마찰계수 f에 기초하여 저면 전단응력 산출과정을 정리하면 다음과 같다:
저면 전단응력 τw는 free stream velocity U∞으로부터 다음과 같이 산출될 수 있으며,
여기서 마찰계수 fw는 다음과 같이 기술될 수 있다.
식(A2)에서 a는 excursion amplitude, kN는 조도길이를 나타내며, 저면 인근 z = δ에서 유속 U∞는 다음과 같이 정의되는 분산 관계식과
천해역이라는 가정으로부터 다음과 같이 기술될 수 있다.



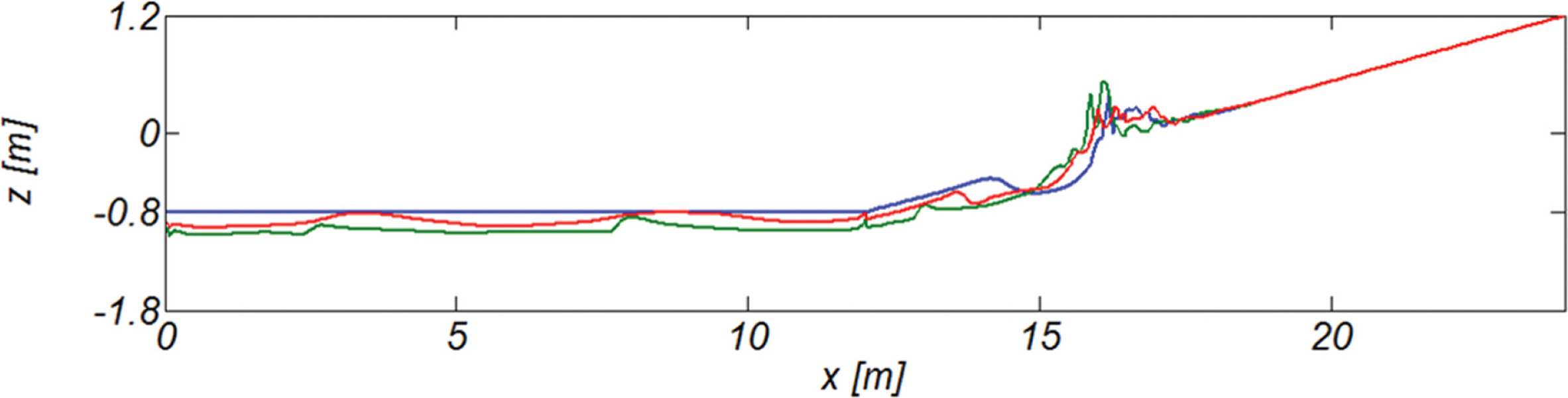
 : Run 1,
: Run 1,
 : Run 2,
: Run 2,
 : Run 3].
: Run 3].