Article information

Abstract

Trans Abstract

1. 서 론

최근 기후변화에 의한 설계파 상향 및 기존 방파제 노후화 등의 영향으로 다수의 방파제를 대상으로 보수보강 사업이 이루어지고 있다. 그 중 케이슨 방파제를 보강하기 위해서는 기존 방파제 전면 또는 후면에 추가로 케이슨을 설치하거나 테트라포드(TTP) 등의 소파블록을 기존 케이슨 전면에 보강하는 방법이 주로 사용되고 있다. 이러한 보강을 효과적으로 시행하기 위해서는 방파제에 작용하는 파압을 정확하게 산정하는 것이 선결 조건이다.

테트라포드로 피복된 방파제를 정확하게 수치 모의하기 위해서는 테트라포드 개체를 하나하나 표현하여 완전 3차원 해석을 수행해야 하며 Dentale et al.(2014)에 의해서 FLOW3D모델을 이용한 3차원 수치모의가 이루어진 바 있다. 그러나 피복된 테트라포드 사이의 공간을 잘 재현하기 위해서는 피복된 영역의 격자를 매우 조밀하게 설정해야 할 뿐만 아니라 3차원으로 해석을 해야 하기 때문에 계산량이 비약적으로 증가하게 된다. 이러한 어려움을 극복하기 위한 일환으로 테트라포드로 피복된 영역을 다공성매체(Porous media)로 대체하여 2차원적으로 해석하는 연구가 진행된 바 있다(Hanzawa et al., 2010).

한편, 수치모델을 이용하여 파랑 수치모의를 수행하는 경우 원하는 파랑조건을 제대로 재현하고 특히 반사파를 제대로 처리하기 위한 조파 방법을 적용하는 것이 중요하다. 최근 여러 연구자들의 관심을 받고 있는 OpenFOAM 기반 모델인 waves2Foam(Jacobsen et al., 2012)은 계산영역에 임의로 수면변위를 부과하는 이완법(relaxation method)을 조파기법으로 사용하여 안정적인 조파 및 소파가 가능하며 최근 Conde(2019)에 의해서도 Stokes 2차 이론 파랑에 대한 성능이 검증된 바 있다. 본 연구에서는 수리실험에서 조파된 파랑조건을 이용해 추가적으로 Stokes 5차 이론 파랑에 대한 조파성능을 검증하였다. 또한, 케이슨 방파제 전면부가 피복되지 않은 조건과 테트라포드로 피복된 조건에 대해 케이슨 전면에 작용하는 파압 수치모의를 수행하여 수리실험 결과와 비교하고 검증하였다. 이로부터 waves2Foam의 파압 수치모의에 대한 타당성을 검증하고 케이슨 전면에 피복된 테트라포드 보강영역의 특성을 다공성 매체로 구현할 수 있는 경험식의 최적 파라미터의 조합을 제시하였다. 이러한 결과는 waves2Foam을 이용하여 테트라포드 피복 영역을 포함하는 수치모의를 수행할 경우 폭넓게 활용 가능할 것으로 기대된다.

2. 수리모형실험

수리모형실험은 한국해양과학기술원에 구축되어 있는 2차원 조파수조(Oh and Lee, 2018)에서 수행되었다. Fig. 1에 보인 바와 같이 케이슨 모형은 조파기로부터 28 m 떨어진 평탄부에 설치되었고, 케이슨 전면에 작용하는 파력을 계측하기 위해 파압계와 로드셀을 사용하였다. 이 중 본 연구에서는 파압계를 이용하여 계측된 파압을 수치모의 결과와 비교하였다. 파압계는 Fig. 2에 보인 바와 같이 케이슨 전면벽을 따라 아래에서부터 위쪽으로 5 cm의 등간격으로 12개(G01~G12)가 설치되었다. Fig. 2에는 케이슨 전면이 피복되지 않은 조건과 중량 300 g의 테트라포드로 피복된 조건의 구조물 단면을 나타내었다. 한편, 케이슨 기초사석 마운드의 전면은 70 g의 테트라포드 2층적으로 피복되었다.

Fig. 1.

Side view of the wave flume.

Fig. 2.

Cross-sections of the caisson models without and with Tetrapods (G01∼G12: location of pressure gauge).

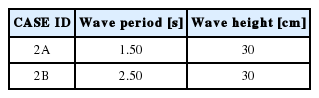
피스톤 형식의 조파기를 이용하여 주기와 파고가 다른 규칙파를 60초 동안 조파하여 실험이 수행되었으며, 본 수치모의는 Table 1에 나타낸 2가지 파랑 조건에 대하여 이루어졌다. Fig. 1의 E01~E07에 보인 것처럼 조파수조의 종방향으로 7개의 파고계를 설치하여 각 위치에서의 시간에 따른 수면변위를 측정하였다. 바닥경사가 시작하기 전과 케이슨 모델 앞쪽에 설치된 파고계의 자료를 통해 목표한 파랑이 잘 조파되었는지 확인하였으며 모델 뒤쪽에 설치된 파고계의 자료를 통해 전달파고의 영향을 확인하였다.

Table 1.

Wave conditions selected for the numerical simulation

수리모형실험 결과 수면 아래쪽에 설치된 파압계에서는 미피복 조건에 비해 전면이 피복된 조건에서 파압이 감소하는 것을 확인할 수 있었다. 반면에 수면 위쪽에 설치된 파압계에서는 피복된 조건에서 오히려 파압이 높게 측정되는 경우가 발생하기도 하였다. 이는 파랑이 TTP로 피복된 사면에서 쇄파가 발생하면서 케이슨 상단부에 있는 파압계에 큰 파압을 미치기 때문인 것으로 판단된다.

3. 수치 모델

본 연구에서는 최근 연안 및 해안공학분야에서도 활발히 사용되고 있는 OpenFOAM을 사용하여 수치 모의를 수행하였다. OpenFOAM(Open source Field Operation And Fluid Dynamics: CFD)은 C++ 언어를 기반으로 한 편미분방정식 솔버(solver) 개발용 클래스 라이브러리로 소스코드가 공개되어 있고 라이센스 비용이 들지 않는다는 점에서 큰 이점을 가지고 있다. 그러나 사용자가 재현하고자 하는 현상을 해석할 솔버가 없을 경우에는 직접 솔버를 개발해야 하므로 경우에 따라 상당한 시간과 지식을 필요로 한다.

파랑의 조파 및 소파기능을 추가하여 개발된 OpenFOAM 라이브러리로는 waves2Foam(Jacobsen et al., 2012), olaFlow(Higuera et al., 2015), IHFOAM(Higuera et al., 2013) 등이 있으며, 본 연구에서는 조파방법으로 이완법(relaxation method)을 적용한 waves2Foam 라이브러리를 이용하여 계산이 수행되었다. waves2Foam 라이브러리는 파랑 수치모의 시 계산 영역의 조건에 따라 3가지의 솔버를 제공한다. 일반적인 계산의 경우 waveFoam, 계산영역 내에 다공성매체가 포함되는 경우 porousWaveFoam, 부유체와 같이 움직이는 격자를 고려해야 할 경우 waveDyMFoam을 각각 이용하여 계산을 수행한다. 본 연구에서는 케이슨제 바닥의 기초사석마운드, 중간피복석, 테트라포드 피복영역 등 다공성 매체를 고려하여 계산을 수행할 필요가 있으므로 porousWaveFoam 솔버가 이용되었다.

4. 조파 성능 검증

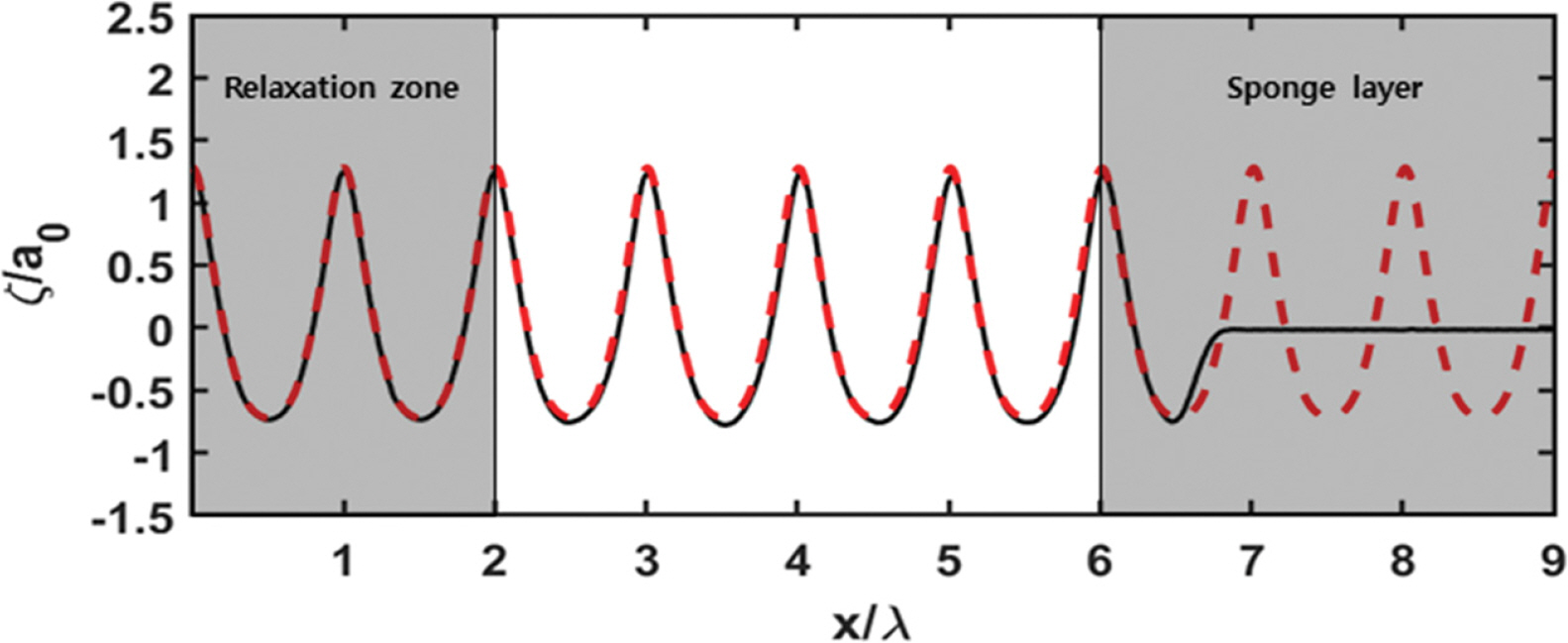
케이슨에 작용하는 파압 수치모의에 앞서 waves2Foam에 적용된 이완법의 조파성능을 Table 2에 제시된 파랑 조건에 대해 검증하였다. 이 파랑 조건은 수리실험에서 적용된 규칙파의 주기 하한 및 상한값에 대하여 파고는 가장 큰 조건에 해당한다. Fig. 3에는 이 파랑 조건들을 Le Mehaute(1969) 파랑이론 한계범위에 표시하였으며, 상당히 비선형성이 큰 파랑조건임을 알 수 있다. 조파영역을 2파장(2λ)로 구성하고 반사파 영향을 최소화하기 위해 소파영역을 3파장(3λ)로 구성하였으며 Stokes 5차 이론의 규칙파를 조파하였다. Fig. 4와 Fig. 5는 수치모의 시작으로부터 30초가 지난 후 조파수조의 수면변위와 해석해를 비교하여 나타낸 것이다. 비교 결과 비선형성이 높은 파랑을 장시간 조파할 경우에도 반사파의 영향이 거의 없으며 목표하는 파랑을 잘 재현하는 것을 확인할 수 있었다.

Table 2.

Test wave conditions for validating numerical wave generation

Fig. 3.

Wave conditions considered in this study (Le Mehaute, 1969).

Fig. 4.

Comparison of water surface elevation calculated using waves2Foam and analytical solution for CASE 2A (solid line: numerical, dashed line: analytical).

Fig. 5.

Comparison of water surface elevation calculated using waves2Foam and analytical solution for CASE 2B (solid line: numerical, dashed line: analytical).

5. 케이슨 방파제 파압 수치해석

5.1 수치해석 조건

수치모델의 조파 구간은 안정적으로 파가 조파될 수 있도록 약 2파장(2λ)로 구성하였으며 그 외의 구간은 수리모형실험과 동일하게 구성하였다. 전체 계산영역의 격자 크기는 수조 길이 방향의 ∆x를 파장의 약 1/150로, 연직방향의 ∆y를 약 0.025 m로 설정하였으며 수조의 폭 방향인 z 방향으로는 한 개의 격자만 설정하였다. 방파제의 수치해석에 중요한 파랑의 형상 및 구조물의 영향을 정확하게 재현하기 위해 파랑이 전파되는 수면부와 구조물 주변부의 격자는 더욱 조밀하게 구성하였다. 본 연구에서는 방파제의 기초사석과 중간 피복석 및 케이슨 전면에 피복된 테트라포드와 같은 투과성 영역을 표현하기 위해 다공성 매체(porous media)를 적용하였다. Fig. 6는 OpenFOAM에서 투과성 영역을 구현한 것을 보여주고 있다.

Fig. 6.

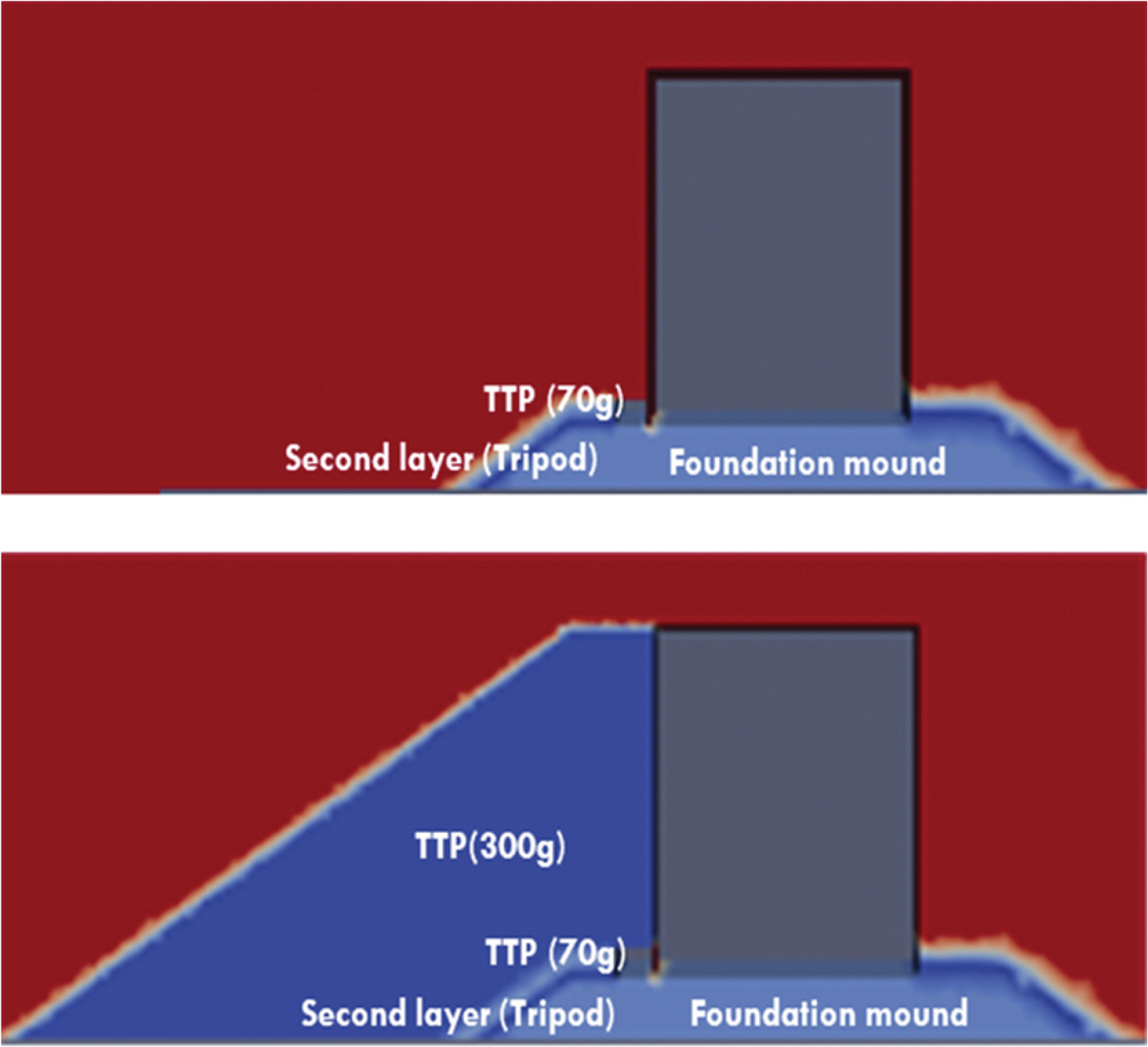
Schematic view of the setup for porous media in the waves2Foam simulation (upper: caisson without protection, lower: TTP-protected caisson).

다공성매체의 설정은 기초사석의 경우 공극률 n = 0.44, 중앙입경 D₅₀ = 0.01m로, 중간 피복석의 경우 공극률 n = 0.3, 중앙입경 D₅₀ = 0.016 m로 설정하였으며, 저항계수로는 Jensen et al.(2014)이 제시한 α = 500, β = 2.0을 적용하였다. 기초사석 전면부에 피복된 70 g 테트라포드 영역은 n = 0.5, 중앙입경 D₅₀ = 0.025 m, 저항계수 α = 500, β = 2.0을 적용하였다. 한편, 케이슨 전면에 피복된 300 g 테트라포드 영역은 n = 0.33, 중앙입경 D₅₀ = 0.075 m, 저항계수 α = 200, β = 0.7을 적용하였다.

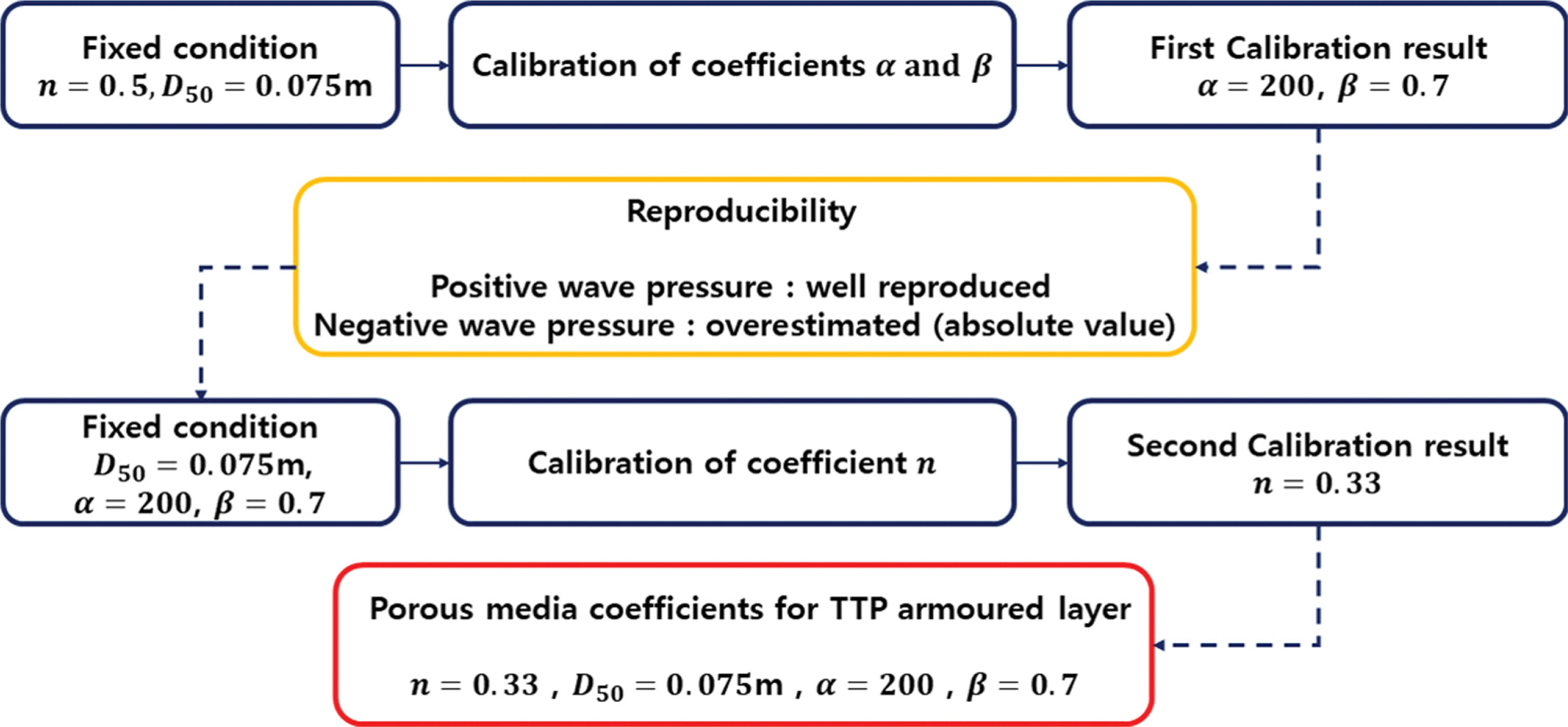
특히, 케이슨 전면에 피복된 테트라포드 영역에 대해서는 Fig. 7에 보인 순서도 절차에 따라 파라미터 보정 절차가 이루어졌다. 파라미터 보정은 케이슨 전면에 설치된 12개의 파압계에서의 실험 자료와 수치모델 결과의 비교를 통해 오차의 값이 최소가 되는 조합을 찾는 방식으로 이루어졌다. 초기에는 수리실험에 사용된 테트라포드의 제원을 이용해 공극률 n = 0.5과 중앙입경 D₅₀ = 0.075m이 고정된 조건에서 α와 β만을 조정하여 이루어졌다. 보정 결과 α = 200과 β = 0.7에서 실험치와 가장 근사한 값을 보이는 것을 확인할 수 있었다. 그러나 이 경우 파압이 음의 값을 나타내는 경우 오차가 크게 발생하였다. 그 이유로는 다공성매체로 모델링한 테트라포드 영역에서의 수위 상승 효과가 실험 결과와 차이를 보이기 때문인 것으로 사료되었다. 이러한 점을 고려하여 공극률 n을 조정하는 추가적인 보정이 이루어졌으며 최종적으로 공극률 n = 0.33, 중앙입경 D₅₀ = 0.075m, 저항계수 α = 200, β = 0.7의 조합에서 실험에서 계측된 파압을 가장 잘 재현함을 확인할 수 있었다.

Fig. 7.

Calibration procedure of porous media for TTP (300 g) armoured layer.

5.2 수치해석 결과

5.2.1 테트라포드 미피복 조건

Fig. 8과 Fig. 9는 각각 미피복 조건에서 Table 1에 보인 두 조건의 파랑을 조파하였을 때 실험과 수치모의에서 얻어진 파압 시계열 자료를 비교한 결과를 보여준다. 12개의 파압계 중맨 밑바닥부터 높이가 높아지는 순서로 1번, 4번, 7번, 9번, 11번 파압계에 대한 비교 결과를 나타내었다. 전반적으로는 수치모델이 실험결과를 잘 재현하고 있어 파압 수치모의에 대한 타당성이 입증되었다고 할 수 있다. 보다 세부적으로는 약 40초 이전까지는 파압 시계열의 계산 결과가 수리실험과 매우 잘 일치하였으나 구조물에 의해 반사된 파랑이 조파판에서 재반사되어 영향을 미치는 약 40초 이후부터는 실험과 모델링 결과의 일치도가 다소 저하되는 것을 확인할 수 있었다.

Fig. 8.

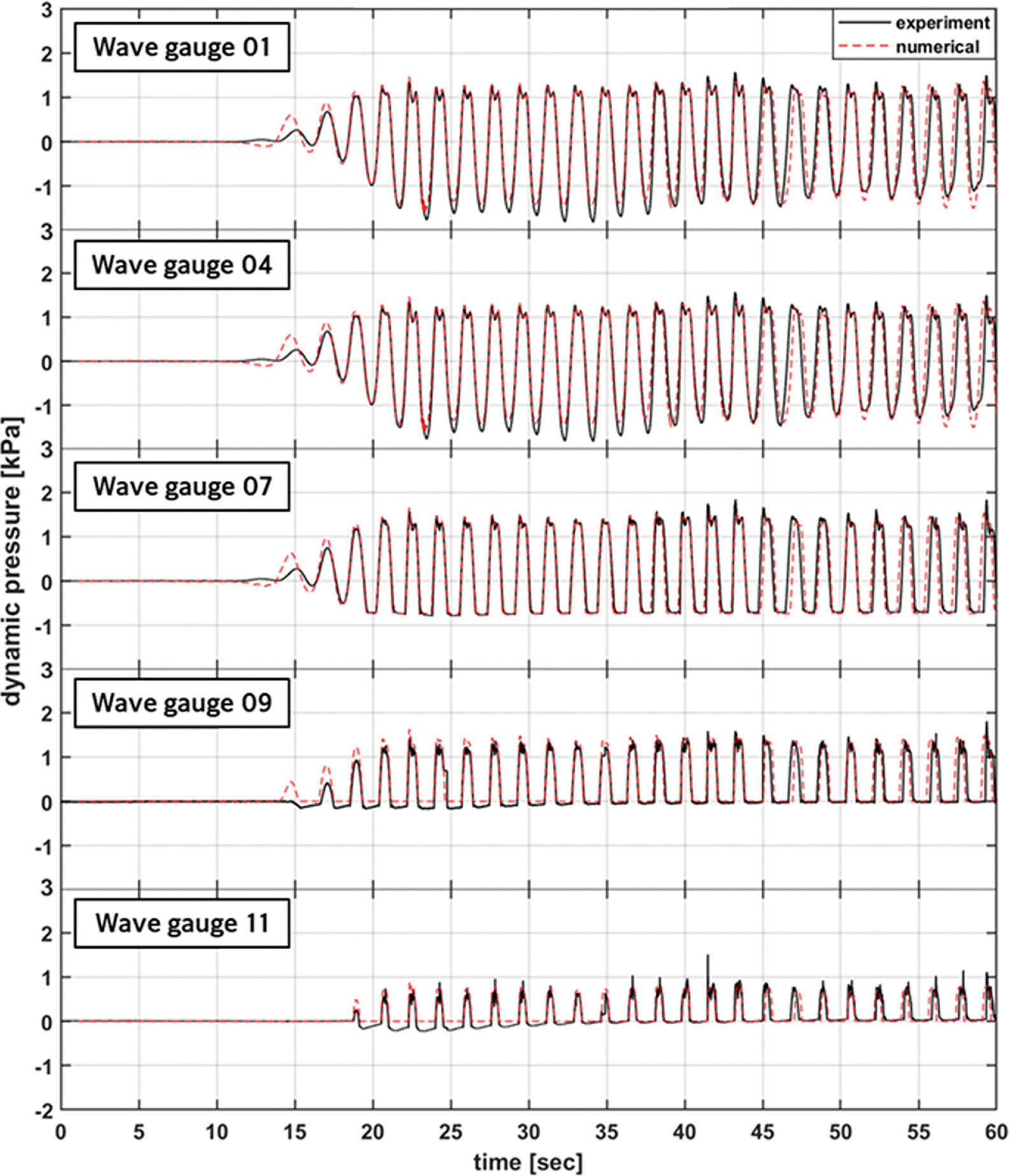
Comparison of the time series of wave pressure on the caisson without placement of Tetrapods (CASE 1A).

Fig. 9.

Comparison of the time series of wave pressure on the caisson without placement of Tetrapods (CASE 1B).

5.2.2 테트라포드 피복 조건

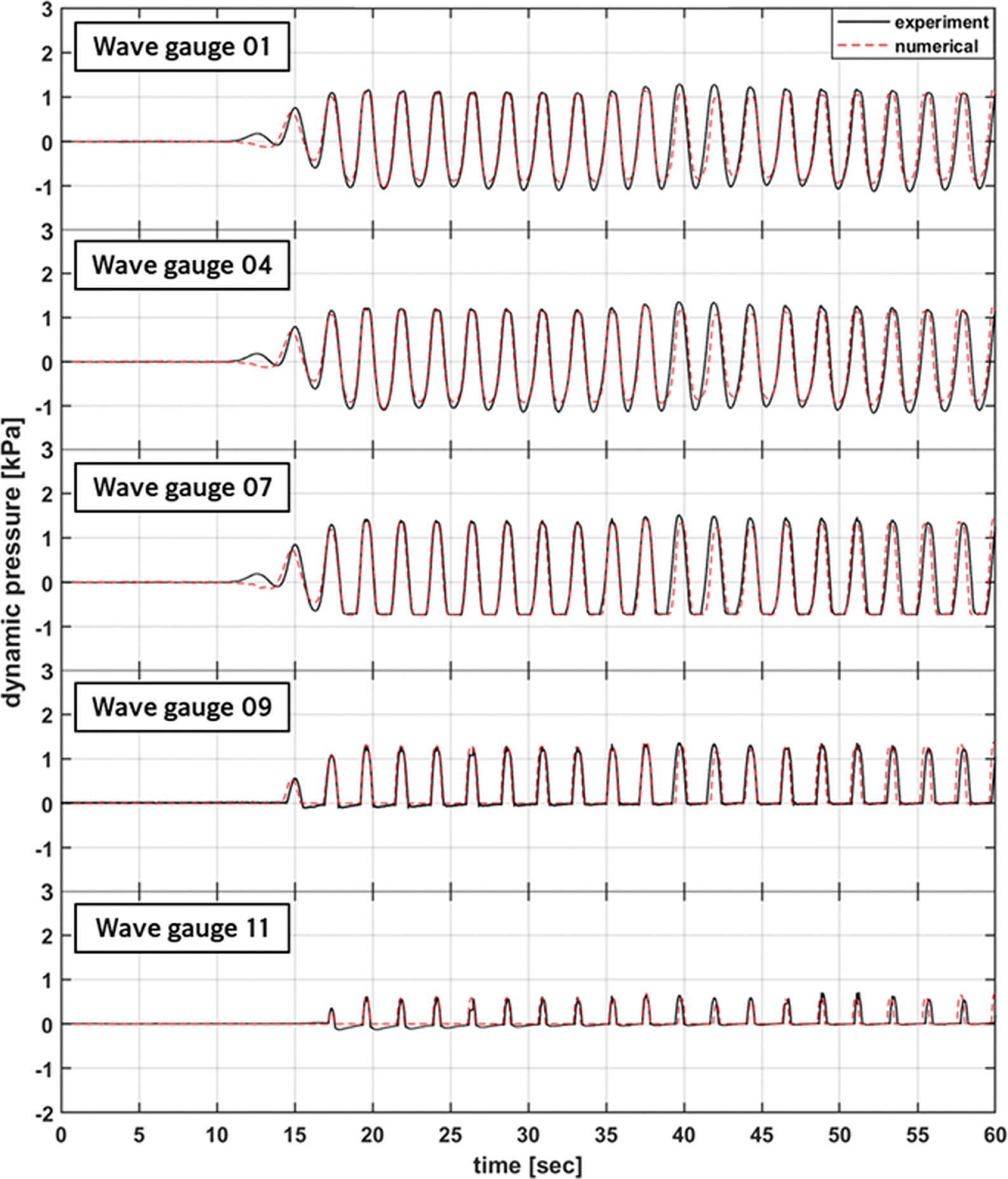
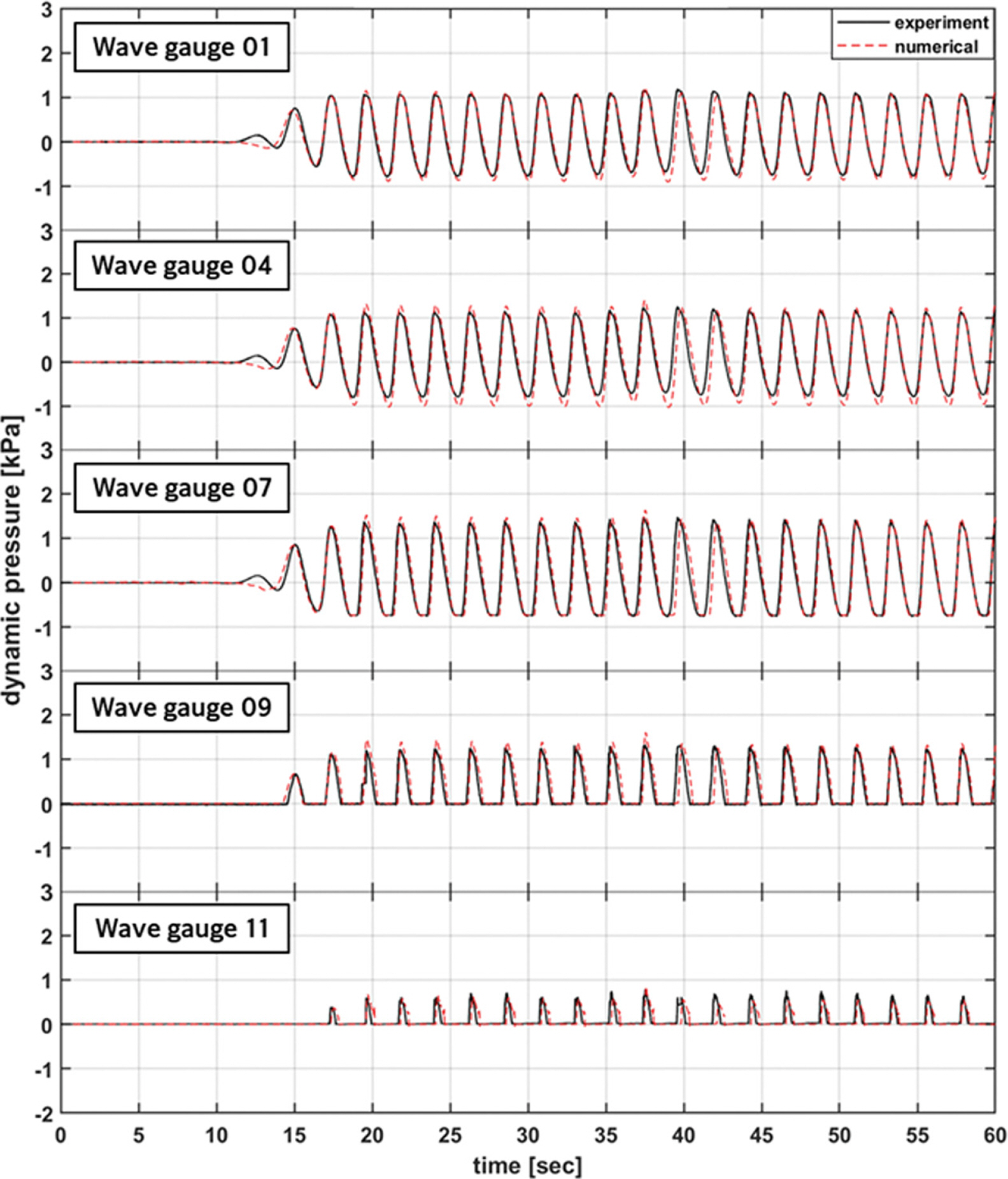
Fig. 10과 Fig. 11은 테트라포드 피복 조건에서의 결과를 나타낸다. 미피복 조건과 마찬가지로 전반적으로 수치모의에 의한 파압 시계열이 수리실험과 잘 일치하였다. 이로부터 본 연구에서 테트라포드 피복 영역에 적용한 다공성 매체 관련 파라미터가 수리실험에서 계측된 파압 특성을 잘 구현함을 확인할 수 있다. 다만 Fig. 8과 9에 보인 미피복 조건에 비해서는 파압의 최대값의 차이가 더 컸으며, 특히 1A 케이스에서 파압 최대값의 차이가 상대적으로 더 큰 편이었다.

Fig. 10.

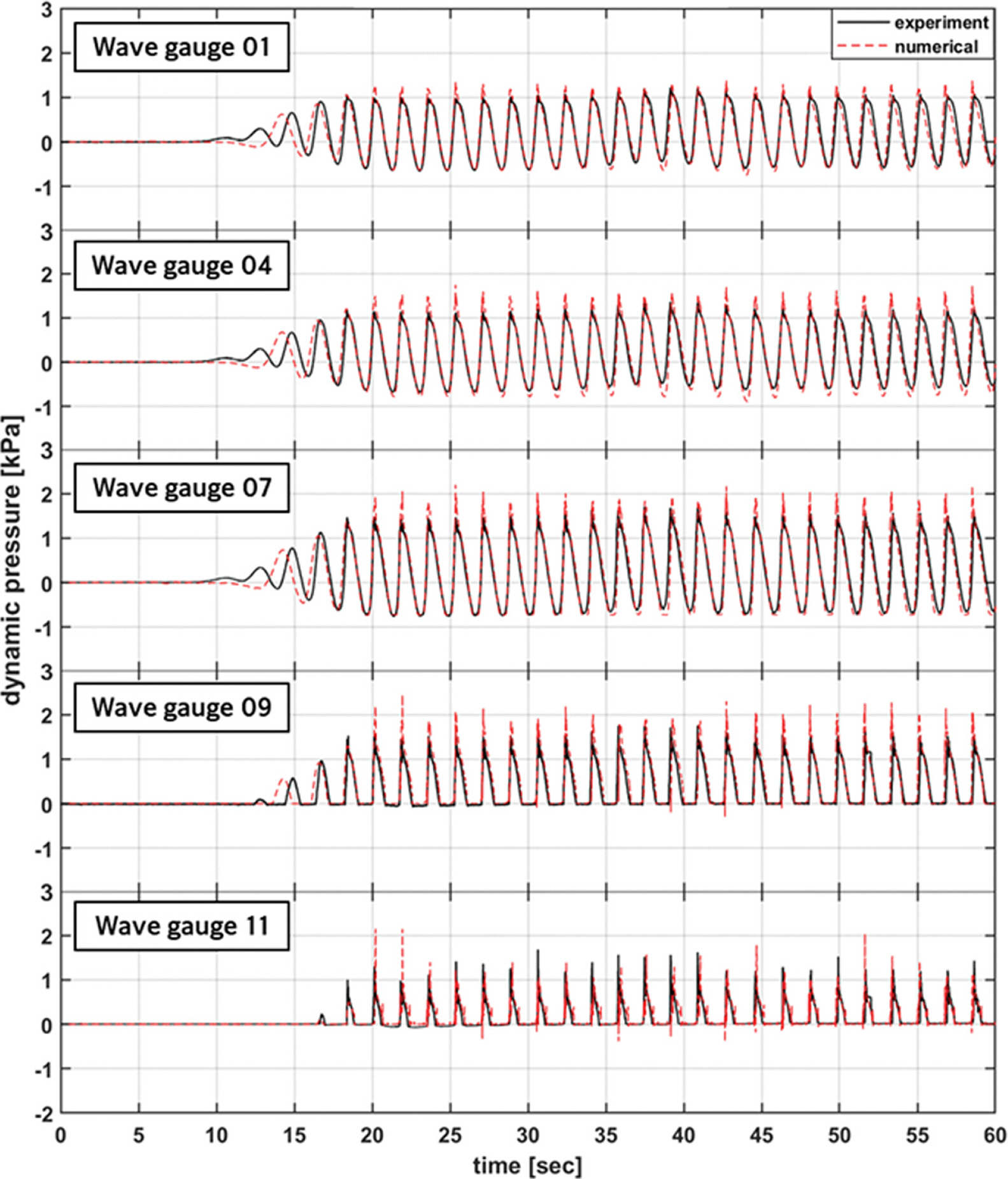
Comparison of the time series of wave pressure on the caisson with placement of Tetrapods (CASE 1A).

Fig. 11.

Comparison of the time series of wave pressure on the caisson with placement of Tetrapods (CASE 1B).

6. 결 론

본 연구에서는 waves2Foam을 적용하여 Stokes 5차 이론의 규칙파에 대한 조파성능을 검증하였으며 이를 근거로 케이슨 방파제에 대한 파압 수치모의를 진행하였다. 케이슨 전면이 미피복된 조건과 피복된 조건에서 규칙파가 작용할 때의 파압을 수리모형실험 결과와 비교하고 특히 테트라포드 피복 영역을 다공성매체로 구현하기 위한 최적 파라미터 조합에 대해 고찰하였다.

미피복 조건의 경우 수치모의된 파압이 실험값과 매우 잘 일치하였다. 이러한 결과로부터 waves2Foam의 파압 수치모의 성능을 충분히 검증할 수 있었다. 한편, 피복 조건에서도 본 연구에서 제안한 다공성 매체 파라미터 조합이 계측된 파압을 상당히 잘 재현함을 확인할 수 있었다. 따라서, 테트라포드 피복 영역을 다공성 매체로 대체하여 2차원 해석을 하는 것이 테트라포드 개체를 하나하나 표현하여 수행하는 완전 3차원 해석의 대안으로 충분히 사용 가능함을 확인할 수 있었다.

또한, 테트라포드 피복 영역을 다공성 매체로 대체하여 수치모의를 진행할 경우 저항계수 α와 β만을 조정하여 보정하는 것에는 한계가 있음을 알 수 있었다. 따라서, 테트라포드처럼 복잡한 형상을 가진 개별 개체들로 구성된 다공성 영역을 다공성 매체로 재현할 경우에는 공극률 n에 대한 추가적인 보정을 통해 더 좋은 결과를 얻을 수 있다. 향후에는 테트라포드 보강 영역의 크기 및 파랑 조건이 다른 경우에 대한 추가 검증을 통해 본 연구에서 제안한 파라미터 조합의 범용적인 적용성을 검토할 수 있을 것으로 전망된다.

Article information Continued