서남해에서 해상풍력구조물의 건설에 의한 해저지형의 변화예측
Prediction of Seabed Topography Change Due to Construction of Offshore Wind Power Structures in the West-Southern Sea of Korea
Article information
Abstract
서남해에서 해상풍력구조물의 건설에 따른 해저지형변화를 예측하기 위하여, 조석, 조류, 부유사 그리고 해저질 등에 대한 현장조사를 수행하였고, 이들 자료를 수치실험에 활용될 수 있도록 하였다. 수치실험에서 표사량 산정은 관련 상수를 시행착오적으로 변화시켜 관측된 부유사농도에 대해 계산치의 오차가 적당할 때에 경험상수들을 결정하는 방법을 사용하였는데, 어떤 농도분포인자가 0.1 그리고 부유사 평형농도 공식의 비례상수가 0.05일 때, 관측치와 계산치가 합리적으로 유사하였다. 부유사농도에 관한 개경계조건은 관측된 부유사농도에 대해 남동측 경계점에서 11.0배, 남서측 경계점에서 0.5배, 서북측 경계점에서 1.0배, 북서측 경계점에서 1.0배 그리고 북동측 경계점에서 1.0배이었을 때, 개경계와 서로 인접한 계산영역 내의 수심변화 계산결과가 단속적이지 않고 매끄럽게 나타났다. 그리고 연간침식퇴적량은 해상풍력 구조물의 건설전후에 대하여 그 변화가 ± 1 cm 이상 발생하는 해역은 거의 나타나지 않았는데, 사용된 대격자 수치모형은 세굴과 같은 국지적 현상을 재현할 수 없고, 해상풍력 하부구조물이 직경 1 m 정도의 자켓타입의 투과식이어서 이들에 의하여 ± 2 cm/s 이상의 유의미한 유속변화역이 거의 나타나지 않았기 때문에, 해저지형변화가 미미한 것은 당연한 결과인 것으로 판단되었다.
Trans Abstract
In order to predict the seabed topography change due to the construction of offshore wind power structures in the west-southern sea of Korea, field observations for tides, tidal currents, suspended sediment concentrations and seabed sediments were carried out at the same time. These data could be used for numerical simulation. In numerical experiments, the empirical constants for the suspended sediment flux were determined by the trial and error method. When a concentration distribution factor was 0.1 and a proportional constant was 0.05 in the suspended sediment equilibrium concentration formulae, the calculated suspended sediment concentrations were reasonably similar with the observed ones. Also, it was appropriate for the open boundary conditions of the suspended sediment when the south-east boundary corner was 11.0 times, the south-west was 0.5 times, the westnorth 1.0 times, the north-west was 1.0 times and the north-east was 1.0 times, respectively, using the time series of the observed suspended sediment concentrations. In this case, the depth change was smooth and not intermittent around the open boundaries. From these calibrations, the annual water depth change before and after construction of the offshore wind power structures was shown under 1 cm. The reason was that the used numerical model for the large scale grid could not reproduce a local scour phenomenon and they showed almost no significant velocity change over ± 2 cm/s because the jacket structures with small size diameter, about 1 m, were a water-permeable. Therefore, it was natural that there was a slight change on seabed topography in the study area.
1. 서 론
서남해 해상풍력 발전단지는 우리나라 전라북도 부안군과 고창군 해역 일대에 건설되고 있다. 이 발전사업은 실증단지, 시범단지 그리고 확산단지의 3단계로 사업이 진행되고 있으며, 2019년 현재 실증단지의 자켓형식 하부구조물이 건설된 상태이다. 이 실증단지의 면적은 289,608 m2이며 20기의 풍력발전기와 1기의 해상변전소가 설치되고 있다(Korea Offshore Wind Power 2019).
이러한 해상풍력단지의 건설로 야기될 수 있는 해양환경영향에 대해 그 평가사례를 조사한 Seo et al.(2019)에 따르면, 영국은 파랑과 조류 및 해저퇴적물의 침식퇴적에 대한 직접적인 영향과 저서생물, 어획, 해안보호 및 수질 등에 대한 간접적인 영향을 평가하고 있다(Department for Communities and Local Government, 2006). 덴마크는 기존자료를 토대로 수리 모델링하여 해저면의 굴착에서 발생하는 부유사농도 및 조류변화가 수질악화에 기여하는 바를 예측하고 있다(Danish Energy Authority, 2006). 네델란드는 풍력발전기의 해저케이블을 위한 굴착, 부식, 침전 등이 지질 및 지형에 미치는 영향과 건설 중 발생하는 해양환경에 대한 영향을 조사하고 있다(The Ministry of Infrastructure and Environment of the Netherlands, 2014). 독일은 수질, 토양 및 기후에 대한 종합적인 조사와 함께 부유사조사를 수행하고 건설중에 해저층이 받는 영향을 평가하였다(Federal Environment Agency, 2010). 스코틀랜드의 환경평가서(Beatrice Offshore Wind Farm Ltd., 2012)는 해상풍력건설시 케이블 설치중 발생하는 부유토사의 영향으로 해양포유류의 포식능력에 영향을 줄 수 있는 먹이서식지의 일시적인 손실 또는 먹이 종의 손실이 발생할 것으로 판단하고 있다. 또한 국내에서는 해상풍력발전단지 건설로 야기되는 환경적 이슈를 파악하고 해양환경관리 및 보전정책수립의 기초환경자료의 제공을 위해 서남해 해상풍력 발전단지를 대상으로 중장기 해양환경 모니터링을 수행하고 있으며, 건설전과 건설중의 해양환경자료가 현재 구축되고 있는 상황으로, 앞으로 운영중의 모니터링에 대한 논의도 진행 중에 있다(Seo et al., 2019).
이 같은 해상풍력단지 설치에 따른 해저지형변화를 예측하고 평가하기 위하여, 본 연구에서는 우선 조석, 조류, 공간부유사, 연속부유사 그리고 해저질 등에 대한 종합적인 동시현장조사를 수행하였고, 이를 자료를 분석하여 현황을 파악하였고 수행될 수치실험에 활용될 수 있도록 하였다. 해저지형 변화를 예측하기 위하여, 수치모형에서 표사량 산정은 검증 지점에서 시행착오적인 방법으로 부유사농도를 계산하여 관측된 부유사농도의 시계열에 대해 그 오차가 적당할 때의 조건에서 여러 가지 경험상수들을 결정하는 방법을 취하였다. 그리고 수치실험에서 계산영역의 각 개경계에서 매시간 간격마다 부유사농도에 관한 개경계조건이 필요한데, 현실적으로 개경계의 각 격자점에 부유사농도를 정확하게 입력하는 것은 불가능하므로, 본 연구에서는 계산영역 내에서 연속관측된 부유사농도값을 이용하여, 각 개경계에서 수심과 관측된 공간부유사 등을 참고하여 경험적·시행착오적 방법으로 이 값에 대해 어떤 비율로 조정하여 각 개경계의 경계조건으로 채택하였다. 한편, 해상에 설치되는 풍력발전기 하부의 자켓구조물은 유수 중에 잠겨서 흐름 변화와 해저지형변화를 일으킬 것으로 예상되므로, 해수 중에 설치된 이들 구조물의 영향을 재현하기 위하여, Park et al.(1998)의 유수저항에 관한 대격자 수치모형을 도입하여 구조물의 형상과 항력을 운동방정식에 도입하여 계산할 수 있도록 하였다.
이상과 같은 현장관측과 수치실험결과로부터, 자켓형 하부구조를 가진 해상풍력구조물 주변에서 해수유동과 같은 물리적 외력현황을 계산하였고 이들 외력으로 인한 해저질의 침식퇴적에 대한 해저지형변화를 분석하였다. 이 연구결과는 앞으로 대규모 해상구조물을 설치함으로서 발생하는 해양퇴적환경의 변동특성을 파악하기 위한 기초자료로 이용될 것으로 기대한다.
2. 대상해역의 특징
서남해 해상풍력 실증단지(Fig. 1의 좌측중앙부 해역의 작은 원들로 표시된 곳)의 북측에 위도항과 격포항 그리고 서측에 구시포항과 같은 국가어항이 있으며, 북동방향으로 곰소만 그리고 남측에 수심이 얕고 퇴적현상이 심각한 백수조간대가 위치한다. 그리고 반경 10 km 이내에 실증단지에 영향을 미칠만한 섬 또는 천퇴 등의 수심변화 구간은 존재하지 않는다(Korea Offshore Wind Power 2019). 이 실증단지는 연안에서부터 약 10 km 떨어져 있으며 평균수심은 10~11 m 정도이다.
The water depth, topography, observation stations and corner points of open boundaries in the study area.
2.1 조석 및 조류
대상해역에서 조석현황을 살펴보면, 위도의 평균해면은 331.5 cm, 약최고고조면 663.0 cm, 구시포항의 평균해면은 334.6 cm, 약최고고조면 669.2 cm, 계마항의 평균해면은 334.5 cm, 약최고고조면 669.0 cm이다. 그리고 Fig. 1의 St. P1과 P2에서 2017년 춘계에 관측된 조석의 4대 분조 진폭은 M2가 각각 191.3 cm, 196.7 cm, S2가 각각 71.9 cm, 74.0 cm, K1이 각각 32.5 cm, 32.6 cm 그리고 O1이 각각 2 7.1 cm, 27.2 cm로 관측되었는데, 조석진폭은 서에서 동으로 갈수록 증가하는 경향을 나타냈으며, 조석형태수는 0.21~0.23로 반일주조가 우세한 조석형태를 보였다.
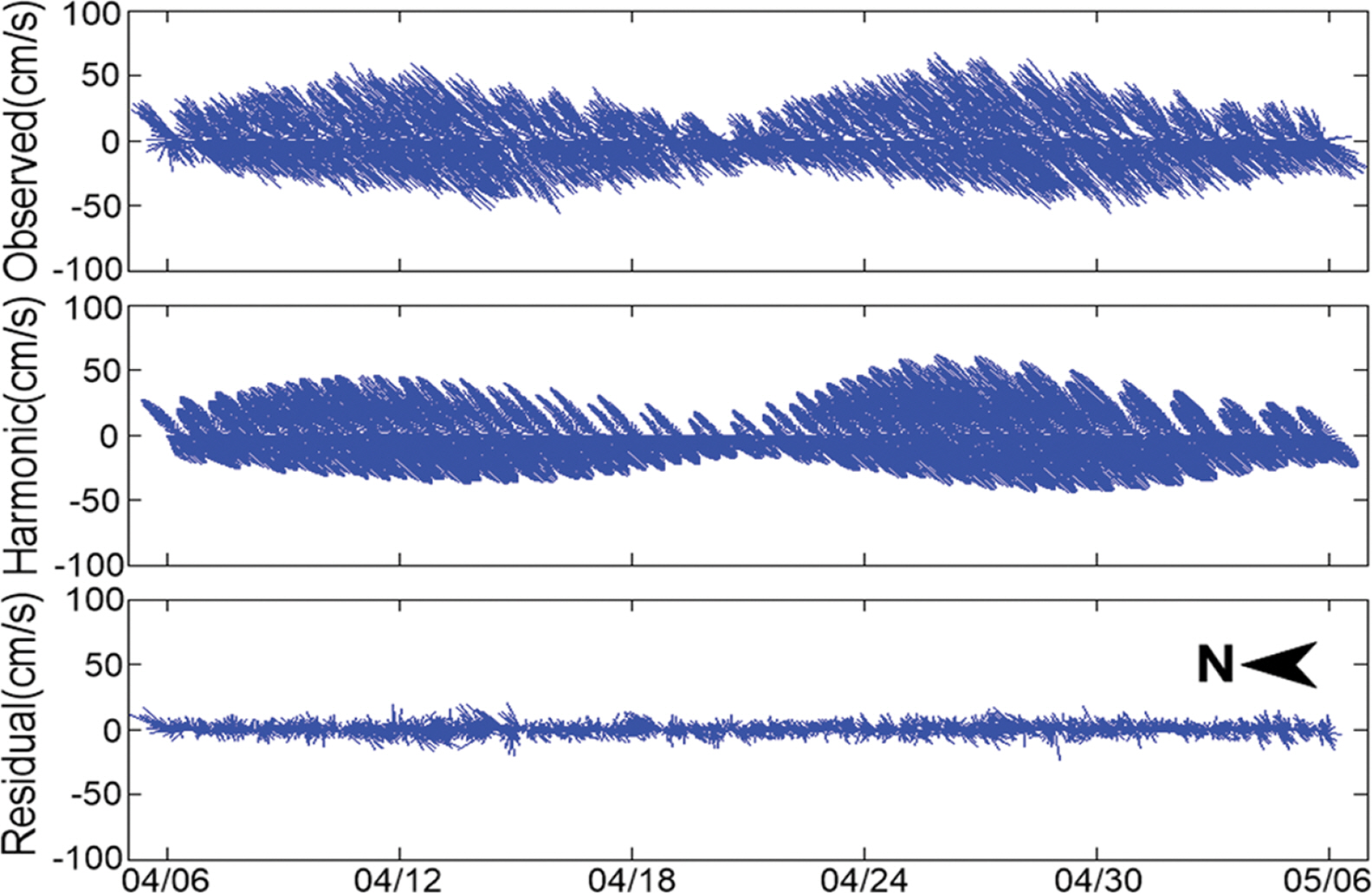
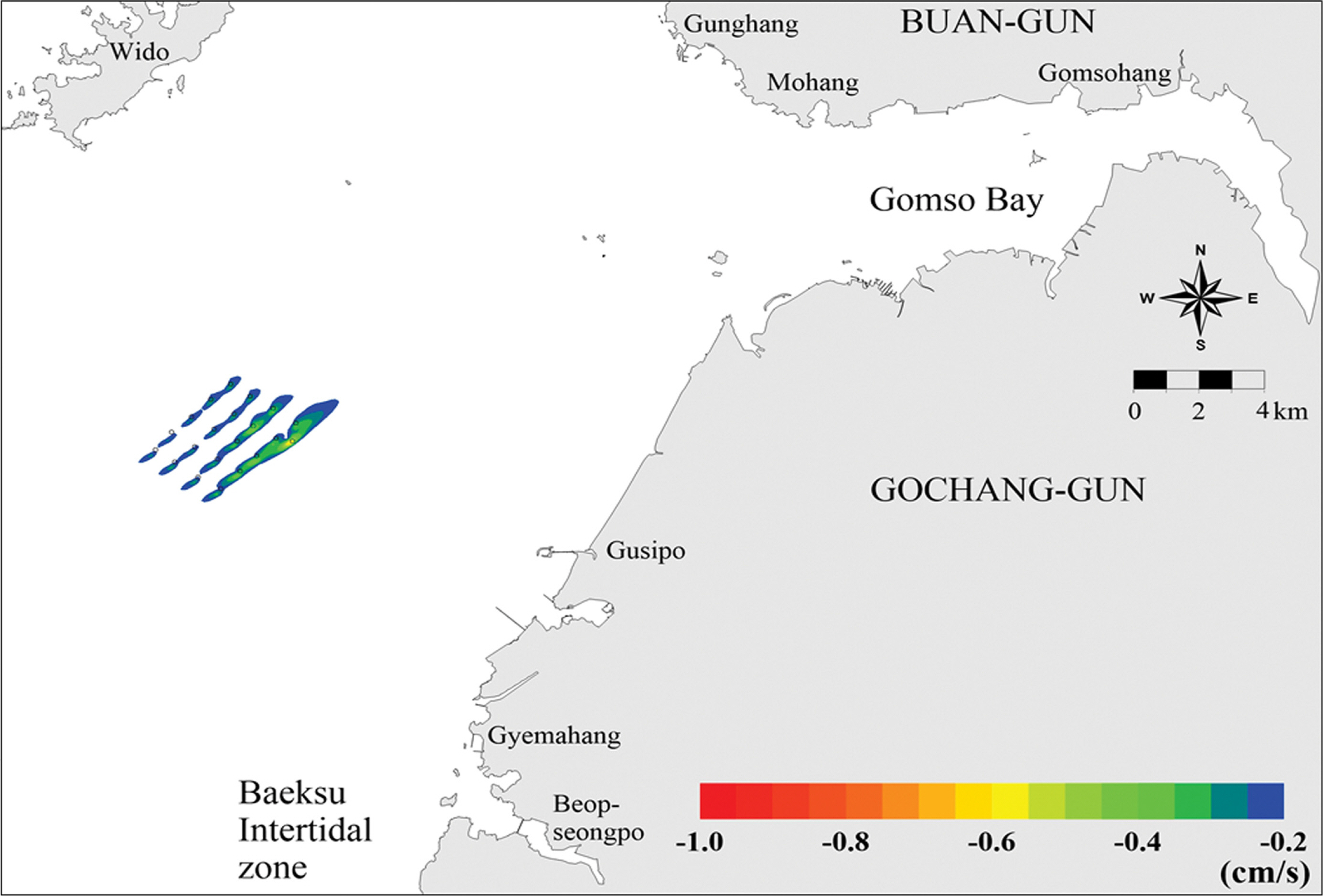
2017년 춘계에 St. P2의 중층에서 관측된 조류를 살펴보면, 흐름 방향은 창조시 북동향류 26.3% 그리고 낙조시 남서향류 27.7%로 우세하였으며, 최강창조류 102.4 cm/s 그리고 최강낙조류 89.7 cm/s로서 창조류의 유속이 더 강하였으나, 평균유속은 창조류 39.4 cm/s 그리고 낙조류 39.2 cm/s로 서로 유사하였다. 이는 지속시간의 차에 따른 것으로 그림에서처럼 창조류는 지속시간은 짧고 최강류가 강하지만 최강류에 버금가는 흐름들의 지속시간이 짧은 편이고, 낙조류는 지속시간이 길고 최강류가 약한 편이지만 최강류에 버금가는 흐름들의 지속시간이 긴 것에 의한 결과로 보인다. 그리고 유속크기별 출현율은 30~40 cm/s가 20.3%로서 가장 빈도가 높으며, 20~30 cm/s는 19.3% 그리고 10~20 cm/s가 17.8%로 나타났다. 또한 평균잔차류는 북북동향의 0.56 cm/s이었다.
The stick diagram for the tidal currents at St. P2 in spring season, 2017.
2.2 부유사
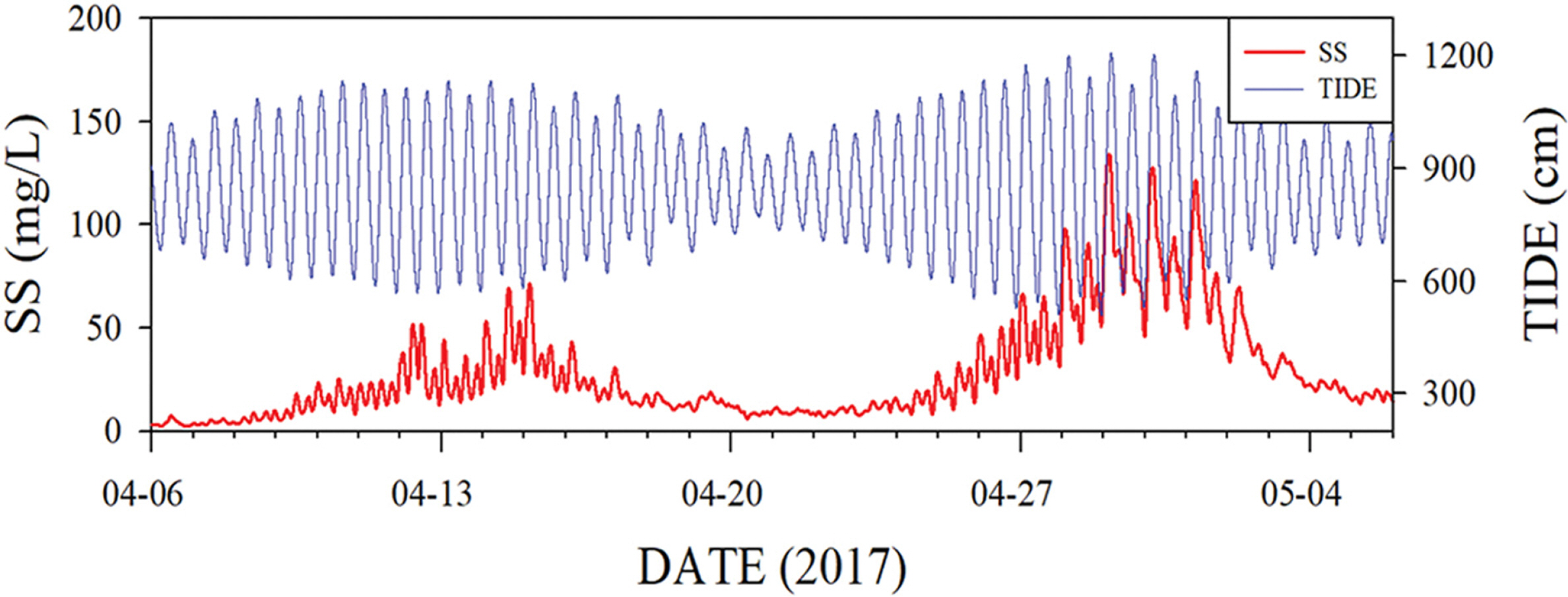
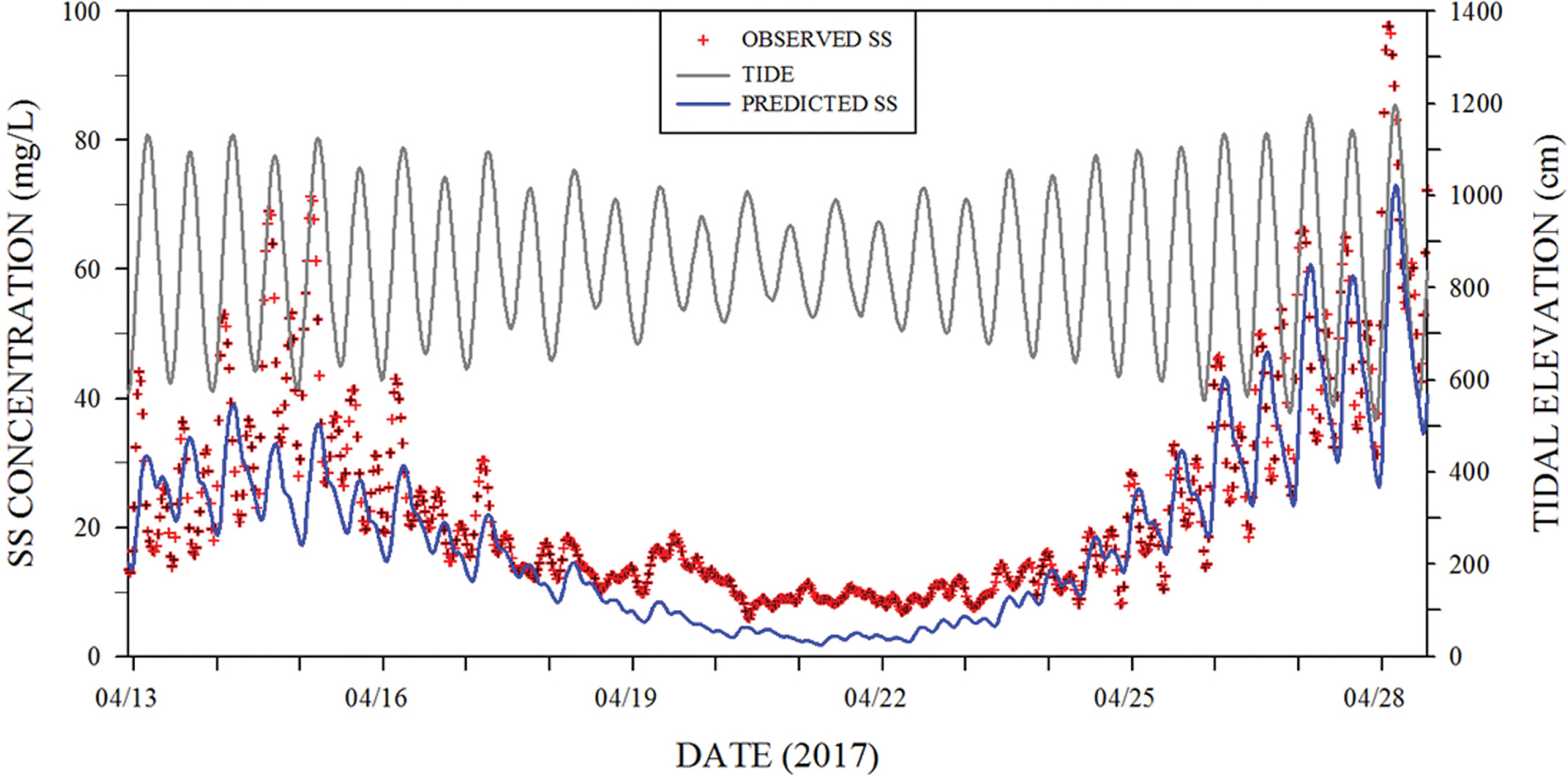
대상해역에서 부유사농도의 시간변화특성을 파악하기 위하여, Fig. 1의 St. P2(평균수심 9 m)에서 2017년 춘계에 해저면상 2m 높이에서 부착생물과 점착성 물질 등이 OBS(Optical Back Scatter) 센서에 침착되는 것을 방지하기 위해 Hydro Wiper가 장착된 탁도계(RBR virtuoso Tu, RBR Co., Canada)를 설치하여 30일간 연속으로 부유사를 관측하였다. 사용된 탁도계의 측정단위는 NTU(Nepthelometric Turbidity Unit)이므로 정량화를 위해 해수를 직접 채수하여 얻은 실제 부유사농도와 비교하여, NTU 단위를 부유사농도인 SS(mg/L) 단위로 변환하여 사용하였다. 이때 두 변수 사이의 상관계수는 0.9 이상이었다.
이같이 얻어진 부유사농도의 시계열을 Fig. 3에 나타내었는데, 그림에서처럼 부유사농도는 조차가 크고 유속이 빠른 대조기에 큰 값을 보였으며, 조차가 작고 유속이 느린 소조기에 작은 값을 보여 이 해역은 유속의 크기와 부유사농도가 상관성이 매우 큰 것으로 보였다. 여기서 관측된 최소값은 2.5 mg/L, 최대값은 134.1 mg/L 그리고 평균값은 28.3 mg/L이었다.
Time series of the observed suspended sediment concentrations at St. P2 in spring season, 2017.
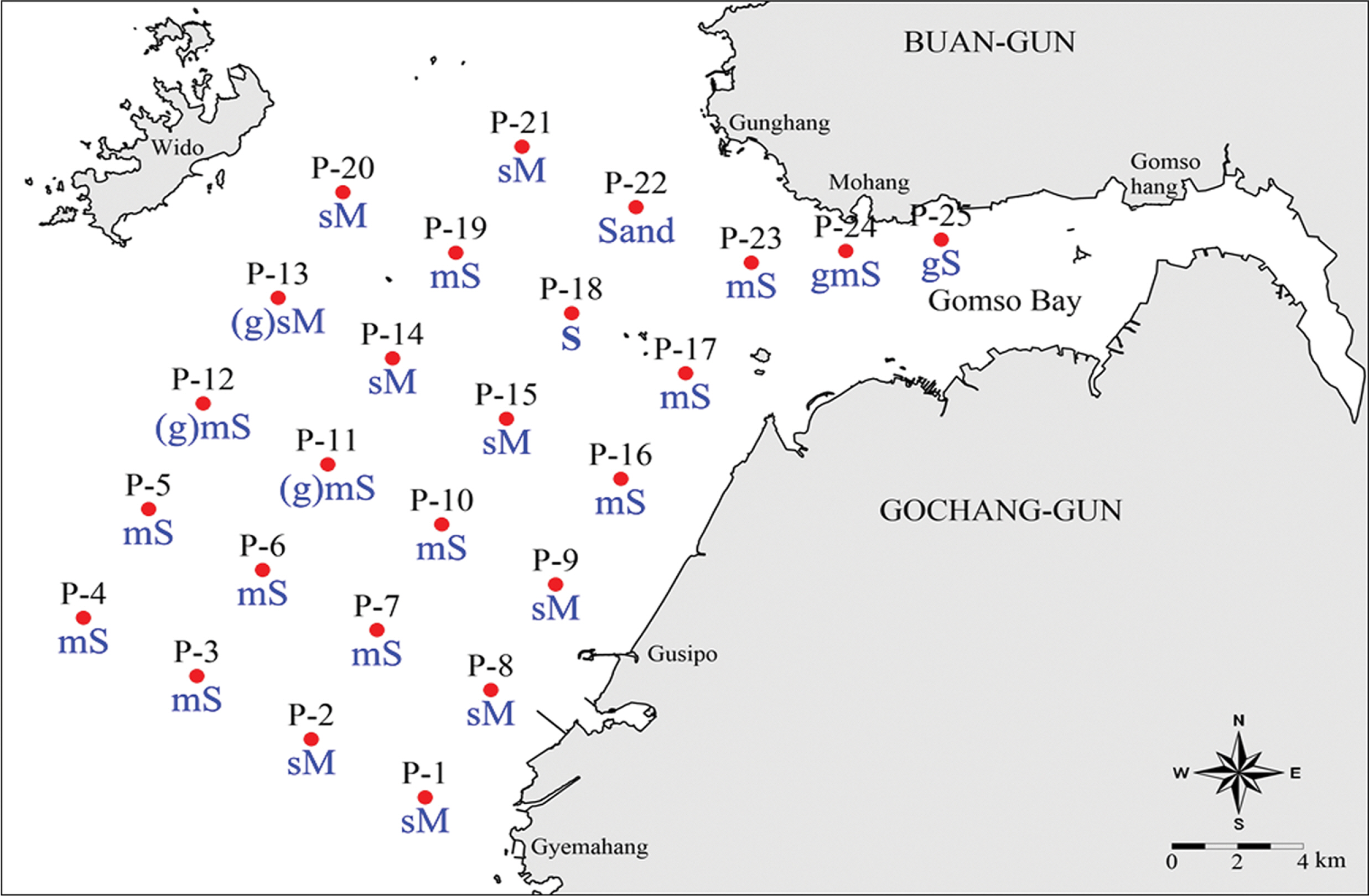
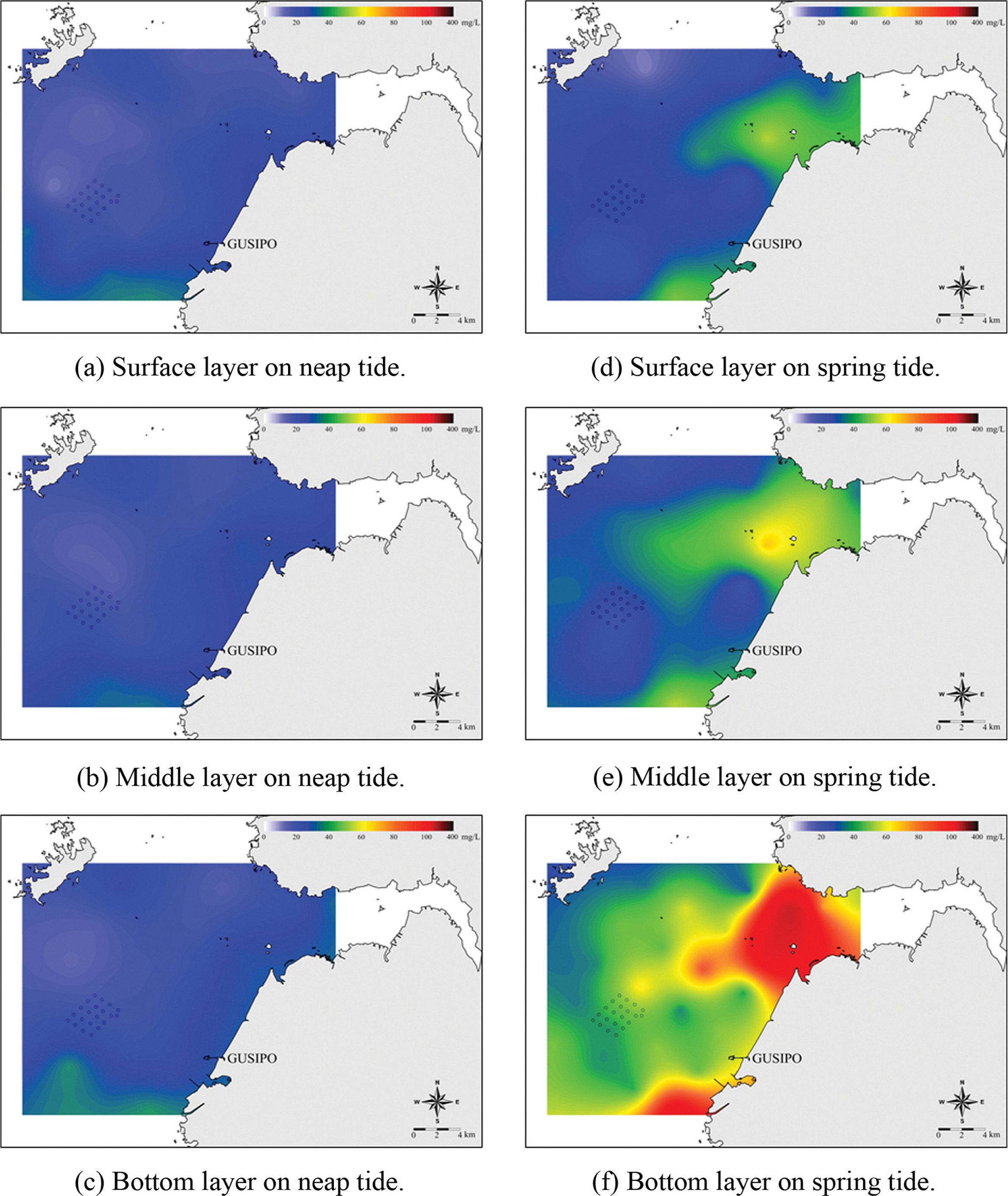
그리고 대상해역에 대해 균등하게 분포하는 25개 정점(위치는 Fig. 5 참조)에서 2017년 춘계에 공간부유사를 채수기로 직접 채수하여 분석한 결과를 Fig. 4에 도시하였다. 관측 결과, 소조기 평균 20.4 mg/L, 대조기 평균 39.1 mg/L이었으며, 표층 평균 23.3 mg/L, 중층 평균 26.9 mg/L 그리고 저층 평균 39.1 mg/L이었으며, 전체 평균은 29.8 mg/L이었다. 전반적으로 유속이 강한 대조기에 소조기보다 부유사농도가 크게 나타났으며, 수층별로 표층보다 중층 그리고 중층 보다 저층에서 부유사농도가 큰 값을 나타내었다. 그리고 대조기에 대상해역 남측의 백수조간대 및 북측의 곰소만 하구에서 고농도의 부유사가 관측되었는데 이곳에서 해저질의 이동이 아주 활발하다는 것을 알 수 있다.
Spatial distributions of the sediment textures in spring season, 2017.
The spacial distribution of suspended sediment concentration in spring season, 2017.
2.3 해저질 특징
Fig. 5와 같은 25개 정점에서 2017년 춘계에 조사된 해저질의 중앙입경은 0.0167~0.5783 mm의 범위로서, 조사정점의 북동쪽에 위치한 곰소항 주변의 St. P-24에서 가장 조립하였고 구시포항 주변의 St. P-9에서 가장 세립하였다. 이들의 퇴적상은 위도주변 및 조사정점들의 남동측에서 전반적으로 사질니(sM)가 우세하였고, 북서측의 곰소만 주변과 남서측의 정점에서 니질사(mS)가 우세하게 나타났으며, 전해역에서 사질이 우세하였다. 표층퇴적물의 조직변수에서 분급도(Sorting)는 1.0~2.4ϕ의 범위로서 거의 모든 정점에서 불량한 분급(Poorly Sorted)을 보였으며, 편왜도(Skewness)는 0.1~2.8의 값으로 매우 큰 양의 왜도(very Positively Skewed) 값을 보여 모든 정점에서 조립한 성분이 우세한 것으로 분석되었다. 그리고 첨도(Kurtosis)는 2.3~20.7의 값으로 대부분 극한의 날카로운(Extremly Leptokurtic) 형태의 값을 보였다.
3. 해저지형변화 수치모형
3.1 비점착성 토사에 의한 해저지형변화
연안역에서 해저질 이동과정의 모형화는 일반적으로 퇴적물이 자연에서 점착성이 있거나(Mud) 점착성이 없는 것(Sand와 Silt)으로 분류되고, 이들은 각각 다른 형태의 표현으로 기술된다. 일반적으로 토사입경이 0.06 mm보다 작은 경우, 중력과 비교할 수 있는 입자간의 정전기력에 의해서 점착성을 가진다(van Rijn, 1993). 그리고 비점착성 토사에 대한 총표사량은 소류사와 부유사 같은 2가지의 다른 유형으로 분리된다. 소류사는 토사가 거의 지속적으로 바닥에 접촉해 있고, 전동(Rolling), 미끄러지거나 도약에 의해 운반되는 표사량의 일부분으로 정의된다. 반면 부유사는 토사가 난류에 의해 부유상태를 유지하는 표사량으로 정의된다. 표사이동에 관한 이 2가지 성분은 2가지 다른 형식으로 표현되고 있고, 그 이동구조는 다르다. 수치모형에서 부유사 플럭스는 수심적분된 이류확산방정식의 수치해에 기초를 두고 있고, 다음의 형태로 쓰인다(Falconer and Owens, 1990).
여기서 S는 수심평균된 부유사농도, H는 전수심, t는 시간, x와 y는 공간좌표, U와 V는 각각 x와 y 방향의 유속성분, Dxx, Dxy, Dyx, Dyy는 각 방향별 확산계수 그리고 E는 저면의 단위면적당 순침식량이다. 그리고 수심평균된 순침식 또는 퇴적률은 다음의 형태로 표현될 수 있다(Owens, 1987).
여기서 γ는 어떤 농도분포인자로서 수심평균된 농도 S에서 저면기준점농도 Sa에 대한 비로 주어지며, Wf는 입자의 침강속도이다. 그리고 Se는 수심평균된 평형농도로서 적절한 표사이동공식으로부터 결정되며, 평형조건은 난류에 의한 표사의 부상 플럭스와 침강 플럭스가 평형을 이룰 때이다. 수심평균된 평형농도에 대한 공식들은 많이 제안되었으나, 연구자들은 Engelund-Hansen 공식(Engelund and Hansen, 1967) 혹은 van Rijn 공식(van Rijn, 1984)과 같은 2가지 공식을 많이 사용한다. 본 연구는 입력매개변수가 단순한 다음의 Engelund-Hansen 공식을 사용하였다.
여기서, 0.05는 비례상수, U*는 흐름 방향의 전단속도, C는 Chezy 계수, g는 중력가속도, ∆는 상대밀도(= (ρs - ρ)/ρ) 그리고 d50은 해저질의 중앙입경이다. 그리고 평형농도 Se는 다음과 같이 주어진다.
여기서, q는 수심적분된 유체의 속력이다. 그리고, 소류사량의 산정은 다음과 같은 Bijker 공식(Bijker, 1967)을 사용하였다.
여기서, qb는 단위폭당 수심적분된 소류사 플럭스, μ는 사련(Sand Ripple)의 영향계수(= (C/C90)1.5), C90은 90% 해저질 입경 d90에 관한 Chezy 계수 그리고 Us는 수심평균된 유체의 속력이다. 이상의 과정과 같이 수심적분된 부유사량과 소류사량의 합에 의해 비점착성 토사이동에 대한 총표사량을 구할 수 있으며, 이 같은 표사이동에 관한 기본식을 바탕으로 DIVAST(Depth Integrated Velocities And Solute Transport) 수치모형(Falconer, 1991; Falconer and Owens, 1990)이 개발되었다.
3.2 저항물체에 의한 흐름변화
수중에 설치된 교량의 교각, 돌핀 부두의 말뚝, 자켓구조물, 수산증양식시설물 그리고 기타 구조물 등은 유수 중에 잠겨서 흐름 저항을 유발시킨다. 이에 따라 이들 구조물 배후에서 후류와가 발생하며, 구조물 주변에서 급격한 유속과 수위의 변화가 발생한다(Park et al., 1998). 따라서 이러한 현상을 재현하기 위하여 기존의 DIVAST(Falconer and Owens, 1987; Falconer, 1991)의 Code를 기본적으로 이용하여 물체에 의한 유수저항을 적용할 수 있도록 수정한 모형(Lee and Park, 1995; Park et al., 1998; Park, 2004; Cho et al., 2010)을 사용하였다. 본 모형에서 사용된 연속방정식과 Navier-Stokes 방정식을 수심적분된 형태로 나타내면 다음의 식(6)~(8)과 같다.
여기서, qx와 qy는 x와 y 방향의 수심적분된 속도성분, f는 Coriolis 계수, ζ는 자유수면변위, h는 수심, τx와 τy는 x와 y 방향의 전단응력성분, ρ는 해수의 밀도, ε은 수심평균된 와 동점성계수이다.
여기에 투과성의 자켓구조물과 같이 구조물의 단면이 계산격자에 비해 작은 경우 이들의 흐름에 미치는 영향을 고려하기 위하여, 식(7)~(8)의 전단응력항에 기존의 바람과 저면에 의한 마찰 이외에 저항물체의 단위면적당 항력을 도입하면, x 방향의 전단응력항은 식(9)와 같이 표현된다. 이 식에서 우변 첫 번째의 바람응력항은 정상등류에 관한 수평분력, 두 번째의 저면전단응력항은 개수로에서 정상등류로부터 유도된 2차의 마찰법칙, 그리고 세 번째의 저항물체에 의한 전단응력항은 항력계수를 도입한 항력을 나타낸다.
여기서, cf는 수면에서 계면저항계수, ρa는 공기의 밀도, Wx는 바람의 x 방향 속도성분, Ws는 바람의 속력, n은 단위면적당 저항물체의 개수, CDx는 x 방향의 항력계수, ADx는 물체의 x 방향 투영면적 그리고 Ua와 Va는 x와 y 방향의 접근유속이다.
이상과 같은 이들 수치모형은 유속과 같은 외력계산을 위한 연속방정식과 운동방정식 그리고 표사에 관한 이류확산방정식을 ADI(Alternating Direction Implicit)법으로 풀며, 이를 위해 공간적으로 엇갈린 격자(Staggered Grid) 체계를 사용하고 있다. 그리고 간석지가 발달된 해역에 대해 수위의 변화에 따라 폐경계의 위치가 변하는 이동경계를 취하고 있다. 수치모형에 대한 내용은 Falconer and Owens(1987, 1990)와 Park et al.(1998)에 자세하게 기술되어 있다. 그리고 식(1)과 같은 표사이동에 관한 이류확산방정식의 개경계조건은 각 개경계에서 시간에 따라 변동하므로, 흐름이 개경계를 Outgoing하는 경우 경계내부의 값을 이용한 외삽법으로 개경계값을 결정할 수 있으나, 흐름이 개경계로 유입되는 경우 개경계값은 관측값으로부터 추정하여 사용하거나 더 큰 계산영역을 설정하여 거칠게 계산된 경계값을 이용하는 Nesting Grid와 같은 기법이 필요하다.
3.3 해상풍력의 자켓구조물
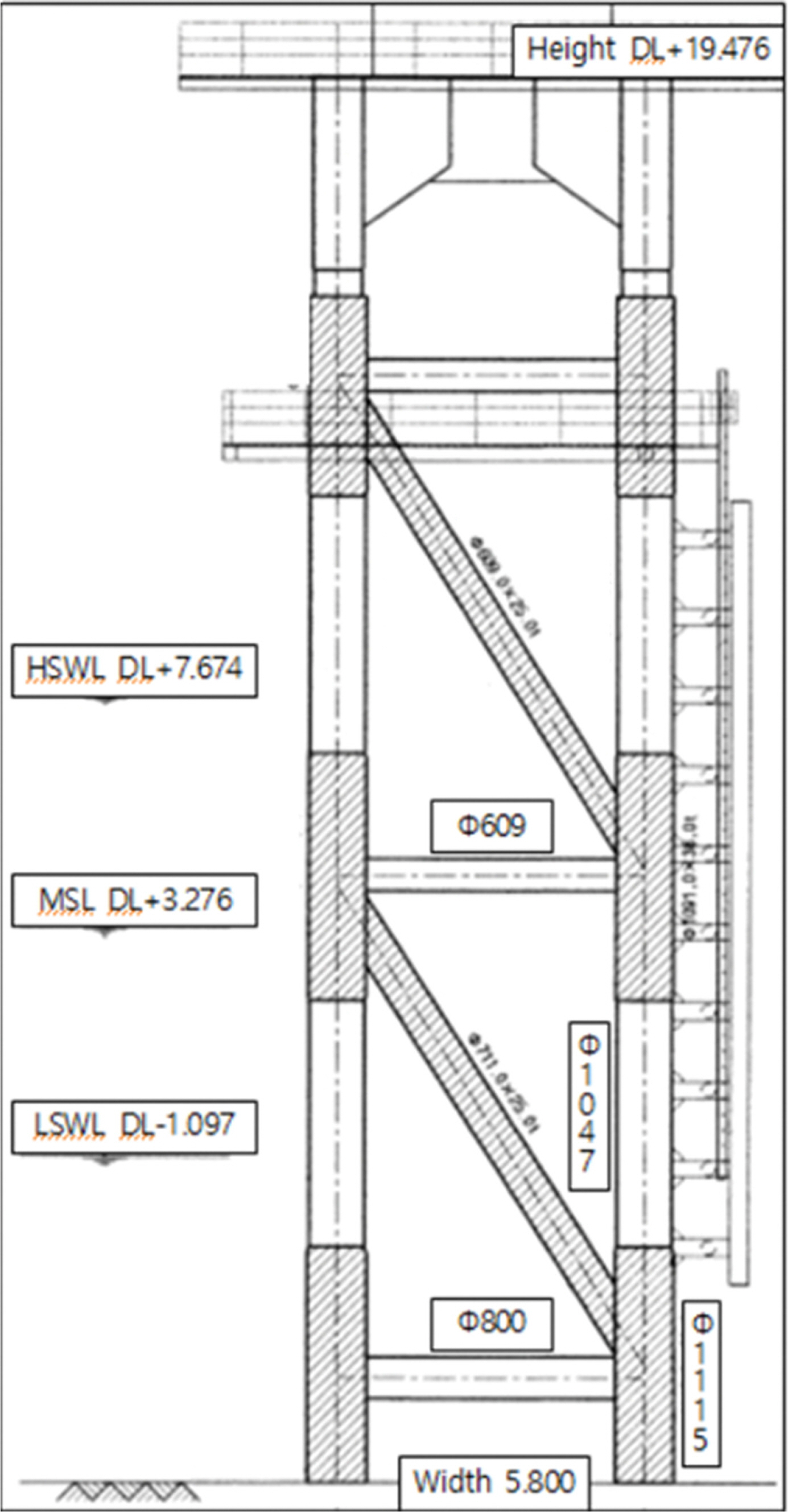
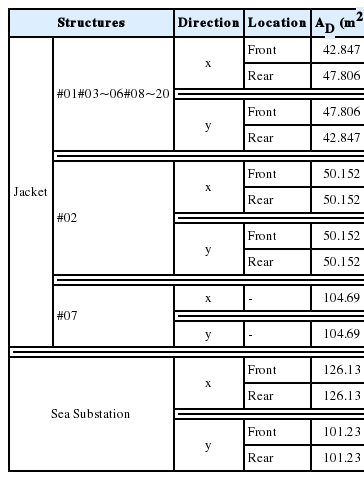
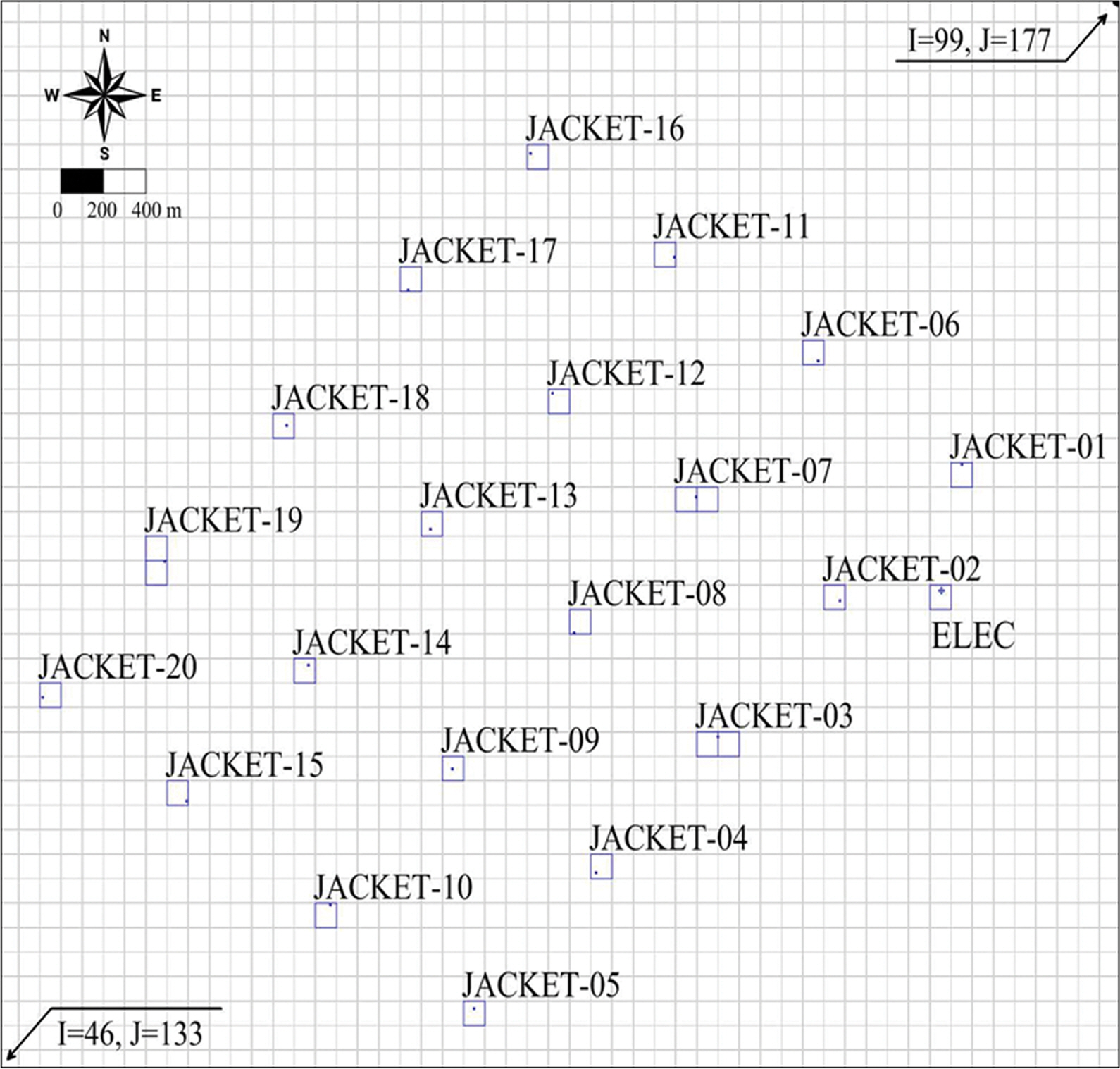
서남해 해상풍력 실증단지에서 설치되는 자켓구조물은 모두 21개로서 모두 4가지 종류가 있으며, Fig. 6에 제시된 구조물은 21개중 18개에 사용된 대표적 구조물로서 예시하였다. 여기서 항력계수는 Fig. 6과 같은 관련도면으로부터 그 입력제원을 구하여, 항력계수에 관한 Akins et al.(1977)의 풍동실험결과와 원형의 말뚝구조물의 항력계수에 관한 Blevins(1984)의 결과를 바탕으로 각 방향별 및 구조물의 위치에 따른 각 항력계수를 Table 1과 같이 산정하였다. 그리고 수치모형의 계산조건에서 21개의 자켓구조물이 설치되는 위치에 대한 격자에 대해, 각 구조물이 각 격자에 포함되는 면적비를 계산하여 단위격자당 구조물의 개수, 구조물의 투영면적 그리고 구조물의 항력계수 등을 수치모형에 입력하여, 이들 구조물에 의한 유수저항을 계산할 수 있도록 하였다. 여기서 Fig. 7은 100 m 간격의 계산격자에 대해 21개의 구조물이 설치되는 위치를 표기한 것으로 파란색으로 표기된 정사각형 격자가 구조물이 존재하는 격자이며 그 격자 내에서 작은 점으로 표시된 것이 구조물이 설치되는 위치이다. 각 격자에서 단위면적당 구조물의 개수 n 값(식(9) 참조)을 수치모형에 입력하였으며, n = 0이면 당연히 구조물의 영향이 없는 것으로 n > 0이면 구조물의 영향을 받는 격자로 처리되도록 하였다.
The example sectional view of the jacket #01.
The projection area (AD) and the drag coefficient (CD) for the structures
The calculation grid numbers and locations for the jacket structures.
이상과 같은 수치실험을 수행하기 위하여 해상풍력 실증단지를 중심으로 주변해역을 격자간격 100 m의 405 × 300(40.5 km × 30 km)로 구성된 모형해역을 설정하였고 이때 모형해역의 수심 및 지형은 Fig. 1에 나타내었다. 여기서 수심자료와 지형자료는 국립해양조사원에서 발행한 수치해도 No.K-3411과 No.K-3451 등을 활용하였다.
4. 계산결과 및 고찰
대상해역에서 표사이동에 따른 해저지형변화를 예측하기 위하여, 관측된 해저질자료와 부유사자료 등과 같은 관련 현장자료를 수치모형에 입력하였고, 외력으로 작용하는 조석과 조류는 사전에 충분한 검증을 거쳐 수치모형으로부터 계산을 선수행하여 그 결과를 이용하였다. 수치모형에서 표사량 산정은 관련상수를 시행착오적으로 변화시켜 Fig. 3의 관측된 부유사농도에 대해 계산값의 오차가 적당할 때에 경험상수들을 결정하는 방법을 사용하였다. 식(2)의 어떤 농도분포인자 γ를 GAMSUS 그리고 식(3)의 부유사 평형농도 공식에서 비례상수 0.05를 HANCON으로 두고 이들 값을 시행착오적으로 변경시켜 관측치와 계산치를 비교검증하였는데, GAMSUS = 0.1 그리고 HANCON = 0.05일 때, Fig. 8과 같이 부유사농도의 관측치와 계산치가 비교적 합리적으로 유사하였다. 여기서 GAMSUS = 0.1은 통상적으로 사용하는 값의 범위이며(Falconer and Owens, 1990), HANCON = 0.05은 식(3)에서 주어진 값 그대로여서 모두 일반적인 사용되는 값으로 결정되었다. 한편, 식(5)의 소류사량은 부유사량에 비해 일반적으로 그 값이 현저히 작으므로 별도로 검증은 수행하지 않고 주어진 공식을 그대로 사용하였다.
Comparison between the observed and the calculated suspended sediment concentrations at St. P2 when the calibration parameters GAMSUS = 0.1 and HANCON = 0.05.
Fig. 8에서 부유사농도의 계산치는 관측치처럼 유속의 크기에 따라 변동하는데 조차가 크고 유속이 빠른 대조기에 크게 나타났고 조차가 작고 유속이 작은 소조기에 작게 나타났다. 그리고 계산치는 관측치와 대체적으로 유사한 변동패턴을 나타내었지만 계산치는 관측치에 비해 다소 작은 값인데, 관측치는 수심의 저층(해저면상 2 m)에서 값이고 계산치는 수심평균된 농도(평균수심 9 m)이므로 관측치가 계산치 보다 다소 큰 값을 나타내는 것은 합리적인 결과인 것으로 판단되었다.
이상과 같은 검증결과로부터 관련상수값을 고정하여 수치실험을 수행하였다. 이때 계산이 수행되는 동안 계산영역의 북측(위측), 서측(좌측) 및 남측(아래측)의 개경계에서 매시간 간격마다 부유사농도에 대한 경계조건이 필요한데, 현실적으로 개경계의 각 격자점에 부유사농도를 정확하게 입력하는 것은 불가능하다. 따라서 본 연구에서는 Fig. 3과 같은 계산영역에서 연속관측된 부유사농도를 개경계조건으로 이용하였는데, 각 개경계에서 모두 이 값과 동일하게 사용하지 않았고, 이 값에 대해 어떤 비율로 조정하여 경계조건으로 주었다. 그 예로서 Fig. 9는 Fig. 3의 부유사농도에 대해 남측개경계 3.0배, 서측개경계 0.8배 그리고 북측개경계 1.0배의 부유사농도를 가정하였을 때의 계산결과인데, 그림에서처럼 남측개경계 부근의 백수조간대는 현상과 다르게 침식하는 경향을 보이고, 수심이 깊은 서측개경계 남단은 약간 퇴적되는 경향을 보인다. 이 결과는 현재 심각한 퇴적양상을 보이는 백수조간대의 현장농도특성을 개경계에서 충분히 반영하지 못하였고 서측 개경계의 남단부근도 현실보다 큰 부유사농도가 사용된 것을 의미하는 것으로 판단할 수 있었다.
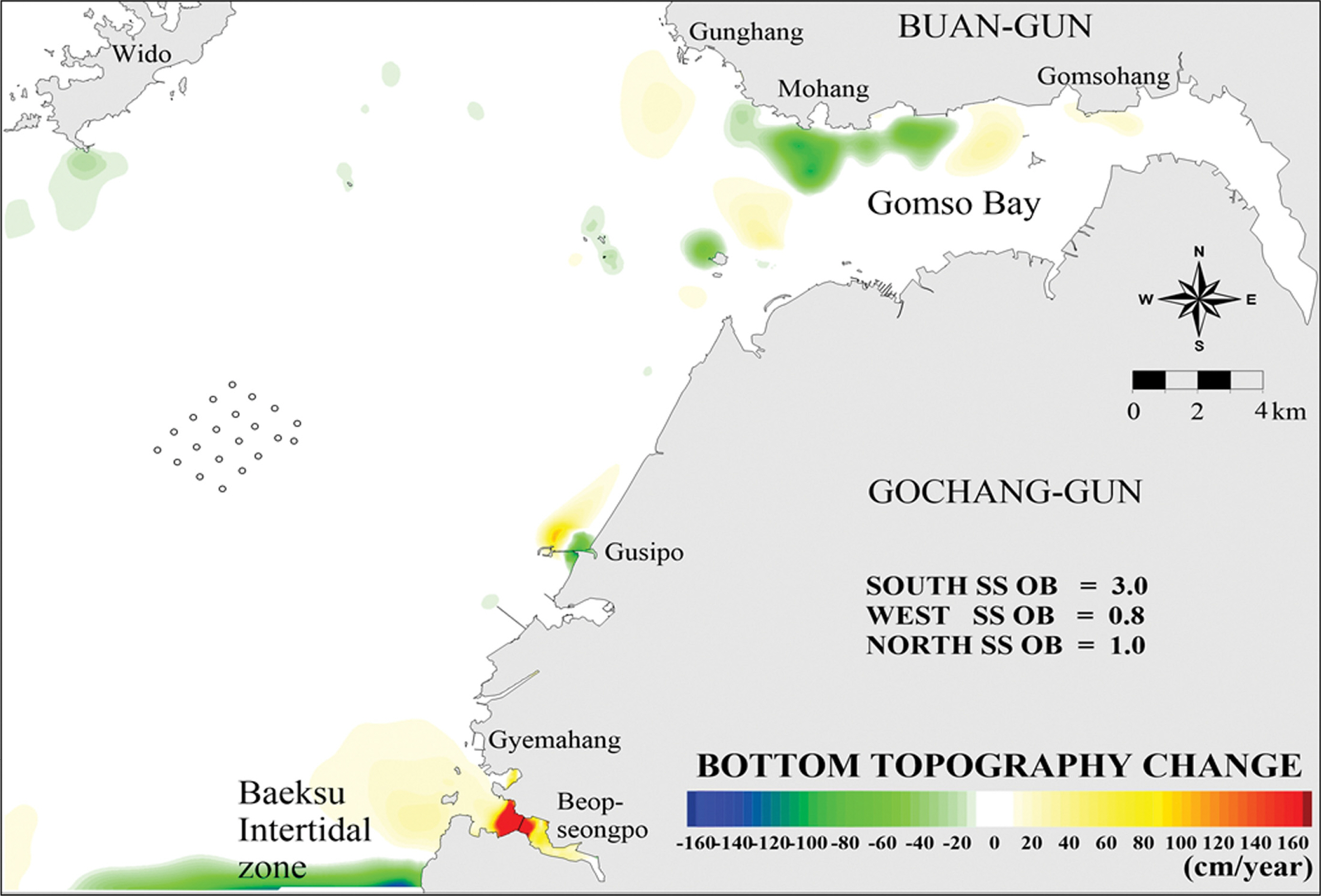
An example result of the bottom topography change given the open boundary conditions for the suspended sediment concentration (South OB = 3.0 rate, West OB = 0.8 rate and North OB = 1.0 rate).
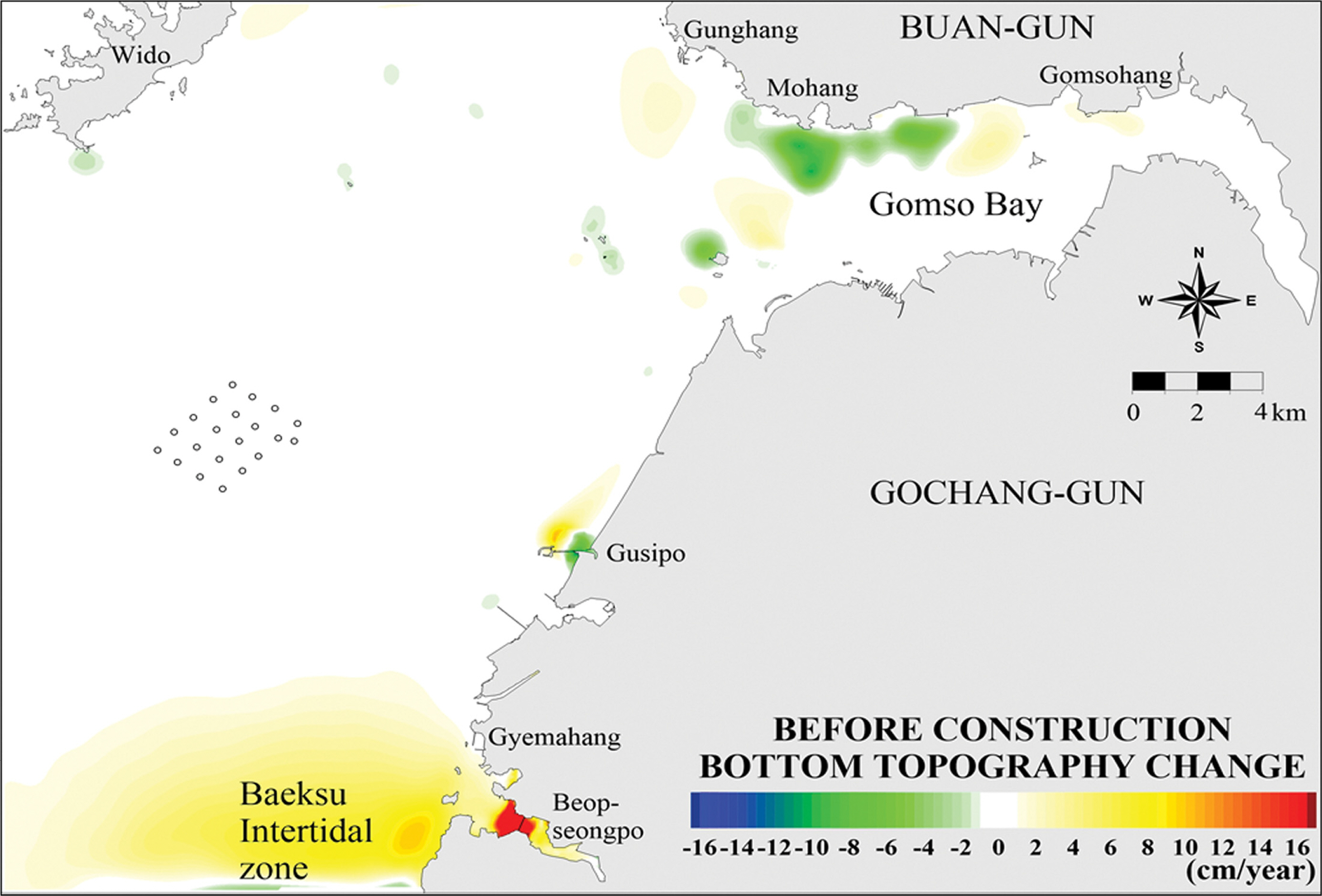
이러한 결과를 응용하여 부유사의 개경계조건을 시행착오적으로 부여하였는데, 적절한 경계조건의 판단기준은 개경계와 서로 인접한 영역에서 수심변화가 단속적으로 나타나지 않고 매끄럽게 나타날 때가 적정한 것으로 판단하였다. 그 결과, 해상풍력구조물 건설전의 연간침식퇴적의 계산결과를 나타낸 것은 Fig. 10이다. 여기서 사용된 개경계의 부유사농도는, Fig. 1의 개경계 코너점으로부터 Fig. 3과 같이 관측된 부유사농도에 대해, OBSS1 = 11.0배, OBSS2 = 0.5배, OBSS3 = 1.0배, OBSS4 = 1.0배 그리고 OBSS5 = 1.0배이었다. 이같이 남측 및 서측 개경계에서 부유사농도를 현장의 수심과 현장의 경험적인 부유사농도분포(Fig. 4 참조) 등을 고려하여 개경계마다 동일한 값을 사용하지 않고 선형적으로 변화하는 값을 부여하였다.
The bottom topography change per year before construction of the wind power farm.
이 그림에서처럼 백수조간대와 맞닿아 있는 남측경계 부근의 법성포 전면해역 및 법성포만 해역은 전반적으로 퇴적되고 특히 법성포만 내는 연간 100 cm 이상 퇴적되는 곳도 있는 것으로 계산되었다. 구시포항 부근은 항 배후 북측에서 퇴적이 일어나고 교량형태로 만들어져 해수소통이 있는 접속교 근처는 침식하는 경향을 보였다. 그리고 북측의 곰소만 해역은 퇴적과 침식이 교번적으로 나타나는데 만구 외측인 궁항 주변해역은 퇴적되고 만구인 모항부터 곰소항 구간까지 비교적 빠른 유속에 의해 침식되며, 만내측으로 가면서 간석지에서 미미하게 퇴적되는 것으로 계산되었다. 그리고 이들을 제외한 대부분의 해역은 연간침식퇴적량이 미미한 것으로 나타났다.
한편, 이러한 연간침식퇴적량은 해상풍력 구조물의 건설전후에 대하여 그 변화가 ± 1 cm 이상 발생하는 해역은 거의 나타나지 않았는데, 사용된 대격자 수치모형은 세굴과 같은 국지적 현상을 재현할 수 없고, 해상풍력 하부구조물이 직경 1 m 정도의 자켓타입의 투과식이므로 이들에 의하여 Fig. 8과 같이 ± 2 cm/s 이상의 유의미한 유속변화역이 거의 나타나지 않았기 때문에 해저지형변화가 미미한 것은 당연한 결과인 것으로 판단되었다.
The flow velocity change area between before and after construction of the jacket type structures around the wind power farm.
5. 요약 및 결론
서남해에서 해상풍력구조물의 건설에 따른 해저지형변화를 예측하기 위하여, 조석, 조류, 부유사 그리고 해저질 등에 대한 종합적인 동시현장조사를 수행하였고, 이들 자료를 수치실험에 활용될 수 있도록 하였다. 수치실험에서 표사량 산정은 관련상수를 시행착오적으로 변화시켜 관측된 부유사농도에 대해 계산값의 오차가 적당할 때에 경험상수들을 결정하는 방법을 사용하였고, 계산영역에서 연속관측된 부유사농도를 개경계조건으로 이용하였는데, 각 개경계에서 이 값에 대해 어떤 비율로 조정하여 경계조건으로 주었다. 한편, 해상에 설치되는 풍력발전기들의 자켓구조물은 유수 중에 잠겨 흐름 변화를 일으키므로, 이를 계산하기 위하여 유수저항에 관한 대격자 수치모형에 이들 구조물의 형상정보와 항력계수 등을 입력하여 흐름을 계산하였다. 이상의 결과를 정리하면 다음과 같다.
(1) 수치실험에서 표사량 산정은 관련상수를 시행착오적으로 변화시켜 관측된 부유사농도에 대해 계산값의 오차가 적당할 때에 경험상수들을 결정하는 방법을 사용하였는데, 어떤 농도분포인자 GAMSUS = 0.1 그리고 부유사 평형농도 공식의 비례상수 HANCON = 0.05일 때, 관측치와 계산치가 비교적 합리적으로 유사하였다.
(2) 개경계에서 부유사농도의 경계조건이 관측된 부유사농도에 대해 OBSS1=11.0배, OBSS2 = 0.5배, OBSS3 = 1.0배, OBSS4 = 1.0배 그리고 OBSS5 = 1.0배이었을 때, 개경계와 서로 인접한 계산영역 내의 수심변화 계산결과가 단속적이지 않고 매끄럽게 나타났다.
(3) 해저지형변화 계산결과, 백수조간대와 맞닿아 있는 남측경계역 부근의 법성포 전면해역 및 법성포만 해역은 전반적으로 퇴적되고 특히 법성포만 내는 연간 100 cm 이상 퇴적되는 곳도 나타났으며, 구시포항 부근은 항 배후 북측에서 퇴적이 일어나고 교량형태로 만들어져 해수소통이 있는 접속교 근처는 침식하는 경향을 보였다. 그리고 북측의 곰소만 해역은 퇴적과 침식이 교번적으로 나타나는데 만구 외측인 궁항 주변은 퇴적되고 만구인 모항부터 곰소항 구간까지 비교적 빠른 유속에 의해 침식되며, 만내측으로 가면서 간석지에서 미미하게 퇴적되는 것으로 계산되었다.
(4) 한편, 이러한 연간침식퇴적량은 해상풍력 구조물의 건설전후에 대하여 그 변화가 ± 1 cm 이상 발생하는 해역은 거의 나타나지 않았는데, 사용된 대격자 수치모형은 세굴과 같은 국지적 현상을 재현할 수 없고 해상풍력 하부구조물이 직경 1m 정도의 자켓타입의 투과식이므로 이들에 의하여 ± 2 cm/s 이상의 유의미한 유속변화역이 거의 나타나지 않았기 때문에 해저지형변화가 미미한 것은 당연한 결과인 것으로 판단되었다.