2.1 지배방정식

SWASH 모형은 수심평균, 비정수압과 자유수면 흐름을 Navier-Stokes 방정식의 질량·운동량 보존 조건으로 유도한 비선형 천수방정식을 적용한다(Zijlema and Stelling, 2005).

연속방정식은

여기서, x와 y는 정수면에 위치하고 있으며 t는 시간, ζ(x, y, t)는 정수면을 기준으로 자유수면까지의 높이, d(x, y)는 정수면, h = ζ + d는 총 수심, u(x, y, t), v(x, y, t)는 x, y 방향에 대한 수심평균유속, q(x, y, z, t)는 비정수압 압력성분, g는 중력가속도, c_f는 무차원 저면마찰계수, τ_xx, τ_xy, τ_yx, τ_yy는 수평난류응력, ν_t(x, y, t)는 쇄파와 Subgrid 난류에 의한 수평와점성계수, 는 혼합거리이다. 식(2)에서 비정수압형태의 압력경도는 식(6)과 같이 표현이 가능하다(Stelling and Zijlema, 2003).

q_b는 저면의 비정수압력이다. 단파에서 주파수분산의 정확한 표현을 위해 Keller-box method를 적용하였고 식(7)과 같다(Lam and Simlson, 1976).

자유수면에서 비정수압력은 0이다. 다음 고려될 변수는 자유수면의 연직속도성분(w_s)과 저면의 연직속도성분(w_b)이다. 수식속도성분에 대한 운동량 방정식은 식(8)과 같다.

식(8)에서는 이류·확산항은 일반적으로 연직가속도에 비해 충분히 작기 때문에 무시한다. 이는 비정수압의 압력경도에 의하여 결정된다. 식(7)과 식(8)을 이용하여 식(9)가 유도된다.

저면의 연직방향 속도성분(w_b)은 운동학적인 경계조건을 이용하여 표현가능하다.

이를 이용하여 국부적인 질량보존이 성립되며 식(11)과 같다.

비정수압 경사의 공간 이산화에는 많은 수치 기법들이 있지만 SWASH 모형에서는 Keller-box 방법과 중앙차분 방법 중 선택할 수 있다. 본 연구에서는 수평 및 수직 운동량 방정식의 이산화는 Keller-Box 기법(Zijlema and Stelling, 2008)을 기반으로 계산하였다.

2.2 격자의 구성 및 반사구조물

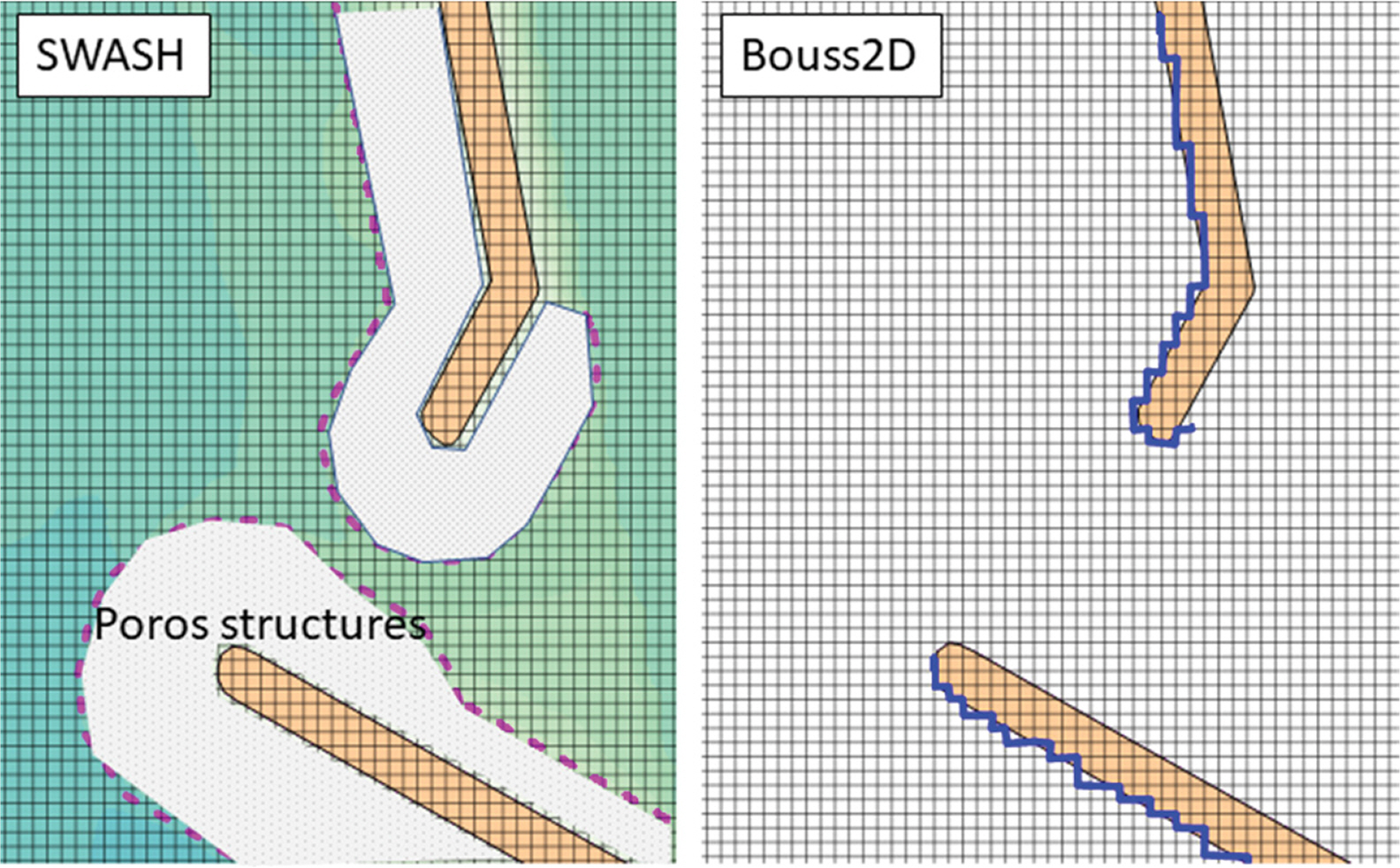
기존 다방향 불규칙파 실험에 사용되던 Boussinesq type의 수치모형인 Bouss2D(Nwogu and Demirbilek, 2001)와 SWASH 모형의 격자 구성 및 반사구조물의 재현에 대해 비교하고 차이점에 대해 검토하였다. Fig. 1에서 이형소파블럭사면을 예를 들어 격자의 구성 및 단면 반사 제어에 대해 도시하였다. SWASH 모형의 반사파 계산은 구조물의 반사경계 처리를 실제 수심 입력 데이터와 구조물의 경사, 공극률, 높이 및 크기에 따라 반사 및 투과파를 계산하고 다공성 구조물은 공극률 계수(0.0~1.0), 구성물질의 크기 및 높이(meter)로 정의된다. 또한, WET/DRY 조건에서 범람 및 월파 계산이 가능하다.

Fig. 1.

One-Dimensional Sectional Grid Control of Reflected Wave near the Breakwater in Numerical Model Experiment (Up: Breakwater cross-sectional shape, middle : Reflection boundary of the Bouss2D model, Down: Reflection boundary of the SWASH model).

방파제 개구부에서 2차원 평면적인 반사파 제어를 Fig. 2에 도시하였다. Bouss2D 모형과 SWASH 모형의 반사율 적용 격자의 개요를 보면 Bouss2D 모형은 하나의 격자면에서의 반사율 감쇄 계수로 반사파를 제어하는 반면, SWASH 모형은 실제 경사의 수심(불투과층)과 평면에 배치된 다공성 구조물의 공극률, 높이 및 크기가 반영되어 반사파를 제어한다. SWASH 모형은 규모가 작은 소규모 항만 및 국부적인 구역에서 파랑의 쇄파, 반사, 굴절 및 회절 현상을 구조물의 형태에 따라 잘 재현할 것으로 판단된다.

Fig. 2.

Two-Dimensional Grid of SWASH and Bouss2D model near the Breakwater in Numerical Model Experiments (Left: Reflection boundary of the SWASH model, Right: Reflection boundary of the Bouss2D model).

2.3 Boussinesq-type 모형과 SWASH 모형의 특징

Boussinesq-type의 파랑모형은 상대 수심이 큰 영역에서는 다소 부정확한 결과를 얻지만 고계도함수의 근사를 사용하며 비선형성을 고려하기 때문에 쇄파대 내의 모의에 정확성을 인정받고 있다. 기존의 Boussinesq-type의 파랑모형은 주파수 분산의 정확성을 높이기 위하여 도함수의 차수를 증가시켜 값을 근사시키는 방법을 사용하지만, 최근 SWASH, COULWAVE와 같이 다층기능을 이용한 수치기법으로 선형분산의 정확성을 개선한 모델들이 있다. 본 연구에서는 사용된 SWASH 모형은 연직방향의 층을 나눌 수 있는 다층기능과 비정수압 기법을 이용하여 선형분산의 정확성이 향상된 파랑변형계산을 수행할 수 있다(Zijlema and Stelling, 2005). 수심평균된 결과값을 얻는 기존의 Boussinesq-type의 파랑모형과 달리 SWASH 모형은 층별 자료를 얻을 수 있어 발전된 형태라고 말할 수 있다.

쇄파되는 파와 도수의 유사성을 고려하여 쇄파에 의한 에너지소산을 계산하고 쇄파조건에서 비선형파의 특징을 잘 재현하고 정수압흐름의 계산이 비정수압의 압력을 무시함으로써 간단하게 계산할 수 있기 때문에 대규모의 조석과 폭풍해일과 같은 계산에 적절하다.

3.1 모형 구성

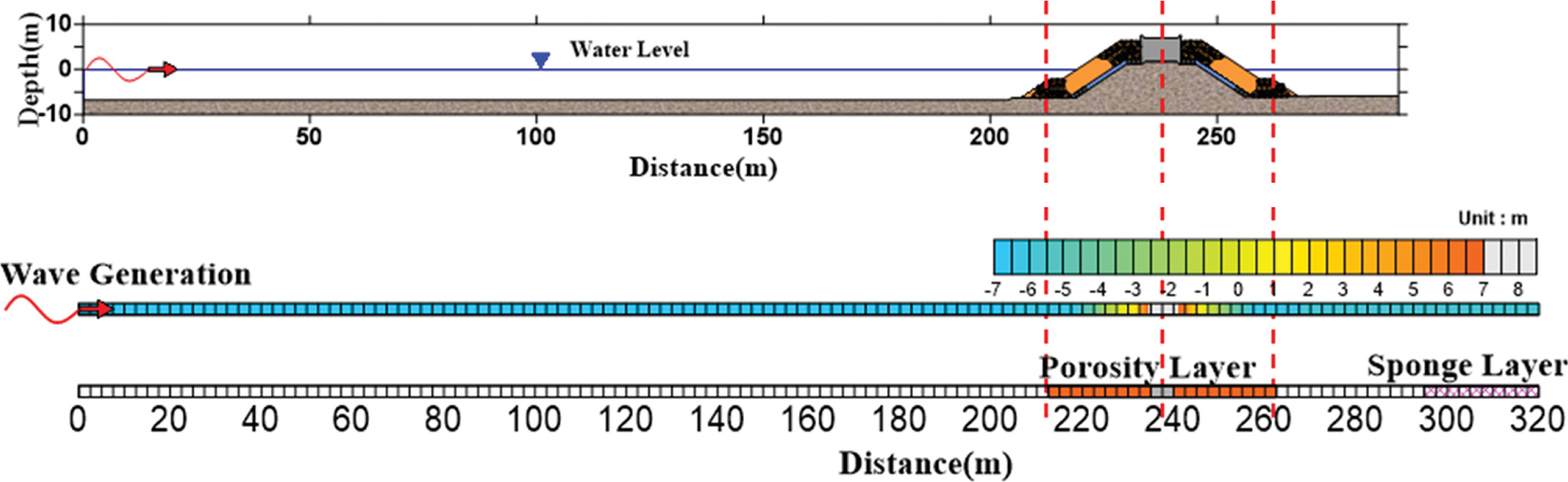
방파제는 1:1.5 경사로 Tetrapod(T.T.P)가 2열로 정적 되어있는 마리나의 방파제 단면을 대상으로 수행하였다. 입사파의 재원은 H_s = 4.0 m, T_p= 15.16 sec이며, 격자의 간격은 2.5 m, 불규칙파는 JONSWAP spectrum을 사용하였다. 입사파 조건에서 파장(L)은 200 m이며, 계산격자 안정조건에서 수심대비 파고비가 H/d << 1 인 경우 한 파장에 50개, 수심대비 파고비가 큰 경우 한 파장에 100개의 격자가 필요하다. 본 실험에서는 수심대피 파고비가 비교적 작은 조건으로 격자의 간격을 2.5 m로 한 파장에 80개의 격자를 나누어 구성하였다. 바닥은 실제 방파제 사면(1:25)의 불투과 지점까지의 수심으로 재현하였으며, 사석 및 T.T.P의 높이는 실제 투수성 구조물의 높이로 정의하였다. 다공성 구조물(C5) 실험에서 구조물의 입력조건인 alpha0, beta0 값은 SWASH 모형의 default 값을 사용하였고, 구조물의 크기(size)는 T.T.P 구조물의 지름을 적용하였다. 실험안은 Table 1과 같으며, 쇄파에 영향을 주지 않는 20 m 등수심(C1)과 실제 지형을 적용한 조건(C2), 직립구조물인 경우(C3), 불투수층 경사구조물(C4)을 적용한 조건 그리고 실제 이형 방파제 구조물 단면과 같이 실제 사석 및 T.T.P를 투수층으로 적용한 실험안(C5)으로 구성하였다.

Table 1.

Computational information of wave reflection numerical simulation

Fig. 3.

Definition sketch of wave reflection numerical simulation.

3.2 단면 반사율 실험결과

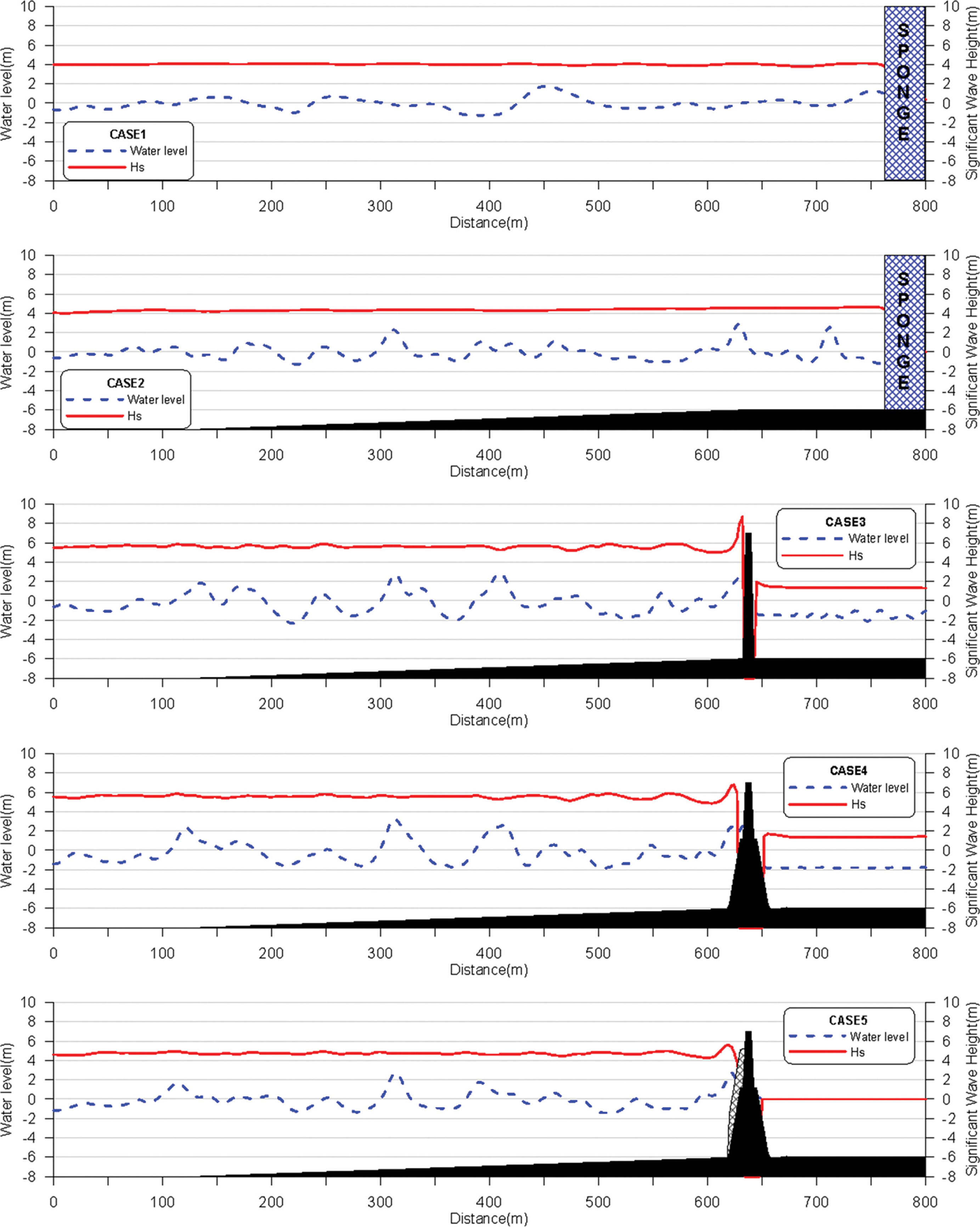
단면의 반사율 실험결과는 Fig. 4와 Table 2에 제시하였다. 파고 계산결과는 SWASH 모형에서 식(12)으로 계산되는 유의파고(H_s)를 사용하였다. E(f)는 스펙트럼 밀도의 분산함수이고, f는 주파수이다. 실험결과에서 계산영역의 최대 유의파고는 H_{s, max}로 정의한다. 등수심 20 m 조건(C1)에서의 실험결과인 Fig. 4와 Table 2를 보면 계산된 유의파고(H_s)가 4.0 m로 외부조파 경계에서 목표 파고값이 잘 계산되는 것으로 판단된다. 입사파고 대비 최대 유의파고(H₀/H_{s, max})는 1.0으로, 반사경계인 sponge layer에서 파의 흡수가 잘 이루어지는 것으로 판단된다.

Fig. 4.

Breakwater cross section reflection simulation results.

Table 2.

Comparison of breakwater cross section reflection simulation results and theoretical values (Stelling and Ahrens, 1981)

실제 지형(C2)에서는 파고비가 1.1로 계산되며, 이는 천수 변형에 의한 wave setup으로 10% 파고 증가가 나타난다. 직립구조물(C3)인 경우 전반사로 최대 2.0의 파고비를 보이고 이는 Ministry of oceans and fisheries(2014)에서 제시한 Stellig and Ahrens(1981)의 직립구조물 전면의 반사율과 유사한 값을 나타낸다. 불투수 사석층(C4)을 적용한 계산 결과 파고비는 1.7로 계산되었다. 실제 투수 사석 구조물(C5)을 적용한 실험의 계산 결과는 파고비가 1.4로 반사율이 0.4로 나타나며, 이는 Stelling and Ahrens(1981)의 이형소파블럭사면의 반사계수 개략치(0.3~0.5)와 유사하게 계산되었다.

SWASH 모형의 수심평균으로 계산된 단면 구조물 반사율 실험결과는 Stelling and Ahrens(1981)이 제시한 반사율의 개략치와 유사한 반사율을 나타내며, 구조물의 형상 및 지형에 따라 반사파가 잘 재현되는 것으로 판단된다.

4.1 불규칙파 입사파 경계조건

불규칙파 입사 조건에서 Goda et al.(1978)에 의해 작성된 불규칙파 회절도는 Bretschneider-Mituyasu 스펙트럼과 Mituyasu 방향함수를 이용하여 S_max로 정의된다. SWASH 모형은 JONSWAP 스펙트럼을 사용하고 방향집중도를 Wrappednormal 방향함수(DSPR, σ_θ)를 사용한 방향분산계수(ms)로 정의한다. Mituyasu형 방향함수(S_max)와 Wrapped-normal 방향함수(σ_θ)는 완전히 일치하지 않지만 Goda et al.(1999)은 두 방향함수와의 관계를 방향각의 표준편차 값을 이용한 비교를 통해 식(13) 및 식(14)를 조합하여 평균 집중도 파라미터를 환산할 수 있다고 제시하였다. 환산된 Wrappednormal형 방향함수(σ_θ)를 방향분산계수(ms)로 환산하기 위해 식(15)을 통해 계산하여 입력하였다. Goda의 회절도에 적용된 방향집중함수 S_max = 10, 75는 방향분산계수 ms = 1.8, 17.2로 환산되어 SWASH 모형을 이용한 수치모형실험에 적용하였다.

Table 3.

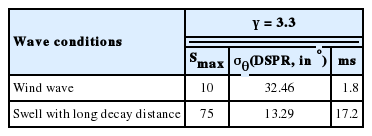
Relation with Mituyasu spreading function (S_max), directional spreading factor (σ_θ) and Directional distribution (ms)

4.2 다방향 불규칙파의 조파

SWASH 모형의 다방향 불규칙파 조파는 주기와 수심의 관계식에 의해 최대 주파수와 최소 주파수를 결정한다. 최대 주파수 영역 밖의 파랑 성분은 제외되고 수심방향으로 layer를 나누어 고주파수의 파랑장 재현성을 향상시킬 수 있다. 본 연구의 실험조건인 주기 10.0 sec, 수심 12.0 m인 실험조건에서 SWASH 모형의 외부조파기법을 사용하여 식(16)에 의해 최소주파수 0.05 Hz와 최대주파수 0.30 Hz 내의 불규칙 파형이 조파되며, 외부조파로 인한 실험영역 내의 재반사를 방지하기 위해 weakly reflective의 경계조건을 사용하였다. 조파시간(2시간)에 계산되는 불규칙파의 단일파 개수는 750개로 식(17)으로 계산된다. 모델의 분산관계식에 의해 허용되는 최대주파수(w_cf, cut-off frequency)는 식(18)에 의해 결정되며 수직 Layer(K)의 증가로 허용 가능한 주파수를 확장할 수 있다.

4.3 모형구성

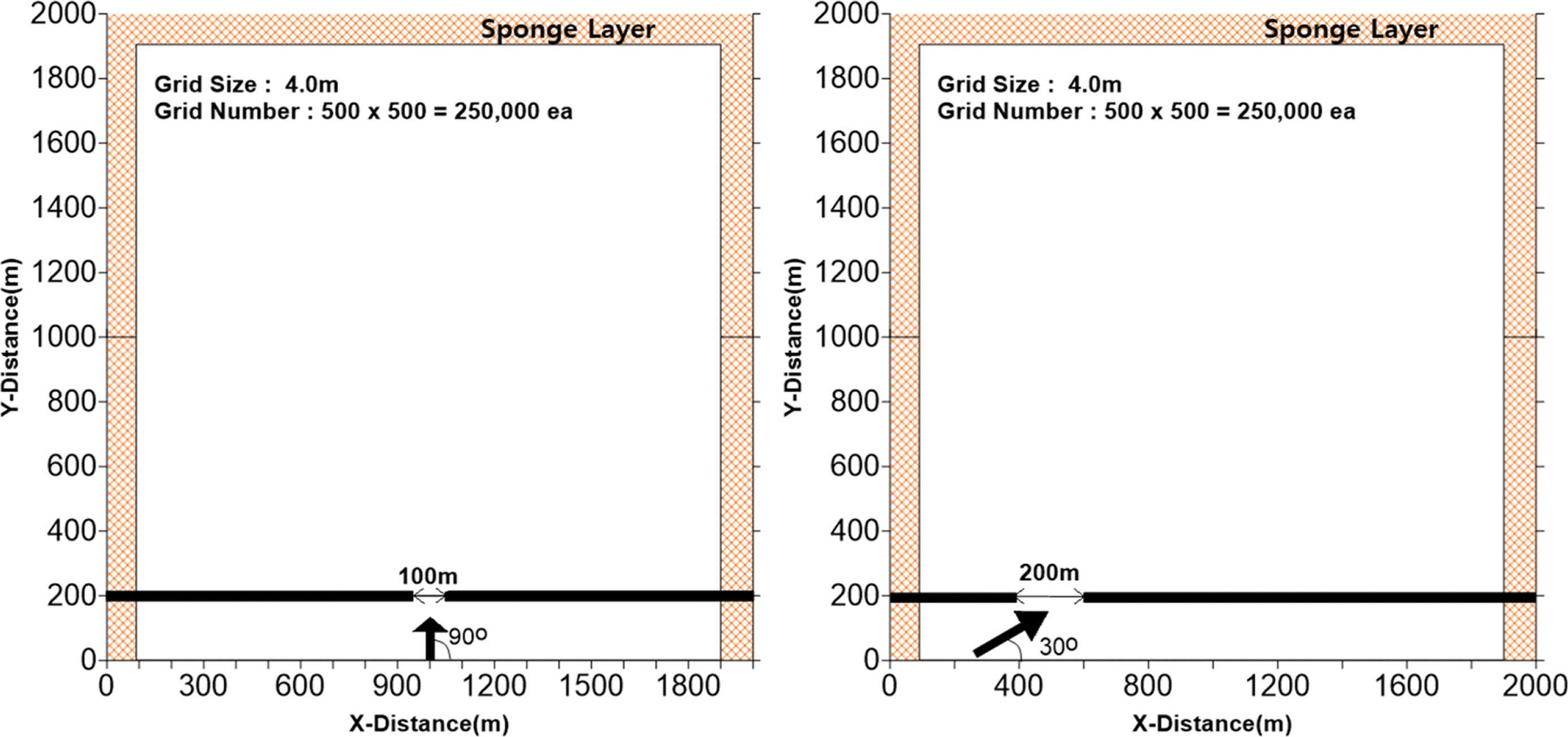
직각으로 입사하는 파에 대한 회절도 실험은 소규모 항만의 좁은 방파제 개구부 폭 재현을 위해 개구부 폭 대비 파장 비가 1.0인 영역을 구성하였으며, 경사로 입사하는 파에 대한 회절도 실험은 개구부 폭 대비 파장 비가 2.0인 영역을 구성하였다. 격자의 크기는 4.0 m, 계산 영역은 남북 동서 방향으로 2.0 km로 구성하였다(Fig. 5). 파랑은 SWASH 모형의 모듈 중 불규칙파 조파 기능을 사용하였다. 불규칙파의 스펙트럼은 JONSWAP(Deutsches hydrographisches institut, 1973)을 사용하였고, 형상계수는 JONSWAP 연구에서 제시한 평균값인 γ = 3.3을 사용하였다. 경계에서의 반사파 제어를 위해 모형의 동, 서와 북측 경계에 100.0m 두께의 Sponge layer를 주었다.

Fig. 5.

Definition sketch of wave diffraction numerical simulation.

Table 4.

Computational informations of wave diffraction numerical simulation

실험안은 Table 5에 제시하였으며, 직각 입사파의 경우 방향분산계수 ms = 1.8, 17.2인 경우에 대해 계산을 수행하였다. 본 실험조건이 불규칙파의 조파 시 최대 허용주파수(w_f=0.29 Hz)가 최대주파수(frequency_max = 0.3Hz)보다 작기 때문에 수직적인 격자구성에 대한 검토를 위해 수심 평균 계산 시와 수직 layer를 2개로 나눈 경우(w_f = 0.58Hz)에 대한 실험을 수행하였다. 경사(30°) 입사파에 대한 회절도 검토를 위해 방향분산계수를 ms = 1.8, 17.2인 경우에 대한 회절도를 검토하였다.

Table 5.

Diffraction simulation plan (case)

4.4 회절도 실험결과

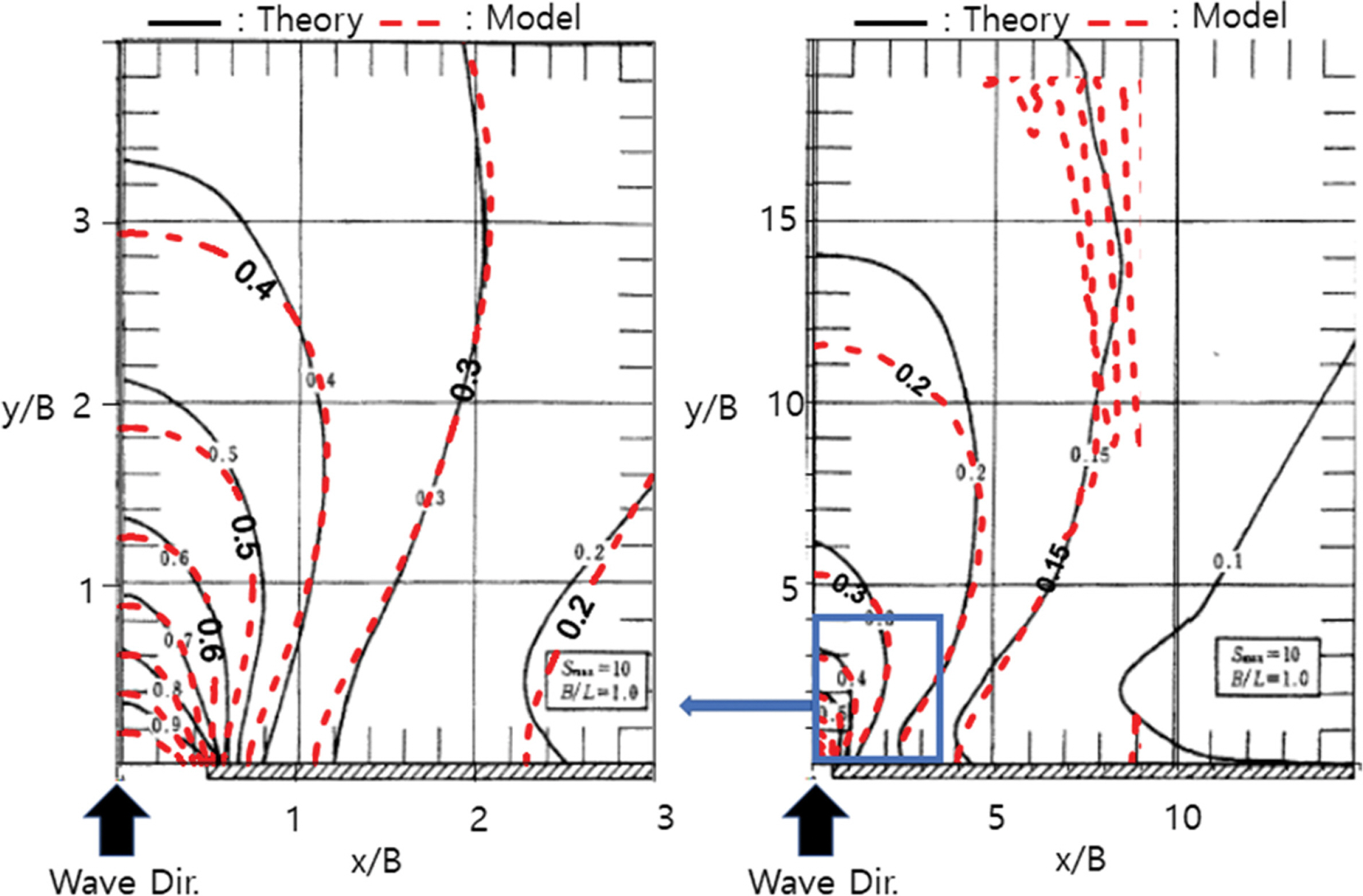
구조물에 직각으로 입사하고 불규칙파의 방향 집중도가 작은(ms = 1.8) 경우의 실험결과를 Fig. 6~7에 도시하였다. 실험안 D1에서의 방파제 개구부 후면에서의 파고비 계산결과, 실험 결과가 이론해의 전파양상을 잘 재현한다. 불규칙파의 방향분산 각도가 큰 경우 수치모형실험의 회절도가 파고비 0.4~0.6 영역에서 일부 저평가되는 것을 확인할 수 있다(Fig. 6). 실험안 D1에서 2개의 수직 layer로 나눈 실험안 D2의 경우 파고비 계산결과, 실험 결과와 이론해의 항내로 진입하는 파의 전파양상는 유사하지만 실험안 D1과 마찬가지로 파고비 0.4~0.6 구간에서 일부 회절도가 저평가되는 것을 확인할 수 있다(Fig. 7).

Fig. 6.

Diffraction diagrams for ms = 1.8, one vertical layer (D1).

Fig. 7.

Diffraction diagrams for ms = 1.8, two vertical layers (D2).

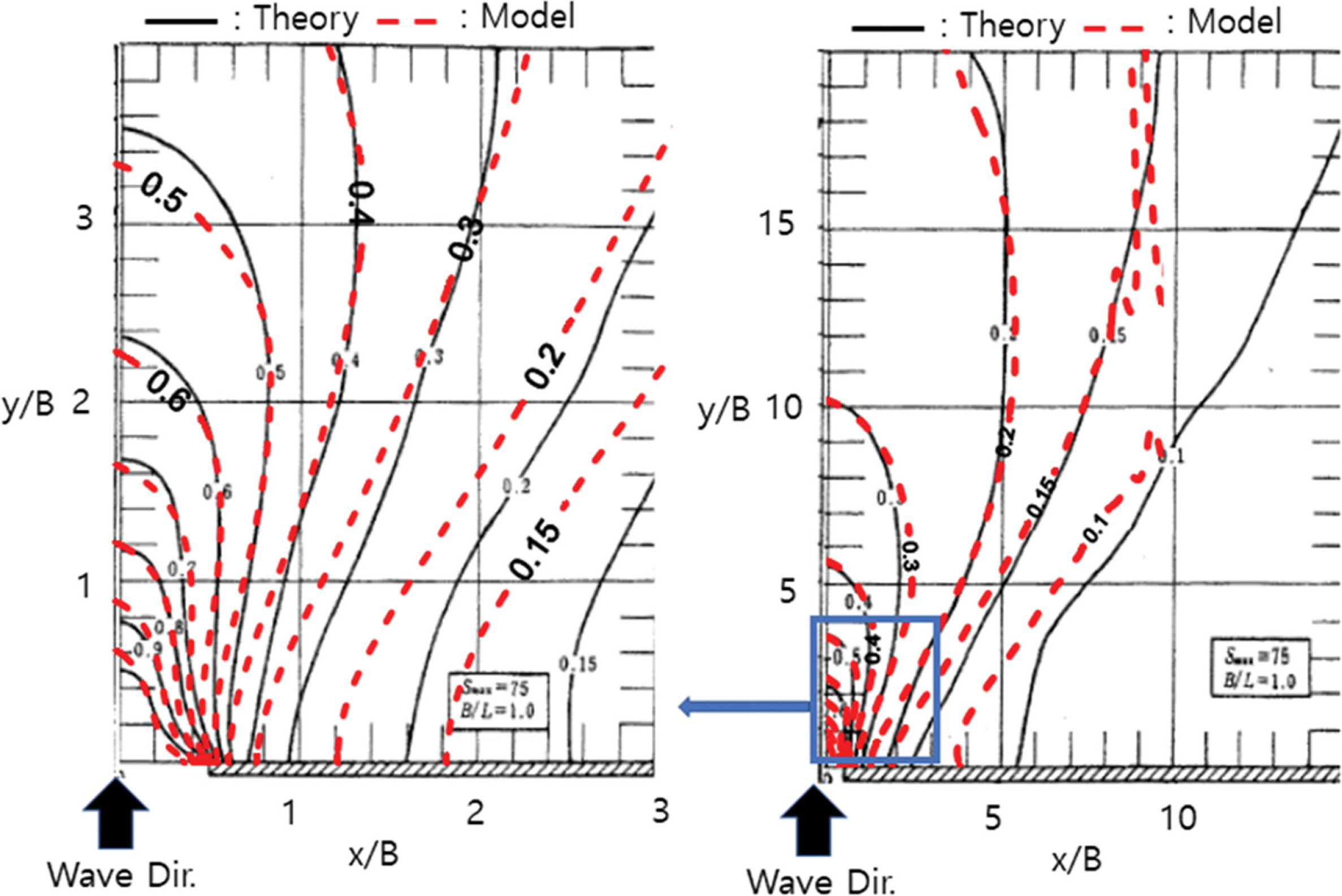
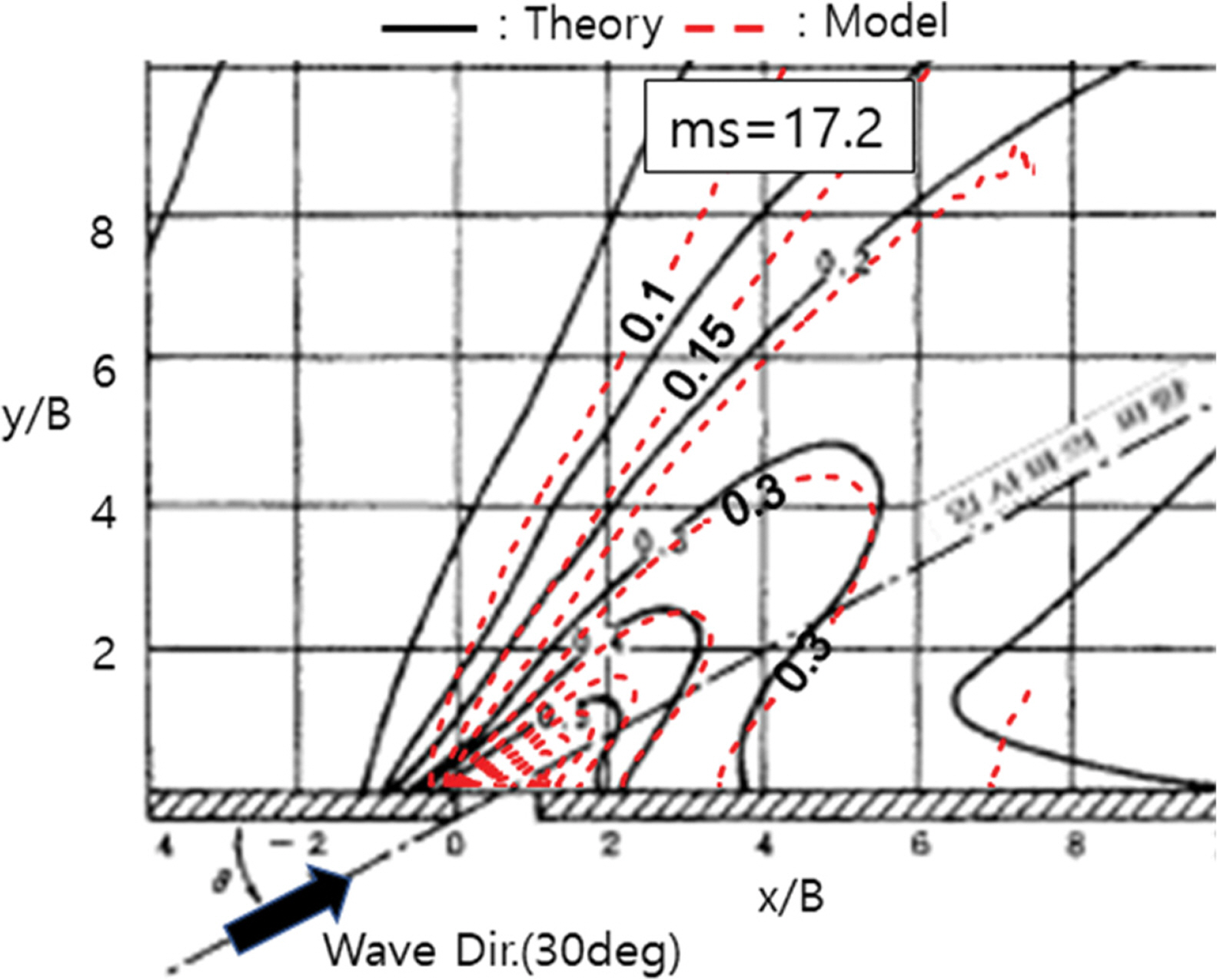
구조물로 직각으로 입사하고 불규칙파의 방향 집중도가 큰(ms = 17.2) 경우의 실험결과를 Fig. 8~9에 도시하였다. 실험안 D3에서의 방파제 개구부 후면에서의 파고비 계산결과, 실험결과와 이론해의 전파 형태는 아주 유사하게 나타나고, 파고비가 0.5~0.6인 구간에서 일부 파랑에너지 전파가 낮은 것으로 판단되지만 아주 유사한 결과를 나타낸다(Fig. 8). 실험안 D3에서 2개의 수직 층을 나눈 실험안 D4의 경우를 보면, 파고비 계산결과가 이론해의 형태와 크기가 유사하며, 수심 평균 실험안 D3에 비해 정확도가 높아진 것을 확인하였다(Fig. 9).

Fig. 8.

Diffraction diagrams for ms = 17.2, one vertical layer (D3).

Fig. 9.

Diffraction diagrams for ms = 17.2, two vertical layers (D4).

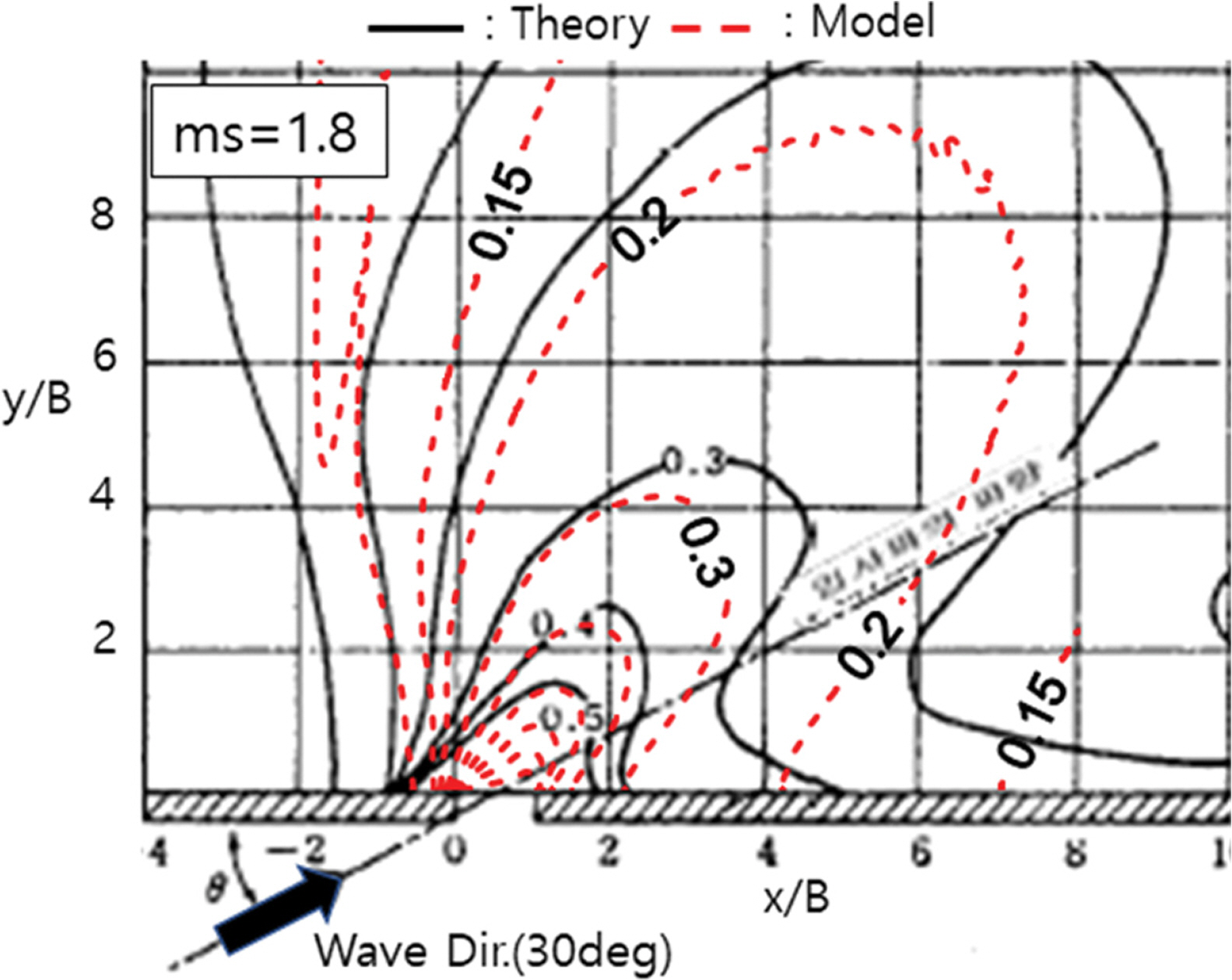
경사 입사에 의한 실험 D5에서의 방파제 개구부 후면에서의 파고비 계산결과는 Fig. 10에 도시하였으며, 불규칙파의 방향분산이 집중도가 작은 경우(ms = 1.8) 진입 각도 및 전파양상은 잘 재현하는 것으로 판단되지만 수치모형 실험결과가 이론해에 비해 영향범위가 저평가 되는 경향을 보인다. 경사 입사에 의한 실험 D6에서의 방파제 개구부 후면에서의 파고비 계산결과는 Fig. 11에 도시하였으며, 불규칙파의 방향 집중도가 큰 경우(ms = 17.2) 수치모형 실험결과가 이론해와 입사파의 진입각도 및 전파양상이 유사한 분포를 보이는 것을 확인하였다.

Fig. 10.

Diffraction diagrams for incident wave at 30^°, ms = 1.8 (D5).

Fig. 11.

Diffraction diagrams for incident wave at 30^°, ms = 17.2 (D6).

회절도 실험결과 직각 입사 및 경사 입사 모두 방향 집중도가 작은 경우, 회절도 이론값 보다 저평가되는 경향을 보인 반면에 방향집중도가 큰 경우, 계산 값과 이론값이 유사한 형태를 보이며 이는 연안에서 충분히 발달된 너울성 파랑의 정온도를 평가하는 경우에는 적용이 가능할 것으로 판단된다. 방향집중도가 낮은 경우가 높은 경우에 대비 파고비가 저평가되는 것을 확인할 수 있었다. 이는 방향집중도가 작을수록 방파제 개구부로 진입하는 파의 에너지 전파 영향 범위가 넓어져서 저평가되는 것으로 사료된다.

수직층을 2개로 나눈 경우의 방파제 회절도 검토 결과, 수직층 증가가 방향집중도가 높은경우의 정확도 향상에 기여했지만 방향 집중도가 낮은 실험의 정확도 향상에는 기여하지 못하였다. 이는 수직층의 최대허용주파수를 증가시켜 허용 가능한 불규칙파의 범위를 키우는 효과보다는 분산항의 기능 향상으로 인한 모형의 정확도 개선의 영향인 것으로 판단된다.