Article information

Abstract

Trans Abstract

1. 서 론

지난 20세기의 전 세계 주요 에너지원인 석탄, 석유, 천연가스 등으로 대표되는 화석연료 에너지들이 과학기술의 발달로 새롭게 등장한 에너지 자원으로 빠른 속도로 대체되기 시작되었다. 세계 각국은 지구온난화로 인한 기후변화에 생존의 위협을 느껴 화석에너지 문제에 적극적으로 대처하고 있어 이들 화석연료들은 매장량에 상관없이 빠른 속도로 다른 에너지로 대체될 것이다. 이러한 추세에 맞춰 선진국을 중심으로 녹색 에너지와 신재생 에너지에 많은 관심을 갖고 이에 대한 지속적인 연구와 투자를 하고 있지만 신재생 에너지 확대에 따른 산림파괴, 자재 생산 및 폐기로 인한 환경오염 등의 문제도 발생하고 있다. 파랑에너지는 개발 및 해체로 발생하는 환경비용이 상대적으로 작고 엄청난 잠재량을 지니고 있어 미래 신재생 에너지의 중요한 부분을 차지할 것으로 전망하고 있다.

진동수주형(Oscillating Water Column, OWC) 파력발전장치는 19 세기 초반에 개발되어 기술의 안정화 단계에 접어든 1세대 파력발전장치로 유럽을 중심으로 현재 가장 많이 설치된 파력발전장치이다. 진동수주형 파력발전장치는 바닥면이 뚫린 콘크리트 또는 철 구조물로 사각형 또는 원기둥 형태를 갖는다. 일정 깊이 잠긴 OWC 파력발전장치 내부의 수면운동은 공기실내의 변동압력을 일으키고, 변동압력은 공기 흐름을 유발하여 공기실 상부에 설치된 터빈을 작동시켜 전기를 생산하게 된다. 터빈과 발전기로 구성된 2차 변환장치인 PTO(Power Take-off) 장치는 공기실 상부에 위치하여 직접 물과의 접촉이 없어 비교적 안전하게 역학적 에너지를 전기에너지로 변환한다. OWC 파력발전장치는 고속으로 회전하는 공기 터빈을 사용하면 높은 주파수에서도 전기를 생산할 수 있으며, 물과 접촉하여 움직이는 구동부가 없어 유지보수가 용이하고, 고정식으로 연근해에 설치가 가능하므로 장거리 수중 송전 케이블이 필요 없다는 장점들을 가지고 있다. 또한 비교적 단순한 형태이므로 제작이 용이하며, 해양공간을 효율적으로 사용할 수 있다. 국내에서는 선박해양플랜트 연구소 등을 중심으로 2000년대부터 연구개발이 추진되었고, 500 kW급 용수시험파력발전소(진동수주형)가 제주도에 구축되어 시험운전을 하며 전력을 생산하고 있다. 최근에는 전력 공급이 어려운 섬지역에 적합한 방파제 연계형 OWC 파력 발전장치도 개발하고 있다.

OWC 파력발전장치의 최적설계를 위해서는 작업 조건(operating condition)에서의 유체역학적 발전성능을 파악하여야 한다. OWC 파력발전장치의 최적형상을 결정하는데 있어서 중요한 핵심은 OWC 장치내 유체의 고유주파수를 입사파의 주파수와 일치시켜 내부 수면운동을 크게 증폭시키는 공진현상을 이용하는 것이다. OWC 장치내의 공진을 유발하는 유체의 고유주파수를 크게 나누면 피스톤과 같이 형태의 변화 없이 상하로 진동하는 피스톤(piston) 모드 고유주파수(ω₀)와 여러 진동모드를 갖는 슬로싱(sloshing) 모드 고유주파수들(ω_n, n = 1, 2, 3…)이 있다. OWC 장치와 같이 입사파에 비하여 내부유체 면적이 작은 경우에는 주로 피스톤 모드 공진주파수가 에너지 밀도가 높은 주파수대에 위치하므로 이를 활용하여 OWC 장치를 설계하는 것이 바람직하다. 즉, 설치해역의 파랑스펙트럼에서 에너지 밀도 가장 높은 주파수 대역에 속하는 에너지 주기(energy period)에 피스톤 모드 고유주파수가 일치하도록 OWC 파력발전장치의 형상을 설계한다.

지금까지 유체역학적 관점에서 OWC 파력발전장치의 성능 평가를 다룬 많은 연구논문들이 발표되었다. Evans(1978)는 OWC 내 자유 수면을 강체 피스톤으로 가정하여 OWC 파력발전장치의 에너지 추출이론을 개발하였다. Evans(1982)는 다수 설치된 OWC 파력발전장치를 통한 추출효율을 구할 수 있도록 해석이론을 확장하였다. Sarmento and Falcão(1985)는 OWC 장치의 최적 효율을 얻기 위한 공기실내의 변동압력에 대한 위상제어의 중요성을 강조하였다. Evans and Porter(1995,1997)는 안벽 앞에 고정된 사각형 진동수주형 파력발전장치가 놓여있을 때 격벽 끝단에서의 유속의 특이거동을 고려하기 위하여 Galerkine 방법을 사용하여 고정식 진동수주형 파력발전장치에 대한 입사파의 회절문제와 공기실내의 변동압력에 의한 파의 방사문제를 고유함수전개법으로 풀어 파랑에너지 추출효율을 계산하였다. Clément(1997)는 비선형 자유표면 경계조건을 고려한 2차원 수치파 수조(numerical wave tank)를 개발하여 2차원 OWC 장치를 포함한 비선형 문제를 다루었다. 더 나가 Clément(1997)는 OWC 장치의 격벽의 깊이와 두께와 형상이 OWC 장치내 수면 운동에 미치는 영향을 분석하였다. Hong et al.(2007)은 직립벽 앞에 놓인 2차원 OWC 파력발전장치의 추출파워를 구하기 위해 공기실 안과 밖에 서로 다른 Green 함수를 적용하여 수치해를 구하였고, 모형실험을 수행하여 수치결과와 모형실험 결과를 서로 비교하였다. 이밖에도 포텐셜이론에 기반을 두고 자유표면의 비선형성을 고려한 시간영역해석법을 OWC 파력발전장치의 성능해석에 적용한 연구들도 있다(Koo and Kim, 2010; Luo et al., 2014; Ning et al., 2015). 또한 점성유체를 다루는 CFD 코드를 OWC 파력발전장치 성능해석에 활용한 연구 논문들도 있는데, 수치 모의는 Reynolds Averaged Navier-Stokes(RANS) 방정식에 기반을 둔 난류 모델을 사용하였고, VOF(Volume Of Fluid) 법을 적용하여 자유수면의 변동을 추적하였다(Hirt and Nichols, 1981; el Marjani, et al., 2008; Paixão, et al., 2008).

본 연구에서는 직립 안벽 앞에 2차원 사각형 진동수주형 파력발전장치가 놓여 있을 때 규칙파와 불규칙파에서의 OWC 파력발전장치의 추출효율과 반사율의 상관관계를 살펴보았다. 해석방법으로 초기설계 단계에서 많이 사용하는 선형포텐셜 이론에 기반을 둔 고유함수전개법을 사용하였다. 여기에 OWC 격벽의 끝단에서의 유속의 특이거동을 고려하기 위하여 Evans and Porter(1995)의 Galerkine 방법을 함께 사용하였다. 공기실이 완전 개방되었을 때 입사파에 의한 산란문제와 닫힌 공기실내의 변동압력에 의한 방사문제를 풀어 OWC 장치내 유량을 구하고 이를 공기실내의 공기 흐름에 대한 연속방정식에 대입하여 변동압력과 추출파워를 구한다. 규칙파 해석에서 얻은 공기실내의 변동압력과 추출파워 그리고 반사율 결과를 불규칙파로 확장하여 추출효율과 반사율을 구하였다. 추출파워를 구할 때 주파수 함수인 최적 터빈계수를 적용하는데 불규칙파인 경우 피스톤 모드 공진주파수에서의 최적 터빈계수를 사용하였다.

2. 문제의 정식화

수심(h)이 일정한 해역에 길이(L), 격벽의 잠긴깊이(d), 높이(H)인 2차원 사각형 OWC 파력발전장치가 직립 안벽 앞에 놓여 있다고 가정한다. Fig. 1과 같이 직교 좌표계(x, z)를 도입하고 원점은 OWC 격벽과 수면이 만나는 위치에 놓여 있으며, z축의 양의 방향을 연직 상향으로 잡았다. x축의 음의 방향으로 들어오는 입사파는 OWC 파력발전장치내 유체의 수면운동을 일으킨다. 선형포텐셜이론을 가정하여 속도포텐셜 Φ(x, z, t)을 도입하고 입사파가 주파수 ω을 갖고 조화 운동을 한다고 가정하면 속도포텐셜, 수면변위, 그리고 공기 실내의 변동압력을 아래와 같이 공간과 시간 함수로 나누어 아래와 같이 쓸 수 있다.

Fig. 1.

Definition sketch of a 2D fixed OWC wave energy converter in front of a seawall.

전체 속도포텐셜은 공기실을 완전히 개방하였을 때의 입사파에 의한 회절을 나타내는 회절포텐셜(ϕ_D = ϕ_I + ϕ_S)과 닫힌 공기실내의 변동압력에 의한 방사포텐셜(ϕ_R)의 합으로 아래와 같이 표현된다.

여기서 A는 입사파의 진폭이다.

식(2)의 회절과 방사 포텐셜은 아래 주어진 경계치문제를 만족한다.

여기서 밑첨자 D는 회절포텐셜을, S는 산란포텐셜을, R는 방사포텐셜을 나타낸다. K = ω²/g이다.

식(3)에 주어진 회절과 방사 경계치문제를 풀어 회절과 방사 속도포텐셜을 구하면 OWC 파력발전장치내 수면운동에 의한 유량(Q(t) = Re{qe^-iωt})를 구할 수 있다. 여기서 복소수 값을 갖는 유량(q)는 다음과 같다.

식(2)을 식(4)에 대입하면 q_D와 q_R은 아래와 같다.

여기서 q_D는 열린 공기실내로 입사하는 파에 의한 내부 유량을, q_R는 닫힌 공기실내 변동압력에 의한 내부 유량을 나타낸다. 특히 q_R의 실수부(B)를 방사컨덕턴스(radiation conductance), 허수부(C)를 방사어드미턴스(radiation admittance)라 부른다.

3. 결과 및 고찰

Fig. 2는 본 해석방법의 신뢰성을 검증하기 위하여 같은 고유함수전개법을 사용한 Evans and Poter(1995)의 해석결과와 비교한 결과를 보여주고 있다. 계산 조건으로 무차원화된 OWC의 길이와 잠긴깊이는 각각 L/h = 0.25, d/h = 0.5이다. 여기서 C¯ = ρgωLC, B¯ = ρgωLB는 무차원화된 방사어드미턴스와 방사컨덕턴스이다. x 축은 무차원화된 주파수 ω² h/g로 잡았다. 계산에 사용한 z 축의 고유함수 개수는 N = 100이며 Galerkin 방법의 전개식의 개수는 M = 10이다. 현재의 해석 결과는 Evans and Poter(1995)의 결과와 일치하였다. 고유함수전개법에 Galerkin 방법을 함께 사용하면 격벽 끝단에서 나타나는 유속의 제곱근 특이성을 전개식(13)안에서 미리 고려할 수 있기 때문에 수렴도가 향상된다. 이후의 모든 계산에서는 N = 100, M = 10을 사용하였다.

Fig. 2.

Comparison of non-dimensional radiation admittance (C̄) and radiation conductance (B̄) with Evans and Porter(1995)’s results for L/h = 0.25, d/h =0.5.

Fig. 3은 공기실이 열려있을 때 입사파에 의한 OWC 장치의 격벽과 안벽 사이의 유체 수면운동에 의한 유량(q_D)을 격벽의 잠긴깊이(d = 2, 3, 4 m)를 변화시키면서 입사파의 주파수 변화에 따라 그린 그림이다. 공기실의 길이(L)과 높이(H)은 각각 5 m와 3 m이며, 수심(h)은 20 m이다. 잠긴깊이가 증가하면서 특정 주파수(1.38, 1.26, 1.16 rad/s)에서 유량의 피크 값이 존재한다. 잠긴깊이가 깊을수록 피크 값은 증가하나 피크 폭은 감소한다. 입사파에 의한 유량(q_D)의 피크 값은 내부유체의 고유주파수와 입사파의 주파수가 일치할 때 생기는 공진으로 발생한다. Fig. 3의 주파수 범위내에 나타난 주된 공진은 형태의 변화 없이 수면이 상하로 진동하는 피스톤 모드(piston mode) 공진주파수(1.38, 1.26, 1.16 rad/s)에서 일어난다. ω = 2.5 rad/s에 나타난 스파이크(spike) 형태의 피크 값은 1차 슬로싱 모드(sloshing mode) 공진에 기인한다.

Fig. 3.

Induced volume fluxes by the incident waves as a function of submergence depth d for h =20m, L =5m, H =3m.

Fig. 4는 Fig. 3과 동일한 계산조건 아래에서 닫힌 공기실내의 변동압력에 의한 유량(q_R = - (B - iC))을 살펴보았다. 방사어드미턴스(C)는 주파수에 따라 증가하다가 피스톤 모드 공진주파수에 가까워지면 양의 값에서 음의 값으로 큰 폭으로 변화한다. 반면에 방사컨덕턴스(B)는 C = 0인 공진주파수에서 최대값을 갖는다. 잠긴깊이가 증가할수록 B의 피크 값은 증가하고 피크 폭은 줄어든다. 이러한 독특한 현상은 안벽과 격벽으로 둘러싸인 닫쳐진 유체영역내에 공진을 유발하는 메커니즘이 존재할 때 발생한다. 이와 비슷한 예로는 안벽에 평행하게 계류된 선박, 2개의 동체가 결합된 쌍동선(catamaran), 문풀(moon pool)을 가진 해상 플랫폼 등이 있다.

Fig. 4.

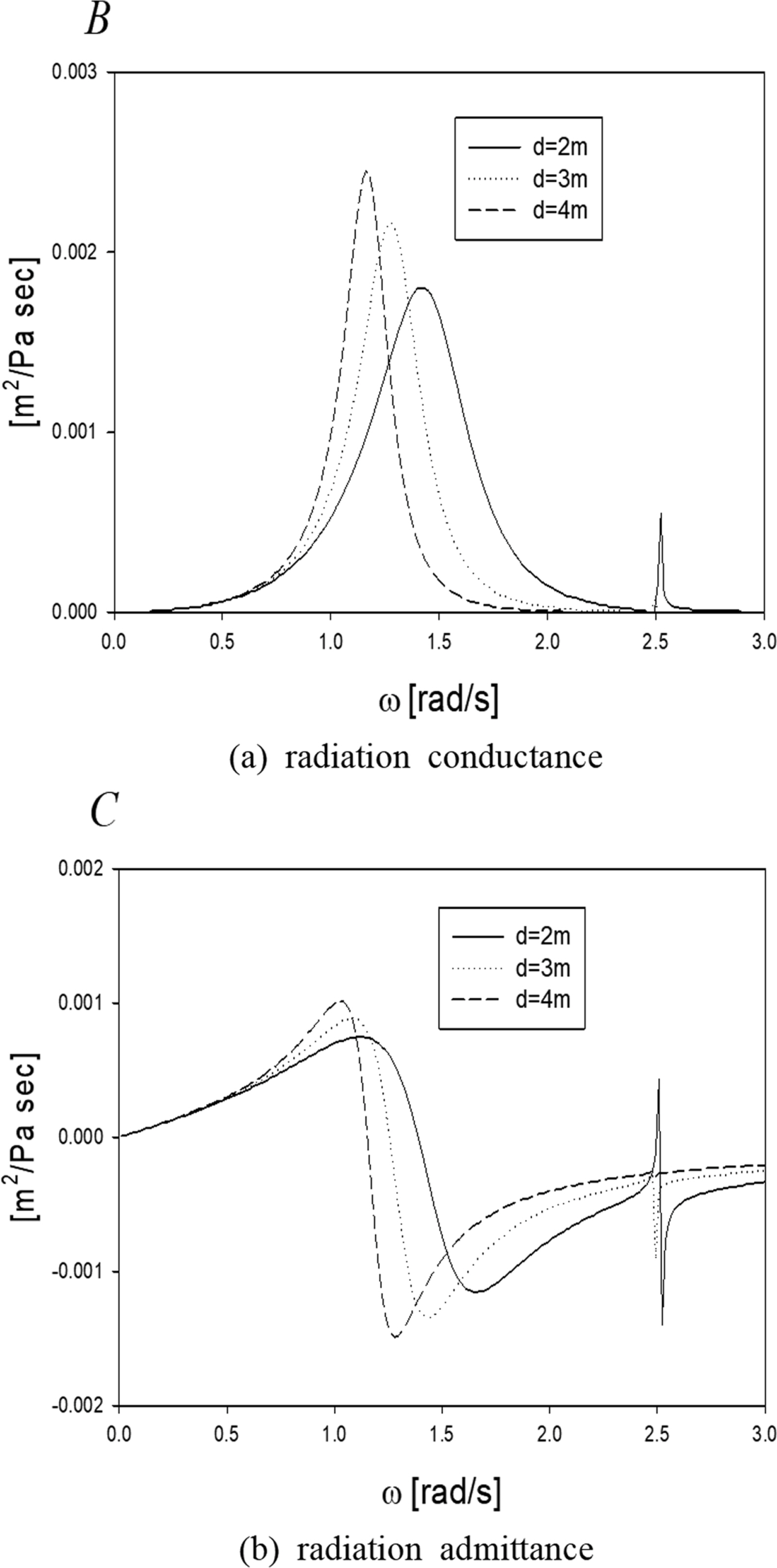
Induced volume fluxes by the oscillating chamber pressure: (a) radiation conductance and (b) radiation admittance as a function of submergence depth d for h =20m, L =5m, H =3m.

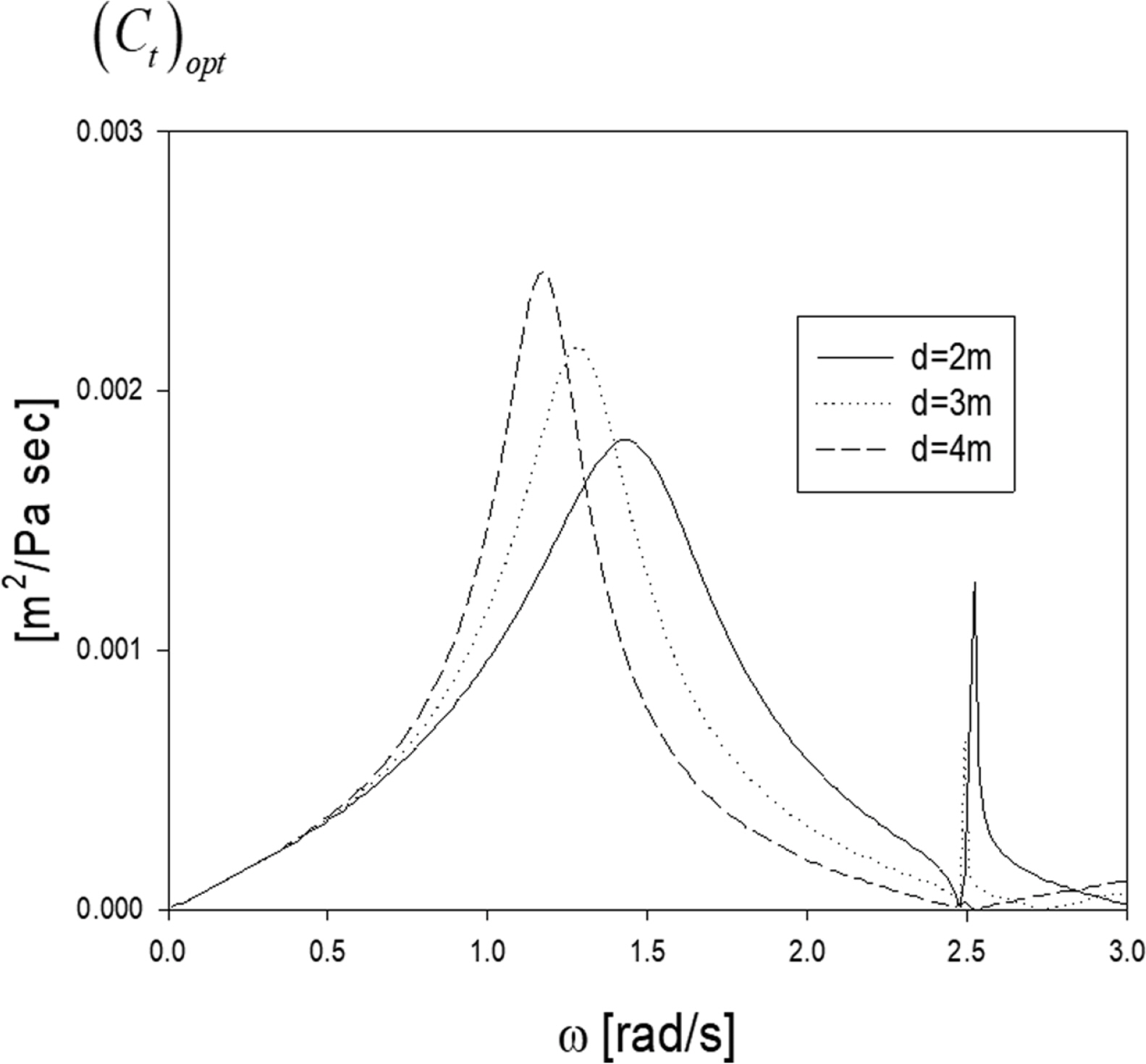
Fig. 5는 식(30)에 주어진 최적 터빈계수((C_t)_opt)를 주파수에 따라 그렸다. 최적 터빈계수 곡선은 피스톤 모드와 1차 슬로싱 모드 공진주파수에서 최대값을 갖는다. 터빈계수는 파력발전장치를 통하여 에너지를 추출할 때 발생하는 PTO 감쇠계수와 비슷한 개념이다. 식(28)에서 보듯이 추출파워는 터빈계수에 따라 선형적으로 증가하나 터빈계수의 증가는 감쇠력의 증가로 이어져 추출파워를 감소시킨다. 따라서 Fig. 5를 참조하여 입사파 주파수의 함수인 최적 터빈계수 값에 따라 적절한 크기와 형상을 갖는 터빈을 설계하는 것이 필요하다.

Fig. 5.

Optimal turbine coefficient as a function of submergence depth d for h =20m, L =5m, H =3m.

앞에서 최적 터빈계수를 적용하여 얻은 추출파워와 효율을 Fig. 6에 그렸다. 예상대로 피스톤 모드 공진주파수에서 추출파워와 효율이 최대가 됨을 볼 수 있다. 1차 슬로싱 모드 공진주파수에서도 추출파워와 효율의 피크 값이 존재하나 크기도 작을 뿐만 아니라 피크 폭이 매우 좁아 전체 OWC 파력 발전성능에 큰 기여를 하지 못한다. 현재의 포텐셜이론에서 고려하지 못한 점성효과를 포함한 여러 감쇠력을 고려하면 추출파워와 효율의 최대값이 감소되리라 예상되지만 현재 이론에서는 피스톤 모드 공진주파수에서 100%의 효율을 보이고 있다. 특히, 흥미로운 사실은 격벽의 깊이가 감소할수록 추출파워와 효율 곡선의 공진 폭이 넓어지면서 발전 가능한 주파수의 범위가 확장됨을 알 수 있다. 즉, 격벽의 잠긴깊이가 전체 에너지 생산량과 추출효율에 큰 영향을 미치고 있음을 Fig. 6을 통하여 확인할 수 있었다.

Fig. 6.

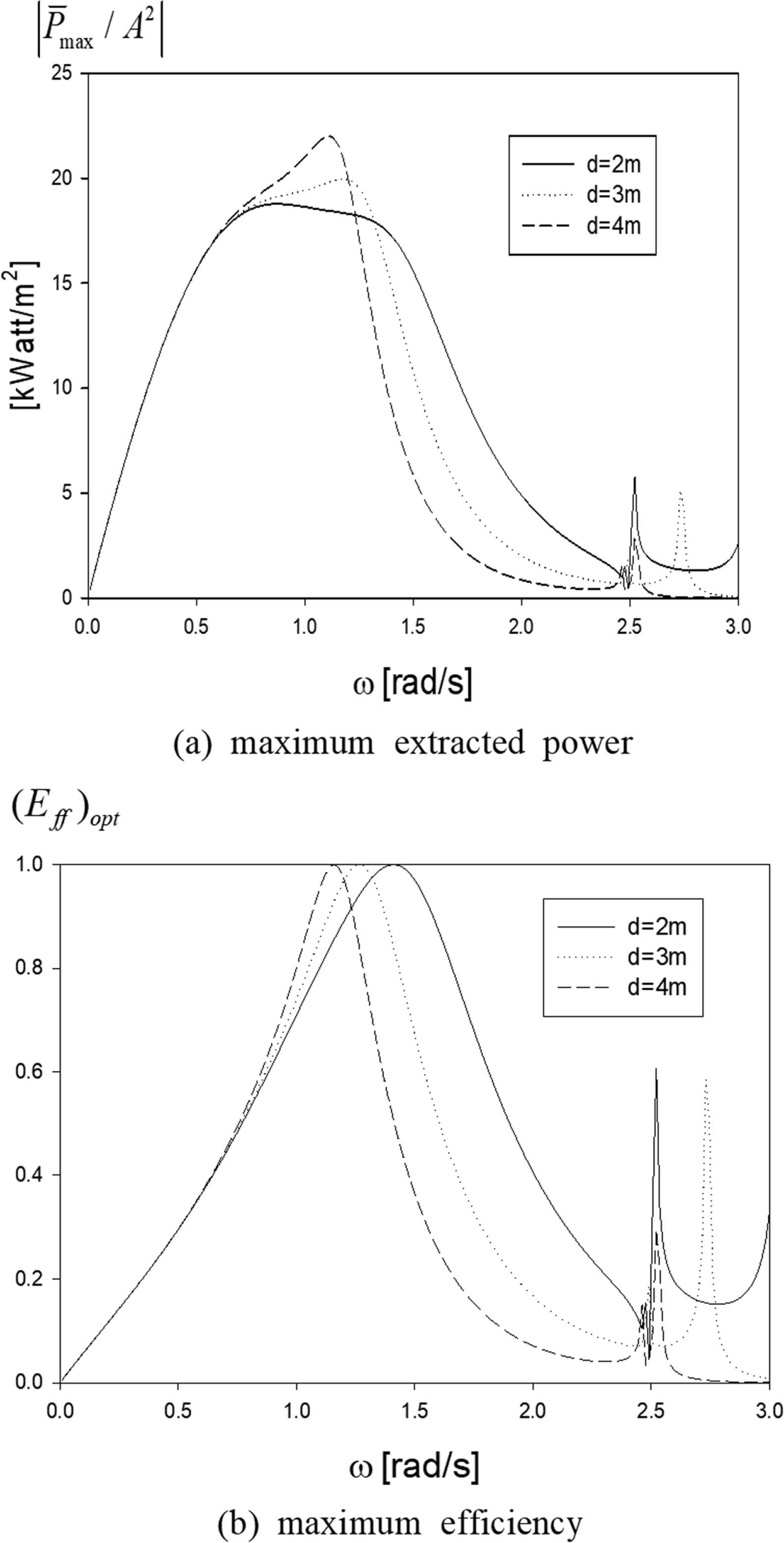
Extracted power (a) and efficiency (b) at the optimal turbine coefficient as a function of submergence depth d for h = 20 m, L =5m, H =3m.

Fig. 7은 최적 터빈계수를 적용하였을 때 안벽 앞에 놓인 OWC 파력발전장치에 의한 반사율을 보여주고 있다. 공기실이 완전히 열린 상태에서 현재의 모델과 같이 별도의 에너지 감쇠기구가 없는 경우에는 입사파는 안벽에 의해 완전 반사되므로 반사율은 1.0이다. 그러나 공기실의 변동압력에 의해 터빈을 돌려 입사파의 에너지를 전기에너지로 변환하였을 때 Fig. 7과 같이 피스톤 모드 공진주파수에서 입사파의 에너지를 모두 흡수하여 반사율이 0인 V자형 반사율 곡선을 보인다. 이러한 결과는 OWC 파력발전장치를 안벽을 따라 설치하면 전기를 생산함과 동시에 반사파를 줄이는 소파제의 역할을 할 수 있어 안벽에 작용하는 파랑하중을 줄이고 주변에 항해하는 선박의 안정성에 도움을 줄 수 있음을 보여준다.

Fig. 7.

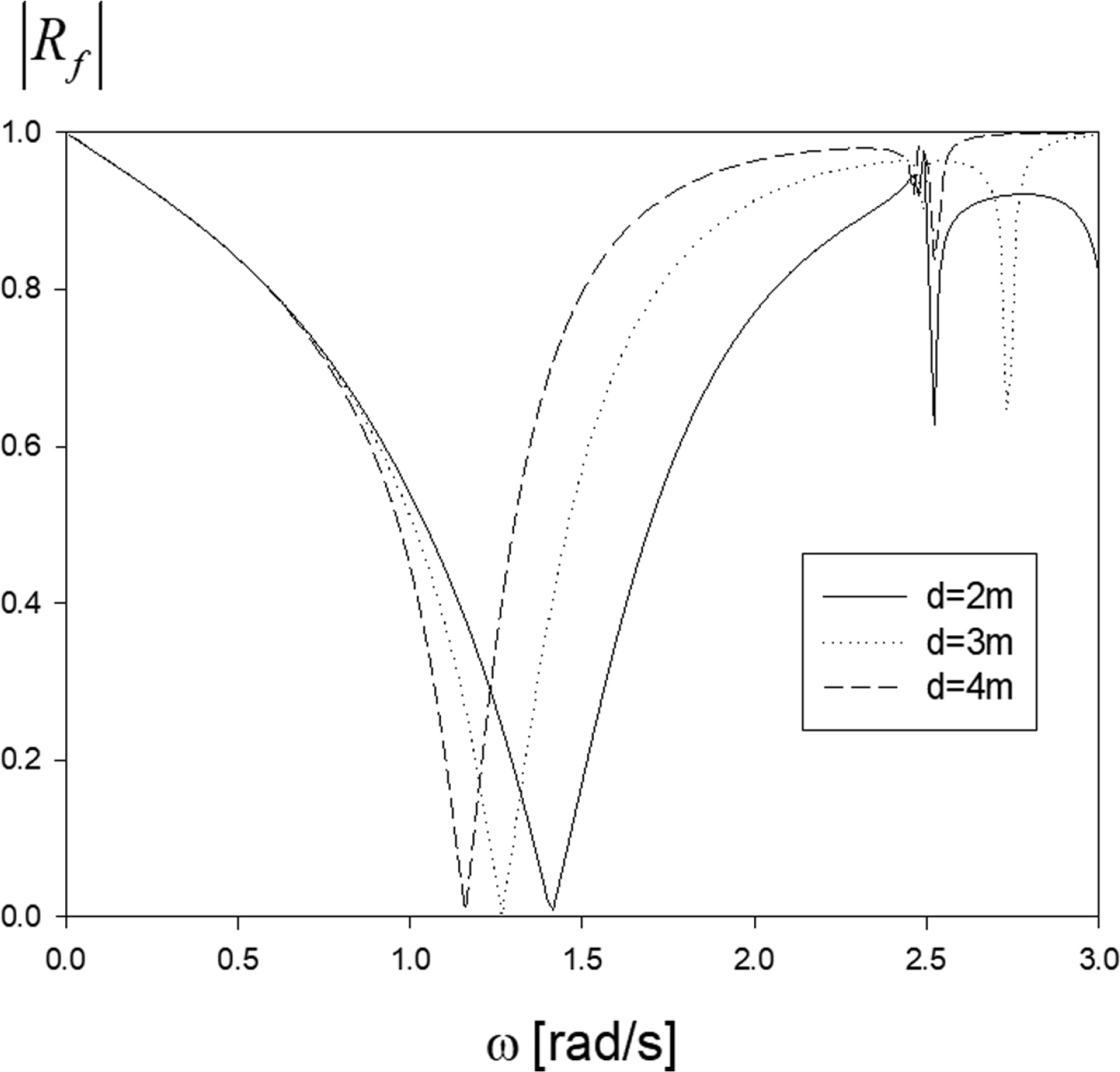
Reflection coefficient at the optimal turbine coefficient as a function of submergence depth d for h =20m, L =5m, H =3m.

Fig. 8은 안벽 앞에 놓인 2차원 OWC 파력발전장치에 불규칙파가 입사하였을 때 반사파 스펙트럼을 입사파 스펙트럼과 함께 그렸다. 계산에 사용한 TMA 스펙트럼의 유의파고는 1.0 m이며 에너지 주기(energy period)는 4.5 s이다. 주파수가 시시각각 변하는 불규칙파인 경우 입사파의 주파수에 따라 터빈계수를 연속적으로 바꾸는 것은 불가능하다. 따라서 불규칙파인 경우 피스톤 모드 공진주파수나 파랑스펙트럼의 에너지 주파수와 같이 특정 주파수에서의 최적 터빈계수 값을 사용해야 한다. 여기서는 피스톤 모드 공진주파수에서의 최적 터빈계수를 사용하였다. 반사파 스펙트럼은 Fig. 7에 주어진 반사율 곡선의 V자형 특징을 반영하므로 입사파 스펙트럼과 달리 이중 피크 곡선을 보여주고 있다. 불규칙 입사파의 에너지가 집중된 에너지 주파수와 피스톤 모드 공진주파수가 일치하도록 OWC 파력발전장치를 설계하면 파랑에너지 추출을 극대화시킴과 동시에 입사파의 에너지 밀도가 높은 주파수 범위내의 반사율을 크게 줄여 전체 반사율을 낮출 수 있다. Fig. 8에서 격벽의 잠긴깊이가 줄어들수록 반사파 스펙트럼의 면적은 줄어들어 전체 반사율은 감소한다.

Fig. 8.

Incident wave spectrum (PM spectrum) and corresponding reflected wave spectrum as a function of submergence depth d for h =20m, L =5m, H =3m, T_e =4.5s, H_1/3 =1m.

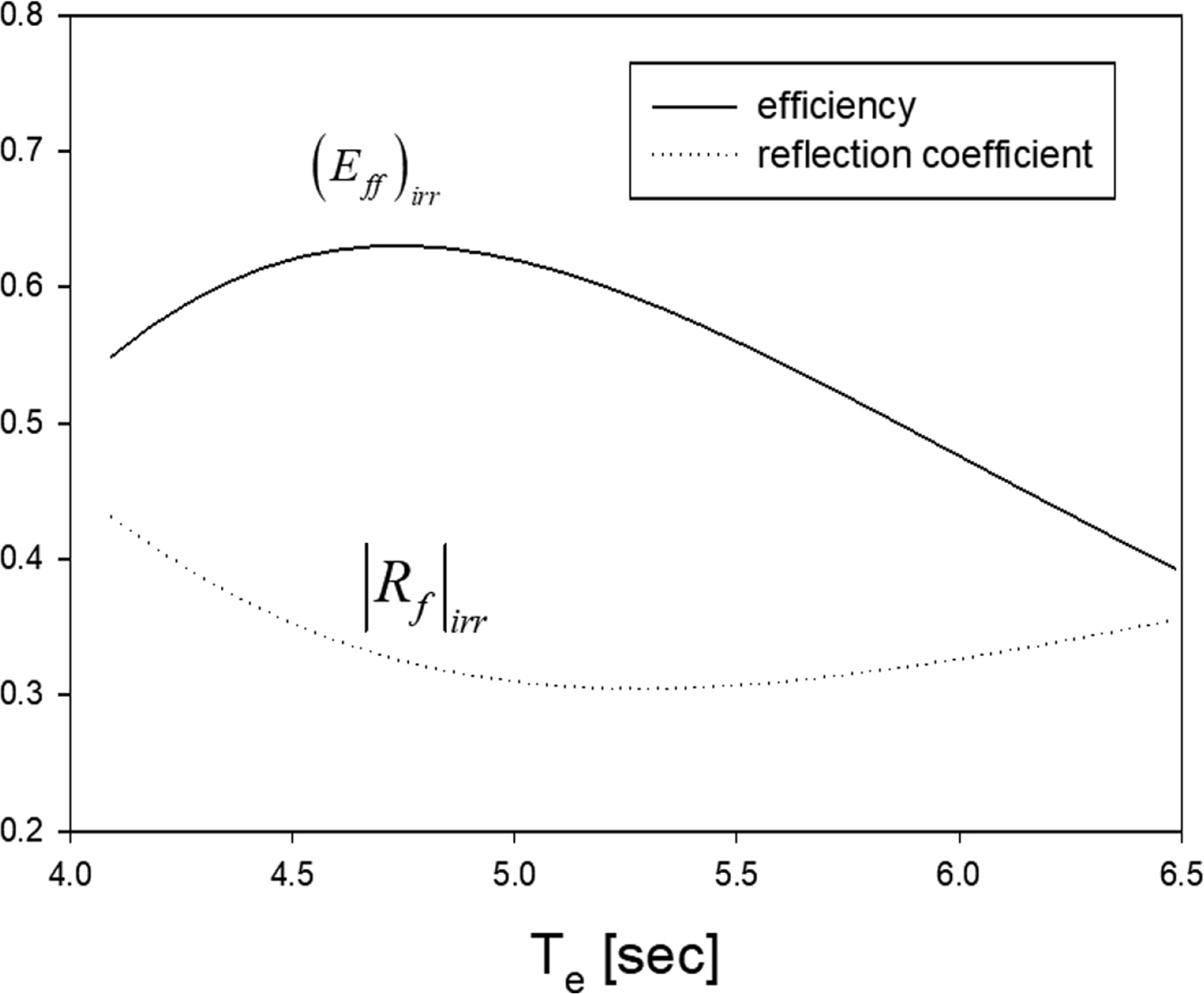
Fig. 9는 Fig. 8과 동일한 계산조건 아래에서 공기실내의 변동압력의 표준편차와 추출파워를 에너지 주기에 따라 그렸다. 길이 5m인 OWC에 해당하는 피스톤 모드 공진주기는 약 5 s이므로 에너지 주기(T_e = 5.25 s)가 피스톤 모드 공진주기 보다 약간 클 때 추출파워와 변동압력이 최대가 됨을 알 수 있다. Fig. 10은 불규칙파 조건에서 추출효율과 반사율을 그렸다. T_e = 4.75 s일 때 추출효율은 최대값을 가지며 최대값은 0.62이다. 반면에 반사율의 최소값 0.3은 T_c = 5.25 s에서 나타났다.

Fig. 9.

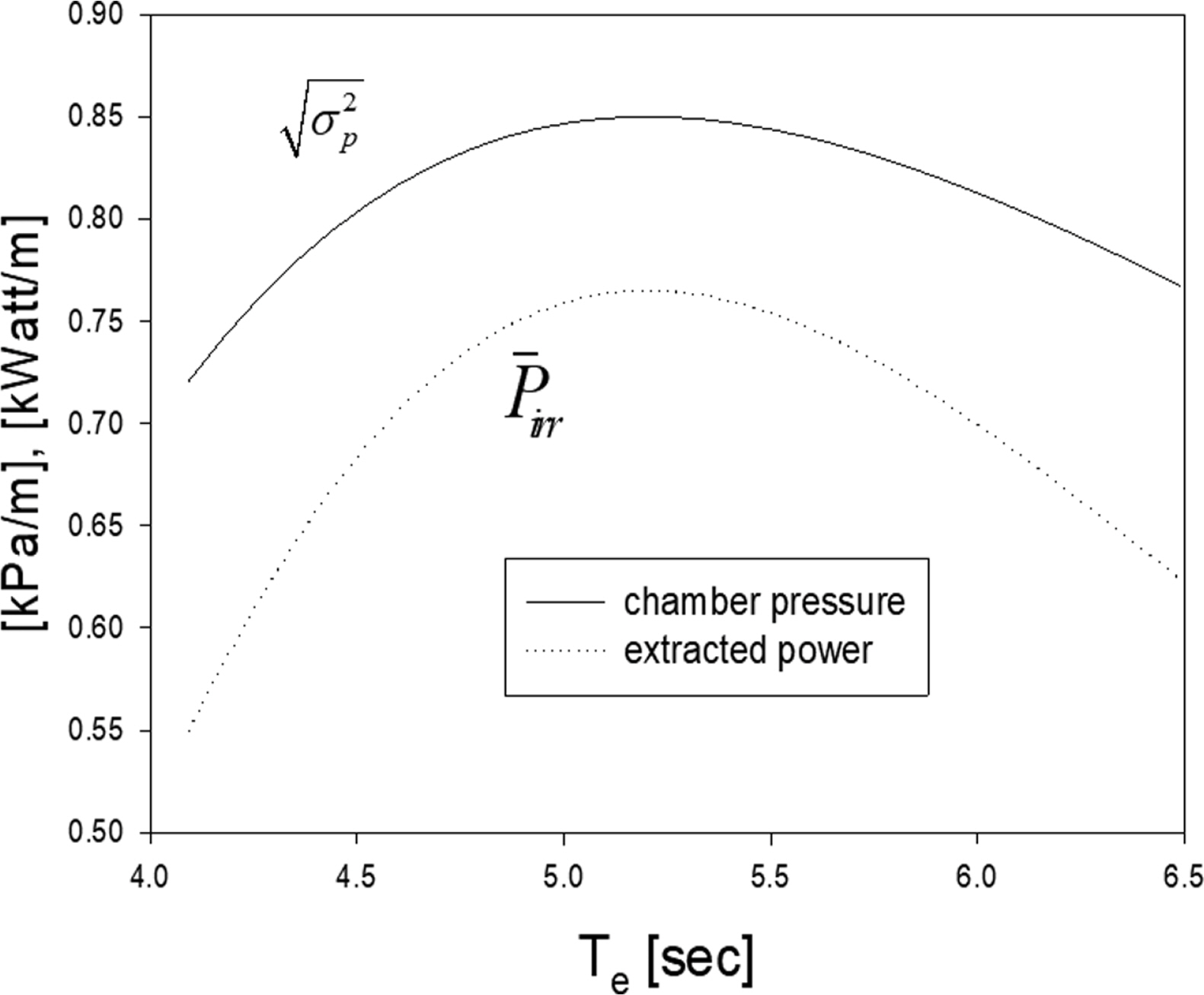
Standard deviation of the oscillation chamber pressure and extracted power as a function of energy period (T_e) in irregular waves for h =20m, L =5m, H =3m, d =3m, H_1/3 = 1m.

Fig. 10.

Reflection coefficient and efficiency as a function of energy period (T_e) in irregular waves for h =20m, L =5m, H =3m, d =3m, H_1/3 =1m.

4. 결 론

안벽 앞에 설치된 2차원 OWC 파력발전장치의 공기실내의 변동압력, 추출파워, 효율, 반사율 등을 규칙파와 불규칙파에 대하여 살펴본 결과 다음과 같은 결론을 얻었다.

1) 입사파의 주파수와 OWC 파력발전장치내 유체의 고유 주파수가 일치될 때 공진이 발생하는데 특히 형태 변화 없이 수면이 상하로 진동하는 모드를 피스톤 고유모드라 부른다. 피스톤 모드 공진주파수에서 입사파에 의한 내부유체 유량은 피크 값을 가지며 격벽 잠긴깊이가 증가할수록 유량의 피크 값은 증가하며 피크 폭은 감소한다. 고주파수 영역에 위치한 1차 슬로싱 모드 공진주파수에서의 피크 값은 상대적으로 작으며 피크 폭이 매우 좁은 스파이크 형태로 나타났다.

2) 공기실내의 변동압력에 의한 유량의 실수부인 방사어드미턴스는 주파수에 따라 증가하다가 피스톤 모드 공진주파수에 가까워지면 양의 값에서 음의 값으로 큰 폭으로 변화한다. 한편 방사컨덕턴스는 방사어드미턴스가 0인 공진주파수에서 최대값을 갖는다. 이러한 독특한 현상은 닫쳐진 유체영역내에 공진을 유발하는 메커니즘이 존재할 때 나타난다.

3) 규칙파인 경우 최대 추출파워를 주는 주파수 함수인 최적 터빈계수를 적용하였을 때, 피스톤 모드 공진주파수에서 추출효율은 최대값 1.0, 반사율은 최소값 0.0이 나타났다. 추출효율과 반사율은 서로 반비례의 관계를 갖는다. 또한 격벽의 깊이가 감소할수록 효율 곡선의 폭이 넓어져 발전 가능한 주파수의 범위가 증가하였다.

4) 불규칙파에서 입사파의 에너지가 집중된 에너지 주파수와 피스톤 모드 고유주파수를 일치시키면 OWC 파력발전장치를 통해 추출 가능한 파랑에너지를 높임과 동시에 에너지 밀도가 높은 주파수 대역에 위치한 반사율을 크게 줄여 전체 반사율을 낮출 수 있음을 확인하였다. 특히, 격벽의 잠긴깊이가 감소할수록 효율은 증가하고 반사율은 줄어드는 경향을 보여주었다.

5) 에너지 주기와 피스톤 모드 공진주기(T_o = 5.0 s)를 완전히 일치시키는 것 보다 에너지 주기(T_e = 5.25 s)가 공진주기보다 약간 클 때 불규칙파에서의 추출파워와 변동압력이 최대가 됨을 확인하였다. 한편 에너지 주기 T_e = 4.75 s일 때 불규칙파에서의 추출효율의 최대값(0.62)이 나타나며, 반사율의 최소값(0.3)은 T_e = 5.25 s에서 나타났다.

Article information Continued