2.1 쇄파에 대한 경험식 고찰

쇄파에 대해 기존에 제안된 이론식이나 경험식은 선형파 이론이나 불투과성 사면 혹은 모래로 구성된 사빈을 대상으로 수행된 수리모형의 실험결과에 기초하고 있다. 진행파의 파봉에서 유체입자의 속도가 파속을 초과하는 경우에 쇄파가 시작된다고 제안한 Miche(1944)의 식(1)이 제안된 이후로 쇄파에 관한 다양한 수리모형실험이 수행되었고, 축적된 실험자료를 이용하여 많은 연구자들은 쇄파지표를 예측하기 위한 경험식을 제안해 왔다(Le Mehaute and Koh, 1967; Goda, 1973; Komar and Gaughan, 1972; Sunamura and Horikawa, 1974; Ostendorf and Madsen, 1979; Rattanapitikon and Shibayama, 2000; Rattanapitikon et al., 2003; Rattanapitikon and Shibayama, 2006).

여기서, H_b는 쇄파 파고, h_b는 해저 경사면으로부터 정수면까지의 연직거리로 정의되는 쇄파 수심, L_b는 쇄파 수심에서의 파장이다. Miche(1944)의 제안식은 Michell(1893)의 최대 심해 파형경사(H_o/L_o = 0.142)에 기초하고 있으므로 쇄파 파고를 과대평가하며, 사면의 기울기를 고려하고 있지 않다. Le Mehaute and Koh(1967)는 최초로 심해 파형경사와 사면경사를 동시에 고려한 쇄파 파고에 대한 식(2)의 경험식을 제안하였다.

여기서, m은 사면경사, H_o는 심해파고, L_o는 심해파장이다. 심해 파형경사와 해저경사를 파라메터로 하는 Le Mehaute and Koh(1967)의 제안식은 이후에 많은 연구자들에 의해 수정되어 왔다. 대표적인 예로 Ostendorf and Madsen(1979)는 사면경사에 따른 쇄파파고를 고려하기 Miche(1944) 식을 수정한 다음의 경험식을 제안하였다.

최근 들어 Rattanapitikon and Shibayama(2006)은 가용한 실험자료를 기반으로 심해파형경사를 이용한 쇄파파고에 대한 식(4)와 쇄파수심에 대한 식(5)를 각각 제안하였다.

한편, 쇄파수심에 대한 식(5)로부터 정선으로부터 쇄파 지점까지의 거리 x_b는 s_b = h_b/m으로부터 다음과 같이 산정할 수 있다.

Goda(2010) 급한 사면경사에 대한 예측성능 개선을 위해 심해 파형경사의 함수로 표현되는 기존의 Goda 쇄파식(Goda, 1973)을 수정하여 쇄파 수심과 심해파장과의 비를 파라메터로 하는 식(7)을 제안하였다.

여기서, A는 상수로 규칙파와 불규칙파에 따라 각각 0.17과 0.12를 갖는다. 한편, Liu et al.(2011)은 사면경사에 독립된 쇄파지표를 산정하기 위해 천해조건에서 미소진폭파이론의 파속을 이용하여 다음과 같은 경험식을 제안하였다.

여기서, λ_b = H_b/L_b, L_b는 쇄파점에서의 파장, ψ_b = gH_b/C_b, g는 중력가속도, C_b는 쇄파 시의 파속으로 다음과 같이 정의된다.

하지만, Liu et al.(2011)의 제안식은 C_b를 계산하기 위해 반복계산이 필요하므로 실무적으로 활용하기가 곤란하다. 최근에는 Xie et al.(2019)에 의해 권파형 쇄파 수심 산정을 위한 식(10)의 반경험 공식이 제안되었다.

2.2 기존의 쇄파 실험결과와의 비교

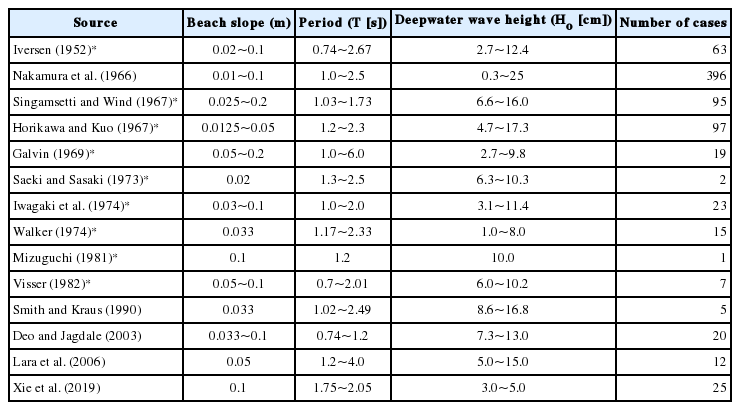
기존의 수리모형의 실험결과는 Deo and Jagdale(2003), Lara et al.(2006) 및 Smith and Kraus(1990)의 연구를 참조하여 취득하였다. 본 연구에서 이용한 실험결과에 대한 범위를 Table 1에 보인다. 기존 연구로부터 총 780개의 실험결과를 획득하였으며 사면 경사는 0.01~0.1의 범위를 갖는다. 단, Xie et al.(2019)의 실험결과는 쇄파파고 만을 제공하고 있지 않으므로 쇄파수심을 예측하는 것으로 제한하였으며, Table 1에서 *은 Smith and Kraus(1990)로부터 획득하였다.

Table 1.

Summary of historical experimental data set on breaking waves

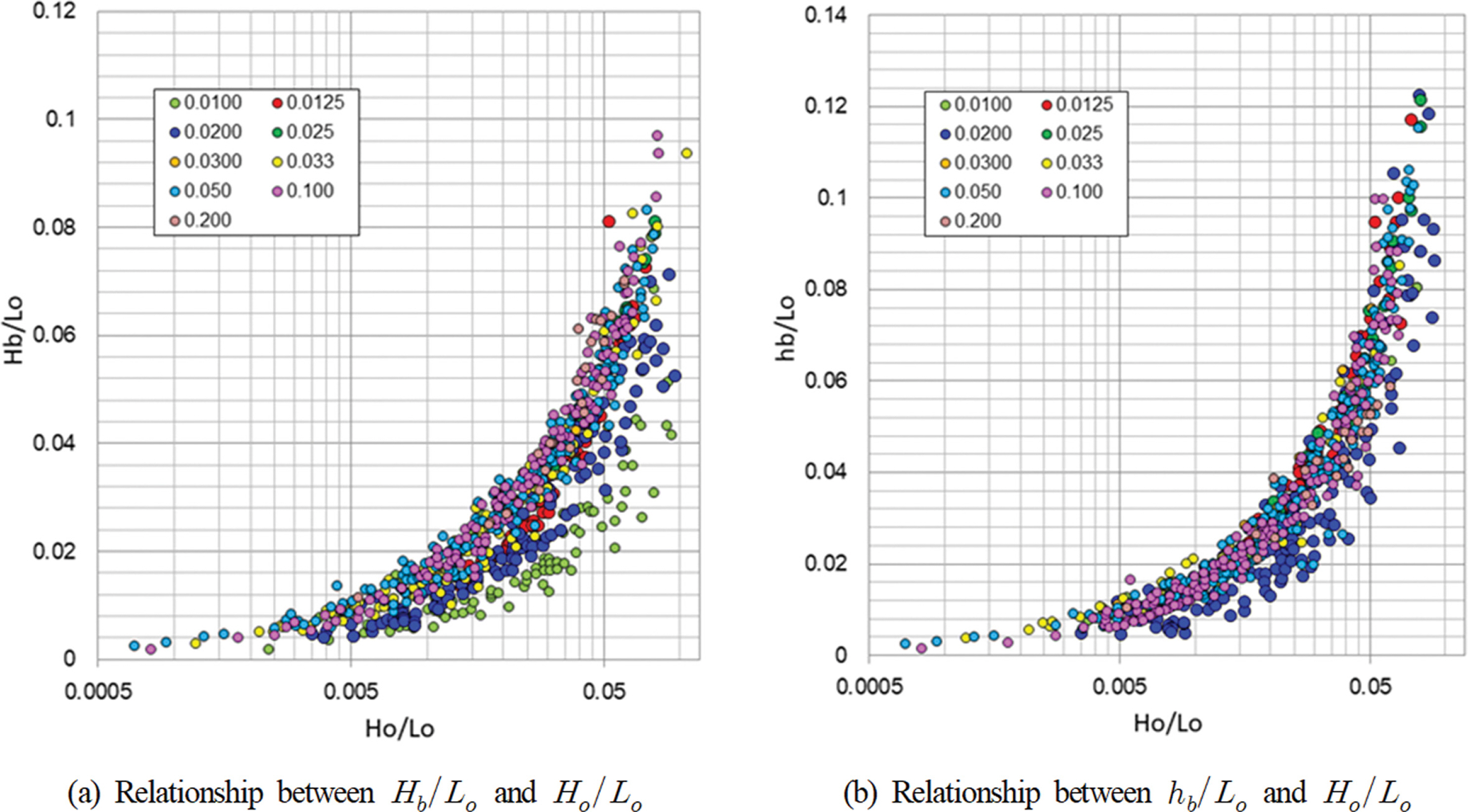
Fig. 1은 Table 1에 보인 기존의 실험결과에 대하여 무차원 쇄파파고 및 쇄파수심을 심해 파형경사의 함수로 도식한 것이다. Fig. 1로부터 확인되는 바와 같이 실험조건에 따라 실험결과가 산포하고 있지만 전체적으로 쇄파파고 및 쇄파수심은 파형경사 H_o/L_o에 비례하여 증가하며, 쇄파지표는 심해 파형경사와 높은 상관관계를 유지함을 확인할 수 있다.

Fig. 1.

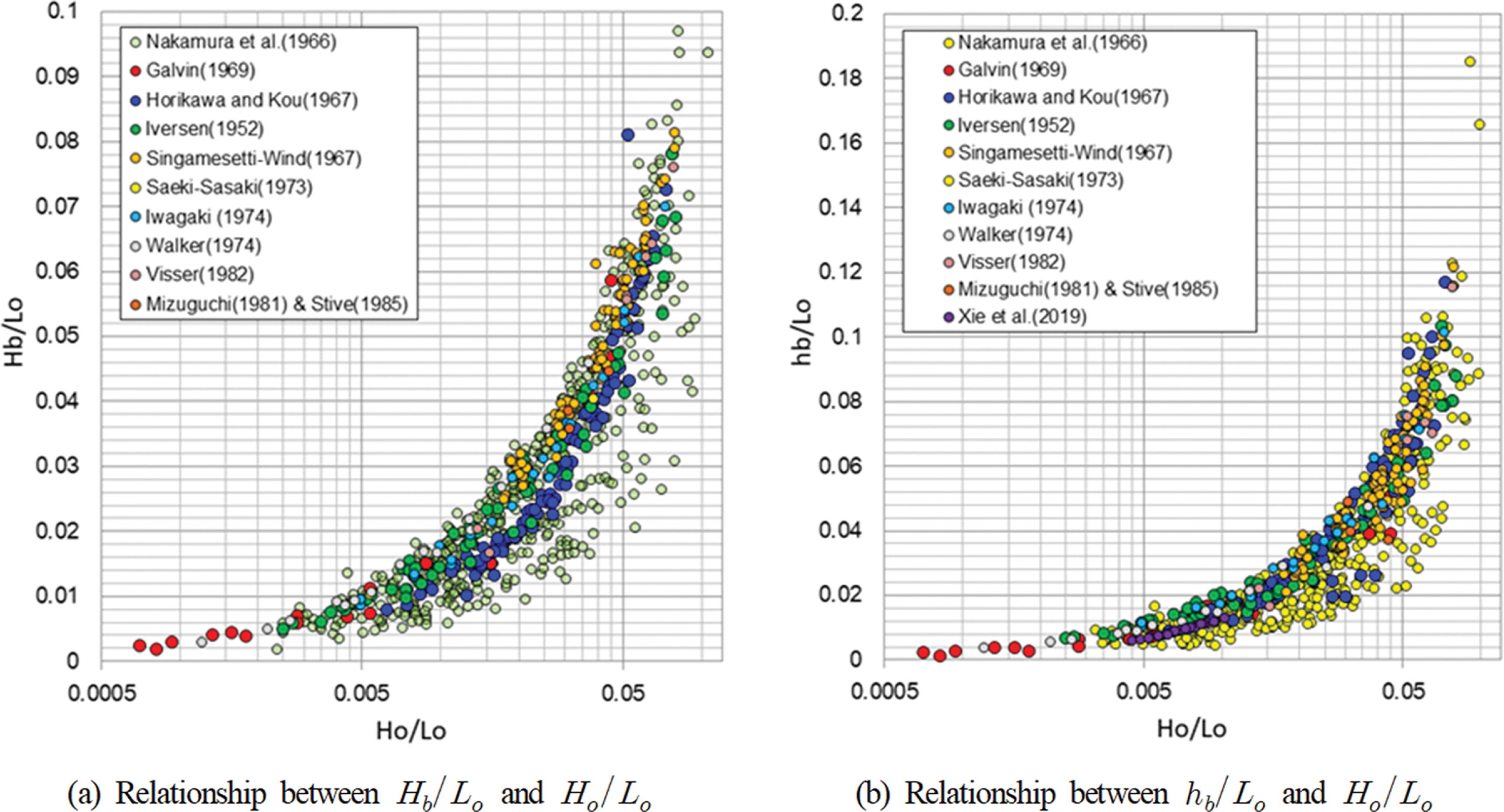
Relationship between wave breaker index and deep water wave steepness by historical laboratory experiments.

Fig. 2는 Table 1의 실험자료에 대해 사면경사 m에 따른 쇄파파고 및 쇄파수심을 정리한 것이다. Fig. 1과 유사하게 실험결과 사이의 차이가 존재하지만 쇄파파고는 사면 경사가 증가할수록 동반되어 증가하는 반면에 쇄파 수심은 쇄파파고에 비해 상대적으로 뚜렷한 차이가 나타나지 않음을 알 수 있다. Fig. 1과 Fig. 2로부터 쇄파지표의 예측을 위해 파형경사와 사면경사를 파라메터로 하는 기존의 경험식이 유용함을 재확인할 수 있다.

Fig. 2.

Relationship between wave breaker index and deep water wave steepness by beach slope.

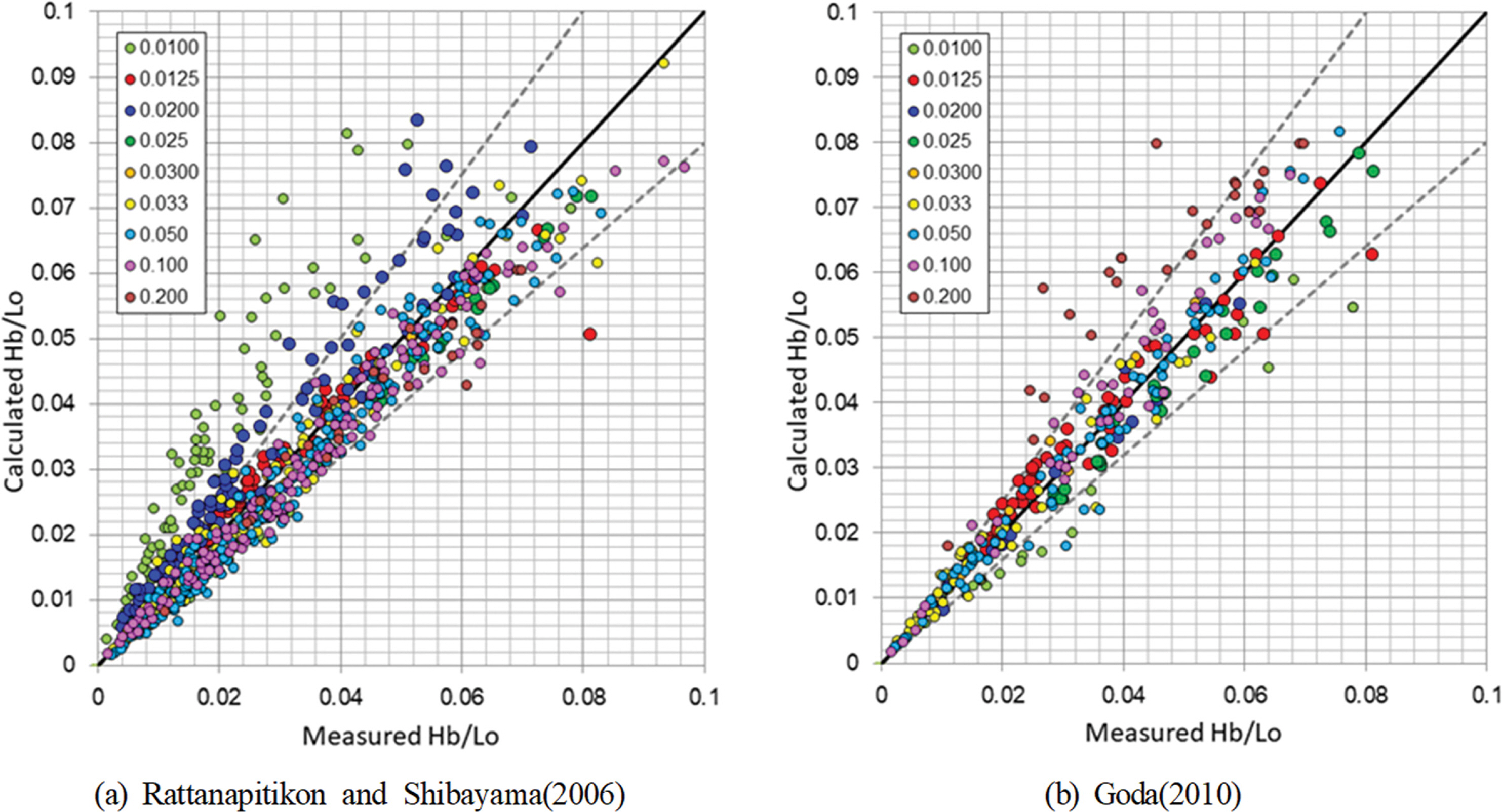
Fig. 3은 앞서 기술한 Rattanapitikon and Shibayama(2006)와 Goda(2010)에 의해 제안된 경험식을 적용하여 쇄파 파고를 예측한 결과이다. 그림 중의 점선은 20%의 오차범위를 나타낸다. Fig. 3(a)의 쇄파파고의 예측결과를 살펴보면 Rattanapitikon and Shibayama(2006)의 쇄파파고에 대한 제안식은 상대적으로 완만한 사면경사에 대해 실험결과를 과대평가하고 있으며, 반대로 상대적으로 급한 사면 경사에 대해서는 과소평가하고 있음을 알 수 있다. 한편, Goda(2010)의 경험식에 의한 결과인 Fig. 3(b)에서는 Rattanapitikon and Shibayama(2006)에 의한 예측결과와 반대로 상대적으로 급한 사면 경사(m ≥ 0.1)에서 쇄파파고를 과대평가하고 있음이 확인된다. Rattanapitikon and Shibayama(2006) 및 Goda(2010)의 경험식에 의한 쇄파파고 예측의 평균오차율은 각각 21.5%와 13.3%를 보였다. 단, Table 1의 Nakamura et al.(1966)의 실험결과는 무차원 쇄파파고 H_b/L_o와 쇄파수심 h_b/L_o의 관계를 제공하고 있지 않으므로 Fig. 3(b)에 보인 Goda(2010)의 경험식에 의한 쇄파파고 예측에는 사용되지 않았음을 밝혀둔다.

Fig. 3.

Comparison of wave breaking height formulas with experimental data.

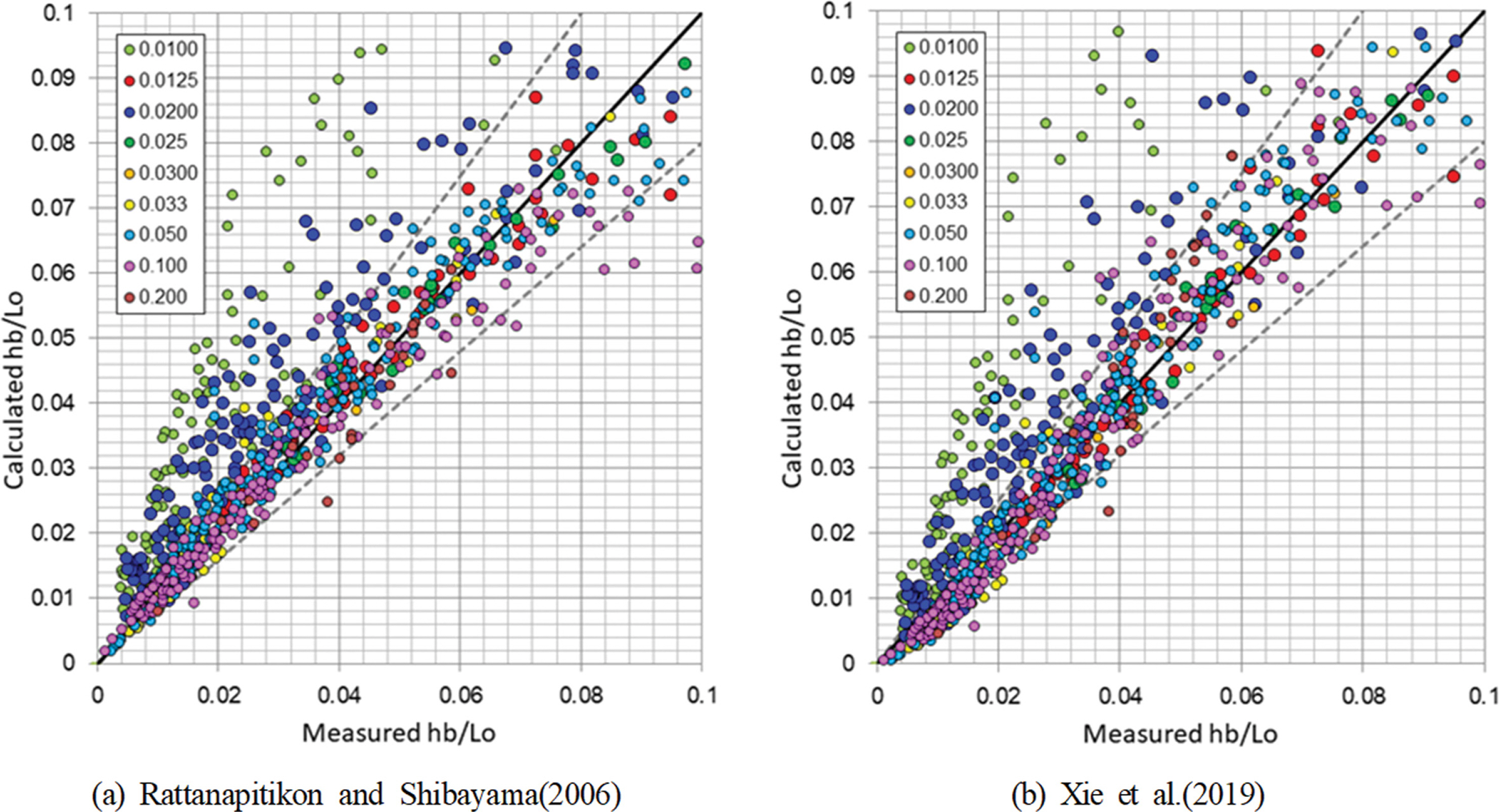
Fig. 4는 Fig. 3과 유사하게 쇄파수심에 대한 Rattanapitikon and Shibayama(2006)과 Xie et al.(2019)의 경험식을 적용하여 쇄파수심의 실험자료를 예측한 결과이다. 쇄파수심에 대한 예측결과는 쇄파파고의 예측결과에 비해 실험결과의 재현 정도가 감소함을 알 수 있다. 특히, Rattanapitikon and Shibayama (2006)과 Xie et al.(2019)의 쇄파수심에 대한 경험식은 쇄파수심을 과대평가하고 있으며, 실험결과와의 평균 오차율은 Rattanapitikon and Shibayama(2006)의 경험식은 31.4%, Xie et al.(2019)의 경험식은 29.8%로 높은 오차율을 보이고 있다.

Fig. 4.

Comparison of wave breaking depth formulas with experimental data.

쇄파파고 및 쇄파수심 대한 기존 경험식의 에측정도를 보다 정량적으로 평가하기 위한 척도로 SI(Scatter Index)와 결정계수(R²)를 적용하였다. SI는 식(11)과 같이 평균 제곱근 오차(Root Mean Square Error; RMSE)를 실험자료의 평균치로써 나눈 무차원 오차척도이며, 식(12)의 결정계수는 예측모델의 추정정도가 실험결과를 표현하는 적합정도를 나타내는 척도이다.

여기서, x_i는 실험자료, y_i는 예측값, x¯와 y¯는 각각 실험결과와 예측값의 평균값, n은 자료의 수 이다. SI는 작을수록 결정계수는 높을수록 실험치와 예측치의 대응이 양호함을 의미한다.

Table 2는 Fig. 3과 Fig. 4에서 논의한 기존의 대표적인 쇄파지표에 대한 경험식의 예측정도를 나타낸다. Table 2에 의하면 기존의 경험식은 쇄파수심에 비해 쇄파파고의 예측성능이 높으며, 본 연구에서 적용한 쇄파실험 자료의 범위에서 쇄파파고는 Goda(2010) 경험식이 쇄파수심은 Rattanapitikon and Shibayama(2006) 경험식이 보다 양호한 예측성능을 보임을 알 수 있다.

Table 2.

Results of error analysis

3.1 신경망의 이론적 배경

머신러닝(machine learning, 기계학습)은 명시적인 프로그래밍을 통해서가 아닌 자료(data)로부터 컴퓨터가 학습을 통해 지식을 주입하는 인공지능(artificial intelligence)의 한 분야이다. 머신러닝의 종류에는 지도학습(supervised learning)과 비지도학습(unsupervised learning)으로 크게 구분될 수 있다. 지도학습은 입력과 출력이 있는 자료들을 학습시킨 후에 테스트 자료를 예측하는 것으로서 선형모델(linear model), 의사결정 트리(decision Tree), KNN(K-nearest neigh_bor), SVM(support vector machine), 신경망(neural network) 등의 알고리즘이 개발되어 있으며, 반면에 비지도학습은 인간이 개입하지 않고 컴퓨터가 스스로 결과를 도출해 내는 것을 말하며, 대표적인 예로 클러스터링(clustering), 비정상 탐지(anomaly detection) 알고리즘 등을 들 수 있다.

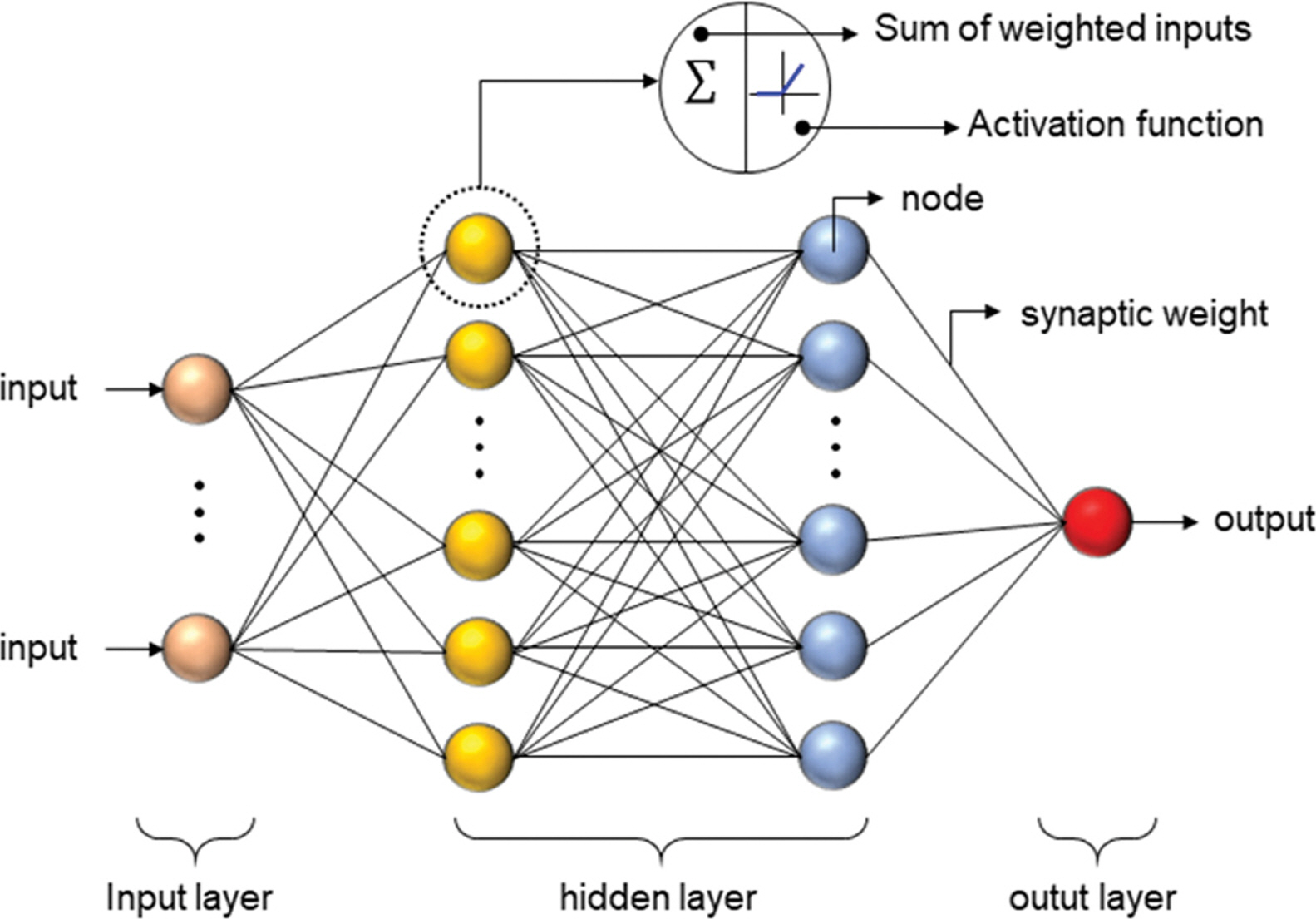
본 연구에서는 이상에서 언급한 다양한 머신러닝의 알고리즘 중에서 신경망(neural network, 이하 NN)을 적용하였다. 한편 최근 들어 등장하기 시작한 딥러닝(deep learning)은 NN 알고리즘을 사용하는 것으로서 기존의 NN 알고리즘의 단점으로 지적된 과대적합(overfitting)을 개선하기 위한 Hinton et al.(2006)의 연구가 발표된 이후로 NN을 대신하여 딥러닝이 보다 포괄적으로 사용되고 있다. 신경망 회로라는 의미의 NN은 엄밀하게 생체의 신경계 네트워크를 의미하는 것은 아니며, 입출력 관계를 부여하는 함수의 공학적 계산을 위해 생체의 신경세포를 모의한 인공소자(node)를 서로 접속시켜 구성한 네트워크이다. Fig. 5에 보인 바와 같이 가장 단순한 형태의 NN의 구조는 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 구성되며, 각각의 층은 한 개 이상의 노드로 구성되어 노드와 노드 사이는 가중치(weight)로 연결되어 있다. 각각의 노드에서는 입력값에 대한 고유한 가중치가 곱해진 합으로 나타나며, 활성함수(activation function)을 적용하여 결과를 출력한다. 한편, 다수의 은닉층이 존재하는 경우를 일반적으로 딥러닝 알고리즘이라고 부른다.

Fig. 5.

General layout of neural network.

NN의 가장 큰 특징은 입력과 출력변수 사이의 비선형적 관계를 추정하기 위해 이론적으로 체계화된 근사기법이라는 점이며, 이를 위해 입력된 자료에 기초해서 필요로 하는 비선형적 규칙성 자동으로 형성하는 학습 알고리즘(learning algorithm)을 갖추고 있다. 이와 같은 학습능력은 노드와 노드를 연결하고 있는 가중치 값을 조정함으로써 수행된다.

3.2 신경망 구성을 위한 Tensorflow 적용

텐서플로(Tensorflow)는 머신러닝 프로그램을 쉽게 구현할 수 있도록 구글(Google)에서 개발되어 2015년에 배포된 오픈소스 머신러닝 플랫폼이다(Abadi et al., 2015). 텐서플로는 Python 기반의 고수준 API(Application Programming Interface)를 제공하고 있어 주로 Java나 C++ 언어를 기반으로 복잡한 알고리즘을 직접 구현해야 했던 기존의 머신러닝 코드들에 비해 비교적 손쉽게 모델 구축이 가능하다. 또한, 텐서플로 코드 자체는 C++ 언어로 구현되어 있으나 Python, Java, Go, R 등의 다양한 언어를 지원하고, 특히 Python을 사용하는 프로그래밍 인터페이스를 통해 사용자가 손쉽게 활용할 수 있는 라이브러리 함수와 클래스를 제공하고 있다. 이를 통해 텐서플로는 머신러닝 이용자들이 알고리즘 구현을 위한 프로그래밍 최적화에 소비하는 비용을 알고리즘의 로직과 네트워크 구축에 집중하게 할 수 있도록 하는 큰 장점이 있다.

텐서플로에서 제공하는 머신러닝 라이브러리는 그 이름에서 드러나는 바와 같이 기본적인 자료(data)의 형태로 다차원 배열(tensor)를 사용하고 유체의 흐름과 유사하게 연산결과와 자료는 그래프 구조를 통한 파이프라인 흐름 형태와 같은 학습 알고리즘을 실행하므로 텐서플로의 코드 구조는 매우 직관적이다. 따라서, 머신러닝 모델을 개발하려고 하는 개발자는 일련의 처리 노드를 통해 움직이는 방법을 기술하는 구조인 자료흐름(data flow) 그래프를 정의하고 입출력 자료를 그래프 구조에 삽입하여 모델을 학습시킬 수 있다. Fig. 6은 Abadi et al.(2016)가 제시하고 있는 자료의 입력, 전처리, 학습 등을 위한 하위 그래프가 포함된 학습 파이프라인에 대한 개략적인 TensorFlow 자료흐름(data flow) 그래프를 나타낸다.

Fig. 6.

A schematic TensorFlow dataflow graph for a training pipeline, containing subgraphs for reading input data, preprocessing, training, and checkpointing state (Abadi et al., 2016).

3.3 신경망의 구조

위에서 언급한 텐서플로 플랫폼을 이용하여 입력층, 은닉층, 출력층으로 구성된 Feed Forward NN을 채용하였으며, 각각의 층에 위치한 노드에서 입력과 출력을 완전-연결하는 Dense 레이어를 이용하였다. 은닉층의 노드에서는 입력된 값과 노드 사이에 연결된 가중치(weight)로 다음과 같은 연산이 수행된다.

여기서, N_j는 j번째의 노드에서의 가중치 곱의 총합, w_ij는 i번째 노드에서 j번째 노드로 연결되는 가중치, x_i는 i번째 노드에서의 입력값, θ_j는 j번째 노드에서의 편향(bias)을 나타낸다. 식(13)으로부터 계산된 각 노드의 값들은 활성화 함수(Activation function)라고 불려지는 비선형 함수를 통해 다음 노드로의 출력이 결정된다. 활성화 함수에는 Step 함수, Sigmoid 함수, Tanh 함수, Softmax 함수, ReLU(Rectified Linear Unit) 함수, Leaky ReLU 함수 등 다양한 함수가 사용되고 있으며, 본 연구에서는 최근 들어 많은 연구자들에 의해 성능이 입증되어 가장 널리 활용되고 있는 다음의 ReLU 함수를 이용하였다.

이상의 연산과정을 통해 입력값으로부터 NN을 통한 출력값을 얻을 수 있지만, 출력값이 기댓값에 근접하기 위해서는 학습과정을 거쳐야 한다. NN의 학습방법으로는 출력값을 역으로 전파하여 오차를 최소화하는 역전파(back propagation) 알고리즘을 이용하였다. 여기서, 오차는 입력값과 출력값의 차 이를 나타내며 NN의 학습지표로써 손실함수(cost function)로 정의된다. 본 연구에서는 식(15)의 평균제곱오차(Mean Squared Error)를 손실함수 E로 정의하였다.

여기서, e_i와 t_i는 각각 NN의 예측값과 목표값(실험결과)이며, n은 전체 자료의 수이다. 식(12)의 손실함수 최적화에는 가중치에 대한 손실함수 기울기 ∂E/∂w가 최소가 되도록 조정하는 경사하강법(Gradient descent method)을 개량한 RMSprop (Tieleman and Hinton, 2012)를 적용하였다. RMSprop는 지수 이동평균 이용하는 방법으로 식(16)으로 표현된다.

여기서, 위첨자 k는 반복회수, α는 학습률(learning rate), ρ는 최근에 업데이트된 값의 반영비율을 높이기 위해 적용되는 가중치인 감쇠계수(decaying factor)이며, ε은 아주 작은 상수를 나타낸다. 본 연구에서는 학습률 α = 0.01, 감쇠계수 ρ = 0.9, ε = 1.e - 10을 각각 적용하였다.

이상의 학습과정을 통해 훈련 자료(Training data)로부터 학습된 NN은 새로운 입력값에 대해서도 예측 가능한 모델의 일반화를 기대할 수 있지만, 학습이 과다하게 수행될 경우 훈련된 자료 이외의 입력값에 대해서는 정확도가 낮은 과대적합(overfitting) 문제가 발생할 수 있다. 텐서플로에서는 이러한 문제점을 해결하기 위한 다양한 최적화(optimization)기법 및 규제화(regularization), 가중치 감쇠(weight decay), 드롭아웃(drop-out), 조기종료(early-stopping) 등의 기법을 제공하고 있으며, 본 연구에서는 손실함수를 이용한 조기종료 기법을 적용하였다.

4.1 입력변수 정규화 및 훈련 자료 결정

NN의 입력변수는 쇄파지표와의 상관성이 높은 심해파형경사 H_o/L_o와 사면경사 m을 적용하였다. 입력변수는 각각의 자료에 대해 동일한 정도의 특성(분포) 스케일로 반영되도록 정규화 과정이 필요하다. 일반적으로 입력자료의 정규화에는 최소-최대정규화(Min-Max normalization)와 z-점수정규화(z-score normalization)이 사용되며, 본 연구에서는 다음과 같이 최소값과 최대값을 이용한 최소-최대정규화를 적용하여 입력변수가 0.1~0.9 범위의 값을 갖도록 정규화하였다.

여기서, 위첨자 x~는 정규화된 자료형, x_max와 x_min은 각각의 입력자료 전체에 대한 최대값과 최소값을 나타낸다.

NN 모델을 학습시키기 위한 훈련 자료(Training data)는 Table 1에 보인 쇄파실험 자료의 70%를 랜덤하게 적용하였으며, 나머지 30%의 자료는 학습된 NN을 평가하는데 사용하였다.

4.2 은닉층 및 노드의 개수 설정

NN을 구성함에 있어서 은닉층의 수와 노드의 수를 결정하는 것은 NN의 성능 및 학습과정의 시간비용과 관계되므로 사용자가 경험적으로 직접 조정되어야 하는 하이퍼 파라메터(hyper parameter) 이다. 본 연구에서는 기존의 연구들로부터 수집한 실험자료를 이용하고 있으므로 훈련 자료가 제한적임을 고려하여 2개 이하의 은닉층을 갖는 소규모 NN을 구축하였다.

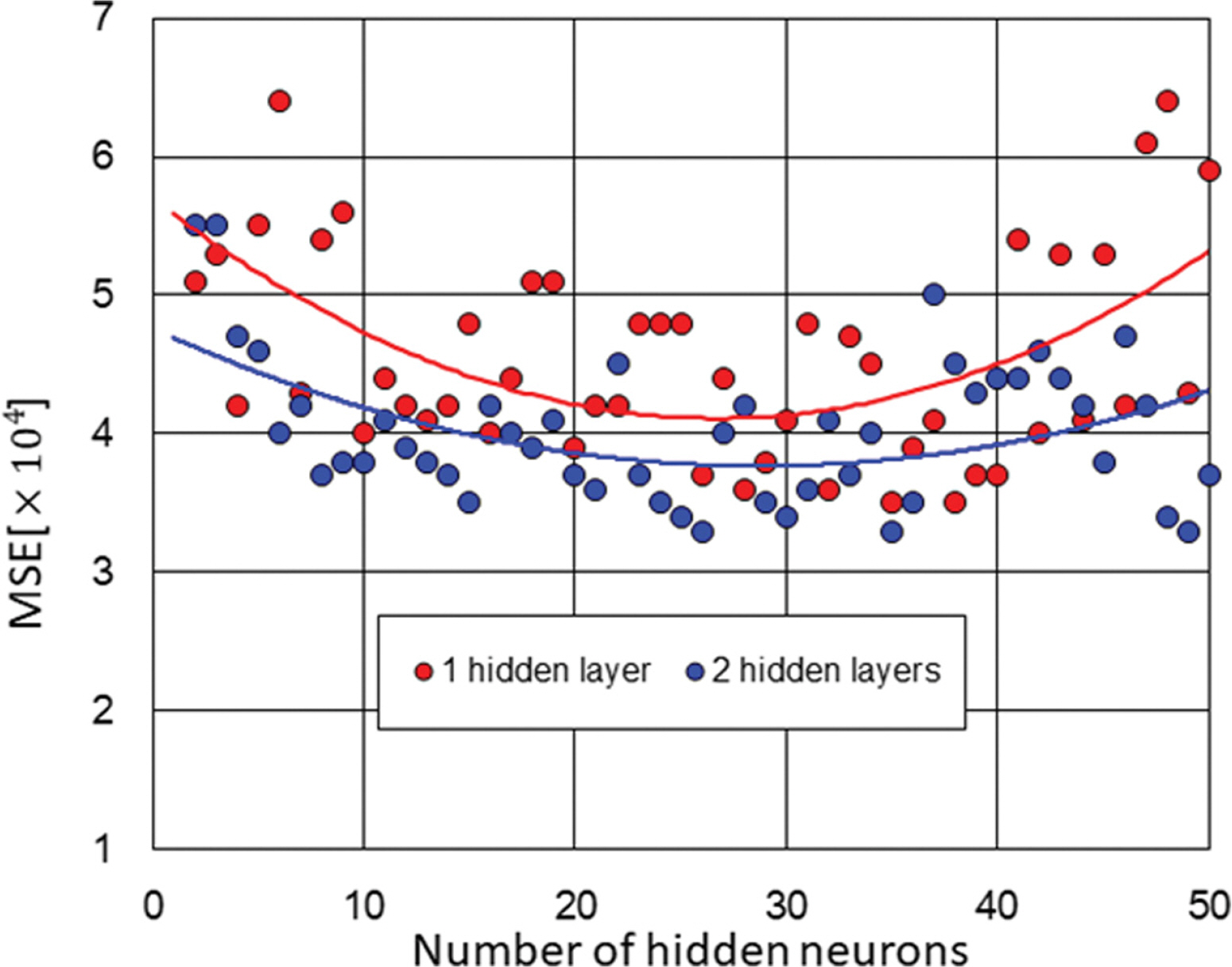
Fig. 7은 은닉층의 개수 및 은닉층의 노드 개수에 따른 훈련결과와 실험결과와의 평균제곱오차를 나타낸다. 그림 중의 실선은 다항식을 이용한 실험결과의 추세선을 나타낸다. 그림으로부터 2개의 은닉층으로 구성하는 경우가 1개의 은닉층에 비해 전체적으로 오차가 감소함을 알 수 있으며, 은닉층에 있는 노드의 수의 따라 오차가 진동하여 경향을 나타낸다. 즉, 노드의 수가 증가함에 따라 일정한 오차범위로 수렴되지는 않는다는 것을 알 수 있다. 본 연구에서는 Fig. 7의 결과로부터 은닉층의 노드 수는 20~30개 범위에서 선택하였다.

Fig. 7.

Mean square error of training data as a function of the number of hidden layer neurons.

4.3 쇄파지표의 예측성능 비교

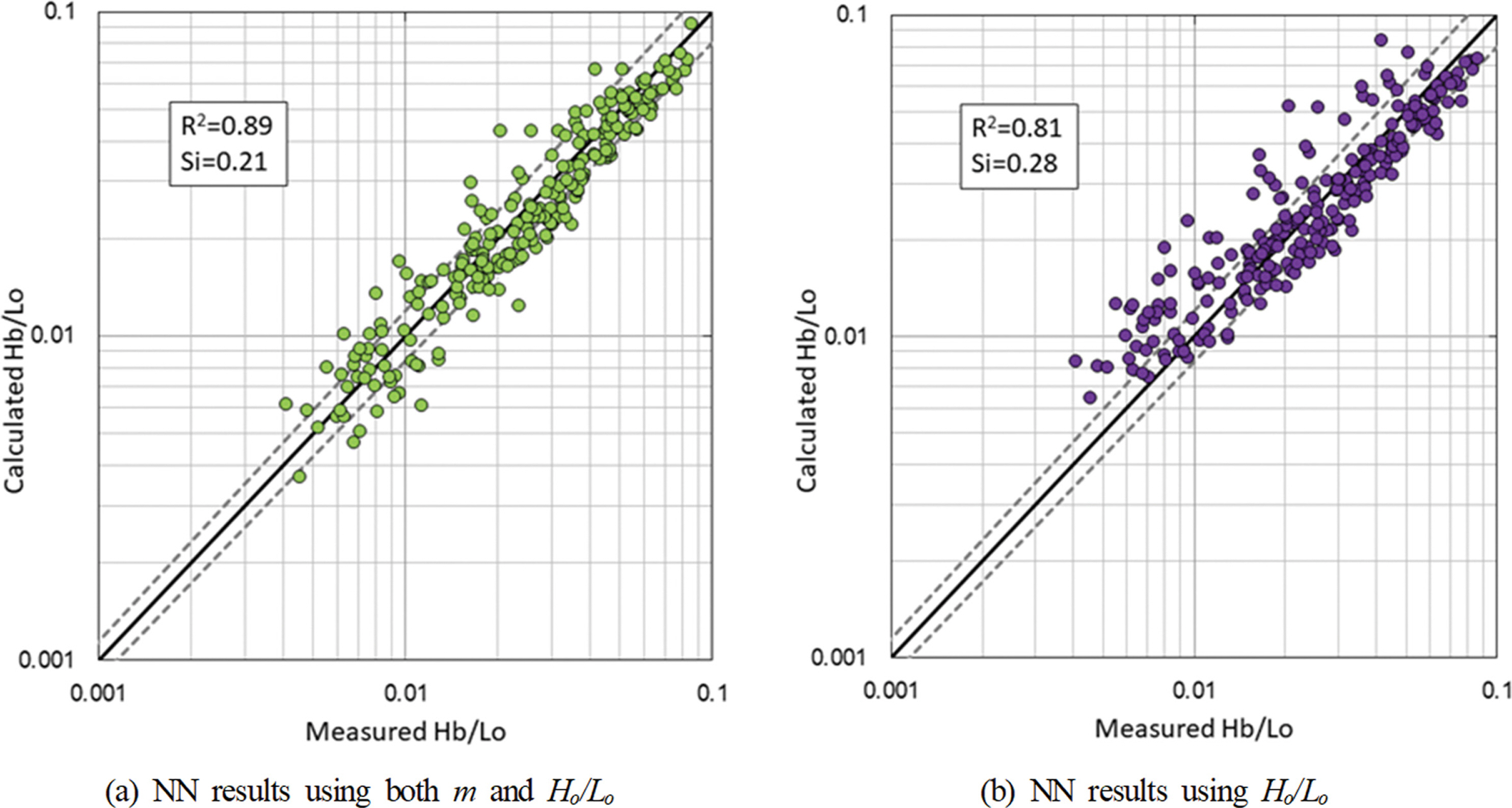
NN의 학습에 이용하지 않은 쇄파실험 자료를 이용하여 학습된 NN을 평가하였다. 평가척도는 앞서 논의한 쇄파지표에 대한 경험식 평가에 적용한 SI(Scatter Index)와 결정계수(R²)를 적용하였다. Fig. 8은 입력변수에 따른 NN의 쇄파지표 예측성능을 검토하기 위해 심해파형경사H_o/L_o 만을 입력변수로 사용하는 경우와 심해파형경사와 사면경사 m을 동시에 고려한 경우에 쇄파파고에 대한 예측결과를 나타낸다. 단, NN 모델은 단일 은닉층을 사용하였으며, 은닉층의 노드 개수는 20개를 배치하였다. 또한, 그림 중의 점선은 20%의 오차범위를 나타낸다. 그림에서 보이는 바와 같이 심해파형경사와 사면 경사를 동시에 입력변수로 고려한 Fig. 8(a)의 결과가 심해파형경사만을 고려한 Fig. 8(b)에 비해 R²은 9.9%, SI는 9.7% 정도의 예측성능이 증가함을 알 수 있다.

Fig. 8.

Comparison of the predicted wave breaking heights applying 1-hidden layer NN for input parameters.

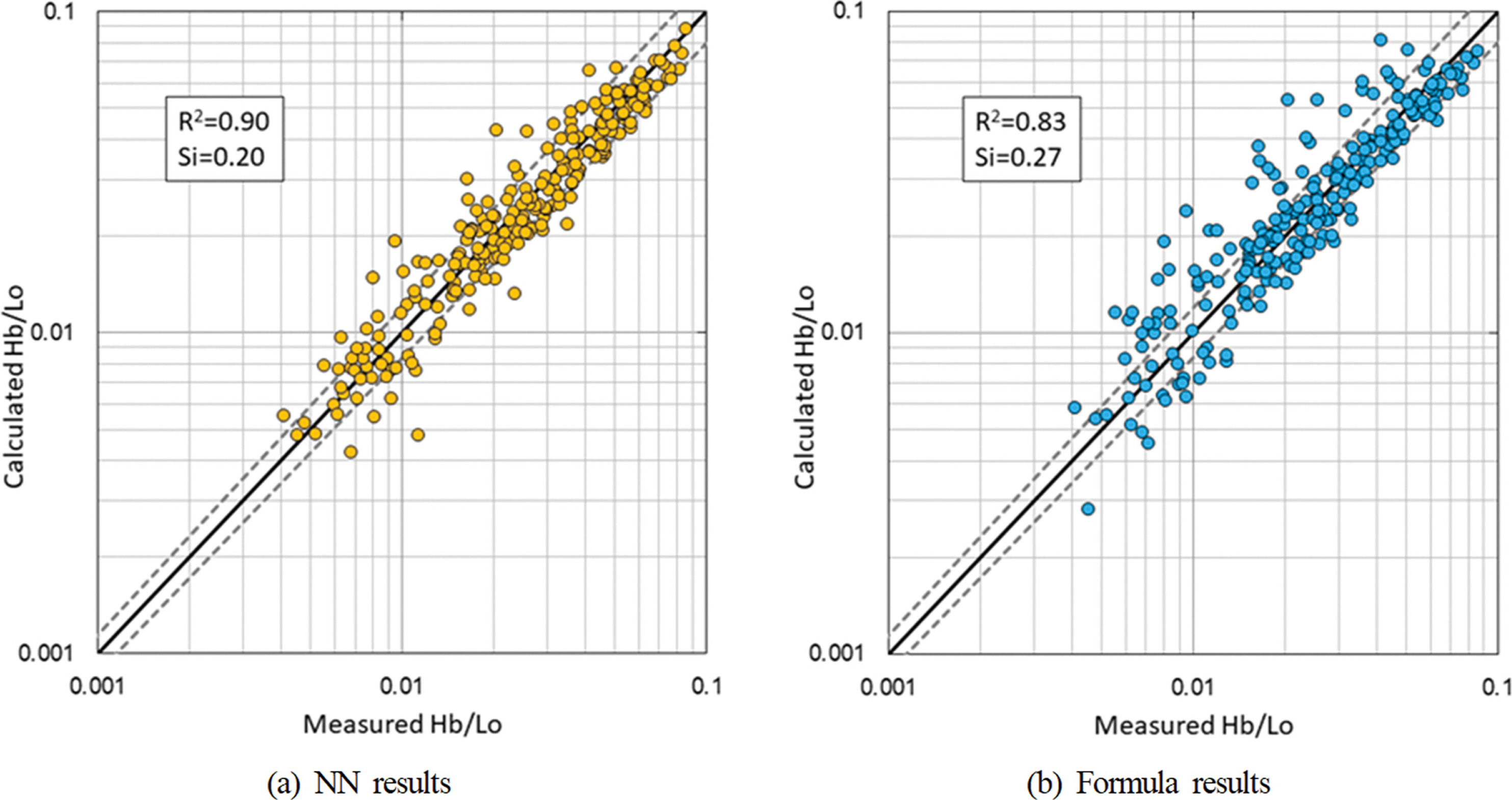
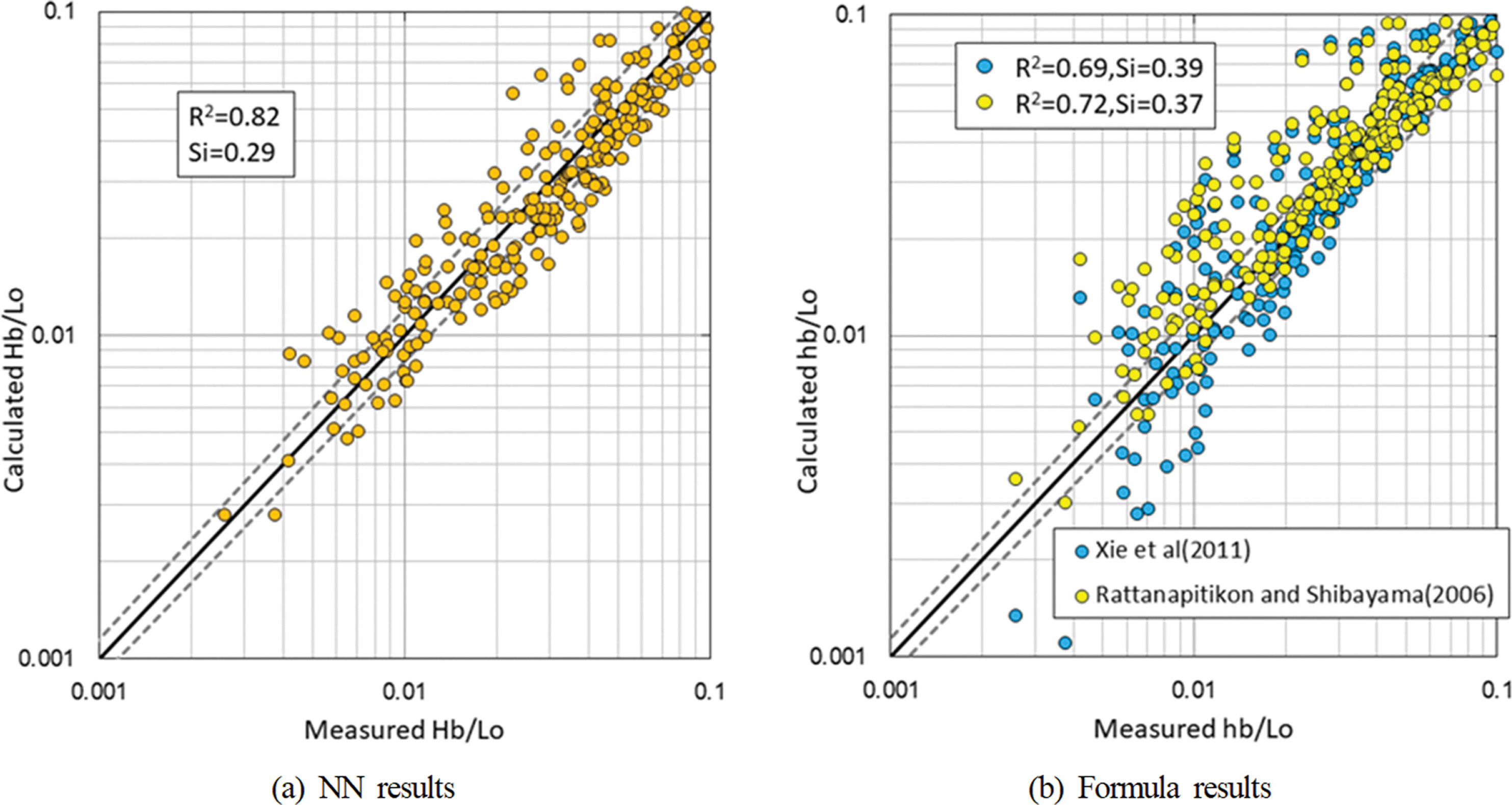
Fig. 9는 NN에 의한 쇄파파고의 예측결과와 경험식에 의한 계산결과를 비교한 것이다. NN 모델은 2개의 은닉층과 은닉층의 노드 개수는 Fig. 8(a)와 동일하게 20개로 설정하였다. 그림 중의 점선은 Fig. 8과 동일하게 20%의 오차범위를 나타낸다. 입력변수는 Fig. 8의 결과로부터 입력변수는 심해파형경사 및 사면경사를 동시에 고려하였다. 또한 경험식은 심해파형경사와 사면경사에 따라 양해적으로 쇄파파고를 산정할 수 있는 Rattanapitikon and Shibayama(2006)의 식을 적용하였으며, NN의 결과와 비교를 위해 경험식에 의한 계산결과는 NN의 예측성능 평가를 위한 훈련자료만으로 한정하였다. 우선, Fig. 9(a)에 보인 2개 은닉층을 고려한 NN 모델과 단일 은닉층을 고려한 Fig. 8(a)의 예측결과를 비교하면 2개의 은닉층을 고려한 딥러닝(deep learning)의 경우가 미소 하지만 약간 증가하는 경향을 보였다. 이는 본 연구에서 적용한 훈련자료의 양이 제한되어 있으므로 은닉층 개수의 증가에 따른 예측성능이 선형적으로 비례하지 않은 것으로 판단되며, 이러한 경향은 NN을 이용한 선행 연구결과와 일치한다. 한편, 경험식에 따른 쇄파파고 예측결과인 Fig. 9(b)에 비해 NN을 적용한 Fig. 9(a)의 경우 R²은 8.4%, SI는 9.5% 정도의 예측성능이 증가하지만, 기존의 쇄파파고에 대한 경험식의 계산결과도 비교적 쇄파수심을 양호하게 예측하고 있음을 알 수 있다.

Fig. 9.

Comparison of wave breaking height for testing data sets.

Fig, 10은 Fig. 9와 유사하게 NN 모델에 따른 쇄파수심의 예측결과를 Xie et al.(2010) 및 Rattanapitikon and Shibayama (2006)에 의한 경험식의 계산결과와 비교한 것이다. NN 모델의 은닉층과 노드 개수는 Fig. 9과 동일하게 설정하였다. Fig. 10의 결과로부터 쇄파수심에 대한 NN 및 경험식의 예측성능은 Fig. 9의 쇄파파고 예측성능 비해 다소 감소함을 알 수 있다. 그러나, 쇄파수심에 대한 NN의 예측결과는 Xie et al.(2010)의 경험식에 비해 R²은 18.89%, SI는 16.4% 정도의 예측성능이 크게 증가함을 알 수 있다. 이는 NN 모델의 경우 입력과 출력자료 사이의 비선형적 관계를 추정할 수 있는 특징이 반영된 결과로 판단된다. 한편, 경험식에 의한 Fig. 10(b)는 쇄파수심이 작은 영영에서 오차가 증가하는 경향을 보이고 있지만, NN에 의한 Fig. 10(a)의 경우 전 영역에 대해 양호한 예측성능을 보였다.

Fig. 10.

Comparison of breaking depth for testing data sets.