항만 환경자료의 정규분포 적합 검정

Normality Test of the Water Quality Monitoring Data in Harbour

Article information

J Korean Soc Coast Ocean Eng. 2021;33(2):53-64

Publication date (electronic) : 2021 April 30

doi : https://doi.org/10.9765/KSCOE.2021.33.2.53

^*Principal Research Scientist, Marine Big-data Center, Korea Institute of Ocean Science and Technology, 385 Haeyang-ro, Youngdo-gu, Busan 49111, Korea

조홍연^,^*

^*한국해양과학기술원 해양빅데이터센터 책임연구원, 과학기술연합대학원대학 KIOST SCHOOL S교수

Corresponding author: Principal Research Scientist, Marine Big-data Center, Korea Institute of Ocean Science and Technology, 385 Haeyang-ro, Youngdo-gu, Busan 49111, Korea, Tel: +82-51-664-3786, hycho@kiost.ac.kr, & Professor, University of Science anf Technology

Received 2021 March 2; Accepted 2021 March 24.

Abstract

환경자료를 이용한 다양한 통계적인 추정에서 요구되는 정규분포 가정 만족 정도를 파악하기 위하여, KOEM(해양환경공단, Korea Marine Environment Management Corporation) 항만환경 모니터링 자료 3,000세트(관측 정점 50, 표층-저층 구분 수질항목 30, 동계-하계 2)를 대상으로 18가지의 방법으로 정규분포 적합도 검정을 수행하고, 각각의 검정방법에 대한 비교 및 평가를 수행하였다. 추가적으로 자료변환 및 이상자료 영향 평가를 위하여 Shapiro-Wilk 방법을 기준 검정방법으로 선택하였다. 선정된 검정 방법을 이용하여 대표적인 정규분포 변환 방법인 Box-Cox 변환 전·후의 정규분포 적합 기각 정도와 Rosner 이상자료 진단방법을 이용한 정규분포 적합 기각 정도를 추정 및 분석하였다. Box-Cox 변환 전·후 정규분포 기각비율은 하나의 수질항목을 기준으로 24-28개 정점에서 3-4개 정도의 정점으로 크게 감소하였으며, 이상자료로 진단된 자료를 제외한 경우에는 Box-Cox 변환 전·후의 기각개수는 6-9개 정도에서 1개 정도로 감소하였다. 따라서 정규분포를 따르지 않는 연안 환경자료를 이용하여 통계적인 추정을 수행하는 경우에는 이상자료 검정 방법과 Box-Cox 변환을 모두 적용할 필요가 있다.

Trans Abstract

Normality test (hereafter NT) is a highly recommended test for statistical estimation because the normality assumption on the data is the basic and essential. NT was carried using the KOEM water quality monitoring data in harbor which are composed of total 3,000 data sets (50 stations, 30 water quality parameters including surface and bottom layers, and two seasons, such as summer and winter). The comparative analysis of the normality are carried out using total 18 methods supported by the R program packages. In addition, the Shapiro-Wilk test method is selected as the references method in this study for the analysis on the data transformation and outliers’s effects in detail. The numbers of normality assumption rejection (NAR) are estimated and compared to these cases, before and after applications of the Box-Cox transformation and Rosner’s outlier test. The NAR numbers are reduced from 24-28 to 3-4 in the “before and after” BC transformation cases with the no outlier-exclusion condition. On the contrary, the NAR numbers are rapidly diminished from 6-9 to below one in the same case with the outlier exclusion condition. Thus, the Box-Cox transformation based on the outlier test of the coastal water quality monitoring data that are not comes form the normal distribution, is highly recommended for the suitable statistical estimation and inferences.

Keywords: 정규분포 검정; 이상자료 검정; Box-Cox 변환; 항만수질 자료; 통계적인 추정

Keywords: normality test; outlier’s test; Box-Cox transformation; harbor WQ monitoring data; statistical estimation

1. 서 론

우리나라 연안에서 수행되는 다양한 환경 항목의 관측으로 자료의 축적은 상당한 정도로 추진되고 있으며, 기본적인 통계 정보 등을 추정하여 주요한 환경관리 정책 및 환경연구 등에 활용되고 있다. 환경 자료를 이용한 다양한 통계적인 추정 절차의 개발 및 활용은 정규분포 가정을 전제로 수행하기 때문에, 정규분포 적합 검정이 자료분석 과정에서 가장 우선적으로, 통상적으로 요구된다(Thode Jr., 2002). 그러나 환경자료를 이용한 통계적인 정보 추정에서 포함하는 정규분포 가정, 이상자료의 영향 등에 대한 검토는 생략되는 경우가 빈번하며, 이로 인하여 편향된 추정 또는 잘못된 통계적 판단을 유발할 수 있다. 따라서, 어떤 자료의 분석-추정을 위한 가장 기본적이고 필수적인 단계는 정규분포 적합 검정이라고 할 수 있다. 본 연구에서는 연안 항만의 수질 환경 모니터링 자료를 대상으로 정규분포 가정의 한계를 입증하기 위하여 정규분포 적합 검정을 수행하였다. 또한 정규분포 가정이 위배되는 경우, 정규분포에 적합한 자료로 변환하는 대표적인 방법에 해당하는 Box-Cox 변환방법의 성능분석을 수행하였다. 또한 대부분의 자료와는 뚜렷한 차이를 보이는 자료로 정의되는 소수의 “이상자료”가 자료 전체를 대표하는 통계측도 추정에 미치는 영향이 상당하고(Barnett and Lewis, 1994; Cho et al., 2016), 정규분포 검정에도 영향을 미칠 것으로 판단하여, 이상자료가 정규 분포 검정 결과에 미치는 영향 분석도 수행하였다.

2. 재료 및 방법

2.1 항만 수질 모니터링 자료

본 연구에서 사용한 항만 환경 관측자료는 해양수산부에서 운영하는 해양환경정보 포털 싸이트(https://meis.go.kr/portal/main.do -> 해양환경관측&조사 -> 해양환경측정망 정보 -> 항만측정망 전체 자료, 1997년-현재)에 접속하여 누구나 다운로드 받을 수 있는 공용 자료이다(MOF, 2021).

항만 수질 관측은 1997년 25개 정점을 시작으로, 2004년 14개 지점, 2006년 1개 지점(이 지점은 부산신항 H₀1 지점으로 2004년 8월 자료가 있으나, 2006년 2월 다시 관측을 개시하여 시작 시점을 2006년 2월로 간주), 2011년 2개 지점, 2013년 8개 지점이 추가되었으며, 2020년 기준 총 50개 지점에서 수질항목 관측을 수행하고 있다(Fig. 1 참조). 관측지점은 전반적으로 동해연안과 부산의 항만에 편중되어 있다. 각각의 지점에서 연2회(동계, 하계) 표층, 저층에서 각각 총 15개 항목(Secchi Depth 항목은 층별 구분과 무관한 항목으로 제외)을 관측하고 있으며, 기본적인 관측 항목은 수온, 염분, pH, DO, COD, NH3-N, NO2-N, NO3-N, TIN(NH3-N + NO2-N + NO3-N), TN, TIP(PO4-P), TP, SiO4-Si(silicate), SS(부유물질), chlorophyll-a(엽록소, 식물 플랑크톤 농도의 간접 지표) 농도이다. 관측 빈도가 연 2회에 불과하기 때문에 최장 24년의 항만 수질자료가 가용함에도 불구하고, 분석에 사용되는 자료의 개수는 동계-하계로 분류하는 경우 최대 24개로 소규모 표본에 해당하며, 최단기간 8년 자료의 경우에는 가용한 표본 개수가 8개, 10개 정도에 불과한 상황이다. 따라서 항만 수질자료의 통계적인 분석-검정은 소표본(small sample, n < 30) 분석에 적합한 비모수적인 분석-검정이 요구된다.

Fig. 1.

Location map of the monitoring stations in harbor (MOF, 2021).

모두 관측 지점에서 하나의 수질항목에 대하여 표층-저층 포함하는 가용한 자료개수는 1,874개(2021년 1월 1일 기준)로, 지점 평균 37.5개 이며, 표층-저층으로 분할하는 경우 18.7개이다(최대 24개, 최소 8개). “-” 기호로 입력된 자료는 결측으로 간주하였으며, 관측 기간동안 완전한 자료 각각의 개수(1,874 × 30 = 56,220)를 기준으로 계산하는 경우, 결측비율은 4.95%이다. 결측 자료는 TN(표층-저층 동일, 249), TP(표층-저층 동일, 249), SiO4(표층-저층 동일, 349), SS(저층, 468), chlorophyll-a(표층-저층 각각 149, 470) 항목에 집중되어 있으며, 결측자료 개수는 2,783개이다(pH, SS 표층 각각 1개 포함). 결측자료를 관측 지점으로 분류하면, 다음과 같이 최근 관측을 개시한 특정 항만에 집중되어 있음을 알 수 있다. 관측 정점은 생태구역(동해, 대한해협, 제주, 서해남부(서남해역), 서해중부 순서로 일련번호 1, 2, 3, 4, 5)으로 분류되어 있으며, 각각의 관측 정점은 다음이 순서대로 일련번호(H1-H50)를 부여하였으며, 수질항목도 순서대로 일련번호(Q1-Q30)를 부여하였다. 항만의 영문 명칭은 다음과 같이 배정하여, 지점과 수질항목을 코드로 정리하였다(Table 1 참조).

Table 1.

Code summary tables for the station and water quality parameters

※ 거진(Geojin, GJ), 속초(Sokcho, SC), 청초(Cheongcho, CC), 주문진(Jumunjin, JMJ), 묵호(Mukho, MH), 동해(Donghae, DH), 삼척(Samcheok, SCK), 임원(Imwon, IW), 죽변(Jukbyeon, JB), 후포(Hupo, HP), 축산(Chuksan, CS), 강구(Ganggu, GG), 포항구항(Pohang OLD, PHO), 포항신항(Pohang, NEW, PHN), 구룡포(Guryongpo, GRP), 감포(Gampo, GP), 울산(Ulsan, US), 대변(Daebyeon, DB), 부산북항(Busan, North, BSN), 부산남항(Busan, South, BSS), 감천(Gamcheon, GC), 다대포(Dadaepo, DDP), 마산(Masan, MS), 옥포(Okpo, OP), 장승포(Jangseungpo, JSP), 삼덕(Samdeok, SD), 통영신항(Tongyeong, NEW, TYN), 삼천포(Samcheonpo, SCP), 광양(Gwangyang, GY), 여수신항(Yeosu, NEW, YSN), 부산신항(Busan, NEW, BSN), 제주(Jeju, JJ), 성산포(Seongsanpo, SSP), 서귀포(Seogwipo, SGP), 한림(Hanlim, HL), 완도(Wando, WD), 목포(Mokpo, MP), 대천(Daecheon, DC), 평택(Pyeongtaek, PT), 인천(Incheon, IC).

KOEM 항만환경 모니터링 자료는 관측정점 50개, 수질항목 30개 항목(표층-저층 포함), 관측 시점은 동계-하계로 분류하였으며, 이 경우 대상자료는 50 × (15 × 2) × 2 = 3,000 세트가 된다. 각각의 자료세트는 정점에 따라 관측 시점이 다르고, 수질항목의 결측이 발생하기 때문에 자료의 개수가 동일하지 않은 방정형 자료로 간주할 수 있다. 이런 자료의 가용 상황은 가용한 자료의 최대 관측기간을 기준으로 하여 관측기간-정점-항목으로구성되는자료결측텐서(missing indicator tensor; 자료가용 = 1, 자료 결측 = 0)를 구성하면 자료의 가용 여부를 쉽게 판단할 수 있다(Little and Rubin, 2002). 이 텐서는 하나 하나의 수질항목에 대하여 행렬로 표시되기 때문에 수질항목에 따라 결측행렬을 도시하면 다음과 같이 자료 가용상황을 도식적으로 파악할 수 있다(Fig. 2 참조). 전체 정점과 항목에 대한 각각의 자료 세트에 대한 가용 자료개수는 행렬형태로 추정되며, 격자그림으로 도시할 수 있다(Fig. 3 참조). 가용 자료개수를 보다 정점을 기준으로 또는 항목을 기준으로 축약하여 정리할 수도 있다(Fig. 4 참조, red line = 평균). 이 그림을 보면 정점에 따라 관측 자료가 유난히 적거나, 최근 관측을 개시한 정점을 간단하게 파악할 수 있으며, 수질항목에 따라 결측이 빈번하게 발생하는 항목을 파악할 수 있는 정점이 있다. 이러한 결측상황 및 가용자료 개수 정보는 가장 필수적이고 기본이 되는 정보로 KOEM 환경 자료와 같은 반정형(semi-formal) 자료의 가용여부(availability) 파악에 중요한 정보를 시각적으로, 정량적으로 정리된 형태로 제공된다.

Fig. 2.

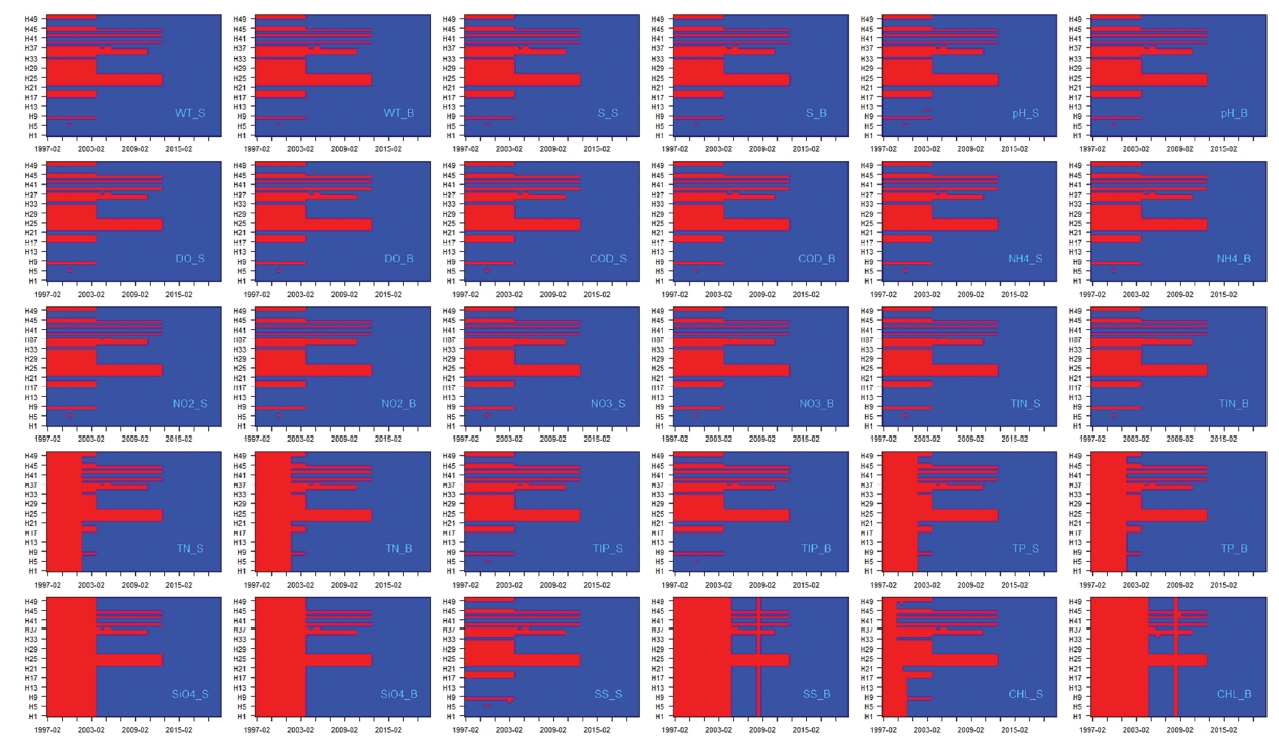
Missing Indicator Matrix (Tensor) plots of the KOEM Monitoring Data in Harbor (Horizontal axis = monitoring month, Vertical axis = Monitoring station codes; red cell = missing or not in operation, bule cell = available).

Fig. 3.

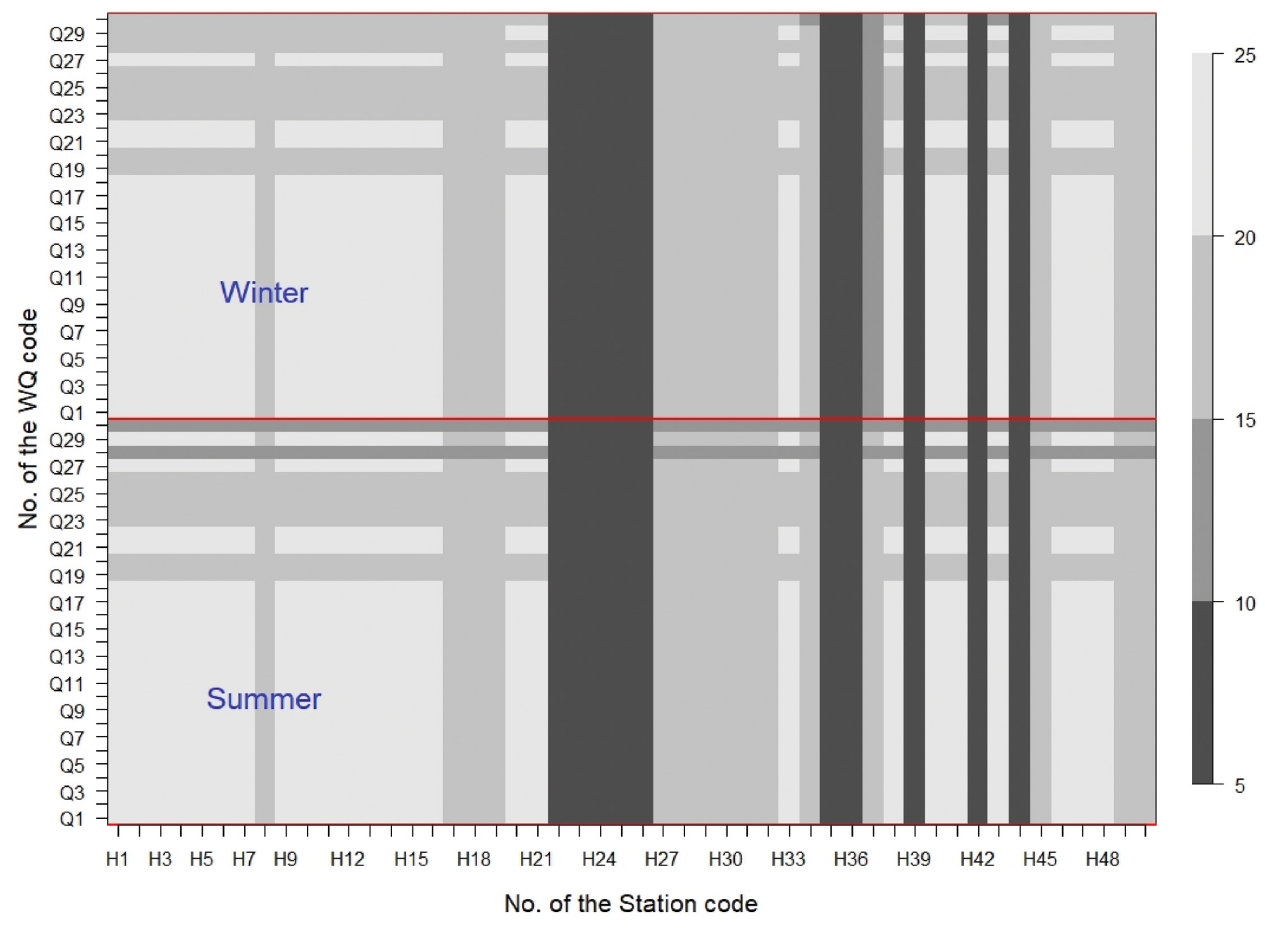
Data numbers of the stations and water quality constituents (No. of the data: n = 8 at H23-26, H39, H42, H44, n = 10 at H35-36 stations).

Fig. 4.

Barplots of the total available data numbers.

2.2 정규분포 검정(normality test, 이하 NT) 방법

(1) 정규분포 적합 검정

정규분포 적합 검정은 그 가정의 중요성으로 매우 다양한 다수의 검정 방법이 제안 및 활용되고 있다. 가장 간단하게 시각적으로 판단하는 방법은 자료의 이론적인 변량과 표본변량을 도시하는 함수를 이용하는 방법이다. 다음 함수(R 프로그램 기본 지원함수: qqnrom(), qqline())를 이용하고 도시하고, 정규분포를 완벽하게 따르는 기준선에서 벗어나는 정도로 정규분포 적합 여부를 판단할 수 있다. 통계량에 근거한 검정 방법은 일반적인 성능 평가에 근거하여 Shapiro-Wilk 검정방법이 우수한 방법으로 제안되고 있으나, 그럼에도 불구하고 다양한 검정 방법이 사용되고 있으며, 자료의 특성에 따라 그 검정 성능이 차이를 보일 수 있다(Thode Jr., 2002; D’Agostino and Stephens, 1986).

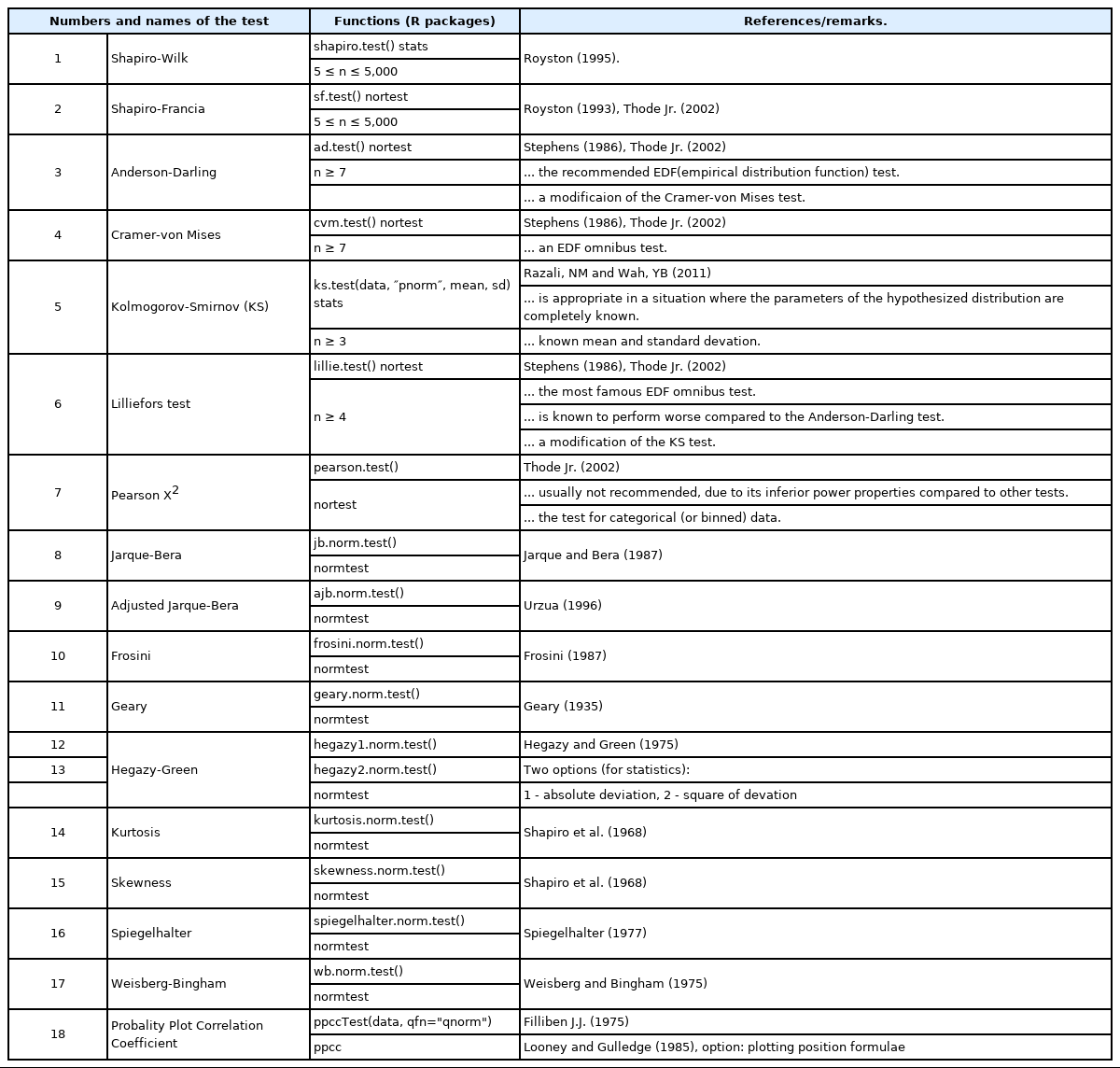
본 연구에서는 일반적으로 제안 및 사용되고 있는 모든 검정 방법에서, R 프로그램 패키지에서 지원하는 방법 총 18가지를 선정하여 정규분포 적합 검정을 수행하였으며, 사용한 방법에 대한 기본적인 설명 및 R 프로그램에서 사용하는 함수를 정리 및 제시한다(Table 2 참조). 이 검정방법의 귀무가설(null hypothesis, H₀)은 “어떤 대상 자료의 분포가 정규분포를 따른다”이고, 대립가설(alternative hypothesis, H_a, H₁)은 “어떤 자료가 정규분포를 따르지 않는다”이다. 따라서 귀무가설이 기각되는 경우, 대상 항만 환경자료는 “정규분포를 따른다”는 가설이 기각되기 때문에, 엄밀한 의미로 “정규 분포를 따른다”고 주장할만한 충분한 근거가 없는 자료로 간주된다.

Table 2.

Summary of the available normality test methods

(2) Box-Cox 변환(‘EnvStats’ 패키지 boxcox() 함수 이용)

자료가 정규분포를 따르지 않는 경우, 정규분포를 따르는 자료로 변환하는 대표적인 방법은 Box-Cox 변환공식을 이용하는 방법이며, 최적의 변환계수 추정은 R EnvStats 패키지(Millard, 2013)에서 제공하는 boxcox() 함수를 이용한다. 이 함수를 이용하여 추정한 최적계수로 변환한 자료를 대상으로 정규분포 적합 검정을 수행하며, Box-Cox 변환이 정규분포 적합을 보장하지는 않는다.

(3) 이상자료 진단 검정(‘EnvStats’ 패키지, Rosner Test 방법, rosnerTest() 함수 이용)

이상자료의 진단방법도 매우 다양한 방법이 제시되고 있으나, 본 연구에서는 단변량(uni-variate) 환경 자료의 이상자료 진단방법으로 이용되는 R EnvStats 패키지(Millard, 2013)에서 제공하는 rosnerTest() 함수를 이용하였다. 환경자료는 다수의 항목으로 구성되는 다변량(multi-variate) 자료에 해당되나, 특정한 하나의 항목만을 대상으로 하는 경우에는 단변량 자료에 해당한다. 이 함수는 Rosner 검정방법으로 이상자료를 진단하는 방법으로, 부산연안 수질 자료의 이상자료 진단에 사용되었으며(Cho et al., 2016), 단 하나의 자료에 대하여 거리 기반(distance-based) 개념으로 이상자료 여부를 판단하는 Grubb’s test, Dixon test 방법과는 달리 다수의 이상 자료 진단이 가능하다.

3. 검정 결과 및 토의

3.1 검정 방법에 따른 정규분포 가정 기각 개수

본 연구에서 사용한 18개의 검정 방법에 따른 정규분포 기각 개수(빈도)는 수질항목에 따른 총50개의 정점에 대한 동계-하계 기각 개수와 정점에 따른 총 60개 세트(15개 항목, 표층-저층, 동계-하계)의 수질항목에 대한 기각 개수를 추정하여 제시한다(Fig. 5 참조). 그림에 제시된 수치는 NT 방법의 번호(Table 2 제시)이며, 번호가 위치하는 높이는 정규분포 가정 기각 개수의 정점 평균, 항목 평균개수에 해당한다.

Fig. 5.

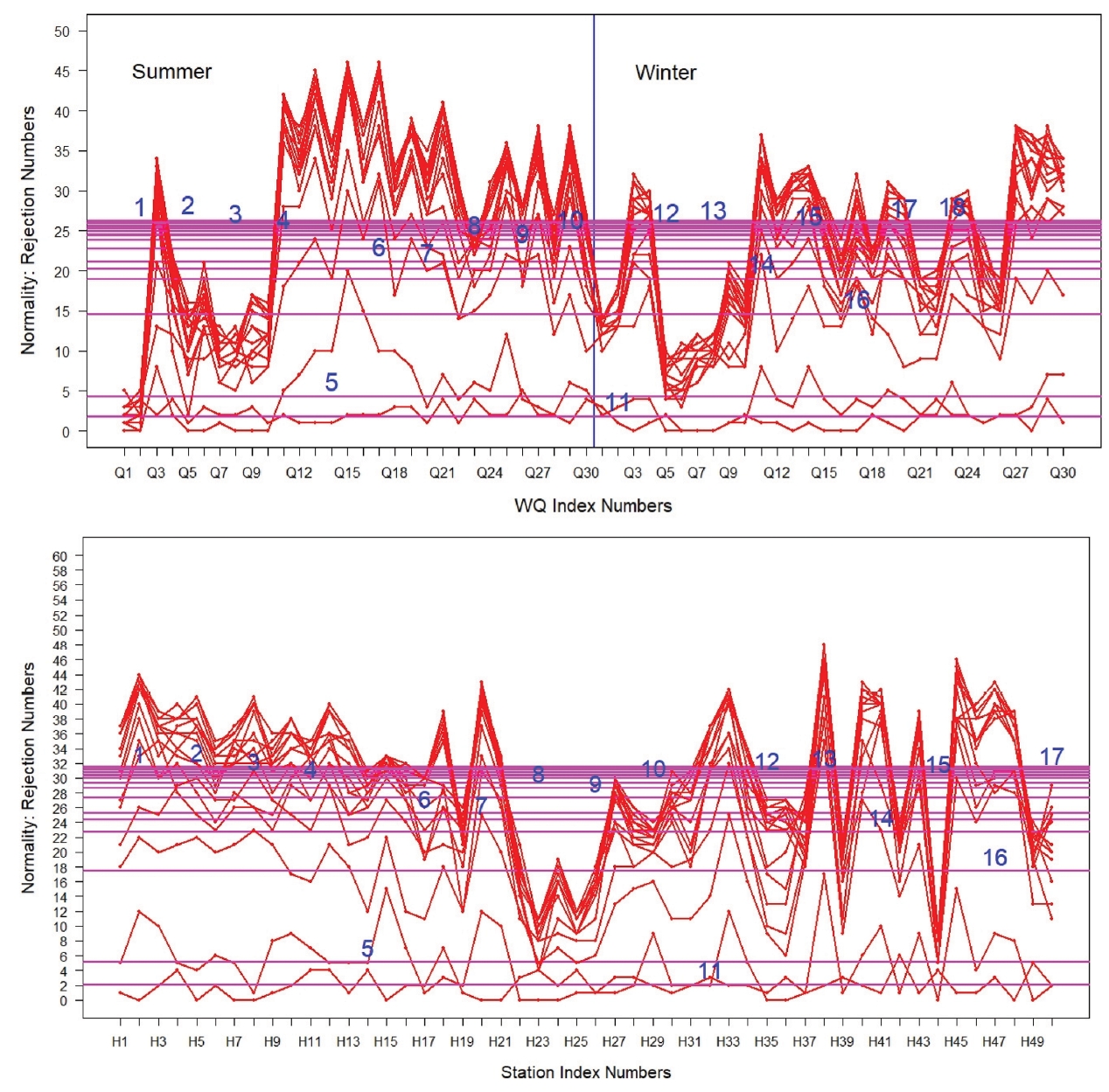
Numbers of the normality assumption rejection for each test method to the stations and water-quality index parameters.

본 연구에서는 선정한 총18개의 정규분포 적합 검정(normality test, 이하 NT) 방법을 사용하여 항만 “수질자료의 정규분포 적합 가정” 기각 여부를 유의수준(significance level) 0.05 조건에서 판정하였다. Fig. 5에서 볼 수 있는 바와 같이, 수질항목에 따른 정규분포 기각 개수는 염분, 영양염류, 엽록소 항목에서 크게 나타나고 있는 것으로 파악되었으며, 동계보다 하계 수질자료에서 보다 높은 빈도로 나타났다. 관측 지점에 따른 차이는 H23-26 정점에서 상대적으로 낮게 나타나고 있음을 알 수 있으며, 정점의 자료개수 영향으로 판단된다. 최근 관측을 수행하여 자료의 개수가 8-10개 정도로 매우 적기 때문에 정규분포 가정을 유의수준에서 기각여부 판단이 크게 제한된다.

한편 정규분포 검정 방법에 따른 차이는 전반적으로 근소한 차이를 보이고 있으나, 유사한 양상의 검정 결과를 보이고 있다. 그러나 KS 검정(No. 5), Geary 검정(No. 11) 방법은 다른 방법과는 NAR(normality assumption rejection) 빈도가 크게 차이가 난다. 또한 정규분포 가정 기각에 엄격한, 기각비율이 낮은 이 두 방법과 더불어, Lilliefors, Pearson’s X², Skewness, Weisberg-Bingham 검정 방법(각각 순서대로 No. 6, 7, 14, 16)도 상대적으로 낮은 기각 정도를 보이고 있는 것으로 파악되었다. 낮은 기각 비율은 Type II 오류 증가의 원인이 되어, 정규분포를 따르지 않는 자료를 정규분포에 적합한 자료로 판정하는 오류가 증가하는 단점이 있다. 따라서 본 연구에서는 일반적으로 검정능력(power)이 우수한 방법으로 추천되는 Shapiro-Wilk 검정 방법을 기준 방법으로 선택한다. 정규분포 적합 검정 방법의 우열 판단은 자료의 특성에 따라 차이를 보일 수 있으나, 전반적으로 KS 방법, Pearson’s X² 등 사용을 제한하는 검정방법과 유사하한 성능을 보이는 방법은 제외할 필요가 있을 것으로 판단된다. 일반적으로 우수하다고 평가되는 정규분포 적합 검정 방법은 Shapiro-Wilk 검정으로 제시되고 있으며(Thode Jr., 2002), 동등한 성능수준으로 Anderson-Darling 방법이 추천되고 있다.

3.2 Box-Cox 변환의 성능평가 - 정규분포 적합 개수 변화

적합검정방법에 따른 차이(3.1절)를 살펴본 바와 같이, 항만의 수질자료는 수질항목과 정점(정점의 가용자료 개수)에 따라 차이를 보이고 있으나, 전반적으로 자료 세트의 상당한 부분이 정규분포 가정이 기각되고 있음을 알 수 있다. 이는 정규분포를 기본가정(underlying distribution assumption)으로 전제하는 대부분의 통계적인 추정 및 검정 등에 직접적으로 영향을 미치기 때문에 정규분포 가정과는 무관한 또는 특정한 분포 가정이 없는 비모수적인 방법을 이용하여야 함을 의미한다. 그러나 일반적으로 비모수적인 방법은 검정능력에 문제가 있기 때문에, 가능하면 환경자료를 적절한 변환을 통하여 정규분포를 따르는 자료로 변환하는 방법이 권장된다. 이러한 정규분포 가정을 만족하기 위한 대표적인 자료 변환 방법으로는 Box-Cox 방법이 있다. 이 방법을 본 연구에서 사용한 항만 환경자료에 적용하였으며, Box-Cox 변환기법 적용 전·후의 정규분포 가정 기각 개수를 추정하고, 다음 그림으로 제시한다(Fig. 6 참조).

Fig. 6.

Numbers of the normality assumption rejection, before/after Box-Cox transformation (Shapiro-Wilk test method, No outlier-detection test – removal condition).

더불어 이상자료도 통계적인 측도 추정 및 검정에 미치는 영향이 상당하기 때문에 이상자료로 진단된 자료의 제거 전·후의 영향을 Box-Cox 변환 적용과 병행하여 비교-분석하는 과정이 필요하다. Box-Cox 변환 적용 전후의 이상자료 진단개수 변화 양상을 분석하기 위하여 이상자료 포함 또는 제외 조건에서 NAR 개수 변화를 추정하였으며, 이상자료 진단 개수 변화도 추정 제시하였다(Fig. 7-8 참조).

Fig. 7.

Numbers of the normality assumption rejection, before/after Box-Cox transformation (Shapiro-Wilk test method, Outlier-detection test – removal condition; excluding the outliers detected by Rosner Test).

Fig. 8.

No. of the detected outliers before/after Box-Cox transformation.

그림에서 볼 수 있는 바와 같이, 전반적으로 동계 자료가 하계 자료보다 정규분포 기각 정도가 다소 높게 나타나는 것으로 파악되었다. 이는 동계에 비하여 하계에 수질 변동이 크게 나타나는 영향으로 판단할 수 있다. Box-Cox 변환 영향은 이상자료 제거 유무조건(Figs. 6-7, (a), (b) 비교)에서 분석하였다. 이상자료를 제거하지 않은 경우, Box-Cox 변환 이전에는 항목별로 24-28개 정도, 지점별로 14-17개 정도의 기각 판정이 나왔으나, Box-Cox 변환 이후에는 항목별로 평균 3.2-3.8, 지점별로 평균 1.9-2.3개 정도로 기각 판정이 크게 감소하였다. 한편 이상자료를 제외한 경우, Box-Cox 변환 이전에는 항목별로 5.5-8.5개 정도, 지점별로 3.3-5.1개 정도의 기각 판정이 나왔으나, Box-Cox 변환 이후에는 항목별, 지점별로 1개 이하로 기각 판정 개수가 크게 감소하였다. 정규분포 기각 판정 저감영향은 Box-Cox 변환 영향이 이상자료 영향보다 크게 나타나는 것으로 파악되었으나. Box-Cox 변환과 이상자료 진단-제외 조건을 적용하는 경우, 대부분의 환경 측정 자료가 정규분포 적합 가정을 만족하게 되는 것으로 파악되었다.

환경자료를 최적 Box-Cox 변환 매개변수를 이용하여 변환한 경우와 변환하지 않은 경우의 이상자료로 진단되는 자료 개수의 변화는 하계가 동계보다 3-4개 정도 크게 진단되었다(Figs. 6, 8 참조). Box-Cox 변환 이전에는 수질항목별로 평균 60-83개, 지점별로 36-50개 정도가 이상자료로 진단되었으나, BC 변환 이후에는 수질항목별로 17-21개, 지점별로 10-13개로 크게 감소하는 양상을 보이고 있다.

4. 결론 및 제언

항만 환경자료를 이용하여 다양한 통계적 추정의 기본 가정으로 전제되는 정규분포 적합 검정을 수행하였다. 정규분포 검정 결과, 저점과 항목에 따라 차이를 보이지만 전반적으로 상당 부분의 자료가 정규분포 가정이 기각되는 것으로 파악되었다. 이상자료를 제거하고, 최적 매개변수를 이용한 Box-Cox 변환 과정을 거치는 경우, 정규분포 기각 비율은 허용할만한 수준으로 크게 감소하였다. 따라서, 항만 환경자료를 이용한 통계적인 추정에서 요구되는 정규분포 적합 검정을 위해서는 Box-Cox 변환과 이상자료 제외 과정이 필요한 것으로 파악되었다. 본 연구에서는 항만 환경자료로 제한하여 분석을 수행하였으나, 가용한 모든 연안 환경자료에 대한 정규분포 적합 검증-분석이 필요하다. 또한 환경자료가 정규분포를 따르지 않는 경우, 적절한 변환 방법의 성능평가에 관한 연구가 필요할 것으로 판단된다. 더불어 환경자료의(모수적 또는 비모수적인, parametric and/or non-parametric) 적절한 분포함수 추정 연구와 추정 분포함수를 이용한 적절하고 효과적인 통계분석 절차에 대한 필요할 것으로 사료된다.

Acknowledgements

본 연구에서 사용한 항만 환경자료를 제공해주신 해양수산부, 해양환경공단(KOEM)에 감사 드립니다.

References

Barnett V., Lewis T.. 1994. Outliers in statistical data John Wiley & Sons.

Cho H.Y., Lee K.S., Ahn S.M.. 2016;Impact of outliers on the statistical measures of the environmental monitoring data in Busan coastal sea, Note. Ocean and Polar Research 38(2):149–159.

D’Agostino R.B., Stephens M.A.. 1986. Goodness-of-Fit Techniques Marcel Dekker.

Filliben J.J.. 1975;The probability plot correlation coefficient test for normality. Technometrics 17:111–117.

Frosini B.V.. 1987. On the distribution and power of a goodness-of-fit statistic with parametric and nonparametric applications. “Goodness-of-fit” In : Revesz P., Sarkadi K., Sen P.K., eds. p. 133–154.

Gavrilov I., Pusev R.. 2014. normtest: Tests for Normality. R package version 1.1. https://CRAN.R-project.org/package=normtest.

Geary R.C.. 1935;The ratio of the mean deviation to the standard deviation as a test of normality. Biometrika 27:310–332.

Gross J., Ligges U.. 2015. nortest: Tests for Normality. R package version 1.0-4. https://CRAN.R-project.org/package=nortest .

Hegazy Y.A.S., Green J.R.. 1975;Some new goodness-of-fit tests using order statistics. Journal of the Royal Statistical Society. Series C (Applied Statistics) 24:299–308.

Jarque C.M., Bera A.K.. 1987;A test for normality of observations and regression residuals. International Statistical Review 55:163–172.

Little R.J.A., Rubin D.B.. 2002. Statistical Analysis with Missing Data Second Editionth ed. John Wiley & Sons.

Looney S.W., Gulledge T.R.. 1985;Use of correlation coefficient with normal probability plots. The American Statistician 39:75–79.

Millard S.P.. 2013. EnvStats: An R Package for Environmental Statistics Springer. New York: ISBN 978-1-4614-8455-4, https://www.springer.com.

Ministry of Oceans and Fisheris. 2012. Marine Environment Information (System) Portal (2021). https://www.meis.go.kr [accessed 2021.02.26.].

Pohlert T.. 2020. ppcc: Probability Plot Correlation Coefficient Test. R package version 1.2. https://CRAN.R-project.org/package=ppcc.

R Core Team. 2020. R: A language and environment for statistical computing R Foundation for Statistical Computing. Vienna, Austria: https://www.R-project.org/.

Razali N.M., Wah Y.B.. 2011;Power comparisons of shapirowilk, kolmogrov-smirnov, lilliefors and anderson-darling tests. Journal of Statistical Modeling and Analytics 2:21–33.

Royston P.. 1995;Remark AS R94: A remark on Algorithm AS 181: The W test for normality. Applied Statistics 44:547–551. doi:10.2307/2986146.

Royston P.. 1993;A pocket-calculator algorithm for the Shapiro-Francia test for non-normality: an application to medicine. Statistics in Medicine 12:181–184.

Shapiro S.S., Wilk M.B., Chen H.J.. 1968;A comparative study of various tests for normality. Journal of the American Statistical Association 63:1343–1372.

Spiegelhalter D.J.. 1977;A test for normality against symmetric alternatives. Biometrika 64:415–418.

Stephens M.A.. 1986. Tests based on EDF statistics. Goodness-of-Fit Techniques In : D’Agostino R.B., Stephens M.A., eds. Marcel Dekker. New York:

Thode H.C. Jr.. 2002. Testing for Normality Marcel Dekker. New York:

Urzua C.M.. 1996;On the correct use of omnibus tests for normality. Economics Letters 53:247–251.

Weisberg S., Bingham C.. 1975;An approximate analysis of variance test for non-normality suitable for machine calculation. Technometrics 17:133–134.

Appendices

부록. Sample R Codes.

1. Box-Cox 최적 매개변수 추정 및 변환 과정 Code (# - comment line)

> ## xx = sample data variable name.

> trn1 <- EnvStats::boxcox(xx, lambda=c(-2,2), optimize=T)

> ## 동일한 이름을 가진 함수 boxcox() MASS 중복을 배제하기 위한 수단.

> trn1$lambda ## 최적의 변환 매개변수

> txx <- (xx^trn1$lambda -1)/trn1$lambda

> txx --> 변환된 변수를 이용하여 정규분포 적합 검정 수행

2. Rosner 검정방법을 이용한 이상자료 진단 Code.

> ## xx = sample data variable name.

> tst1 <- rosnerTest(xx, k=length(xx))

> nout <- tst1$n.outliers

> oval <- tst1$all.stats$Value[1:nout]

> oidx <- tst1$all.stats$Obs.Num[1:nout]

> rxx <- xx[-oidx] ## Rosner 검정방법으로 진단된 이상자료를 제외한 자료

> plot(xx); points(oidx, oval, pch=12, cex=1.8, col="red")

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Hcode	H. Stations	Hcode	H. Stations	Hcode	H. Stations
H1	GJ H01	H18	DB H01	H35	YSN H02
H2	SC H01	H19	BSN H02	H36	YSN H03
H3	CC H01	H20	BSS H02	H37	BSN H01
H4	JMJ H01	H21	GC H02	H38	JJ H01
H5	MH H01	H22	BSN H03	H39	JJ H02
H6	DH H01	H23	BSN H01	H40	SSP H01
H7	SCK H01	H24	BSS H01	H41	SGP H01
H8	IW H01	H25	GC H01	H42	SGP H02
H9	JB H01	H26	DDP H01	H43	HL H01
H10	HP H01	H27	MS H01	H44	HL H02
H11	CS H01	H28	OP H01	H45	WD H01
H12	GG H01	H29	JSP H01	H46	MP H01
H13	PHO H01	H30	SD H01	H47	MP H02
H14	PHN H01	H31	TYN H01	H48	DC H01
H15	GRP H01	H32	SCP H01	H49	PT H01
H16	GP H01	H33	GY H01	H50	IC H01
H17	US H01	H34	YSN H01	-	-

Qcode	Q. Symbol	Qcode	Q. Symbol	Descriptions (S, B = surface, and bottom layers, respectively)
Q1	WT_S	Q2	WT_B	Water temperatures (°C)
Q3	S_S	Q4	S_B	Salinity (PSU)
Q5	pH_S	Q6	pH_B	pH (-)
Q7	DO_S	Q8	DO_B	Dissolveld Oxygen (mg/L)
Q9	COD_S	Q10	COD_B	Chemical Oxygen Demand (mg/L)
Q11	NH4_S	Q12	NH4_B	Ammonia-N (μg/L)
Q13	NO2_S	Q14	NO2_B	Nitirte-N (μg/L)
Q15	NO3_S	Q16	NO3_B	Nitrate-N (μg/L)
Q17	TIN_S	Q18	TIN_B	Total Inorganic N (μg/L)
Q19	TN_S	Q20	TN_B	Total Nitrogen (μg/L)
Q21	TIP_S	Q22	TIP_B	Total Inorganic P (μg/L)
Q23	TP_S	Q24	TP_B	Total Phosphorus (μg/L)
Q25	SiO4_S	Q26	SiO4_B	Silicate-Si (μg/L)
Q27	SS_S	Q28	SS_B	Suspended Solids (μg/L)
Q29	CHL_S	Q30	CHL_B	Chlorophyll-a (μg/L)

Table 2.

Summary of the available normality test methods

Numbers and names of the test		Functions (R packages)	References/remarks.
1	Shapiro-Wilk	shapiro.test() stats	Royston (1995).
1	Shapiro-Wilk	5 ≤ n ≤ 5,000	Royston (1995).
2	Shapiro-Francia	sf.test() nortest	Royston (1993), Thode Jr. (2002)
2	Shapiro-Francia	5 ≤ n ≤ 5,000	Royston (1993), Thode Jr. (2002)
3	Anderson-Darling	ad.test() nortest	Stephens (1986), Thode Jr. (2002)
		n ≥ 7	... the recommended EDF(empirical distribution function) test.
			... a modificaion of the Cramer-von Mises test.
4	Cramer-von Mises	cvm.test() nortest	Stephens (1986), Thode Jr. (2002)
4	Cramer-von Mises	n ≥ 7	... an EDF omnibus test.
5	Kolmogorov-Smirnov (KS)	ks.test(data, ″pnorm″, mean, sd) stats	Razali, NM and Wah, YB (2011)
		ks.test(data, ″pnorm″, mean, sd) stats	... is appropriate in a situation where the parameters of the hypothesized distribution are completely known.
		n ≥ 3	... known mean and standard devation.
6	Lilliefors test	lillie.test() nortest	Stephens (1986), Thode Jr. (2002)
		n ≥ 4	... the most famous EDF omnibus test.
			... is known to perform worse compared to the Anderson-Darling test.
			... a modification of the KS test.
7	Pearson X²	pearson.test()	Thode Jr. (2002)
		nortest	... usually not recommended, due to its inferior power properties compared to other tests.
		nortest	... the test for categorical (or binned) data.
8	Jarque-Bera	jb.norm.test()	Jarque and Bera (1987)
8	Jarque-Bera	normtest	Jarque and Bera (1987)
9	Adjusted Jarque-Bera	ajb.norm.test()	Urzua (1996)
9	Adjusted Jarque-Bera	normtest	Urzua (1996)
10	Frosini	frosini.norm.test()	Frosini (1987)
10	Frosini	normtest	Frosini (1987)
11	Geary	geary.norm.test()	Geary (1935)
11	Geary	normtest	Geary (1935)
12	Hegazy-Green	hegazy1.norm.test()	Hegazy and Green (1975)
13		hegazy2.norm.test()	Two options (for statistics):
		normtest	1 - absolute deviation, 2 - square of devation
14	Kurtosis	kurtosis.norm.test()	Shapiro et al. (1968)
14	Kurtosis	normtest	Shapiro et al. (1968)
15	Skewness	skewness.norm.test()	Shapiro et al. (1968)
15	Skewness	normtest	Shapiro et al. (1968)
16	Spiegelhalter	spiegelhalter.norm.test()	Spiegelhalter (1977)
16	Spiegelhalter	normtest	Spiegelhalter (1977)
17	Weisberg-Bingham	wb.norm.test()	Weisberg and Bingham (1975)
17	Weisberg-Bingham	normtest	Weisberg and Bingham (1975)
18	Probality Plot Correlation Coefficient	ppccTest(data, qfn="qnorm")	Filliben J.J. (1975)
18	Probality Plot Correlation Coefficient	ppcc	Looney and Gulledge (1985), option: plotting position formulae

Basic references:

* R Core Team (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

* Gross J. and Ligges, U. (2015). nortest: Tests for Normality. R package version 1.0-4. >https://CRAN.R-project.org/package=nortest

* Gavrilov, I. and Pusev, R. (2014). normtest: Tests for Normality. R package version 1.1. https://CRAN.R-project.org/package=normtest

* Pohlert, T. (2020). ppcc: Probability Plot Correlation Coefficient Test. R package version 1.2. https://CRAN.R-project.org/package=ppcc