Article information

Abstract

Trans Abstract

1. 서 론

바람은 시간과 고도에 따라 변화하는 풍속과 풍향 정보를 포함하고 있으며 해양구조물 설계 및 풍파 추정 등에 있어서 매우 중요한 인자이다. 일반적으로 바람은 특정한 하나의 고정된 고도에서 연속적으로 관측되기 때문에 다양한 고도에서 연속적으로 측정한 바람 자료는 매우 제한되어 있다. 바람의 고도 분포는 대기 역학적인 관점에서 매우 복잡한 기상 인자의 영향을 받기 때문에 충분한 기상인자의 추가적인 관측 자료가 미흡한 경우에는 고도에 따른 풍속 분포 예측이 곤란하다. 또한 특정 고도에서의 바람 관측도 관측 여건(목표)에 따라 관측 고도가 다르기 때문에 풍속의 상대적인 비교를 위해서는 동일한 기준 고도로 환산하여 비교하는 과정이 요구된다. 또한 관심을 가지는 영역에 따라 관심 고도도 차이를 보이고 있다. 파랑을 발생시키는 풍속의 경우는 기준 고도로 2 m, 10 m 조건이 일반적이며, 육상에서는 기준 고도 10 m 조건을 유지하는 경우가 일반적이다. 반면 해상풍력의 경우 터빈 크기에 따라 차이를 보일 수 있으나, 터빈이 위치하는 고도인 약 100 m 정도의 고도에 대한 풍속 정보를 필요로 한다. 그러나 대부분의 경우, 관심 고도에서의 관측 자료가 가용하지 못한 경우가 빈번하기 때문에 특정 고도에서의 측정한 바람 자료를 이용하여 다른 고도에서의 풍속을 추산하는 과정을 거치게 된다. 이러한 추산과정에서 가장 활발하게 사용되는 공식은 다음 식(1)과 같은 Power 함수를 이용한 경험 공식이다. 경험적으로 일정한 범위를 가지지만, 실질적으로 관측 자료를 이용한 검토가 곤란하기 때문에 n = 7 조건에서 특정 고도(기준고도)에서의 풍속자료를 이용하여 관심 고도에서의 풍속을 간단하게 산정하는 방법이 공학 분야에서는 널리 이용되어 왔다(Coastal Engineering Manual, 2008; Mwanykia and Kainkwa, 2006). 대표적인 풍속 추정 연구는 풍력 하중 추정이었으나 최근에는 풍력자원 추정을 위한 연구의 일환으로 풍속 분포 추정 및 관측 연구가 진행되고 있는 상황이다(Choi and Kanda, 1990).

여기서 u(z)는 지면으로부터의 높이 z에서의 풍속, u(z_r)은 기준 높이 z_r에서의 풍속, 1/n은 고도분포지수이다. 그러나 이 지수분포는 고도 분포를 추정할만한 가용한 자료가 없는 경우에 사용되는 공식이며, 기존 공식의 지수에 대한 검토도 일반적으로 고정된 육상에서, 중립 대기조건에서 선별된 자료를 이용하여 제안된 활용 범위가 제한된 공식이다. 본 연구에서는 유동적인 표면에서 풍력발전 평가 목적의 고도에 해당하는 20~100 m 정도의 범위에서 측정한 고도에 따른 풍속 자료이기 때문에 기존의 공식 이용 조건과는 큰 차이가 있다.

반면 이론에 근거한 함수로 제시되는 방정식은 다음 식(2)와 같은 대수함수 형태가 사용되고 있으며 보다 정밀한 보조 관측 정보가 지원되는 경우, 비교적 정확한 풍속 추정이 가능하다. 이 함수의 매개변수(u_*, z₀)는 각각 대기 저면(수면) 마찰속도(friction velocity, m/s), 수면의 거칠기에 해당하는 조도(roughness, m)로 물리적인 의미를 가지고 있다. 마찰속도는 수면에서의 마찰 전단응력의 함수(u* = τs/ρ, τ_s = 수면 또는 지면에서의 전단응력, ρ = 대기 밀도)로 주어지기 때문에 고도화된 관측 자료가 지원되는 경우, 자료를 이용한 직접적인 추정이 가능하다. 그러나 실질적으로 가용한 관측 정보나 관측 환경 여건에 따라 관측이 제한될 수 있기 때문에 실질적으로 적절한 방법의 선택과 추정 오차 분석이 요구된다.

한편 식(3)은 다양한 대기조건을 포함하는 함수 형태로 선형 변환이 제한되기 때문에 비선형 매개변수 추정 과정을 거쳐야 한다(Pena et al., 2008; Emeis, 2014). 식(3)의 경우 난류 규모에서의 추가 관측 자료가 요구되기 때문에 일반적으로는 가용 자료의 제한으로 매개변수 추정에 한계가 따른다. Molina-Garcia et al.(2019)는 함수 형태의 매개변수 추정이 아니라 분류 기법을 이용하여 풍속 분포를 추정하는 연구를 수행한 바 있다.

여기서, ϕ_m(·) 함수는 대기조건에 따라 다음 식(4)~(6)과 같이 비선형 함수로 정의된다(Sozzi et al., 2001). 한편 Moller et al.(2009)은 보다 세분화된 대기조건으로 분류하여 풍속의 분포 분석 기준으로 사용하였다. 이론적으로 명확한 수식이라 할지라도 미분 형태의 함수로 표현되는 경우가 대부분이므로, 현장 관측 자료를 이용한 추정의 경우, 불연속적인 형태가 발생하는 경우를 다양하게 분류하는 연구이다.

- 대기가 불안정한 조건(in unstable condition, L < 0, γ > γ_a)

- 대기가 안정한 조건(in stable condition, L > 0, γ < γ_a)

- 대기가 중립인 조건(in (near) neutral condition, L = 0 ≒ 0, γ = γ_a)

여기서, L = Monin-Obukhov 안정거리(stability length), γ = - dT/dz(= lapse rate, 고도에 따른 기온 감률), γ_a = 0.98 (≒ 1.0°C/100 m, 건조공기 조건), T = 기온(°C)이다.

대기조건을 판단하는 대표적인 방법은 아래 식(7)과 같이 정의되는 L, 또는 Richardson 계수(Ri)를 이용하여 분류할 수도 있다.

해양에서 바람을 관측하기 위해 부이를 이용하는 경우에는 관측 고도 2~3 m 정도로 제한되며, 고도 변화에 따른 풍속 관측이 매우 곤란하다. 반면 고정 관측 타워를 이용하는 경우에는 다양한 고도에서 풍속 관측이 가능하나, 해상 관측타워 설치에 따른 과도한 비용이 소요된다. 또한 조석의 영향이 있는 해역에서는 수면과 가까운 고도 자료는 조위에 따라 관측 고도가 변화하는 양상을 보일 수 있으며, 수면에서 가까운 관측이 제한될 수 있다. 해안 지역의 등대와 같은 고정 구조물에서 관측하는 경우에도 해상부이보다는 높은 고도에서 관측이 가능하지만, 특정 고도에서의 관측으로 제한되고, 육상에서는 급격한 변화 양상을 보이기 때문에 관심 해역 바람 자료와 상관정도가 작으면 해상에서의 바람과는 상이한 특성을 가지게 되어 실질적으로 사용이 곤란하다. 따라서 어떤 고도에서의 풍속 추정은 가용한 자료 환경에 따라, 관측 고도에 따라 최적 방법의 선택이 불가피하다.

이에 본 연구에서는 한국전력공사에서 국내 서남해안 2.5 GW 풍력발전 사업을 수행하기 위하여 설치한 HeMOSU-1 바람 관측 자료를 이용하여 Power 함수 지수의 변동 양상 분석과 고도에 따른 풍속 추정 오차 분석을 수행하였다. 대수함수 형태의 풍속 추정형태는 이론적으로 제시되고 있는 함수이지만, 풍속에 따라 풍속 추정 함수에 포함된 매개변수가 달라지고, 중립 조건(neutral condition)에서의 사용으로 제한되기 때문에 현실적으로 사용에 큰 제약이 따른다. 다양한 기상 조건을 포함하는 함수를 사용하는 경우에는 Obukhov 길이를 추정하여 매개변수를 추정하여야 하기 때문에 이론적인 지원이 확실하지만, 실질적인 사용에는 한계가 따른다. 또한 복잡한 함수 또는 방법인 경우, 그 방법에서 필요로 하는 고도화된 입력 자료의 관측이 요구되기 때문에 실질적으로는 목표 정도에 따른 최적 관측의 설계가 중요한 요소가 된다.

2. 재료 및 방법

2.1 HeMOSU-1 바람 관측 자료

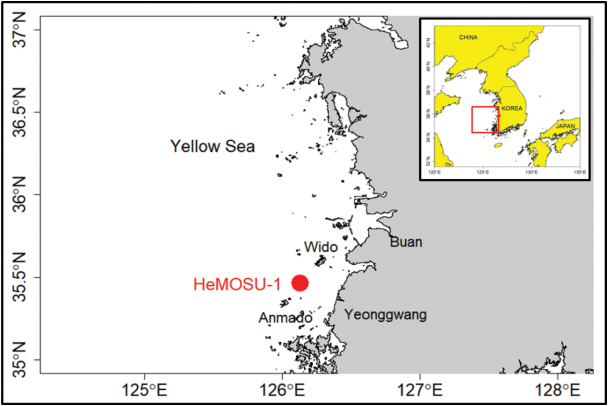
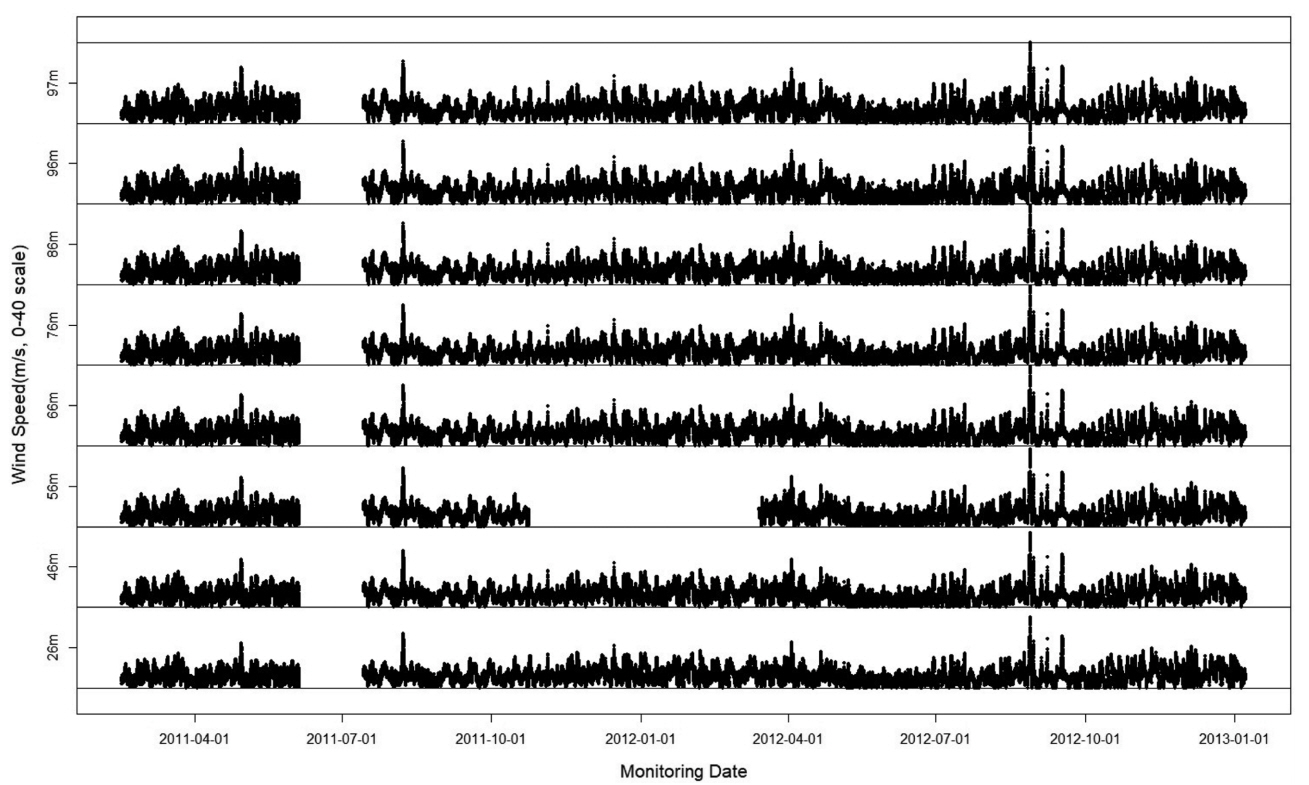
본 연구에서 사용한 바람 자료는 2011년 2월 15일 14:20부터 2013년 1월 8일 7:10까지 HeMOSU-1 관측타워의 MSL (+) 26 m, 46 m, 56 m, 66 m, 76 m, 86 m, 96 m, 97 m(총 8개 지점) 높이에서 관측한 10분 평균 바람 자료이다. HeMOSU-1 관측타워는 한국전력공사에서 해상풍력사업의 추진을 위하여 2010년 설치한 국내 최초의 해상 기상타워로서 최고 높이 100 m(수심 DL 기준 13.5 m), Jacket 형식으로 우리나라 서남해역 안마도와 위도 사이 해역(Fig. 1 참조)에 위치하고 있으며, 이 관측 타워에 대한 정보와 자료 분석 결과는 연구 논문을 통해 발표된 바 있다(Kim and Kim, 2017; Ko et al., 2012; Kim et al., 2013; Lee et al., 2014).

Fig. 1.

Location map of the HeMOSU-1 platform.

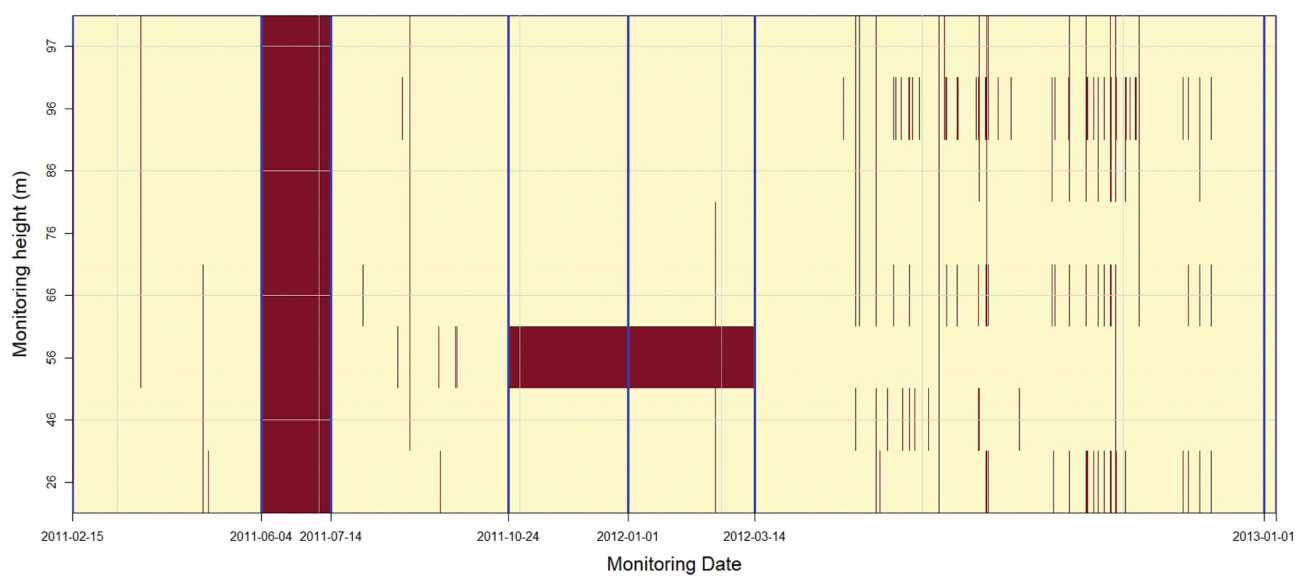
한편 관측 자료의 결측 양상은 관측 기간 시점과 종점을 기준으로 모든 시간을 관측 간격(10분)으로 포함하는 경우를 완전한(complete) 자료로, 그 외는 결측 자료로 판단할 수 있다. 본 연구에서는 실질적으로 무풍 조건에 해당하는 자료 또는 zero 자료(frozen data) 등도 결측 자료로 간주하였다. 또한 각 고도에서의 결측 상황은 관측시간에 따른 자료의 유무를 판단하는 결측 인자 이진 행렬(0 = missing, 1 = non-missing, missing indicator binary matrix)의 이미지 도시(image plot)로 간단하게 파악할 수 있다(Fig. 2 참조).

Fig. 2.

Missing indicator map of the vertical wind-profile data (Brown line cell = missing).

Fig. 3에서 보는 바와 같이 모든 고도에서 결측이 발생한 시기는 2011년 6월 4일 23:50~2011년 7월 14일 10:00(총 42일)이고, 고도 57.65 m 관측 지점에서 발생한 결측은 2011년 10월 24일 15:40~2012년 3월 14일 12:40(총 143일)로 평균적으로 풍속이 강한 시기에 해당하는 자료가 결측되어 편향(bias)이 우려되는 자료이다. 또한 월별 풍속 변화 양상 분석을 수행하는 경우, 월별 자료가 편중된 경우에도 편향이 우려된다. 본 연구에서는 ‘list-wise deletion’ 원칙으로 관측 고도에서 하나 이상의 결측이 발생하는 경우, 관측 시점의 모든 고도 자료를 분석 대상에서 제외하였다. 또한 무풍(calm) 조건에 해당하는 풍속 자료도 분석에서 제외하였다. 모든 관측 기간에 대하여 결측이 없는 경우, 완전한 자료의 개수는 99,750개이지만, ‘list-wise deletion’ 조건과 무풍 조건(풍속 < 0.5 m/s)에 해당하는 자료를 제외하면, 제외되는 자료의 개수는 각각 7,390개(26 m), 6,705개(46 m), 26,814개(56 m), 7,339개(66 m), 6,278개(76 m), 6,824개(86 m), 9,450개(96 m), 6,358개(97 m)이다. 결측 시점의 중복을 고려하면, 제거되는 자료의 개수는 30,734개로 전체 자료의 30.8%, 장기 결측이 존재하는 57.65 m 관측 자료를 제외하는 경우 제거되는 자료의 개수는 10,297개로 전체 자료의 10.3% 정도를 차지하고 있다.

Fig. 3.

Time-series plot of the vertical wind speed profile (Wind-speed range: 0~40 (m/s) in each cell. The cell-center located characters are the monitoring elevation).

2.2 기본적인 통계 정보

관측 자료의 기본적인 통계 측정 파악을 위하여 각각의 고도에서의 풍속 평균과 표준편차, 그리고 95% 신뢰구간을 추정하여 Table 1에 제시하였다. 여기서, 각각의 고도에 대한 평균 풍속의 하한-상한 구간의 중복 여부로부터 판단하면, 고도 66 m~76 m, 86 m~96 m 구간은 유의미한 평균 차이를 보이고 있지 않은 것으로 판단되며, 96 m~97 m 고도는 1m 정도의 작은 고도 차이에도 불구하고 유의미한 차이를 보이고 있음을 알 수 있다. 반면 다른 고도의 평균은 유의미한 차이를 보이고 있음을 알 수 있다. 표준편차는 66 m~76 m, 96 m~97 m 구간에서 유의미한 차이를 보이고 있지 않는 것으로 파악되었다. 이러한 차이는 관측타워와 풍속 측정 기기 설치 지점의 상대적인 영향으로 판단된다.

Table 1.

Basic statistical information of the wind speed data at the different elevations (n = 69,016, 10-minute interval data; SD = the standard deviation, L, and U = the lower and upper limits of the measures, respectively)

2.3 연직분포 함수의 매개변수 추정 방법

Power 함수와 대수함수 모두 선형 변환 자료를 이용하여 매개변수를 추정할 수 있다(Hsu et al., 1994). 추정오차로 간주되는 잔차는 변환 자료를 다시 변환하여 평균 절대편차를 기준으로 분석하였다. 평균 절대편차(mean absolute deviation)는 자료와 단위가 동일하기 때문에 오차의 정도 파악에 유리한 절대오차 측도이다.

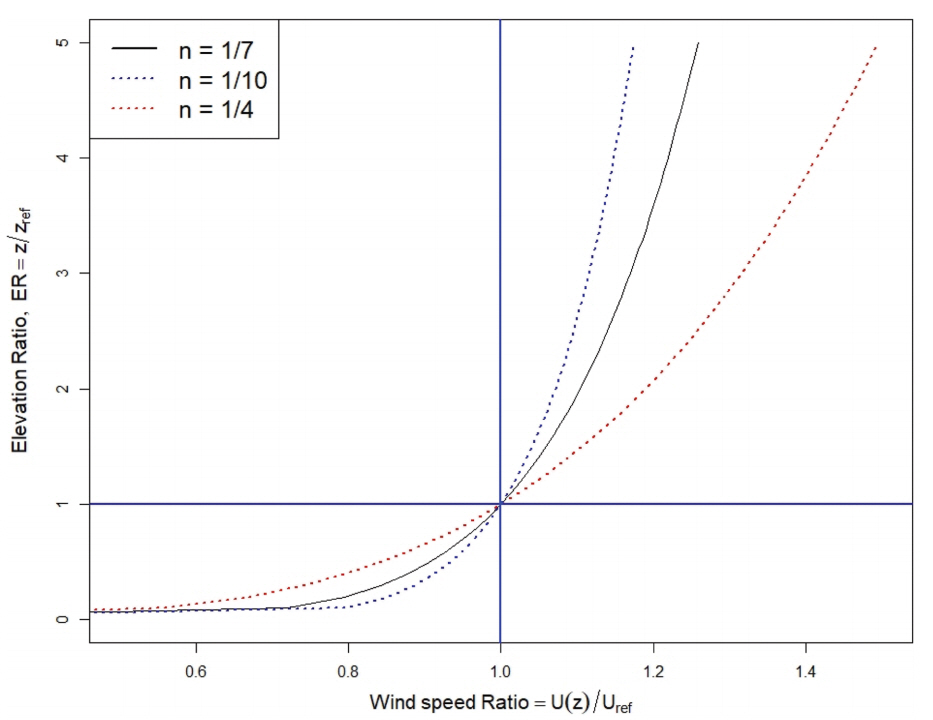
한편 식(1)과 같은 Power 함수의 경우, y = ax의 형태로 선형 변환 할 수 있고, 일반적으로 사용되는 지수(n = 1/7 = 0.14) 조건을 기준으로 하는 경우, 지수가 0.1보다 작은 경우에는 고도 함수의 경사가 급격하게 증가하기 때문에 고도와 무관하게 비교적 일정한 풍속 분포가 형성된다. 지수함수는 기본적으로 단조증가(monotonic increasing) 함수이기 때문에 풍속크기분포가 고도에 따라 역전되는 경우 또는 거의 일정한 경우는 본 분석에서 제외하였다. 한편 지수 매개변수가 0.14 조건보다 큰 경우에는 고도에 따른 풍속 차이가 크게 차이나기 때문에 0.14 조건을 일률적으로 사용하는 경우, 풍속의 과소 추정이 발생할 수 있다. 반면 이 함수는 기준 고도를 기준으로 그 고도보다 작은 경우에는 이러한 변화와 상반되는 양상을 보이기 때문에 기준 고도를 기준으로 관심 고도가 기준 고도보다 큰 경우와 작은 경우에 대하여 지수함수 매개변수 영향이 다르게 나타난다(Fig. 4 참조).

Fig. 4.

Range effects of the Power function exponent parameter.

또 하나의 대표적인 연직 분포함수는 식(8)과 같은 형태의 대수(logarithmic) 함수이다. 이 함수도 단조증가 함수이기 때문에 풍속이 고도에 따라 감소하거나 일정한 양상을 보이는 조건에서는 적용이 불가하다. 수학적으로 매개변수는 추정되더라도, 물리적인 의미를 가지는 매개변수가 의미의 범위를 벗어나는 ‘음수’ 추정이 발생할 수 있다.

Hsu(1988)는 대수함수 법칙에 대하여 y = ax + b 형태의 풍속을 독립변수로 가진 선형 변환 공식을 제안하였다. 그러나 독립변수는 풍속 함수의 형태, u(z)로서 고도를 독립변수로 하는 것이 적절하며 다음 식(8)과 같이 나타낼 수 있다.

(8) u(z)=u*κlnzz0=u*κlnz-u*κlnz0

또한 식(8)은 다시 y = ax + b의 형태에 따라 y = u(z), x = ln(z), a = u_*/κ, b = - (u_*/κ)·ln(z₀), κ = 0.4로 나타낼 수 있으며, 최종적으로, u_* = κa, z₀ = exp[-(b/a)] 식을 이용해 간단하게 매개변수를 추정할 수 있다.

3. 풍속자료의 고도에 따른 상관분석

모든 고도 자료에 대하여 상관분석을 실시한 결과, Pearson 상관계수 최소는 0.948 이상으로 높은 상관관계를 보였다(Fig. 5 참조). 상관계수 추정 결과는 모든 고도 구간에서 유의미한 높은 상관관계를 보이는 것으로 파악되었으며, 이러한 높은 상관계수는 인접한 고도에서의 결측 자료 추정에도 높은 신뢰수준을 보일 수 있다. 더불어 특정 고도에서의 결측 자료 추정에 다양한 고도의 모든 가용 자료를 이용한 추정도 가능하며, 보다 안정적인 추정이 가능할 것으로 판단된다.

Fig. 5.

Correlation plot of the wind-speed data-set at the different elevations.

또한 고도 차이에 따른 상관계수는 예상되는 바와 같이 고도 차이가 적을수록, 즉 인접한 고도에서의 자료일수록 상관계수가 크게 나타나고 있음을 알 수 있다. 전반적으로 고도 차이에 따른 상관계수는 매우 크게 나타나지만, 가장 작은 0.948, 0.958 조건은 고도 차이가 가장 크게 나타나는 26 m~96 m, 97 m 구간에서 발생하고 있으며, 이는 일반적인 경향과 일치하는 것으로 판단할 수 있다.

4. 연직 분포 함수 매개변수 추정 및 오차분석

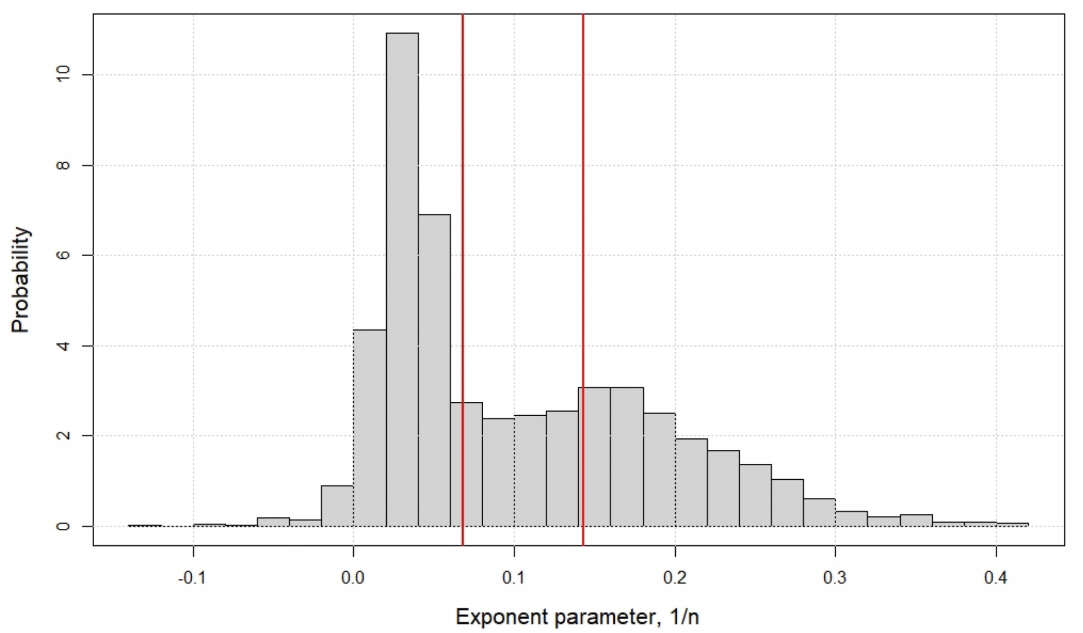
Calm 조건(풍속 < 0.5 m/s) 자료를 제외한 모든 풍속 자료의 시간 평균 자료를 이용하여 연직 분포 매개변수를 추정한 결과, Power 함수의 지수는 1/10 = 0.1 정도로 일반적으로 제안되는 1/7 = 0.14 보다 작은 수준으로 추정되었다. 한편 대수함수의 매개변수인 마찰속도(u_*, friction velocity)와 조도 길이(z₀, roughness length, roughness height)는 각각 0.25 (m/s), 1.6·10^-3 (m) 정도로 추정되었다. 그러나 추정 매개변수는 풍속에 따라 차이를 보이고 있으며, 풍속의 시간적인 변동 정도를 완화하기 위하여 대략 3시간 간격으로 평균한 풍속 자료에서 고도에 따른 변화가 뚜렷할 것으로 판단되는 5.0 m/s 이상 조건을 만족하는 풍속 자료를 추출하여 Power 함수조건과 대수함수 조건에 대하여 각각의 매개변수를 최적 추정하였고 그 결과를 나타내었다. Fig. 6에서 보는 바와 같이 일반적으로 사용되는 0.14(= 1/7) 수치는 전체 분포에서 두 번째 첨두를 차지하고 있지만, 본 연구에서 사용한 자료의 경우에는 고도에 따른 풍속 변화가 상대적으로 미미한 조건에 해당하는 구간(0.0~0.1)에서 다수의 빈도를 차지하는 것으로 나타났다. 이러한 영향은 관측 고도가 풍속이 급변하는 표면 경계 저층(surface boundary sub-layer) 범위를 벗어나는 비교적 높은 고도에서 측정한 자료를 사용한 영향으로 판단된다. 관측 고도 10 m 이내의 고도에서의 해상 풍속 관측 자료가 미흡하기 때문에 자료에 근거한 입증에는 한계가 있으나, 육상에서의 고정 조도(roughness) 조건에서의 변화양상을 감안하면 적절한 추론으로 판단된다. 또한 HeMOSU-1 기상타 워에서 동시에 관측한 13 m, 94 m 높이의 기온 자료를 이용하여 계산되는, 대기의 조건을 판단하는 지표로 사용되는 Lapse 비율(lapse rate, γ, Eqs. (4)~(6) 참조)로 추정한 결과, 불안정 대기조건은 68%, 안정 대기조건 비율은 32% 정도를 차지하고 있다. 이론적으로 정확하게 중립을 차지하는 자료는 존재할 수 없으며, 건조공기, 습윤공기 조건의 Lapse 비율 범위를 거의 중립(near neutral) 대기조건으로 가정하는 경우, 그 비율은 약 7% 정도이다. 따라서 일반적으로 중립 대기조건은 이론적인 기준으로 사용할 수는 있지만, 전체 대기조건을 대표하기에는 무리가 있는 가정 조건으로 판단된다.

Fig. 6.

Histogram of the power function exponent parameter, 1/n.

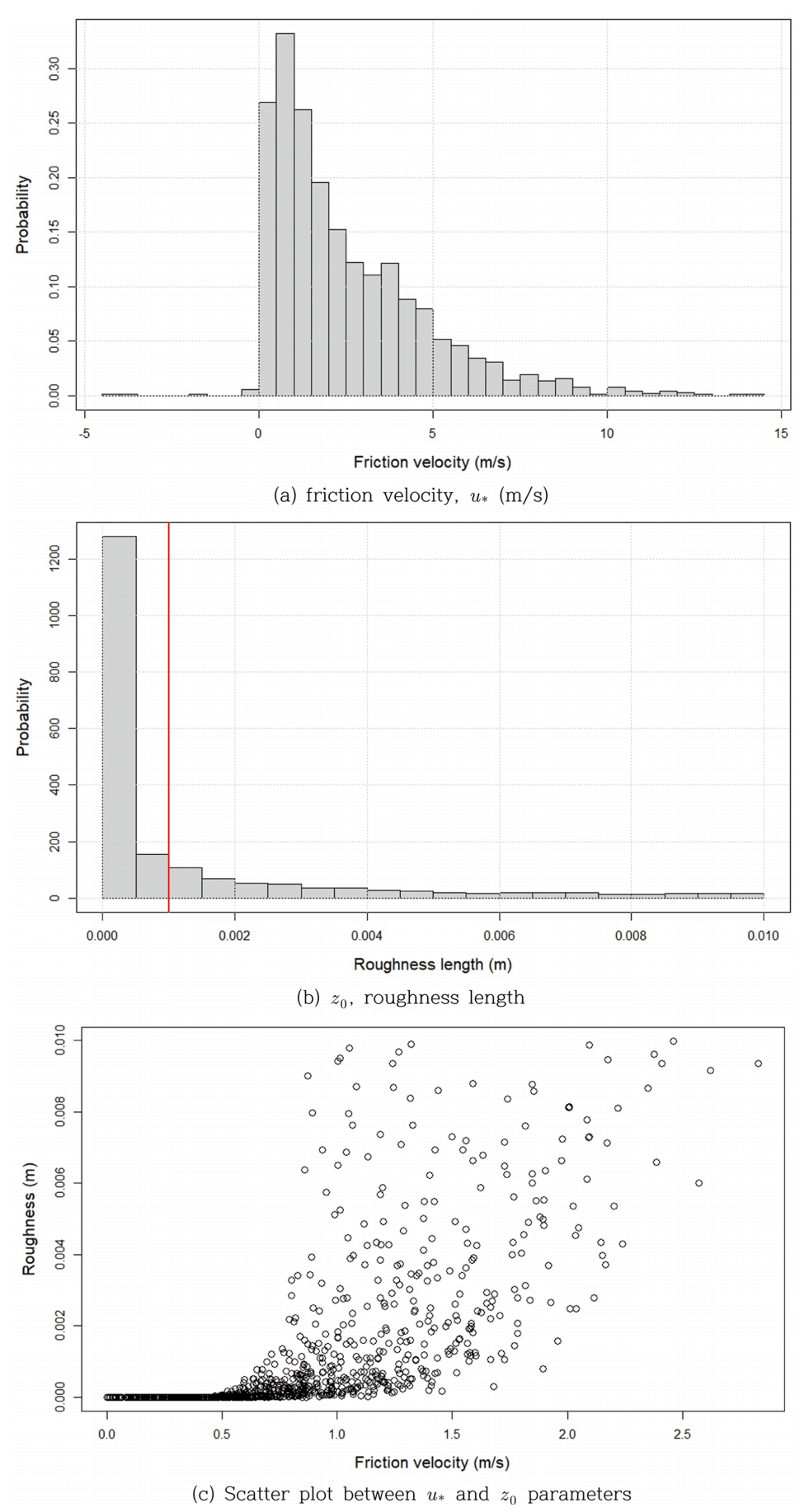
대수 분포 함수를 사용하는 조건에서의 매개변수 추정 결과는 매우 비현실적인 추정 결과를 보이는 자료를 제외하고 분석하였다. 그림에서 볼 수 있는 바와 같이, 마찰속도는 적절한 분포양상과 변화 범위를 보이고 있음을 알 수 있다(Fig. 7. (a) 참조). 반면, 조도 길이는 그 물리적인 범위의 정도가 cm 수준이기 때문에, 1.0 cm(0.01 m) 이하 범위의 자료만을 도시하였다. 전체적인 범위는 비현실적인 결과를 보이고 있으나, 대부분의 자료는 적절한 범위에 집중되는 경향을 보이고 있음을 알 수 있다(Fig. 7. (b)). 또한 마찰 풍속 증가에 따른 조도 길이 증가 양상도 그 변화 범위가 매우 크지만 예상되는 경향을 보이고 있다(Fig. 7. (c)).

Fig. 7.

Histogram of the log-profile function parameters.

한편, 기상관측타워가 위치하고 있는 해역은 조차가 약 6m 정도 발생하는 한반도 서남해역에 위치하고 있기 때문에 규칙적인 조위변동으로 고정된 관측고도가 상대적으로 변화하는 양상을 보이게 된다. 또한 입력 고도 자료도 시간에 따라 달라지기 때문에 조위영향을 고려하여 보정된 고도 자료를 입력하여, 매개변수 추정에 미치는 영향을 분석하였다. 조위 영향을 포함한 결과, 그 차이는 최저 고도 26 m 기준으로 최대 범위 23~29 m 정도로 무시할만한 정도는 아니지만 규칙적인 변동과 상쇄효과의 영향으로 매개변수 추정 결과에 미치는 영향은 미미한 수준으로 파악되었다.

5. 결론 및 제언

HeMOSU-1 풍속 자료를 이용하여 다양한 고도에서의 풍속 추정을 수행하는 함수의 매개변수를 추정하고 그 변동 범위를 분석과 결과 다음과 같은 결론을 도출하였다.

(1) 기존의 Power 함수, 대수함수를 이용한 풍속 추정은 대기의 중립 조건을 가정하기 때문에 다양한 대기조건에서의 풍속 추정에는 한계가 있다.

(2) 대기의 중립 조건 가정에서 사용되는 함수의 매개변수도 관측 자료에 따라 큰 변동 범위를 가지고 있다. Power 함수의 지수(exponent) 매개변수의 경우, 일반적으로 0.14(= 1/7) 조건을 제안하고 있으나, 본 연구에서는 평균 0.1 조건에 가장 적합한 수치로 파악되었다. 또한 지수 매개변수의 범위도 특정 수치에 집중되는 양상을 보이지 않고 0.0~0.3 정도의 범위로 분포하고 있다. 대수 분포함수의 경우, 조도 매개변수는 그 물리적인 의미에 근거하면 cm 정도가 적절한 수치이지만, 최적 추정한 조도 매개변수의 범위는 그 발생 빈도가 상대적으로 작으며, 0.1 cm~1.0 cm 범위에 골고루 분포하고 있는 것으로 파악되었다. 또한, 마찰속도 매개변수도 풍속 5.0 m/s 이상의 조건과 비교하는 경우, 그 범위는 0~5 m/s 범위로 제한되고 있음을 알 수 있었다.

(3) 따라서, 어떤 측정 함수를 이용한 목표 고도에서의 풍속 추정은 고정된 매개변수를 사용하는 경우, 추정오차가 상당한 수준으로 발생할 수 있으며, 그 원인은 대기조건을 중립 조건으로 가정한 영향이 가장 대표적인 원인인 것으로 판단되었다.

다양한 고도에서의 풍속 측정 자료는 풍속의 연직 분포 함수 및 매개변수 추정에 직접적인으로 활용이 가능하다. 그러나 이러한 자료는 제한되어 있으며, 관측 고도와 관측 환경도 자료에 따라 범위가 다르기 때문에 기존의 고정된 함수를 이용한 방법을 개선하는 연구가 필요하다. 또한 대기조건은 다양한 인자로 구분되고, 계절의 영향에 따라 다양한 특성을 보일 수 있기 때문에 계절, 대기 구조 등 다양한 조건을 고려하여 분석하는 연구도 필요할 것으로 판단된다.

한편 고도에 따른 풍속 추정 오차의 유의미한(significant) 상당한 절감을 위해서는 보다 고도화된 난류 규모의 정밀 관측도 요구된다. 더불어 대기와 해양 경계에서의 flux 측정과 같은 관측도 중요하지만, 가용한 모든 조각 자료 등을 수집하고 분석하여 대기 상태를 간단하게 판단하는 지표, 공식 등의 개발도 필요할 것으로 사료된다.

Article information Continued