2.1 관측자료

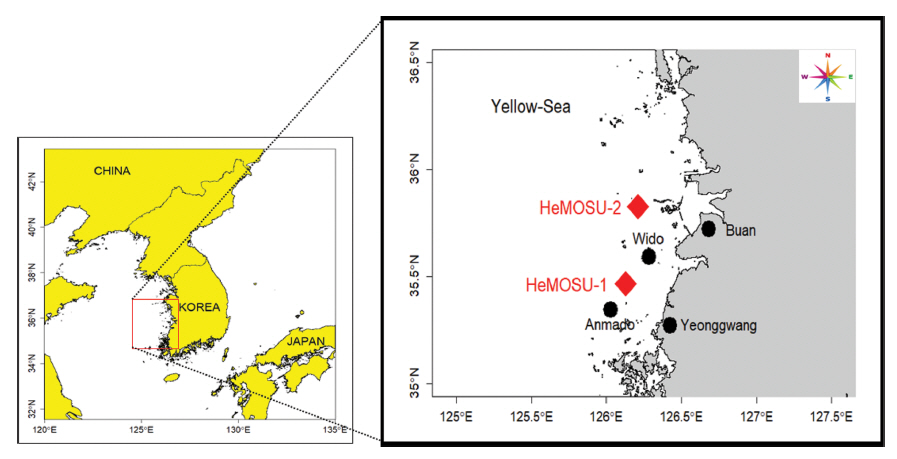
한국전력공사에서는 해상풍력 단지 구축을 위해 서해안에 해상기상관측타워 2기(Oceanographic and Meteorological Observation Tower)를 설치하고 풍황 및 해황을 조사하고 있다. 해양기상학적 연구 구조물의 시초라는 의미의 HeMOSU (Herald of Meteorological and Oceanographic Special research Unit)는 부안 위도면 인근 해역과 군산 옥도면 해역에 2010년과 2013년에 각각 설치되어 풍황 자료(풍속, 풍향, 3차원 풍속, 온습도, 대기압, 강우)와 해황 자료(파랑, 유속, 조위)를 실시간으로 취득․분석하여 운영 중에 있다(Kim and Kim, 2017). 운영방식은 CDMA 통신 및 위성채널을 상호보완 운영하고 있으며, 이러한 자료를 바탕으로 대상 부지의 설계, 유지관리, 환경영향평가 등에 활용하고자 지속적으로 데이터를 축적하고 있다. Table 1은 기상관측 타워에 대한 설명을 정리한 표이다.

Table 1.

Introduction to HeMOSU-1 & 2

Fig. 1은 국내 서해안에 설치되어 있는 해양기상관측탑(offshore meteorological tower)인 HeMOSU-1호와 2호의 위치를 도시한 것이다.

Figure 1.

Location map of HeMOSU-1 & 2 in the west sea of Korea.

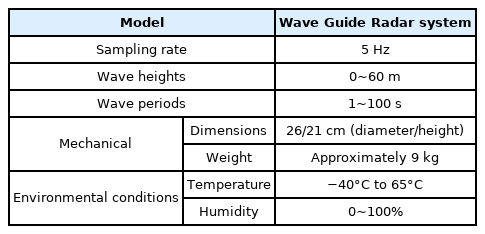
HeMOSU-1은 4개의 강관으로 이루어진 자켓식 기초로 설치 되어있으며, 적용 수심은 기본 수준면(D.L.) 기준 13.5 m이다. HeMOSU-2는 석션 트라이포드 형태의 기초를 적용하여 설치되었으며, 적용 수심은 HeMOSU-1에 비해 약 2배 이상 깊은 30 m이다. 파랑 관측장비로는 1996년 Delft사의 WaveGuide 장비가 사용되었으며(Choi et al., 2017), 해당 장비는 3개의 초음파 센서를 이용하여 수면 변위를 동시에 측정하고 있다. 이 장비는 관측된 수면 변위 자료에서 북/남 및 동/서 방향의 경사가 계산되며, 경사와 세 개의 수면 변위 사이의 위상 관계를 사용하여 파랑의 방향 정보까지 계산이 가능하다. Table 2와 같이 WaveGuide는 직경 26 cm, 높이 21cm이며, 관측 해역의 온도가 -40~60°C 사이에 사용이 가능하고 수면 변위의 관측 간격은 5 Hz(0.2 s) 간격으로 관측하는 고해상도 장비이다(RADAC, 2012).

Table 2.

Specifications of the Wave Guide Radar system

본 연구의 분석에서 사용한 관측 자료 기간은 HeMOSU-1의 경우 2013.07.28.~2014.07.06.(169일)이며, HeMOSU-2의 경우 2013.11.26.~2014.04.23.(131일)이다. 이 기간 중 HeMOSU-1&2의 결측율은 각각 28.5%와 12.1%이며, 이는 WaveGuide 장비 이상으로 인해 관측이 중단 된 것으로 나타났다.

2.2 분석 방법

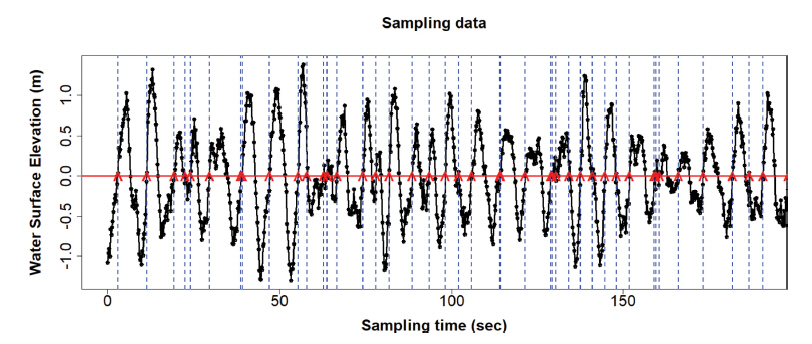
본 연구에서 사용한 파고와 주기는 파열분석법과 스펙트럼 분석법을 사용하여 계산하였다(Dean and Dalrymple, 1991). 두 방법 모두 분석을 수행하기 전 기본적인 관측 자료 보정이 필요하며, 관측 데이터 내 조석과 같은 외부 영향으로 인한 자료의 추세로 인해 데이터의 등질성이 허물어지기 때문에 추세를 반드시 제거해야 한다(Goda, 2010; Molenat et al., 1999; Hanson et al., 2004). 파열 분석법은 보정된 데이터를 통해 Fig. 2와 같이 영점 상향 교차(Zero-up-Crossing)방법으로 개별파를 결정하게 되는데, 매우 작은 주기들이 발생하는 현상에 대한 문제를 해결하기 위해 반파 처리기법을 도입하여 주요 파랑 변수를 산정하였다(Choi et al., 2017).

Figure 2.

Principle of wave-train analysis method.

한편, 파랑 스펙트럼 분석법은 시간영역에서 주파수 간격(△f)의 정수배(n△f)가 아닌 영역에서 발생하는 에너지 손실(leakage)을 최소화하기 위해 식(1), (2)와 같이 ‘10% Cosine Window’ 과정을 통해 추가로 관측 자료를 보정한다.

여기서, η^(t*)는 Data Window의 결과, W(t_*)는 Data Window 값, η(t_*)는 보정된 평균 수위 값, N은 자료의 개수, l은 데이터의 처음과 끝의 10%(0.1*N) 범위를 나타낸다. 관측 자료에 대하여 시간 영역에서의 보정을 충분히 수행한 후, FFT(Fast Fourier Transform) 기법을 통해 주파수 영역으로 변환하여 해석을 수행하게 되며, 스펙트럼의 면적(m₀)을 산정하여 이를 통해 유의파고(H_s)를 계산한다. 이때, 첨두 주파수(f_p)의 역수를 취함으로서 첨두주기(T_p)를 산정하게 된다(Goda, 2010).

전술한 과정을 통해 산정된 주요 파랑 변수에 대하여 상관성 분석을 수행하였으며, 분석 방법은 식(3)과 같이 통상적으로 사용되는 Pearson의 상관계수 공식을 사용하였다(Pearson, 1895).

여기서 x, y는 서로 독립인 변수이며, N은 자료의 전체 길이, x¯, y¯는 각 변수의 평균값을 의미한다.

이에 본 연구에서는 파랑 변수간 상관성 분석을 통하여 상관계수를 산정하였으며, 기존에 제안된 선형 상관관계식과의 비교를 수행하였다. 또한, 대상 해역의 유의파고(H_1/3)와 유의파 주기(T_1/3)의 분포 특성을 파악하고, 비선형 회귀분석을 통하여 두 변수 사이의 관계식을 도출하였다.

3.1 대표 파고간 상관관계 분석

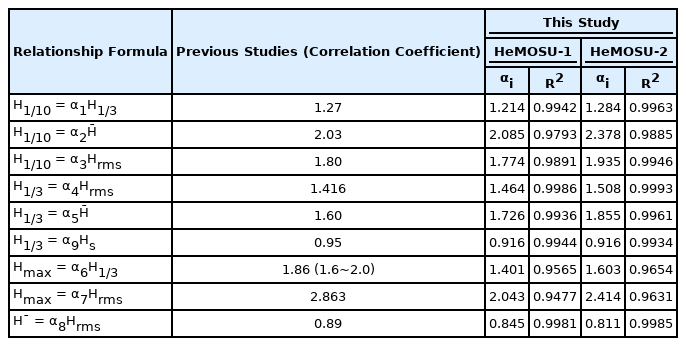
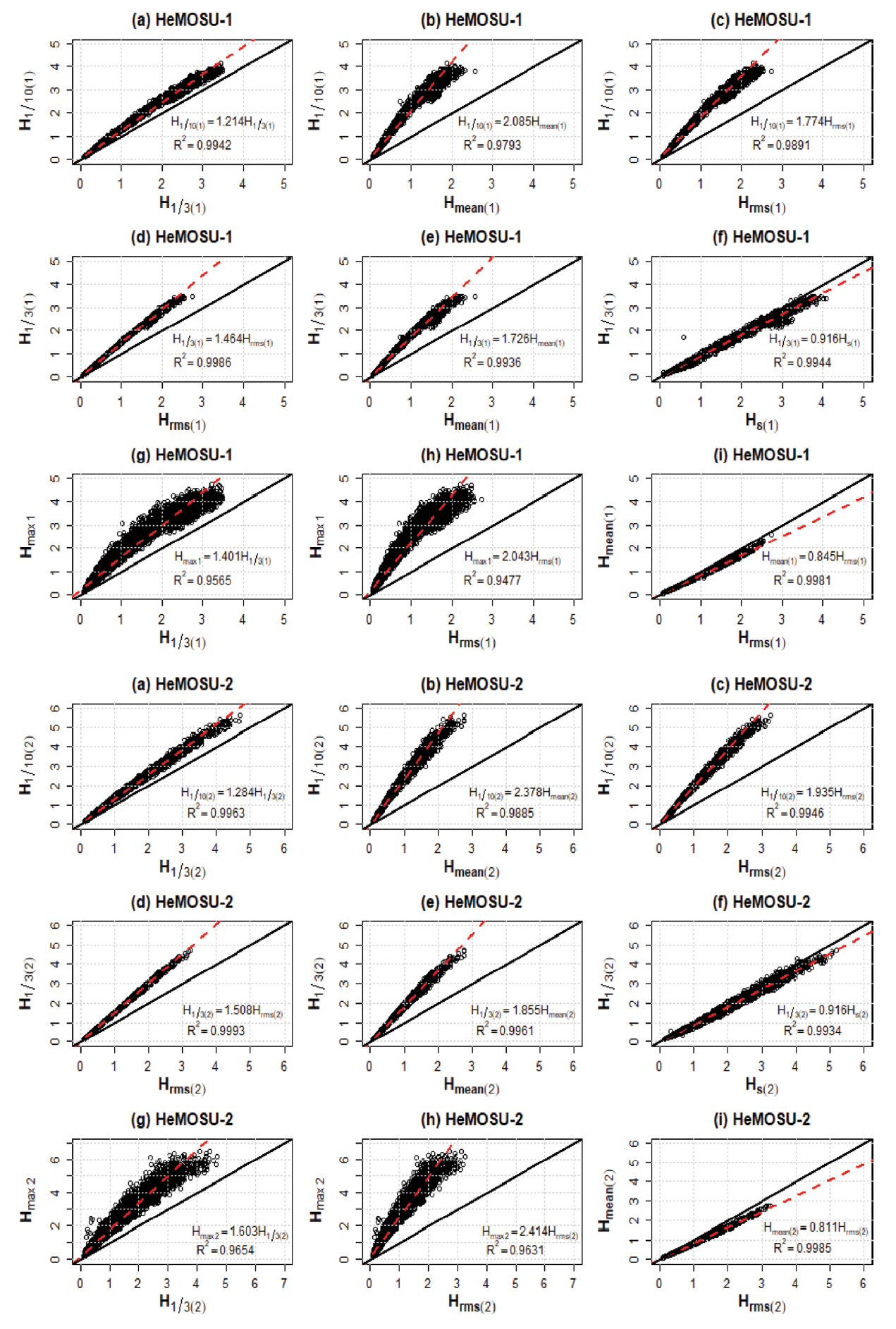
대표 파고 사이의 상관관계식은 상관 분석을 통해 산출 할 수 있으며, 결정 계수를 사용하여 추정 된 선형 모델의 우수성을 판단할 수 있다(Ang and Tang, 2007). 다음 Table 3과 Fig. 3에는 대표파고 간 상관 분석을 통해 산출한 상관 계수와 결정 계수를 제시하였다. 분석 대상 지점의 상관 분석 결과, 대부분의 파고 간 상관 계수는 기존에 제안된 상관 계수와의 오차율이 0.1% 미만으로 산정됨으로서 Goda(2010), Rattanapitikon and Shibayama(2007)에 의해 제안된 상관 계수와 큰 차이를 보이고 있지 않았으며, 결정계수 또한 매우 높은 수준으로 나타났다. H_max와 비교를 하는 경우에는 최대 약 29% 차이가 나타났는데, 이는 분석 대상 지점의 수심이 각각 13.5 m와 30 m 수준으로 심해영역에 포함되지 않기 때문에 최대파고의 쇄파로 인한 영향으로 사료되며, Jeong et al.(2019)의 연구 결과에서도 H_max의 관계가 기존에 제안된 상관 계수보다 과소 추정되는 결과를 확인할 수 있다.

Table 3.

Correlation coefficient between representative wave heights

Figure 3.

Relationships between the representative wave heights observed in HeMOSU-1&2.

한편, Fig. 3에는 상관관계 분석 결과를 제시하였는데, 스펙트럼법에 의해 산정되는 유의파고(H_s)는 파열분석법에 의해 산정되는 유의파고(H_1/3) 보다 약 1.05배 크게 나타나는 것을 확인할 수 있으며(Goda, 2010), 대부분의 대표 파고 간 상관관계가 선형관계를 이루고 있지만 Fig. 3의 (g), (h)와 같이 파고가 어느 정도 커짐에 따라 선형 관계를 추정함에 있어 한계를 보이고 있었다.

3.2 대표 주기간 상관관계 분석

Goda(2010)는 T_1/3, T_1/10, T_max, T¯, T_p 사이의 관계식을 제안한 바 있으며, 본 연구에서 파열분석법 및 스펙트럼 분석법을 통해 산정 된 HeMOSU-1과 HeMOSU-2의 주기를 이용하여 관계식을 산정하였다(Table 4, Fig. 4 참조).

Table 4.

Correlation coefficient between representative wave periods

Figure 4.

Relationships between representative wave periods observed in HeMOSU-1 & 2

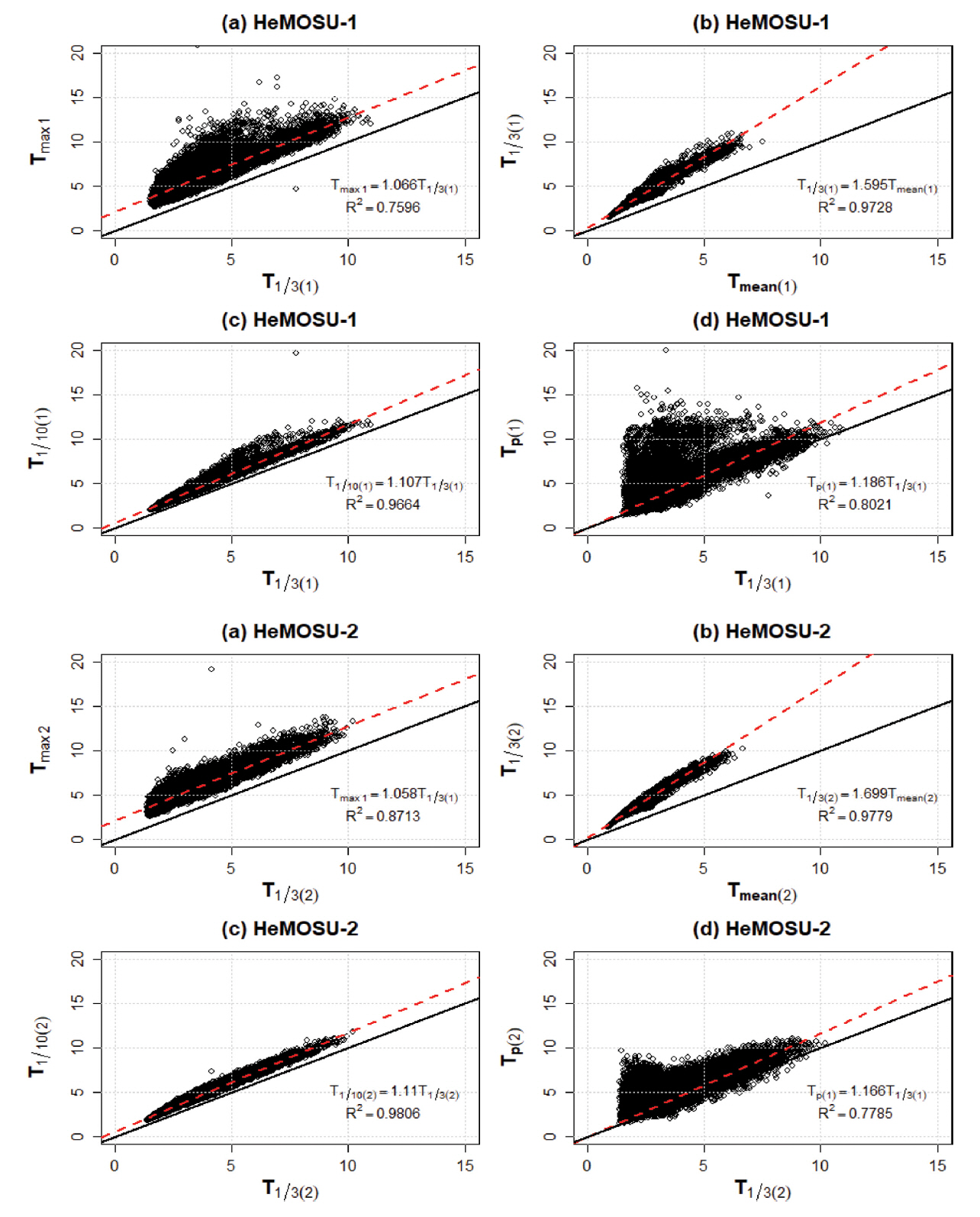
대표 주기 사이의 상관 관계 분석 결과, 대부분의 상관 계수는 기존에 제안된 상관 계수와 매우 유사한 수치를 보이고 있었다(Table 4 참조). 유의파 주기(T_1/3)와 평균파 주기(T¯)사이에는 기존에 제안된 상관 계수의 상한값인 1.4에 비해 약 12%, 17%의 차이를 보이고 있었으며, HeMOSU-1&2에서 평균파 주기가 커짐에 따라 비선형 관계를 가지는 것으로 확인된다(Fig. 4의 (b) 참조). 또한, 최대파 주기(T_max)와 유의파주기(T_1/3)의 상관 분포에서 상관계수는 기존에 제안된 상관계수의 평균값과 유사하지만, 최대파 주기의 분산이 매우 크게 나타나고 있으며, 이러한 현상으로 평균파 주기의 비해 유의파 주기가 크게 발현하는 것으로 사료된다(Fig. 4의 (a) 참조).

한편, 유의파 주기(T_1/3)와 첨두주기(T_p)의 경우 기존에 제안된 상관 계수와 유사하게 나타났지만, Fig. 5에서 보는 바와 같이 첨두 주기가 유의파 주기보다 매우 큰 분포를 보이는 경향도 나타났다. 이는 스펙트럼 분석법을 통해 첨두 주기를 산정하는 경우 주로 단봉형태의 스펙트럼 분포가 대다수 이지만, 스펙트럼 밀도가 작게 추정되는 구간에서 풍파의 성장이 충분하지 않아 첨두 주파수(f_p)가 2개 이상 출현하는 현상이 발생하는 문제 때문인 것으로 사료된다(Soares, 1984; Jeong et al., 2019). 그러나 그 비율이 HeMOSU-1&2에서 각각 전체 자료의 2.5%, 1.3%로 매우 적고 대부분의 유의파 주기(T_1/3)와 첨두주기(T_p)는 5초 이하에서 분포함을 확인할 수 있다.

Figure 5.

Distribution of peak wave periods (Tp) and significant wave periods (T_1/3).

3.3 유의파고와 유의파 주기 분포

유의파고와 유의파 주기는 대상 해역의 파랑 특성을 파악하기 위한 매우 중요한 파랑 변수이며, 항만 및 해안 구조물 설계에 주로 사용된다. 이 파고와 주기는 파 추산 등에 입각하여 결정하더라도 양자는 파의 발달 및 감쇠 과정에 따라 특정 관계를 유지하고 있다. 이에 Goda(2003)는 바람에 의해 발달한 파에 대하여 Wilson의 파 추산식으로부터 T_1/3 ≈ 3.3(H_1/3)^0.63의 관계식을 제안하였으며, SPM(Shore Protection Manual, 1977)에서는 T_1/3 = 3.85(H_1/3)^0.5의 관계식을 제안하였다. 또한, Suh et al.(2008)의 연구 결과를 살펴보면, 서해안에 위치한 홍도에서 관측된 자료를 통해 유의파고 및 유의파 주기에 대한 관계식을 T_1/3 = 5.59(H_1/3)^0.20과 같이 제안하였다. 이에 본 연구에서는 국내 서해안의 유의파고 및 유의파 주기의 관계에 대하여 비선형 회귀분석을 통해 관계식을 산정하였으며, 앞서 소개한 3가지 식과 비교하였다.

그 결과, 유의파고가 작을수록 유의파 주기의 변동성이 증가하였다. HeMOSU-1의 경우(Fig, 6(a), (c) 참조) 파고가 1m 이하의 경우와 2 m~2.5 m 범위에서 이상 주기가 발현하였으며, 이는 너울 및 파의 중첩으로 발생하는 영향으로 사료된다.

Figure 6.

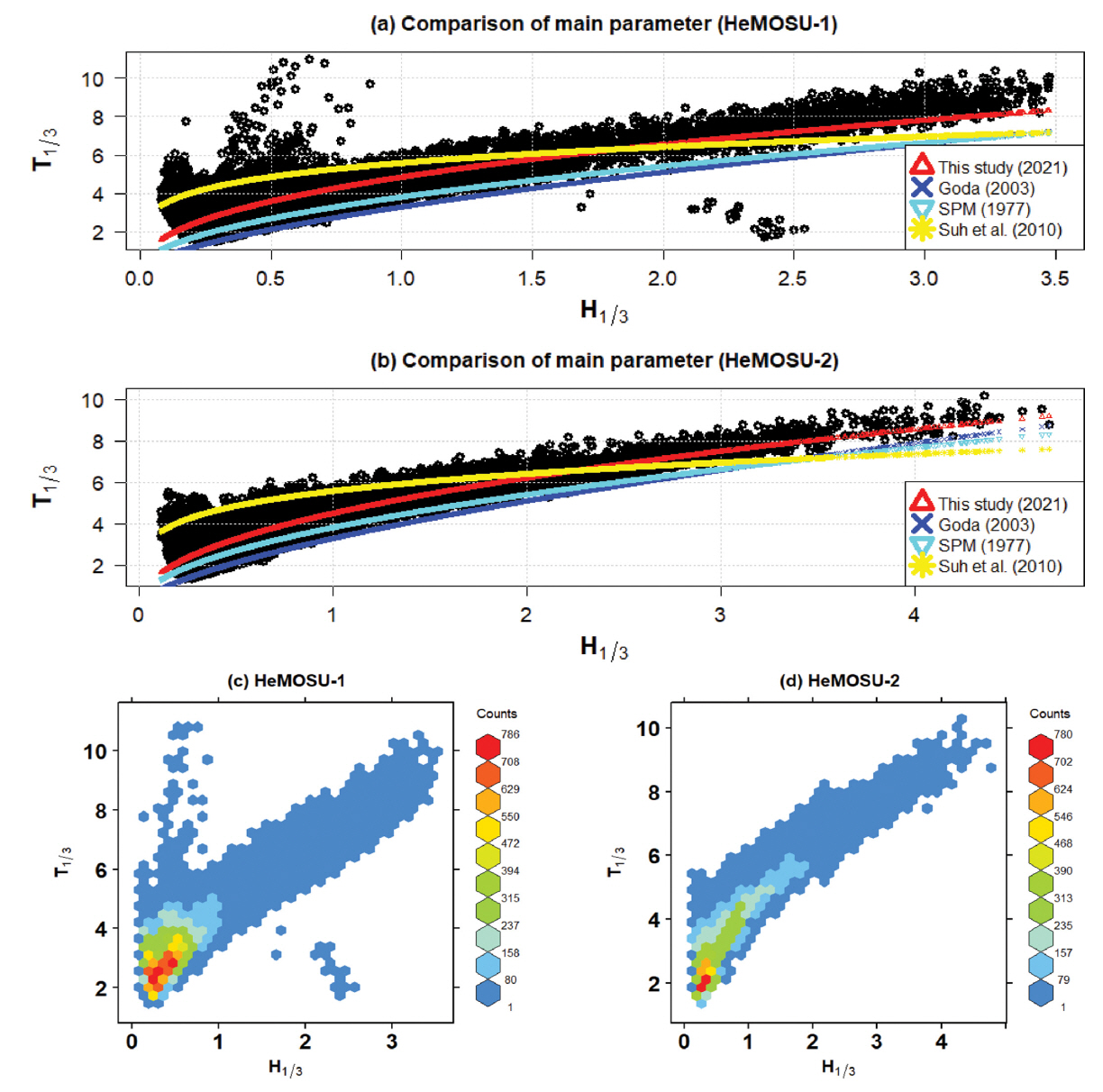
Scatter plot and non-linear regression between significant wave heights (H_1/3) and wave periods (T_1/3).

또한 서해안의 유의파고 분포는 약 1 m 이하에 주로 분포하였고, 유의파 주기의 경우 대부분 5초 이하에 머물고 있었다(Fig. 6(c), (d)). 또한, Goda(2003) 및 SPM(1977)의 관계식은 유의파고와 유의파 주기 분포의 하한선을 따라가는 경향을 보이고 있었고, Suh et al.(2008)에서 제안한 관계식은 파고가 낮은 경우 어느 정도의 경향성을 보이고 있었다(Fig. 6(a), (b)). 기본적으로 유의파고와 유의파 주기의 관계식은 멱함수 형태의 T_1/3 = α(H_1/3)^β로 이루어져 있으며, 본 연구에서 수행한 비선형 회귀분석을 통해 산정된 HeMOSU-1과 HeMOSU-2의 관계식은 다음 식(4), (5)와 같이 나타났다.

관계식에서 α 값은 기존에 제안된 Goda(2003)과 SPM(1977)에 적용된 수치보다 약 1.2~1.5배 크게 산정됐으며, β 값은 약 1.4~1.6배 낮게 산정되었는데, 이는 풍파가 우세한 경우의 파랑에 대하여 제시된 공식이기 때문이다. 한편, α, β 값은 Suh et al.(2008)의 관계식과도 약간의 차이가 발생하는데, 이는 대상 수심 및 쇄파 영향 등 관측 해역의 물리적 요인에 기인할 것으로 판단된다.