능동적 지진해일 생성을 고려한 지진해일 수치모형 개발
Development of a Numerical Model Considering Active Tsunami Generation
Article information
Abstract
단층파괴에 의한 해저지형변화는 공간적으로 시간차를 가진다. 특정 지점에서 파괴가 발생하면 이웃지점으로 단층파괴가 전파하면서 시간차에 따른 단층파괴가 발생하며, 단층파괴시 연직방향으로 상승하면서 지진해일을 야기한다. 해저 지형의 상승속도는 지진해일 초기파형에 영향을 주며 결과적으로 지진해일의 도달시간 및 크기에 영향을 준다. 본 연구에서는 단층파괴에 의한 해저 지형의 수평적 및 수직적 변화를 능동적 및 동적으로 고려하여 지진 해일의 생성 및 전파를 모의할 수 있는 수치모형을 개발하였다. 모델의 검증을 위하여 2011년 동일본대지진에 대해 적용하였으며 기존의 수동적 및 정적 모형에 비해 정확성이 개선되는 것을 확인하였다.
Trans Abstract
Seabed deformation due to the fault failure have both a spatial variation and temporal history. When the faulting process initiates at a certain point beneath seabed, the failure spreads out to neighboring points, resulting in temporal changes of deformation. In particular, such a process induces tsunami waves from the vertical motion of seabed. The uprising speed of seabed affects the formation of initial surface profile, eventually altering the arrival time and runup of tsunamis at the coast. In this work, we developed a numerical model that can simulate the generation and propagation of tsunami waves by considering the horizontal and vertical changes of seabed in an active and dynamic manner. For the verification of the model, it was applied to the 2011 Tohoku-oki earthquake in Japan and the results confirmed that the accuracy was improved compared to the existing passive and static model.
1. 서 론
해저 지형 내부에서 발생하는 단층파괴는 해저 지형을 시시각각 변화하게 만든다. 특정 지점에서 발생한 단층파괴는 단층파열속도(rupture velocity)를 가지며 수평적으로 진행한다. 이러한 시간차를 지닌 다수의 단층파괴는 개별적인 단층파괴에 의해 발생하는 수면상승에 중첩현상을 야기하여 지진해일 초기파형에 막대한 영향을 끼친다(Jung and Son, 2018). Ohmachi et al.(2001) 및 Suppasri et al.(2010)는 진원에 가까운 지역일수록 시간차를 지닌 단층파괴의 영향을 크게 받는 것을 확인하였으며 Imai et al.(2010)은 시간차에 따른 단층파괴활동으로 인해 해안에서 지진해일고가 크게 증가할 수 있음을 보였다. 이 외에도 시간차를 지닌 단층파괴가 지진해일의 전파에 미치는 영향이 다수의 학자들에 의해 수행되었다(Ishii et al., 2005; Saito and Furumura, 2009; Suzuki et al., 2011; Lee et al., 2015; Jung and Son, 2020a, 2020b).
단층파괴에 의한 해저 지형의 수직적 상승이 지진해일 초기파형에 미치는 영향은 주로 해석해를 이용하여 검토되었다. Kajiura(1963)는 Green 함수를 이용하여 해저 지형의 변화가 근거리 및 원거리 자유수면 변위에 미치는 영향을 검토하였으며, Hammack(1973)은 선형파 이론에 Fourier-Laplace 변환을 적용하여 해석해를 유도한 뒤, 해저 지형의 다양한 상승속도에 따른 자유수면의 변화를 연구하였다. 이후 Dutykh et al.(2006), Dutykh and Dias(2007), Kervella et al.(2007) 및 Jung and Son(2018) 등에 의해 해석해를 활용한 다양한 연구가 수행되었다.
해석해를 활용한 연구는 수치오차 없이 빠르고 정확하게 해를 구할 수 있다는 장점이 있지만 해석해 자체가 가지는 한계로 인하여 제한된 상황에서만 사용이 가능하다. 많은 연구자들에 의해 활용되고 있는 Hammack(1973)의 해는 선형파이론 및 일정수심이라는 한계로 인하여 이상적인 지형조건에서 선형파에 의한 영향만 고려할 수 있다. 따라서, 본 연구에서는 실제 지형에서 발생하는 단층파괴에 의한 해저 지형의 동적 거동이 지진해일에 미치는 영향을 검토하기 위하여 지진해일 수치모형을 활용하였다. 지진해일은 장파의 거동을 보이기 때문에 통상적으로 선형 또는 비선형 천수방정식을 사용하며 이를 기반으로 다양한 모형들이 개발되었다(Tivot and Synolakis, 1998; Wang, 2009; Kowalik et al., 2005). 본 연구에서는 이 중에서 한반도 주변 지진해일 수치모의에 가장 빈번하게 사용되는 COMCOT 모형(Cornell Multi-grid Coupled Tsunami model)을 사용하여 분석하였다.
2. 수치 모의
2.1 수치모형
COMCOT모형은 적용 대상에 따라 다양한 선택이 가능하다. 통상적으로 광역에 적용할 경우에는 구형 좌표계의 선형천수방정식을 사용하며 상세역에 대해서는 직교 좌표계의 비선형 천수방정식을 사용한다. 각각에 대한 지배방정식은 다음과 같다.
선형천수방정식(구형좌표계):
비선형천수방정식(직교좌표계):
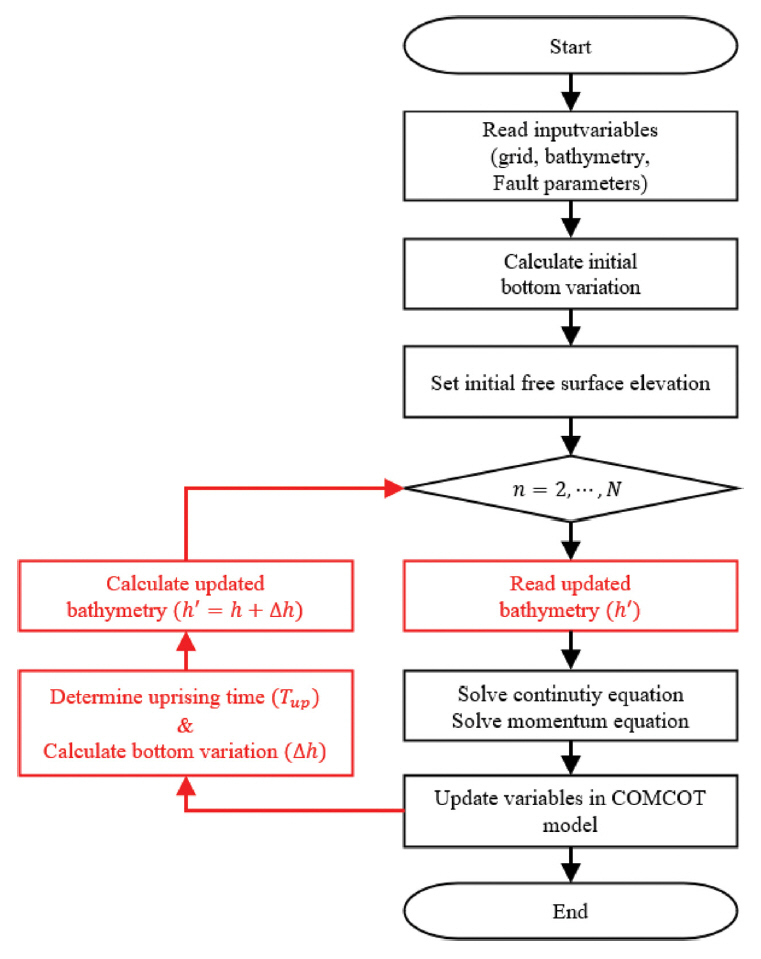
지배방정식에 수심에 관한 시간미분항이 포함되어 있으나 실제 배포된 코드상에서는 해저 산사태 경우에만 수심을 실시간으로 반영할 수 있다. 단층파괴와 같은 지진활동에 의한 해저지형의 변화와 이로 인한 지진해일 초기파형의 생성은 수동적 지진해일 생성(해저지형의 변화 = 자유수면의 변화)을 가정하여 지진해일 수치모의를 수행하고 있다. 해저지형의 상승속도가 짧은 경우는 해저지형의 변화와 자유수면의 변화는 거의 동일하지만 상승속도가 느린 경우에는 먼저 상승한 자유수면이 좌우로 이동하기 때문에 단층파괴가 완료된 후의 자유수면변화는 해저지형변화와 그 양상이 많이 다를 수 있다. 본 연구에서는 단층파괴에 의한 지진해일 모의시 기존의 연구처럼 수동적으로 지진해일 초기파형을 생성하는 것이 아니라 Fig. 1의 순서도에서와 같이 변화된 수심을 실시간으로 업데이트하여 연속방정식과 모멘텀 방정식을 통해 지진해일 초기파형이 능동적으로 생성되도록 하였다. 기존의 연구방법에서는 단층파괴에 의해 해저지형에 변화가 생기면 이러한 변화량을 자유수면 초기조건으로 할당하여 수치해석을 진행하였다. 반면, 본 연구에서는 해저지형에 변화가 생기면 연속방정식의 ∂h/∂t 및 운동량 방정식의 ∂P/∂t, ∂Q/∂t에 영향을 줘서 지배방정식을 통해 지진해일 초기파형(η)이 계산되도록 하였다.
Algorithm for tsunami numerical model considering time-dependent water depth.
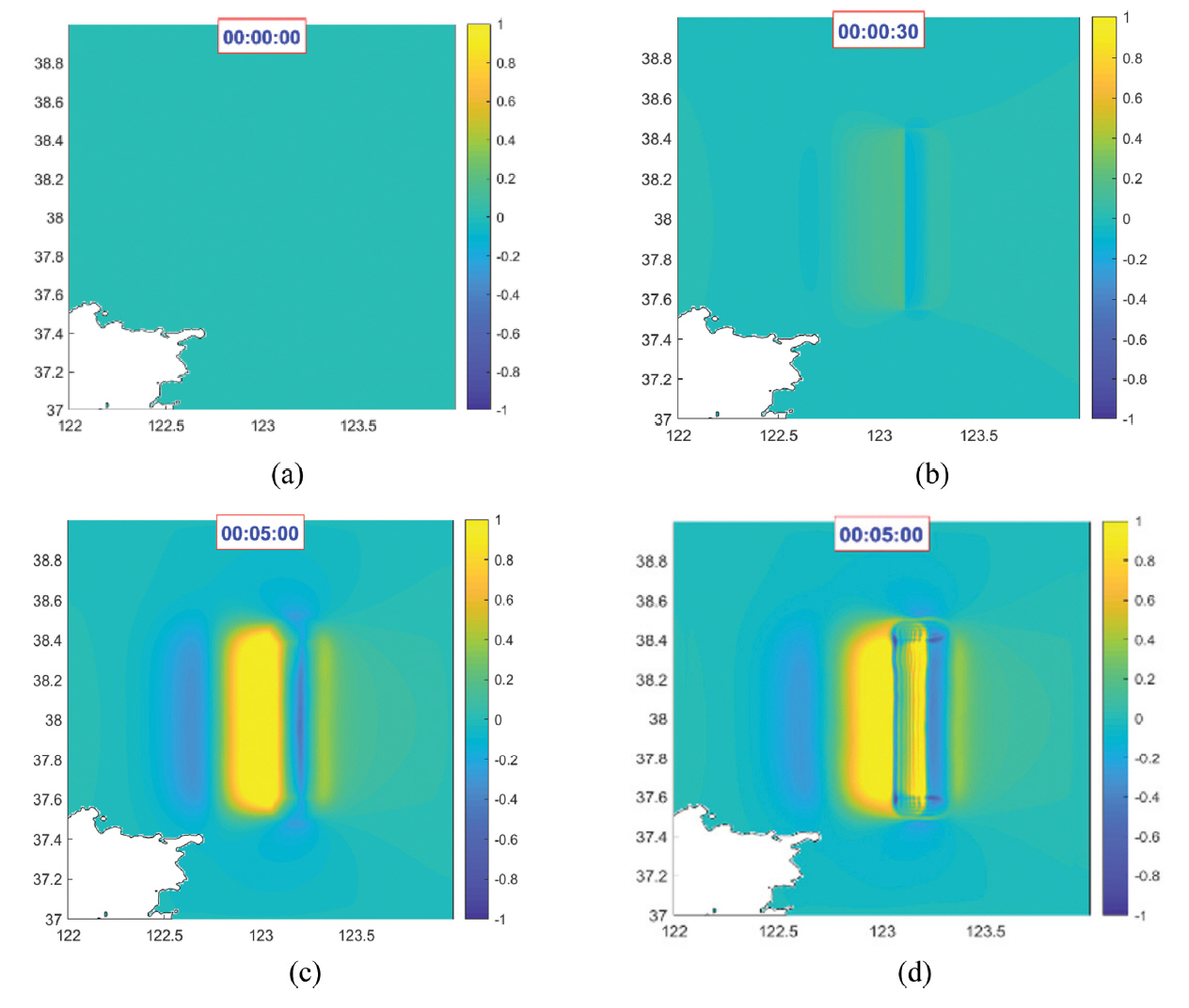
Fig. 2는 본 연구에서 제안한 능동적 지진해일 초기파형과 기존의 수동적 지진해일 초기파형을 비교한 그림이다. Fig. 2(a)~(c)는 능동적 지진해일 생성에서 상승시간(Tup)을 5분으로 한 뒤에 0초, 30초 및 5분 지난 후의 자유수면을 나타난 결과이며 Fig. 2(d)는 0초에서 수동적 지진해일 생성 후 5분이 지난 후의 자유수면을 나타낸 결과이다. 능동적 지진해일 생성에서는 5분이 지난 후 지진해일 생성이 완료되어 전파가 시작되지만 수동적 지진해일 생성에서는 이미 전파가 시작되어 두 방식에 의한 초기파형에 차이가 있음을 알 수 있다.
Comparison of free surface elevation between active (a, b and c) and passive (d) tsunami generations.
2.2 격자구성 및 단층정보
본 연구에서 개발한 지진해일 수치모형을 동일본대지진에 적용하여 타당성을 검토해보았다. 동일본대지진은 2011년 3월 11일 일본 산리쿠 연안(38.322°N, 142.36°E)에 발생한 규모 9.0~9.1의 대지진이다. 지진 및 쓰나미로 인해 약 16,000명의 사망자, 220,000명의 난민과 더불어 추정 2,350억 달러의 피해액이 발생하였다. 동일본대지진은 다른 지진과 달리 단층파괴가 발생한 지역의 중심에 위치한 후쿠시마현 이와키시에서 약 3분 동안 진도 4 이상의 진동이 발생하여 시간이력 단층운동의 중요도가 크기 때문에 본 연구에서 개발한 지진해일 수치모형을 적용하기 적합하다. 지진을 재현하기 위해 Table 1 및 Fig. 3과 같이 6개의 소단층을 사용하였다.
Fault information for 2011 Tohoku-Oki earthquake
The location of sub-faults for 2011 Tohoku-Oki earthquake (Wei et al., 2014 발췌).
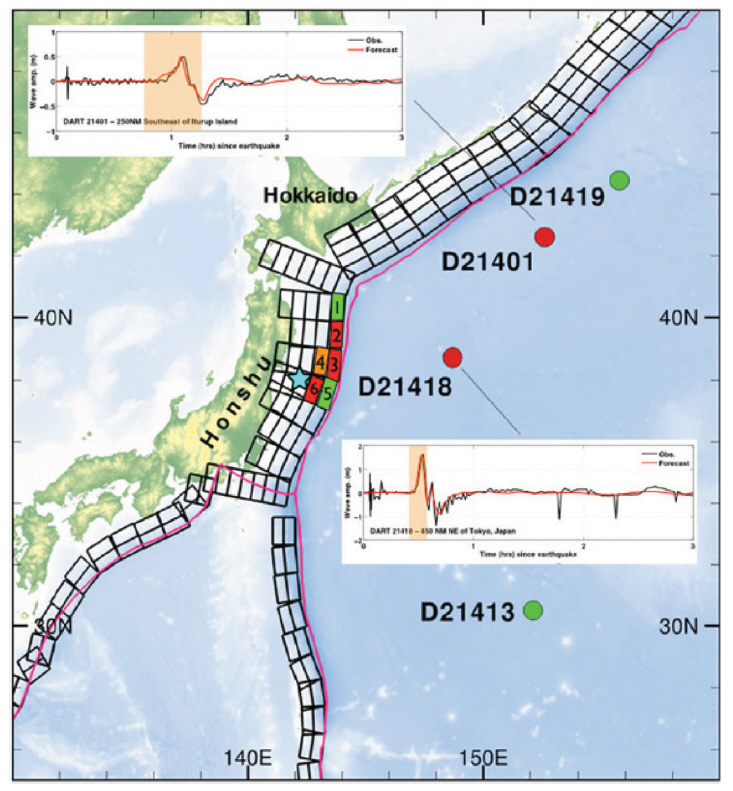
Okada 모형을 이용하여 해저지형 변화를 계산하였으며 각 소단층의 파괴 시작 시간을 달리 설정하여 남쪽에서 북쪽으로 단층파괴가 발생하도록 설정하였다. 일본 동쪽에서 발생하는 지진해일을 고려하면서 태평양 및 미국 서쪽에서 관측된 지진해일고와 비교하기 위해 Fig. 4와 같이 위도 0°~60°N 및 경도 130°~280°E 범위에서 2'의 간격으로 격자를 구성하였다.
Computational domain.
수치모형의 검증을 위해 National Data Buoy Center(NDBC)에서 제공하는 Deep-ocean Assessment and Reporting of Tsunamis(DART) 자료를 활용하였다. Fig. 4에서 표시된 바와 같이 총 14개 지점의 자료를 사용하였으며 2차 Butterworth band-pass 필터를 적용하여 조석 성분을 제거하였다. 단층파괴의 동적 거동을 고려하기 위하여 단층파괴속도 및 해저지형 상승시간은 각각 2.5 km/s 및 60 sec.로 설정하였다.
2.3 수치모의 결과
Fig. 5는 시간별 지진해일 수치모의결과를 나타낸다. 단층파괴의 동적거동이 지진해일 생성 및 전파에 미치는 영향을 보기 위하여 기존 지진해일 수치모형의 결과는 위에, 개선된 지진해일 수치모형의 결과는 아래에 배치하였다. 기존 지진해일 수치모형에서는 단층파괴로 인한 지진해일 초기파형이 지진발생 직후 생성되었으나 본 연구에서 개발한 수치모형에서는 단층파괴로 인한 해저지형의 변화와 이로 인한 자유수면의 변위가 발생하기까지 시간이 소요되기 때문에 지진발생 직후에는 수면이 정지되어 있음을 알 수 있다. 이후 지진해일이 전파하는 동안의 지진해일 공간분포는 국지적으로 차이가 있으나 두 결과 모두 대체로 유사하게 모의되고 있음을 알 수 있다.
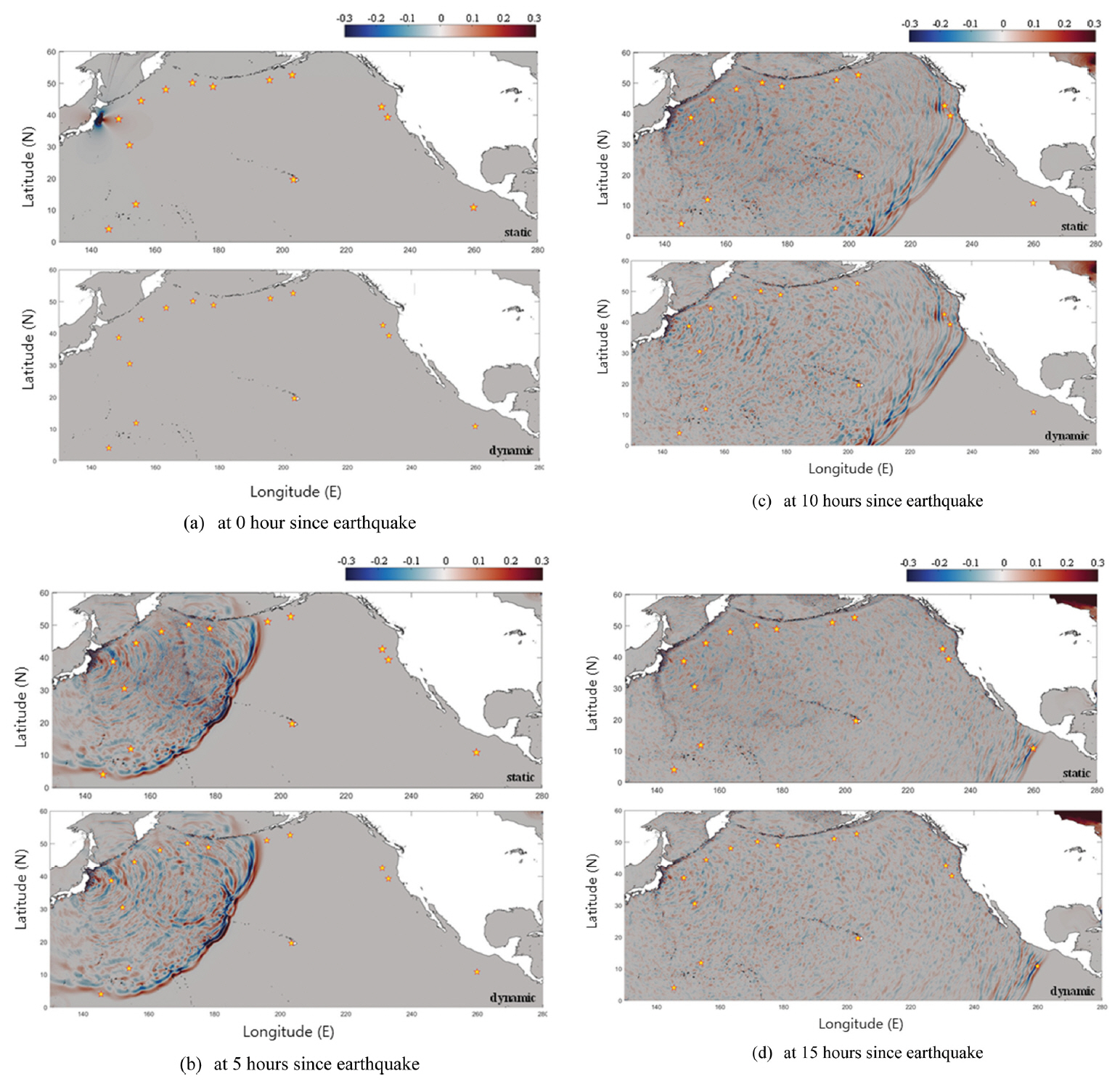
Numerical results of tsunami propagation for different times (up: previous model, down: present model).
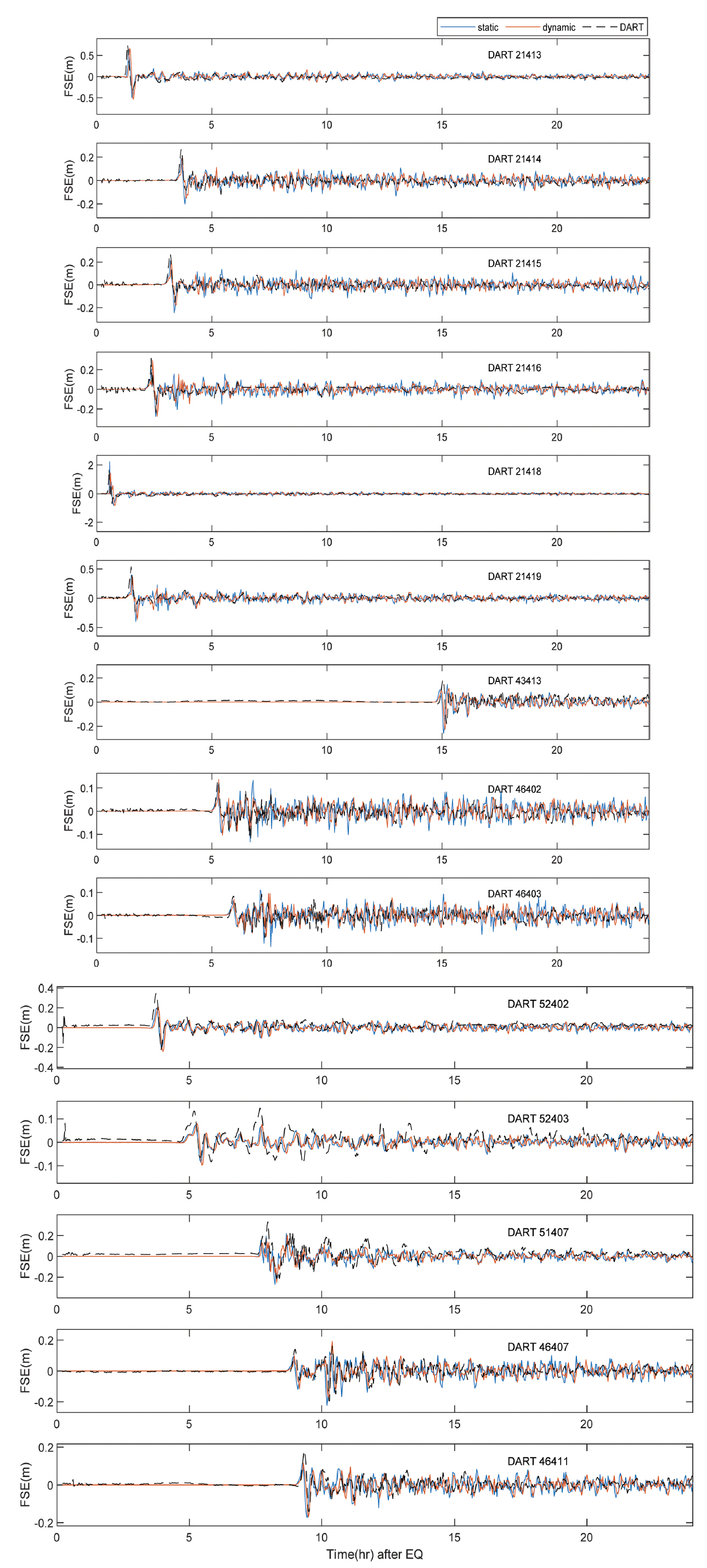
Fig. 6은 지진이 발생한 후 24시간 동안 14개의 DART 지점에서 관측된 수면변위와 두 수치모형에 의해 계산된 수면 변위를 비교한 결과이다. 국부적으로는 두 모델사이에 위상차 및 파고차이가 발생하지만 전체적으로 관측결과와 잘 일치하고 있다. 지진해일에 의한 자유수면변위는 불규칙한 양상을 나타내기 때문에 전체 모의시간에 대한 평균 제곱근 오차(Root Mean Square Error, RMSE)로 모형의 성능을 평가하기에는 무리가 있다. 따라서 본 연구에서는 지진해일 모의시 중요한 인자인 최대수면변위 및 지진해일 도착시간에 대해 비교하였다.
Comparison between previous and present models for different DART’s location.
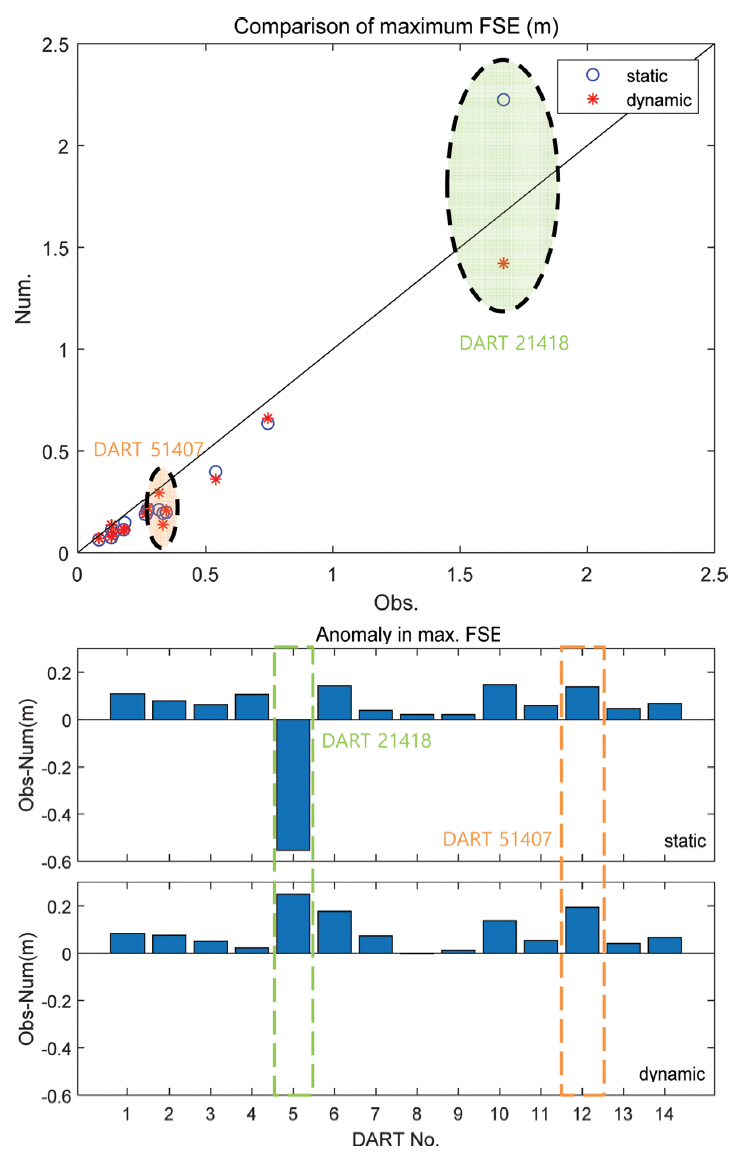
Fig. 7은 DART 지점에서의 최대수면변위를 비교한 결과이다. DART 21418을 제외하면 두 지진해일 모형으로 계산된 최대수면변위는 관측값과 비교했을 때 과소추정되는 것을 알 수 있다. 단층파괴의 동적거동을 고려하지 않은 지진해일 모형의 경우 관측값과의 상관계수는 0.98, RMSE는 0.17로 계산되었으며 동적거동을 고려한 수치모형의 경우에는 상관계수 0.99, RMSE는 0.11로 계산되었다. 태평양 중심인 하와이에 위치한 DART 51407에서는 수치모델 결과와 관측값이 큰 차이를 보였다. 이는 아마 관측지점 일대에 섬이 많아 복잡한 지형을 이루고 있어 수치모형에서 이를 제대로 고려하지 못한 결과로 판단된다. DART 21418에서는 동적거동을 고려하지 않은 경우에는 관측값과 0.5 m 이상의 오차가 발생하였으나 동적 거동을 고려함에 따라 오차는 절반으로 줄어들었다.
Comparison of maximum surface elevation for different DART’s location.
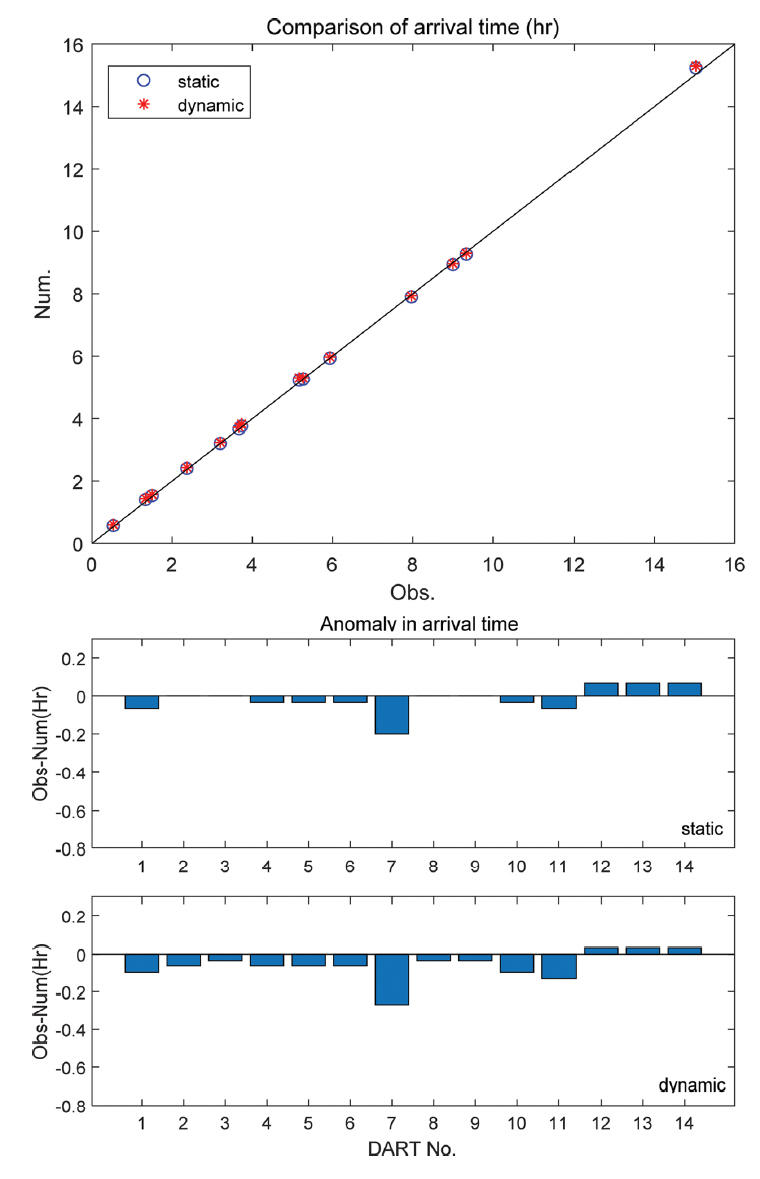
Fig. 8은 DART 지점에서의 지진해일 도달시간을 비교한 결과이다. 동적거동을 고려하지 않은 경우 상관계수와 RMSE는 각각 0.9999 및 0.0690으로 산정되었으며 동적 거동을 고려한 경우에는 각각 0.9998 및 0.0976으로 산정되었다. 최대 수면변위와는 달리 지진해일 도달시간은 두 모델 모두 관측값과 대체로 잘 일치하는 것을 확인할 수 있다.
Comparison of arrival time for different DART’s location.
4. 토의 및 결론
단층파괴로 인한 해저 지형의 동적거동을 모의할 수 있는 수치모형을 개발하여 기존 지진해일 사례에 적용해보았다. 해저지형 내부에서 지진이 발생할 경우 특정 지점에서 단층파괴가 시작하여 주변으로 이동한다. 이러한 과정을 통해 공간적으로 다수의 지점에서 단층파괴가 시간차를 가지며 발생하고 이로 인하여 지진해일 초기파형도 시간차를 가지며 생성된다. 아울러, 단층파괴에 의해 해저지형이 상승 또는 하강할 시에도 움직이는 시간에 따라 지진해일 초기파형은 달라진다. 기존의 모형은 시간차에 의한 단층파괴는 모의가능하였으나 해저지형의 변화에 의한 지진해일 초기파형의 생성은 물리적으로 구현하지 못하였다. 해저지형의 변화와 자유수면의 변화가 동일하다는 수동적 지진해일 생성원리를 사용하여 대부분의 수치모의를 수행하였으며 이는 경우에 따라 큰 오차를 야기할 수도 있다. 수심변화에 의한 지진해일 초기파형에 관한 연구는 해석적인 방법을 통해 수행된 바가 있으나 해석해의 한계로 인하여 제한된 조건에서만 연구가 수행되었다.
본 연구에서는 기존의 수치모형을 개선하여 실제 지진해일 발생 메카니즘을 수치모형에서 그대로 구현하였다. 즉, 자유수면에 인위적으로 지진해일 초기파형을 설정하지 않고 단층파괴에 의해 해저지형이 변화하는 것을 실시간으로 수치모형에 반영하여 연속방정식과 모멘텀 방정식을 통해 지진해일 초기파형을 자연스럽게 생성되도록 하였다. 개발된 지진해일 수치모형은 2011년 동일본대지진에 적용하여 성능을 검토하였다. 태평양에 설치된 DART의 관측자료 및 기존 수치해석의 결과와 비교한 결과, 최대수면변위는 기존모형에 비해 정확하게 예측할 수 있었으나 지진해일 도달시간은 별다른 차이를 보이지 않았다. 기존 모형에 비해 계산결과가 크게 개선되는 않는 것은 다음과 같은 이유를 생각할 수 있다. 첫째, 본 연구에서 사용한 단층매개변수는 단층의 동적거동을 고려하지 않은 상황에서 추정된 값들이다. 둘째, 본 연구에서는 단층의 동적 거동을 모의하기 위하여 2.5 km/s의 단층파열속도와 60 sec.의 상승시간을 사용하였으나 이는 실제의 지반거동을 정확하게 묘사하기에는 한계가 있다. 따라서, 추후 수치모형의 성능을 정밀하게 검토하기 위해 단층파괴의 동적거동을 고려한 새로운 매개변수 추정 및 실제 지진 발생시 지반의 정확한 거동 등을 보완할 필요가 있다.