2.1 신뢰성해석

방파제 하중저항계수 보정을 위한 첫 번째 단계는 기존 방파제에 대한 신뢰성해석을 수행하여 방파제들의 신뢰성수준을 파악하고 각 방파제들의 한계상태함수 민감도 정보를 구하는 것이다. 소파블록 피복제의 파력에 대한 활동과 전도 파괴모드에 대한 신뢰성해석을 위하여 식(1) 및 (2)의 한계상태 함수를 사용한다.

여기서 f_c, W_i, B, U 및 P는 각각 제체와 마운드의 마찰계수, 제체 중량, 부력, 양력 및 파력이며 x_i와 y_i는 전도시 방파제의 회전 중심에서 하중까지의 수평 및 연직거리이다. 제체중량은 다시 무근콘크리트(W_c), 철근콘크리트(W_rc), 채움재(W_f) 등으로 나눌 수 있다. 식(1)과 (2)에서 거리에 대한 변수(x_i, y_i)를 제외한 모든 변수는 확률변수이다. 파력과 양력은 독립 매개변수 G를 이용하여 다음과 같이 정의하였다.

여기서, P₀와 U₀는 파력 및 양력의 설계 값이고 G는 고다 파압식에 의한 파력과 양력이 가지는 불확실성을 나타내기 위한 확률변수이다. 고다의 파압식에 의한 파력과 양력은 실험에 의하면 실제보다 과대평가되는 경우가 많으며 그 변동성을 신뢰성해석에서 고려하기 위하여 독립 확률변수로 G를 사용하며 이것은 결과적으로 파력과 양력이 동일한 위상을 갖도록 하였다(Kim, 2020). 식(1) 및 (2)에서 제체에 작용하는 부력은 식(5)와 같다.

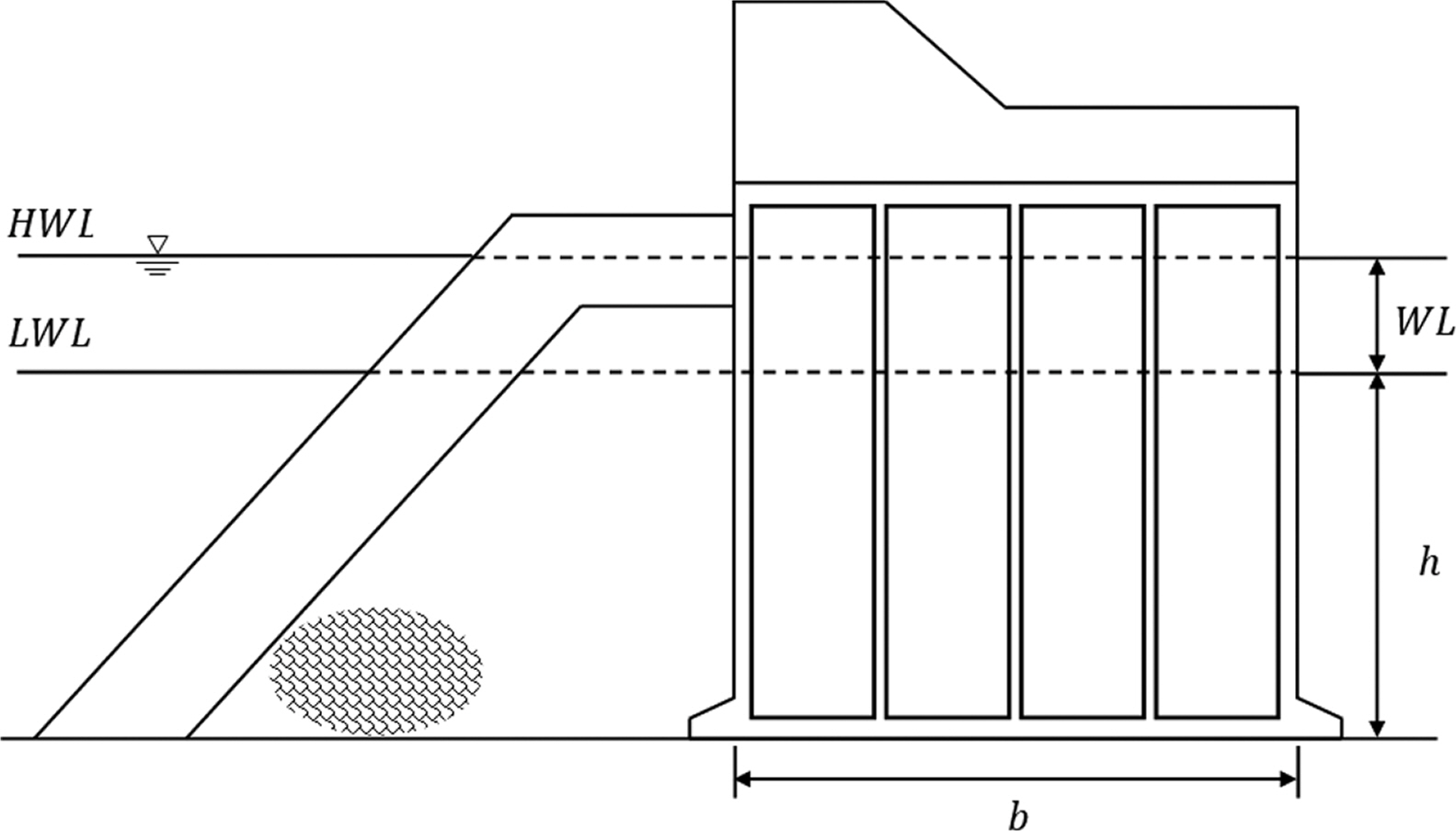
위 식에서 r_w는 해수 단위중량이며 h, WL, b, v_f는 Fig. 1에서 보는 바와 같이 수심, 설계조위, 케이슨 폭, 앞굽과 뒷굽의 부피를 의미한다.

Fig. 1.

Geometry of caisson breakwater.

방파제 신뢰성해석은 Level II 방법인 일계신뢰도법(FORM) 을 적용한다. 그 이유는 하중저항계수 보정에서 필요한 한계 상태의 민감도 정보를 얻을 수 있는 방법이기 때문이다. FORM에서는 한계상태함수를 파괴점(X^*)에서 선형화한 근사 한계상태함수(g~ )에 대하여 파괴면(< 0)이 평균으로부터 떨어진 거리(β)를 구한다. β는 감소 변수(reduced variable) 평면상에서 파괴점과 원점사이의 거리로서 한계상태함수의 민감도를 이용하여 다음과 같이 표현할 수 있다(Hasofer and Lind, 1974).

2.2 부분안전계수

하중저항계수 보정을 위해 수집한 방파제 설계사례를 이용하여 신뢰성해석을 수행하면 설계확률변수에 대한 한계상태 함수의 민감도를 얻을 수 있다. 신뢰성해석 결과 얻을 수 있는 민감도계수를 이용한 부분안전계수는 식(7)과 같다.

여기서 α_X, β_T, σ_X, μ_X, X_k는 각각 민감도계수, 목표신뢰성 지수, 표준편차, 평균 및 설계특성값을 나타낸다. 부분안전계수는 사용한 확률변수의 수만큼 생성되며 사용한 설계사례와 동일한 수만큼의 부분안전계수 군이 만들어 진다.

2.3 하중저항계수

부분안전계수를 이용한 한계상태설계법은 설계변수 개별적으로 안전율을 적용하므로 설계변수의 개수만큼의 계수가 필요하지만 하중저항계수를 이용한 방법은 저항값과 하중값에만 안전율을 적용하므로 계수가 2개로 줄어드는 편리한 점이 있다. 이러한 설계의 편리성 때문에 부분안전계수법보다 하중저항계수법을 선호하는 경우가 있다(JHS, 2018).

부분안전계수를 하중저항계수로 변환하는 방법은 다음과 같다. 우선, 부분안전계수법의 활동 저항값은 식(1) 우항의 첫번째 항인 마찰력이며 각 확률변수를 설계특성값(X_k)과 부분 안전계수(γ_X)의 곱으로 표현한다. 하중저항계수법의 활동 저항값은 마찰력에 저항계수(γ_R)를 곱한 것이다. 두 설계법의 저항값이 같다는 것을 식으로 표현하여 정리한 것이 식(8)이다 (Kim, 2019). 활동 하중값을 동일한 방법으로 전개하면 하중 계수(γ_S)를 식(9)와 같이 구할 수 있다. 하중계수는 결국 불확실성 변수 G의 부분안전계수와 같게 된다.

여기서 γ_fc, γ_Wi, γ_WL, γ_G는 각각 마찰계수, 케이슨 요소의 중량, 조위, 파력의 부분안전계수이고 하첨자 k가 붙은 값들은 설계특성값이다.

2.4 하중저항계수 최적화

앞서 구한 부분안전계수와 하중저항계수들은 원칙적으로 특정 방파제 설계에 종속된 값들이다. 설계조건이 달라지면 민감도계수, 특성치 등이 영향을 받아 결과적으로 하중저항계 수가 달라진다. 하중저항계수를 표준화하여 하나의 기준값을 만든다는 것은 다양한 사례에 적용했을 때에도 목표로 설정한 신뢰성지수보다 큰 값을 갖도록 보장해야 한다. 따라서, 여러 하중저항계수 쌍을 이용하여 표준적인 하나의 쌍을 만들되, 최종 계수의 쌍을 적용한 어떠한 방파제도 그 신뢰성지수가 목표값보다 커야한다는 조건을 만족해야 한다. 이러한 것을 수식화하여 표현하면 식(10)과 같은 최적화문제를 정의할 수 있다.

여기서, 가격함수의 첫 번째 중괄호는 하중저항계수를 적용하여 재설계한 방파제의 신뢰성지수 β_j(γ_R, γ_S)와 목표신뢰성지수(β_T)의 거리를 최소화시키기 위한 것이며 두 번째 중괄호는 개별 방파제의 하중저항계수인 γ_Rj와 γ_Sj가 최종 하중 저항계수 γ_R와 γ_S의 거리를 최소화시키기 위한 것이다. W_β와 W_γ는 각 제곱항의 가중치 값이다. 제약식(10b)는 하중저항계수를 적용하여 설계한 방파제의 신뢰성지수를 목표값보다 크게 만들기 위한 것이다.

하중저항계수 최적화 과정에서 γ_R와 γ_S를 적용하여 설계한 방파제는 신뢰성지수가 목표신뢰성지수보다 커야 한다. 그렇다고 해서 중량을 지나치게 증가시켜 과도하게 안전성을 높인다면 하중저항계수가 충분히 최적화되었는지를 판별할 수없게 된다. 따라서, 하중저항계수를 적용하여 재설계한 방파제는 저항과 하중이 균형을 이루도록 최소설계를 해야 하며 그 상태에서 재설계한 방파제의 신뢰성지수를 평가해야 하중 저항계수가 충분히 최적화 되었는지 판별할 수 있다.

식(10)을 이용한 최적화 과정에서 하중계수와 저항계수를 각각 γ_S* 와 γ_R*로 사용한다고 가정하자. 하중저항계수법의 활동안정 조건은 다음과 같다.

즉, 하중저항계수 설계법에서는 마찰저항력에 저항계수를 곱한 값이 파력에 하중계수를 곱한 값보다 크거나 같을 때 안정성을 확보한 것으로 본다. 좌항의 값이 우항보다 클 경우는 안정성이 증가하므로 문제가 되지 않는다. 그러나 그 정도가 지나칠 경우 과도한 안정성이 발생하고 제체의 활동 한계상태에서 신뢰성지수가 목표신뢰성지수보다 훨씬 크게 된다. 이것은 신뢰성지수의 최적화에서 의도한 결과가 아니므로 식(11)에서 마찰저항력을 감소시켜 등식이 성립하는 조건을 만들어야 한다. 이러한 조건에서는 활동안정성도 확보하면서 신뢰성지수를 최적화할 수 있기 때문이다. 식 (11)에서 등식을 만드는 방법은 제체의 무게를 감소시키는 것과 채움재 중량을 감소시키는 것이 있는데 케이슨의 형상에 변화를 주기 않으면서 가능한 것은 채움중량을 조절하는 것이다. 즉, 식(11)의 등식 조건에서 채움중량을 유도하면 다음과 같다.

여기서, W_c, W_rc, W_f는 무근, 철근, 채움중량이며 P_k, U_k는 파력과 양력, B_k는 부력을 나타낸다. 이 식은 활동에 의한 케이슨의 평형식에서 외력과 저항력을 등식화하여 만든 채움중량 재설계식이다. 최적화를 완료한 하중저항계수를 설계사례 방파제에 모두 적용하여 신뢰성해석을 수행하고 목표신뢰성 지수보다 큰 값을 보이면 최적화가 완성된다.

3.1 설계사례

수치해석을 위해 전국 항만에 시공된 9개의 소파블록 피복제를 이용하였다. Table 1은 각 방파제의 주요제원을 보여준다. 각 방파제의 무근콘크리트 중량(W_c), 철근콘크리트 중량 (W_rc), 채움채 중량폭(W_f), 케이슨 폭(b), 조위(WL), 앞뒷굽 부피(v_f), 수심(d) 등이 정리되어 있다. 그 밖에 해수단위중량은 10.3 kN/m³ 마찰계수는 0.6을 사용하였다.

Table 1.

Design parameter for front cover breakwaters (dim: kN, m)

3.2 신뢰성해석

6개의 확률변수에 대한 변동특성 값은 Table 2와 같다(JHS, 2007; US Army, 2006; Kim, 2019). 표에서 a는 편이계수로서 평균값을 설계특성값으로 나눈 값이며 V는 변동계수로서 표준편차를 평균값으로 나눈값이다. 확률변수는 모두 정규분포를 따른다고 가정하였다.

Table 2.

Distribution characteristics of design parameters

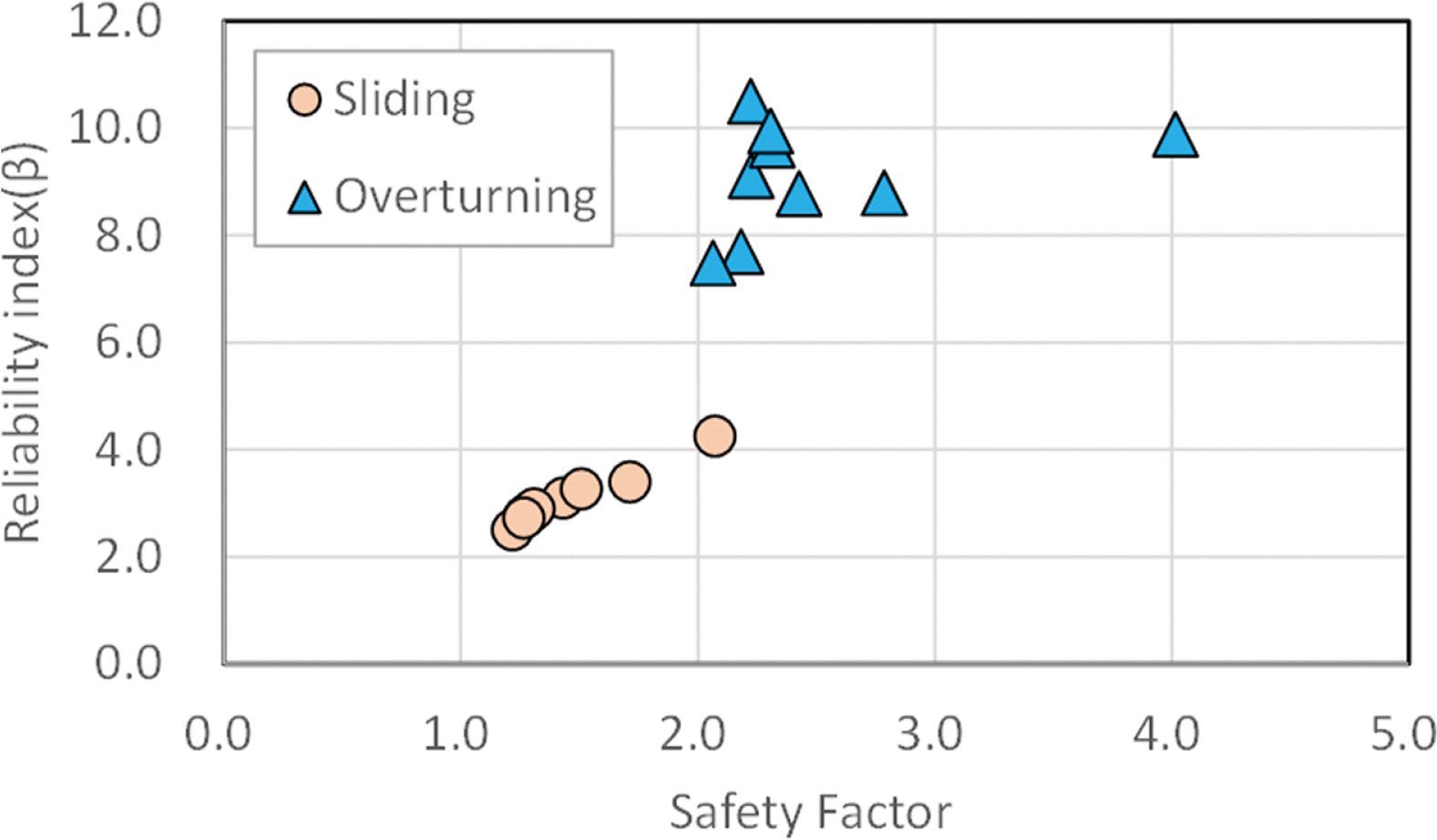
FORM을 적용하여 방파제의 활동 및 전도 한계상태 신뢰 성해석을 수행한 결과 신뢰성지수와 안전율을 Fig. 2에 그렸다. 안전율은 활동한계에서 1.22~2.07, 전도한계에서 2.06~ 4.02의 범위에 있으며 신뢰성지수는 활동한계는 2.5~4.26, 전도한계는 7.49~10.51의 분포를 보였다. 활동한계에서는 안전율이 높을수록 신뢰성지수도 증가하는 경향을 보였으나 전도 한계는 그렇지 않았다.

Fig. 2.

Reliability indices and safety factor of the breakwaters.

확률변수에 대한 활동 한계상태의 민감도는 Fig. 3과 같다. 민감도의 절대값 크기는 각 확률변수가 활동한계에 미치는 영향의 정도를 의미한다. 마찰계수(f_c)와 파력계수(G)에 대한 민감도의 절대값은 다른 것에 비해 월등히 크며 활동파괴에 지배적인 확률변수라는 것을 의미한다. 민감도의 부호가 음인 것은 활동에 기여하며 양인 것은 저항에 기여하는 변수이다. 조위와 파력계수의 부호가 음인 것으로 보아 활동에 기여하는 변수임을 알 수 있다.

Fig. 3.

Sensitivities of design parameters.

3.3 하중저항계수 보정

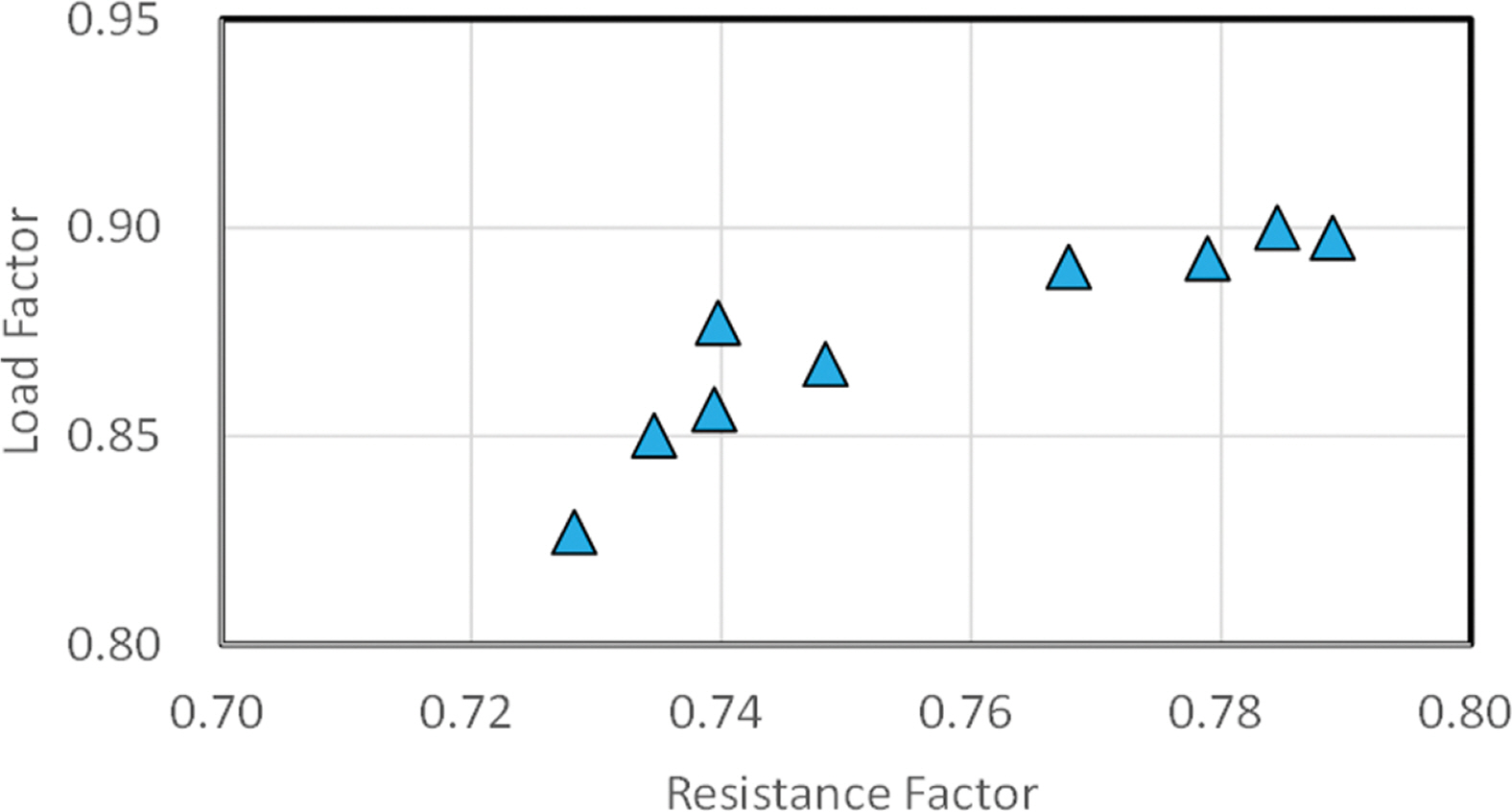
목표신뢰성지수를 β_T = 2.4로 설정하여 방파제 9개에 대하여 하중저항계수를 구하면 Fig. 4와 같다. 일반적으로는 저항계수가 1.0보다 작고 하중계수가 1.0보다 크다. 그러나 소파 블록 피복제 제체의 경우 파력계수에서 편이계수가 0.702로써 작기 때문에 식(7)에서 평균과 특성치의 비를 편이계수로 적용하면 부분안전계수가 1.0보다 작게 되어 최종 하중계수가 1.0보다 작아지는 결과가 나타났다.

Fig. 4.

Load and resistance factors.

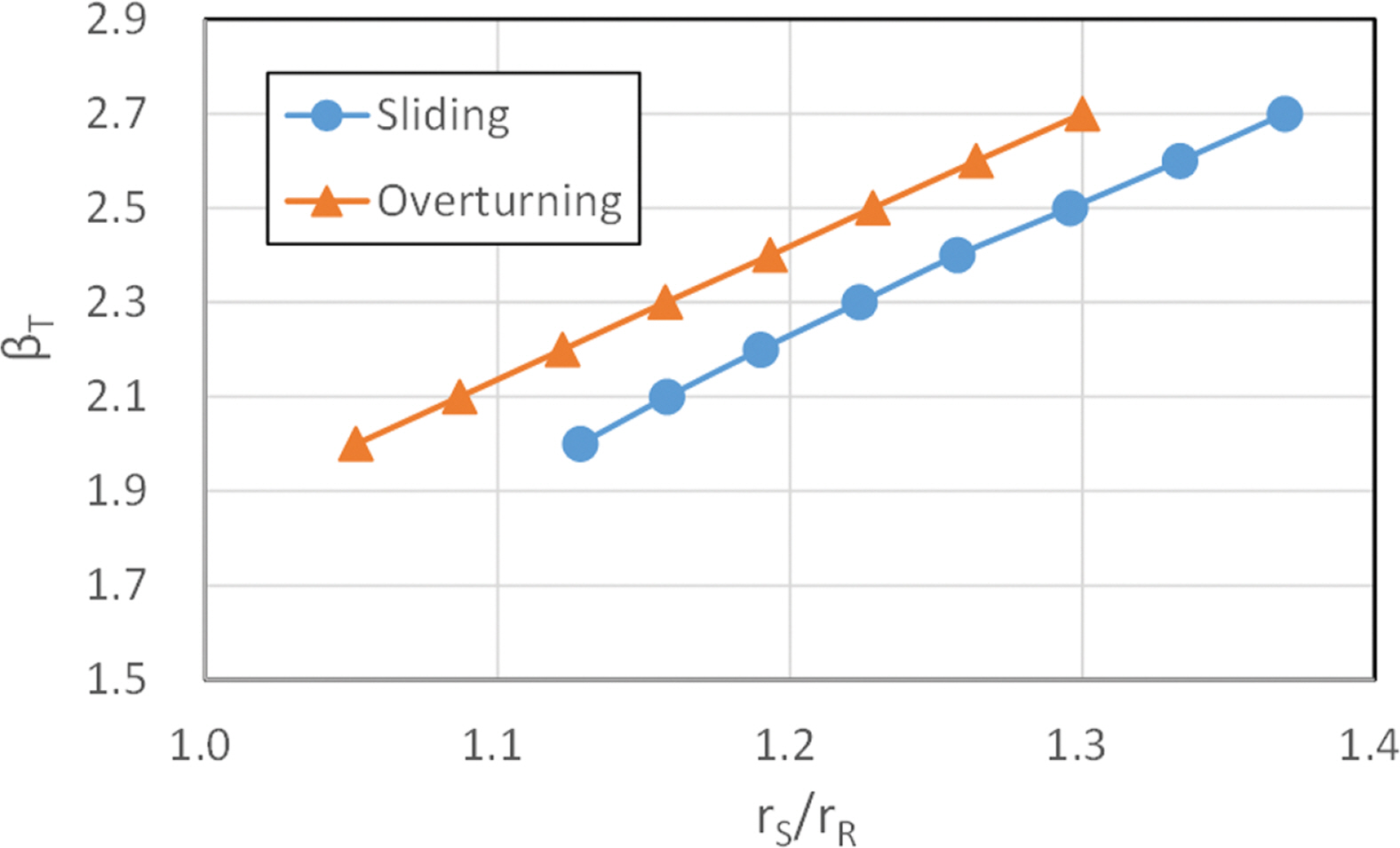
목표신뢰성지수를 2.2에서 2.8까지 변화시켜 최적화한 하중계수와 저항계수를 Table 3과 같이 구하였다. 하중계수를 저항계수로 나눈 값을 하중저항계수비라 하면 현행 결정론적설계의 안전율과 동일한 역학적 의미를 가진다. 따라서 현행 안전율(1.2)을 목표신뢰성지수로 환산할 수 있다. Fig. 5는 하중저항계수비와 목표신뢰성지수를 그래프로 표현한 것이다. 두 값사이의 회귀식을 추정하면 활동한계 및 전도한계에 대하여 각각 식(13) 및 (14)와 같다. 여기서 γ_S/γ_R에 1.2를 대입하면 각각 β_{T, S} = 2.22, β_{T, O} = 2.42를 얻는다. 이 값이 우리나라 소파블록 피복제의 신뢰성에 근거한 현행 안전율 1.2에 해당하는 목표신뢰성지수이다.

Table 3.

Load & resistance factors according to target reliability index

Fig. 5.

Load resistance factor ratio vs target reliability index.

3.4 하중저항계수 검증

본 연구에서 구한 하중저항계수를 비교하기 위하여 하중저항계수 설계법을 사용하고 있는 일본항만설계기준(JHS, 2018) 의 값과 비교하였다. 일본항만기준에서 소파블록 피복제에 대한 목표신뢰성지수는 그동안 일본에서 설계시공된 방파제의 신뢰성지수 평균값으로 정한 것으로 그 값은 Table 4와 같다 (Sato et al., 2016). 일본기준의 활동, 전도 한계상태의 목표 신뢰성지수는 각각 2.409와 2.290이다. 이 값과 동일하게 목표신뢰성지수로 설정한 후 본 연구의 하중저항계수 최적화를 다시 수행한 결과를 표에서 비교하였다. 하중저항계수비를 기준으로 활동한계는 10.5% 전도한계는 2%의 차이가 발생한다. 이 차이는 하중저항계수 보정에 사용한 일본과 우리나라의 기존 방파제가 가지는 신뢰성지수의 수준이 다르기 때문 이다. 즉, 일본의 설계사례와 우리나라 설계사례의 활동안전율 평균은 각각 1.24와 1.45로서 우리나라가 일본보다 더 높은 안전율로 설계되었기 때문으로 볼 수 있다(Sato et al., 2016).

Table 4.

Comparison of load & resistance factors with Japanese code