수리실험을 통한 수평 2열 쉬라우드 조류에너지 변환장치 성능평가
Performance Assessment of Two Horizontal Shroud Tidal Current Energy Converter using Hydraulic Experiment
Article information
Abstract
본 연구에서는 저유속 조건에서도 발전이 가능한 수평 2열 쉬라우드 조류에너지 변환장치를 개발하였다. 쉬라우드 시스템의 형상을 결정하기 위해 3차원 수치모의 실험을 수행하였으며, 1/6 축소모형을 제작하여 수리모형 실험을 수행하였다. 수리모형 실험은 4가지 유속 조건하에서 수행하였으며, 각각의 실험 케이스별로 유속, 토크 및 RPM을 계측하였다. 수치모의 실험 결과, 노즐을 통과한 유속은 실린더에서 약 2~3배 유속이 증폭되는 것을 확인하였으며, 연장비가 2:1일 때, 가장 높은 유속 증폭율을 보였다. 또한 노즐과 실린더의 직경비는 1.5:1일 때 유속이 2.8배 증가하는 것으로 나타났다. 한편 수리모형 실험 결과, TSR이 1.75~2 일 때, 0.32~0.34의 출력 성능을 보이는 것으로 나타났다.
Trans Abstract
In this study, the two horizontal shroud tidal current energy converter, which can generate power even under low flow speed conditions, was developed. In order to determine the shape of the shroud system, a three-dimensional numerical simulation test was conducted, and a 1/6 scale down model was made to perform a hydraulic model experiment. The hydraulic model experiment was performed under four flow conditions, and the flow speed, torque, and RPM were measured for each experimental case. As a result of the numerical simulation test, it was found that the flow speeds passing through the nozzle were increased by about 2~3 times in the cylinder, and when the extension ratio was 2:1, the highest flow speed was shown. In addition, it was found that the flow speeds increased 2.8 times when the diameter ratio between the nozzle and the cylinder was 1.5:1. Meanwhile, as a result of the hydraulic model experiment, it was found that when the tip speed ratio was between 1.75 and 2, the power coefficient was 0.32 to 0.34.
1. 서론
지난 몇 세기 동안 세계 경제는 크게 성장하였으며, 이에 따라 에너지수요도 증가하였다. 그러나 화석 연료의 소비로 인한 CO2 배출 증가는 지구온난화 문제에 큰 영향을 미치게 되었고 이에 대한 문제가 국제사회에서 큰 의제가 되었다. 지구온난화 문제를 해결하기 위해 UN 기후변화협약(1992), 교토의정서(1997), 파리협정(2015), UN 기후정상회의(2019) 등 전 세계 국가 간에 국제적 협의가 진행되며 탄소중립이 새로운 국제적 패러다임으로 대두되고 있다(UN, 1992; UN, 1998; UN, 2015). 이에 세계 각 주요 국가들은 2050 탄소중립을 목표로 탄소중립 선언을 가속화하고 있으며, 우리 정부 역시 최근 탄소중립을 선언한 바 있다. 국내 탄소중립 정책에서는 화석연료에 대한 의존도를 낮추고 재생에너지로의 전환을 추진하면서 에너지 전환 가속화의 필요성을 언급하고 있다.
한편 우리나라는 삼면이 바다로 둘러싸인 반도국가로서 풍부한 해양에너지 자원을 보유하고 있으며, 이를 이용한 조류 발전, 조력발전 및 파력발전은 재생에너지 생성에 따른 에너지 전환 가속화에 기여할 수 있다. 해양에너지원 중 조류발전은 조석에 의한 해수의 흐름을 이용하여 발전하는 방식으로 지속가능한 발전과 발전량 예측이 가능한 장점을 가지고 있으며, 세계적으로 타 해양에너지원에 비해 상용화에 가장 근접한 기술로 평가받고 있다. 또한 조류발전장치는 조류의 운동에너지를 이용하여 기계적 운동을 거쳐 전기에너지로 변환하는 장치로서 시스템 효율은 장치 및 블레이드의 기하학적 형상에 영향을 받게 된다. 이러한 조류발전장치는 회전축에 따라 수직축(VAT, vertical axis turbines)과 수평축(HAT, horizontal axis turbines)으로 구분할 수 있으며, 최근에는 수중익 방식(hydrofoil type) 및 쉬라우드 형식(shroud type)과 같은 다양한 형태의 조류발전기에 대한 연구가 진행되고 있다.
조류발전은 유속의 크기에 비례하여 발전량이 높아지기 때문에 높은 유속을 갖는 환경을 만드는 것이 중요하다. 그러나 유속이 빠른 해역은 한정적이고 수심에 따른 블레이드 크기 확장에 제약이 발생하면서 저유속 및 저수심 조건에서도 고효율의 발전장치를 개발하기 위한 연구가 필요하다. 이로 인해 풍력발전 산업에서는 디퓨저와 같은 쉬라우드를 갖춘 풍력발전장치에 대한 연구가 진행되었다(Van Bussel, 2007). 그러나 블레이드 길이 확장에 제약이 없는 풍력산업에서는 쉬라우드 시스템에 대한 필요성이 상대적으로 낮은 상황이며, 이 아이디어를 바탕으로 조류발전에서는 쉬라우드를 적용한 발전장치가 개발 되고 있다. 대표적인 쉬라우드가 부착된 조류발전장치로는 OpenHydro, Lunar Energy 사 및 독일의 MittelrheinStrom 사에서 개발한 조류발전 장치가 있다(Fig. 1 참조).
Shrouded open centre tidal turbines manufactured by OpenHydro (left), and duct type tidal turbines developed by Lunar Energy (right) (IEA-OES, 2021; Mehmood et al., 2012).
조류발전장치의 형상 중 덕트를 수반한 쉬라우드 형식의 기하학적 구조는 터빈 효율에 중요한 영향을 미친다(Zhou et al., 2013). 이에 Khunthongjan and Janyalertadun(2012)은 전산유체역학 기법을 이용하여 조류발전 장치의 디퓨저 각도 효과에 대한 연구를 수행하였으며, Wang and Shen(2018)은 쉬라우드의 형상 파라미터 변화를 통해 최적 형상화를 결정하는 연구를 수행한 바 있다. 또한 Shahsavarifard et al.(2015)는 디퓨저 유무에 따른 성능을 평가하였고 1.0 m/sec를 초과하는 유속 조건에서는 디퓨저의 출구 직경과 동일한 직경의 프로펠러형 조류발전장치가 디퓨저가 있는 조류발전장치와 동일한 출력을 보이고 있음을 발견하였으며, 디퓨저를 통해 블레이드의 직경을 줄일 수 있음을 실험을 통해 발표하였다. 또한 저유속, 저수심 및 해양 생물이 우려되는 곳에서는 쉬라우드 조류발전장치가 유리함을 나타내었다. 이외에도 Gaden and Bibeau(2010)는 수치해석을 통한 덕트의 형상 각도에 따른 출력 효율 산정한 바 있다. 국내에서도 쉬라우드 조류발전장치에 대한 연구는 활발히 진행되었다. Kim and Lee(2012)는 조류발전 시스템용 쉬라우드의 형상각도별 해수유동 변화를 수치모의 한 바 있으며, Lee et al.(2018; 2019a; 2019b)은 단일 쉬라우드 조류발전 장치의 상부 두께에 따른 유속변화와 블레이드의 형상에 따른 유속변화를 수리모형실험과 수치해석을 이용해 분석한 바 있다. Han et al.(2019; 2020)은 쉬라우드 조류발전장치의 축소모형 실험을 통해 발전 성능을 분석한 바 있으며, 다중 채널구조에 따른 해수유동장을 분석한 바 있다.
이에 본 연구에서는 흐름 단면의 차이를 통해 유속을 증가시켜 저유속 조건에서도 고효율의 출력을 나타내는 쉬라우드 조류발전장치를 개발하였다. 또한 본 장치의 최적형상은 수치모의 실험을 통해 결정하였으며, 수리모형 실험을 통해 수평축 배열에 따른 쉬라우드 조류발전장치의 성능평가를 수행하였다.
2. 쉬라우드 형상 결정을 위한 수치모의 실험
2.1 쉬라우드 조류발전기 개념
쉬라우드 조류발전타입의 개념은 유입구의 단면적을 축소하여 속도에너지를 증가시키는 노즐과 유출부에 유속을 줄이고 정압을 유지하기 위한 디퓨저가 적용되어 있다. 이러한 쉬라우드 조류발전타입은 비교적 낮은 유속을 증폭시킬 수 있어 저유속 조건에서도 고효율의 성능을 보일 수 있다는 장점을 가지고 있으며, Fig. 2와 같이 배열형태에 따라 단독형 혹은 다중형으로 설치하여 사용할 수 있다.
Single and multi array concrete tidal current energy converters.
쉬라우드의 성능은 유입구 노즐 직경과 실린더의 직경, 구조체 길이 등에 따라 영향을 받게 되므로 유속 증가가 가능한 최적 형상을 결정하여야 한다. 이에 본 연구에서는 쉬라우드의 최적 형상을 결정하기 위해 수치모의 실험을 진행하였다.
2.2 쉬라우드 연장비 및 직경비
본 실험에서 사용한 쉬라우드형 조류발전 형상체의 형상화는 SolidWorks 프로그램을 이용하였으며, 구조물의 기본 형상은 하단 길이 6 m, 높이 5 m, 외부직경 3 m, 내부직경 1 m로 형상화하였다(Solidworks, 2018). 저유속의 조건에서도 발전이 가능하도록 유속을 증폭시킬 수 있는 쉬라우드 조류발전 형상의 최적화를 위하여 3차원 유동해석 프로그램인 FLOW-3D를 이용하였다. FLOW-3D 모델은 미국 Flowscience가 개발한 범용 유동해석 프로그램으로서 좌표계는 직교 좌표계를 사용하였으며 복잡한 3차원 형상의 표현을 위하여 FAVOR 기법(Fractional Area/Volume Obstacle Representation Method)을 사용하였다. 또한 직교좌표계에서 비압축성 유체의 3차원 흐름을 해석하기 위한 지배방정식으로는 연속방정식과 운동 방정식이 사용되었으며, 난류모형으로는 수치모의 정확도가 비교적 우수하다고 평가받고 있는 RNG(renormalized group) k-ε Model을 사용하였다(FLOW Science, Inc., 2017; Kaheh et al., 2010).
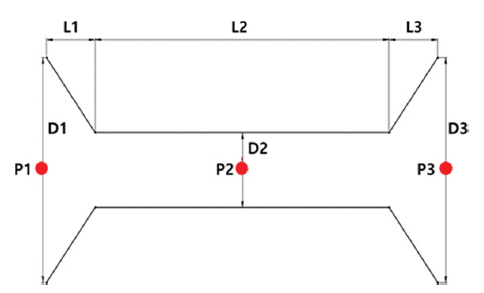
3차원 수치모의실험은 100초 동안 수행하였으며, 쉬라우드 형상 및 내부 유속을 재현하기 위하여 격자간격을 최소 0.1 m~ 최대 0.3 m의 가변격자로 구성하였으며, 계산영역은 길이 (x) = 46 m, 폭(y) = 15 m, 높이(z) = 10 m이다. 수치모의 실험은 수심 8 m, 유속 1 m/sec 조건에서 노즐(L1), 실린더(L2), 디퓨저(L3)의 연장 비율에 대하여 각각 실험을 수행하였으며, 외부직경(D1, D3)과 내부직경(D2) 비율에 대하여 실험을 수행하여 터빈이 위치하게 될 실린더 유속이 최대 유속으로 증폭되는 최적의 형상 조건을 도출하였다. 다음 Table 1은 수치모의 실험 개요이다.
Numerical simulation test for determination of shroud shape
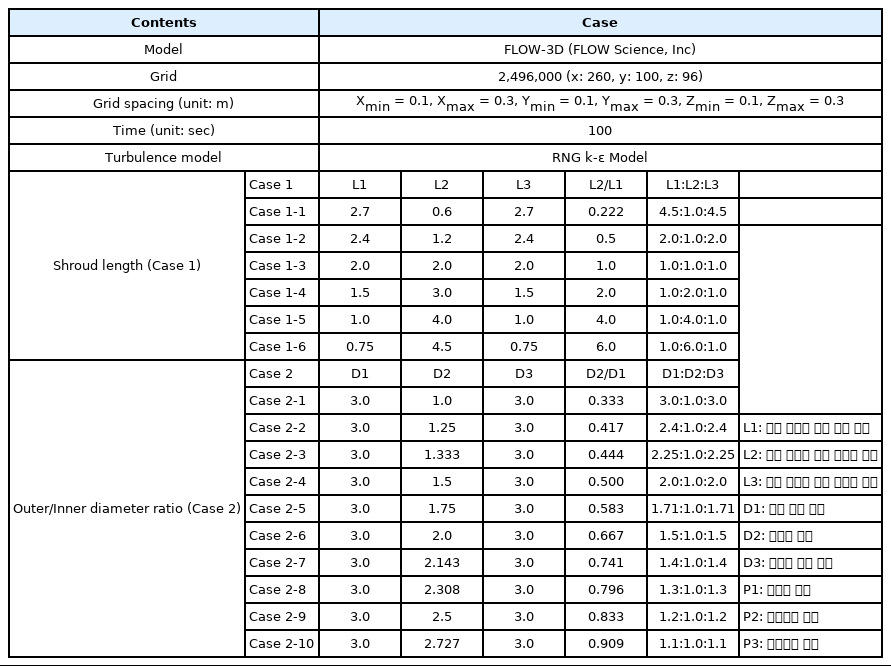
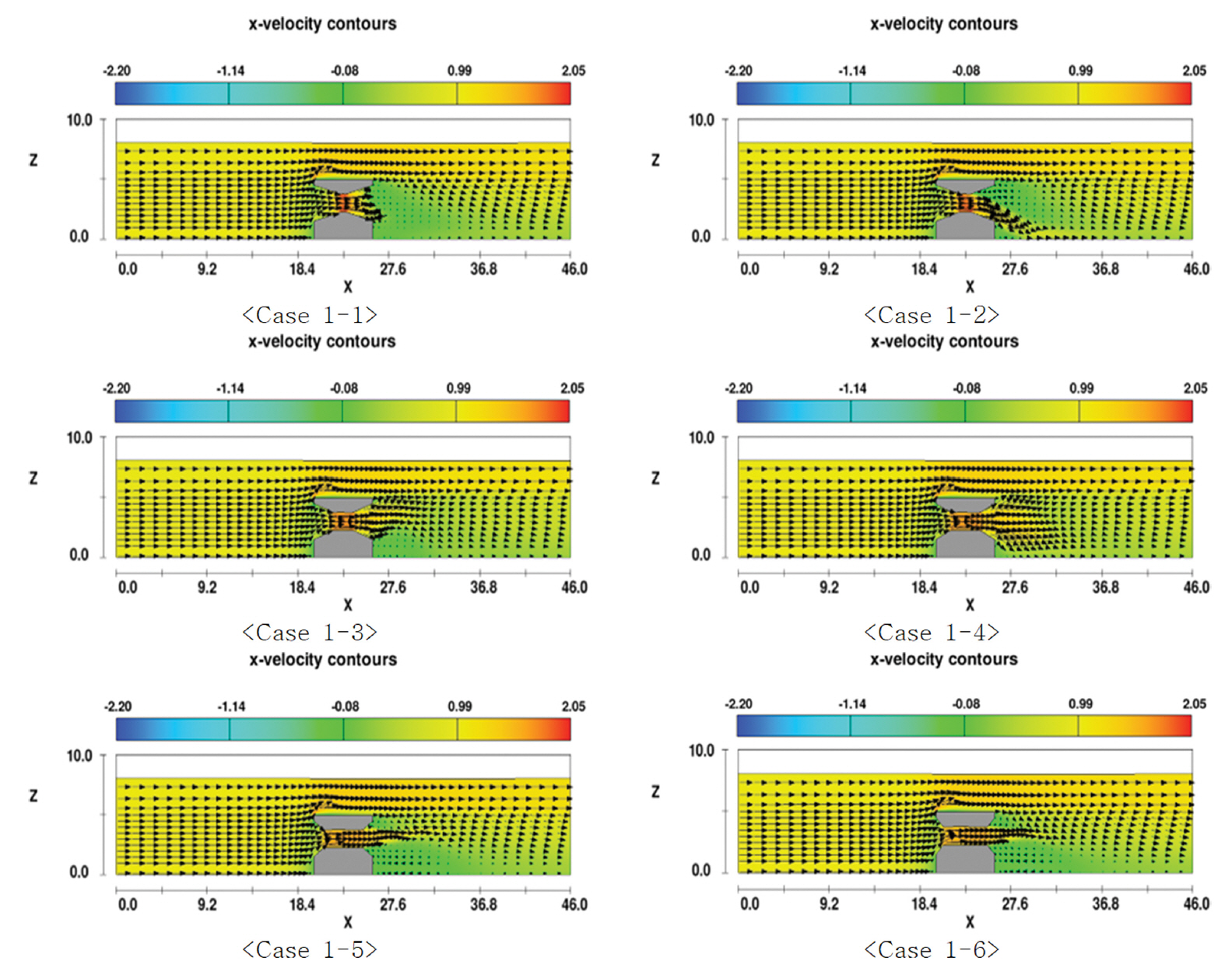
수평 2열 쉬라우드의 형상 최적화를 위하여 노즐(L1), 실린더(L2), 디퓨저(L3)의 길이 연장 변화에 따른 유동을 재현하였으며, 노즐부(P1), 실린더부(P2), 디퓨저부(P3)에서의 유속을 분석하여 P1과 P2의 유속 분포 및 최대 유속 비를 산정하였다. 초기 유속은 쉬라우드 형상에 따라 P1 지점에서 감소하는 경향을 보였고, 상대적으로 좁은 공간을 지난 후 P2 지점에서 유속이 증가하였으며, 디퓨저 출구 지점인 P3 지점 에서는 P2 지점에 비해 상대적으로 유속이 감소하는 것으로 나타났다. 각 지점에서 최대 유속은 L1, L2, L3의 길이 변화에 따라 다르게 나타났으며, P1에서 최대 유속은 0.54 m/sec ~ 0.67 m/sec, P2에서 최대 유속은 1.50 m/sec~1.73 m/sec, P3 에서 최대 유속은 0.15 m/sec~1.31 m/sec로 나타났다. P1과 P2 최대 유속 비는 2.23~3.16로 나타났으며, L1, L2, L3 길이의 연장비가 Case 1-2(2:1:2) 일 때 최대 유속비가 3.16으로 산정되었고, 이때 P2 최대 유속은 1.73 m/sec로 가장 높게 나타났다. 또한, 연장비 변화와 상관없이 모든 경우에서 쉬라우드 구조체 뒷면으로 후류가 나타나고 있으며, 이는 Lee et al.(2018)의 수치해석 결과와 유사한 변화 양상을 보였다.
Fig. 3은 L1, L2, L3 연장비율에 따라 쉬라우드 시스템 내실린더에서 최대 유속일 때, 흐름 분포를 보여주고 있으며, Fig. 4에 시간에 따른 지점별 유속 변화를 나타내었다. Fig. 4의 P1과 P2의 유속비를 살펴보면 Case 1-1과 1-2가 유속 증폭율이 비교적 높게 나타났으나 Case 1-2가 높은 유속 증폭율을 보이는 것으로 나타났다.
x-z plane velocity distributions for >Case 1-1>~>Case 1-6>.
Velocity changes at P1, P2, P3 and P1 to P2 ratio for >Case 1-1>~>Case 1-6>.
쉬라우드의 L1, L2, L3와 함께 노즐 직경(D1), 실린더 직경(D2), 디퓨터 직경(D3)의 크기는 유속 증폭을 결정하는 중요한 요소로서 수치모의 실험을 통해 직경변화에 따른 유속 변화를 분석하여 최적 직경비를 결정하였으며, 그 결과를 Fig. 5에 나타내었다.
Velocity changes at P1, P2, P3 and P1/P2 ratio for <Case 2-1>~<Case 2-10>.
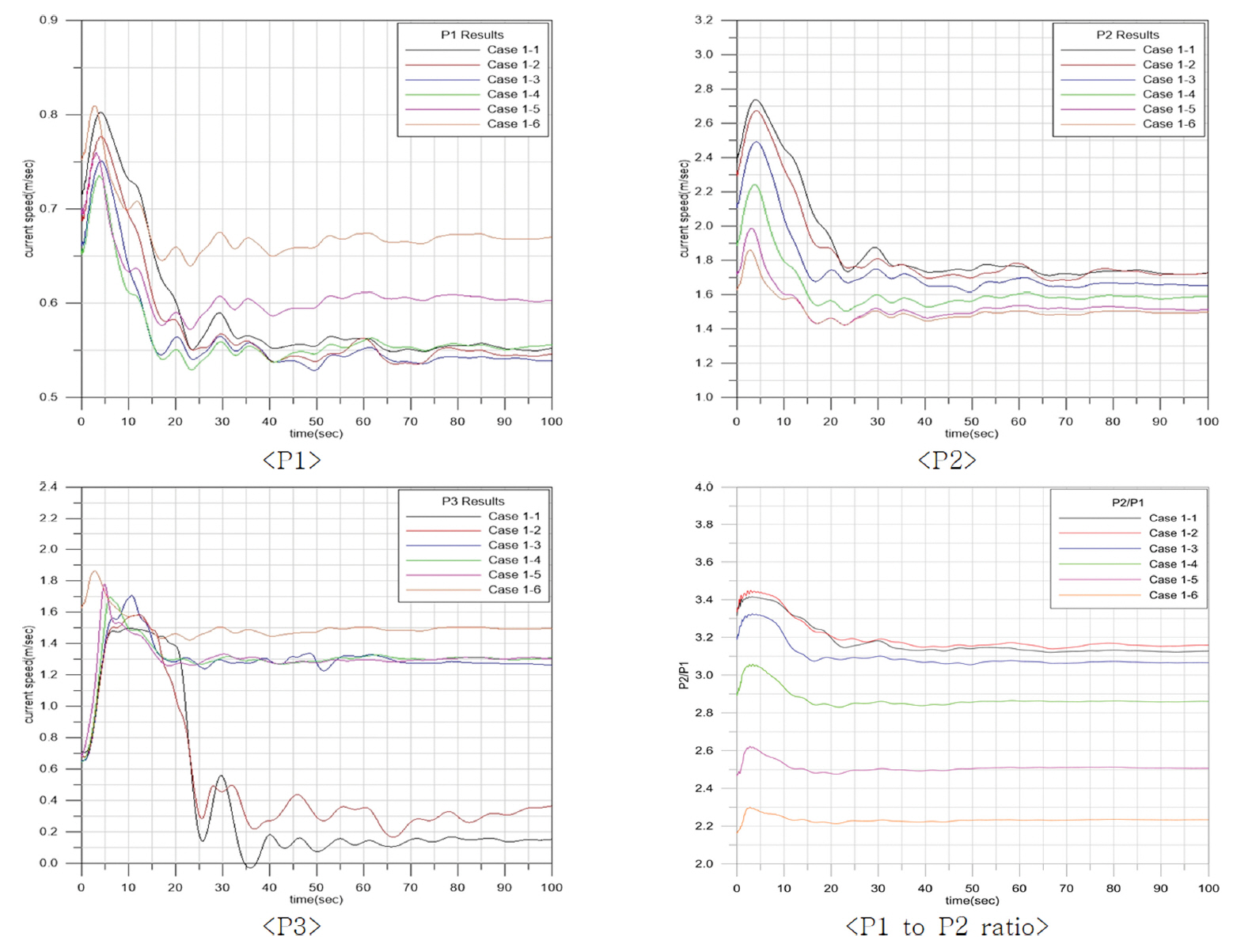
각 지점에서 최대 유속은 D1, D2, D3의 직경 변화에 따라 다르게 나타났으며, P1 지점에서 최대 유속은 0.34 m/sec ~ 1.06 m/sec, P2 지점에서 최대 유속은 1.60 m/sec~2.07 m/sec, P3 지점에서 최대 유속은 0.04 m/sec~1.26 m/sec로 나타났다. 유속 증폭은 Case 2-1에서 5.38로 큰 증폭률을 보였으나, 급속한 D2의 직경 감소로 P1에서의 유속이 가장 낮게 나타났다. 또한, Case2-9와 Case2-10에서 유속 증가율이 급격이 감소하는 것은 D1과 D2의 차이가 매우 작아짐에 따라 발생하는 현상으로 사료되며, 쉬라우드 형상체의 단면적의 적정비는 최소 1.3배 이상에서 발전이 가능함을 확인할 수 있다.
수치모의 실험에서 D2/D1이 증가할수록 P1의 유속이 증가하였고, P2에서의 유속은 Case 2-6과 Case 2-8에서 가장 큰 유속을 보였으며, 이에 본 연구에서는 L1, L2, L3의 연장비를 Case 1-2(2:1:2), 직경비를 Case 2-6(1.5:1:1.5)를 최적 형상 치수로 결정하여 이를 바탕으로 수리모형을 제작하였다.
3. 수리모형 실험
3.1 수리모형 제작
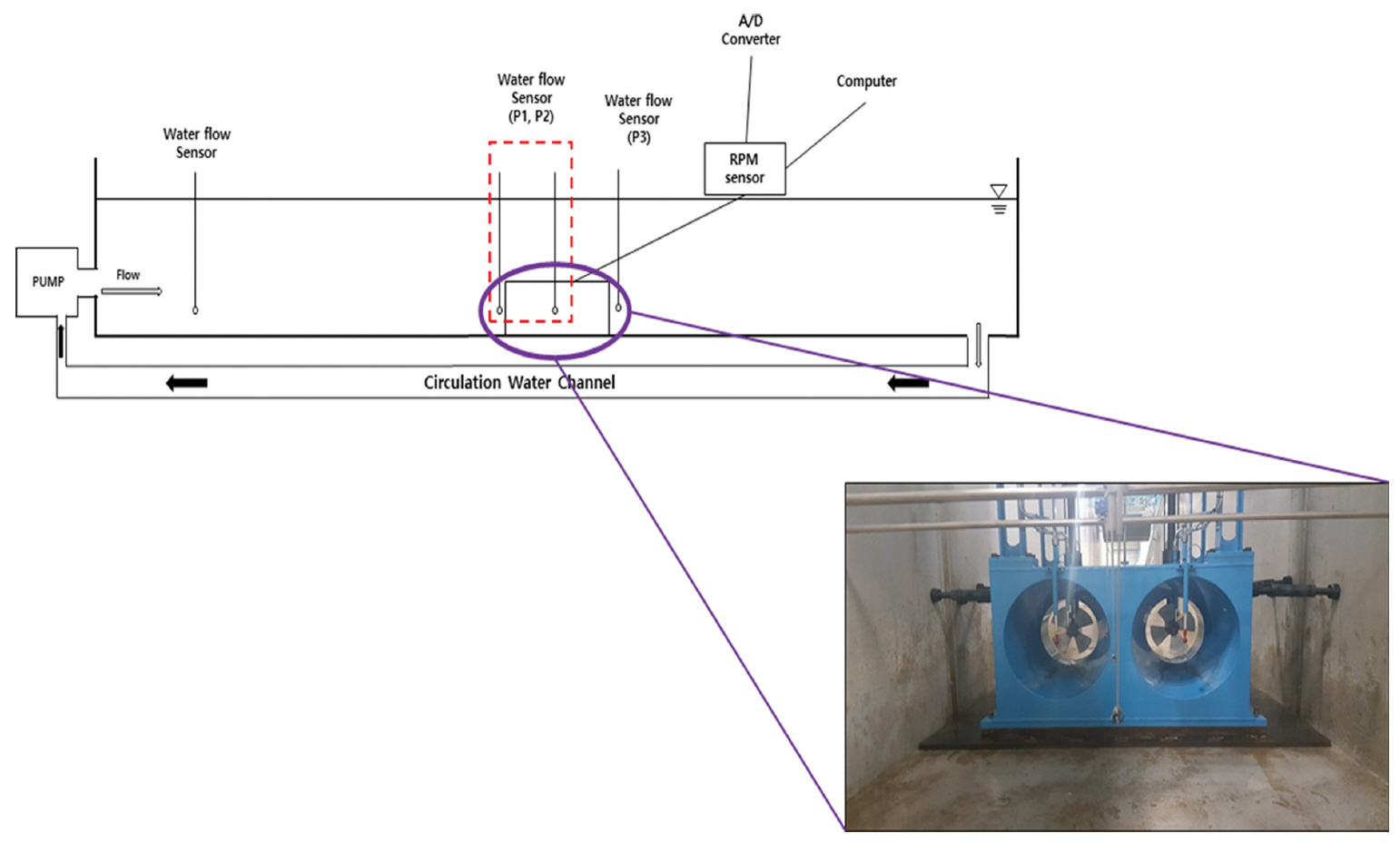
본 연구에서는 수치모의 실험 결과를 바탕으로 Fig. 6과 같이 수평배열형 쉬라우드 조류발전 발전체를 제작하였다. 수리모형 실험은 1/6로 축소모형 실험으로 진행하였으며, D1은 0.5 m, D2는 0.33 m, D3는 0.5 m로 제작하였다. 또한 좌측과 우측의 유입구 간격은 0.1 m, 전면부 폭은 1.26 m, 높이는 0.7 m이다. 쉬라우드 주흐름 방향의 길이는 총 1 m이며, L1과 L3은 0.4 m, L2는 0.2 m이다.
Front view (left) and side view (right) of the shroud tidal current energy converter.
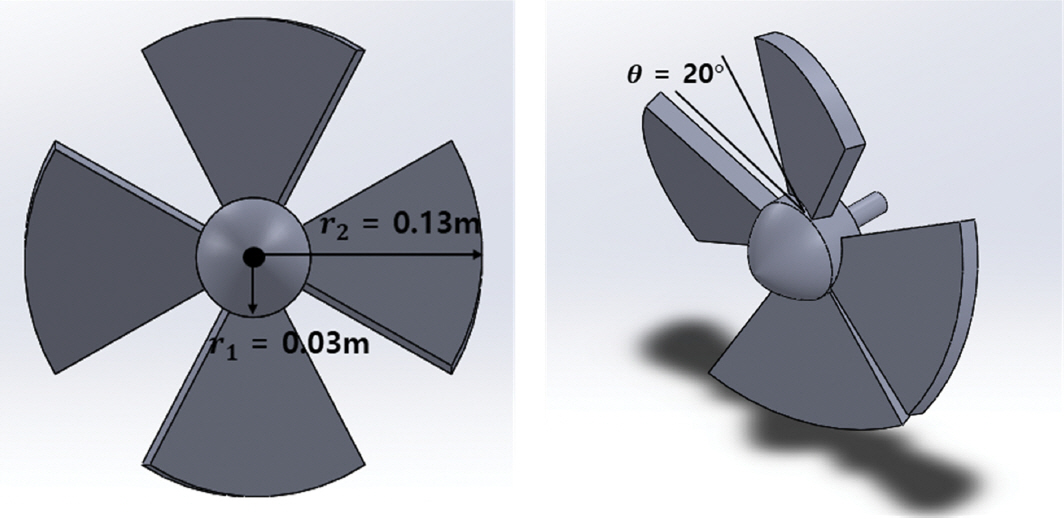
또한 쉬라우드 조류발전 장치의 성능평가를 위해 기본 블레이드(conventional blade)를 제작하여 실험을 수행하였다 (Fig. 7 참조). 조류발전 블레이드 수는 총 4개이며, 조류발전 블레이드 직경은 0.265 m, 피치각은 20°이다. 블레이드 및 시험 장치에 대한 형상 치수는 Table 2에 정리하였다.
Front view (left) and side view (right) of the rotor blade.
Specification of a shroud system and blade
3.2 실험 조건
수평 2열 쉬라우드 시스템 내 유속 변화 및 성능평가를 위해서 전남대학교 해안항만실험센터에 설치된 대형 조파 수로에서 수리모형실험을 수행하였다. 수로의 전체 길이는 100 m, 폭 2 m, 높이 3 m이며, 발전장치의 거동을 방지하기 위해 바닥에 고정대와 양측에 지지대를 설치하였다. 단면수로는 전기 서보 피스톤식 조파기와 대용량 펌프 및 회류수조가 설치되어 있으며, 회류수조의 흐름을 안정화 시킬 수 있는 허니컴과 누름판이 수조 전면부에 설치되어 있고 독취된 계측자료를 바탕으로 유속 제어가 가능하다.
실험에 적용된 유속은 0.84~1.04 m/sec 유속이며, 계측은 Fig. 8과 같이 수조 가장 앞쪽, 노즐부 유입부 전면, 실린더 내부, 유출부에 각각 유속계를 설치하여 총 4개 지점에서 유속을 측정하였다. 또한, 블레이드 후면에는 샤프트를 이용하여 토크, RPM 및 전력 측정 장치를 설치하였다.
Schematic profile and picture of hydraulic experiments.
유속계는 정확도 ± 5%인 Schiltknecht swiss사에서 개발한 Mini Air 64이며, RPM 계측장치는 검출거리가 4 mm까지 정밀 계측이 가능한 장비를 사용하였으며, 시스템 상단부분까지 연결한 후, 수면 밖으로 노출시켜 설치하였다.
3.3 성능평가
조류는 해수의 흐름이므로 조류가 갖는 운동에너지를 모두 추출해 내는 것은 조류발전장치의 후방 흐름이 완전히 정지하는 것을 의미하므로 이는 현실적으로 불가능하다. 따라서 조류발전장치를 움직일 수 있는 기계적 에너지는 조류가 가진 운동에너지를 사용해야만 얻을 수 있으므로 이를 효율적으로 추출해 내는 것이 매우 중요하다. 조류발전장치의 성능 평가 요소로는 출력계수(Cp, power coefficient)와 주속비(TSR, tip speed ratio)가 있다. 조류발전장치를 이용하여 조류로부터 추출해 낼 수 있는 출력 비율을 출력계수라고 하며 조류발전장치의 성능을 평가하는 중요한 지표가 된다. 또한 주속비는 블레이드 선단속도와 조류속의 비로 정의되며, 조류터빈의 블레이드 선단속도(tip speed)란 블레이드가 회전할 때 블레이드 끝이 움직이는 속도로서 블레이드 길이가 증가 함에 따라 선속도가 증가한다. 출력계수와 주속비는 식(1)~(2) 와 같이 산출할 수 있다.
여기서 ρ는 유체의 밀도(kg/m3), V는 유속(m/s), T는 토크 (Nm), w는 각속도(rad/s), r은 로터의 반경(m), A는 실린더의 단면적(m2)을 나타낸다.
4. 수리모형실험 결과
4.1 계측 결과
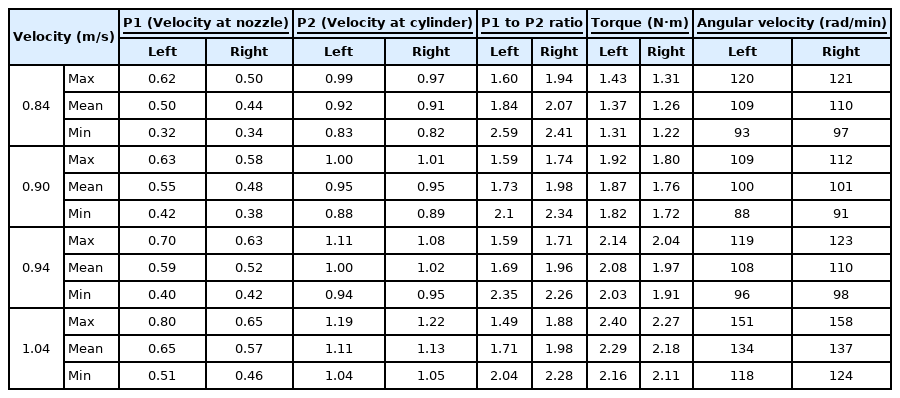
본 연구에서는 초기 유속 조건에 따른 조류발전용 쉬라우드 시스템 내 유속 변화와 성능을 파악하기 위해 블레이드의 토크 및 각속도를 계측하였으며, 계측은 초기 유속이 안정화된 이후, 1 Hz 간격으로 측정하였다. 실험조건은 유속조건에 따라 0.84 m/sec, 0.90 m/sec, 0.94 m/sec, 1.04 m/sec 총 4가지이며, 각 케이스 별 실험 결과를 Table 3에 정리하였다. 그결과, 블레이드 토크 및 각속도는 초기유속 조건과 비례하는 경향을 보이고 있었으며, 토크의 범위는 좌측 쉬라우드 시스템에서에서 1.37~2.29 N‧m, 우측 쉬라우드 시스템에서는 1.26~ 2.18 N‧m로 계측되었으며, 각속도는 좌측의 경우, 109~134 rad/min, 우측의 경우, 110~131 rad/min로 양측이 비교적 유사하게 계측되었다.
Flow velocity ratio measurement results in left and right shroud systems
한편, P1 지점에서의 유속을 계측한 결과, 좌측의 평균 유속 범위는 0.50~0.65 m/sec, 우측은 0.44~0.57 m/sec로 약 10% 내외의 차이를 보였으며, P2 지점에서 좌측의 평균 유속 범위는 0.92~1.11 m/sec, 우측은 0.91~1.13로 매우 유사하게 나타났다. 또한, 유속 증가율의 평균 범위는 좌측의 경우 1.69~1.84, 우측의 경우 1.96~2.07로서 우측에서 약 10~12% 더 증가하는 것으로 나타났다. 또한 초기 유속 조건이 가장 낮은 0.84 m/sec인 경우 가장 높은 유속 증가율을 보였다. 한편, P2/P1을 나타내는 유속 증가율은 수치해석과 수리모형실험(1.04 m/s)의 결과가 약 2.0~2.2배로 유사하게 났지만, 수치 해석에서 계산된 P1, P2의 유속값에 비해 수리모형실험을 통해 계측된 유속값은 절반 수준으로 나타났다. 이러한 차이는 블레이드 설치로 인한 실린더부의 단면적 차이로 판단된다.
4.2 블레이드 성능 및 시스템 효율 평가
수평 2열 쉬라우드 시스템 내 유속, 토크 및 RPM을 계측한 후, 이를 이용하여 TSR-Cp 곡선을 다음 Fig. 9에 제시하였다. 유속조건 0.84 m/s의 경우, 좌측 쉬라우드 시스템의 출력계수는 TSR이 약 2일 때, 0.33으로 높게 나타났으며, 우측 쉬라우드 시스템은 TSR이 1.87일 때 0.31로 가장 높게 나타났다. 유속조건 0.90 m/s의 경우, 좌측과 우측의 출력계수, Cp는 TSR이 1.75와 1.73일 때 0.33과 0.34로 나타났다. 또한 0.94 m/s의 경우, 좌측과 우측의 최대 출력 계수는 1.75와 2.17일 때 0.32와 0.37로 추정되었고, 실험값으로는 TSR이 1.75와 1.6일 때 0.32와 0.33의 출력계수값을 보였다. 마지막으로 유속조건 1.04 m/s의 경우, 좌측과 우측의 출력 계수는 TSR이 1.98과 1.85일 때 0.34와 0.32로 최댓값을 보였다. 본 연구에서 실험한 수평 2열 쉬라우드 시스템은 TSR이 1.75~2의 조건에서 0.32~0.34의 출력 성능을 보이는 것으로 나타났으며, 낮은 유속 조건에서도 출력 성능을 확보할 수 있는 것으로 나타났다.
TSR (λ) and power coefficient (Cp) curves.
4. 결론
수평 2열 조류발전 쉬라우드 시스템은 단일 조류발전 쉬라우드 시스템에 비해 공사비와 발전량 측면에서 장점을 가지고 있다. 그러나 단일시스템 비해 수평배열에 따른 상호 간섭으로 인한 성능저하가 발생할 수 있어 성능평가가 사전에 수행되어져야 한다. 따라서 본 연구에서는 수치모의 실험과 수리모형 실험을 통해 수평 2열 쉬라우드 시스템의 성능평가를 수행하였으며 다음과 같은 결론을 도출하였다.
1) 수평 2열 쉬라우드 시스템의 최적 형상을 설계하기 위해 노즐, 실린더, 디퓨저의 길이 연장 변화 및 직경을 3차원 범용 유동해석 프로그램인 Flow-3D를 이용하여 결정하였다. 그 결과, 노즐, 실린더, 디퓨저의 연장비는 유속 증가율이 가장 높은 Case 1-2(2:1:2)를 선정하였으며, 직경비는 실린더에서 가장 높은 유속을 보이는 Case 2-6(1.5:1:1.5)을 최적 형상 치수로 결정하였다.
2) 쉬라우드 시스템의 P1, P2 지점에서 계측된 유속을 이용하여 유속 증가율을 산정한 결과, 초기유속 조건 0.84 m/sec에서 좌측과 우측 시스템이 각각 1.84, 2.07배로 가장 높은 변화율을 보이고 있었으며, 수리모형실험과 수치해석을 통해 산정된 P1, P2의 유속 증가율은 약 2배 내‧외로 유사한 비율을 보이고 있었다. 한편, 블레이드의 토크 및 각속도는 좌측과 우측이 유사한 범위 내에서 계측됐으며, 초기유속과 비례하는 경향을 보였다.
3) 특정 유속에서 로터에 의하여 발생하는 출력은 블레이드 끝단과 유속에 의해 영향을 받게 된다. 또한 출력계수는 주속비에 따라 달라지게 되는데 결국 최대 출력이 나타나는 주속비가 최적 주속비가 된다. 본 수평배열형 쉬라우드 시스 템의 최적 주속비를 결정하기 위해 실험데이터를 이용하여 Fig. 9와 같이 TSR-Cp 곡선을 나타내었고, 최적 주속비는 1.75~2로 나타났다.
Acknowledgements
본 논문은 해양수산부 해양산업 성장 기술개발 사업인 “항만시설물 전력공급용 1 KW급 조력발전장치 개발(과제번호: 20210224)” 과제의 일환으로 수행되었습니다. 연구지원에 감사드립니다.
