2.1 Data analysis

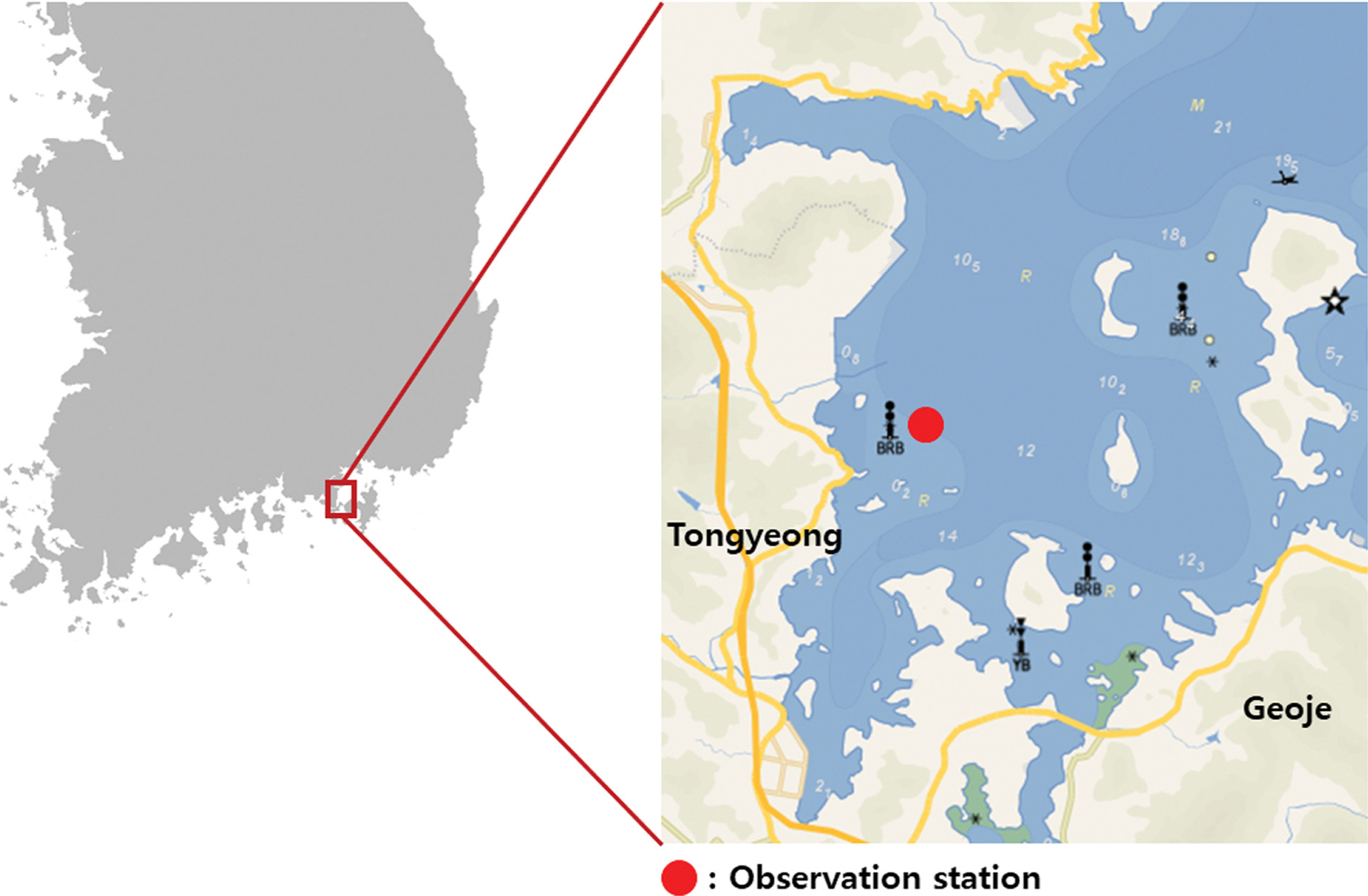
본 연구에서는 진해만 내에 있는 국립수산과학원의 ‘실시간 해양환경 어장정보시스템’에서 제공하는 ‘통영 안정’ 정점(34.9395° N, 128.4456°E) 자료를 취득하여 사용하였다(Fig. 1; NIFS, 2022). 항목은 표·저층의 수온, 염분, 탁도, Chl.a, 용존산소포화도(DO-S), 용존산소농도이며, 42개월간(2015.07.01.~2018.12.31.) 1시간 간격으로 관측되었다. 결측치(missing)와 이상치(outlier)는 선형보간하여 자료의 약 70%를 기계학습에 이용하였고 나머지 30%를 모형 검증에 사용하였다. 각 항목의 평균, 표준편차, 최대, 최소, 중앙값을 Table 1에 제시하였다. 저층 DO 농도를 종속변수, 그 외 항목들을 독립변수로 하여 다중선형회귀 및 t-검정(t-test)를 진행하여 그 결과를 Table 2에 나타내었으며, DO 농도와 각 항목의 상관분석(correlation analysis)을 진행하여 그 결과를 Table 3에 나타내었다. 선형회귀의 t-test는 회귀예측에서 예측변수를 선별하는 방법의 하나로 ‘독립변수의 계수(또는 가중치)는 0이다’라는 귀무가설 검정을 진행한다. 검정 결과 그 확률(p-value)이 0.05 이하일 경우 가설은 기각되며 해당 항목은 예측변수로 선별된다. t-test 결과 모든 항목의 p-value가 0.05 이하로 나타나 모두 예측변수로 선별하였다. 상관분석에서는 상관계수(correlation coefficient, R)의 절대값(|R|)에 따라 두 변수의 상관성을 평가할 수 있다. 항목 중 수온이 DO 농도와 가장 높은 상관성을 보였으며, 탁도와 Chl.a 농도는 상대적으로 낮은 상관성을 보였다.

Fig. 1.

Location of observation station in Jinhae Bay.

Table 1.

The mean, standard deviation, min, max, median of features

Table 2.

The t-test results of linear regression between features and bottom DO concentration

Table 3.

The |R| values between DO concentration and features

LSTM을 이용한 DO 농도의 장·단기 예측에는 전체 자료 중 2017.01.01.~2018.07.01. 자료를 사용하였다. 시간 예측에는 기존 관측자료를 사용하였으며, 일 예측에는 자료를 일 평균하여 사용하였다. 자료의 수(Data point)는 시간 예측과 일 예측 각각 n_hour = 13,101, n_day = 546이다. 자료는 평균=0, 표준편차 = 1로 표준화(standardization)하였다.

결정 트리를 이용한 빈산소수괴 발생 예측에는 전체 자료(2015.07.01.~2018.12.31.)를 일 평균하여 일 예측만을 진행하였다(n = 1280). DO 농도는 3 mg L^-1를 기준으로 빈산소수괴 발생(HWM) 및 미발생(nonHWM)으로 범주화(categorical)하여 반응변수(response variable)로 사용하였다. 단, 전체 자료 중 빈산소수괴 발생 사례와 미발생 사례의 데이터 포인트는 각각 n_HWM = 97, n_nonHWM = 1183으로 데이터의 불균형이 존재한다. 이 불균형을 해결하기 위해 빈산소수괴 발생 사례에 대한 데이터 증식(augmentation)을 진행하여 미발생 사례와 데이터 수를 일치시켰다. 데이터 증식은 예측변수(predictor)인 수온, 염분, 탁도, Chl.a, DO-S에 -0.1~0.1 사이의 무작위 잡음을 추가하여 수행하였다.

2.2 LSTM

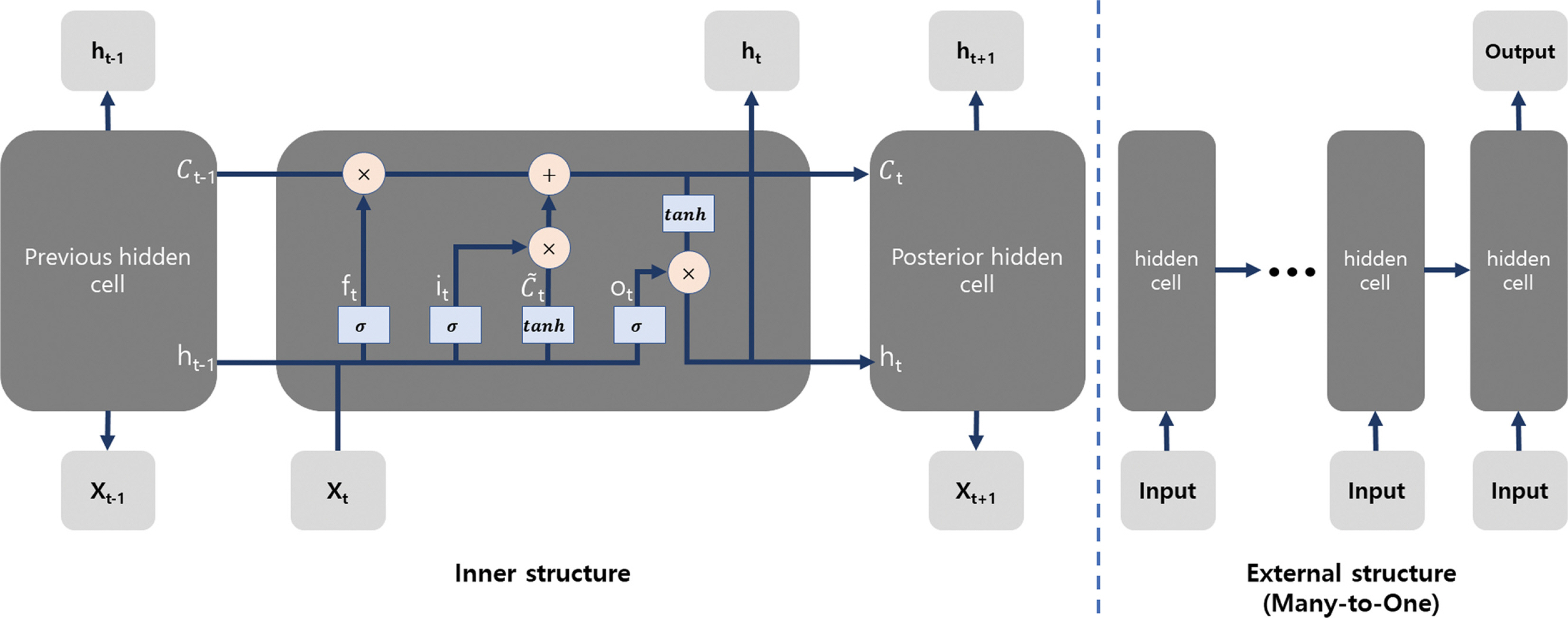
Long Short-Term Memory(LSTM)은 Recurrent Neural Network(RNN) 계열의 모형으로 기존 인공신경망 모형과 달리 Hidden cell간의 순환구조를 이루고 있다(Fig. 2). 이러한 순환구조로 LSTM은 sequence data 처리에 적합하다고 평가받는다(Dupond, 2019; Tealab, 2018). LSTM의 하이퍼파라미터(hyperparameter)는 Epoch, Number of hidden node, sequence length가 있다. 하이퍼파라미터의 값에 따라 정확도와 필요비용이 결정되기 때문에 비용과 성능을 고려하여 하이퍼파라미터를 최적화(optimization)하는 것이 중요하다. LSTM은 입력자료의 길이(sequence length)와 출력의 개수에 따라 다음과 같은 4가지 구조를 갖는다. one-to-one, one-tomany, many-to-many 그리고 many-to-one. 본 연구의 LSTM 모형은 sequence length가 1인 경우를 제외하고 many-to-one의 구조를 갖는다. 즉, 본 연구에서는 과거 일정 기간의 시계열 자료를 입력받아 수일 후의 DO 농도를 예측하였으며, case study를 통해 적합한 하이퍼파라미터 조건을 찾는 것을 목적으로 한다. LSTM의 각 gate와 state에 대한 식은 아래와 같다.

Fig. 2.

The inner and external structure of LSTM.

여기서, f_t는 forget gate, i_t는 input gate, o_t는 output gate, C_t는 Cell state, h_t는 hidden state, W는 가중치(weight), b는 편향(bias)이다.

2.3 Decision tree

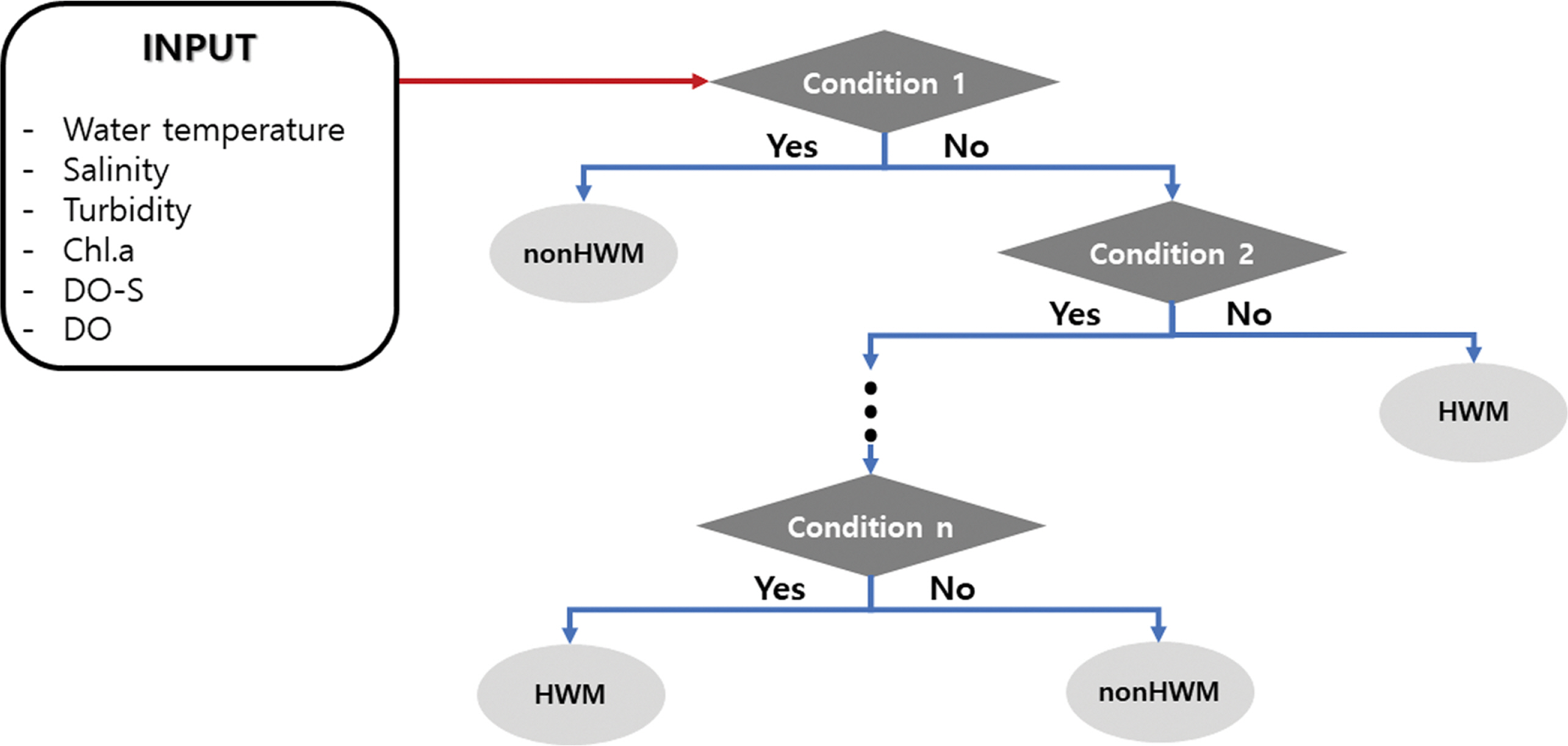
결정 트리(Decision tree)는 기계학습 기반의 데이터 분류(classification) 기법이다. 결정 트리는 나무 형태의 구조로 뿌리 노드(root node)로부터 분기된 노드들이 모여 의사결정나무를 형성한다. 각각의 노드는 분기 조건을 가지며 최종적으로 말단 노드(leaf node)에서 객체의 클래스가 결정된다. 각 분기마다 불순도가 감소하는 방향으로 노드를 형성하여 의사결정나무를 완성한다. 이후 모형의 과대적합(overfitting)을 방지하기 위해 부적절한 분기 조건을 갖는 노드를 제거하는 가지치기 과정을 거친다. 결정 트리에 대한 구조를 Fig. 3에 나타내었다.

Fig. 3.

The structure of decision tree.

2.4 Experiment model condition

LSTM 모형을 이용한 DO 농도의 장·단기 예측 연구에서는 모형의 하이퍼파라미터에 따른 예측 정확도를 비교하였다. 하이퍼파라미터 항목으로는 LSTM 모형의 number of Hidden node, Epoch, Sequence length이다. 예측 시간 간격은 시간 예측에서 1, 6, 12, 24, 36, 48 hour, 일 예측에서 1, 3, 6, 10, 15, 30 day를 고려하였다. 위 실험을 통해 DO 농도의 장·단기 예측에 적합한 LSTM 모형의 하이퍼파라미터 값을 찾고자 하였다.

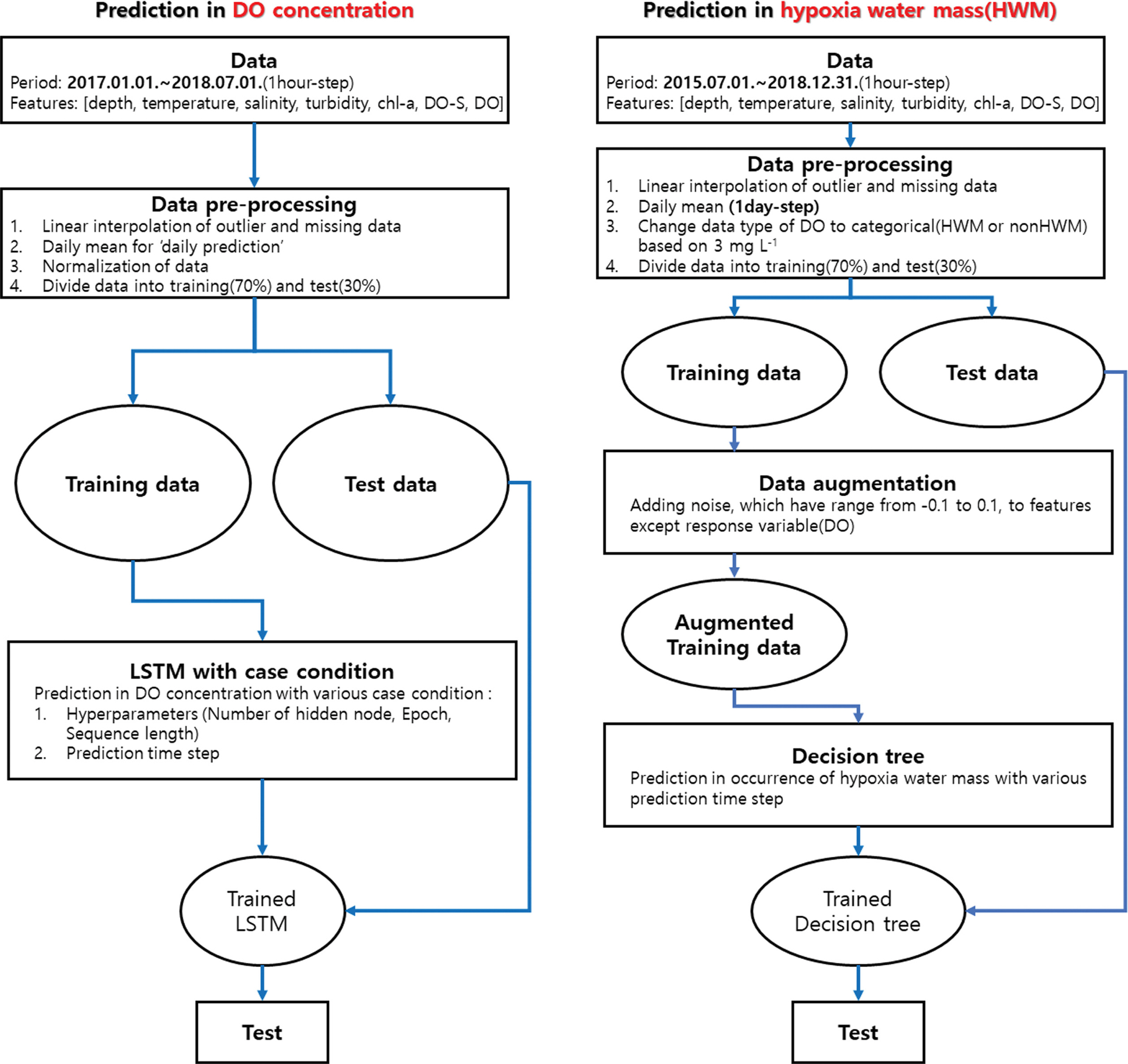
결정 트리를 이용한 빈산소수괴 발생 예측에서는 일 예측만을 진행하였으며, 예측 시간 간격은 1, 3, 6, 10, 15, 30 day를 고려하였다. 트리의 분기 조건에는 지니 지수(Gini index)를 사용하였으며, 예측 결과는 빈산소수괴 발생(HWM)과 미발생(nonHWM) 2가지 범주형 변수로 표현하였다. 본 연구에서 고려된 LSTM 모형 조건과 결정 트리 모형 조건을 Table 4에 제시하였다. 연구의 진행도를 Fig. 4에 요약하여 나타내었다.

Table 4.

Experiment model condition

Fig. 4.

The flowchart of prediction in DO concentration and hypoxia water mass.

3.1 Prediction in DO concentration based on LSTM

본 연구에서는 진해만 DO 농도의 장·단기 예측에 적합한 LSTM 모형의 하이퍼파라미터값을 찾기 위한 case study를 진행하였다. 여러 하이퍼파라미터값 조건에서 DO 농도를 장·단기 예측하였으며, 그 결과를 결정계수(R²) 값으로 비교·평가하였다. Hidden node의 개수에 따른 예측 정확도를 Fig. 5에 나타내었으며, Sequence length와 Epoch에 따른 예측 정확도를 heat map으로 Fig. 6과 Fig. 7에 나타내었다. 그 이후에 모형의 시계열 예측성을 평가하기 위해 [1 hour, 48 hour]과 [1 day, 30 day] 예측 시간 간격에 대한 예측값과 관측값의 시계열 비교 그래프를 Fig. 8에 나타내었다.

Fig. 5.

DO prediction result R² values with respect to number of hidden node.

Fig. 6.

DO prediction R² values with respect to Epoch and Sequence length in hourly prediction.

Fig. 7.

DO prediction R² values with respect to Epoch and Sequence length in daily prediction.

Fig. 8.

Time series of observed (line) and predicted (dotted line) DO concentration.

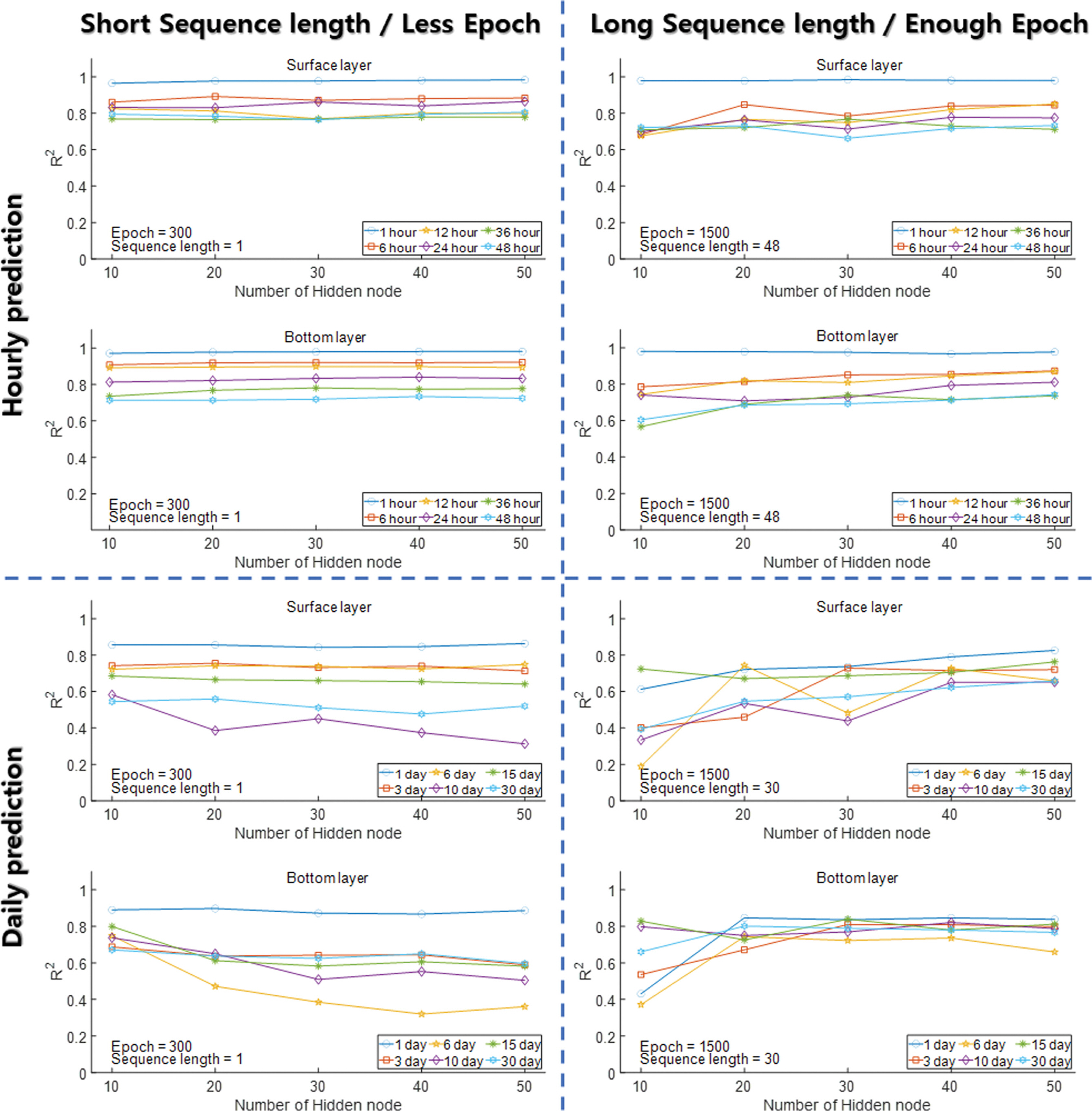
Short Sequence length, Less Epoch과 Long Sequence length, Enough Epoch 조건에서 Hidden node의 개수에 따른 예측 정확도를 R² 값으로 나타내었다(Fig. 5). Short Sequence length, Less Epoch 조건의 시간 예측에서 Hidden node의 개수에 따른 정확도 차이는 나타나지 않았다. 일 예측에서는 Hidden node의 개수가 많아질수록 R² 값은 감소하는 결과를 보였다. 저층 DO 농도 예측에서 Hidden node = 10일 때 6 day와 10 day 예측의 R² 값은 각각 0.75, 0.74에서 Hidden node가 증가함에 따라 0.36, 0.50으로 감소하였다. 이는 Hidden node의 개수 증가로 모형의 복잡도가 증가하면서 Epoch = 300 조건에서 모형이 과소적합(Underfitting)된 것으로 판단된다. 반면에 Long Sequence length, Enough Epoch 조건의 일 예측에서는 Hidden node의 개수가 많아질수록 R² 값은 증가하는 결과를 보였다. 표층 DO 농도 예측에서 Hidden node = 10일 때 모든 예측 시간 간격의 평균 R² 값은 0.44에서 Hidden node가 50으로 증가함에 따라 0.71로 증가하였으며, 저층 DO 농도 예측에서도 평균 R² 값이 0.60에서 0.78로 증가하는 결과를 보였다. 이는 Hidden node = 10일 때 Epoch = 1500 조건에서 과대적합(Overfitting)이 발생한 것으로 판단되며, Hidden node = 50에서 모형의 복잡도가 증가함에 따라 요구되는 Epoch도 증가하여 과대적합이 해소된 것으로 판단된다.

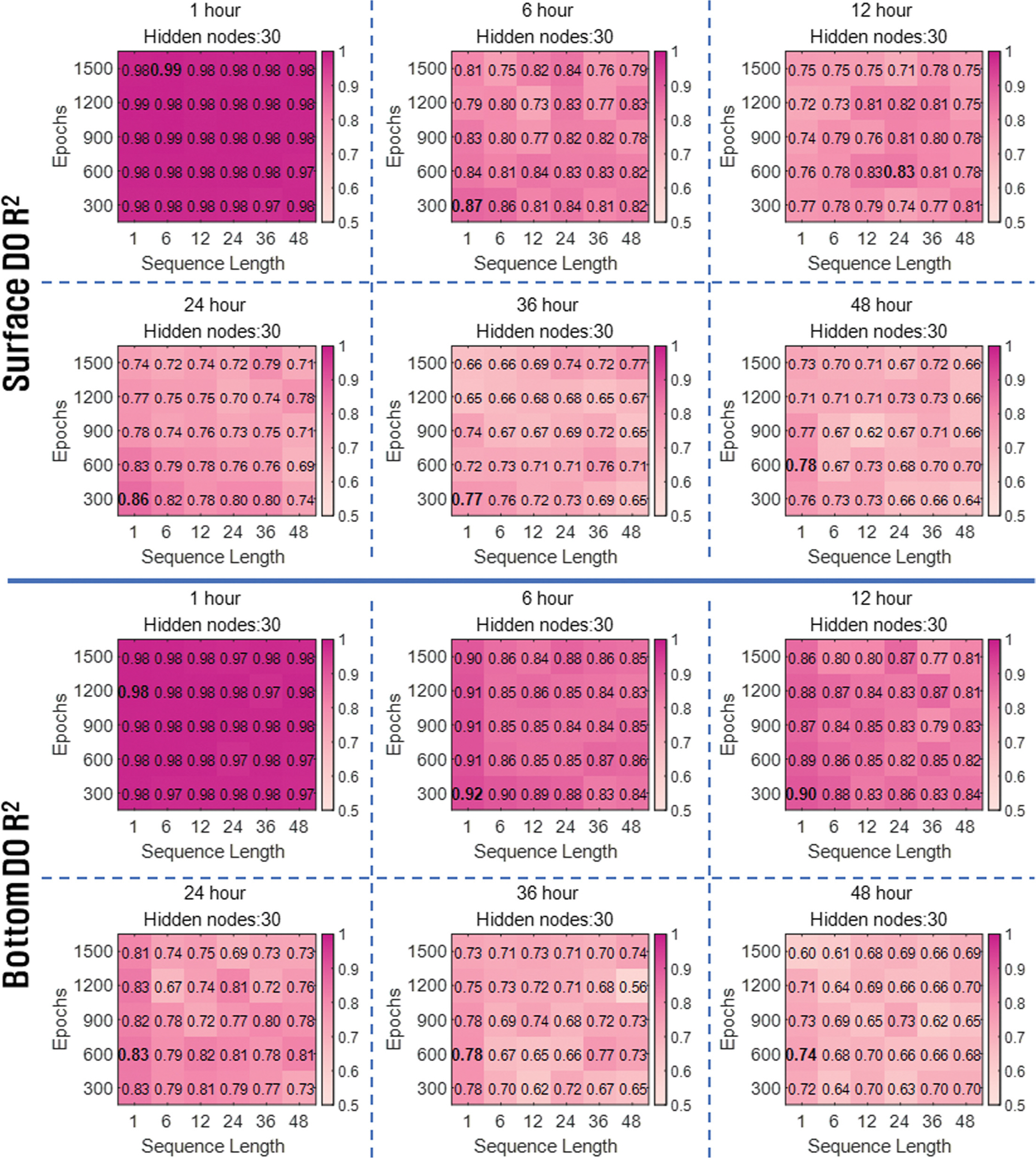
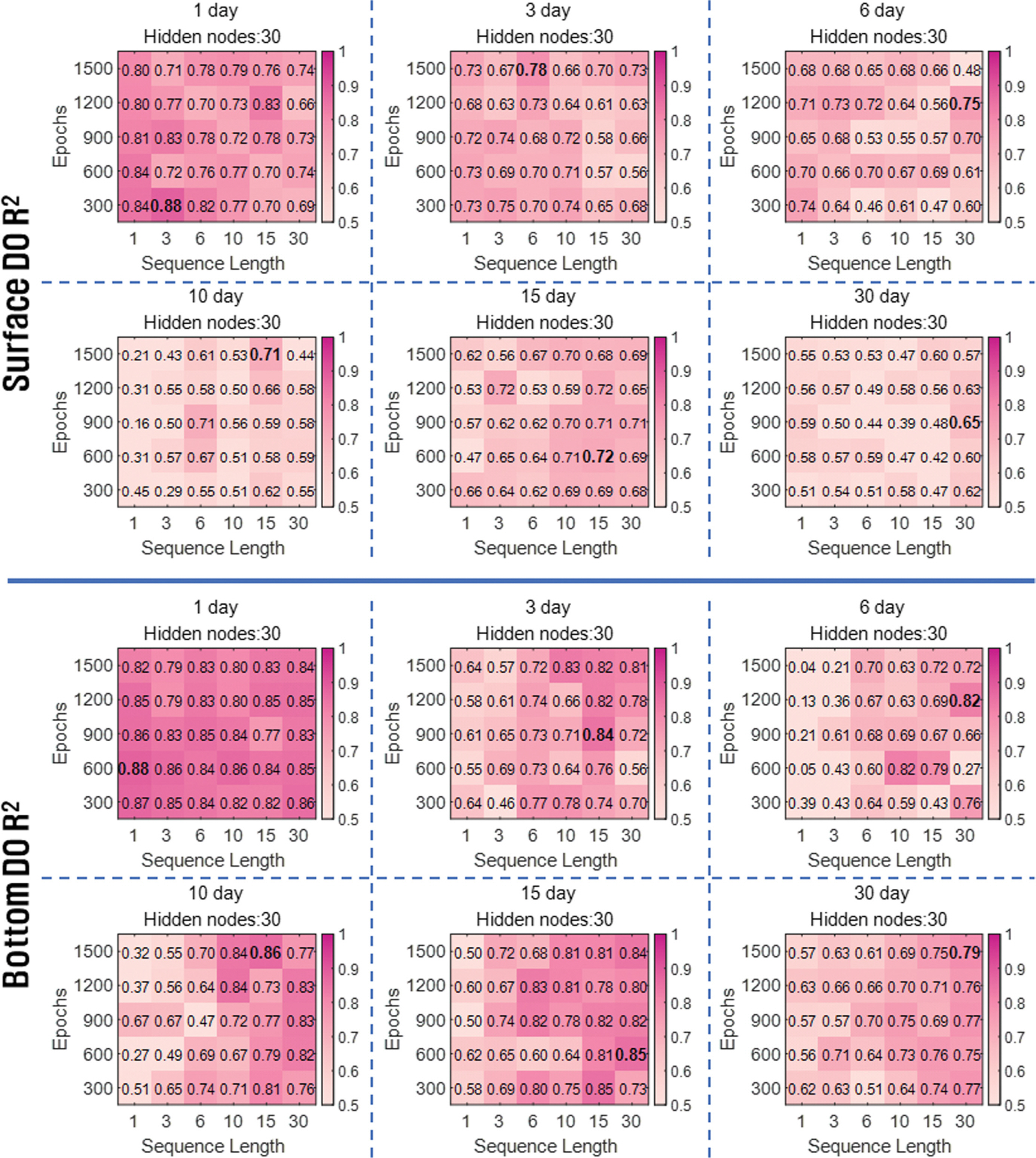
Sequence length와 Epoch에 따른 예측 정확도를 비교하기 위해 Hidden node의 수를 30으로 고정하고 R² 값을 heat map으로 나타내었다(Fig. 6; Fig. 7). 시간 예측 결과, 표·저층 DO 농도의 1 hour 예측에서 하이퍼파라미터 조건에 따른 R² 값의 유의미한 차이는 보이지 않았다. Epoch에 따른 시간 예측 정확도는 Epoch = 300 또는 Epoch = 600의 낮은 Epoch 조건에서 상대적으로 높은 R² 값을 보였다. 낮은 Epoch 조건에서 상대적으로 높은 R² 값을 보인 것은 900 이상의 Epoch 조건에서 과대적합이 발생한 것으로 판단된다. Sequence length에 따른 예측 정확도는 표층의 12 hour 예측을 제외하고 표·저층 예측의 모든 예측 시간 간격에서 Sequence length = 1일 때 가장 높은 R² 값을 보였다. Sequence length = 1에서 높은 R² 값을 보인 것은 상대적으로 짧은 예측 시간 간격에 의한 결과로 판단된다. 시간 예측에서 고려된 예측 시간 간격은 최대 48 hour로 DO 농도의 시계열 변화 특성이 나타나지 않아 긴 Sequence length 조건에서 낮은 R² 값을 보인 것으로 판단된다. 예측 시간 간격이 1 day에서 최대 30 day까지 고려된 일 예측에서는 예측 시간 간격이 길어짐에 따라 긴 Sequence length 조건에서 상대적으로 높은 R² 값을 보였다. 저층 DO 농도의 1 day 예측에서 R²의 최댓값은 0.88로 Sequence length = 1 조건에서 나타났다. 이후 3 day 예측에서는 Sequence length = 15 조건에서 0.84의 R² 최댓값이 나타났으며, 15 day와 30 day 예측에서는 Sequence length = 30 조건에서 각각 0.85, 0.79의 R² 최댓값을 보였다. 표층 DO 농도 예측에서도 R²의 최댓값이 나타난 Sequence length 조건은 [1, 3, 6, 10, 15, 30] day 예측에서 각각 [3, 6, 30, 15, 15, 30]으로 나타나 예측 시간 간격이 길어질수록 긴 Sequence length를 요구하는 경향을 보였다. 이는 예측 시간 간격이 길수록 DO 농도의 시계열 변화 특성이 강하게 반영되어 나타난 결과로 판단된다.

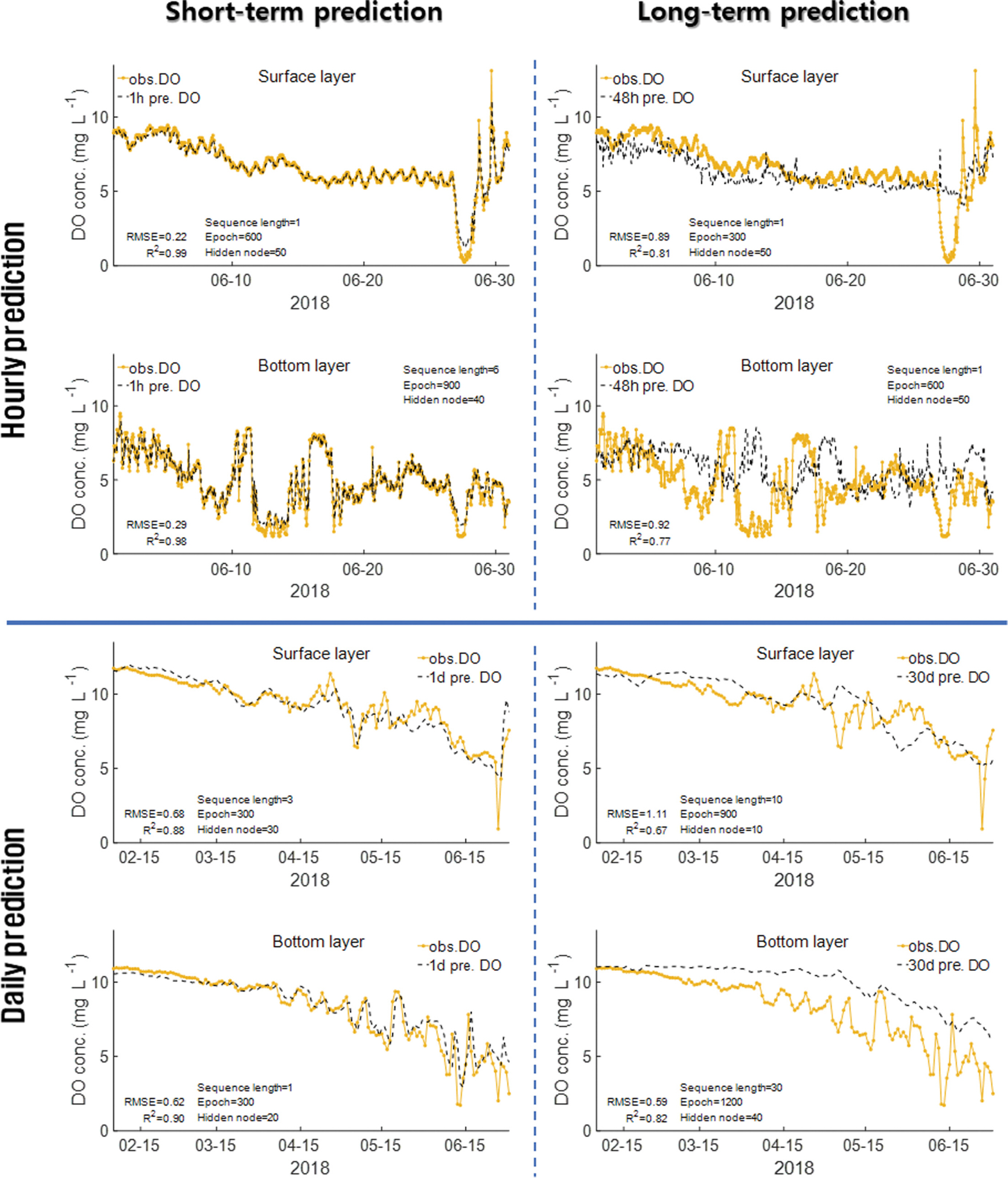
LSTM 모형의 시계열 예측 성능을 평가하기 위해 시간 예측과 일 예측의 장·단기 예측 결과를 관측값과 함께 시계열 그래프로 나타내었다(Fig. 8). 시간 예측과 일 예측의 예측 기간은 각각 약 1개월과 5개월이며, 장·단기 예측 시간 간격은 다음과 같다. 시간 예측: [단기, 장기] = [1 hour, 48 hour]/일 예측: [단기, 장기] = [1 day, 30 day]. 모형 조건은 각각의 예측에서 R² 값이 가장 높게 나온 하이퍼파라미터 조건을 사용하였다. 단기 예측(Short-term prediction)의 경우 시간 예측과 일 예측의 예측값 모두 관측값을 잘 재현하는 것으로 나타났다. 단기-시간 예측의 표층과 저층 R² 값은 각각 0.99, 0.98로 나타났으며, 단기-일 예측의 경우 표층과 저층 각각 0.88, 0.90으로 나타났다. 장기-시간 예측에서 표층의 경우 06-27 이후에 급격히 변하는 DO 농도 변화는 재현하지 못했다. 저층의 경우 관측값과 비교했을 때 예측값이 일정 시간 간격 뒤로 밀리는 모습을 보였다. 이러한 결과는 Li et al.(2021a)의 연구에서도 확인할 수 있으며, 이는 DO 농도의 비정상성(non-stationary)과 복잡성에 기인한 것으로 판단된다. 장기-일 예측의 경우 표층과 저층 모두 단기적인 재현성은 떨어지는 모습을 보였다. 그러나 30 day라는 긴 예측 시간 간격을 고려하여 그 목적을 장기적인 추세 예측으로 제한했을 때 높은 재현성을 보였다.

3.2 Prediction in hypoxia water mass based on decision tree

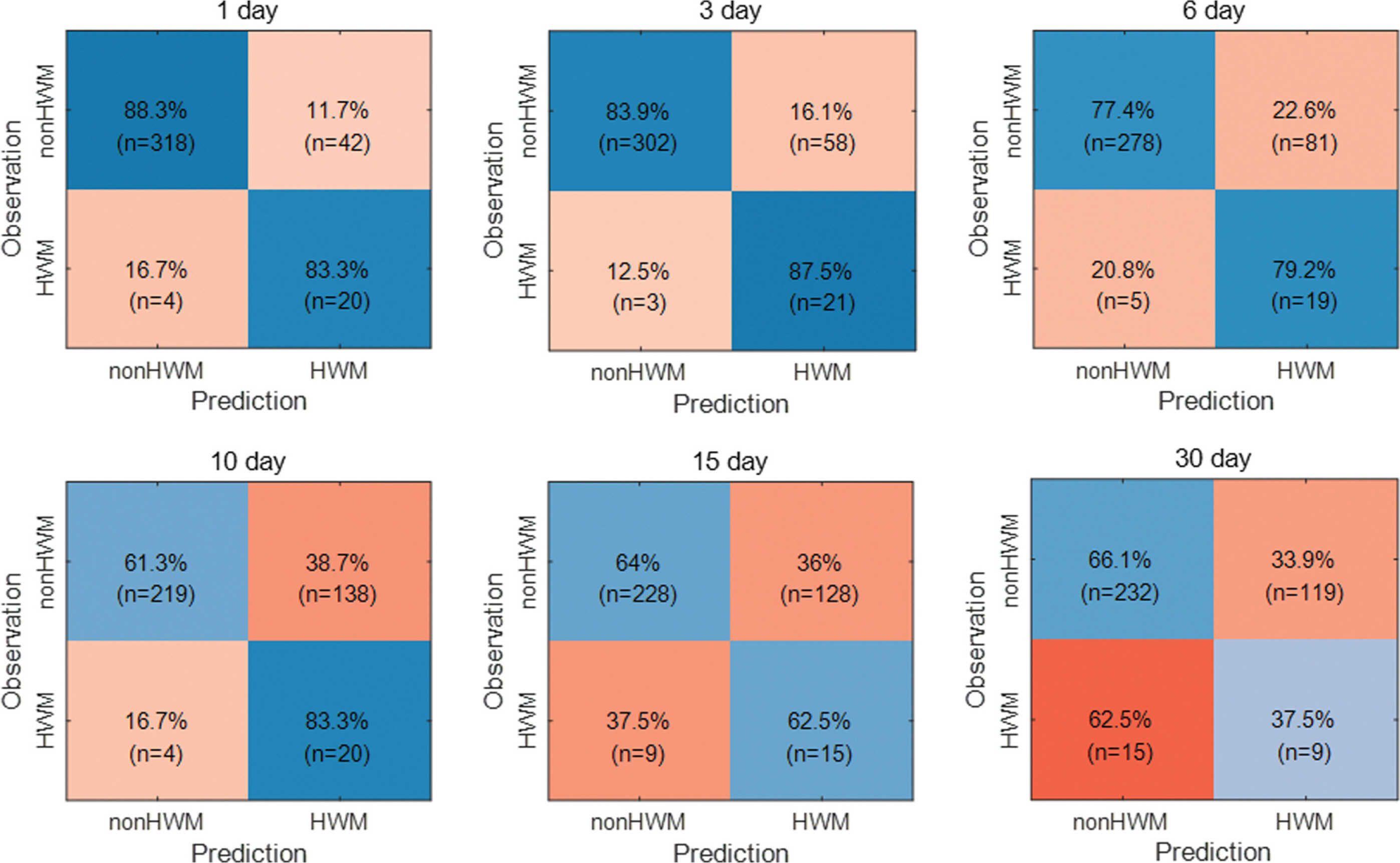
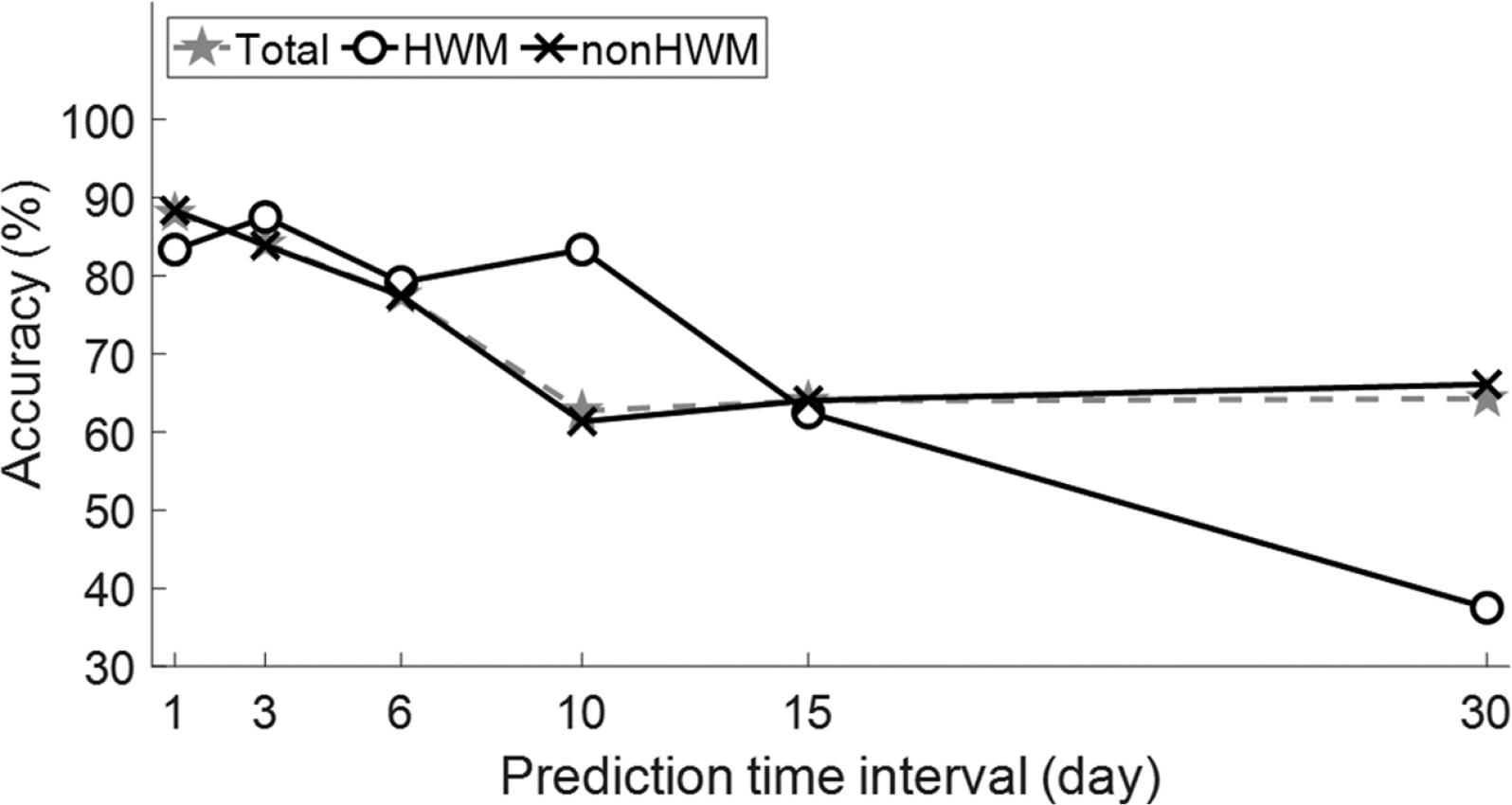
본 연구에서는 결정 트리를 이용한 저층의 빈산소수괴 발생 예측 연구를 진행하였다. 그 결과를 정오분류표(confusion matrix)로 Fig. 9에 나타내었으며, 예측 시간 간격별 예측 정확도 그래프로 Fig. 10에 요약하여 나타내었다. 반응변수는 빈산소수괴 발생(HWM) 또는 미발생(nonHWM)의 범주형 변수이다. 예측 시간 간격으로는 1, 3, 6, 10, 15, 30 day를 고려하였다. HWM 케이스의 예측 결과, 예측 시간 간격 10 day 이하의 단기 예측에서 약 80% 이상의 높은 예측 정확도를 보였다. 이후 예측 시간 간격이 늘어남에 따라 예측 정확도는 급격히 감소하였다. HWM 케이스의 예측 정확도는 [[1, 3, 6, 10, 15, 30] day 예측에서 각각 [83.3, 87.5, 79.2, 83.3, 62.5, 37.5]%로 나타났다. nonHWM 예측에서도 단기 예측에서 장기 예측으로 갈수록 예측 정확도는 감소하는 결과를 보였다. 1 day 예측의 정확도는 88.3%이었으며, 30 day 예측에서 66.1%로 감소하였다. 단, [[10, 15, 30] day 예측만을 봤을 때는 오히려 정확도가 증가하는 결과를 보였다. 장기 예측에서 HWM 예측 정확도의 급격한 감소와 nonHWM 예측 정확도가 증가하는 결과를 봤을 때, 결정 트리 모형이 DO 농도를 관측치보다 고평가(overestimate)하는 경향이 있는 것으로 판단된다. 전체 케이스에 대한 정확도는 nonHWM 케이스의 정확도와 큰 차이를 보이지 않았다(Fig. 10). 이는 전체 데이터 포인트 수(n = 1280)에서 nonHWM 케이스의 데이터 수(n = 1183)가 차지하는 비중이 커서 나타난 결과로 판단된다.

Fig. 9.

Confusion matrix of prediction accuracy (%) in HWM and nonHWM.

Fig. 10.

Prediction accuracy in hypoxia water mass for HWM, non-HWM and total cases.