Article information

Abstract

Trans Abstract

1. 서 론

일반적으로 케이슨의 마루에 설치되는 상치구조물은 제체의 안정성 확보, 구조물 배후로의 월파량 감소, 접근 도로 제공, 친수공간 제공 등을 목적으로 사석경사제의 천단에 설치되는 일체식 콘크리트 구조물로 정의할 수 있다. 하지만, 최근 들어 건설되는 케이슨 혹은 콘크리트 블록을 이용한 직립식 해안·항만구조물의 경우에도 구조물의 천단상에 다양한 형태의 상치구조물을 설치하여 월파의 발생을 방지하거나 친수 공간을 확보하는 사례가 증가하고 있으며, 이와 같은 직립식 구조물이 호안으로 적용되는 경우 적정한 상치구조물의 설치를 통해 월파 방지를 위한 마루높이 확보와 경제성을 동시에 확보할 수 있다.

과거부터 사석경사제 천단에 설치되는 상치구조물에 대한 작용파력 및 파괴모드에 대한 연구는 유럽을 중심으로 지속적으로 수행되어 왔다. 대표적으로 Pedersen and Burcharth (1992)은 상치구조물의 파괴 모드로 연직벽의 파괴, 상치콘크리트 저판의 파괴, 상치구조물의 이동, 제체 파괴에 의한 상치구조물 파괴 등을 언급하였으며, Nørgaard et al.(2013)는 사석경사제 천단에 설치되는 상치구조물의 경우 가장 중요한 파괴 모드로 수평 슬라이딩을 지적하였다. 최근 Molines et al.(2018)은 사석경사제의 월파량으로부터 상치구조물의 작용 파력을 예측할 수 있는 신경망을 제안하였으며, 월파량이 10배 이상 증가하는 경우 상치구조물의 작용파력과 전도 모멘트가 11%~60% 정도 증가함을 확인하였다. 그러나, 사석제체 위에 설치되어 상치구조물의 이동이 비교적 자유로운 경우와는 상이하게 케이슨과 같은 구조물의 경우 상치구조물에 작용하는 외력이 과소평가되는 경우에는 상치구조물의 파손과 더불어 구조물 제체의 전체 외력의 증가로 다양한 파괴 모드가 발생할 수 있다. 실제로, Fig. 1에 보이는 바와 같이 설계 한계파고를 초과하는 입사파랑이 내습하는 경우에 케이슨 상치구조물이 심각하게 파괴되는 현상이 발생하며, 제체의 안정성에도 영향을 미칠 수 있다. 또한, 과거 수십년동안 연직벽 형태의 상치구조물이 대부분의 해안 및 항만구조물에 광범위하게 적용되어 왔지만 케이슨을 포함한 직립식 구조물 천단에 설치되는 구조물에 대한 일반적인 적용 가능한 설계기준은 부재한 것이 현실이다.

Fig. 1.

Destruction of the upper structure of Gamcheon Port breakwater by typhoon.

한편, 케이슨을 포함한 직립식 구조물에 작용하는 파압산정은 Goda(1974, 1985)에 의해 제안된 파압산정식(이하 Goda 파압식)이 가장 널리 활용되고 있다. 특히, Goda 파압식은 경사입사파를 고려할 수 있는 유일한 예측식으로 우리나라의 항만설계기준뿐만 아니라 영국을 포함한 유럽에서도 직립식 및 혼성제 구조물에 작용하는 파압산정을 위해 Goda 파압식을 적용하고 있다. Goda 파압식은 구조물의 파괴를 발생시킬 수 있는 단일의 극한파를 대상으로 하는 결정론적인 파력산정방법이며, 구조물 전면에서 발생하는 압력은 정수면에서 최대 파압이 발생하고 구조물의 설치바닥까지 선형적으로 감소하는 사다리꼴 분포로 가정한다. 또한, 정수면보다 높은 지점에서의 압력은 가상의 처오름 지점(직각 입사파일 경우 최대파의 1.5배)에서 0으로 감소한다. 비록 Goda 파압식이 쇄파에 의한 파압성분을 고려하고 있지만 보다 상세한 파압에 따른 구조물의 안정성 검토나 유공케이슨 등과 같은 이형 직립식 구조물 검토를 위해 수리모형실험 혹은 전산유체역학(CFD)을 활용한 수치모델을 이용한 연구들이 활발하게 수행되어왔다(Oh et al., 2013; Ji et al., 2015; Choi et al., 2020). 특히, Lee et al.(2020)은 수치계산을 통해 비충격파 조건에서 케이슨 상부에 설치된 연직벽의 위치에 따른 케이슨 방파제의 안정성을 평가하였으며, 연직벽의 위치가 케이슨 후면에 위치할수록 구조물 전면의 최대 파압 및 파력을 저감시킬 수 있음을 지적하였다.

본 연구에서는 케이슨 직립제의 상부에 설치된 상치구조물에 대한 Goda 파압식의 적용성의 한계를 분석하고 상치구조물의 설치 위치에 따른 파압특성을 고찰하기 위해 단면 수리모형실험과 수치계산을 동시에 수행하였다. 또한, 수리모형실험과 수치계산으로부터 분석된 상치구조물의 작용 파압을 Goda 파압식과 비교하여 파압의 발생크기를 고찰하였다.

2. 수리모형실험

2.1 실험방법 및 조건

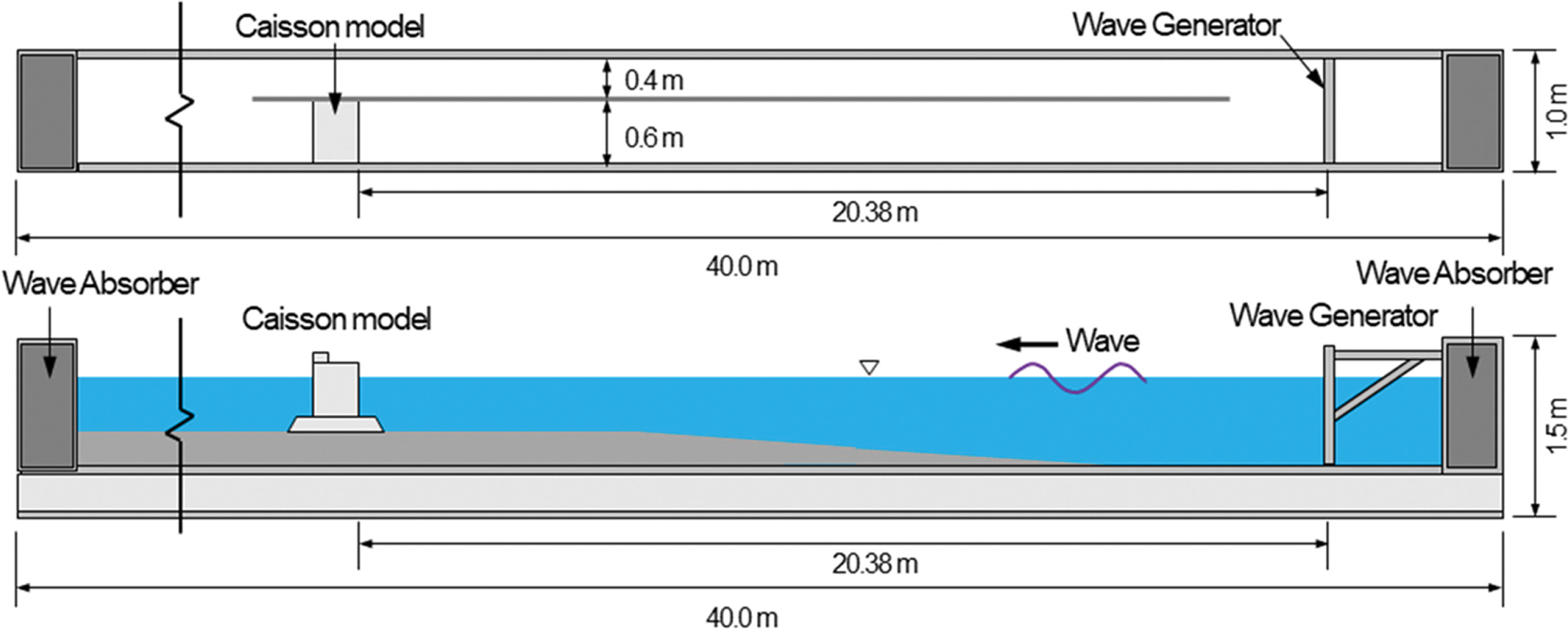
수리모형실험은 Fig. 2에 보인 바와 길이 40 m, 폭 1 m, 높이 1.5 m의 2차원 단면수조에서 수행되었다. 단면수조에는 목표파랑의 조파를 위한 서보 피스톤형식의 조파기가 설치되어 있으며, 수조의 양끝단에는 반사파 제어를 위한 소파제가 설치되어있다. 또한 수로 폭을 6:4로 분할하여 대상 구조물은 광폭을 갖는 수로에 설치하여 실험을 진행하였다.

Fig. 2.

Schematic diagram of the wave flume.

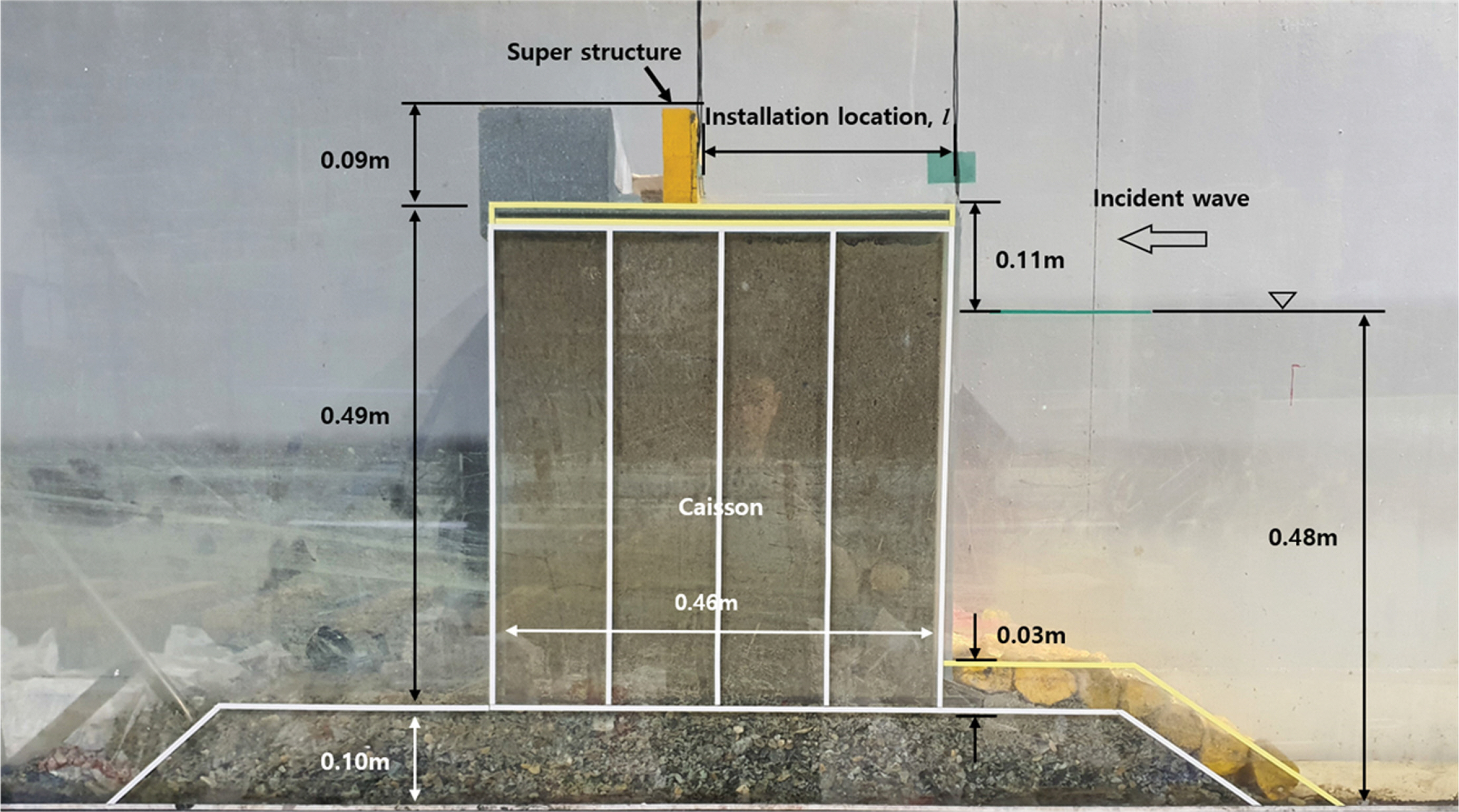
수리모형실험의 축적은 조파수조의 크기, 조파기의 가동범위 및 대상 구조물의 크기 등을 고려하여 1/25 축척을 적용하였으며, 축소된 모형구조물은 조파판으로부터 20.38 m 이격된 거리에 설치되었다. 또한, 케이슨 전면의 단면형상이 상치구조물 작용파압에 미치는 영향을 최소화하기 위하여 단순한 무공 직립제 케이슨을 적용하였다. 상치구조물의 설치 위치는 케이슨 전면에서부터 입사파랑의 진행방향으로 이격거리(l = 0.0~25.5 cm)를 증가시켜 총 6가지 실험조건을 적용하였다. 케이슨 모형구조물은 너비 0.46 m, 높이 0.49 m이며, 케이슨 직립제의 상부에 설치된 상치구조물은 너비 0.122 m, 높이 0.09 m로 제작되었고, Fig. 3에 수조내에 설치된 케이슨 모형구조물을 보인다.

Fig. 3.

The caisson model in the experiment.

본 연구에서는 상치구조물에 작용하는 파압의 기본적인 특성을 검토하기 위한 것이므로 구조물에 작용하는 입사파랑은 비쇄파조건의 규칙파를 적용하였다. 입사파랑은 구조물이 미설치된 조건에서 용량식 파고계(CHT6-60, KENEK)로부터 측정되었으며 Table 1에 실험파의 제원을 보인다. Table 1에서 h는 수심, T는 주기, L은 파장, H는 파고를 각각 나타낸다. 상치구조물의 이격거리 l에 따라 서로 다른 주기조건 5가지를 적용하여 총 30가지의 케이스에 대한 실험을 수행하였다.

Table 1.

Incident wave conditions

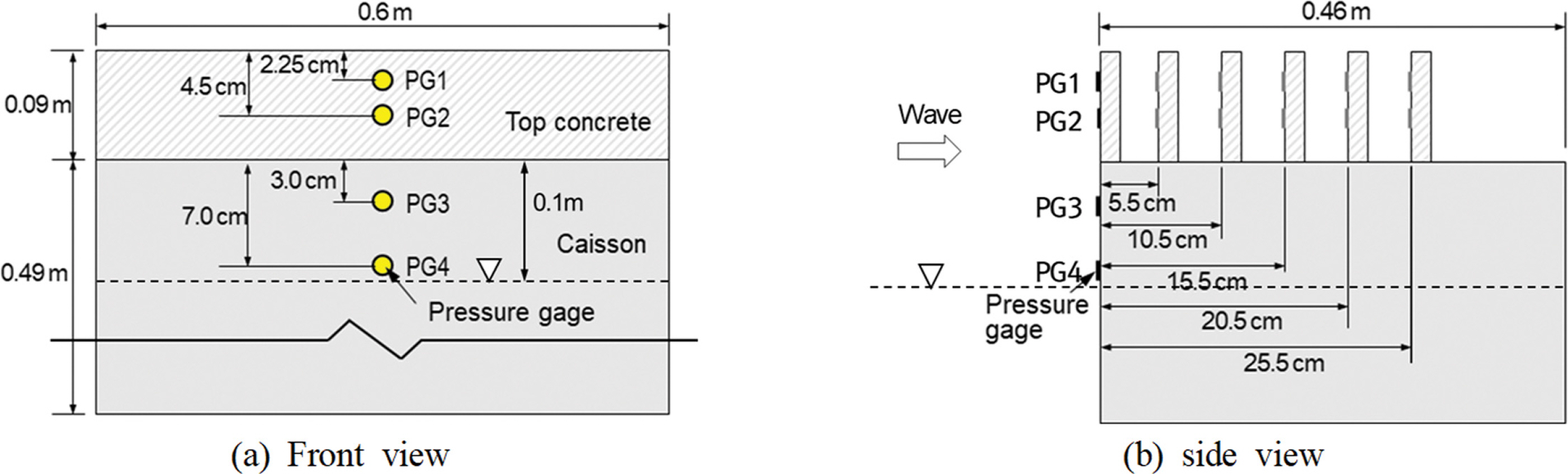
파압측정은 파압센서(PS-05KC, KYOWA)를 케이슨 전면 2개소와 상치구조물에 2개소를 각각 설치하여 동일한 파랑조건에서 케이슨의 전면과 상치구조물에서의 파압을 동시에 측정하였다. 파압계의 설치위치는 Fig. 4에 나타낸 것과 같이 상치구조물의 상단에서 수심방향으로 2.25 cm와 4.5 cm, 직립제 케이슨의 마루로부터 수심방향으로 3cm와 7 cm 이격된 위치에 파압계를 설치하였고 이는 모두 수심위에 위치하는 지점으로 대기중에 노출되어있는 지점이다. 파압계의 위치에 따라 상치구조물의 상단과 가까운 파압계부터 PG1, PG2, PG3, PG4로 각각 정의하였다. 순간적인 파압 변화를 정밀하게 측정하기 위해 부착된 모든 파압계의 독취시간 간격은 100 Hz로 설정하였다.

Fig. 4.

Schematic layout of wave pressure measurement.

2.3 파압 측정 결과

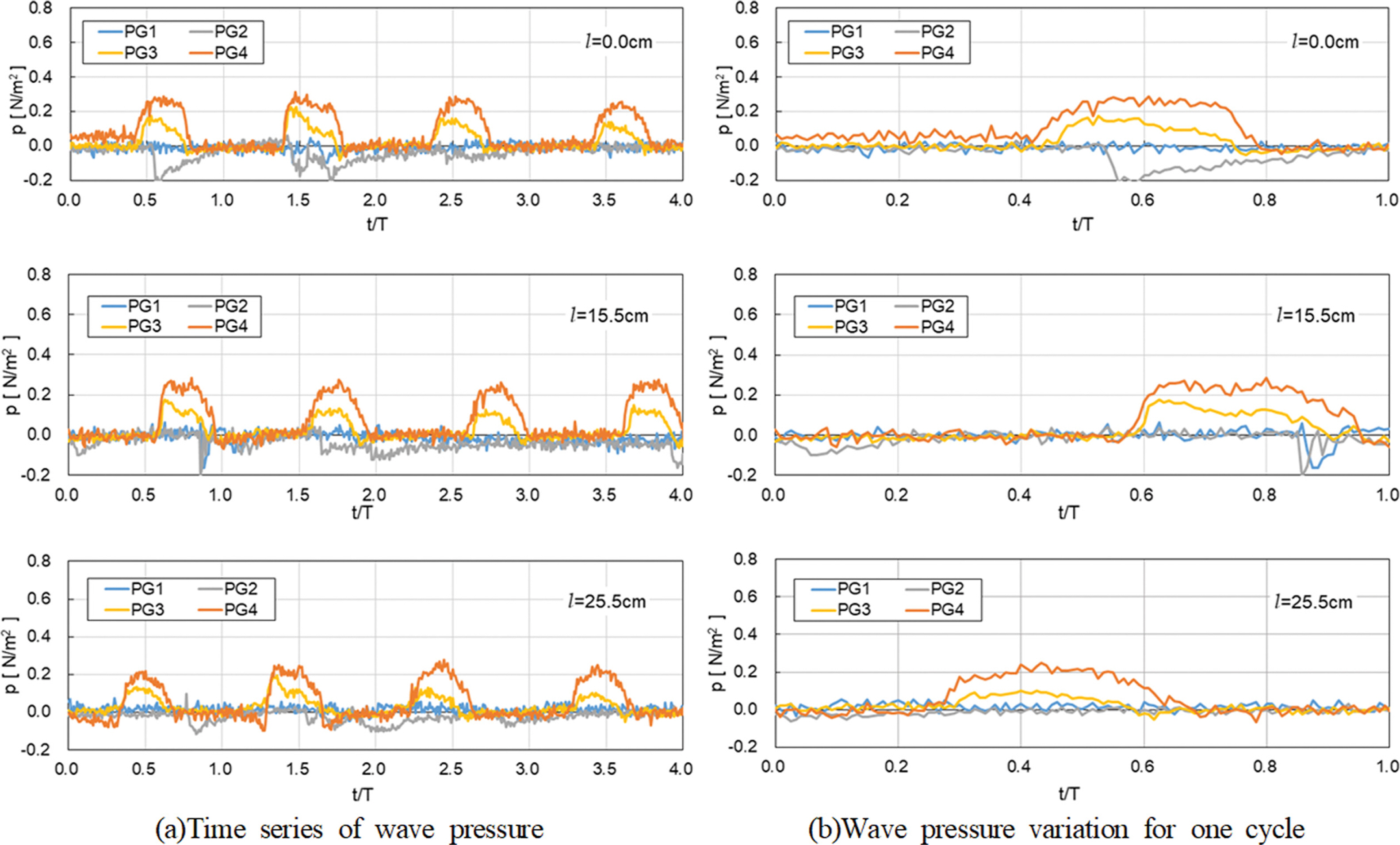
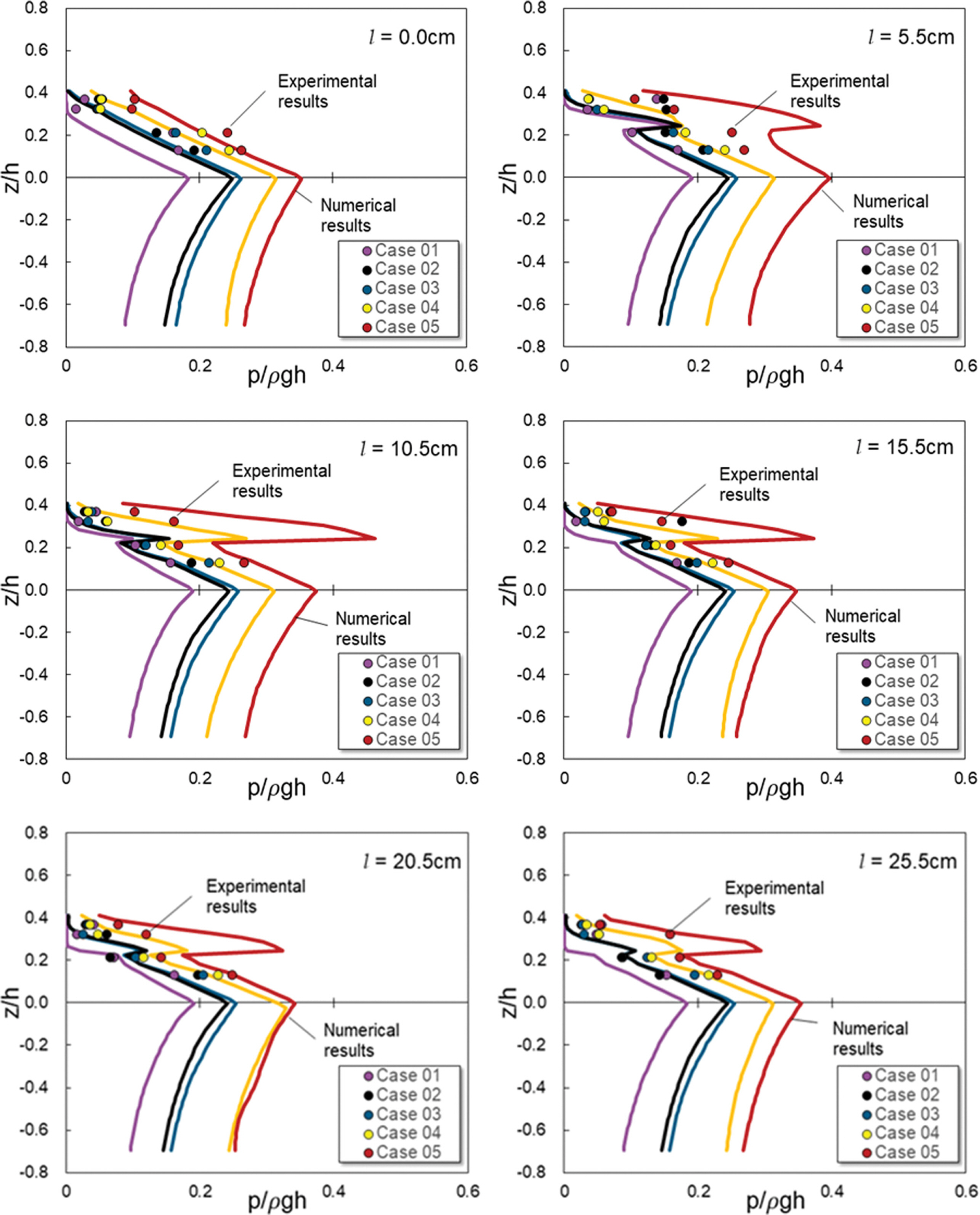
케이슨 전면부 및 케이슨의 마루에 설치한 상치구조물에 작용하는 파압의 변동특성을 고찰하기 위해 상치구조물에 파압이 작용하지 않는 경우와 구조물의 마루로 월류가 발생하여 상치구조물에 파압이 작용하는 경우에 대한 측정 파압의 시계열을 Fig. 5와 Fig. 6에 각각 보인다. Fig. 5는 파고 Table 1의 Case 1의 조건에 대한 결과이며 Fig. 6은 Case 5에 대한 결과이며, Fig. 5(b)와 6(b)에는 측정 위치별 파압발생 형태의 관찰을 위해 한주기동안 파압변화를 보인다. Fig. 5의 경우는 케이슨의 마루 위로 월파(월류)가 거의 발생하지 않음에 따라 케이슨 전면에 설치된 파압계(PG3, PG4)로부터만 파압이 측정되며 구조물 전면에서의 수위변동에 대응하여 파압이 변동하고 있음을 확인할 수 있다. 구조물의 마루 위로 월파가 발생하는 Fig. 6에서는 상치구조물에 작용하는 파압이 확인된다. 또한, 상치구조물이 구조물의 전면으로부터 이격된 l = 15.5 cm와 l = 25.5 cm의 경우에 상치구조물에 작용하는 파압(PG2)은 케이슨 전면에 작용하는 파압(PG3)을 상회하고 있으며, 이격거리에 따른 최대파압에 대한 위상차도 확인된다. 이는 상치구조물의 설치 위치에 따라 케이슨 전면에 비해 상치구조물에 오히려 큰 파압이 작용할 수 있음을 시사하며, 정수면에서 처오름을 고려하여 구조물의 마루높이까지 선형적으로 감소하는 파압분포를 적용하는 Goda 파압식은 상치구조물에 작용하는 파압을 과소평가할수 있음을 의미한다. 특히, 구조물의 전면으로부터 이격된 상치구조물에 작용하는 파압은 일반적인 진동파압과는 다른 파압(이하 충격성 파압으로 정의)의 형태를 보이고 있음을 알 수 있다.

Fig. 5.

Time variations of pressure by separation distance for Case 1.

Fig. 6.

Time variations of pressure by separation distance for Case 5.

3. 수치파동수조의 재현성

수리모형실험에서 확인된 바와 같이 상치구조물에 작용하는 파압의 변동특성을 보다 상세하게 고찰하기 위해 수치파동수조를 이용한 수치실험을 동시에 수행하였다. CFD 기반의 수치파동수조는 수리모형실험과 유사한 조건에서 물리현상의 재현이 가능하므로 수리모형실험에서 측정되는 제한된 물리량을 보다 상세하게 검토가 가능하다는 장점이 있다. 이하에는 본 연구에서 적용한 CFD 기반의 수치파동수조에 대하여 간략히 기술하고, 수리모형실험의 결과에 대한 재현성을 검증한다.

3.2 실험결과의 재현성

수치파동수조를 이용한 수치실험에서는 직립제 케이슨 전면에 작용하는 파압을 계산 격자별로 측정하였다. 직립제 케이슨 전면의 피복블록은 불투과 조건을 적용하여 구조물 전면에서 상치구조물의 최상단까지의 높이는 0.55 m이며 연직 방향의 격자 크기는 0.01 m이므로 구조물 전면에서 총 55개 지점의 파압결과를 취득하였다. Fig. 7은 수치실험으로부터 산정된 최대 작용파압과 수리모형실험의 결과를 비교하여 나타낸 것이다. 그림에서 연직축은 정수면을 기준으로 연직 상방향을 양(+)의 값으로 나타내었으며 수평축은 정수압으로 정규화된 최대 작용파압을 나타낸다.

Fig. 7.

Maximum wave pressure distribution of experiments and numerical method.

Fig. 7로부터 수치실험에서 산정된 케이슨 및 상치구조물의 전면에 작용하는 최대파압은 수리모형실험에서 측정된 파압을 입사파랑의 조건별로 다소 과대 혹은 과소평가하고 있으나 정수면 위에서 발생하는 파압의 분포형태를 전체적으로 양호하게 재현하고 있다고 판단된다. 특히, 수치실험으로부터 산정된 최대파압은 입사파랑의 주기가 상대적으로 단주기인 Case 1의 경우에 수리모형실험결과를 과소평가하며 반대로 주기가 가장 큰 Case 5의 경우는 과대평가함을 확인할 수 있다. 이는 입사파랑에 주기에 따른 공간해상도에 따른 수면파형의 분해능에 따른 결과로 판단된다. 또한, 수리실험에서 산정된 최대파압의 결과는 제한된 위치에서 측정된 수리모형실험결과에서 확인되지 않은 상치구조물에 작용하는 충격성 파압이 확인된다. 이와 같은 상치구조물에 작용하는 파압은 동일한 입사파랑의 조건하에서도 케이슨의 전면에서부터 상치 구조물의 이격거리에 따라 상이하게 발생하는 것을 확인할 수 있으며, 이러한 상치구조물의 위치는 케이슨 전면에서 형성되는 중복파동장에도 영향을 미치므로 동일한 입사파랑조건에서도 정수면에서 발생하는 최대파압이 상이하게 발생함을 확인할 수 있다.

Fig. 8은 Fig. 7에서 확인되는 바와 같이 상치구조물에 충격성 파압이 발생하지 않는 l = 0.0 cm 조건과 상치구조물이 케이슨의 전면에서 가장 후퇴되어 설치된 l = 25.5 cm 조건에서 수치실험과 수리모형실험의 자유수면 거동에 대한 snapshot을 보이며, 수치실험에서 재현한 구조물은 상치구조물의 높이까지 포함하여 모델링한 것이다. 특히, 수치실험은 상치구조물의 설치위치에 따른 일련의 자유수면 변화를 양호하게 재현하고 있음을 확인할 수 있다. 특히, 상치구조물에 충격성 파압이 발생하지 않는 l = 0.0 cm 조건에서는 입사파랑이 상치구조물을 월파하고 있음에도 Fig. 8에 보인바와 같이 충격성 파압이 발생하지 않는 반면에 동일한 월파에 의해 상치구조물이 케이슨 전면으로부터 이격된 l = 25.5 cm에서는 충격성 파압이 발생함을 알 수 있다.

Fig. 8.

Measured and computed free-surface snapshots at the moment of wave impact.

4. Goda 파압식의 적용 가능성

케이슨 전면에 작용하는 압력강도에 대한 산정식은 식(4)와 같이 사다리꼴 분포의 가정하에 Goda(1974)에 의해 최초로 제안되었으며, 이후에 Tanimoto et al.(1976)는 경사입사 파랑에 대한 효과를 보정하였고, Takahashi et al.(1991)은 케이슨 전면의 형상을 고려할 수 있는 수정파라미터 λ를 고려한 수정식을 제안하였다.

여기서, p₁과 p₂는 각각 정수면과 해저바닥에서 작용하는 최대파압으로 p₁에서부터 수심방향으로 p₂까지 선형적으로 변화하며, H_max는 설계파고, β는 입사파향, w_o는 비중량, λ₁과 λ₂는 각각 중복파 및 충격파 성분에 의한 파력의 변화를 나타내는 수정파라미터이며, α₁과 α₂는 각각 변화하는 파동성분과 쇄파성분에 대한 추가적인 첨두값을 나타내는 압력계수로 다음과 같이 산정된다.

여기서, h는 케이슨 전면의 수심, h_b는 케이슨에서 해측으로 5H_1/3의 위치에서의 수심, d는 사석마운드에서의 수심을 각각 나타낸다. 또한, 식(4)에서 정수면에 작용하는 최대파압 p₁은 식(6)의 처오름을 높이 η^*까지 선형적으로 감소하여 작용하는 것으로 가정한다.

한편, 본 연구에서는 무공케이슨을 대상으로 하고 있으므로 λ = 1을 적용하였다.

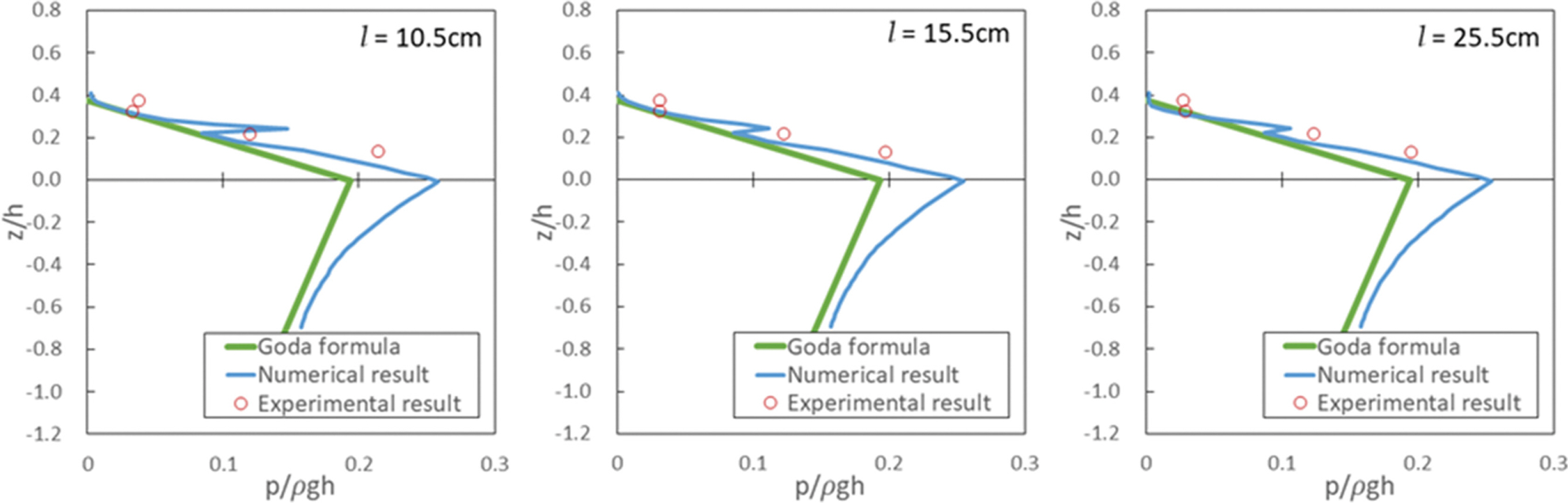
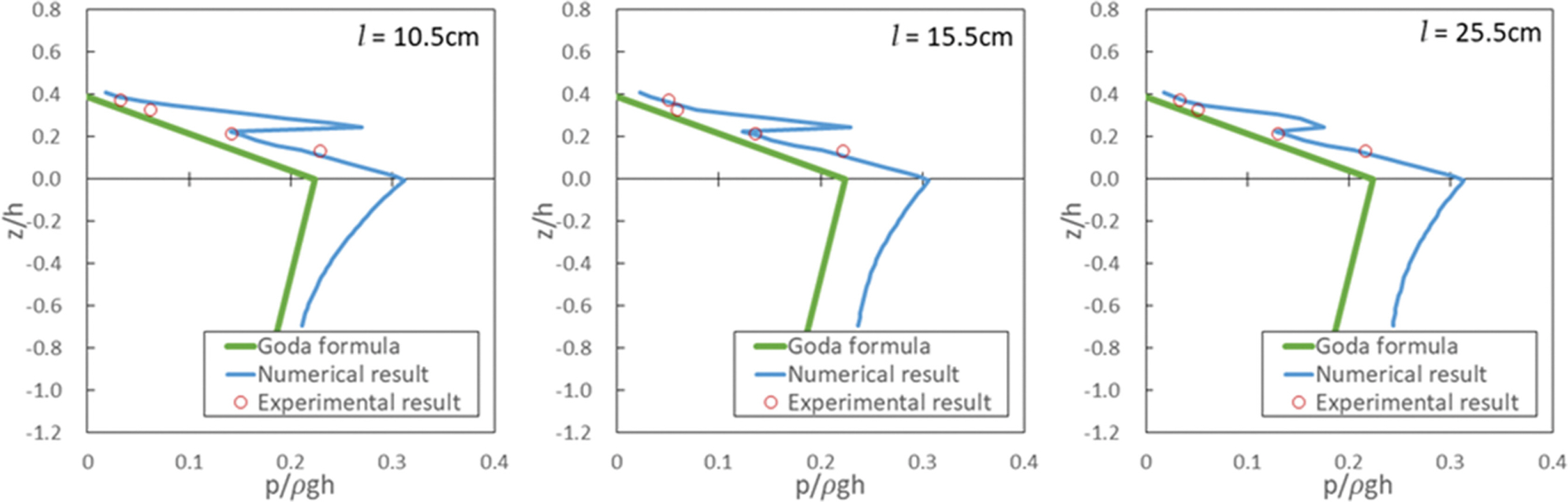
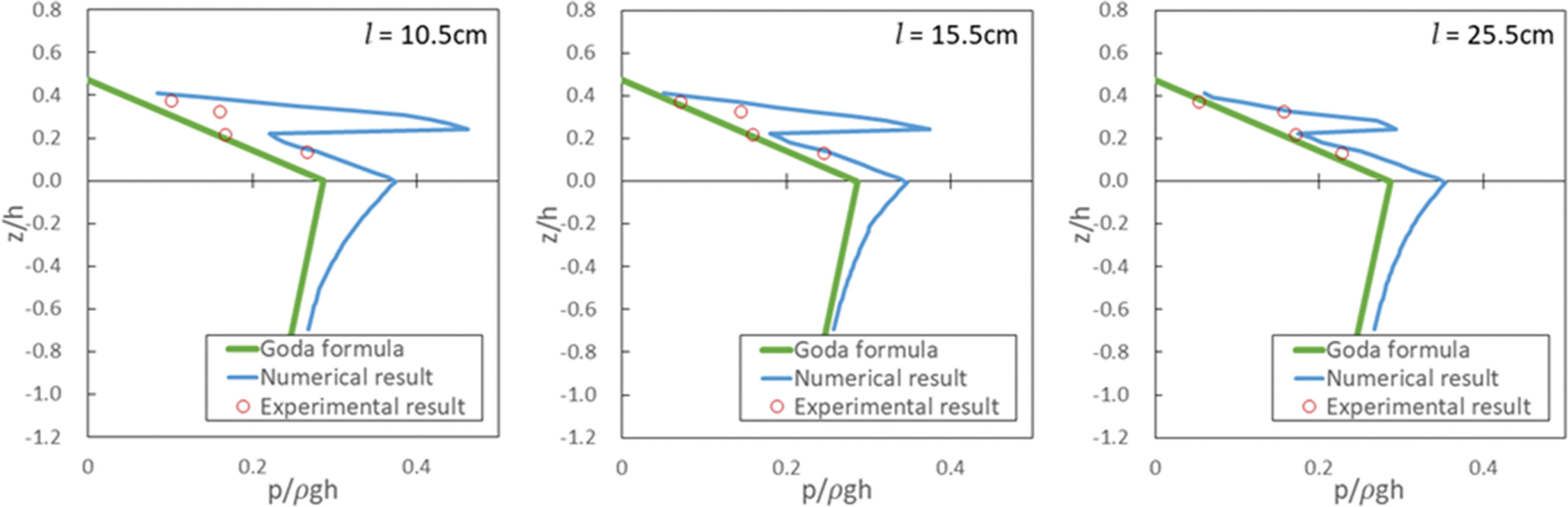
Fig. 9는 Case 3 조건에서 구조물 전면에 작용하는 파압분포에 대한 수리 및 수치실험결과를 Goda 파압식과 비교한 것이다. 그림으로부터 확인되는 바와 같이 정수면에서부터 입사파랑의 처오름 높이까지 선형적인 감소를 고려한 Goda 파압식은 수리모형실험에서 확인된 충격성 파압이 고려되지 못하는 반면에 수치파동수조에 의한 수치실험결과는 상치구조물에 작용하는 파압을 잘 재현하고 있음이 확인된다. 또한, 정수면 위에서 발생하는 파압은 Goda 파압식의 최대파압인 p₁을 상회하는 파압이 작용하고 있음을 확인할 수 있다.

Fig. 9.

Comparisons of wave pressure with Goda formula and experimental and numerical results (Case 3).

Fig. 10과 Fig. 11은 Fig. 9와 유사하게 각각 Case 4와 Case 5에 대한 결과를 나타낸다. 정수면 상부에 작용하는 작용파압의 분포 양상은 Fig. 9와 유사하며, 모든 입사파랑조건에 걸쳐 수치실험에 의한 정수면 위치에서의 작용파압은 Goda 파압식에 의해 산정된 파압을 상회하였으며 정수면으로부터 수심이 증가함에 따라 지수함수적으로 감소함을 알 수 있다. Figs. 9-11에 보인 바와 같이 입사파랑이 케이슨 마루 높이를 초과하는 월파가 발생하는 경우 상치구조물에 작용하는 파압은 케이슨 전면으로부터 이격거리에 따라 충격성 파압이 발생하며, 이러한 충격성 파압은 기존의 Goda 파압식으로는 산정될 수 없음이 확인된다. 한편, 수치실험에서 산정된 정수면 아래에서 발생되는 파압과 Goda 파압식에 의해 산정된 파압과의 차이는 수치실험의 경우 계산비용의 감소를 위해 Fig. 8에 보인바와 같이 사석마운드와 피복석의 투수층을 불투과 구조물로 모델링한 결과에 따른 것으로 판단된다.

Fig. 10.

Comparisons of wave pressure with Goda formula and experimental and numerical results (Case 4).

Fig. 11.

Comparisons of wave pressure with Goda formula and experimental and numerical results (Case 5).

Table 2에는 상치구조물에 작용하는 파압의 정량적인 비교를 위해 입사파랑의 주기에 따른 정수면의 작용파압과 상치구조물에 작용하는 파압의 비를 제시하였다. 단, 정수면에 작용하는 파압과 상치구조물에 작용하는 파압에 대한 결과는 수치실험으로부터 산정된 결과를 이용하였다. 입사파랑의 주기가 T = 1.2 s, 1.4 s 및 1.6 s인 경우 l = 5.5 cm에서 84.73, 70.99, 63.54%로 가장 높았고, T = 2.0 s 및 2.2 s에서는 l = 10.5 cm에서 65.78, 123.80%로 가장 높게 나타났다. 이와 같이 전면 케이슨으로부터 상치구조물의 이격거리에 따라 파압의 발생크기가 상이하지만 상치구조물에 작용하는 최대파압은 정수면의 위치에서 작용하는 파압의 약 60~120%의 범위에서 발생함을 알 수 있다.

Table 2.

Ratio of shock wave pressure to maximum pressure at the still water level

Table 2에 제시한 바와 같이 상치구조물에 작용하는 최대파압은 입사파랑의 조건 및 구조물의 이격거리에 따라 발생 크기가 매우 상이하다. 따라서, 상치구조물에 작용하는 최대파압을 정량적으로 예측하기 위하여 케이슨 상부에서 월파에 의해 발생하는 유속성분을 이용하여 최대파압의 크기를 식(7)의 Froude number에 따른 함수로 정의하였다.

여기서, V는 직립제 케이슨 마루에서 월파에 의해 발생하는 흐름속도이며, 이는 수치실험으로부터 케이슨의 마루위에서 발생한 단면평균유속이다. 한편, 구조물 마루에서 월파수괴 상단까지의 연직거리 D로부터 gD의 계산이 가능하지만 간략화를 위해 입사파랑의 파속 C를 적용하였다.

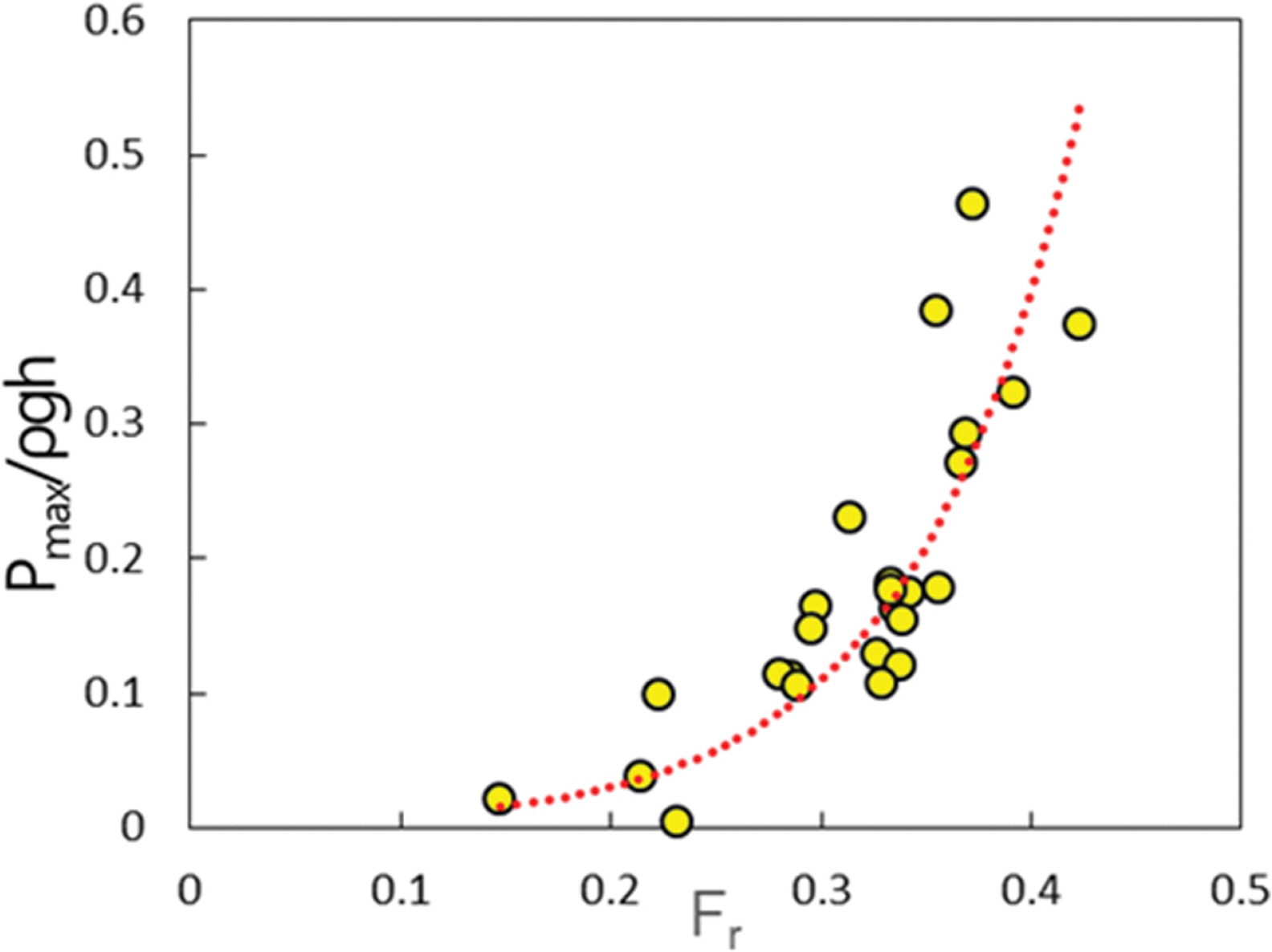
Froude number에 η파압의 크기를 Fig. 12에 보인다. 그림으로부터 F_r이 증가함에따라 상치구조물에 작용하는 최대파압이 지수함수적으로 증가함을 확인할 수 있으며, 본 연구의 실험조건하에서는 정수압의 최대 46%까지 최대파압이 작용함을 확인할 수 있다. 또한 Fig. 12에는 지수함수를 기저로 회귀분석으로부터 산정된 다음의 식 (8)로 표현되는 적합곡선을 동시에 도식하였다.

Fig. 12.

Comparing the Froude number with the distribution of wave pressure.

식(8)의 무차원 최대파압에 대한 경험식은 Fig. 12에서와 같이 본 연구의 실험범위인 0.14  F_r  0.43에서만 적용가능하며, 상관계수는 R² = 0.65로 최대파압이 갖는 다양한 발생조건을 고려하면 양호한 대응성을 갖는 것으로 판단된다.

5. 결론 및 향후 연구과제

본 연구에서는 직립제 케이슨 상부에 설치된 상치구조물에 작용하는 파압 특성을 고찰하기 위하여 수리모형실험과 오픈소스 CFD 모델인 REEF3D를 사용하여 수치실험을 수행하였으며, 수리모형실험과 수치실험의 결과를 Goda 파압식과 비교하여 현재 설계에 적용하고 있는 Goda 파압식의 상치구조물 위치에 따른 적용 가능성에 대해 검토하였다. 케이슨 마루높이를 초과하는 월파가 발생하는 경우 상치구조물에 충격성 파압이 발생함을 확인하였고 이러한 파압은 사다리꼴 파압분포를 가정한 기존의 Goda파압식과는 매우 상이함을 확인하였다. 상치구조물에 작용하는 최대파압은 정수압에 작용하는 파압 대비 60~120%인 것으로 확인되었으며, 상치구조물의 설치위치 및 입사파랑의 조건에 따라 상이한 결과를 보였다. 이와 같은 상치구조물에 작용하는 최대파압의 예측을 위해 정수압으로 정규화된 최대파압을 케이슨 마루에서 월파에 의해 발생하는 유속에 기반한 Froude number의 함수로 정의하였으며, Froude number에 따른 무차원 최대파압은 Froude number가 증가함에 따라 지수함수적으로 증가함을 확인하였다. 또한, 이러한 지수함수를 바탕으로 상치구조물에 작용하는 최대파압의 예측을 위한 경험식을 제안하였다. 하지만 최대파압에 대한 경험식은 케이슨 마루에서 발생하는 평균유속이 추가적으로 요구되므로 향후 추가적인 수리실험을 통해 보다 적용성이 높은 산정식이 제안되어야 할 것으로 사료된다.

본 연구에서는 수리모형실험 과정에서 제한된 파압계와 측정위치에 따른 한계를 극복하기 위하여 고정도의 CFD 기반의 수치실험을 동시에 수행하였으나, 향후, 상치구조물의 설치 위치뿐만 아니라 형상까지 고려한 보다 상세한 추가적인 실험이 필요할 것으로 판단된다.

Article information Continued