Article information

Abstract

Trans Abstract

1. 서 론

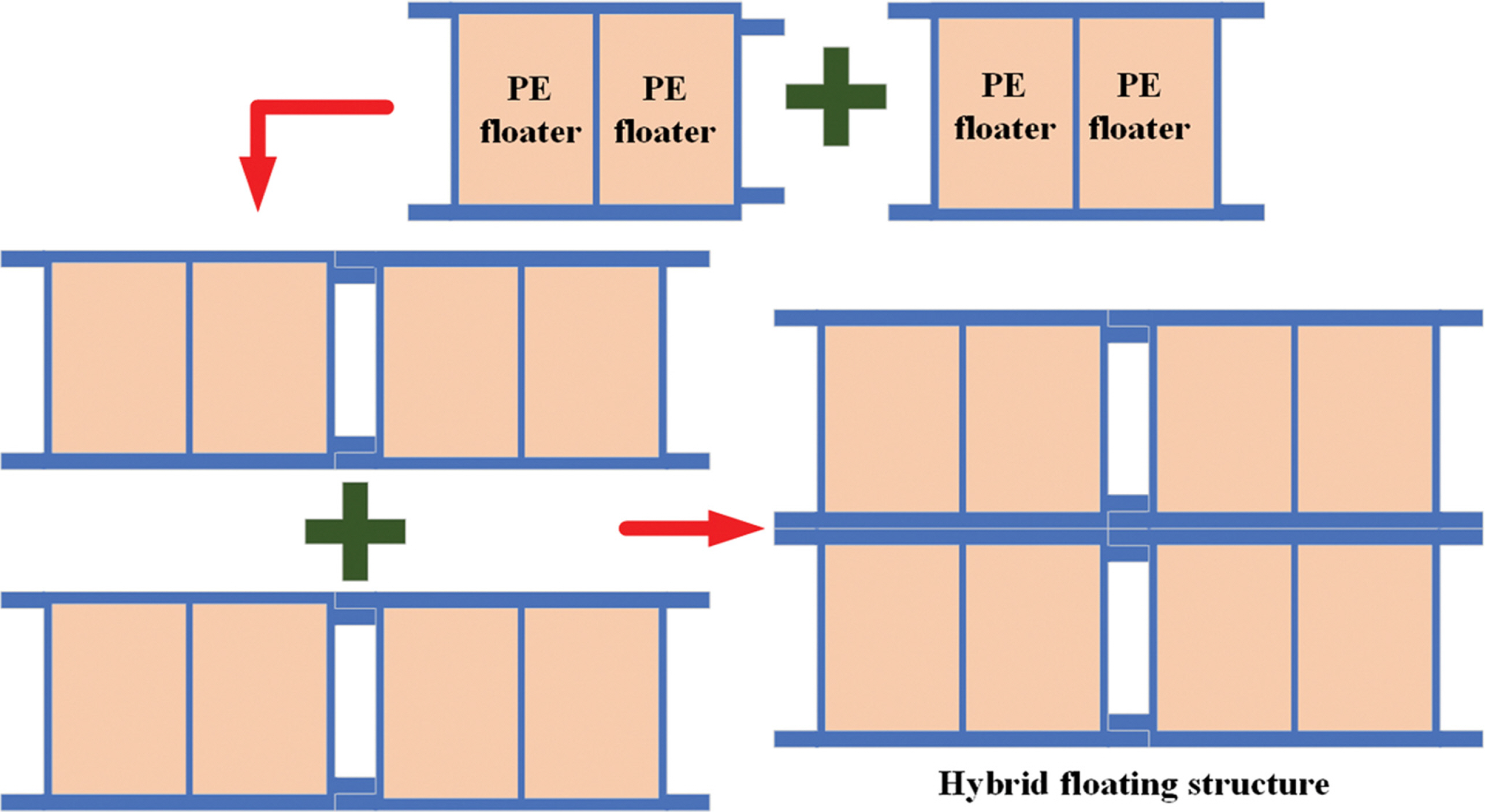
최근 연안에서 해상관광레저, 플로팅 건축 등의 사업발굴이 활발히 진행 중에 있어 해상조건에 적합한 부유식 구조물의 필요성이 대두되고 있다. 기존의 부유체는 건설 현장에서 제작되거나 또는 기 제작된 부유체를 물에 띄워서 건설 현장으로 이동하는 방식을 취하고 있다. 만약 건설 현장의 여건이 좋지 않거나 물에 띄워서 이동할 수 없는 경우에는 공장에서 부유체를 제작하여 육상으로 이동해야 한다. 육상으로 이동할 경우에는 부유체의 크기에 제한으로 대형화가 불가능하다. 따라서 본 연구에서는 육상이동 조건 및 이동에 따른 부유체 파손 등을 방지하기 위해 기존 수상조건에서 사용 중인 다수의 PE 부력체를 내부에 그룹화하고 외부를 콘크리트로 둘러싼 표준 부력체 단위 모듈을 고안하였다. Fig. 1에서와 같이 본 연구에서 제안된 하이브리드 부유식 구조물은 표준 부력체를 수직 및 수평 적층으로 크기 조절이 가능하고, 하부에 수평감쇠판(Damping plate)이 설치되어 해상조건에서 부유체의 안정성이 향상되면서 계류장치와의 연결도 원활하게 할 수 있도록 하였다.

Fig. 1.

Extension method of hybrid module for floating structure.

주로 제작이 용이하고 내파안전성이 뛰어난 폰툰형 부유식 방파제가 이용되어 왔으나 일반적으로 내습파를 외해로 반사시켜 전달파를 저감하기 때문에 충분한 크기의 폭과 자중이 요구되는 문제점이 있다(Lee et al., 2013). 이러한 문제점을 보완하기 위해 폰툰형 부유식 방파제 하부에 수평판을 적용하여 상하 동요를 저감하기 위한 연구가 Chen et al.(2012)에 의해 수행되었다. 해양구조물에 수평감쇠판을 부착하여 상하 동요를 줄이기 위한 연구는 많이 수행되어져 왔으며 주로 TLP와 SPAR platform 형태의 원통형 부유체를 대상으로 많이 이루어졌다(Lim et al., 2015). 최근 부유식 풍력 부유체에 수평감쇠판을 적용한 연구들이 진행되고 있다(Lopez-Pavon and Souto-Iglesias, 2015; Bezunartea-Barrio et al., 2020; Jiang et al., 2022).

구조물과 구조물이 매우 근접하게 설치될 경우 구조물에 의해 둘러싸인 유체가 특정 주기에서 상하로 크게 진동하는 공진현상이 발생하는데 포텐셜이론 기반의 수치해석에서는 점성유동(Viscous flow)의 영향이 고려되지 않아 구조물에 작용하는 하중이 과도하게 산출되는 현상이 발생한다. 이러한 문제를 해결하기 위해 구조물들에 의해 둘러싸인 유체영역에 감쇠존(Damping zone) 영향을 고려한 수치해석들이 Chen(2005), Fournier et al.(2006), Pauw et al.(2007), Bunnik et al.(2009), Watai et al.(2015), Ganesan T and Sen(2016) 및 Chen et al.(2021)에 의해 수행되었다.

본 연구에서는 육상 이동이 가능한 단위 모듈의 수직 및 수평 적층으로 확장된 하이브리드 부유식 구조물의 안정성을 향상시키기 위해 수평감쇠판을 적용하였다. 적용된 수평감쇠판의 길이 변화에 따른 부유식 구조물의 거동 특성을 상용 프로그램인 ANSYS AQWA를 이용하여 분석하였다. 하지만 제안된 하이브리드 부유식 구조물의 경우 단위 모듈 결합에 의해 구성되기 때문에 구조물에 의해 둘러싸인 유체영역이 존재하고 이로 인해 특정 주기에서 공진이 발생할 가능성이 있다. 따라서 구조물에 의해 둘러싸인 유체영역에 ANSYS AQWA에서 제공되는 감쇠존 효과를 고려하여 부유식 구조물의 거동 특성을 면밀하게 분석하였다. 또한 새롭게 제안된 하이브리드 부유식 구조물의 동적거동 특성을 일반적으로 사용되는 폰툰형 부유식 구조물과 비교하였다.

2. 수치해석 조건 설정

ANSYS AQWA는 해양외력(파도, 바람, 조류 등)의 영향으로 인한 해양구조물의 동적거동을 시뮬레이션하는 프로그램으로, 다수의 구조물이 존재하는 경우 한 구조물의 움직임이 다른 구조물의 움직임에 영향을 줄 수 있으므로 이러한 인접 구조물 사이의 유체 역학적 상호작용 효과를 고려할 수 있다. 또한 최대 50개의 구조물과 50개의 관절 구조로 결합된 해양구조물의 유체 역학적 및 기계적 동적 구성의 모델링이 가능하다. 3차원 포텐셜 이론 기반의 ANSYS AQWA의 기본 속도 포텐셜은 식(1)과 같다.

여기서, ϕ_I는 입사파(Incident wave) 속도 포텐셜, ϕ_D는 회절파(Diffraction wave) 속도 포텐셜, ϕ_R는 구조물의 6자유도 운동에 의한 방사파(Radiation wave) 속도 포텐셜을 나타낸다.

파랑 중 부유체의 운동은 3개의 병진운동과 3개의 회전운동으로 구성되는 총 6개의 운동 중첩으로 나타난다. 병진운동으로는 전후 동요(Surge), 좌우 동요(Sway) 및 상하 동요(Heave)가 있으며, 회전운동으로는 횡 동요(Roll), 종 동요(Pitch) 및 선수 동요(Yaw)가 있다. ANSYS AQWA에서 파랑에 의한 부유체의 운동방정식은 주파수 영역에서 다음과 같이 나타낼 수 있다.

여기서, ω는 파주파수(Wave frequency), M_s는 구조물의 중량, M_R은 부가질량(Radiation added mass), C_R는 감쇠(Radiation damping), K는 유체정역학적 강성(Hydrostatic stiffness), F는 파랑 강제력(Wave exciting force)을 의미한다.

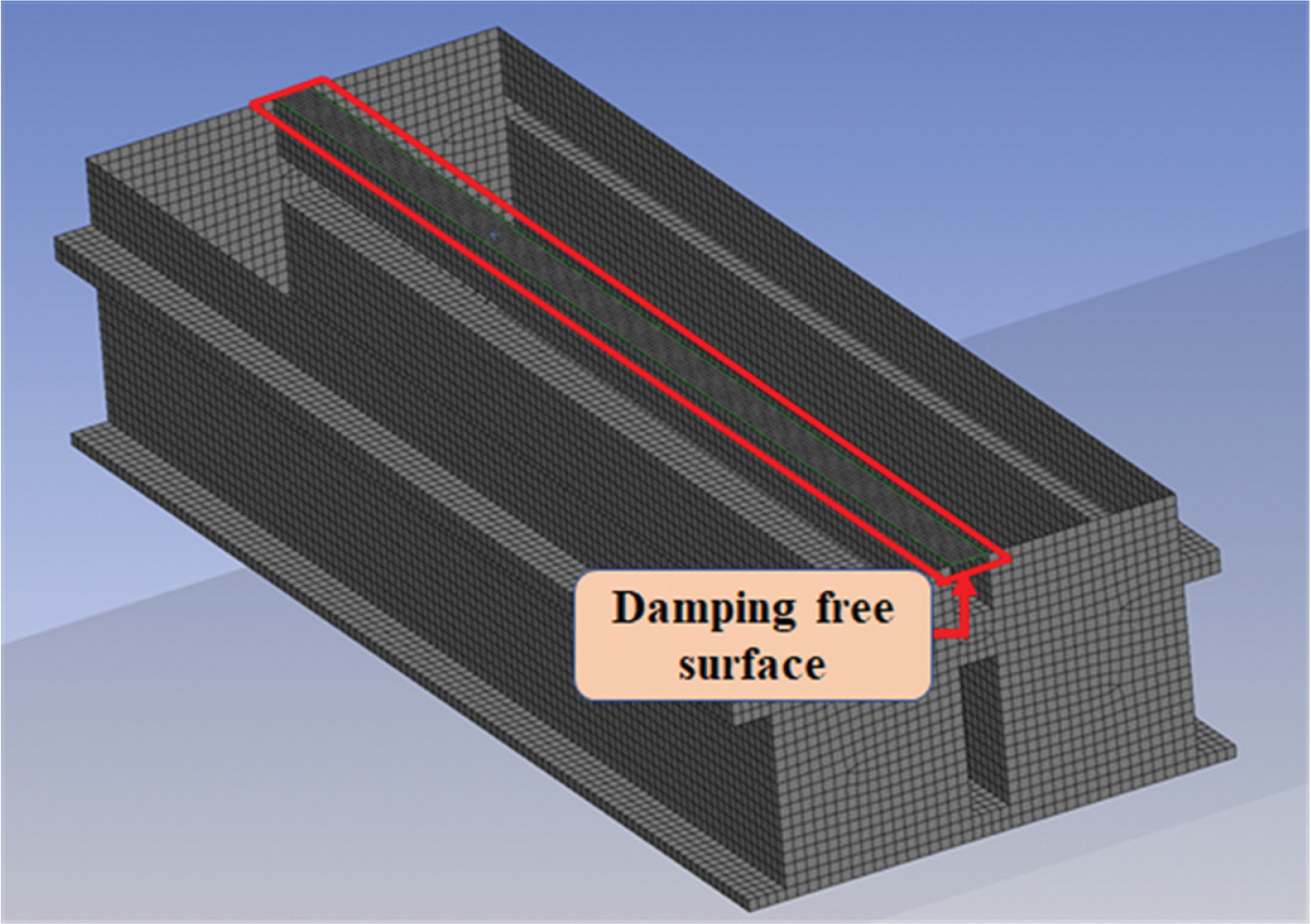
또한 포텐셜이론 기반의 수치해석에서 점성유동의 효과가 고려되지 못해 인접한 구조물에 의해 둘러싸인 유체영역에서 비정상적인 공진으로 유체가 상하로 크게 진동하여 구조물에 작용하는 하중이 과도하게 평가되는 것을 방지하기 위해 Fig. 2와 같이 구조물과 구조물 사이 유체영역에 감쇠 자유수면 경계조건인 식(2)를 비선형 시간영역 방정식에 적용할 수 있다. 이때 ANSYS AQWA는 Cheetham et al.(2007)에 의해 제안된 감쇠계수(Damping factor) 기반으로 수치해석이 수행된다.

Fig. 2.

Damping free surface in ANSYS AQWA.

여기서, g는 중력가속도, α_d는 감쇠계수(Damping factor), f₁는 구조물간의 간격과 관련된 함수이다.

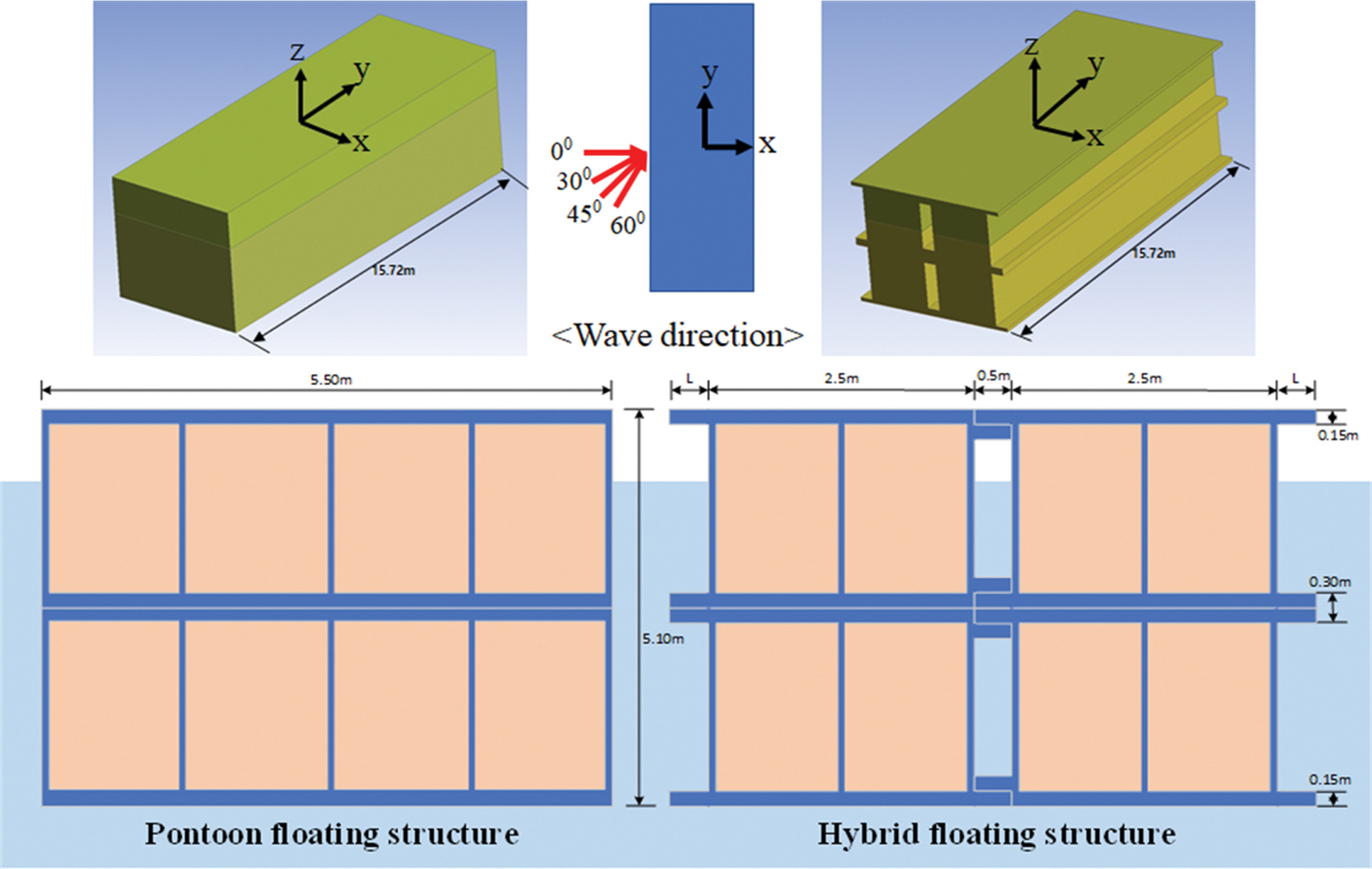
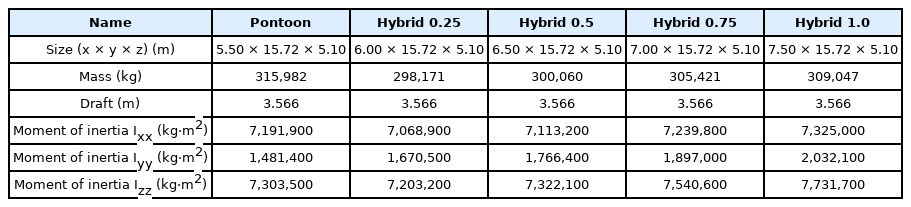
수평감쇠판(Damping plate)의 길이 변화(L)에 따른 부유식 구조물의 거동 특성을 분석하기 위해 Fig. 3과 Table 1에 나타낸 것과 같이 총 4개의 하이브리드 부유식 구조물(L = 0.25 m, L = 0.5 M, L = 0.75 m, L = 1.0 m)과 일반적으로 사용되고 있는 폰툰형 부유식 구조물에 대해 수치해석을 수행하였다. 부유식 구조물의 거동은 작용하는 파랑 하중에 민감하게 반응하며 구조물에 작용하는 하중은 부유체의 흘수(Draft)에 매우 큰 영향을 받는다. 따라서 모든 수치해석 조건에서 부유체의 흘수는 3.566 m로 설정하고 수심은 10.0 m로 고정하였다.

Fig. 3.

Definition sketch of numerical model for floating structures.

Table 1.

Properties of floating structures

ANSYS AQWA(2022R1 64bit)는 구조물 요소 개수에 제한(최대 60,000 절점, 40,000 요소)이 있어 모든 부유식 구조물의 최대 요소 사이즈를 0.25 m, 그리고 구조물과 구조물 사이에 존재하는 유체 감쇠존은 0.1 m로 설정하여 최대 요소 개수 제한 조건에 맞게 조절하여 수치해석을 수행하였다.

3. 수치해석 결과 및 고찰

부유체가 정수상태인 잔잔한 물에 떠 있는 상황에서 초기 경사에 대해 원래의 자세로 돌아가려고 하는 성질을 정적 복원성이라고 한다. 경사 각도가 증가함에 따라 복원력이 커지다가 감소하면서 음이 되는 각도까지 가게 되는데, 이러한 각도까지 가게 되면 부유체는 전복하게 된다. 이러한 곡선을 정복원력 곡선(Statical curve) 또는 부유체 경사 각도에 따른 GZ 곡선이라고 하며, 이 GZ 곡선을 이용하여 부유체의 복원력 크기를 확인할 수 있다. 또한, 동복원력은 경사각 θ로 경사시키기 위하여 필요한 일의양(Work done)으로 정의된다. 따라서 이는 식(4)와 같이 정의되며, 이것은 정복원력 곡선 하부의 면적을 의미한다.

여기서, GZ = GM × sin(θ)는 식(5)에 의해 계산되는 롤링주기(Rolling perriod)에 직접적인 영향을 미치므로 값이 너무 크면 문제가 발생할 수 있다. 부유체가 바로 서있는 직립상태에서 외력에 의해 기울어지게 되면 부심(부력중심)의 위치도 이동하게 되는데, 이때 기울어진 후에 이동된 부심에서 수면에 수직방향으로 향하는 새로운 부력의 작용선과 기울어지기 전의 부력의 작용선은 한 점에서 만나게 되는데, 이 점을 경심(Metacenter, M)이라고 한다. 경심 높이(Metacentric height, GM)란 부유체의 무게 중심으로부터 경심까지의 높이를 의미한다.

여기서, T는 롤링주기(sec)이며, k는 롤링 관성반지름(m)이고, g는 중력가속도이다.

부유체의 복원성을 검토하기 위해 ANSYS AQWA에서 제공되는 Large angle stability check 기능을 이용하여 부유체 모델을 경사시켜 가며, 경사된 상태에서의 잠긴 체적을 계산한 정복원력 곡선(GZ curve)을 Fig. 4에 나타내었다. Fig. 4 에서 구조물 좌표계의 x축에 대한 회전운동은 횡 동요(Roll)이고 y축에 대한 회전운동은 종 동요(Pitch)를 나타낸다. 횡 동요에 대해서는 폰툰형과 하이브리드형이 거의 유사한 패턴을 보이고 있는데 이는 부유식 구조물의 횡 동요 길이 15.72 m 대비 수평감쇠판의 길이가 상대적으로 짧고 부유체가 경사지더라고 배수량에 큰 변화가 발생하지 않기 때문으로 판단된다. 하지만 종 동요인 경우 하이브리드형이 폰툰형과는 눈에 띄게 다른 패턴을 나타내고 있으며 수평감쇠판의 길이가 길어질수록 GZ 값이 증가하고 이는 곡선 하부의 면적과 밀접한 관련이 있는 부유식 구조물의 복원력을 증가시키는 것을 알 수 있다. 따라서 기존 폰툰형 부유식 구조물에 수평감쇠판을 적용하면 부유식 구조물의 복원력 향상에 기여할 수 있다.

Fig. 4.

Comparison of GZ curve.

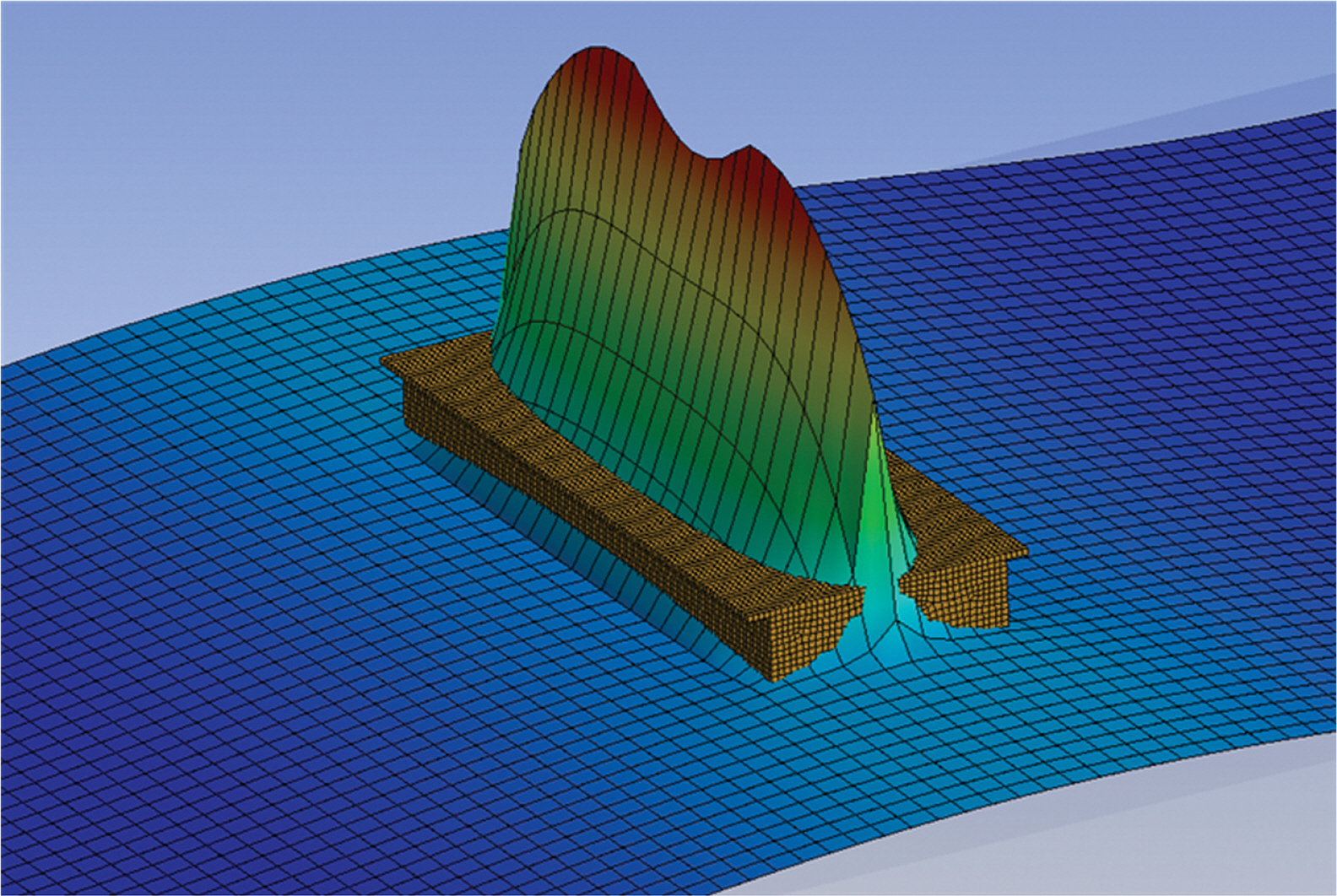
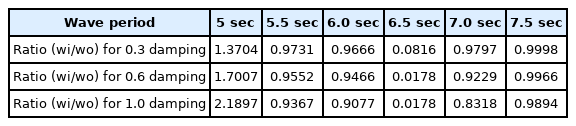
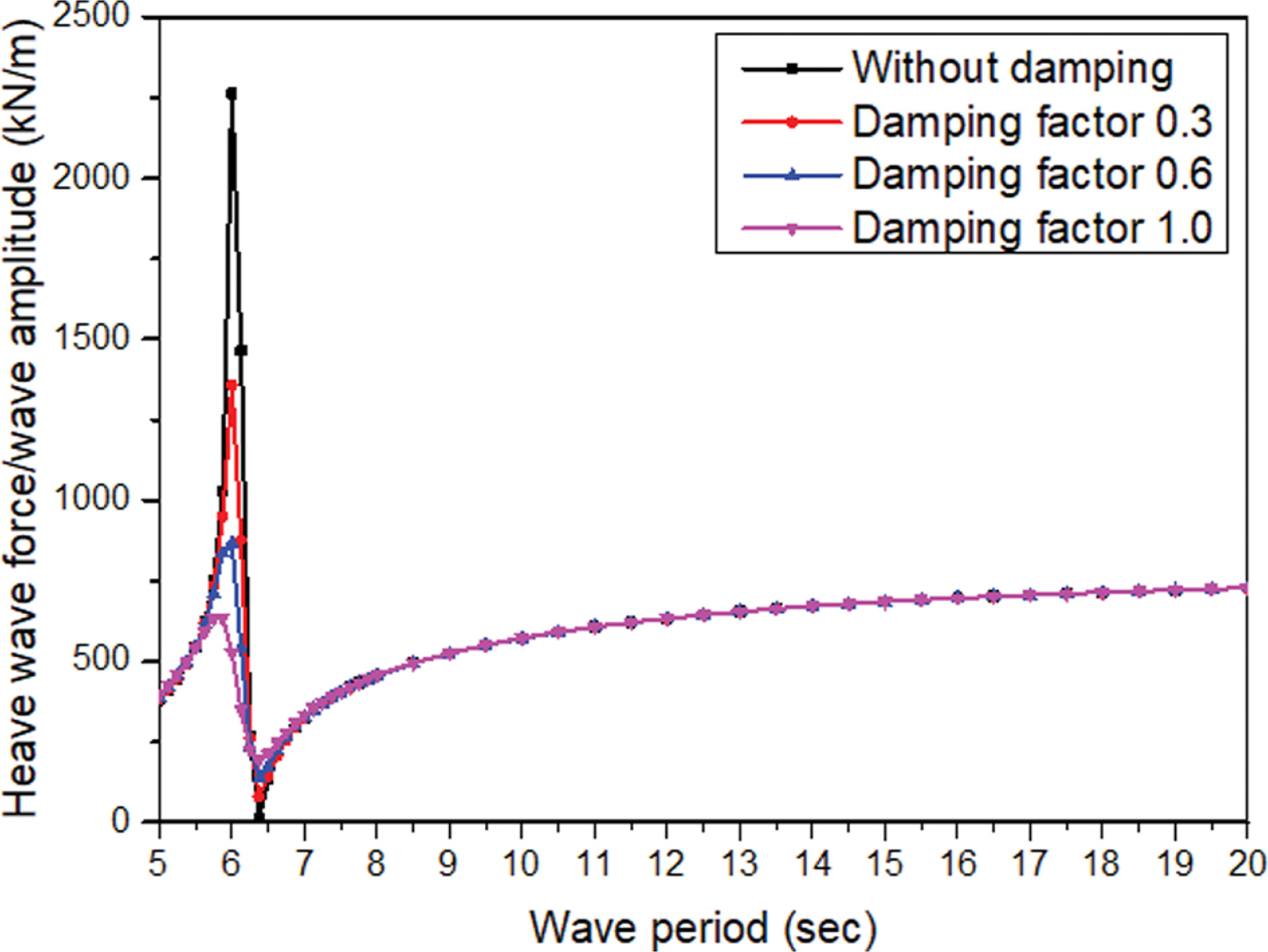
본 연구에서 제안된 하이브리드 부유식 구조물의 경우 단위 모듈 결합에 의해 구성되기 때문에 Fig. 3에서 나타낸 것처럼 구조물에 의해 둘러싸인 유체영역이 해수면 근처 부유식 구조물의 가운데 존재한다. 따라서 Fig. 5와 같이 유체가 상하로 크게 진동하는 비정상적인 공진으로 중복파(Standing wave)가 발생되어 구조물에 작용하는 하중이 특정 주기에서 과하게 산출되는 문제가 발생할 수 있다. 이 부분에 대한 검토를 수행하기 위해 구조물에 의해 둘러싸인 유체영역에 ANSYS AQWA의 감쇠존 옵션을 적용하여 비교하였다. ANSYS AQWA의 Workbench(2022R1)에서는 감쇠존의 감쇠계수(Damping factor)를 최대 1.0까지 적용할 수 있는데 감쇠계수 증가에 따른 해수면에서의 파랑 높이 비를 Table 2에 나타내었는데 주기 5.0초를 제외하고는 검토된 주기영역에서 감쇠계수가 증가할수록 파랑 높이가 감소하는 것을 알 수 있다. 이는 구조물에 의해 둘러싸인 유체영역에 감쇠존을 적용할 경우 유체의 공진주기에 변화가 발생하여 주기 5.0초에서 파랑 높이가 감쇠존 적용 전보다 높게 나타나는 현상이 나타났으나 구조물에 작용하는 하중 변화에는 큰 영향을 주진 않는 것을 Fig. 6에서 확인할 수 있다. Fig. 6의 감쇠계수 변화에 따른 상하 파력에서도 감쇠계수가 증가할수록 공진에 따른 구조물에 작용하는 파력이 감소하였으며 이는 Park et al.(2022)의 연구결과와 유사하다. 따라서 본 연구에서도 감쇠계수를 1.0으로 설정하여 감쇠효과를 최대화하였다.

Fig. 5.

Standing wave without damping for hybrid 0.5.

Table 2.

Ratio (with damping/without damping) of wave surface elevation for hybrid 0.5

Fig. 6.

Comparison of damping factor for hybrid 0.5.

하이브리드 부유식 구조물의 수평감쇠판 길이 변화에 따른 거동 분석에 ANSYS AQWA가 적절한지 검토하기 위해 원형 실린더에 수평감쇠판을 적용한 Koh and Cho(2016)의 연구 결과와의 비교를 Fig. 7에 나타내었다. Koh and Cho(2016)는 부유체의 점성감쇠력을 선형화된 점성 감쇠계수로 나타내어 MEEM(Matched Eigenfunction Expansion Method)과 ANSYS AQWA를 이용하여 수치해석을 수행하고 수리모형 실험을 통해 수치해석 결과를 검증하였다. Fig. 7에서 ANSYS AQWA의 결과는 Koh and Cho(2016)의 결과와 매우 좋은 일치를 보이는 것을 확인할 수 있다. 본 연구에서는 특정 주기에서 구조물에 둘러싸인 유체영역의 공진현상이 하이브리드 부유식 구조물의 거동에 미치는 영향을 주로 검토하기 위해 부유체의 점성감쇠력은 고려하지 않았다.

Fig. 7.

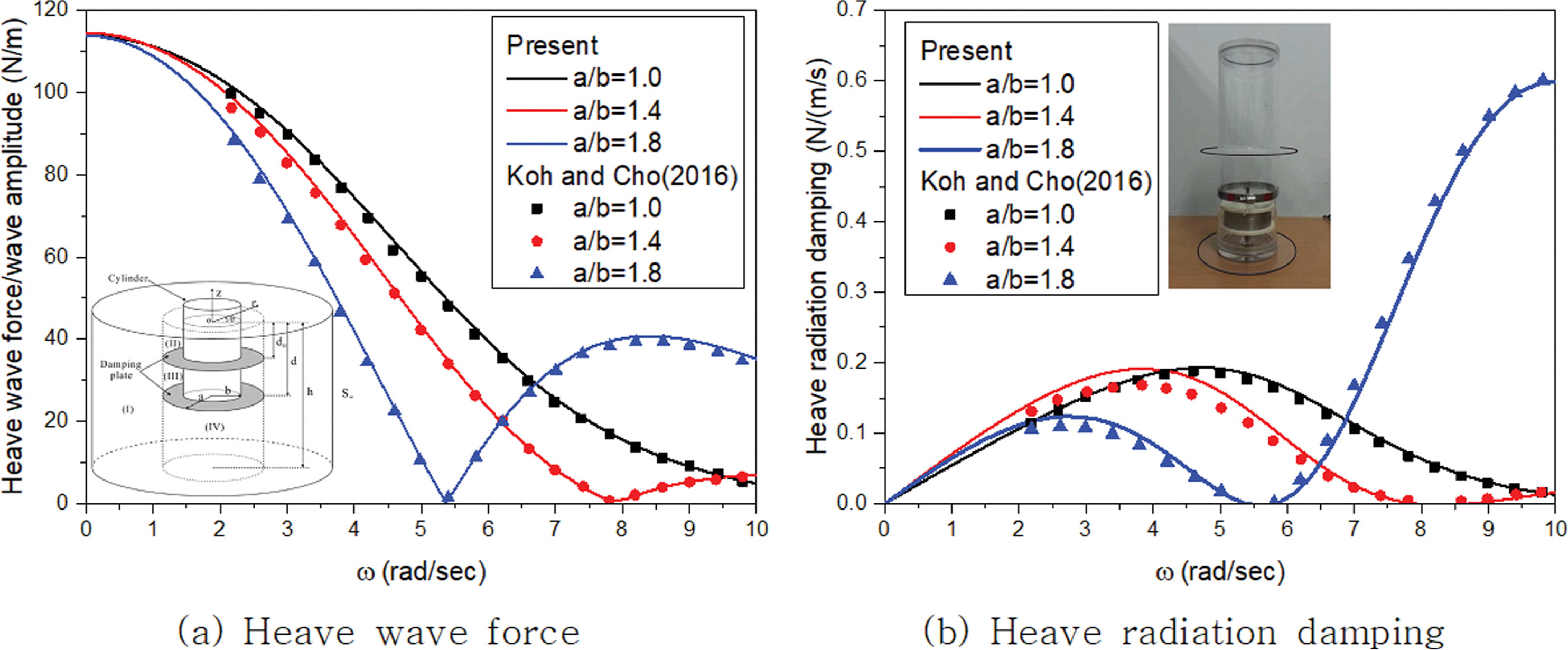
Comparison between present method and Koh and Cho (2016) for b/h = 0.1, b/d = 0.228, d₀/d = 0.54, and h =0.6m.

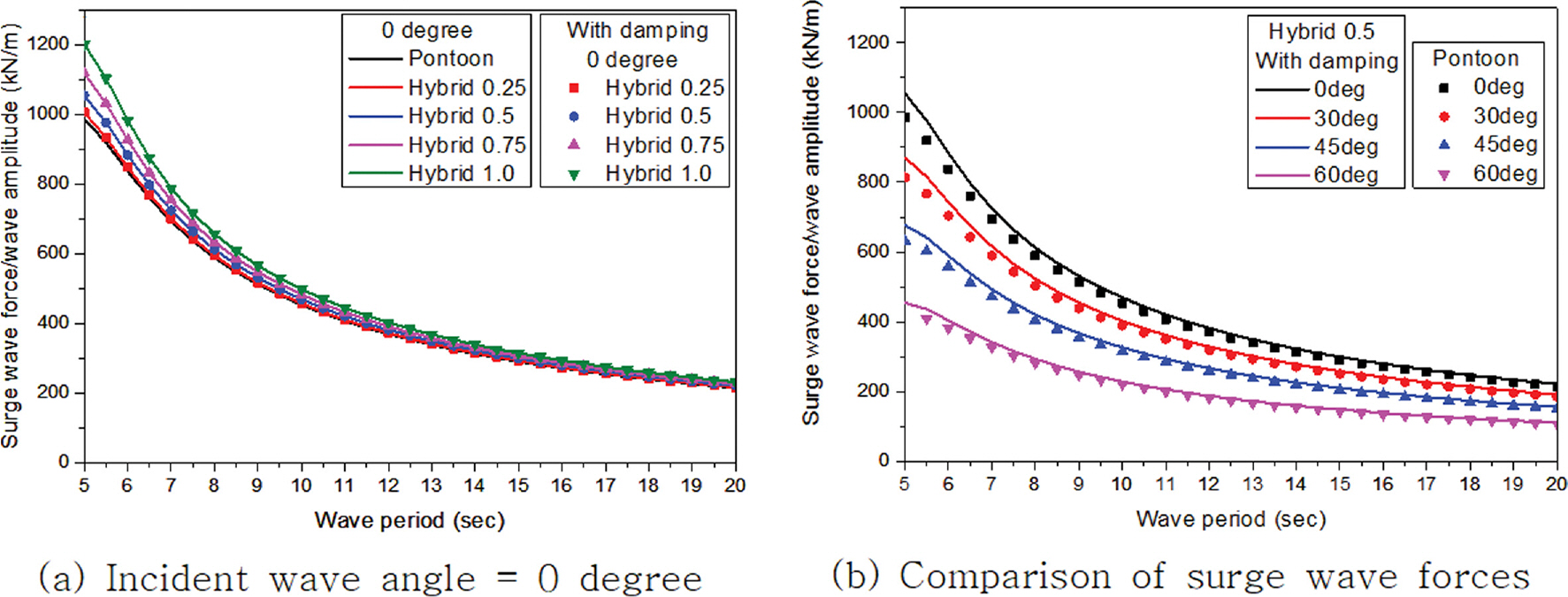
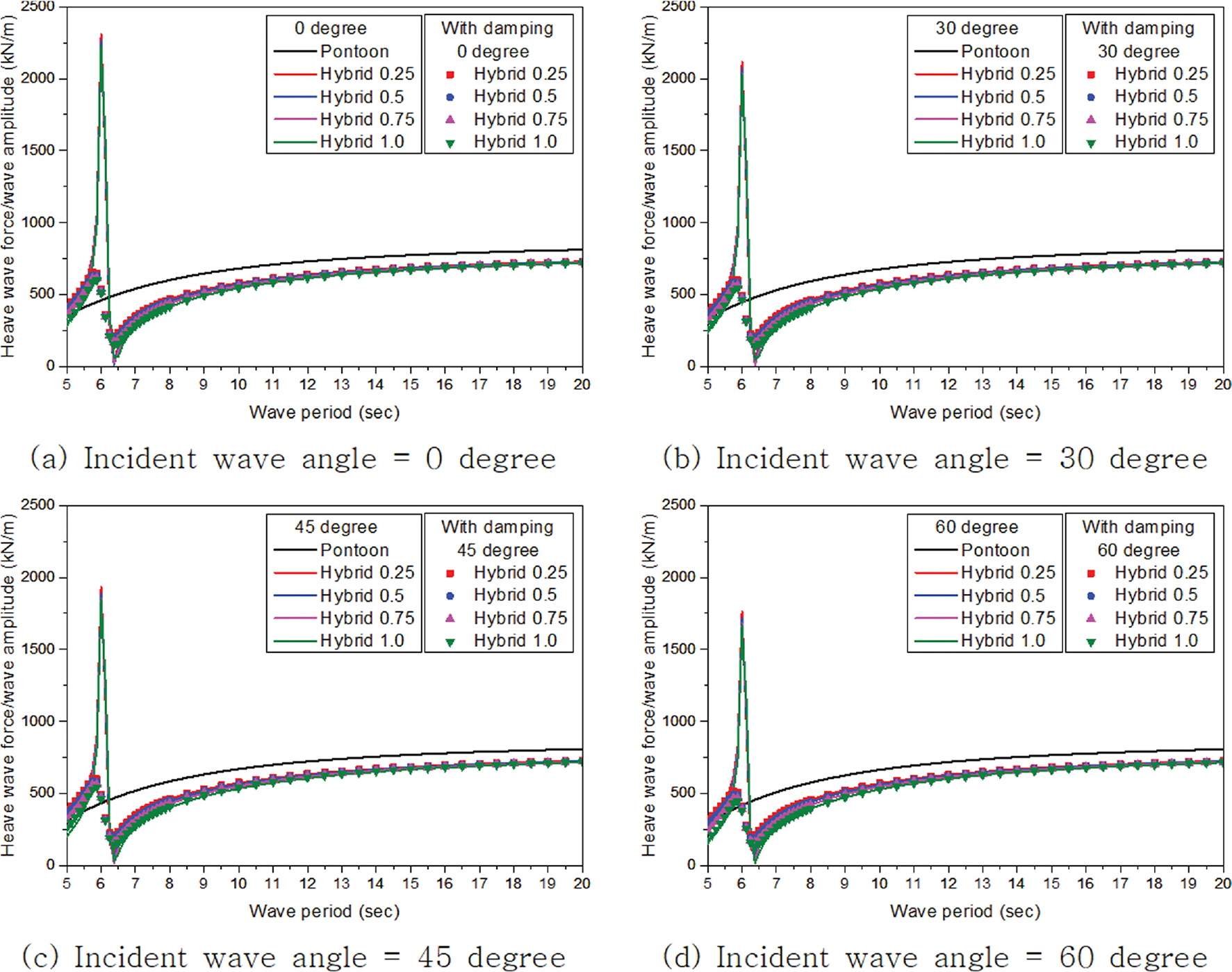
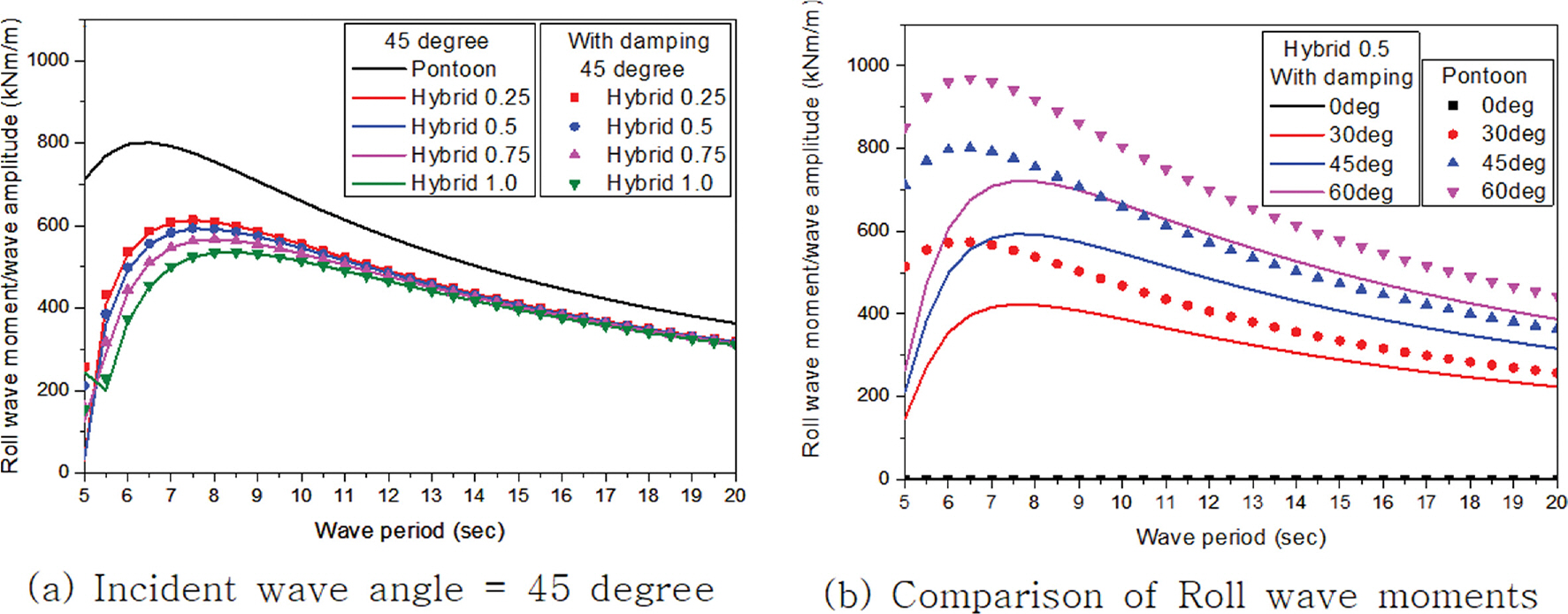
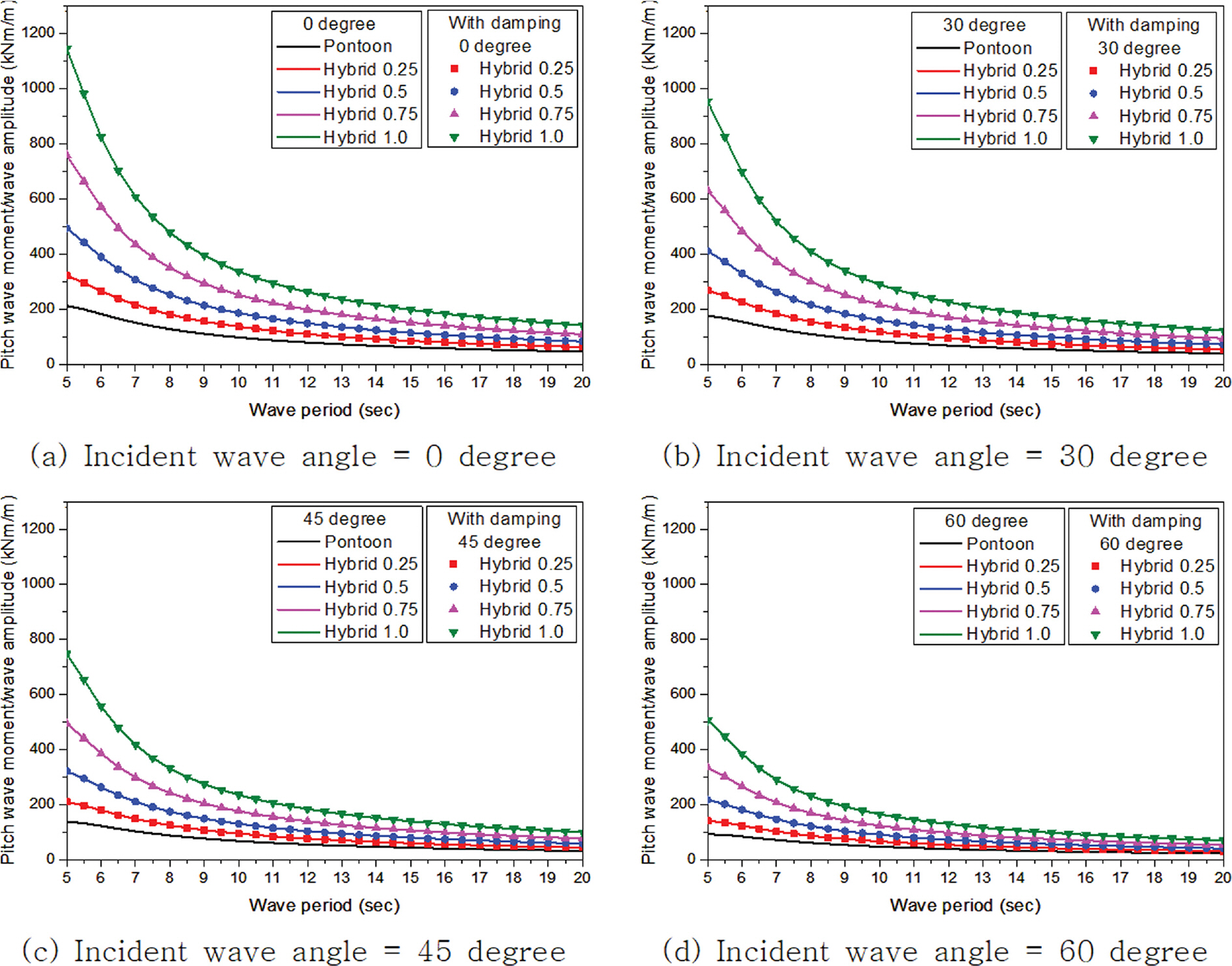
부유체가 수중에 고정되어 있다고 가정할 때 입사하는 파랑이 부유체에 작용하는 힘을 파랑 강제력(Wave exciting force)이라 한다. Fig. 8~13은 입사하는 파랑의 입사각도 변화(0도, 30도, 45도, 60도)에 따른 부유체에 작용하는 각 자유도별 파랑 강제력을 보여주고 있으며, Fig. 8~13에서 가로축은 입사하는 파랑의 주기를 나타내고 있으며, 세로축을 구조물에 작용하는 파력 및 모멘트를 입사하는 파랑의 진폭(= 입사파 파고(H)/2)으로 나눈 값이다. Fig. 10에서 수평감쇠판의 길이 변화에 관계없이 주기 6.0초에서 공진이 발생하였으며 감쇠효과가 적용될 경우에는 이러한 공진이 발생하지 않는 것을 확인할 수 있었다. 그리고 이러한 특정 주기에서의 공진은 상하로 구조물에 작용하는 파력(Heave force)에만 영향을 주고 구조물의 전후 파력(Surge force)과 좌우 파력(Sway force)에는 영향이 나타나지 않았다. 특히 부유체의 회전력(Roll moment, Pitch moment)은 상하 파력(Heave force)과도 밀접한 관련이 있는데 특정 주기에서의 공진에 의한 급격한 상하 파력 증가는 회전력에 거의 영향을 주지 않는 것으로 나타났다. 이는 구조물에 의해 둘러싸인 유체영역이 하이브리드 부유식 구조물의 가운데 위치하고 부유체의 회전력을 발생시킬 수 있는 상하 파력의 회전 팔길이가 매우 짧기 때문으로 판단된다. 전후 파력의 경우 입사하는 파랑 각도 변화에 관계없이 검토된 전 주기에서 폰툰형에 작용하는 파력이 하이브리드형보다 작은 값을 보이고 있다. 하이브리드형에 작용하는 전후 파력은 수평감쇠판의 길이가 길어질수록 주기가 짧은 단파에서는 값이 증가하는 경향을 나타내고 있으나 주기 12.0초 이상인 장파에서는 거의 차이가 발생하지 않고 폰툰형 부유식 구조물에 작용하는 파력과 유사한 값을 가지고 있다. 부유식 구조물에 작용하는 좌우 파력은 주기 6.0초 이하를 제외하고는 폰툰형의 파력이 하이브리드형보다 높게 나타나고 있으며 수평감쇠판의 길이가 길어질수록 주기가 짧은 단파에서는 파력값이 증가하지만 주기가 길어질수록 거의 차이가 발생하지 않은 경향이 나타났다. 상하 파력은 수평감쇠판의 길이가 길어질수록 파력이 감소하며 공진이 발생하는 주기 6.0초 이하에서는 폰툰형보다 높은 값을 가지지만 그 외 주기에서는 폰툰형보다 작고 주기가 길어질수록 폰툰형과의 차이가 감소하는 경향이 나타났다. 수평감쇠판의 길이가 길어질수록 상하 파력이 감소하는 원인을 Koh and Cho(2016)의 연구에서는 파랑강제력은 Froude-Kryloff력과 회절력(Diffraction force)의 합으로 표시되는데, 감쇠판의 길이가 길어질수록 회절력이 증가하여 회절력과 Froud-Kryloff력의 교차점에서 발생하는 상쇄 주파수(Cancellation frequency)가 증가하기 때문이라고 서술하고 있다. 횡 모멘트(Roll moment)는 폰툰형이 하이브리드형보다 높게 나타나고 있으며 수평감쇠판의 길이가 길어질수록 주기가 짧은 단파에서는 감소하는 경향을 보이다가 주기 12.0초 이후부터는 거의 유사한 값을 가지고 있다. 이는 횡 모멘트가 좌우 파력과 상하 파력에 의해 발생되는데 좌우 파력의 회전 팔길이보다 상하 파력의 회전 팔길이가 길어 상하 파력의 지배적인 영향을 받는 것으로 판단된다. 종 모멘트(Pitch moment)는 검토된 전 주기에서 폰툰형이 하이브리드형보다 작게 나타나고 수평감쇠판의 길이가 길어질수록 증가하고 주기가 길어질수록 감소하는 경향이 나타났다. 즉, 종 모멘트는 전후 파력과 상하 파력에 의해 발생되는데 주로 전후 파력의 지배적인 영향을 받는 것을 알 수 있다. 선수 모멘트(Yaw moment)는 폰툰형과 하이브리드형 간의 차이가 미소하게 나타나 수평감쇠판의 길이 변화에 큰 영향을 받지 않는 것으로 나타났다.

Fig. 8.

Comparison of surge wave exciting force for various incident wave angles.

Fig. 9.

Comparison of sway wave exciting force for various incident wave angles.

Fig. 10.

Comparison of heave wave exciting force for various incident wave angles.

Fig. 11.

Comparison of roll wave exciting moment for various incident wave angles.

Fig. 12.

Comparison of pitch wave exciting moment for various incident wave angles.

Fig. 13.

Comparison of yaw wave exciting moment for various incident wave angles.

정수 중에서 부유체가 정해진 자유도로 강제 동요할 때 부유체로부터 방사하는 파에 의하여 발생하는 힘을 방사력(Radiation forces)이라고 한다. 강제 동요로 인하여 발생하는 유체동역학적 힘 중에서 실수부는 가속도와 위상이 같아 부유체의 질량에 더해지는 부가질량(Radiation added mass)되고, 허수부는 속도와 위상이 같아 부유체의 감쇠(Radiation damping)가 된다. Fig. 14와 15는 부유체의 각 자유도별 강제 동요로 발생하는 부가질량과 감쇠를 보여주고 있다. Fig. 14에서 감쇠효과는 전후 및 좌우 부가질량에는 나타나지 않고 상하 부가질량에서만 발생되고 있다. 상하 부가질량의 경우 주기 6.5초 이하에서는 감쇠효과에 따른 차이가 발생하고 공진 주기인 6.0초에서 매우 큰 변화를 보이고 있으나 그 외 주기에서는 차이가 없었다. 이러한 감쇠효과에 따른 상하 부가질량의 변화는 횡 부가질량에만 영향을 주고 그 외 회전에는 영향이 나타나지 않았다. 좌우 부가질량을 제외하고는 폰툰형의 부가질량이 하이브리드형보다 작은 것을 알 수 있으며 하이브리드형의 경우 수평감쇠판의 길이가 길어질수록 부가질량이 증가하는 경향이 나타났다.

Fig. 14.

Comparison of added mass.

Fig. 15에서도 감쇠효과는 전후 및 좌우 감쇠에는 나타나지 않고 주기 6.5초 이하인 상하 감쇠에서만 발생하고 있으며 이러한 상하 감쇠 변화는 횡 감쇠에 매우 큰 영향을 주는 것을 알 수 있다. 폰툰형과 하이브리드형의 감쇠 차이는 주로 주기 짧은 단파에서 큰 차이가 나타나고 주기가 길어질수록 거의 유사한 값을 갖는 것을 볼 수 있다. 특히 횡 감쇠와 종 감쇠에서 뚜렷한 차이가 발생하고 있으며 하이브리드형인 경우 수평감쇠판의 길이가 길어질수록 횡 감쇠는 감소하지만 종 감쇠는 증가하는 반대의 경향이 나타나고 폰툰형의 경우에는 횡 감쇠는 하이브리드형보다 높은 값을 가지지만 종 감쇠는 낮은 값을 가지는 경향을 보였다.

Fig. 15.

Comparison of radiation damping.

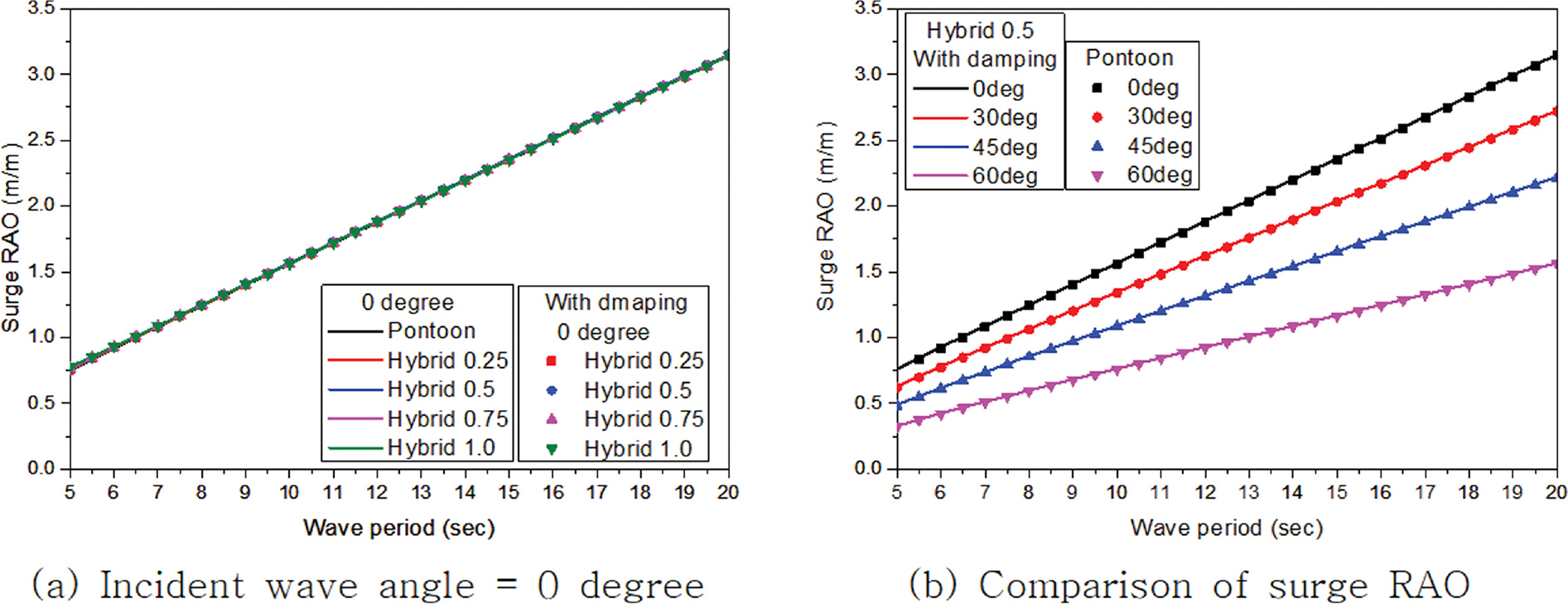
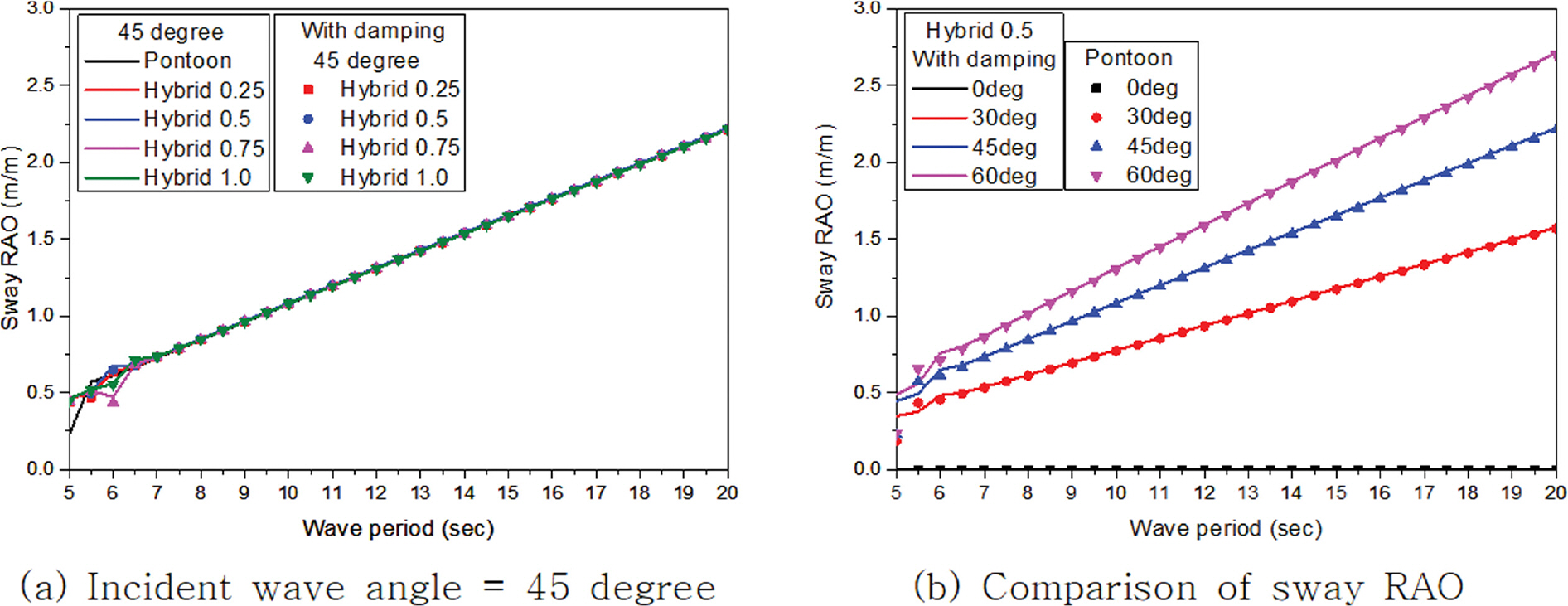
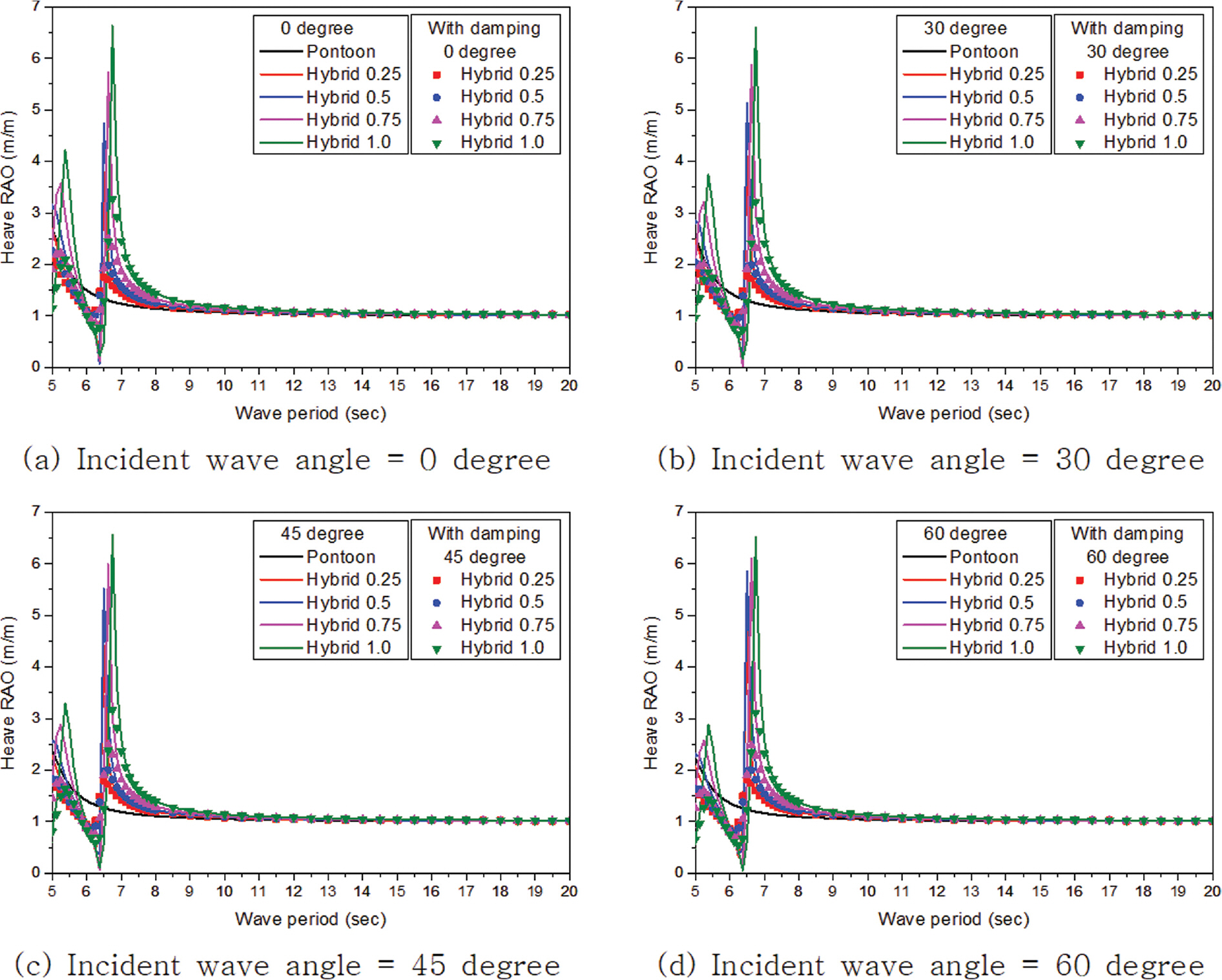
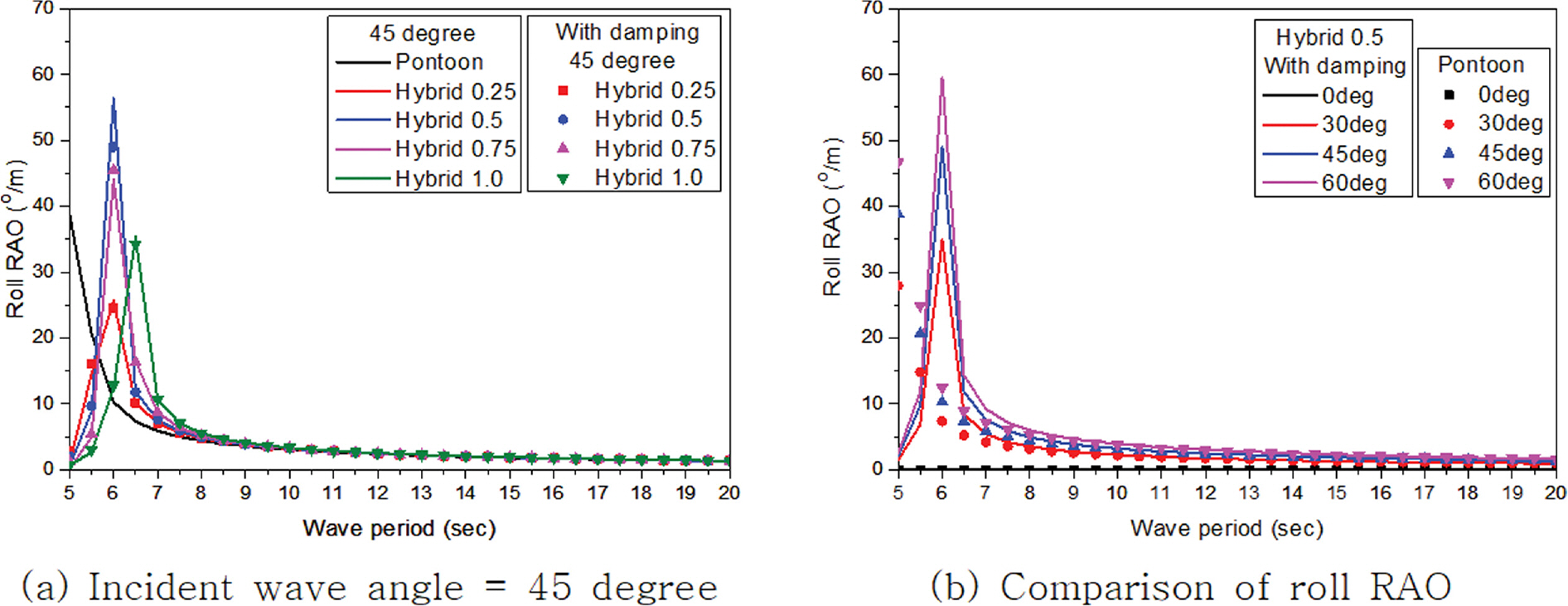
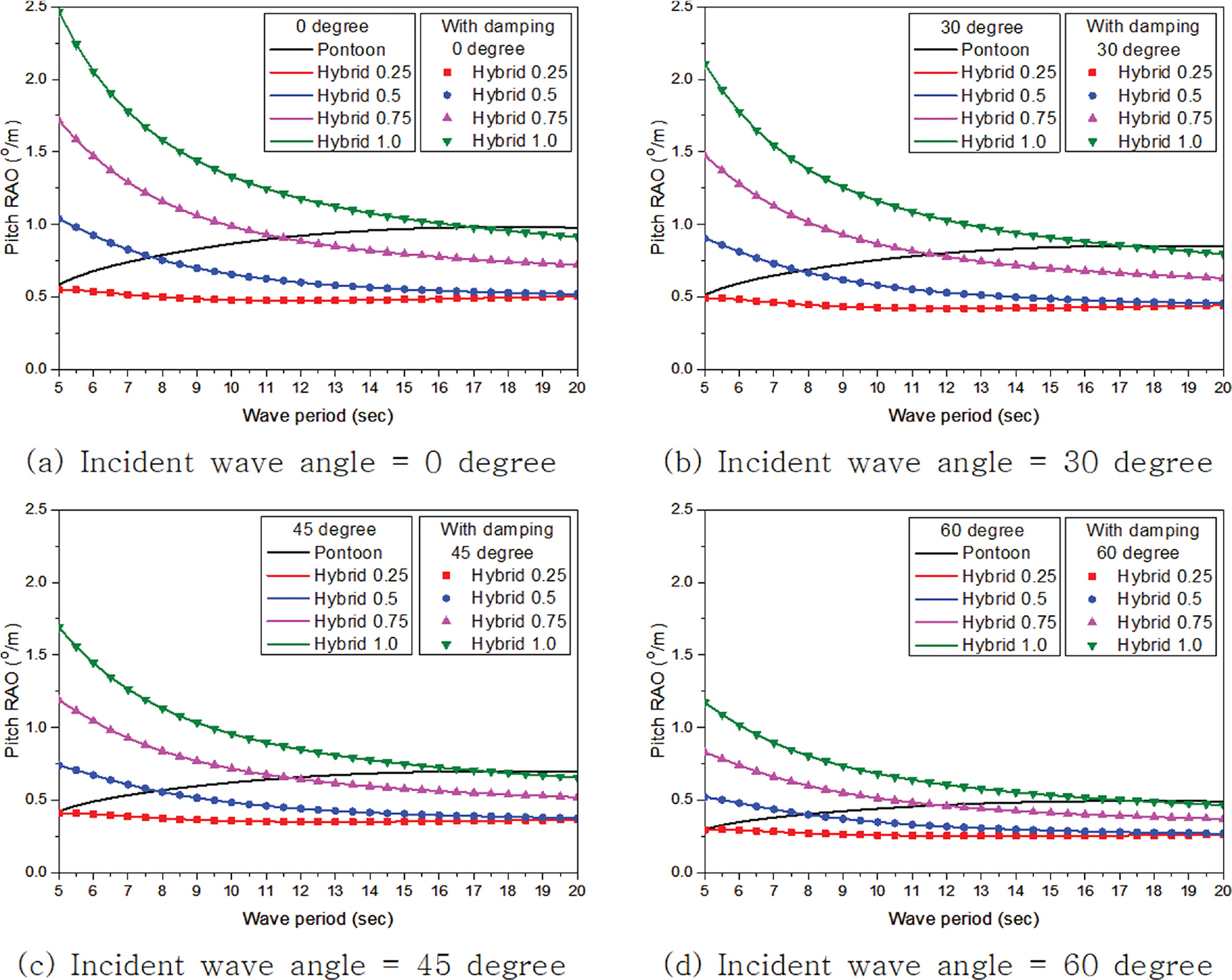
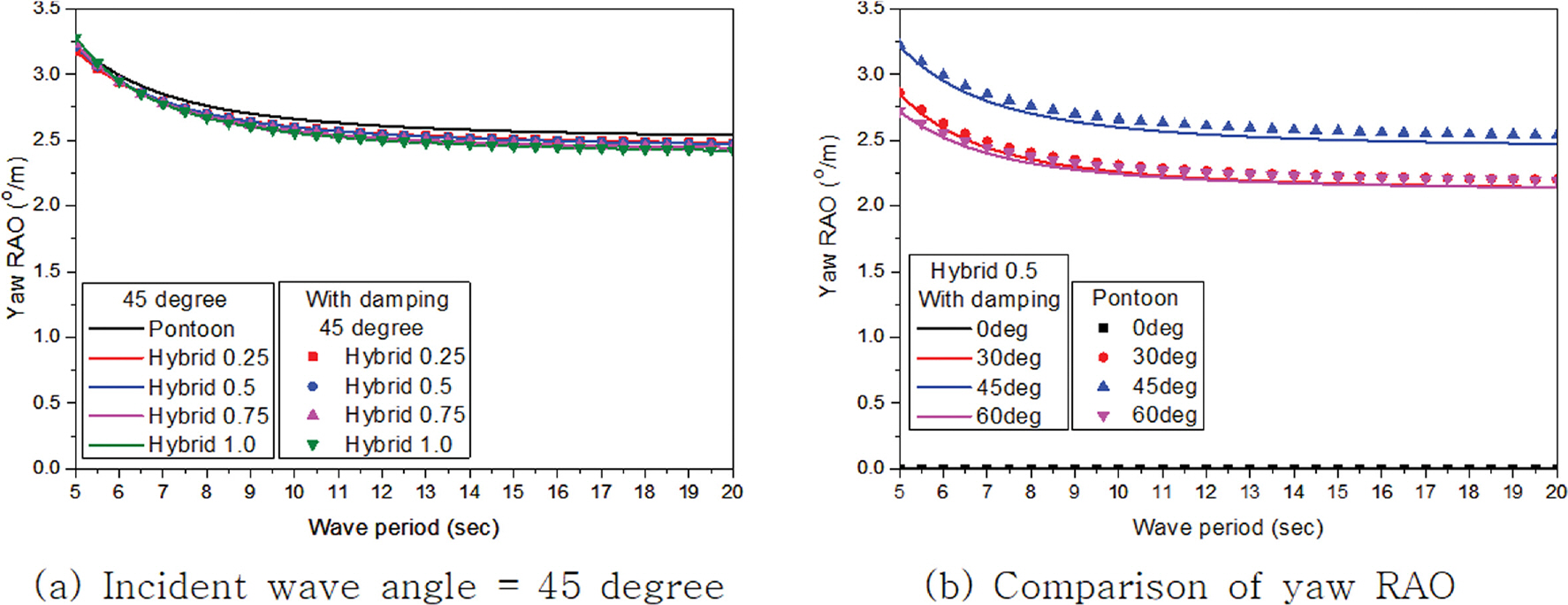
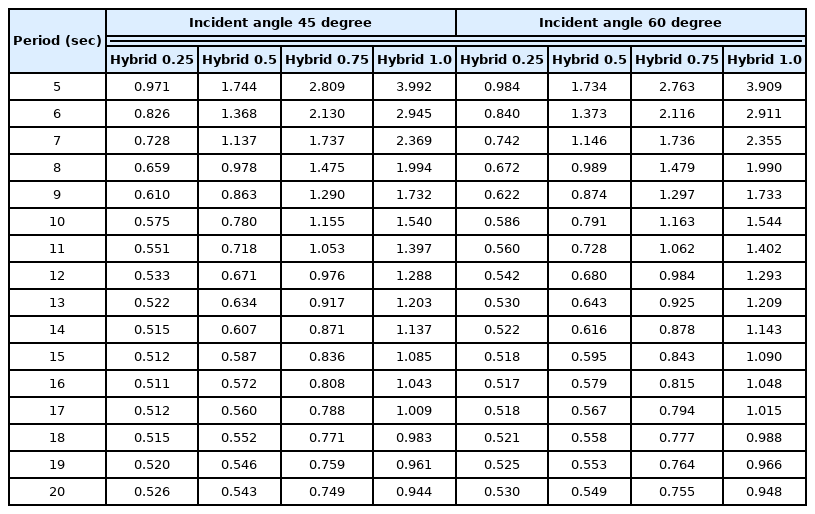
주파수에 따른 부유체의 동요 진폭과 입사파 진폭과의 비율을 응답진폭함수(Response Amplitude Operator, RAO)라 하며 이를 이용하여 입사하는 파랑조건에 따른 부유체의 거동 특성을 분석할 수 있다. Fig. 16~21은 입사하는 파랑의 각도 변화에 따른 부유체의 각 자유도별 RAO를 나타내고 있다. 감쇠존 적용에 따른 차이는 좌우 동요, 상하 동요, 횡 동요의 주기 7.5초 이하에서만 나타나고 그 외 주기에서는 발생하지 않고 있다. 이는 감쇠효과가 공진이 발생하는 주기 부근에서만 나타나고 그 외 주기에서는 발생하지 않는 기존 연구들(Chen, 2005; Fournier et al., 2006; Pauw et al., 2007; Bunnik et al., 2009; Watai et al., 2015; Ganesan T and Sen, 2016; Chen et al., 2021)과 같은 경향을 보이는 것을 알 수 있다. 종 동요와 선수 동요를 제외하고는 폰툰형과 하이브리드형 부유식 구조물의 거동 특성은 공진이 발생하는 주기를 포함해 주기 8.0초 이하에서는 다소 차이가 발생하고 있지만 그 이상의 주기에서는 수평감쇠판의 길이 변화에 관계 없이 두 형식이 매우 유사한 값을 가지는 것을 알 수 있다. 선수 동요인 경우 하이브리드형이 폰툰형보다 거동이 작아 부유체가 안정적인 것으로 나타났다. 하지만 부유식 구조물의 거동에서 가장 중요한 종 동요인 경우 수평감쇠판의 길이 변화에 따라 거동 특성이 서로 다르게 나타났으며 수평감쇠판 길이가 길어질수록 종 동요가 증가해 부유체의 안정성이 감소하는 것을 알 수 있다. Table 3와 4는 수평감쇠판 길이 변화에 따른 하이브리드형의 종 동요를 폰툰형 종 동요로 나눈 비를 보여주고 있다. 검토된 전 주기에서 Hybrid 0.25가 폰툰형보다 종 동요 값이 작고 하이브리드형 중에서도 가장 작은 종 동요가 발생하였다. 그리고 수평감쇠판의 길이가 길어짐에 따라 주기가 짧은 단파에서는 종 동요값이 증가하는 경향이 발생하여 특정 주기 이하에서는 폰툰형보다 종 동요 값이 높아 부유체의 안정성이 감소하였다. 특히 수평감쇠판이 길이가 가장 긴 Hybrid 1.0은 대부분의 주기에서 폰툰형보다 종 동요 값이 높게 나타나 부유체의 안정성을 향상시키기 위해 적용된 수평감쇠판이 반대로 부유체의 안정성을 감소시켰다. 따라서 부유체의 안정성을 향상시키기 위해 수평감쇠판을 적용할때에는 6자유도 운동 기반의 분석을 통해 부유체의 요구성능을 만족할 수 있는 적절한 길이 선택이 매우 중요하며 이러한 결과는 Park et al.(2018)의 연구에서도 확인할 수 있다.

Fig. 16.

Comparison of surge RAO for various incident wave angles.

Fig. 17.

Comparison of sway RAO for various incident wave angles.

Fig. 18.

Comparison of heave RAO for various incident wave angles.

Fig. 19.

Comparison of roll RAO for various incident wave angles.

Fig. 20.

Comparison of pitch RAO for various incident wave angles.

Fig. 21.

Comparison of yaw RAO for various incident wave angles.

Table 3.

Ratio(Hybrid/Pontoon) of pitch RAO for incident angle 0 and 30 degree

Table 4.

Ratio (Hybrid/Pontoon) of pitch RAO for incident angle 45 and 60 degree

4. 결 론

본 연구에서는 육상 이동이 가능한 단위 모듈의 수직 및 수평 적층으로 확장된 하이브리드 부유식 구조물의 안정성을 향상시키기 위해 수평감쇠판을 적용하고 상용 프로그램인 ANSYS AQWA를 이용하여 부유식 구조물의 거동 특성을 분석하였다. 제안된 하이브리드 부유식 구조물의 경우 단위 모듈 결합에 의해 구성되기 때문에 구조물에 의해 둘러싸인 유체영역이 해수면 근처에 존재하여 특정 주기에서 공진이 발생할 가능성이 있다. 따라서 ANSYS AQWA에서 제공되는 감쇠존 효과를 구조물에 의해 둘러싸인 유체영역에 적용하여 부유식 구조물의 거동 특성을 면밀하게 분석하고 일반적으로 사용되는 폰툰형 부유식 구조물과 비교하였다. 부유체의 복원성(GZ curve) 검토결과 하이브리드형이 폰툰형과는 눈에 띄게 다른 패턴을 나타내고 있으며 수평감쇠판의 길이가 길어질수록 GZ 값이 증가하여 복원력이 증가되는 것을 확인할 수 있었다. 감쇠존 적용에 따른 차이는 좌우 동요, 상하 동요, 횡 동요의 주기 7.5초 이하에서만 나타나고 그 외 주기에서는 발생하지 않았다. 부유체의 회전운동은 상하 동요와 밀접한 관련이 있는데 특정 주기에서의 공진에 의한 급격한 상하 동요 증가는 회전운동에 거의 영향을 주지 않는 것으로 나타났다. 이는 구조물에 의해 둘러싸인 유체영역이 하이브리드 부유식 구조물의 가운데 위치하고 부유체의 회전력을 발생시킬 수 있는 상하 운동의 회전 팔길이가 매우 짧기 때문으로 판단된다. 부유식 구조물의 거동에서 가장 중요한 종 동요의 경우 수평감쇠판의 길이 변화에 따라 거동 특성이 서로 다르게 나타났으며 수평감쇠판 길이가 길어질수록 종 동요가 증가해 폰툰형보다 부유체의 안정성이 감소하는 것을 알 수 있었다. 따라서 부유체의 안정성을 향상시키기 위해 수평감쇠판을 적용할때에는 6자유도 운동 기반의 분석을 통해 부유체의 요구성능을 만족할 수 있는 적절한 길이 선택이 매우 중요하다. 부유체의 안정성을 면밀하게 검토하기 위해서는 주파수영역 및 시간영역의 수치해석 결과를 바탕으로 수리모형실험 데이터와 비교가 이루어져야 한다. 따라서 향후 본 연구에서 고려되지 못한 부유체의 점성감쇠력을 적용한 시간영역의 수치해석과 수리모형실험을 통해 하이브리드 부유식 구조물에 대한 분석이 추가로 수행되어야 할 것으로 생각된다.

Article information Continued