국내 서해안 파랑 관측자료를 이용한 대표주기 산정 및 최적 확률밀도함수 추정
Estimation of Representative Wave Period and Optimal Probability Density Function Using Wave Observed Data around Korean Western Coast
Article information
Abstract
본 연구에서는 서해안 해상기상타워 2기에서 관측된 수면변동자료를 이용하여 해양특성을 구분하는 주요 인자인 첨두주기 Tp와 평균주기 T02와 Tm-1, 0를 산정하고 이상자료의 비율, 상관관계 분석 및 최적 확률밀도함수를 추정하였다. 산정된 대표주기 중 첨두주기의 경우, 이상 자료의 비율은 각각의 지점에서 5.73 %, 0.67 %로 나타났으며, T02는 4.35%, 0.01%, Tm-1, 0는 2.82%, 0.03%로 나타났다. 한편, T02와 Tp 사이의 관계를 분석한 결과 각 지점별로 0.53, 0.63의 관계로 산정됐으며, Tm-1, 0와 Tp의 관계는 각각 1.15, 1.32로 나타났다. T02와 Tm-1, 0는 서로 1.18, 1.22의 관계를 보이고 있었다. 산정된 대표주기의 최적 확률밀도함수를 추정한 결과, Tp는 각각의 지점에서 ‘Lognormal’, ‘Normal’ 분포를 따르고 있었으며, T02는 ‘Gamma’, ‘Normal’ 분포, Tm-1, 0는 각각 ‘Log-normal’, ‘Normal’ 분포가 우세한 것으로 나타났다. 이러한 결과는 서해안을 대상으로 수행되는 파랑 분석에 기초자료로 사용될 수 있을 것으로 판단된다.
Trans Abstract
In this study, the peak wave period Tp and mean wave period T02 and Tm-1, 0, which are major parameters for classifying ocean characteristics, were calculated using water surface elevation data observed from the second west coast oceanographic and meteorological observation tower. In addition, the ratio of abnormal data, correlation analysis, and optimal probability density function were estimated. In the case of Tp among the calculated representative periods, the proportion of abnormal data was 5.73% and 0.67% at each point, and T02 was 4.35% and 0.01%. Tm-1, 0 was found to be 2.82% and 0.03%. Meanwhile, as a result of analyzing the relationship between T02 and Tp, the relationship was calculated to be 0.53 and 0.63 for each point. The relationship between Tm-1, 0 and Tp was 1.15 and 1.32, respectively, and T02, Tm-1, 0 was 1.18 and 1.22. As a result of estimating the optimal probability density function of the calculated representative period, Tp followed the ‘Log-normal’ and ‘Normal’ distributions at each point, and T02 was ‘Gamma’, ‘Normal’ distribution and Tm-1, 0 showed that ‘Log-normal’ and ‘Normal’ distribution were dominant, respectively. It is decided that these results can be used as basic data for wave analysis conducted on the west coast.
1. 서 론
해양에서 주로 수행되는 해양구조물 설계, 극치 분석, 파랑 스펙트럼 분포형 추정 등의 다양한 분석에서는 주로 파고와 주기가 이용된다. 파고와 주기는 파열분석법(Wave Train Analysis)과 파랑 스펙트럼 분석법(Wave Spectrum Analysis)을 통해 산정되며, 이를 산정하기 위한 기초 자료로 수면변동자료(WSE, Water Surface Elevation)가 이용된다. 최근에는 다양한 해양 특성을 분석하기 위해 유의파고(Hm0 ≈ Hs)와 첨두주기가 적용되고 있기 때문에 파랑 스펙트럼 분석이 주로 사용되고 있으며, 이를 통해 정확한 파랑 변수를 산정하는 것이 매우 중요하다(Karunarathna et al., 2014; Vanem, 2018; Shao et al., 2018).
파랑 스펙트럼 분석을 통해 산정되는 유의파고(Hs)의 경우, 추정되는 스펙트럼의 면적을 통해 계산되기 때문에 산정되는 유의파고에 대한 불확실성 문제는 발생하지 않는다. 그러나, 첨두주기의 경우, 파랑 스펙트럼에서 최대 주파수에 해당되는 값을 이용하여 산정되고 있지만 낮은 파고에서 주로 발현하는 다중 첨두 스펙트럼(Bimodal Spectrum) 형상으로 인하여 첨두주기 산정에 불확실성 문제가 발생하고 있다. 이에 다중 첨두 스펙트럼으로 인해 발생하는 파랑 변수 산정 및 매개변수 추정의 문제점을 해결하기 위해 수치모델 및 관측자료 분석이 다양하게 이루어지고 있다(Vettor and Soares, 2020; Garcia-Gabin, 2015). 또한, Lee et al.(2022)는 최적 평활화 기법과 신뢰구간 추정 기법을 적용하여 최적 첨두주기를 추정하는 연구를 수행하였으며, 파랑 스펙트럼 에너지 밀도가 작은 경우 및 다중 첨두 스펙트럼 형상이 발생하는 경우 정확한 첨두주기를 추정함에 한계가 있음을 확인한 바 있다.
일반적으로 파랑 스펙트럼 분석 과정을 거쳐 산출되는 첨두주기뿐 아니라 0차 모멘트(m0), 1차 역모멘트(m-1), 2차 모멘트(m2)를 이용하여 산정되는 평균주기도 매우 중요한 파랑 변수로 강조되고 있으며, 최근 유럽에서는 파랑 스펙트럼을 통해 추정되는 첨두주기의 불확실성 문제로 인하여 평균주기 사용의 중요성이 대두되고 있다(IHAR, 1989; Goda, 2010; Allsop et al., 2016). 대상 해역의 파랑 분포 특성을 파악하기 위해서는 스펙트럼 분포 모델(PM, BM, JONSWAP, TMA 스펙트럼 등)에서는 첨두주기를 주로 사용하지만, 첨두주기는 불연속적인 주파수에 대하여 계산되기 때문에 첨두주기 또한 불연속적인 값이 되며, 높은 파고에서 시간 변화를 확인했을 때, 첨두주기는 불연속적으로 변화할 수 있기 때문에 평균주기를 추정하는 것이 필요하다(Goda, 2010).
한편, 해양에서 주로 분석되고 있는 극치분석의 한 방법으로 결합확률분포 분석이 요구되고 있다. 결합확률분포 분석은 해양의 다양한 주요 변수(파고, 주기, 파향 등)는 각각의 항목이 독립적인 항목이 아닌 상호 어느 정도의 관계가 예상되는 항목으로 기존 단변량 분석 방법으로 추정 정보가 제한되는 한계가 있기 때문에, 각각의 항목에 대한 상관성을 고려한 조건에서 목표 초과확률에 대한 범위를 산정하는 연구가 수행되어지고 있으며, 국제 표준에서도 I-FORM(Inverse First Order Reliability Method)을 이용한 분석이 요구되고 있는 실정이다(Veritas, 2010; Lee et al., 2023). 이러한 분석을 수행함에 있어 각각의 파랑 변수에 대하여 정확한 확률밀도함수를 추정하는 것이 매우 중요하게 여겨지고 있으며, 이에 따라 이에 본 연구에서는 산정된 대표주기에 대하여 두 가지 분포 적합도 검정을 통한 최적 확률밀도함수를 추정하였다.
2. 자료 및 방법
2.1 분석 자료
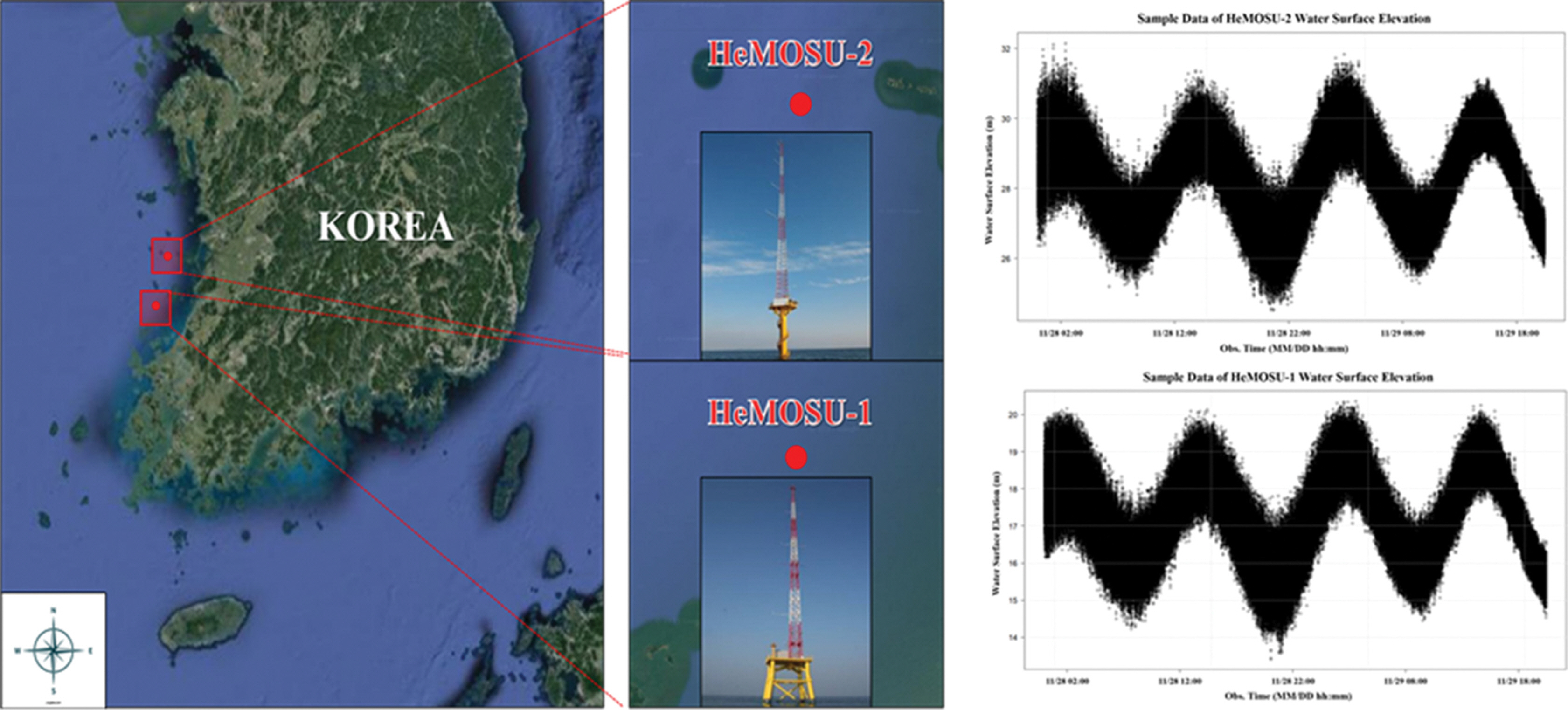
본 연구에서 파랑 스펙트럼 분석을 통해 대표주기를 산정하기 위해 사용된 자료는 해상풍력 단지 구축을 위해 설치된 HeMOSU 기상타워 2기에서 관측된 수면변동자료를 이용하였으며, 이때, HeMOSU-1의 설치 위치는 126o07'45''E, 35o27'55''N, HeMOSU-2의 설치 위치는 126o12'45''E, 35o49'40''N 이다(Fig. 1 참조).
Location map and water surface elevation data of HeMOSU-1, 2 in the western coast of the Korea.
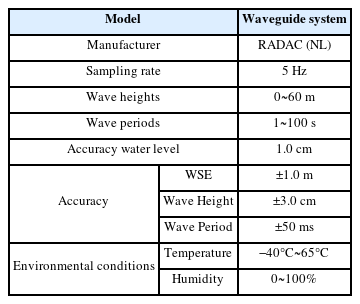
수면변동자료는 파랑 스펙트럼 분석에 사용되는 가장 기본적인 관측자료이며, 관측에 사용된 Waveguide 장비는 Radac B.V.에서 1996년 개발된 장비로서, 수면변동자료를 200 ms(0.2 s) 간격으로 관측하는 고해상도 장비이다. HeMOSU-1의 관측 기간은 2013.07.28부터 2014.07.06이며, 결측을 제외한 총 170일 관측자료를 사용하였다. 또한, HeMOSU-2의 관측 기간은 2013.11.26부터 2014.04.23이며, 결측을 제외한 총 133일 관측자료로서, 각각의 지점에 결측률은 각각 28.5%, 12.1%이다. 자료의 결측은 장비의 시스템 결함 및 유지보수 기간으로 인하여 발생된 것으로 판단된다. 두 지점의 수심은 각각 13.5 m와 30.0 m이며, 관측장비의 수면변동 관측 정확도는 ±1.0 cm이다(Table 1 참조).
Waveguide server details
2.2 대표주기 산정
해양에서 주로 사용되는 인자는 파고와 주기이며, 본 연구에서는 주기에 대한 분석을 수행하였다. 일반적으로 해양구조물 설계, 파랑 분포모델 산정 등에 주로 사용되는 주기는 첨두주기이며, 이는 파랑 스펙트럼 분석을 통해 계산되는 스펙트럼 에너지밀도에서 첨두주파수의 역수(1/fp)로 산정이 다. 첨두주기 산정을 위해 파랑 스펙트럼 분석은 Lee et al. (2022)에서 사용된 분석 방법을 적용하였다. 해당 스펙트럼 분석 방법은 시간 영역에서 관측된 수면변동자료를 영점보정한 후, 데이터 윈도우가 적용된 자료를 변환을 통해 주파수 영역에서 최적 첨두주기를 산정하였으며, 신뢰구간 문제를 해결하기 위한 평활화를 수행한다. 본 연구에서 사용한 첨두주기 자료는 해당 방법을 통해 산정된 값을 이용하였다. 또한, 최근 중요성이 강조되고 있는 평균주기에 대한 추가 분석을 수행하기 위하여 추정된 스펙트럼 정보를 통해 평균주기를 산정하였다. 파랑 스펙트럼 분석을 통해 산정 가능한 평균주기는 T02와 Tm-1, 0이 있으며, 파열분석법을 통해 산정되는 평균주기
여기서, m-1, m0, m2은 각각 스펙트럼 에너지 밀도에서의 n차 모멘트를 의미하며, 이는 다음과 같이 산정할 수 있다.
한편, CIRIA et al.(2007)은 파랑 스펙트럼 분석을 통해 산정되는 두 개의 평균주기 중, Tm-1, 0에 대하여 수리실험을 통해 관측된 스펙트럼을 기반으로 Tm-1, 0와 Tp 사이의 선형관계를 다음 식(6)과 같이 산정하였다. 해당 선형관계식을 통하여 특별한 정보 없이 첨두주기만을 알고 있는 경우 Tm-1, 0을 추정할 수 있으나, 수심이 매우 낮은 지점 및 다중 피크의 영향이 주로 발생하는 경우에는 수치 해석을 통해 보다 정확한 값을 결정하여 사용하여야 한다.
2.3 최적 대표주기 확률밀도함수 추정
일반적으로 주기의 최적 확률밀도함수는 대수정규분포(Log-normal distribution)가 제시되고 있다(Kamphuis, 2000; Holthuijsen, 2007). 본 연구에서는 대표주기(T02, Tm-1, 0, Tp)에 가장 적합한 확률밀도함수를 추정하기 위해 일반적으로 가장 널리 사용되고 있는 최우도법(MLE, Maximum Likelihood Estimation)을 사용하였다(Venables and Ripley, 2013). 최우도법은 표본자료의 확률이 최대가 되도록 추정하는 방법이며, 점 추정에 의한 방법이다. 이러한 최우도법은 매개변수를 추정하는 방법 중 하나이며, 이를 위해 다음 식(7), (8)과 같이 우도 함수 또는 대수 우도 함수를 사용한다.
여기서, f는 변수 δ로 결정되는 확률변수들의 확률 밀도함수를 의미한다.
첨두주기의 최적 확률밀도함수 추정에 사용된 후보함수는 ‘Normal’, ‘Lognormal’, ‘Gamma’ 분포를 적용하여 최적 확률밀도함수를 산정하였다(식(9)-(11) 참조).
- Normal distribution
- Log-normal distribution
- Gamma distribution
여기서, μ는 평균(Mean), σs는 표준편차(Standard Deviation), λ는 척도계수(Scale parameter), k는 형상계수(Shape parameter), ξ는 위치계수(Location parameter), X는 대표주기를 나타낸다.
한편, 분포 적합도 검정을 수행하기 위해 K-S test(Kolmogorov-Smirnov Test)를 통해 산정된 p-value를 이용하여 첨두주기의 확률 밀도 분포와 분포 적합도 검정을 수행하였다. 그러나, K-S test는 확률 밀도 분포의 양 끝단과 같은 무의미한 작은 차이까지 계산이 이루어지기 때문에 적절한 분포 차이 검정에는 한계가 있다. 이에 따라 본 연구에서는 산정된 대표주기 자료의 1%를 무작위로 샘플링하여 1,000번 반복 계산한 후, 산정된 p-value의 평균을 이용하여 대표주기와 가장 유사한 분포를 추정하였다(Lazariv and Lehmann, 2018). 이후, 다음 식(12)와 같이 KL Divergence(Kullback-Leibler Divergence)를 이용하여 각 확률 밀도 분포의 차이가 최소가 되는 최적 분포를 결정하였다. 여기서, KL Divergence 는 관측 스펙트럼의 분포와 추정 스펙트럼의 분포의 차이를 계산하는 방법으로서, DKL 값이 작을수록 두 분포가 유사함을 의미한다(Belov and Armstrong, 2011).
여기서, P(i)는 추정된 스펙트럼 에너지 밀도, Q(i)는 비교를 위해 사용된 확률 밀도 분포 함수를 의미한다.
3. 분석 결과
3.1 대표주기 산정 및 대표주기 간 상관관계
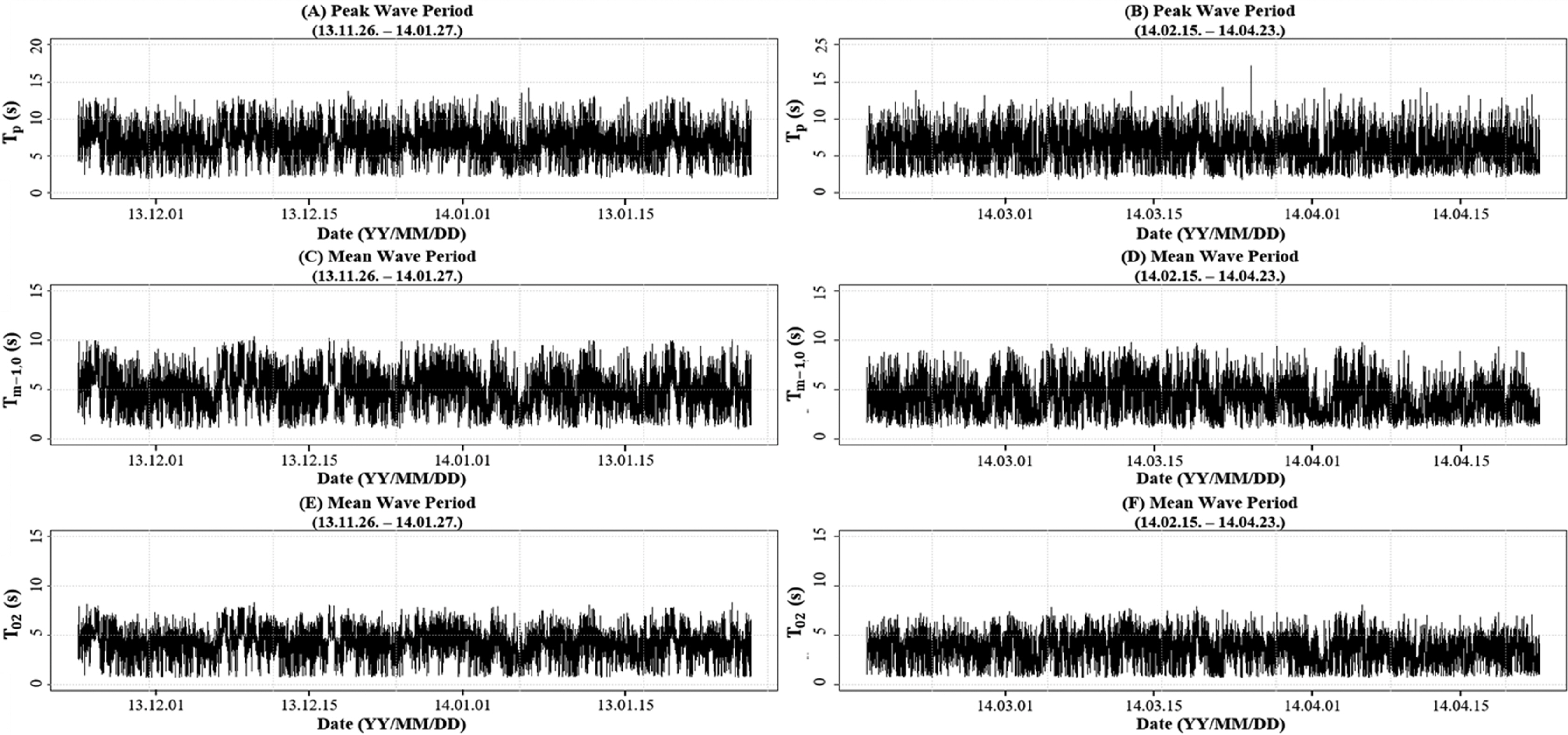
본 연구에서 산정한 대표주기의 시계열 그림은 다음 Fig. 2~3과 같다. 분석에 사용된 수면변동자료의 결측으로 인하여 Fig. 2의 (A)~(C)는 HeMOSU-1의 첨두주기, (D)~(F)는 Tm-1, 0, (G)~(I)는 T02의 시계열 그림을 기간에 따라 나눠서 제시하였다. 이와 마찬가지로 Fig. 3의 (A)~(B)는 HeMOSU-2의 첨두주기, (C)~(D)는 Tm-1, 0, (E)~(F)는 T02의 분석 결과 그림을 제시하였다.
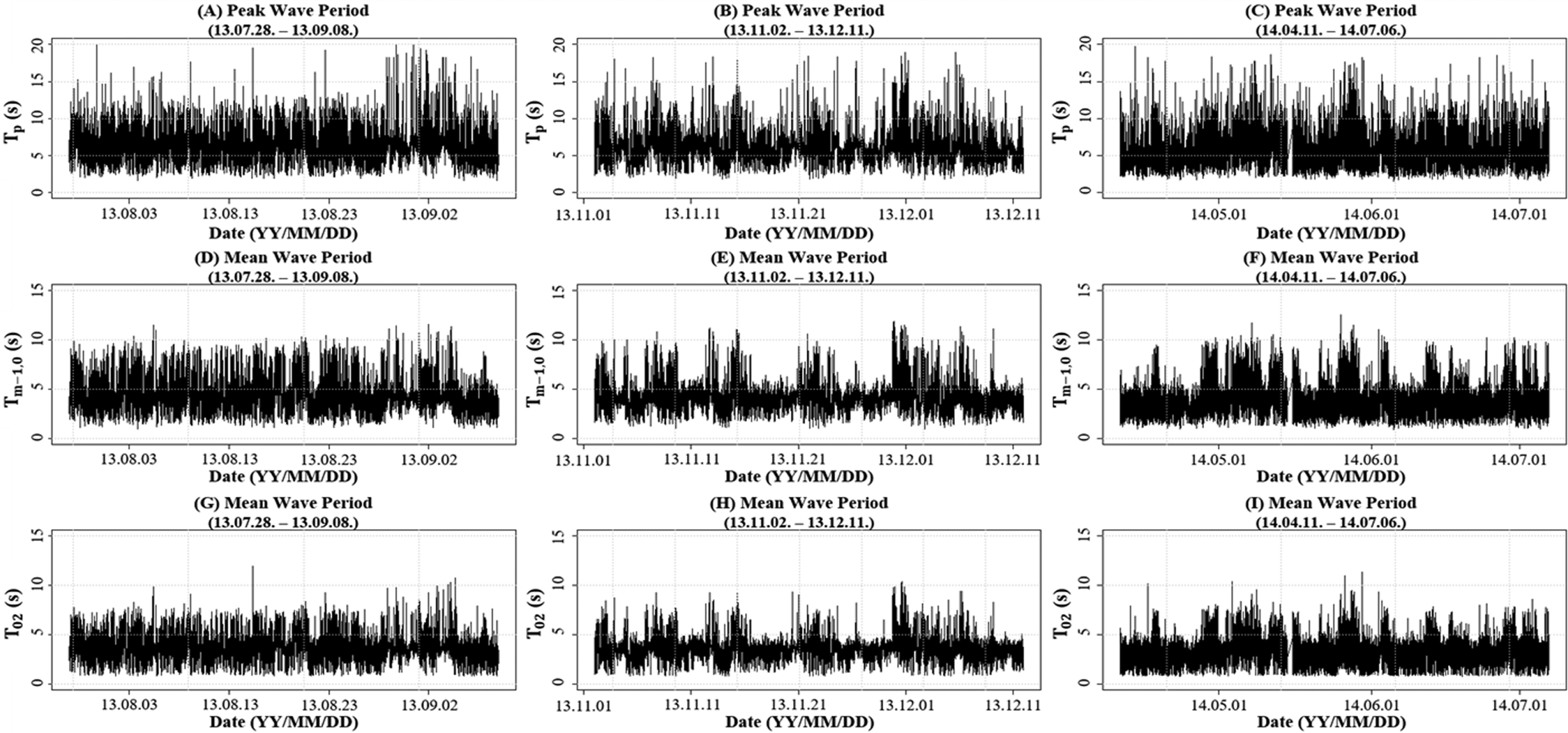
Time series of representative wave period at HeMOSU-1 (A, B, C: Tp, D, E, F: Tm−1, 0, G, H, I: T02).
Time series of representative wave period at HeMOSU-2 (A, B: Tp, C, D: Tm−1, 0, E, F: T02).
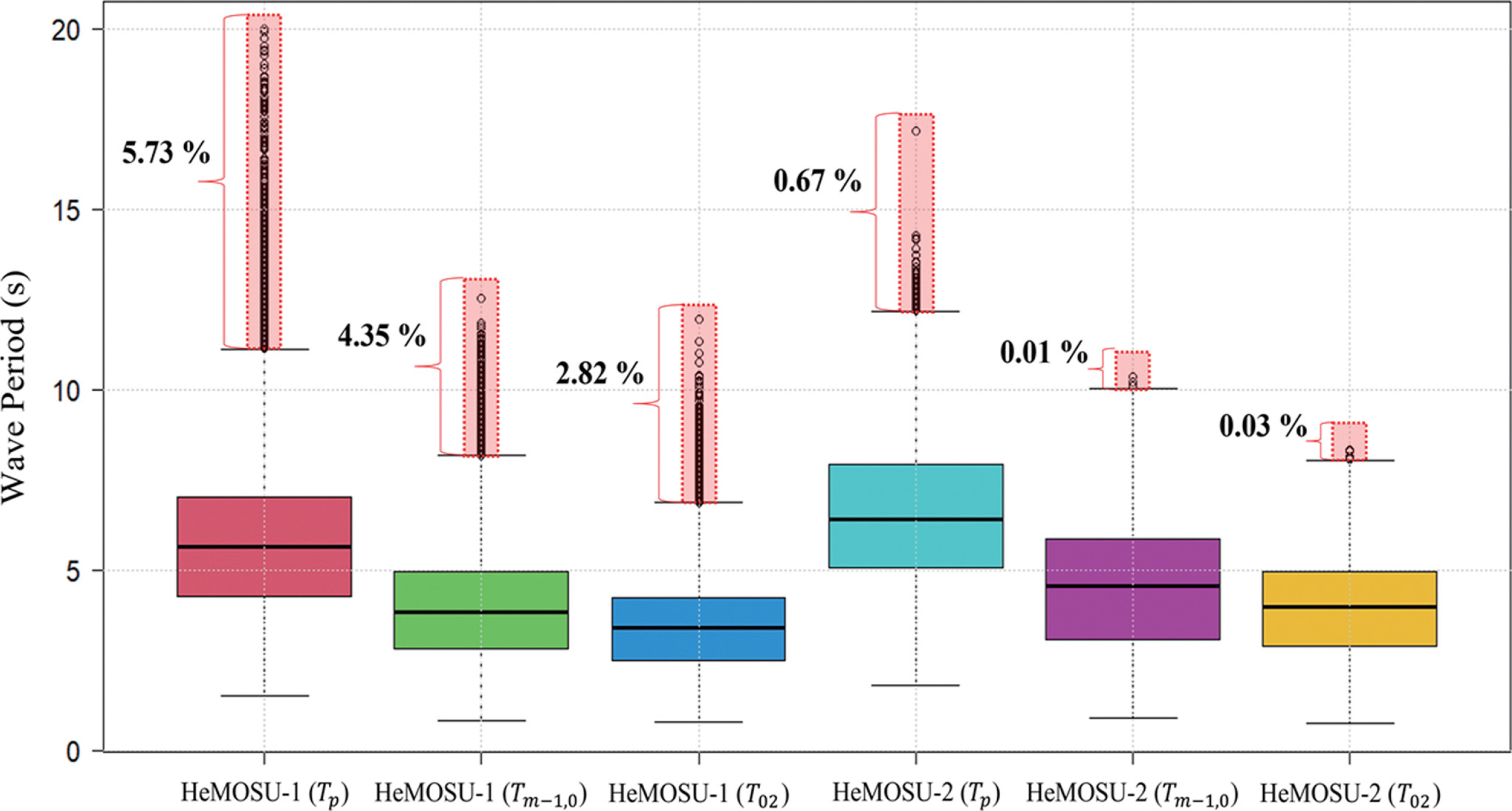
본 연구에서 파랑 스펙트럼 분석 방법을 통해 산정된 대표주기의 통계적 특성을 분석하기 위해 다음 Fig. 4와 같이 박스플롯을 제시하였다. 대표주기 중 첨두주기의 경우, HeMOSU-1, 2 각각의 평균은 6.01 s, 6.53 s으로 나타났으며, Tm-1, 0의 평균은 각각 4.11s, 4.56 s로 산정됐다. 또한, T02의 평균은 3.48 s, 3.90 s으로 나타났다. 또한, HeMOSU-2의 대표주기의 평균이 HeMOSU-1의 대표주기보다 크게 산정됐으며, 이는 상대적으로 HeMOSU-2 지점의 깊은 수심으로 인해 발생하는 것으로 판단된다. 산정된 대표주기의 이상자료 비율은 박스플롯을 통해 계산하였으며, 그 결과는 다음 Fig. 4에 제시하였다. 이상자료 비율 산정은 3분위수(75%)에 1.5IQR을 더한 값(Q3 + 1.5IQR)을 기준으로 이를 넘어가면 이상자료라고 판단하였다. 그 결과, 두 지점의 첨두주기의 이상자료 비율은 5.73%, 0.67%로 나타났으며, Tm-1, 0는 각각 4.35%, 0.01%, T02는 각각 2.82%, 0.03%로 산정됐다. HeMOSU-1에서 추정된 첨두주기의 이상자료 비율은 HeMOSU-2에 비해 높은 수준으로 나타났다. 이는 HeMOSU-1에서 주로 발생하는 낮은 파고의 영향으로 인해 추정되는 스펙트럼의 형상이 다중첨두형상(Bimodal Spectrum)으로 정확한 첨두주기 추정에 한계가 있는 것으로 판단된다(Lee et al., 2022).
Boxplot of calculated peak wave period and mean wave period (HeMOSU-1, HeMOSU-2).
일반적으로 대표주기 사이의 관계는 Tp,
Relationships between Tp and T02, Tp and Tm−1, 0, Tm−1, 0 and T02.
The relationships between representative wave period
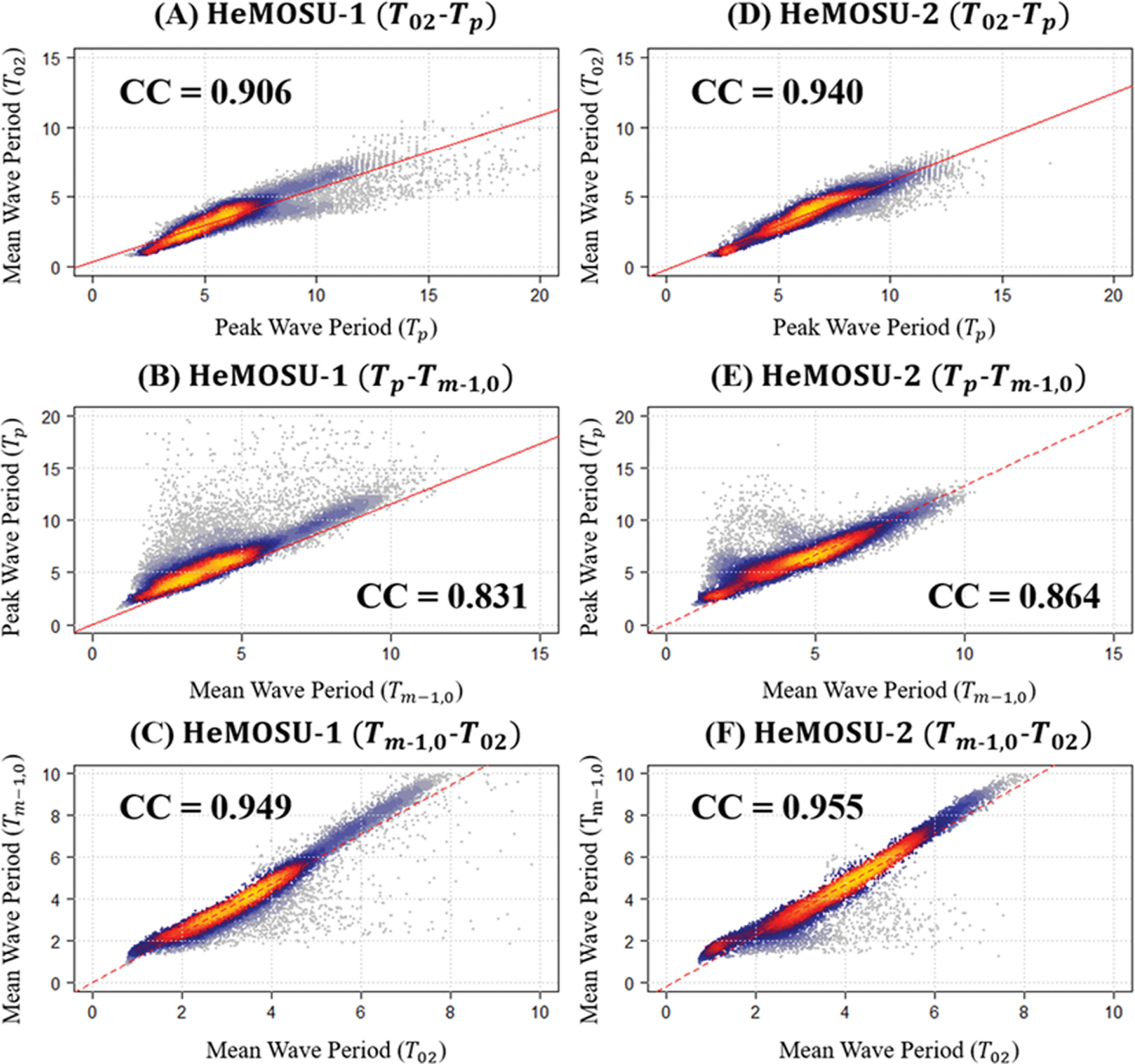
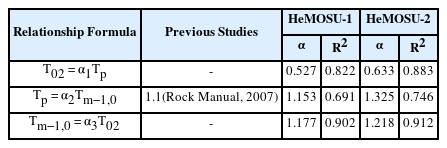
분석 결과, HeMOSU-1, 2에서 첨두주기와 T02의 선형 관계는 각각 0.53, 0.63으로 나타났으며, 이때 상관 계수 값(CC, Correlation Coefficient)은 각각 0.91, 0.94, 결정 계수값(R2)은 0.82, 0.88로 매우 높은 상관관계를 보여주는 것으로 나타났다(Fig. 5(A), (D) 참조). 또한, HeMOSU-1, 2에서 Tm-1, 0, T02 사이의 관계를 분석한 결과, 두 지점에서 각각 1.18, 1.22의 관계를 보였으며, 이때 상관 계수 값은 각각 0.949, 0.955, 결정 계수 값은 0.90, 0.91로 매우 높은 상관관계를 보이고 있었다(Fig. 5(C), (F) 참조). 한편, 두 지점에 대하여 Tm-1, 0와 첨두주기 사이의 관계를 분석한 결과, HeMOSU-1의 경우, Tm-1, 0와 첨두주기의 관계는 1.153으로 CIRIA et al.(2007)에서 제안하고 있는 1.1과 유사하게 나타났으며, 이때, 상관 계수 값은 0.831, 결정 계수 값은 0.691로 나타났다. HeMOSU-2의 경우, Tm-1, 0와 첨두주기의 관계는 1.325로 다소 기존에 제안되고 있는 계수값보다 높게 산정됐으며, 상관계수 값은 0.864, 결정 계수 값은 0.746으로 나타났다(Fig. 5(B), (E) 참조).
3.2 대표주기 최적 확률밀도함수 추정
HeMOSU-1, 2의 대표주기 분포 특성을 확인하기 위하여 본 연구에서 산정된 Tm-1, 0, T02와 첨두주기에 대하여 최적 확률밀도함수를 추정하였다. 이를 추정하기 위해 사용된 후보 함수는 해양에서 주기 추정에 주로 사용되는 ‘Log-normal’, ‘Gamma’, ‘Normal’ 분포를 적용하였으며, 정량적인 평가를 위해 K-S Test를 통해 산정되는 p-value(Pv)와 KL-Divergence를 통해 산정되는 DKL을 이용하여 평가하였다(Fig. 6, Table 3 참조).
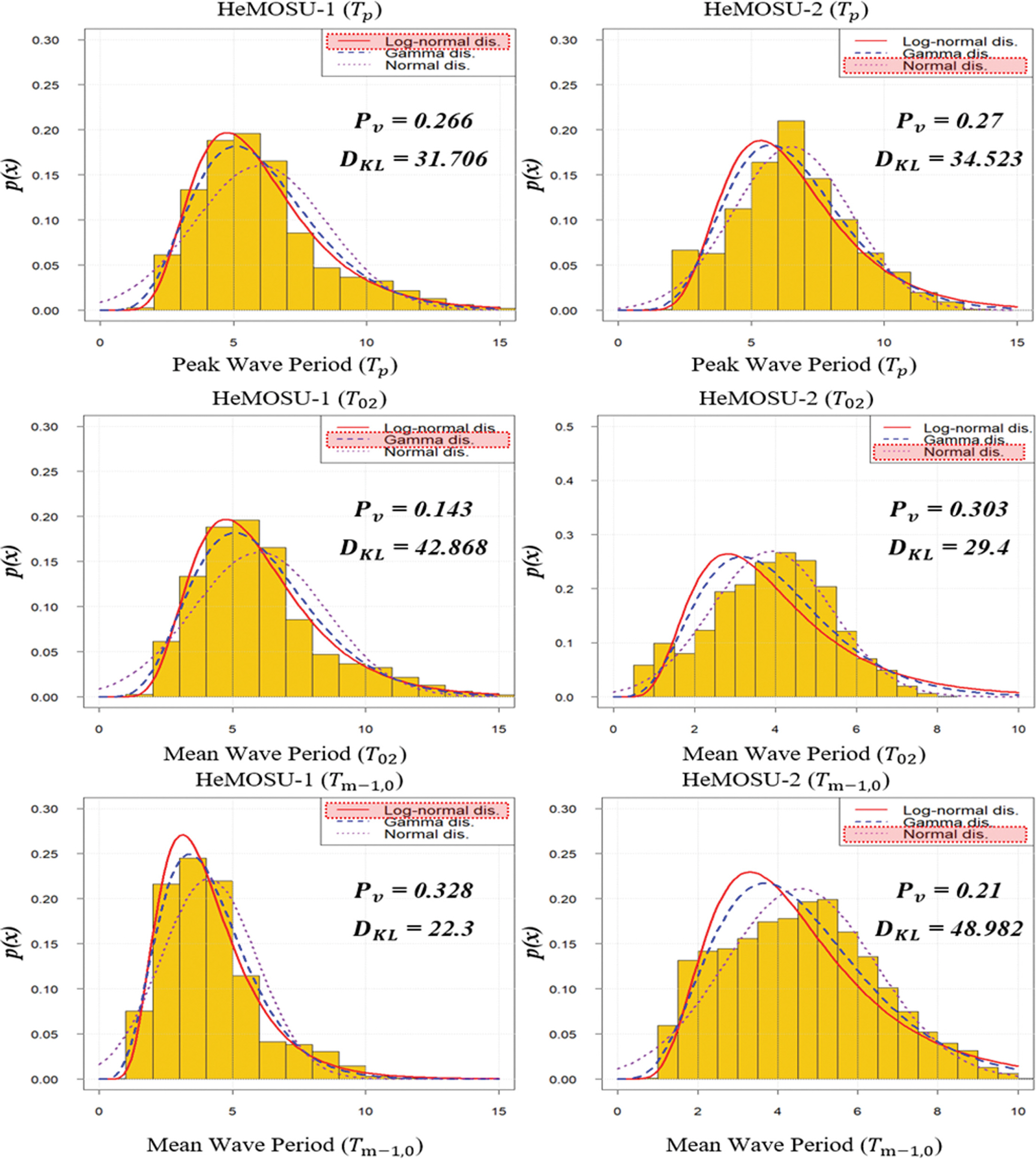
Estimation results of the optimal probability density function of the calculated representative wave period.
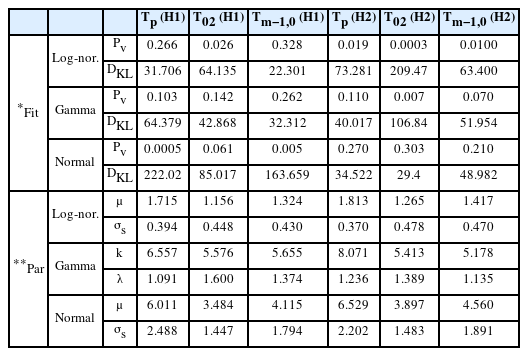
Distribution goodness-of-fit test results and optimal probability density function parameter estimation results (* Goodness-of-fit test, ** Parameter)
HeMOSU-1의 첨두주기에 대하여 최적 확률밀도함수 추정을 위한 분포적합도 검정 결과, ‘Log-normal’과 ‘Gamma’ 분포의 Pv 값이 0.05 이상으로 산정되어 적합한 확률밀도함수로 나타났으며, DKL를 계산한 결과, ‘Log-normal’ 분포의 DKL 값이 ‘Gamma’ 분포의 DKL 값보다 작게 나타나면서 HeMOSU-1의 첨두주기는 ‘Log-normal’ 분포에 더 적합한 확률밀도함수인 것으로 산정됐다. HeMOSU-2의 첨두주기의 최적 확률밀도함수를 추정한 결과, Pv 값은 ‘Gamma’와 ‘Normal’ 분포가 0.05보다 크게 산정되었으며, DKL 계산을 통해 ‘Normal’ 분포가 다른 후보 함수에 비해 작게 산정됨에 따라 더욱 우세한 것으로 나타났다. 한편, HeMOSU-1의 T02의 Pv를 산정한 결과, ‘Gamma’ 분포와 ‘Normal’ 분포가 우세하였으며, DKL 값은 ‘Gamma’ 분포가 더 적합한 확률밀도함수인 것으로 산정됐다. HeMOSU-1의 Tm-1, 0의 최적 확률밀도함수는 Pv 값과 DKL 값을 통해 ‘Log-normal’ 분포가 가장 적합한 것으로 나타났다. HeMOSU-2의 T02, Tm-1, 0는 Pv 와 DKL 값을 통해 ‘Normal’ 분포가 우세하게 나타나는 것으로 산정됐다.
4. 결론 및 제언
본 연구에서는 한국 서해안에 설치된 HeMOSU-1, 2에서 관측한 수면변동자료를 이용하여 첨두주기와 T02, Tm-1, 0를 산정하였으며, 산정된 대표주기를 이용하여 상관관계 분석 및 각각의 대표주기의 최적 확률밀도함수를 추정하였다. 최적 확률밀도함수 추정을 위해 분포 적합도 검정은 K-S Test를 통한 Pv 값과 KL Divergence를 통해 산정되는 DKL을 이용하였으며, 본 연구의 주요 결론은 다음과 같다.
1) 파랑 스펙트럼 분석을 통해 산정된 첨두주기, T02, Tm-1, 0 의 이상 자료 비율을 확인하기 위해 박스플롯과 Q3 + 1.5IQR 기준을 이용하여 계산하였다. HeMOSU-1의 첨두주기의 이상자료는 약 5.73%로 산정됐으며, HeMOSU-2의 첨두주기는 0.67%로 나타났다. 또한, HeMOSU-1, 2의 T02 이상 자료 비율은 각각 4.35%, 0.01%로 나타났으며, Tm-1, 0의 이상 자료 비율은 각각 2.82%, 0.03%로 산정됐다. 또한, 대부분의 주기는 HeMOSU-1에 비해 HeMOSU-2에서 더 높게 산정됐으며, 이는 HeMOSU-2의 수심의 영향으로 HeMOSU-1에 비해 더 높은 파랑이 발생하여 생기는 현상으로 판단 된다.
2) 산정된 대표주기를 각각의 파주기 간 상관분석을 수행한 결과, T02와 첨두주기의 선형관계는 HeMOSU-1, 2에서 각각 약 0.53, 0.63으로 나타났다. 이 때 계산된 상관계수는 각각 0.906, 0.940으로 계산됐으며, 결정계수는 약 0.822, 0.883으로 높은 선형 상관관계를 보였다. 또한, 첨두주기와 Tm-1, 0의 선형관계는 약 1.15, 1.325로 산정됐다. 특히, 두 관계는 기존에 1.1로 제안되고 있으며, HeMOSU-1에서 산정된 결과와 매우 유사하게 나타났지만, HeMOSU-2의 경우 기존 제안값에 비해 약 20% 크게 산정됐다. 마지막으로 Tm-1, 0, T02의 선형 상관관계를 분석한 결과 두 주기 간 약 1.17, 1.22의 관계를 보임으로서, Tm-1, 0가 T02에 비해 크게 나타났다.
3) 또한, 첨두주기, 평균주기에 대하여 최우도법을 이용한 최적 확률밀도함수를 추정하였다. 첨두주기의 경우, HeMOSU-1, 2 각각 Pv와 DKL을 통해 분포 적합도 검정을 수행한 결과 ‘Log-normal’ 분포와 ‘Normal’ 분포가 우세한 것으로 나타났으며, T02의 경우, ‘Gamma’ 분포와 ‘Normal’ 분포가 적합한 확률밀도함수로 산정됐다. 또한, Tm-1, 0의 최적 확률밀도함수를 추정한 결과, ‘Log-normal’ 분포와 ‘Normal’ 분포가 적합한 것으로 산정됐다.
일반적으로 파랑 분석을 수행하는 경우, 대부분의 파랑 분석에서 유의파고와 첨두주기를 이용한 분석이 주로 수행되고 있다. 그러나, 최근 유럽의 해안공학 분야에서는 첨두주기 산정에 대한 문제점으로 인하여 대부분의 파랑 분석을 수행하는 경우 평균주기를 사용하는 경우가 증가하고 있기 때문에 정확한 파주기를 산정하는 것이 중요하며, 파주기에 대한 다양한 연구가 이루어져야 할 것으로 판단된다. 또한, 본 연구에서 분석 대상지점으로 다루고 있는 HeMOSU-1, 2는 서해안 지역에 위치하고 있지만, 서해안 전해역에 대하여 대표성을 갖지 못하는 한계가 있다. 그러나, 대표주기를 분석함에 있어 본 연구 분석 방법 및 결과는 기초자료로 활용될 수 있을 것으로 사료된다.
Acknowledgements
본 연구는 산업통상자원부의 신재생에너지핵심기술개발 사업인 “해상풍력 전주기 HSE 운영지원 모델 개발(과제번호: 20213030020130)”의 일환으로 수행되었습니다. 연구지원에 감사드립니다.