1.1 연구배경 및 목적

세계 인구의 약 30%가 연안 지역에 거주하고 있으며 바다를 낀 해양도시는 항만, 산업단지 등 국가 기반 시설 및 주거지 등이 밀집해 있어 육상 공간 활용이 포화 상태에 이르고 있다. 그간 인간활동의 대부분은 육상 공간을 중심으로 이뤄졌으나 기후변화 및 기술 발전 등에 의해 빠르게 해상공간으로 확장되고 있으며, 전 세계적으로도 부유식 구조물을 통해 해상공간의 활용성을 높이려는 노력이 활발히 이뤄지고 있다. Fig. 1과 같이 싱가포르는 부유식 태양광, 문화시설 등을이미 운영하고 있고 2016년에 국토확장을 위한 부유식 구조체 연구를 위한 국가 R&D 센터를 구축하였으며, 사우디아라비아도 최근 옥사곤 해상 산업단지 프로젝트를 발표해 해상 공간 활용 의지를 보인 바 있다.

Fig. 1.

Examples of offshore floating structures: (a) Solar in Singapore, (b) Football in Singapore, (c) Merchandise store in Singapore, (d) Deep Ocean Basin (DOB) research facility in Singapore, and (e) Octagon project in Saudi Arabia.

한편 최근 기후변화로 인해 해수면 상승이 가속화되고 있어 연안 지역의 해상공간 마련 필요성도 증가하고 있다. 정부간 협의체인 IPCC는 최대 15 m까지 해수면 상승이 가능하다고 전망하고 있으며(IPCC, 2007), 실제 인도네시아 자바섬 등은 해수 상승으로 인해 매년 수 cm 단위로 가라앉는 상태이다(KIMST, 2023). 해수 상승과 세계 인구의 약 30%가 연안 지역에 거주하고 있는 점을 고려할 때 향후 연안 지역을 중심으로 부유식 구조물을 활용한 사회·경제적 해상공간 창출이 기대된다.

그러나 기존에 설치된 대부분의 부유식 구조물은 자원 채굴 및 전기 생산 등 산업 목적으로 설치된 것으로 사람의 거주나 사회·경제활동에 적합한 환경을 제공하기 어렵다. 기존의 부유식 항만시설물은 구조적인 안전성 및 사용성 측면을 고려하여 설계 범위 내에서 바람, 파랑, 조류 등의 해양환경 노출에 따른 동요 및 진동을 허용하고 있다. 그렇지만 이를 저감할 수 있는 부유식 구조물의 사용성 개선 방법이 요구된다. 구조물의 진동 및 동요는 인간의 건강, 안락성, 인지 등에 대해 영향을 미치며, ISO 2631-1, 6954:2000 등의 기준은 공간 활용 목적에 따른 진동 및 동요에 대한 주파수, 변위, 가속도 기준 등을 제시하여 인간의 거주 및 작업 환경 마련을 권고하고 있다. 이러한 이유로 본 연구는 부유식 구조물의 사용성 개선을 위한 방법으로 유공을 포함한 외곽 부유체를 제시하고, 이를 적용했을 경우 부유체의 운동 특성 및 사용성 변화를 분석하였다.

1.2 연구동향

해양구조물의 파랑 저감을 위해 외부에 유공벽을 활용한 연구는 대부분 고정식 구조물을 대상으로 이뤄져 왔다. Kim and Lee(2014)는 단면수리실험을 통하여 유공1실을 갖는 유공케이슨을 대상으로 최적 유공부 길이를 제안하였으며, Lee et al.(2013)은 수리모형실험을 통해 경사 입사파를 받는 유공 및 무공 구조물 전면의 파고분포를 계측함으로써 유공 구조물이 경사 입사파에 대해서도 소파 효과가 있음을 보였고 무공 구조물 대비 낮은 상대파고를 가져 유공이 해양 구조물의 안정성 확보에 도움이 될 수 있음을 밝혔다. Ko et al.(2015)는 단일 유공벽 및 이중 유공벽을 갖는 파일지지식 방파제 모형체에 대한 수리실험을 통해 이중 유공벽 사용을 통한 파랑 에너지의 소산이 Goda 파압 대비 최대 64%까지 감소할 수 있음을 보였다. Kim(2019)는 유공케이슨의 유수실을 골재로 채워 안정성을 확보하고, 수리특성을 확보할 수 있는 방법에 대하여 수리실험을 수행하였다.

한편 유공벽을 갖는 부유식 구조물에 대한 실험 연구도 수행된 바 있다. Yoon et al.(2011)은 수리모형실험을 통해 유공을 갖는 부유식 방파제가 무공 및 투수성 방파제 비해 높은 방파성능을 가지고 유공률이 커질수록 장주기 파랑에 대해 낮은 투과성능을 가짐을 확인하였다. Yoon et al.(2021)은 파력발전을 위한 유공을 갖는 부유식 방파제에 대한 연구를 수행하였다. 규칙파 조건에서의 실내모형실험을 수행하여 전기에너지를 생산할 수 있음을 보였으나, 해당 부유체의 전기 생산 가능성을 검토하기 위한 것이어서 유공 효과 및 사용성 등이 다뤄진 것은 아니다. Lee(2023)는 수리모형을 이용해 부유식 방파제의 방파성능을 조사하였고, Han and Wang(2022)는 슬릿형 유공 대신 내관이 설치된 부유식 방파제를 제안하고 내관형상에 따른 파력 저감효과를 수리실험을 통해 분석하였다. 그러나 두 연구는 각각 계류조건과 내관형상에 따른 부유체의 방파성능 분석에 초점이 맞춰져 있고, 유공의 배치 및 유공률 변화로 인한 부유체의 동요 영향을 분석한 것은 아니다.

유공 구조물에 대한 수치해석적 연구도 존재하였다. Hur et al.(2014)는 경사 입사파에 대한 고정식 이중 유공 슬릿 케이슨의 3차원 반사 특성을 조사함으로써 이중 유공 슬릿 케이슨에 입사되는 파랑의 각도가 작아질수록 반사계수가 감소하는 것을 확인하였다. Kee(2001)은 횡 방향으로 길게 배치된 이중 부유체를 연결하는 유공 유연막 소파시스템에 대한 2차원 수치모델을 사용해 해당 시스템의 공진 및 응답을 조사하고, 유공 유연막에 의한 소파 효과를 조사하였다. Han and Wang(2021)은 하이브리드 경계요소법을 제안하고 이를 수평 슬릿형 유공을 갖는 부유 방파제 해석하고, 이를 통해 유공이 해수면 근처에 배치될 때 회절 등의 파랑 감소에 유리함을 밝혔다.

기존 연구에 대한 동향 분석을 통해, 유공을 적용해 해양 구조물에 작용하는 외력을 감소시키고 이를 통한 구조물의 운동을 저감 시키려는 연구들이 있어 왔으나 고정식 구조물에 대한 실험 및 수치해석 연구가 다수였다. 또한 부유식 구조물의 경우 유공이 있는 부유체 연구는 소수였으며 유공으로 인한 운동 응답이 주된 관심 사항이 아니었음을 확인하였다. 본 연구는 외벽에 슬릿형 유공을 갖는 부유체의 운동 응답을 조사하고 유공 조건에 따른 운동 응답 변화를 분석하고자 한다.

2.1 해석방법 및 대상

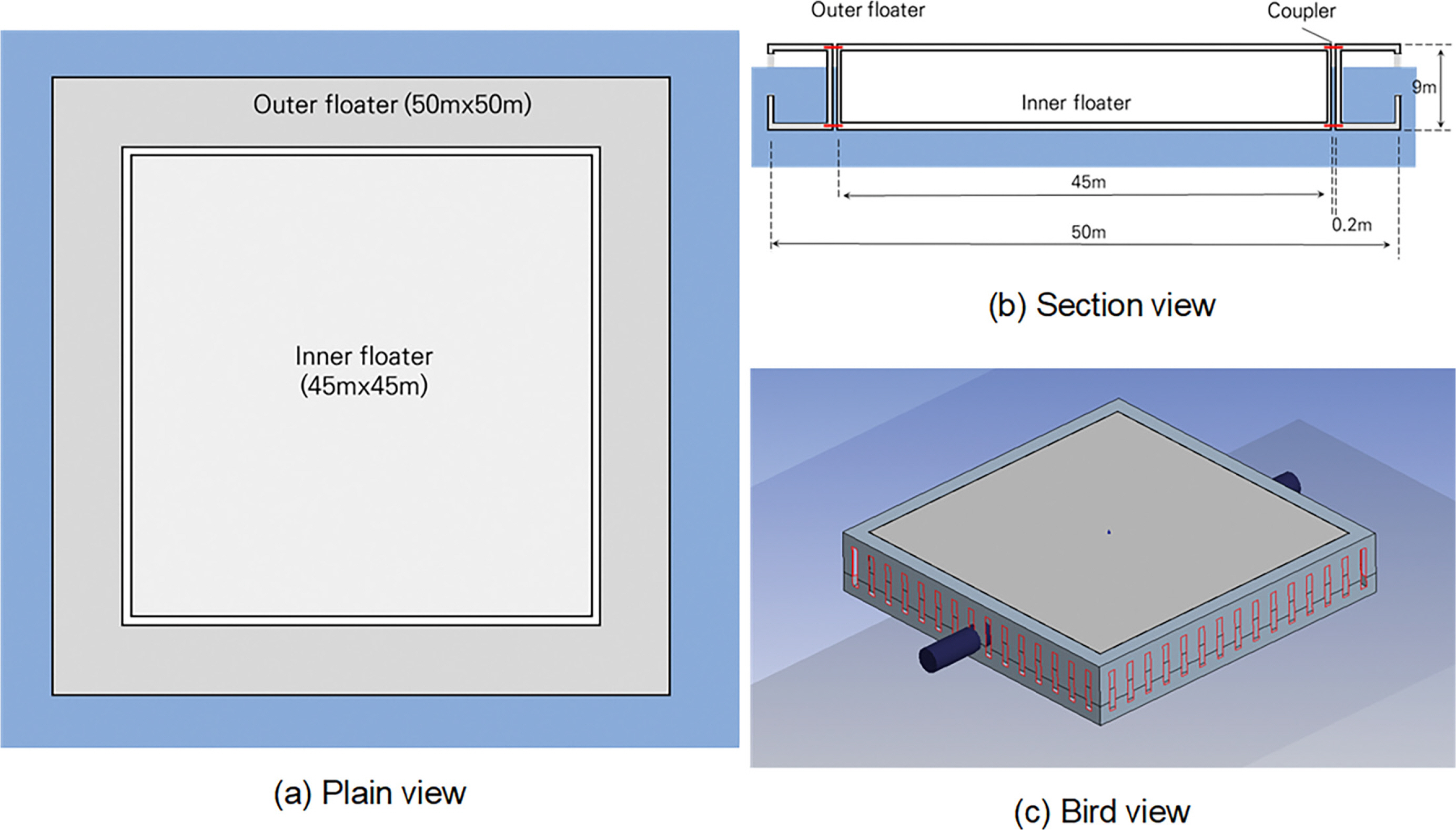
본 논문에 적용된 전체 부유식 구조물의 외곽 제원은 50 m × 50 m이다. 부유체는 내부 부유체와 외곽 부유체로 구성되어 있으며, 내부 부유체 외부에 외곽 부유체를 결합하는 형태이다. 외곽 부유체에는 유공벽이 설치되어 있으며, 외부 부유체의 폭은 10 m로서 부유체의 형상은 Fig. 2를 참고할 수 있다. 외곽 부유체 벽면에 설치된 유공부의 유공률, 유공부 위치를 달리함에 따라 전체 부유체의 동요 특성 비교하였다. 파랑 조건에 대한 외곽 부유체의 유공 조건 변화에 따른 운동 응답을 조사하기 위해 ANSYS AQWA를 이용해 주파수 영역 해석을 수행하였으며, 사용된 해석모델은 별도의 계류 조건의 설정 없이 부유체와 해수 간 상호작용만 고려하도록 하였다. 해석모델의 외곽 부유체 벽면에 종방향 슬릿형태의 유공벽이 설치되어 있으며, 유공벽의 유공률이 0~30%가 되도록 해석모델을 각각 생성하였다.

Fig. 2.

Schematic diagrams of a floating structure with porous outer floater.

2.2 주파수 영역 수치해석 방법

본 논문에서 사용하는 ANSYS AQWA는 해양구조물의 동적 거동을 수치해석적으로 분석하는 프로그램으로, 지배방정식인 Laplace 미분방정식에 3차원 포텐셜 해를 계산해 파랑과 다중 부유체 간의 움직임 간의 상호작용을 고려한 운동 응답을 제공한다. 따라서 해수의 비압축성 및 비회전 유동을 가정하게 되며 점성유동의 효과가 고려되지 않는 주파수 영역 해석을 통해 부유체의 운동 응답이 식(1)을 통해 계산된다.

여기서 ω는 파랑 주파수, M_s는 구조물 질량행렬, M_a는 부가 질량, C는 감쇠행렬, K는 유체정역학적으로 결정되는 강성행렬, X는 부유체 운동벡터, F는 파랑 강제력 벡터를 각각 나타낸다. 식(1)로부터 단위 파고에 대한 파랑 주파수 변화에 따른 부유체의 운동 응답(Response Amplitude Operator, RAO)를 구함으로써 규칙파 입사에 따른 부유체의 최대 운동 응답을 예측할 수 있다.

해양파의 선형성을 가정하면 불규칙파는 수많은 규칙파가 중첩된 것으로 고려할 수 있다. 본 논문은 부유체의 변위 및 가속도 응답을 평가하기 위해 파랑의 불규칙성을 통계적으로 고려할 수 있는 스펙트럼법을 사용하였다. 1차원 파랑 스펙트럼과 부유체 운동별 RAO를 식(2)와 같이 계산해 응답 스펙트럼을 도출하고 식(3)과 (4)의 응답 스펙트럼 모멘트를 계산해 부유체의 동적 응답을 평가할 수 있다.

여기서 S_ζ는 파랑 스펙트럼, ηj¯는 규칙파 조건의 운동방향에 대한 RAO 크기, µ₀는 위상각, S_j는 운동방향에 대한 응답 스펙트럼, X_S는 유의 변위 진폭, A_S는 유의 가속도 진폭을 의미한다. AQWA를 이용해 규칙파 조건에서 전체 부유체에 대한 RAO 산출결과를 도출한 후, 동요에 대한 응답 스펙트럼과 유의 변위 및 가속도를 계산하였다.

2.3 수치해석 모델 케이스 및 해석조건

외곽 유공부 영향을 분석하기 위해 다음과 같은 유공 조건을 부여하였다. 외곽 부유체 측면의 수직방향으로 배치된 슬릿형 유공을 배치하였으며, 개별 유공은 가로와 세로가 각각 1 m, 6 m인 직사각형 형상을 갖도록 하였다. 이 때 유공의 중심점은 외곽 부유체 측면의 중심선 위에 있도록 하였다. 해당 직사각형 유공 개수를 증감시켜 외곽 부유체의 측면 면적 대비 유공 면적(유공률)을 조정하였고, 유공률이 각각 10%, 20%, 30%이 되도록 해석모델을 각각 생성하였다. 또한 Fig. 2와 같은 부유체의 기본 동요 특성을 확인하기 위해 유공이 없는 외곽 부유체에 대한 해석도 함께 수행하였다(유공률 0%).

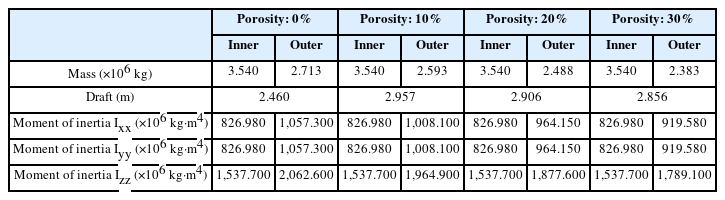
파랑에 대한 부유체의 동적 응답을 결정하기 위해 부유체의 질량 및 관성모멘트 정보가 요구된다. 본 논문은 Fig. 2의 부유체의 두께를 50 cm로 가정하였으며, 철근콘크리트 재질로 이뤄져 있다고 고려해 단위질량 2,500 kg/m³를 적용하였으며, 해수 단위질량은 1,025 kg/m³을 적용하였다. 케이스별 부유체 중심점의 질량 및 관성모멘트 산정을 위해 ANSYS Mechanical을 사용하였고, 외곽 부유체로의 해수 유입을 고려해 전체 부유체의 흘수를 계산하였다. 흘수 산정 시 내부 및 외곽 부유체는 커플러에 의해 강결된 것으로 고려해 전체 부유체의 중량과 부력 간의 평형조건으로부터 흘수를 계산하였고, 부유체의 질량 및 관성모멘트, 그리고 흘수 조건 등을 정리해 Table 1에 나타내었으며, 수심과 입사파 방향은 각각 30 m와 0^o로 가정하였다. 규칙파 조건에서 Table 1의 정보를 입력한 수치모델을 활용해 부유체의 임의 지점에서의 운동 응답을 추정할 수 있다. 본 논문은 부유체 중심점에서의 Heave와 Pitch, 그리고 부유체 중심으로부터 파랑 진행방향으로 ±22.5 m 떨어진 점의 Heave 응답을 관측한다.

Table 1.

Input parameter of hydrodynamic analysis for floating bodies with a porous outer

한편 흘수는 부유체 거동에 매우 큰 영향을 받는다(Park et al., 2022). 본 논문에서 다루는 부유체는 유공률에 따라 외곽 부유체의 중량이 달라져 해석 케이스마다 흘수 차이가 불가피하게 발생하나, 외곽 부유체의 유공 형상으로 인한 전체 부유체의 동요 영향을 확인하기 위해 추가로 흘수 조건을 동일하게 설정하여 응답을 비교하였다. 해석모델의 흘수가 모두 2.957 m(Porosity: 10%)가 되도록 하였고, 해당 흘수가 정온 상태(Calmness)에서 물리적으로 유지되도록 가상의 점 질량(Point Mass)을 내부 부유체에 추가하였다. 단, 점 질량을 가정하였으므로 관성모멘트의 변화는 발생하지 않는다.

추가로 유공 부유체의 불규칙파 해석을 통한 변위 및 가속도를 평가하기 위해 파랑 스펙트럼의 정의가 필요하다. 본 논문은 동해 남항진의 고파 파랑 관측 자료를 바탕으로 제시된 Cho et al.(2020)의 연구 결과를 참고하여 불규칙파 해석을 수행하였다. Cho et al.(2020)는 JONSWAP Spectrum을 사용하였고, 계측 정보를 바탕으로 첨두 증대계수를 통상적으로 사용되는 3.3보다 작은 1.4를 제안하였다. 본 논문도 JONSWAP Spectrum을 채택해 1.4의 첨두 증대계수를 적용하고 남항진의 평균 첨두 주기 및 유의파고 조건을 적용하였다(T_p= 0.096, Hz = 10.417 s, H_s = 4.356 m). 규칙파 해석과 동일한 부유체 위치에서 Heave와 Pitch에 대한 응답 스펙트럼을 추출하고, 유의 변위 및 가속도를 계산하였다.

AQWA을 통한 동적 응답 평가에서도 흘수 산정에 적용한 가정 사항과 논리적 모순이 없도록 내부 및 외곽 부유체가 서로 강결로 운동하도록 하였으며, AQWA의 요소 제한조건 및 해석 대상의 유공 크기를 고려해 요소의 최대 크기를 1.0 m로 설정하여 수치해석을 수행하였다.

3.1 규칙파 조건의 Heave 및 Pitch RAO

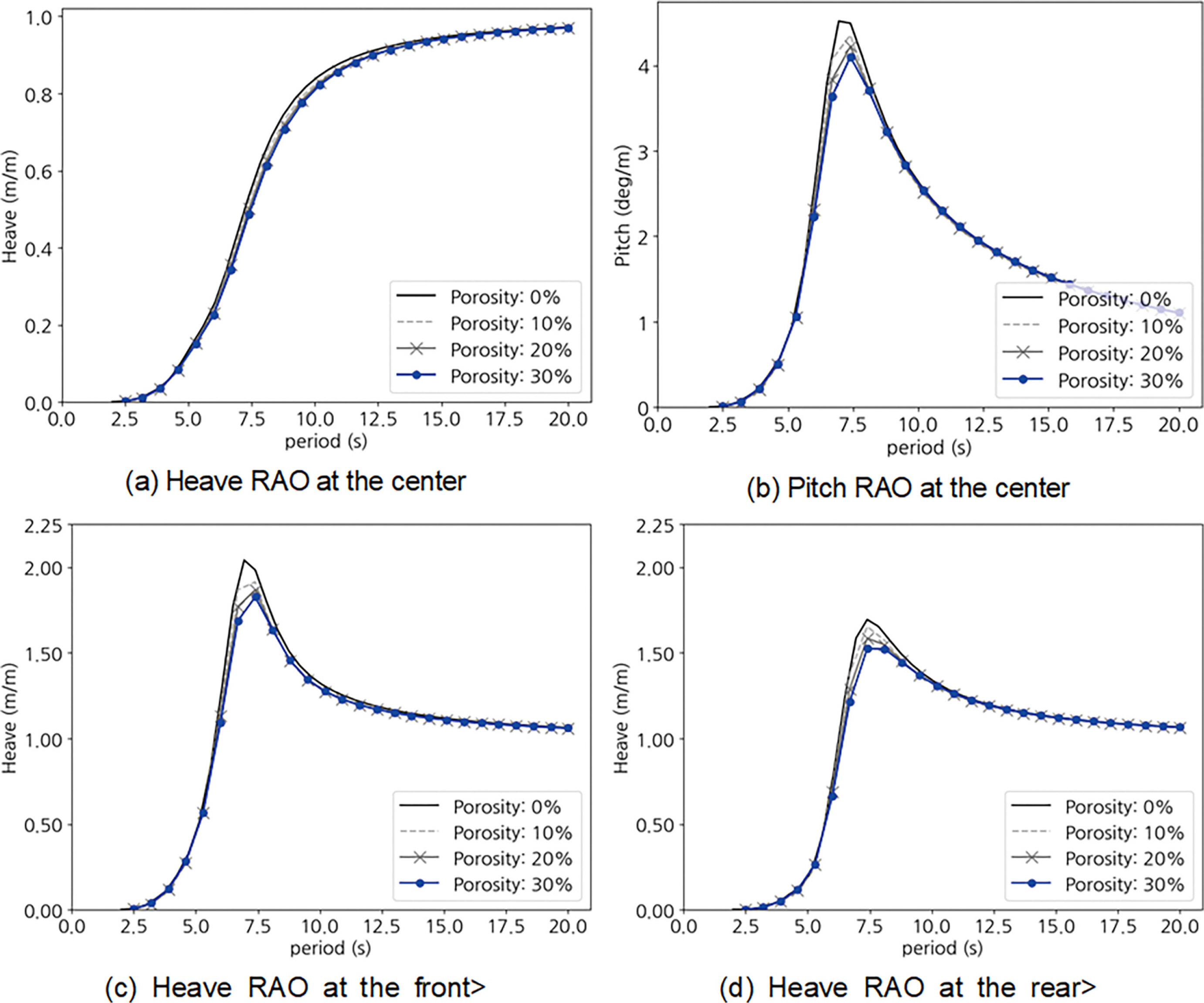
Table 1 조건을 갖는 유공률별 부유체 모델의 Heave 및 Pitch RAO를 비교하였다. Fig. 3에 나타낸 바와 같이 외곽 부유체의 유공률이 증가함에 따라 단위 파고에 대한 부유체의 최대 Heave 및 Pitch 응답은 감소하였다. 중심점(Fig. 3(a))에서의 Heave RAO에서는 유공율 증가 대비 유의미한 최대 응답 감소를 확인하기 어려우나 전체 주파수 영역에서 응답이 감소하였고, 주기가 감소함에 따라 단조 감소하고 있어 부유체와 해수 사이의 방사 감쇠(Radiation Damping)가 부력에 의한 복원력 대비 크게 작용하고 있음을 알 수 있다. 한편 파랑 전·후면의 Heave RAO는 파랑 주기 7~7.5 s에서 최대 응답이 나타났으며, 유공률이 증가함에 따라 최대 응답이 감소함을 확인할 수 있다. 최대 응답이 발생하는 파랑 주기가 Pitch RAO의 파랑 주기와 일치하고 있으므로 Pitch 운동 응답이 반영된 결과로 해석할 수 있다. 또한 파랑을 직접 부딪치는 부유체 전면에서의 최대 응답이 후면보다 크게 발생하였다. 이는 부유체 형상이 대칭적이나 최대 응답 시 파랑 주기에서 전면 파고는 후면 파고 대비 상승해 있기 때문이다. Fig. 4는 유공률 0% 조건일 때 최대 응답 발생 시 파랑 진폭 변화를 보여주며, 파랑 진폭의 분포가 파랑의 입사파가 산란 및 회절됨에 따라 비대칭을 가지게 된다(Kim et al., 2021). 그 결과 파랑 진행 방향에 대해 부유체 전/후면의 Heave 운동 응답도 비대칭으로 나타나게 된다.

Fig. 3.

RAO of a floating structure with porous outer floater.

Fig. 4.

Distributions of wave surface elevation for floating structure without porosity.

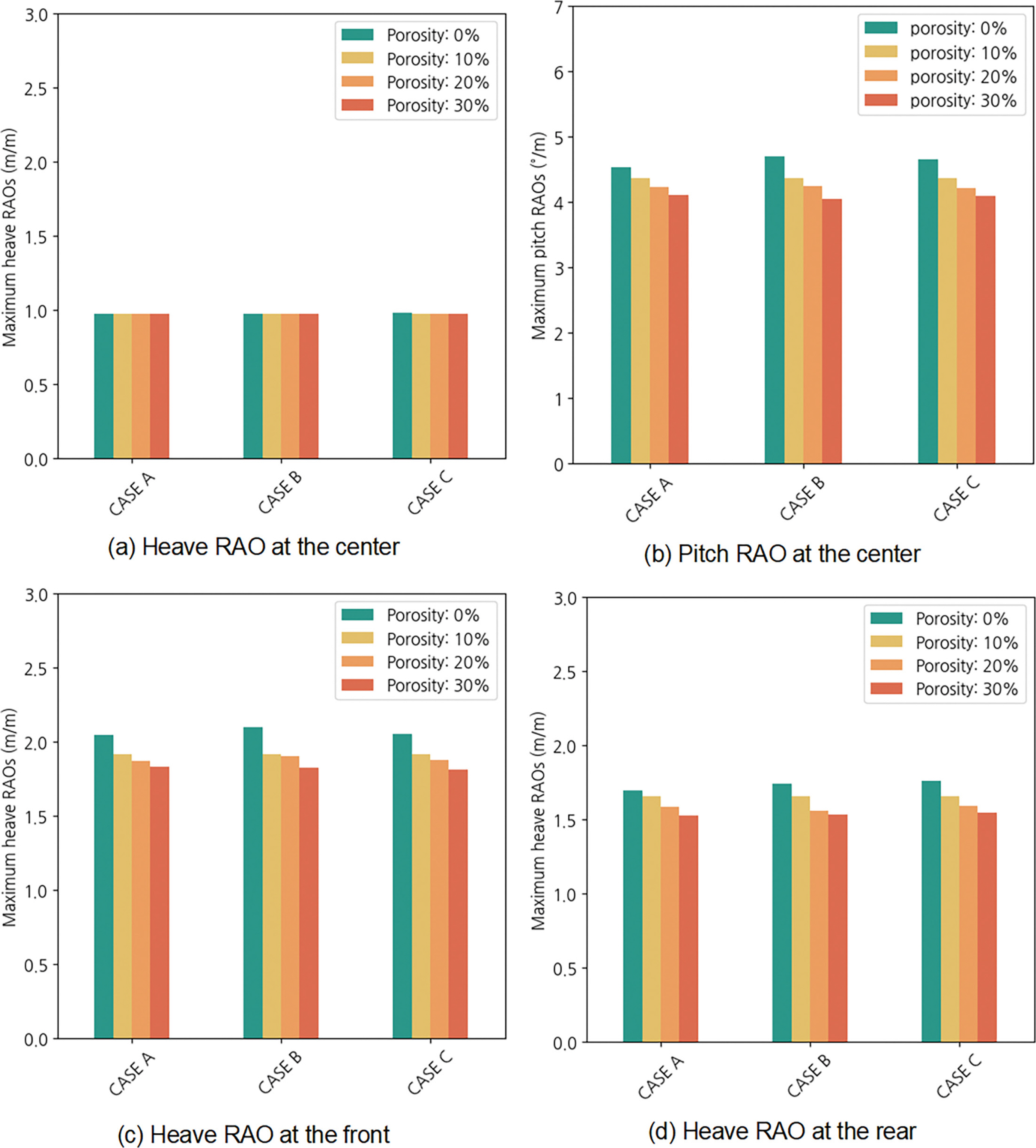
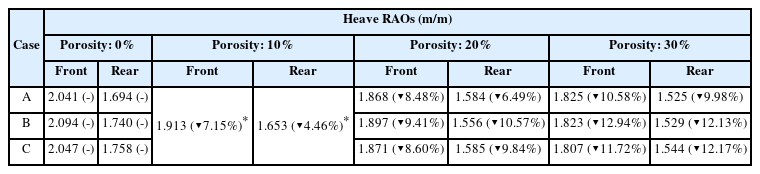
Fig. 3의 결과는 유공률 뿐만 아니라 각 해석모델의 질량 및 흘수 간 차이가 있어, RAO 응답 요인이 복합적으로 반영되어 있다. 외곽 부유체 유공 형상에만 기인한 운동 응답 저감 영향을 파악하기 위해 동일한 흘수 및 질량 조건을 적용하여 얻은 해석결과에서 최대 응답을 추출해 Fig. 5와 같이 정리하였다. Fig. 5는 유공률 변화에 따른 위치별 Heave 및 Pitch 응답의 최댓값을 막대 그래프(Case A: Table 1 조건, Case B: Table 1에서 흘수만 2.957 m로 설정, Case C: Case B 조건 및 점 질량 추가)로 나타낸 것으로, 모든 해석 조건에 대해 유공률이 증가됨에 따라 최대 응답이 감소하고 있음을 보여준다. 부유체 중심점에서 유공률 차이는 미미하였고, 해수 표면의 Heave 운동 최대 진폭과 거의 동일한 응답을 보였다. 반면 부유체 가장자리에서의 Heave는 Pitch 영향으로 인해 유공률 증가에 따른 일관된 최대 응답 감소를 보여주며, Table 2에 나타낸 바와 같이 유공이 없는 부유체 대비 약 10%의 Pitch 감소(Porosity: 30%) 효과를 가질 수 있음을 확인 할 수 있다. 참고로 Heave 및 Pitch RAO 곡선 형상은 Fig. 3과 거의 동일한 형상을 가진다.

Fig. 5.

Comparison of maximum RAOs between floaters with different porosity ratio.

Table 2.

Maximum Heave RAOs at the front and the rear of floater with different porosity ratio

한편 Fig. 5와 Table 2에서 확인할 수 있듯이, 흘수 및 질량 조건 변경에 따른 규칙파 조건에서의 부유체 최대 응답 변화는 점 질량 및 조정된 흘수 조건의 영향이 규칙파 진폭 대비 0.01 수준에 불과하였고, 유공률 대비 미치는 영향이 작아 일관된 경향성을 확인하기 어려웠다. 이를 통해 주어진 부유 시스템에서 0.5 m 이내 흘수 변동은 유공률 대비 영향이 작아 무시할 수 있는 인자로 판단된다(Case B). 또한 Case C는 정온 상태의 부력 평형을 충족하도록 관성모멘트의 증가 없이 점 질량만 부유체 무게중심에 추가된 것이므로, 부유 시스템의 Pitch 응답에 미치는 영향이 미미한 것으로 추론되며, 이 때문에 추가된 점 질량이 부유체 가장자리의 Heave 응답에 미치는 영향도 작은 것으로 판단된다. 따라서 외곽 부유체 유공률이 Pitch에 대해 가장 큰 영향을 미치는 인자임을 알 수 있다.

3.2 불규칙파 조건의 부유체 유의 응답 분석

3.1절의 규칙파에 대한 RAOs에 대한 분석을 통해 Case B와 Case C에서 추가된 흘수 및 점 질량 영향이 크지 않음을 확인하였으므로, 불규칙파 조건에서 외곽 부유체의 유공 영향은 Case A에 대해서만 정리하였다.

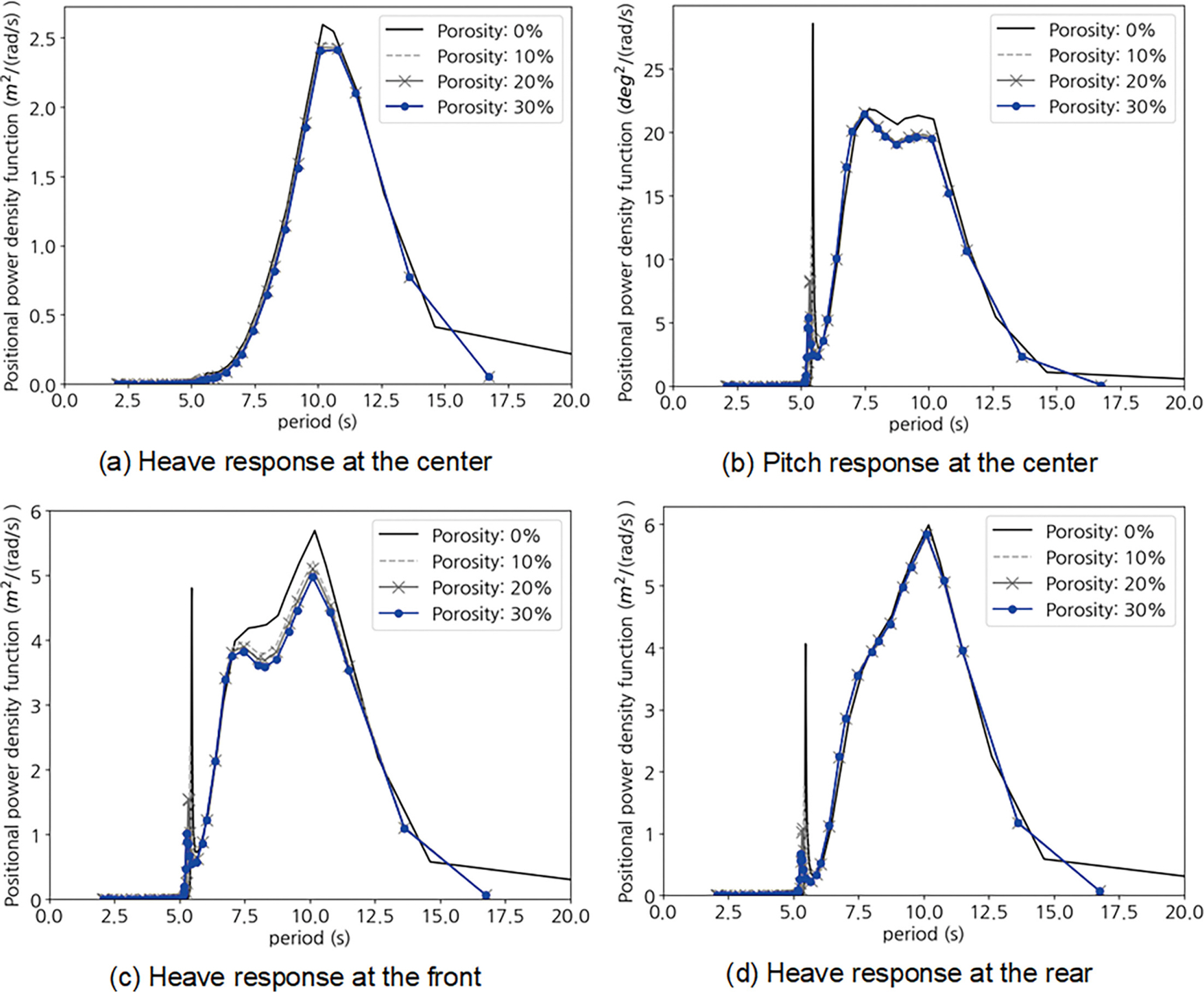
Fig. 6은 2.3절에서 설명한 불규칙파 조건에 대한 부유체의 Heave 스펙트럼을 보여준다. 먼저 전체 부유체의 중심에서의 스펙트럼 결과는 규칙파 조건에서의 RAO와 마찬가지로 외곽 부유체의 유공이 없는 조건에서 파랑 응답의 최대 진폭이 가장 크게 나타남을 보여주며, 파랑 스펙트럼의 첨두 주기인 10.4 s 전후(5.0~17.5 s)에서 전체 부유체의 응답이 증폭되고 있다. 유공률 증가에 따라 파랑에 의한 부유체의 최대 가진 크기가 감소하는 경향도 확인된다. 또한, 유공이 없는 부유체의 경우, 파랑 주기 5.0~20.0 s에서 부유체의 Heave 가진이 발생하는 반면 유공이 존재하는 경우 5.0~17.5 s 구간에서만 가진이 확인되므로, 이를 통해 유공이 포함된 외곽 부유체를 사용함으로써 Heave의 증폭이 진전되는 파랑 주기의 범위를 축소할 수 있음을 알 수 있다.

Fig. 6.

Positional response spectrum: Heave and pitch.

한편, Fig. 6에서 Pitch 및 Pitch의 영향을 받는 부유체 전·후면 위치에서의 응답은 파랑 주기 5 s에서 가진이 크게 발생되고, 파랑 주기 7.5 s 및 10.4 s에서 가진이 증폭되는 경향을 보인다. 단, 여기서 파랑 주기 5 s의 가진은 비정상적인 응답 증폭으로 분석된다. 본 연구에서 제안된 부유체 시스템이 구조물이 둘러싼 유체영역을 포함하고 유동에 대한 포텐셜 해를 기반으로 하는 ANSYS AQWA가 해수의 점성 감쇠를 고려하지 못한다. 또한 모듈형 부유체를 다룬 수치해석 연구에서도 유사한 결과가 보고된 바 있어(Chen et al., 2021; Park et al., 2022), 물리적으로 발생하는 응답으로 보기는 어렵다고 판단된다. 따라서 부유체 중심점의 Heave와 마찬가지로 파랑 주기 5 s 이후에 부유체의 Pitch 또한 증폭되는 경향이 확인되며 Pitch 응답의 공진 주기인 7.5 s 및 파랑 스펙트럼 첨두 주기인 10.4 s 전후로 공진이 발생할 가능성이 높다고 분석된다.

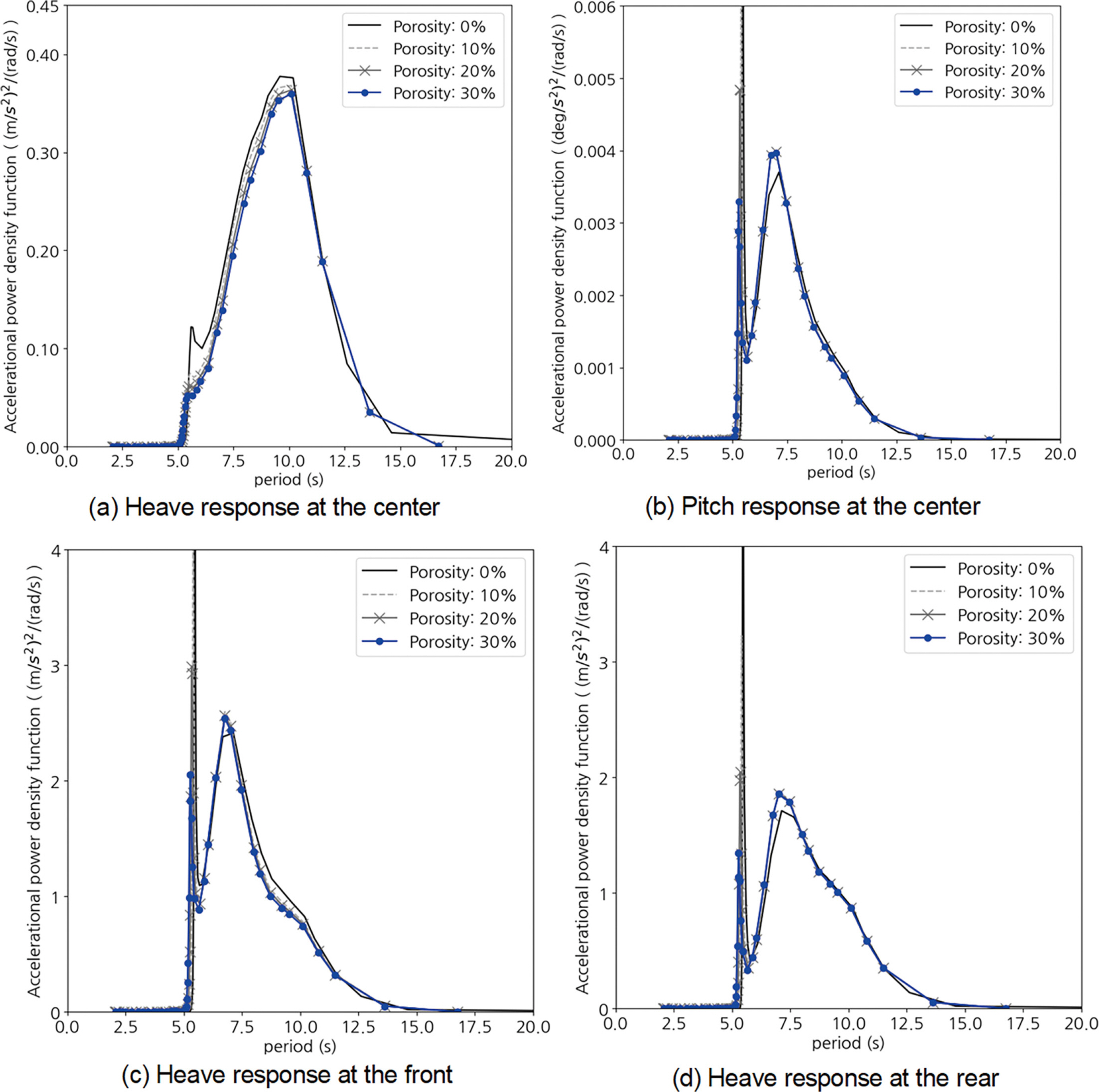
Fig. 7은 부유체 중심 및 가장자리에서의 가속도 스펙트럼을 보여준다. 변위 응답 스펙트럼과 마찬가지로 부유체 중심점의 Heave 방향 가속도는 외곽 부유체에 유공이 증가함에 따라 가속도 밀도가 감소하는 경향을 보여준다. 반면, Pitch 방향 가속도 응답 경향성은 차이를 보인다. Pitch RAO가 최대가 되는 7.5 s 전후로 가속도 공진이 발생할 수 있으며, 유공이 포함된 부유체의 Pitch 방향 가속도 스펙트럼의 최댓값은 유공이 없는 부유체보다 크게 나타났다.

Fig. 7.

Acceleration response spectrum: Heave and pitch.

Figs. 6과 7은 부유체 응답이 증폭되는 주기 정보를 제공하나 절대 크기를 판단하기 어려우므로, 각 응답 스펙트럼에 대한 유의 크기를 통해 유공률에 따른 응답 크기를 비교하였다. Table 3에 나타낸 바와 같이 유의 변위 및 가속도 모두 유공이 존재하는 부유체에서 응답 크기가 감소하였으며, 유공률이 증가함에 따라 응답의 크기가 일관되게 감소하는 경향을 보였다. 유공률 30%일 때 부유체 변위 및 가속도가 가장 작게 평가되었으며, 유공이 없는 부유체의 변위 및 가속도 대비 최대 4.6%, 6.3%의 감소 효과를 보였다. 그러나 불규칙파 조건의 유공에 의한 응답 크기 감소 효과는 규칙파 결과에 비해 감소하였다. 규칙파 조건에서 유공 부유체 Heave 운동 감소 효과는 최대 12% 수준이나(Porosity: 30%, Rear), 동일한 유공 및 위치에서의 유공에 따른 Heave 방향 변위 감소 효과는 1% 이하로 평가되었다.

Table 3.

Significant heave and pitch responses