FUNWAVE-TVD 모델을 이용한 경사구조물의 월파량 산정
Estimate of Wave Overtopping Rate on Armoured Slope Structures Using FUNWAVE-TVD Model
Article information
Abstract
FUNWAVE-TVD 모델을 이용한 경사구조물의 월파량 산정 Estimate of Wave Overtopping Rate on Armoured Slope Structures Using FUNWAVE-TVD Model본 연구에서는 완전비선형 Boussinesq 방정식을 사용한 FUNWAVE-TVD 모델에 경사구조물의 월파 계산이 가능하도록 EurOtop(2018)의 경험식을 추가하여 프로그램을 수정하였다. 수정된 수치 모형은 경사제에 대한 CLASH data 및 수리모형실험 자료와 비교하여 그 타당성이 검증되었다. 본 모형은 피복 블록의 조도계수 차이에 따른 월파량의 변화를 정확히 재현하였고, 상대여유고 증가에 따른 월파량의 감소율을 잘 재현하였다. 경사제의 월파량은 피복 블록의 배치 상태에 따라서 큰 차이를 보였다. Tetrapods를 정적(regular positioning)으로 배치한 경우는 난적(random positioning)으로 배치한 경우보다 월파량이 크게 증가하였고 Rocks로 배치했을 때와 일치하였다. 한편, Rocks를 1열로 배치한 경우는 2열로 배치한 경우보다 월파량이 커졌으며 이는 구조물 표면의 조도와 투수성의 영향 때문으로 판단된다.
Trans Abstract
In this study, the program was modified by adding the empirical formula of EurOtop (2018) to enable calculation of wave overtopping on armoured slope structures in the FUNWAVE-TVD model using the fully nonlinear Boussinesq equation. The validity of the modified numerical model was verified by comparing it with CLASH data and experiment data for the rubble mound structure. This model accurately reproduced the change in wave overtopping rate according to the difference in the roughness factor of the armoured block, and well reproduced the rate of decrease in wave overtopping rate due to the increase in relative freeboard. The overtopping rate of the armoured slope structures showed significant differences depending on the positioning condition of the armoured blocks. When Tetrapods were placed with regular positioning, the overtopping rate increased significantly compared to when they were placed with random positioning, and it was consistent with when they were placed with Rocks. Meanwhile, when rocks were placed in one row, the wave overtopping rate was greater than when rocks were placed in two rows, which is believed to be due to the influence of the roughness and permeability of the structure’s surface.
서 론
최근 태풍의 강도와 내습 빈도가 커지면서 남해안 및 동해안은 월파 피해가 크게 증가하였다. 월파는 파랑의 수면 변위가 해안구조물의 마루높이보다 높을 때 다량의 해수가 구조물 내측으로 전달되는 현상으로 침수 피해를 유발한다. 해안 제방, 호안 등의 해안구조물은 대부분 경사구조물로 이루어져 있으며 월파 피해 대책을 마련하기 위해서는 넓은 평면 파랑장에서 경사구조물에 대한 월파 예측 수치모형이 필요하다.
월파에 대한 수치모형은 크게 두 범주로 나눌 수 있다. 하나는 Nonlinear Shallow Water equation model(NLSW model)이고 다른 하나는 Navier-Stokes equation model(NS model)이다. NLSW model은 Navier-Stokes equation의 단순화된 형태로서 시간과 공간상에서 수심과 수평 흐름속도를 구하여 수평에 가까운 수심 적분된 자유표면 흐름을 해석한다. 즉, 연직 속도는 무시하고 압력은 정수압으로 가정한다. 이 모델의 제약은 천해 역(h/L < 0.05)에서 단파(bore)로 전파하는 파랑에 적합하다. 따라서 쇄파 거동은 상당히 단순화되며 외해 경계는 구조물 선단에서 미리 주어져야 하고, 바닥경사는 완만하여 연직 흐름 성분이 작아야 한다. 이들 모형은 RBREAK, ODIFLOCS, AMAZON, the ANEMONE, suite(OTT-1D, OTT2D), Tuan and Oumeraci(2010) 등이 있다(EurOtop, 2018). 최근에는 Boussinesq 형식의 모형들이 월파 연구에 널리 사용되고 있다. 이 모형의 장점은 NLSW model에 비하여 파랑을 중간수심 역까지 계산할 수 있는 점이다. 이것은 NLSW model보다 구조물로부터 더욱 멀리 떨어진 곳에 외해 경계 조건을 설정할 수 있고 쇄파의 시작을 파악할 수 있도록 한다. 이 방법은 전빈(foreshore)에서의 파랑 전파와 쇄파 과정을 더 잘 표현할 수 있다. 이와 같은 모형은 Stansby(2003), Lynett et al.(2010), McCabe et al.(2013), Tonelli and Petti(2013) 등이 있다. 또 다른 최신의 경향은 월파 수치해석에 SWASH 모형을 적용하는 것이다. SWASH 모형은 분산성 Nonlinear Shallow Water equation을 기본 식으로 사용하여 흐름의 연직 구조와 비정수압(non-hydrostatic)을 해석할 수 있다. SWASH 모형을 이용하여 천해 역에서 제방의 월파 현상을 해석한 연구가 있다(Suzuki et al., 2014).
3차원 Navier-Stokes equation은 시간과 공간상에서 3개의 속도성분과 압력, 난류를 해석함으로써 흐름을 가장 잘 모의할 수 있다. 일반적으로 NS model은 난류흐름을 재현하고 정확히 모의하기 위해서 난류모형으로 확장시킨다. 그러나 이 모형은 NLSW model보다 많은 계산량을 필요로 한다. Navier-Stokes equation은 기본적으로 Eulerian 방법과 Lagrangian 방법으로 푼다. 일반적으로 Eulerian 방법은 유체를 연속체로 간주하고 흐름 영역은 검사 체적으로 이산화한다. 해석 알고리즘은 유체 영역의 각 검사 체적에서 운동량 보존이 만족되도록 한다. 그리고 Lagrangian 방법은 Lagrangian 틀에서 이산 단위가 입자이고 시간 내에 입자 집단의 상호작용과 운동을 수치적으로 풀어서 흐름의 진화가 계산된다. 자유표면 흐름에서 Eulerian 방법을 사용하면 자유표면 운동에 대해서 특별한 처리가 필요하다. 파랑과 투과성 구조물의 상호작용에 대한 적용과 검증을 시도한 프로그램은 SKILLA, COBRAS, VOFbreak, IH-2VOF, IH-3VOF, ComFLOW, LFLOW 등이 있다. 또한 자유롭게 사용할 수 있도록 개방된 OpenFOAM CFD, 상용프로그램인 FLOW-3D 등은 파-구조물의 상호작용에 대해서 성공적으로 적용되었다. 그러나 NS 모델은 매우 작은 공간격자 및 시간 간격이 필요하여 많은 계산 비용이 소요된다(EurOtop, 2018).
최근에는 자유표면 흐름에 대해서 Lagrangian 방법을 적용한 모델이 개발되었는데 무격자법(meshless method)과 SPH(Smooted Particle Hydrodynamics) 모델이 해안공학에 적용되었다. SPH 모델은 복잡한 격자가 필요 없으며 자유표면 흐름에 대해서 특별한 처리도 필요 없다. 그러나 이 방법은 계산에서 많은 노력이 필요하고 파-구조물 상호작용에 대해서 넓은 계산 영역과 긴 지속시간의 파열을 해석하기에는 아직 어려움이 있다(EurOtop, 2018).
한편, 경사구조물에 대한 월파 연구들을 수리실험 및 수치 모델로 구분하여 살펴보면 다음과 같다. 먼저 수리실험 연구로는 EU의 연구프로그램인 CLASH 프로젝트를 통하여 데이터베이스(Steendam et al., 2004)를 구축하고 여러 구조물에 대한 10,000개 이상의 월파 테스트 결과를 수집하였다. 경사진 투과성 구조물의 사석 경사면과 다양한 피복 블록에 대한 월파 수리실험이 수행 되었고, 경사면의 거칠기 영향인자(roughness factor, ϒf)를 실험 결과로부터 도출하여 CLASH 데이터베이스에 수록하였다(Bruce et al., 2009). CLASH 프로젝트 이후 새로운 콘크리트 피복 블록이 발명되고 수리 실험으로 테스트되었다(Molines and Medina, 2015). 이 실험은 피복 블록의 여유고(Ac)와 구조물의 여유고(Rc)가 같도록 설정된 CLASH의 실험 조건과 비교하여 큰 차이가 있었다. 2열 배치된 큐비포드(Cubipods)는 Ac/Rc = 0.57-0.79 조건으로 1열 배치 큐비포드는 Ac/Rc = 0.42-0.63으로 수행되었다. 이는 많은 경우에 구조물 천단이 피복 블록의 천단보다 훨씬 위에 있었고 이러한 구성이 일반적으로 월파 공식에 영향을 미친다는 것을 의미한다. 실험 결과를 보면 큐비포드는 1열과 2열 배치의 큐브(Cubes)와 다소 유사한 결과를 나타내었다(EorOtop, 2018). 그리고 투수성 및 불투수성 전빈 해안에서 경사구조물에 대한 월파 실험이 수행되었으며 투수성의 전빈 해안에서는 기존 불투수성 전빈 해안 조건일 때 측정된 평균월파량보다 4배 정도 감소한 결과를 나타내었다. 그러나 개별 최대월파량은 유의미한 차이를 나타내지 않았다(Salauddin and Pearson, 2020). 마루높이가 낮고 제체 경사면의 기울기가 급한 경사구조물에 대한 월파 수리 모형실험이 수행되었으며 실험 조건과 유사한 구조물에 대한 EurOtop(2018)의 예측 식은 정확성이 부족하다는 것을 확인하고 새로운 예측 식을 제안하였다(Gallach-Sánchez et al., 2021).
국내의 실험 연구로는 단순형, 소단형, 복합단면형(S형) 등 경사제 형상에 따른 월파량을 측정하고 동일한 파랑조건에서 복합단면형 경사제의 월파량이 가장 적음을 확인한 연구가 있으며(Sohn et al., 2005), 원호 호안 및 경사 호안에 대한 월파량을 계측하고 반파구조물에 의한 월파량 저감 효과를 정량적으로 분석한 연구가 있다(Oh, 2016). 그리고 낮은 마운드 높이에 높은 상치구조물을 갖는 경사 호안의 월파량을 실험으로 계측하고 EurOtop(2016)의 월파량 산정식과 비교한 연구가 있다(Jung and Yoon, 2019). 또한 비쇄파 조건에서 경사식 구조물의 개별 최대월파량을 실험으로 계측하고 평균 월파량을 이용하여 최대월파량을 산정하는 경험식을 제안한 연구가 있으며(Lee and Jeong, 2021), Tetrapods로 피복된 경사식구조물의 평균월파량을 실험으로 산정하고 EurOtop(2018)의 월파량 산정식과 비교한 연구가 있다(Lee and Kim, 2023).
수치모델을 이용한 경사제의 월파 해석 연구는 먼저 NLSW 모델을 이용한 연구로서 경사구조물의 월파 현상을 AMAZON으로 해석하고 COBRAS-UC(NS 모델) 모델과 월파량을 비교한 연구가 있다(Neves et al., 2008). SWASH 모델을 이용한 연구로는 경사제의 월파 현상을 SWASH 모델로 해석하고 DualSPH, FLOW-3D 모델과 비교한 연구가 있으며(Vanneste et al., 2014), 경사제의 월파량을 SWASH 모델로 해석한 연구가 있다(Zhang et al., 2020). 그리고 NS 모델을 이용한 연구로는 경사제의 월파량을 COBRAS-UC 모델로 해석하고 경험식과 비교한 연구가 있으며(Losada et al., 2008), RANS/VOF 모델을 이용하여 Coreloc과 Rocks의 피복 블록에 대한 경사제의 월파를 해석하고 월파량을 비교한 연구가 있다(Cavallaro et al., 2012). 또한 FLOW-3D 모델을 이용하여 Antifer, Xbloc, Tetrapod의 피복 블록에 대한 경사제의 월파를 해석하고 월파량을 비교한 연구와(Ghasemi et al., 2021), OpenFOAM 모델을 이용하여 경사제 피복 블록의 조도계 수와 월파량의 변화를 해석한 연구가 있다(Castiglione et al., 2023). 그리고 SPH 모델을 이용한 연구로는 경사식과 직립식 케이슨 구조물에 대한 월파를 해석하고 월파량을 비교한 연구가 있다(Pu and Shao, 2012).
한편, 완전비선형 Boussineq 방정식이 유도되어(Wei et al., 1995; Chen, 2006) 고파랑 내습 시 천해 역에서 수심 진폭비의 증가에 따른 파랑의 강비선형 현상을 더욱 정밀하게 모의할 수 있게 되었다. Kirby et al.(1998)은 Wei et al.(1995)의 식을 사용하여 완전비선형 Boussinesq 모델(FUNWAVE)을 수립하였고, Shi et al.(2012)은 Chen의 식을 사용하고 이동경계조건 처리를 위하여 TVD기법을 도입한 FUNWAVE-TVD 모델을 수립하였다. 최근에 FUNWAVE-TVD 모델은 연안의 다양한 동수역학 문제들을 해석하기 위해서 널리 사용되고 있다.
본 연구에서는 고파랑 내습 시 천해 역에서 파랑의 비선형성을 정밀하게 해석할 수 있는 완전비선형 Boussinesq 모델을 주목하였다. 여기서는 FUNWAVE-TVD 모델에 경사구조물의 월파 계산이 가능하도록 EurOtop(2018)의 경험식을 추가하여 프로그램을 수정하였다. 수정된 수치모형은 경사제에 대한 CLASH data(EurOtop, 2018) 및 Tetrapods로 피복된 경사제의 수리모형실험 자료(Lee and Kim, 2023)와 비교하여 그 타당성이 검증되었다.
2. 수치모형
2.1 지배방정식
FUNWAVE-TVD 모델은 Chen(2006)이 유도한 완전비선형 Boussinesq 방정식을 지배방정식으로 사용하고 있으며 미분방정식의 이산화 기법인 MUSL-TVD 기법과 이동경계조건을 해석할 수 있는 HLL 기법을 사용하여 플럭스 항을 계산한다. 지배방정식은 보존식 형태의 Boussinesq 방정식 형태로 표시하면 다음과 같다.
여기서 ψ와 ϴ(ψ)는 보존변수의 벡터 성분과 flux 벡터 함수로서 각각 다음과 같이 주어진다.
여기서
H는 H = h + η이고, h는 정수 면까지의 수심, η는 수면 변위를 나타낸다. u, v는 za = (β - 1)h + βη, β = 0.47 위치에서의 유속이고, 식(5), (6)의 첨자 x, y, t는 각각 공간과 시간에 대한 미분을 의미한다. 그리고 U'1, V'1, U"1, V"1, U2, V2, U4, V4 는 분산 항을 의미하고, U3, V3는 수직 와도 항을 나타낸다. Rx, Ry는 바닥 마찰, subgrid lateral turbulent mixing, 쇄파, 바람효과 등의 확산과 소실 항을 포함한다.
공간의 이산화는 유한체적법과 유한차분법을 혼합하여 적용하고 있다. Flux항과 1차 미분 항들은 high-order 및 loworder MUSCL-TVD(Monotonic Upstream-centered Scheme for Conservation Laws-Total Variation Diminishing) 기법을 사용하는데 high-order 기법에는 Erduran et al.(2005)의 fourthorder MUSCL-TVD 기법이 적용된다. 그리고 시간 스텝은 비선형 공간 이산화에 대해서 third-order Strong Stability-Preserving(SSP) Runge-Kutta 기법을 사용한다(Shi et al., 2012; Choi and Seo, 2018).
2.2 경사구조물의 월파량 계산방법
본 연구에서는 FUNWAVE-TVD 모델의 계산시간에 영향을 주지 않고 넓은 평면 파랑장 해역에서 월파량을 빠른 시간에 계산하는 한편 다양한 피복 블록의 조도계수를 반영하기 위하여 많은 실험 자료로부터 얻어진 EurOtop(2018)의 경험식을 이용하였다. 여기서는 먼저 경험식을 코딩하고 불규칙 파랑의 스펙트럼 유의파고(Hmo)와 주기(Tm)를 이용하여 구조물 전면의 격자점에서 월파량을 산정할 수 있도록 서브루틴을 구성하여 기존의 FUNWAVE-TVD 모델에 추가하였다.
본 수치모형에 사용된 경험식은 식(9)로 나타낸 EurOtop (2018)의 평균월파량 산정식이며 주요 변수가 구조물 전면의 스펙트럼 유의파고(Hmo)와 피복 블록의 조도계수(ϒf)이다. 본 연구에서 스펙트럼 유의파고(Hmo)는 TMA 스펙트럼을 이용한 내부 조파 기법으로 불규칙파를 재현하고 완전비선형 Boussinesq 방정식으로부터 파랑장을 엄밀하게 해석하여 구하였으며, 피복 블록의 조도계수는 다양한 블록을 대상으로 많은 실험 자료로부터 제시된 EurOtop(2018)의 조도계수 값을 사용하였다.
여기서, q는 단위 폭 당 월파량(wave overtopping rate), Hmo는 스펙트럼 유의파고(
3. 모형의 검증
3.1 CLASH data와 비교
모형의 검증은 먼저 경사제에 대한 많은 실험 자료로부터 얻어진 CLASH data(EurOtop, 2018)와 비교하고 불규칙파에 대한 본 수치모형의 월파량 계산 과정을 검토하였다. EurOtop(2018)의 매뉴얼에는 CLASH data의 구체적인 물리적 실험 조건은 제시되어 있지 않으나 구조물의 여유고(Rc)와 피복 블록의 여유고(Ac)가 동일하고, 구조물 표면의 경사가 1:1.5인 것을 알 수 있었다. 따라서 CLASH data와 비교 검증을 위한 물리적 계산 조건은 상대여유고 범위를 고려하여 임의로 설정하였다.
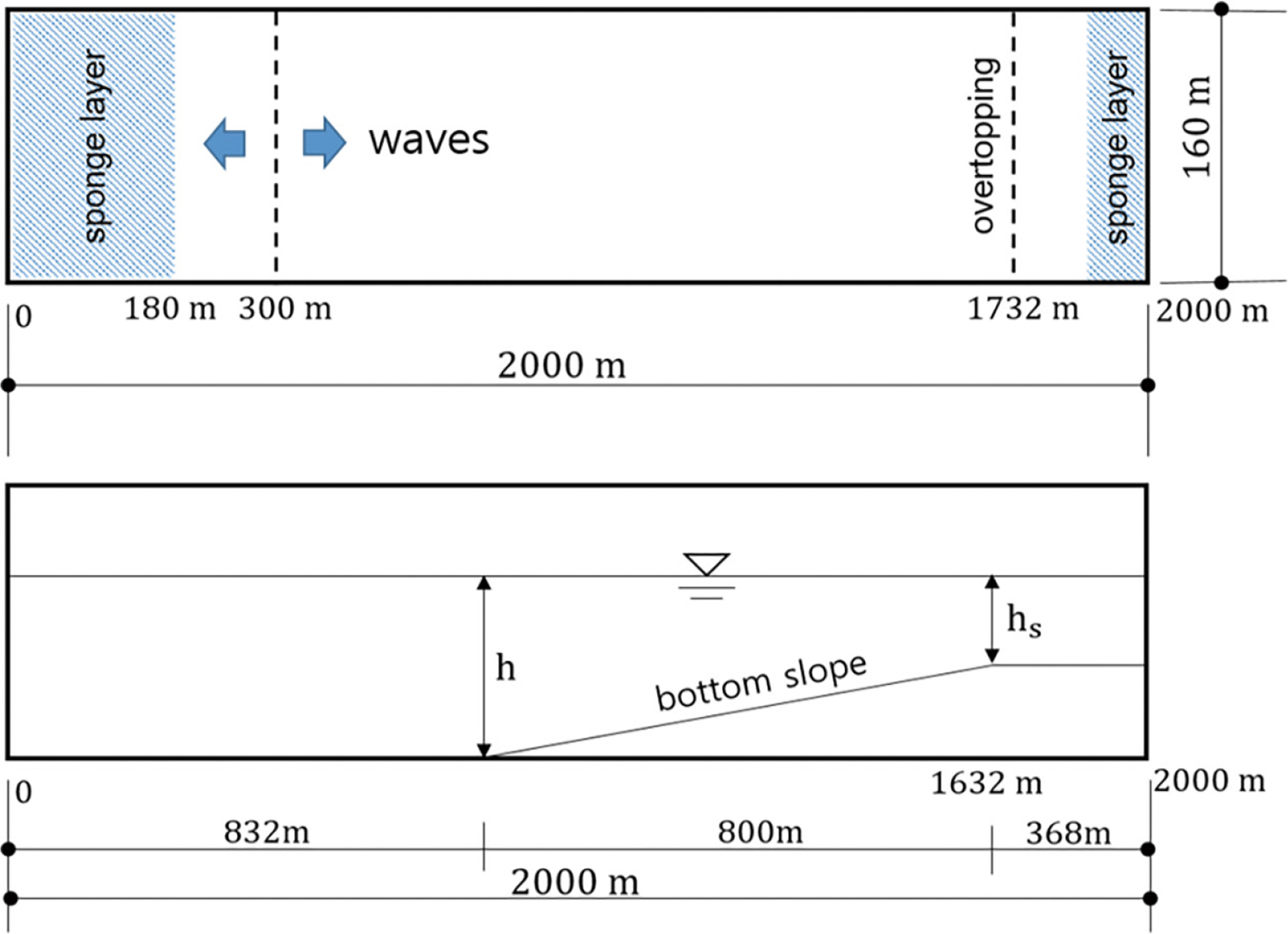
검증계산을 위한 계산영역은 2000 × 160 m의 2차원 조파수조 형상으로 구성하였고, 계산격자는 CFL 조건을 만족하도록 간격을 ∆x, ∆y = 2.0 m로 설정하여 총 1001 × 81개의 격자망을 구성하였다. 그리고 내부 조파 경계는 입사역 300 m 지점에 설정하였고, TMA 스펙트럼을 사용하여 불규칙파를 조파하였다. 내부 조파 시간은 1 case 당 600 sec로 하였는데 샘플 계산 case에 대해서 600 sec와 3,600 sec의 월파량 계산 결과를 비교하였으나 차이가 없어서 모든 case를 600 sec로 계산하였다. 그리고 외해 측에 폭 180 m, 해안 측에 폭 100 m의 스폰지 경계를 설정하여 양측 경계로부터의 반사파를 제어하였다. 계산영역의 측면경계는 periodic boundary condition을 적용하여 측면으로부터의 반사를 제어하였다(Fig. 1).
Sketch of simulation domain (upper) and bottom condition (lower).
한편, EurOtop(2018)의 경험식에 사용되는 구조물 전면의 스펙트럼 유의파고(Hmo)는 구조물에 의한 반사파를 포함하지 않는 입사파의 파고이다. 수치계산의 경우는 중복파로부터 입·반사파 분리가 어려우므로 중복파가 발생하지 않도록 수치 모의하는 방법을 검토하였다. 검증계산에서는 진행파만을 재현하기 위하여 계산영역의 1,732 m 지점에 경사제 모양의 구조물을 설치하지 않고 구조물 없이 파랑이 통과하도록 하였다. 그리고 월파량은 구조물 위치의 각 격자점에 월파 계산을 위한 경계조건을 부여하고 통과파의 스펙트럼 유의파고로부터 계산하였다.
CLASH data와 비교 검증을 위한 계산 조건은 구조물 전면의 수심은 10.8 m, 14.4 m, 18.0 m의 3 cases이고, Rc는 1.8~7.2 m의 7 cases, 내부 조파의 스펙트럼 유의파고(Hmo,i)는 1.8~7.2 m의 7 cases, 내부 조파 형식은 TMA 스펙트럼을 이용한 불규칙파 조파, 내부 조파 시간은 600 sec, 구조물 전면의 저면 경사는 1/40로 하였다. 그리고 피복 블록의 조도계수(ϒf)는 피복 블록이 없는 매끈한 표면인 경우 1.0과 CLASH data의 다양한 피복 블록의 조도계수 평균값인 0.45를 적용하였다. 또한 경사 입사파의 영향계수(ϒβ)는 1.0(normal wave attack)으로 하였다(Table 1).
Computer simulation conditions for model verification with CLASH data
Fig. 2는 다양한 피복 블록에 대한 경사제의 평균월파량을 수리모형실험으로 측정하고 상대 여유고에 대한 무차원 월파량으로 나타낸 CLASH data와 본 수치모형에 의한 계산 결과를 비교한 것이다. CLASH data의 실험에 사용된 피복 블록 종류는 매끈한 표면(Smooth), Cube rough, Anitfer, Tetrapods, Accropode, Xbloc, Rock, Cube flat, Haro, Cube-1 layer, Coreloc 등이다. 먼저 CLASH data 결과를 살펴보면 다양한 피복 블록에 대한 경사제의 월파량이 제시되어 있으며 Tetrapods(+)일 때 월파량이 가장 적은 반면에 피복 블록이 없는 매끈한 표면(Smooth, △)일 때 월파량이 가장 많은 것을 알 수 있다. 그 밖의 블록들은 조도계수의 차이에 따라서 월파량의 차이가 뚜렷이 분포한다. 그림에서 파선은 조도계수가 1.0일 때, 실선은 조도계수가 0.45일 때 경험식으로부터 얻어진 월파량이다. 이 때 조도계수 0.45는 실험에 사용된 피복 블록들의 조도계수 평균값을 의미한다. 경사제의 월파량은 피복 블록의 조도계수에 따라 크게 달라진다. 즉, 경사제 표면이 매끈할수록 월파량이 증가하는 것을 CLASH data를 통해서 확인할 수 있다.
Comparison results of mean overtopping rate on armoured slope structures.
본 모형의 계산 결과는 회색 원은 조도계수가 1.0일 때(Model gf = 1.0), 노란색 원은 조도계수가 0.45일 때(Model gf = 0.45)의 월파량이다. 본 모형의 결과는 CLASH data에 제시된 경험식의 월파량과 정확히 일치하는 것을 알 수 있다. 이것은 당연한 결과로서 본 모형은 CLASH data로부터 얻어진 경험식을 사용하였기 때문이다. 본 수치모형은 Fig. 2의 비교 결과로부터 조도계수가 다른 피복 블록의 경사구조물에 대한 월파량을 잘 재현할 수 있음을 확인할 수 있다.
3.2 수리모형실험 자료와 비교
본 연구에서는 경사제에 대한 평균월파량 실험 자료(Lee and Kim, 2023)와 본 수치모형에 의한 계산 결과를 비교하여 모형의 타당성을 검증하였다. 실험에 사용된 경사제는 피복재의 높이와 상치 콘크리트의 높이가 동일한 조건(Ac = Rc)이고, 제체의 사면경사는 1:1.5이다. 그리고 실험 단면은 전면은 Tetrapods로 2층 피복되었고 중간층은 Tripods로 피복되었다(Fig. 3).
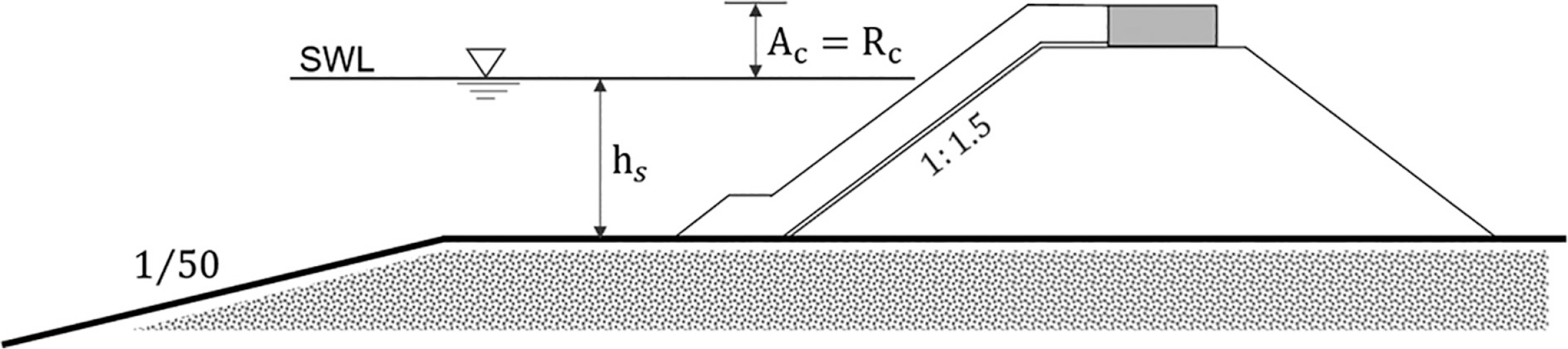
Cross section of model structure with armoured slope (Lee and Kim, 2023).
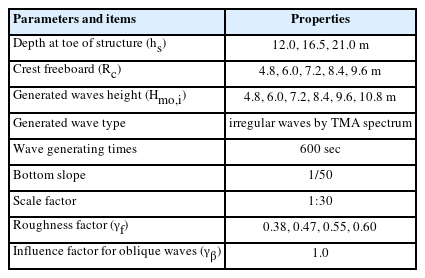
본 모형을 적용하기 위한 계산 영역 및 격자간격, 경계조건 설정 등은 위의 Fig. 1과 같게 하였고, 구조물 전면의 저면경사는 수리모형실험의 수조와 동일하게 1/50으로 구성하였다. 물리적 계산 조건은 수리모형실험의 제원을 1:30의 scale factor를 적용하여 실해역 scale로 환산하였다. 수치 계산에서 구조물 전면의 수심은 12.0 m, 16.5 m, 21.0 m의 3 cases이고, 구조물의 여유고(Rc)는 4.8~9.6 m의 5 cases, 내부 조파의 스펙트럼 유의파고(Hmo,i)는 4.8~10.8 m의 6 cases, 내부 조파 형식은 TMA 스펙트럼을 사용한 불규칙파 조파, 내부 조파 시간은 1 case 당 600 sec로 하였다. 그리고 피복 블록의 조도계수(ϒf)는 EurOtop(2018)에 제시된 조도계수를 참조하여 0.38(Tetrapods), 0.47(Cubes 2 layers, random positioning), 0.55(Rocks 2 layers, impermeable), 0.60(Rocks 1 layer, impermeable) 등 4종류를 적용하였으며, 경사 입사파의 영향계수(ϒβ)는 1.0(normal wave attack)으로 하였다(Table 2).
Computer simulation conditions for model verification with experiment data
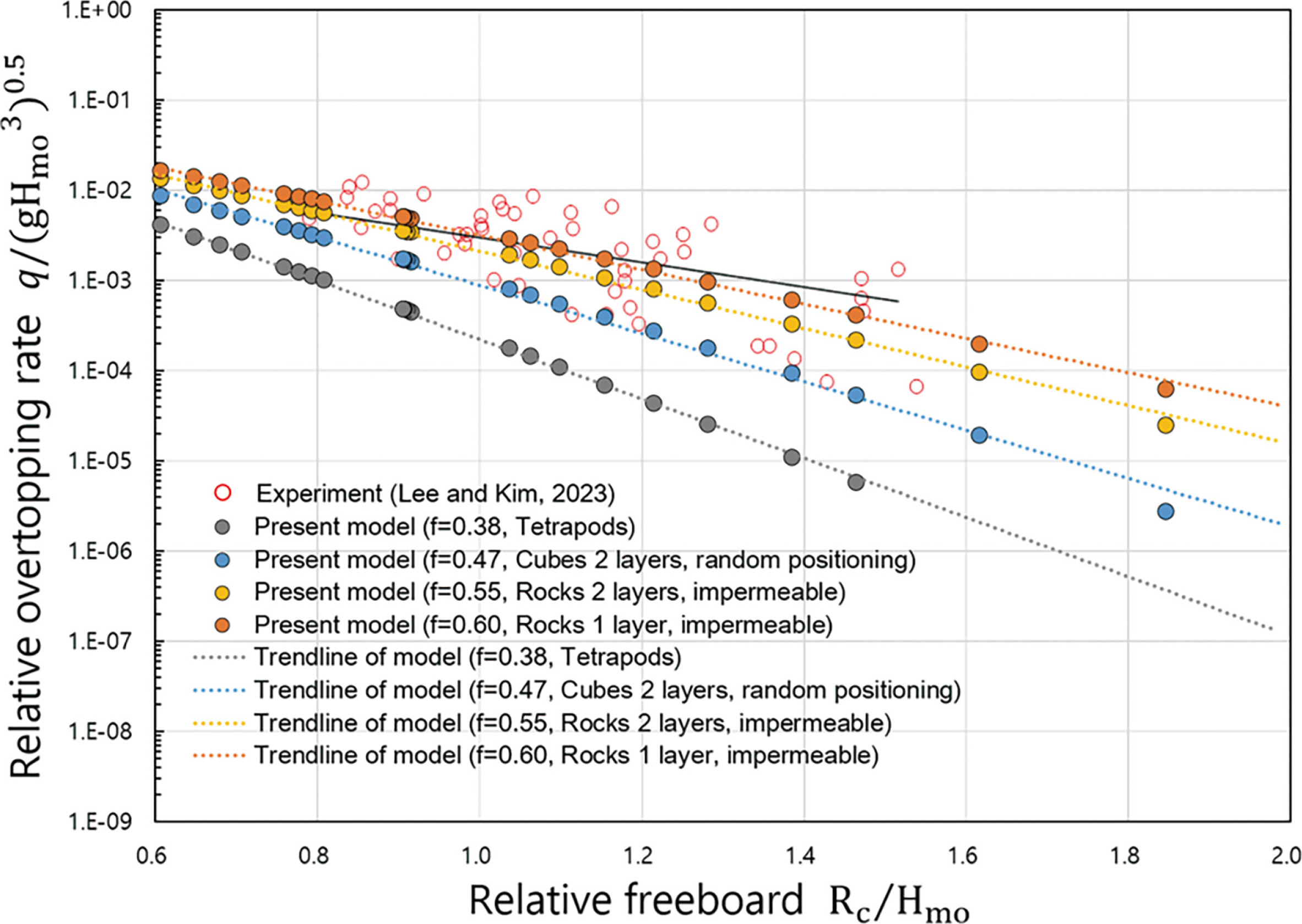
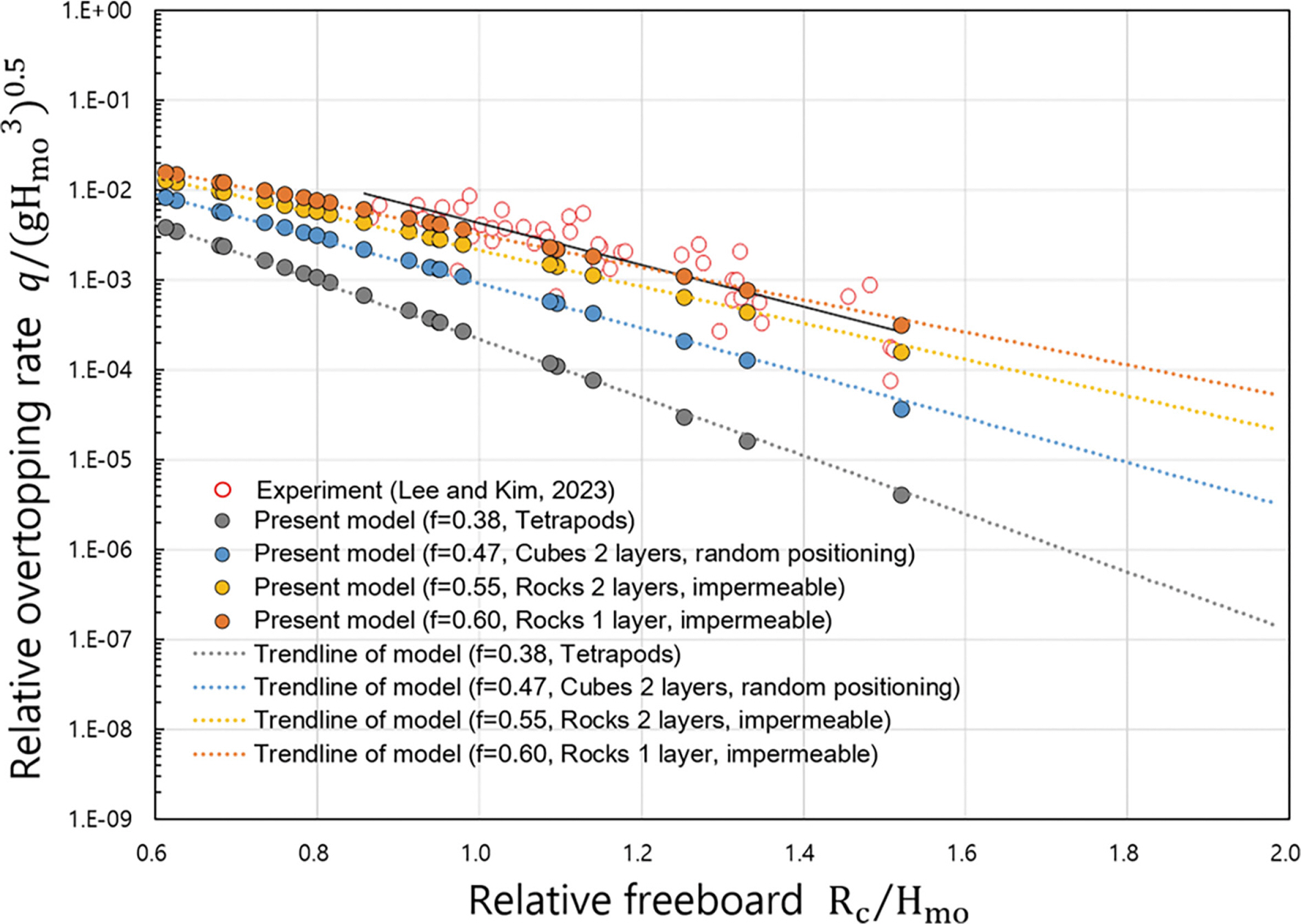
Fig. 4는 구조물 전면의 수심이 12.0 m인 조건에서 경사제의 평균월파량을 수치계산하고 수리모형실험 결과와 비교한 것이다. 그림에서 속이 빈 빨간색 원은 Lee and Kim(2023)의 실험 결과이고, 속이 찬 회색, 파란색, 노란색, 빨간색 원은 수치계산 결과이다. 수치계산 결과는 상대여유고의 증가에 따른 월파량의 감소율이 실험과 유사하고, 피복 블록의 조도계수 차이에 따른 월파량의 변화를 뚜렷이 보여주고 있다. 수치계산 결과는 피복 블록이 Rocks 1 layer 및 2 layers일 때 수리모형실험 결과와 일치하지만 Tetrapods일 때는 실험 결과보다 과소평가되었음을 알 수 있다. 수치계산에 사용된 Tetrapods의 조도계수는 EurOtop(2018)에 제시된 실험값 0.38을 사용하였다. EurOtop(2018)에서 Tetrapods의 조도계수 실험 사진을 살펴보면 난적(random positioning)으로 배치된 것을 알 수 있었다. 반면에 국내의 경사제는 Tetrapods를 대부분 정적으로 배치하고 있는 것을 감안하면 Lee and Kim(2023)의 수리모형실험에서는 Tetrapods를 정적(regular positioning)으로 배치했을 것으로 추측된다. 따라서 Tetrapods일 때의 월파량은 수치계산과 Lee and Kim(2023)의 수리모형실험 사이에 조도계수 및 투수계수의 차이 때문에 서로 상이한 결과를 나타낸 것으로 판단된다. 다르게 표현하면 정적으로 배치된 Tetrapods의 조도계수는 Rocks 1 layer 및 2 layers 배치의 조도계수와 유사한 것으로 생각할 수 있다.
Comparison results of mean overtopping rate on armoured slope structure (hs = 12.0 m).
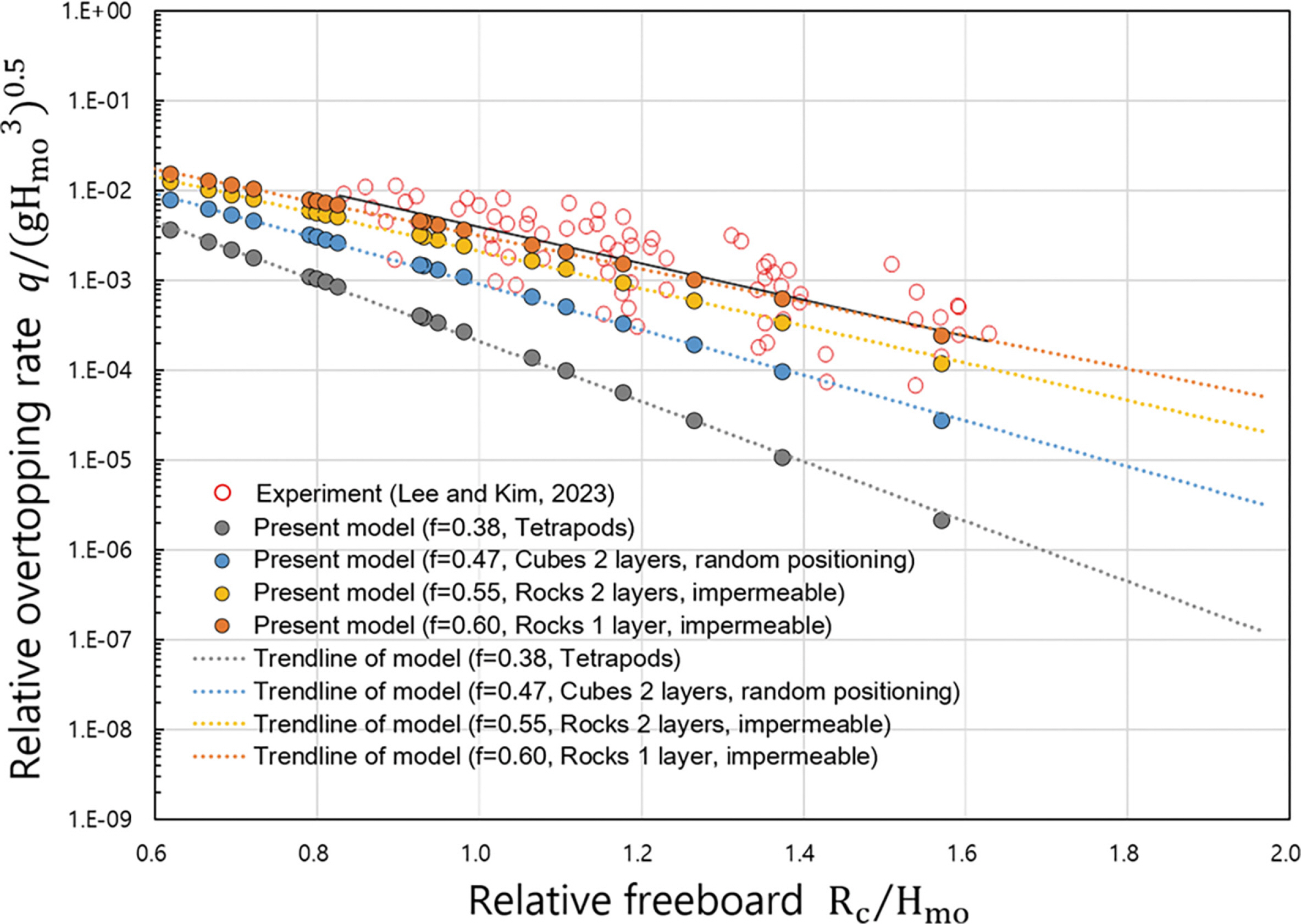
Fig. 5는 구조물 전면의 수심이 16.5 m인 조건에서 경사제의 평균월파량을 수치계산하고 수리모형실험 결과와 비교한 것이다. 수치계산 결과는 Rocks 1 layer 및 2 layers일 때 수리 모형실험 결과와 잘 일치하였고, Tetrapods일 때의 수치계산 결과는 실험 결과보다 과소평가되었음을 알 수 있다. 수치계산 결과는 상대여유고의 증가에 따른 월파량의 감소율이 실험과 일치하였다.
Comparison results of mean overtopping rate on armoured slope structure (hs = 16.5 m).
Fig. 6는 구조물 전면의 수심이 21.0 m인 조건에서 경사제의 평균월파량을 수치계산하고 수리모형실험 결과와 비교한 것이다. 앞에서 검토한 결과와 마찬가지로 수치계산 결과는 Rocks 1 layer 및 2 layers인 경우에 수리모형실험 결과와 잘 일치하였으며, Tetrapods의 수치계산 결과는 수리실험 결과보다 과소평가되었음을 알 수 있다.
Comparison results of mean overtopping rate on armoured slope structure (hs = 21.0 m).
결 론
본 연구는 완전비선형 Boussinesq 방정식을 사용한 FUNWAVE-TVD 모델에 EurOtop(2018)의 경험식을 추가하여 평면 파랑장 해역에서 경사구조물의 월파량을 해석할 수 있는 수치모형을 수립한 것이다. 본 수치모형은 CLASH data와 비교 검증을 통하여 피복 블록의 조도계수 차이에 따른 월파량의 변화를 정확히 재현할 수 있음을 알 수 있었다. 또한, 본 모형은 수리모형실험 자료와의 비교 검증을 통하여 상대여유고의 증가에 따른 월파량의 감소율이 실험과 일치하는 것을 확인하였으며, 월파량이 Tetrapods의 배치 상태에 따라서 크게 달라지는 것을 알 수 있었다. 즉, Tetrapods를 정적(regular positioning)으로 배치한 경우는 난적(random positioning)으로 배치한 경우보다 월파량이 크게 증가하였고 Rocks로 피복한 경우와 유사하였다. 한편, Rocks를 1열로 배치한 경우는 2열로 배치한 경우보다 월파량이 증가하였는데 이는 1열로 배치한 경우가 2열 배치보다 구조물 표면의 조도가 작기 때문으로 판단된다.