우리나라 해역별 해양환경에 최적화된 확률모형 개발
Development of Probabilistic Models Optimized for Korean Marine Environment Varying from Sea to Sea Based on the Three-parameter Weibull Distribution
Article information
Abstract
본 연구에서는 먼저 우리나라 해역별 해양환경 특성이 담긴 장기 파랑 관측자료로부터 Goda 모형을 활용하여 파력과 양력 시계열자료를 생성하였다. 이어 이렇게 생성된 시계열자료부터 Three-parameter Weibull distribution에 기반한 파력과 양력 확률모형을 개발하였다. 해역별로 다른 우리나라 해양환경은 파력과 양력 확률모형 모수에서도 그 차이를 확연하게 드러내었다. 충분히 발달한 풍성 파가 우월한 남해안의 경우 큰 Scale Coefficient, 작은 Location Coefficient, 1.3 전후의 Shape Coefficient로 특정되는 것을 확인하였다. 이에 비해 파랑의 성장이 취송거리에 의해 제한되는 서해를 마주하고 있는 군산의 경우 작은 Scale Coefficient, 큰 Location Coefficient, 2.0 전후의 Shape Coefficient로 특정되었다. 서해와 남해가 만나는 해역을 마주하고 있는 목포의 경우 작은 Scale Coefficient, 큰 Location Coefficient, 제일 작은 Shape Coefficient를 지녀 남해와 서해의 해양환경이 혼재한다는 사실도 확인할 수 있었다.
Trans Abstract
In this study, probabilistic models for the wave- and lifting forces were derived directly from long-term in-situ wave data embedding the Korean marine environment characteristics varying from sea to sea based on the Three-Parameter Weibull distribution. Korean marine environment characteristics varying from sea to sea carved out their presence on the probability coefficients of probabilistic models for wave- and lifting forces. Energetic wave conditions along the southern coast of Korea distinguish themselves from the others with a relatively large scale coefficient, small location coefficient, and shape coefficient around 1.3. On the other hand, mild marine environment along the western coast has a small variability, leading to small scale-coefficient, large location coefficient and shape coefficient around 2.0. In the sea off Mokpo, near the boundary between the South- and West Seas, marine environment was characterized by small scale-coefficient, large location coefficient, and shape coefficient around 1.2, implying that marine environments characteristics of the South-and West Sea coexist in the sea off Mokpo.
1. 서 론
최근 우리나라에서 항 외곽시설의 구조양식으로 선호되는 케이슨을 활용한 직립식 방파제 신뢰성 기반설계는 아직 여명기에 불과하여 개선의 여지가 상당하며, 이러한 판단의 논거를 정리하면 다음과 같다:
첫째, 직립식 방파제 활동 파괴 여부를 결정하는 확률변수인 진행 방향 파력과 양력의 성격은 파고뿐만 아니라 주기에 의해서도 결정되나(Kortenhaus and Oumeraci, 1998)., 현재 우리나라에서 마련 중인 직립식 방파제 신뢰성 기반설계는 파고에만 천착하여 진행되는 듯하다. 이 과정에서 파력이 작용하는 공간적 범위는 첨두 주기만을 활용하여 추정되는 등 지나치게 단순화되어, 주기라는 확률변수가 지니는 추계학적 성정이 온전하게 반영된 것으로 보기 어렵다. 이러한 판단의 근거는 신뢰성 기반설계를 다룬 국내연구에서 파고와 주기의 결합분포를 다룬 예를 찾아보기 어렵다는 사실에서도 찾을 수 있다(Lee et al., 2009).
둘째, 우리나라 해양환경은 신뢰성 설계의 이론적 체계가 완성된 유럽 혹은 미국의 그것과는 다른 구조적 차이를 지닌다(Park et al., 2021). 따라서 신뢰성 설계가 효율적으로 구현되기 위해서는, 우리나라 해역별 해양환경 특성을 담아낸 확률모형 개발이 선행되어야 하나, 현재 유럽 혹은 미국에서 선호하는 확률모형을 단순수용하여 신뢰성 기반설계가 수행되고 있어 시정되어야 할 것이다. 이러한 구조적 차이는 반 시계 방향으로 틀어지고, 남북으로 길게 늘어선 모양의 동해와 서해의 지형적 특성에 기인하며, 이러한 특성으로 인해 서해와 동해의 경우 풍성 파 발달에 필요한 취송거리가 제한적인 방위에서만 확보된다. 이러한 지형적 특성으로 인해 우리나라 서해와 동해의 경우 파랑의 성장이 취송거리에 의해 제한되며, 이로 인해 서해안과 동해안의 경우 긴 너울이 우세한 미국 혹은 구주와는 달리 다양한 성격의 너울이 출현한다. 특히, 서해안의 경우 주기가 파고에 선형비례 하는 것으로 관측되나(Cho and Cho, 2022), 이러한 거동은 파고가 큰 경우 파고와 주기 사이의 상관관계가 옅어진다는 해안공학계의 정설과는 각을 세우는 것으로 우리나라 해양환경을 담아낼 수 있는 확률모형 개발이 필요하다는 사실을 방증한다(Cho and Cho, 2022). 이에 비해 남해안의 경우 가장 거친 해양환경에 노출되어 완전히 성장한 풍성파[Fully Developed Wind Waves]가 관측되며, 해안공학계에 잘 알려진 것처럼 파고가 상대적으로 큰 경우 파고와 주기의 상관관계가 옅어지는 것을 관측할 수 있다(Cavanie et al., 1976).
셋째, 항 외곽시설에 대한 여러 설계안을 차별화할 수 있는 지표이자 신뢰성 기반설계의 중요한 성과물인 파괴확률이 구조물 생애주기, 혹은 특정한 해에서의 파괴확률을 나타내는지가 불분명한 경우가 대부분으로 보인다. 그러나, 이러한 혼선은 일종의 최적화 과정인 신뢰성 해석으로 설계조합, 신뢰 지수를 찾아내고, 이렇게 특정된 설계조합을 구성하는 파력과 양력으로부터 하중계수와 저항계수를 역설계하는 우리나라 신뢰성 기반설계 관행에 오류가 있을 수 있다는 추정을 가능하게 해 명징한 기준마련이 시급해 보인다.
넷째, 전술한 파고와 주기의 상관관계에서 확연하게 드러나듯, 우리나라 해양환경은 유럽 혹은 미국의 그것과는 다른 구조적 차이를 지닌다. 따라서 이러한 구조적 차이가 결과하는 파고와 주기의 상관관계, 주기가 직립식 방파제에 작용하는 파력의 공간적 범위에 미치는 영향 등을 고려하면 우리나라 해역별 해양환경 특성이 담긴 파력과 양력 관측자료로부터 파력과 양력에 대한 직접적인 확률모형을 개발하고, 이에 기반하여 신뢰성 설계가 수행될 필요가 있으나, 현재 이러한 시도가 문헌에서는 찾아볼 수 없어 개선이 시급하다(Park et al., 2021; Cho and Park, 2023).
다섯째, 직립식 방파제의 활동 파괴 여부를 결정하는 두 가지 확률변수인 파력과 양력은 밀접하게 연계된 사상으로 보이나, 이러한 파력과 양력 간의 상관성은 우리나라에서 수행된 직립식 방파제 신뢰성 관련 연구에서 간과된 것으로 보인다. 현재 우리나라 신뢰성 기반설계 관련 연구의 대부분에서 파력과 양력은 재현 빈도가 오십 년 혹은 백 년인 설계 파랑과 Goda 모형을 활용하여 추정하며, 이 과정에서 Goda 모형의 over-shooting 문제와 계측상에서 있을 수 있는 오류를 해결하기 위한 bias 계수가 도입된다(Kim and Suh, 2009). 이렇게 도입된 여러 bias 계수는 서로 다른 정규분포를 따르는 확률변수로 취급되나 이러한 연구 관행은 후속하는 신뢰성 해석과정에서 파력과 양력이 상호 독립적으로 정규분포를 따른다는 가정을 수행한 것과 다르지 않다. 그러나, 파력과 양력 간의 상관성이 큰 경우 직립식 방파제 활동에 저항하는 방파제 유효 자중이 양력으로 감소한 채 큰 진행 방향 파력에 노출된다는 사실을 상기하면 전술한 상관성은 직립식 방파제 파괴확률에 적지 않은 영향을 미칠 수 있어 시정이 시급해 보인다(Kim and Cho, 2023).
이상의 논의를 토대로 본 연구에서는 먼저 주기가 파력에 미치는 영향을 살펴보기 위해 Goda 모형을 활용하여 1979.1.1.부터 2019.12.31까지의 파고와 주기 관측자료[WINK, Jeong et al.(2018)]로부터 파력과 양력 값을 산출하고, 파력과 양력 간의 상관 정도를 살펴보았다. 이어, 이렇게 생성된 파력과 양력의 시계열자료로부터 파력과 양력의 연 최댓값 FHMAX와 FVMAX을 특정하고, 이렇게 특정된 연 최댓값으로 시계열자료를 구성하고 빈도 해석하여 우리나라 해양환경에 최적화된 파력과 양력의 확률모형을 산출하였으며, 이 과정에서 기저 확률분포로는 대표적 극치분포로 알려진 Three-parameter Weibull 분포를 사용하였다.
본 논문의 구성을 정리하면 다음과 같다: 논의 전개를 위해 2장에는 파랑 in-situ data로부터 파력을 산출과정에서 현재 해안공학계에서 가장 선호되는 Goda 파력 모형을 정리하였다. 3.1절에는 직립식 방파제 신뢰성 기반설계 관행에서의 파력 산출과정을 비판적 시각에서 들여다보았으며, 3.2절에는 이 과정에서 드러난 문제를 정리하여 수록하였다. 3.3절에는 우리나라 신뢰성 기반설계 관행에서는 주기라는 확률변수가 지니는 추계학적 성정이 온전하게 반영하지 못한다는 문제를 해결하기 위해 본 논문에서 제시한 파력과 양력 확률 모형의 필요성과 유도과정을 정리하였다.
2. Goda 파력 모형
Goda and Fukumori(1972), Goda(1974, 1975, 2000)의 연구성과에 따르면 직립식 방파제에 작용하는 충격 쇄파압의 수평 방향 성분 FH, 연직 방향 성분 FV은 각각 다음과 같이 산출될 수 있으며[Fig. 1 참조],
Definition sketch of physical parameters affecting the impulsive wave force on the vertical type breakwater using Caisson [reproduced from Goda (2000)].
여기서 B는 Caisson 두께를 나타내며, p1, p3, p4, pu, h*c, η*는 각각 다음과 같이 기술될 수 있다.
상기 식에서 β는 파랑 접근 각도를 나타내며, α1, α2, α3는 파랑 주기가 미치는 영향을 설명하기 위해 도입된 계수로 다음과 같이 산출될 수 있으며,
여기서 h는 수심, hb는 방파제에서 5H1/3만큼 떨어진 지점에서의 수심, d는 기초 사석 층 정점에서의 수심을 각각 나타낸다.
3. 확률모형
3장에서는 논의 전개를 위해 직립식 방파제의 활동 파괴 여부를 결정하는 세 가지 확률변수인 파력, 양력, 저항계수에 대한 확률모형 중 현재 문헌에서 빈번하게 언급되는 모형을 비판적 시각에서 다루었다. 먼저, 3.1절에서는 기존 우리나라 해안공학계의 문법에서 파력 산출과정에 중요한 역할을 하는 최대파고 확률모형을 정리하였으며, 3.2절에서는 상당한 공학적 가치에도 불구하고 기존의 해안공학계 문법에서 소홀히 다루어진 주기의 추계학적 성정이 파력에 미치는 영향에 관해 기술하였다. 이어 논의과정에서 드러난 한계를 해결하기 위해 본 논문에서 제안한 파력과 양력에 대한 직접적인 확률모형 산출과정은 3.3절에 정리하였다.
3.1 HMAX
현재 문헌에서 단위 폭풍 사상에서 관측되는 HMAX의 확률분포모형으로 가장 빈번하게 언급되는 모형은 Three parameter Weibull 분포로 보이며 이를 기술하면 다음과 같으며(Ang and Tang, 1984)
여기서 μHMAX, a, b는 확률 모수로 각각 Location, Scale, Shape Coefficients로 불린다.
Burcharth et al.(1994)는 전술한 Weibull 분포에 준거하여 구조물의 생애주기 T 동안 최대파고 HMAX가 HMAX를 초과하는 확률을 다음과 같이 제시한 바 있으며,
여기서 λ는 연간 태풍 발생 횟수를 나타낸다.
3.2 첨두 주기 Tp
주기는 상당한 공학적 가치를 지니나 우리나라 해안공학계에서는 소홀히 다루어졌으며, 이러한 예는 직립식 방파제 신뢰성 해석을 위한 파력 산출과정에서 파력이 작용하는 공간적 범위가 첨두 주기 Tp와 식(9), (10), (11)을 활용하여 산출하는 관행에서 찾을 수 있다. 이러한 관행은 수행과정에서의 편의를 위한 것으로 보이나, Weibull 분포를 활용하여 HMAX가 모의 되더라도, 이렇게 모의 된 HMAX에 연계된 Tp 산출과정을 제시한 단 한 편의 논문도 찾을 수 없다. 이러한 사실로 미루어 보면 우리나라에서 그동안 수행된 신뢰성 해석에서 주기라는 확률변수가 지니는 추계학적 성정이 온전하게 반영된 것으로 보기 어렵다.
파고와 주기는 해양환경이 온화한 경우 같이 움직이며, 해양환경이 거친 경우에는 상관관계가 옅어지며, 이렇게 다양한 상관관계가 우리나라를 둘러싼 세 해역에서 극명하게 드러나 HMAX와 Tp의 관계식이 해역별로 마련되어야 할 것으로 판단되며, 향후 상당한 논의가 필요해 보인다(Cho, 2021a, 2021b, 2021c, 2021d).
3.3 파력과 양력
서해안에서 관측되는 파고와 주기의 선형 상관관계에서 알 수 있듯 우리나라 해양환경은 유럽 혹은 미국의 그것과는 다른 구조적 차이를 지닌다. 이러한 구조적 차이가 결과하는 파고와 주기의 선형 상관관계, 주기가 직립식 방파제에 작용하는 파력의 수직 분포에 미치는 영향 등을 고려하면 신뢰성 설계가 상당한 정도로 수행되기 위해서는 우리나라 해양에서 출현한 파고와 주기에 의해 결과된 파력과 양력 관측자료로부터 파력과 양력의 확률모형을 직접 개발할 필요가 있어 보인다.
이러한 인식에 기초하여 본 논문에서는 주기가 파력에 미치는 영향을 살펴보기 위해 먼저 Goda 모형을 활용하여 1979.1.1.부터 2019.12.31까지의 파고와 주기 관측자료[WINK, Jeong et al.(2018)]로부터 파력과 양력을 한 시간 간격으로 먼저 산출하였다. 수심은 직립식 방파제의 일반적인 거치 수심을 고려하여 20 m로 취하였으며, d는 18.5 m, hc는 5 m, B는 10 m로 각각 취하였다.
이어 이렇게 생성된 파력과 양력의 시계열자료로부터 파력과 양력의 연 최댓값 FHMAX와 FVMAX을 특정하고, 이렇게 특정된 연 최댓값 시계열자료를 빈도 해석하여 우리나라 해양환경에 최적화된 파력과 양력의 확률모형을 산출하였으며, 이 경우 전술한 확률모형으로 신뢰성 해석을 수행하여 얻게 되는 파괴확률은 특정 연도에 직립식 방파제가 활동으로 파괴될 수 있는 확률을 의미한다.
3.3.1 해운대
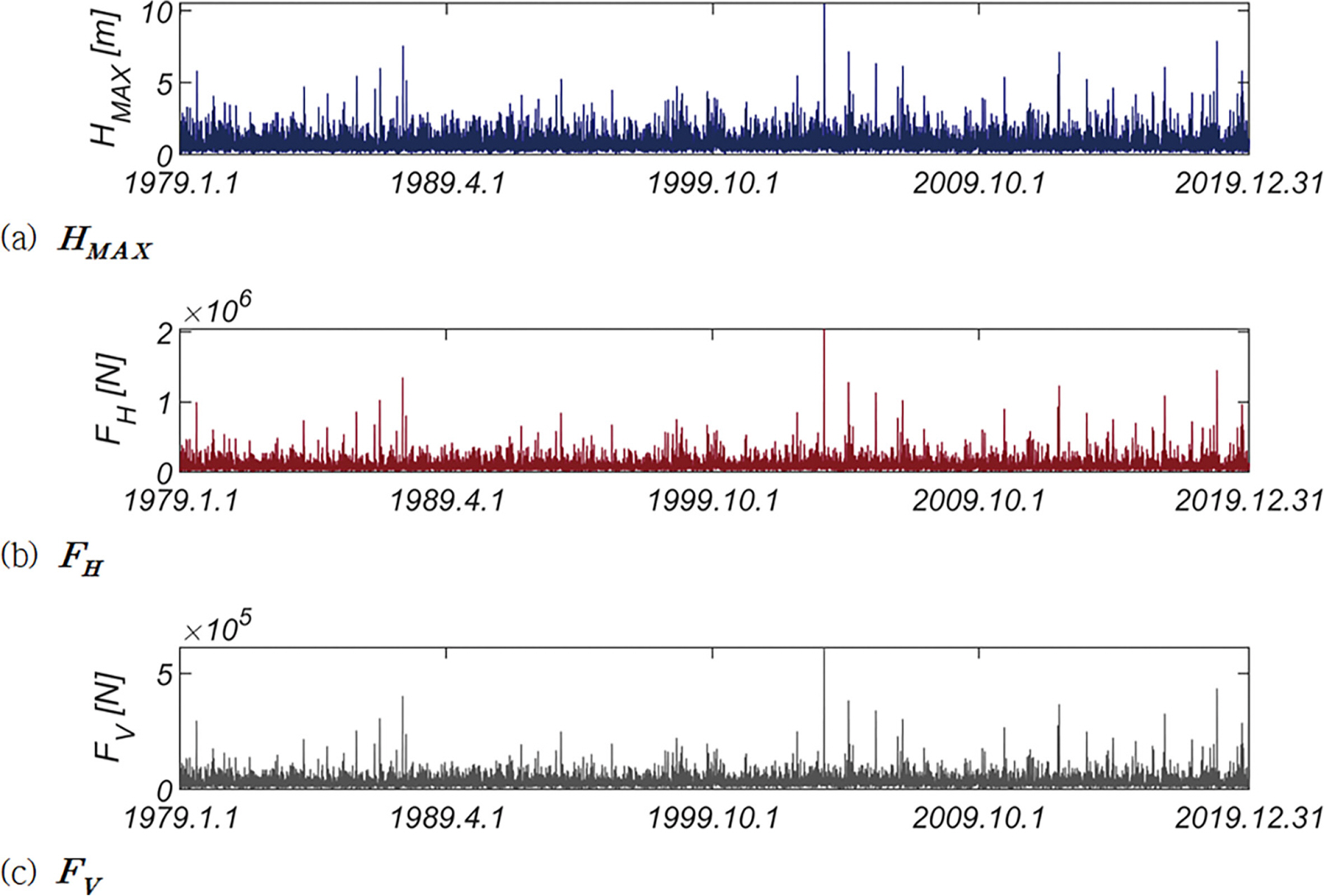
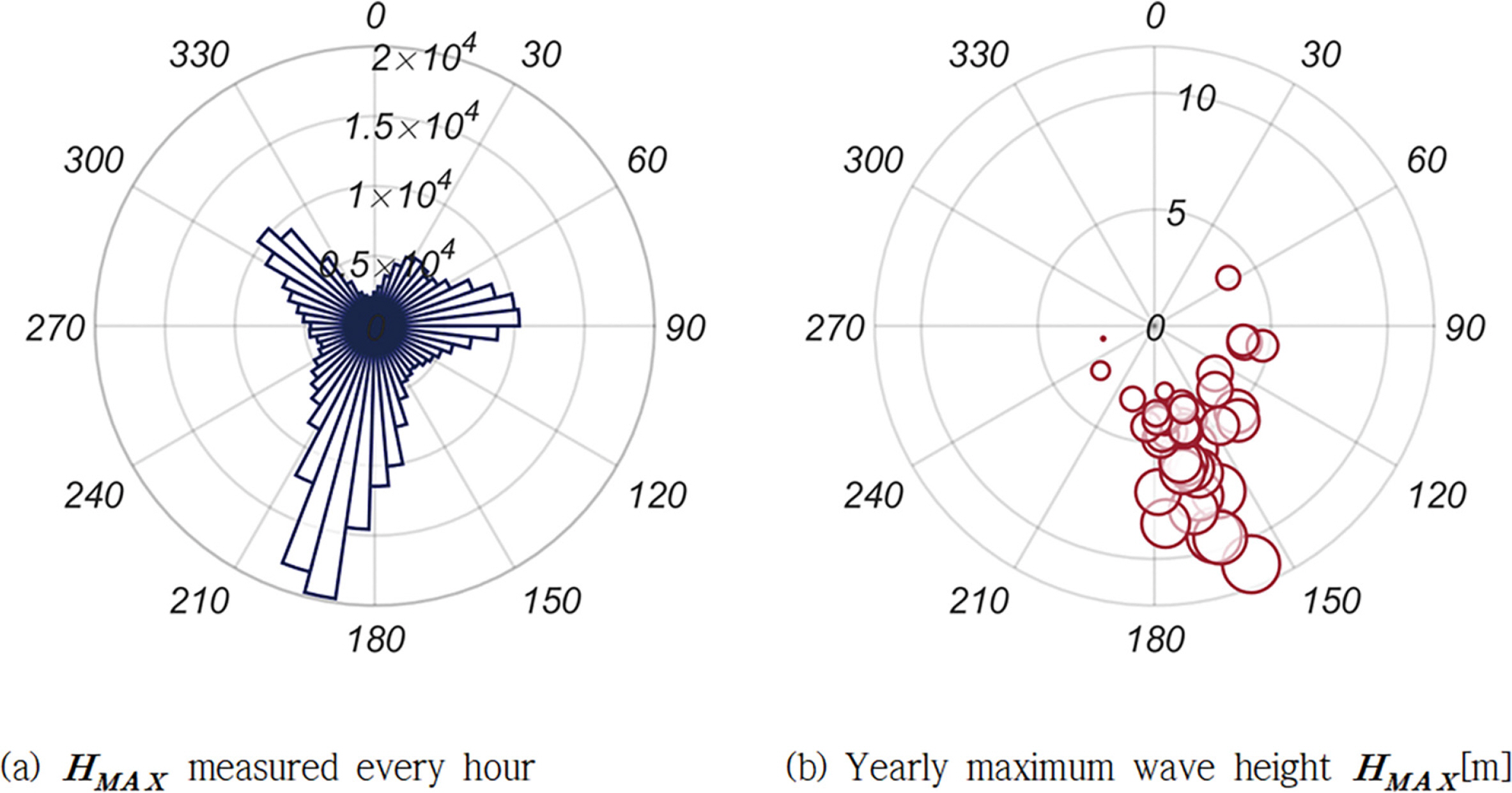
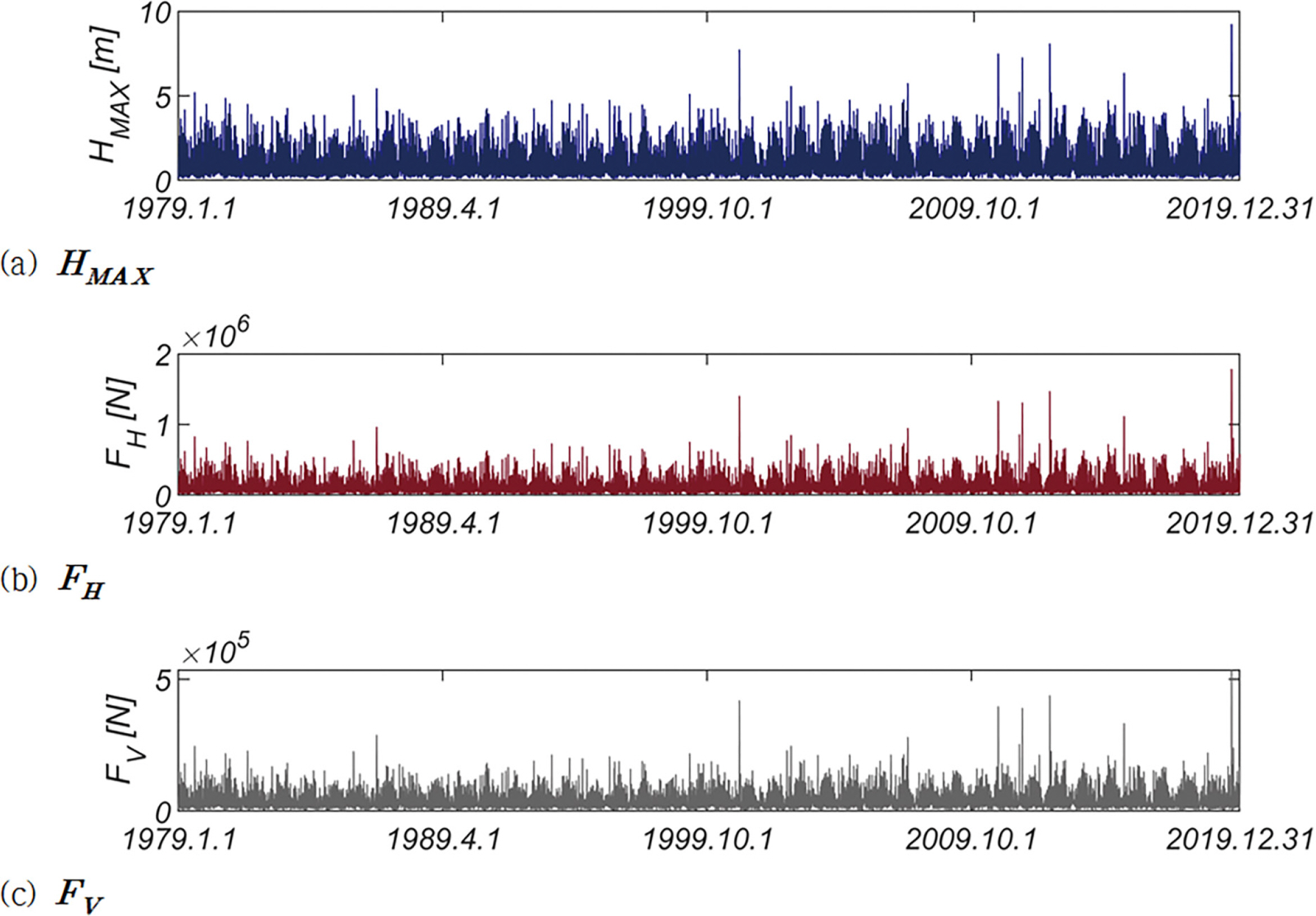
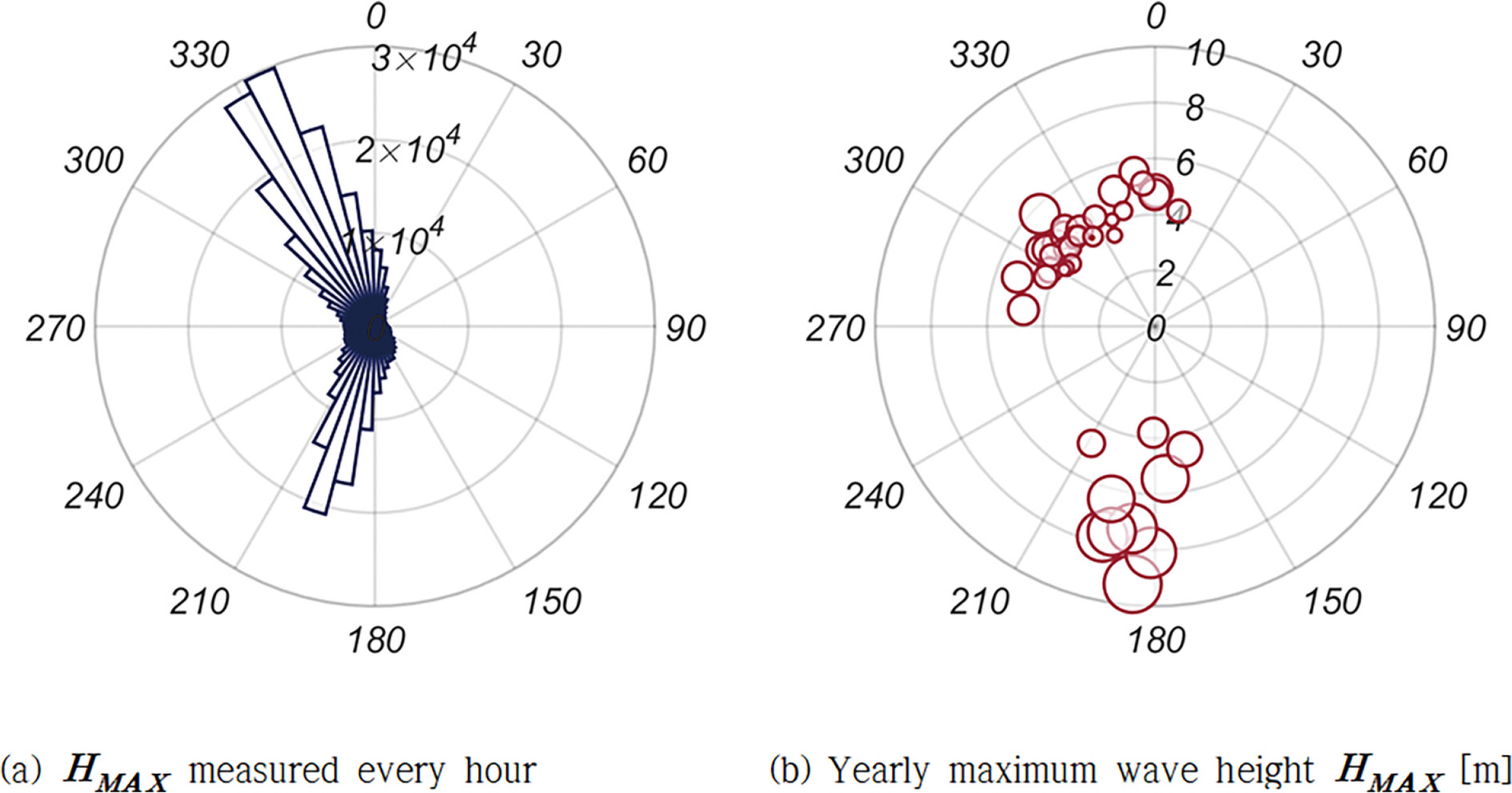
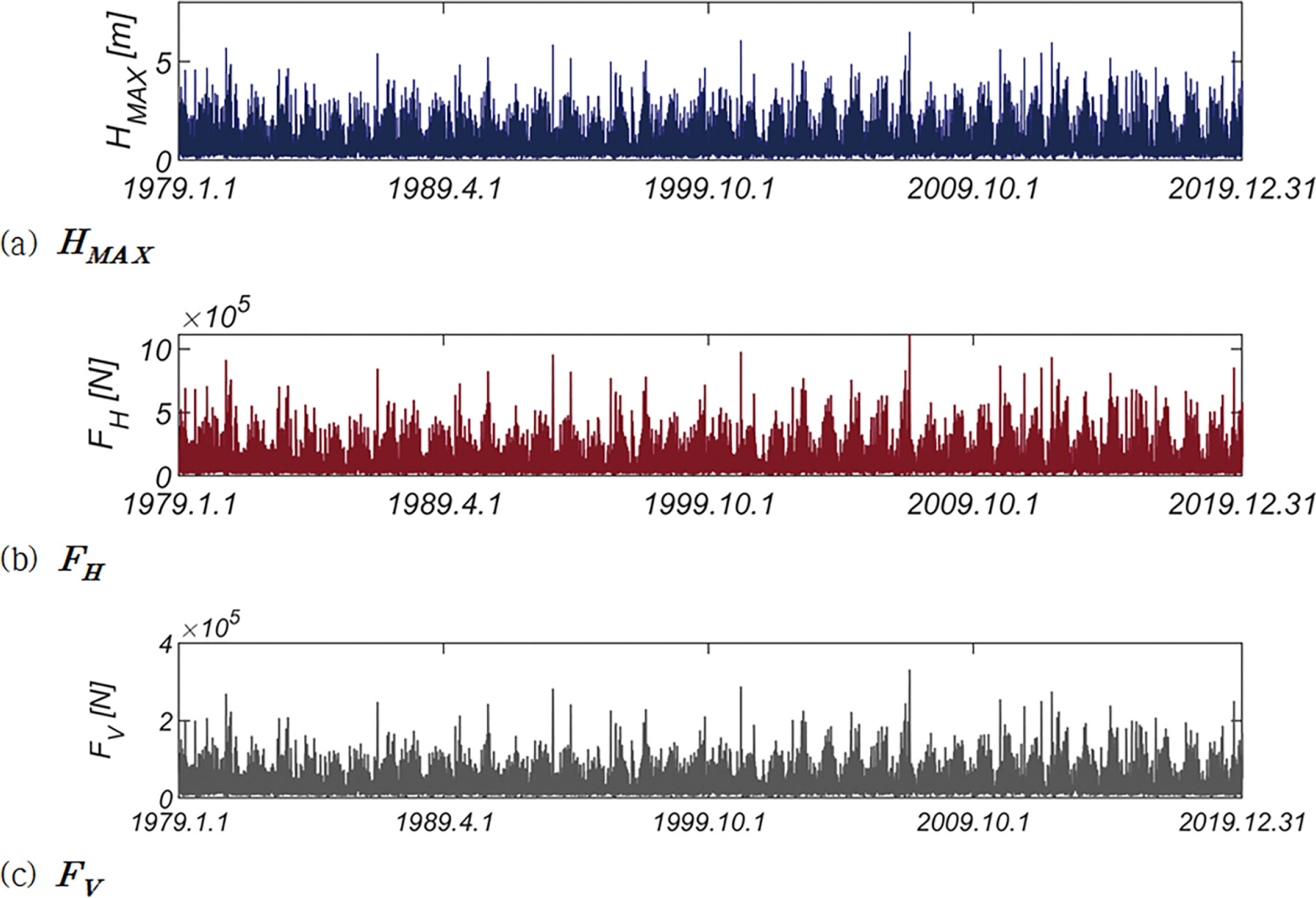
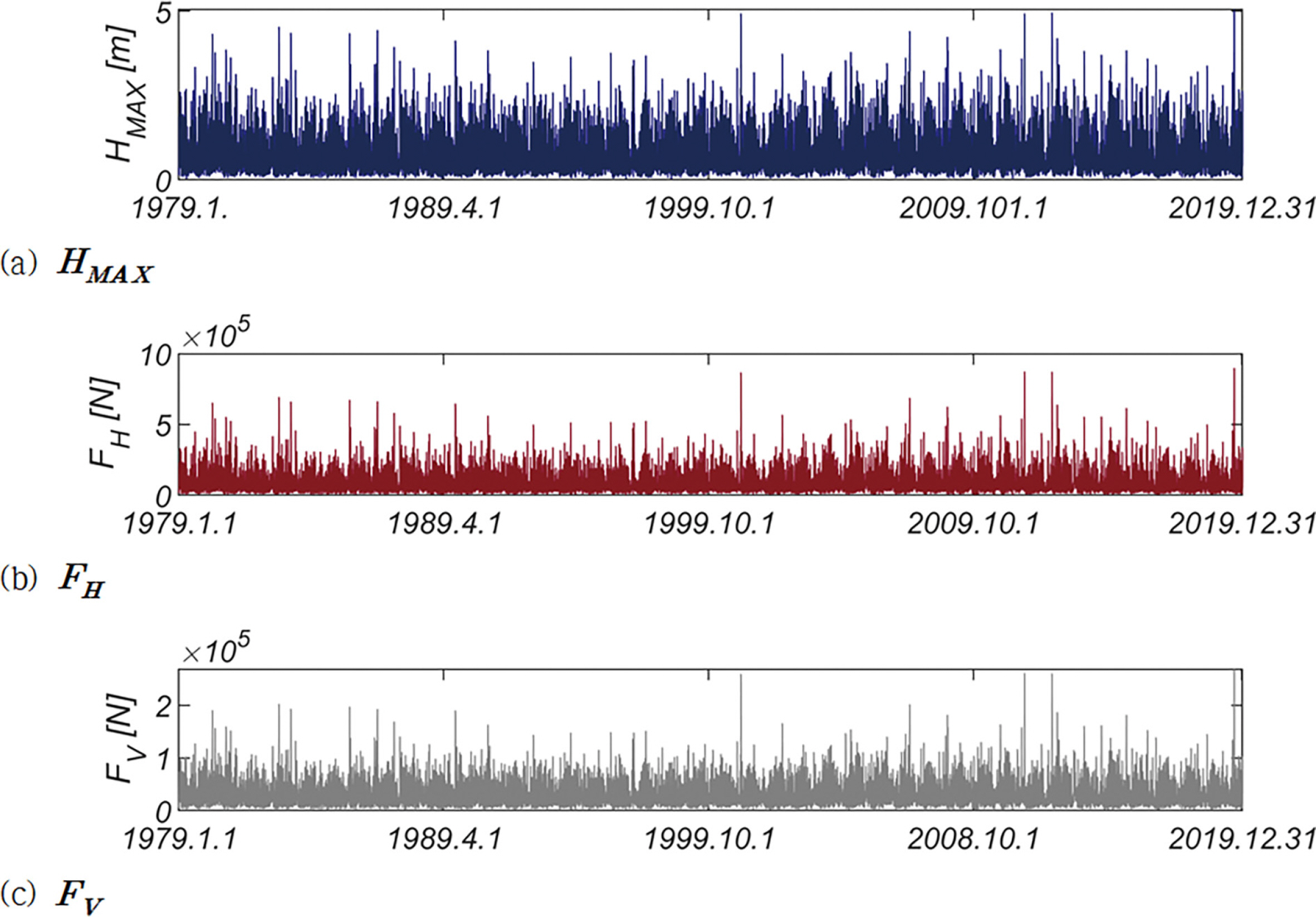
Fig. 2에는 HMAX, 파랑 진행 방향 파력 FH, 양력 FV의 1979.1.1부터 2019.12.31까지의 시계열자료를 도시하였다 [Grid NO 107-3]. Fig. 3(a)에는 한 시간 간격으로 계측된 모든 파랑을 대상으로 한 파랑 장미도, Fig. 3(b)에는 41개의 년 최대파랑을 대상으로 한 파랑 장미 도를 정리 하였으며, Fig. 3(b)에서 원점으로부터의 거리는 파고[m], 원의 면적은 주기를 나타낸다. 출현 빈도는 상대적으로 낮으나 S 계열로부터 파고가 10m 내외인 큰 파랑이 십여 차례 접근한 것을 확인할 수 있다.
Time series of measured HMAX, FH, and FV from 1979.1.1. to 2019.12.31.
Wave rose at the sea off Haeundae.
년 최대파고 HMAX와 주기 간의 상관관계를 살펴보기 위해 Fig. 4에는 HMAX[m]와 주기 Tpeak[s]의 결합확률 분포, HMAX와 주기 상관관계 회귀분석 결과를 도시하였다. 기보고된 것처럼 파고가 거친 경우 파고와 주기의 상관 정도가 옅어지는 것을 확인할 수 있으며, 회귀분석 결과를 정리하면 다음과 같다.
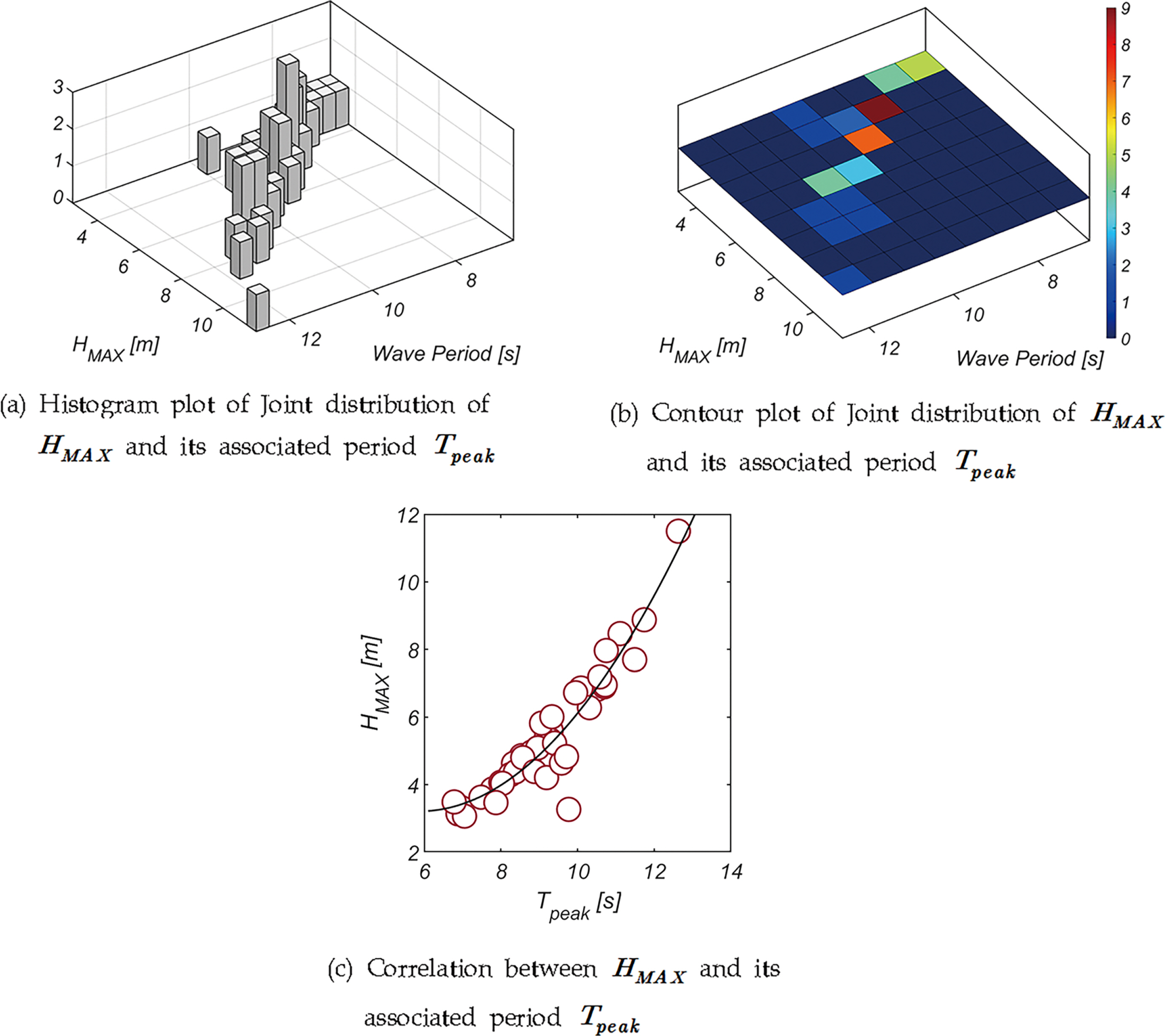
Joint distribution of yearly maximum wave height HMAX and its associated period Tpeak, and the inter-correlation between HMAX and Tpeak.
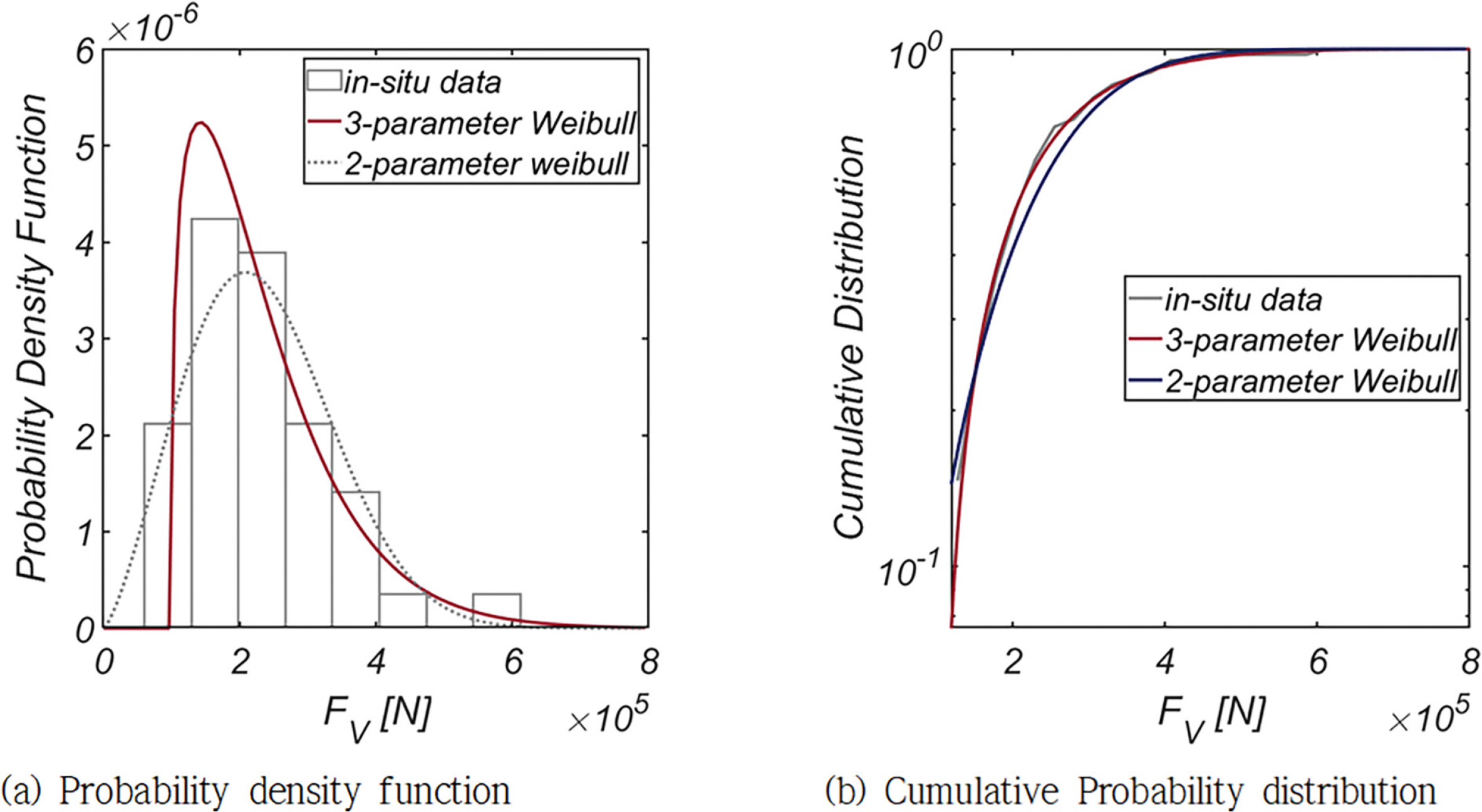
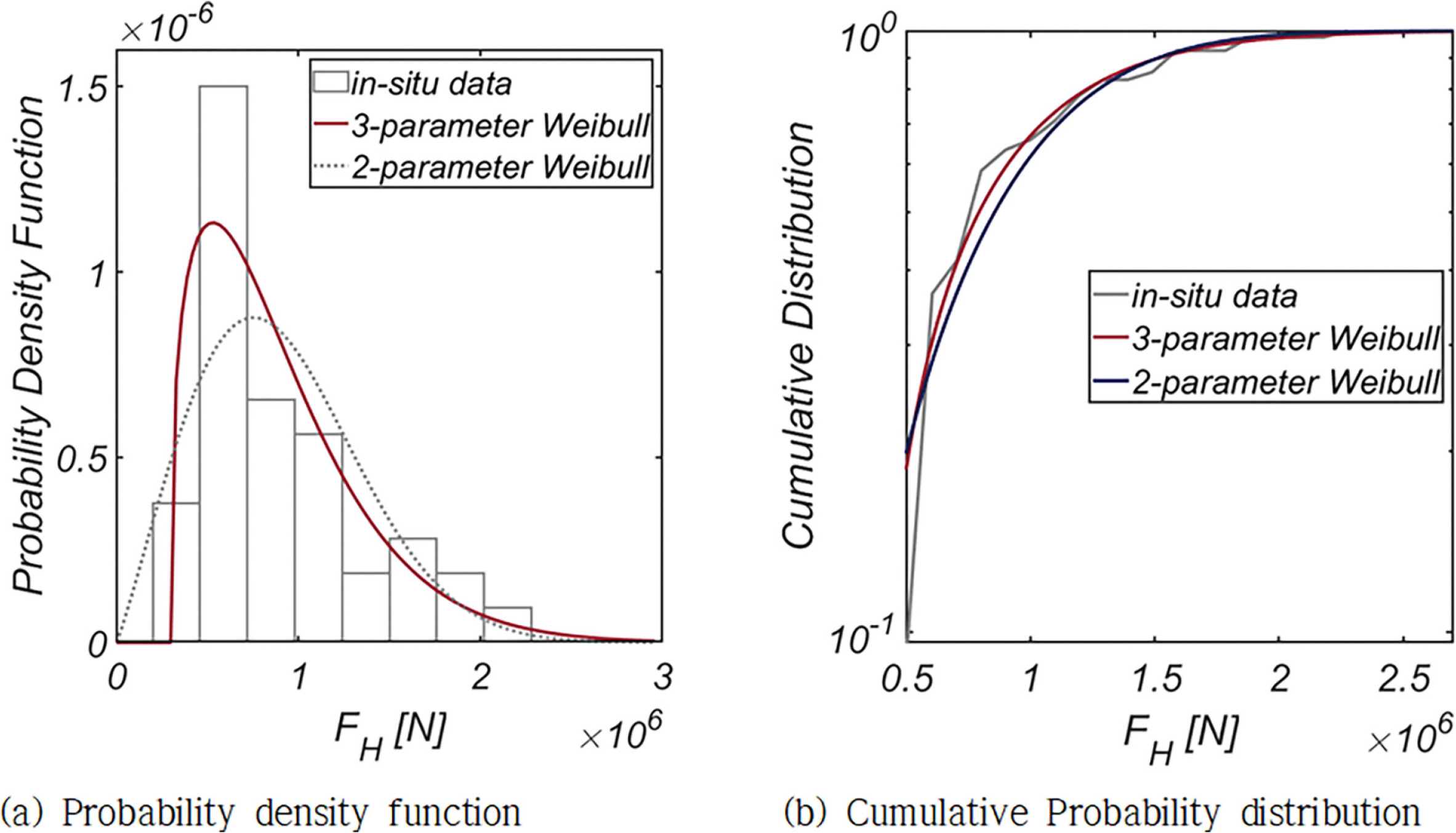
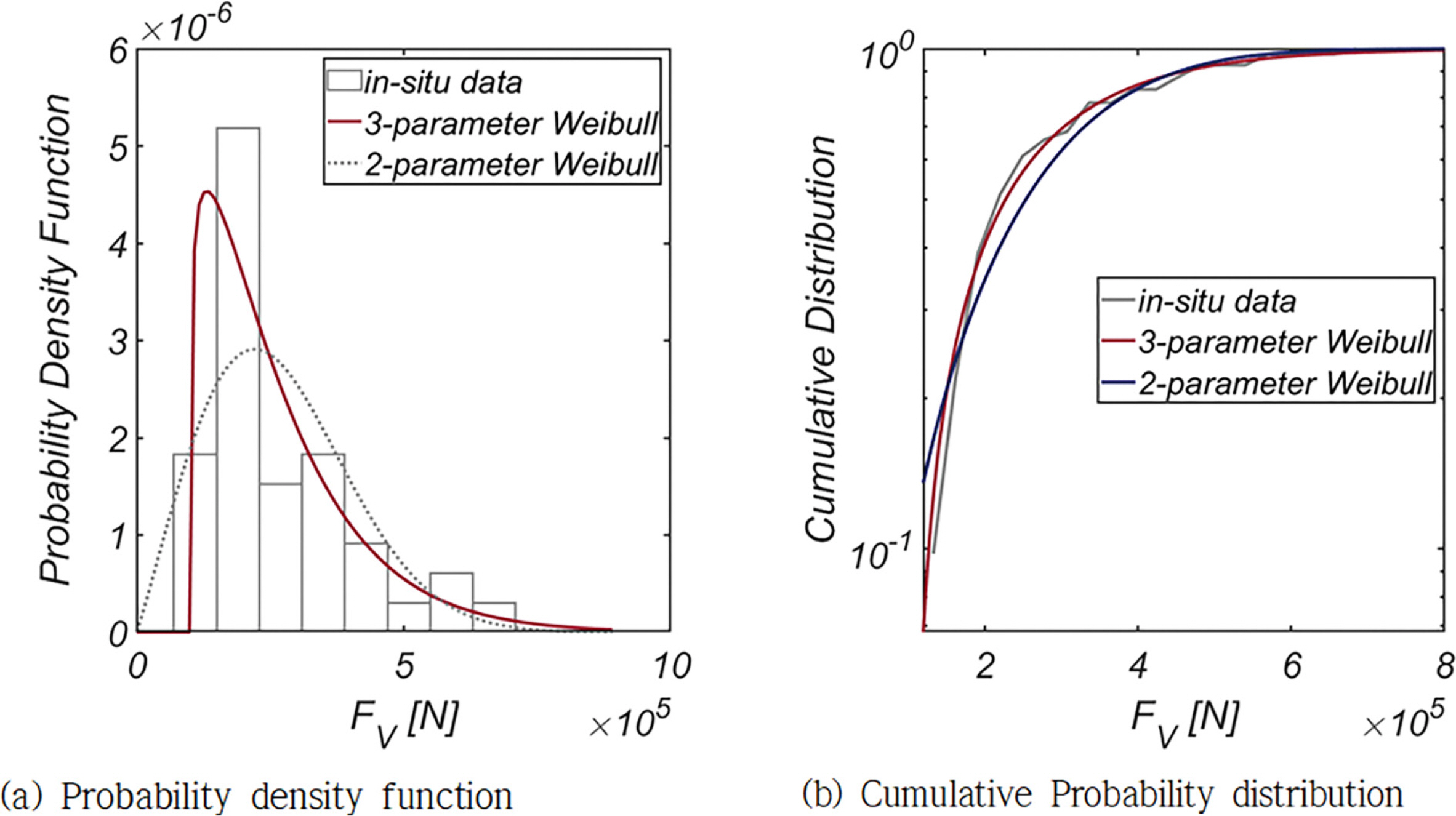
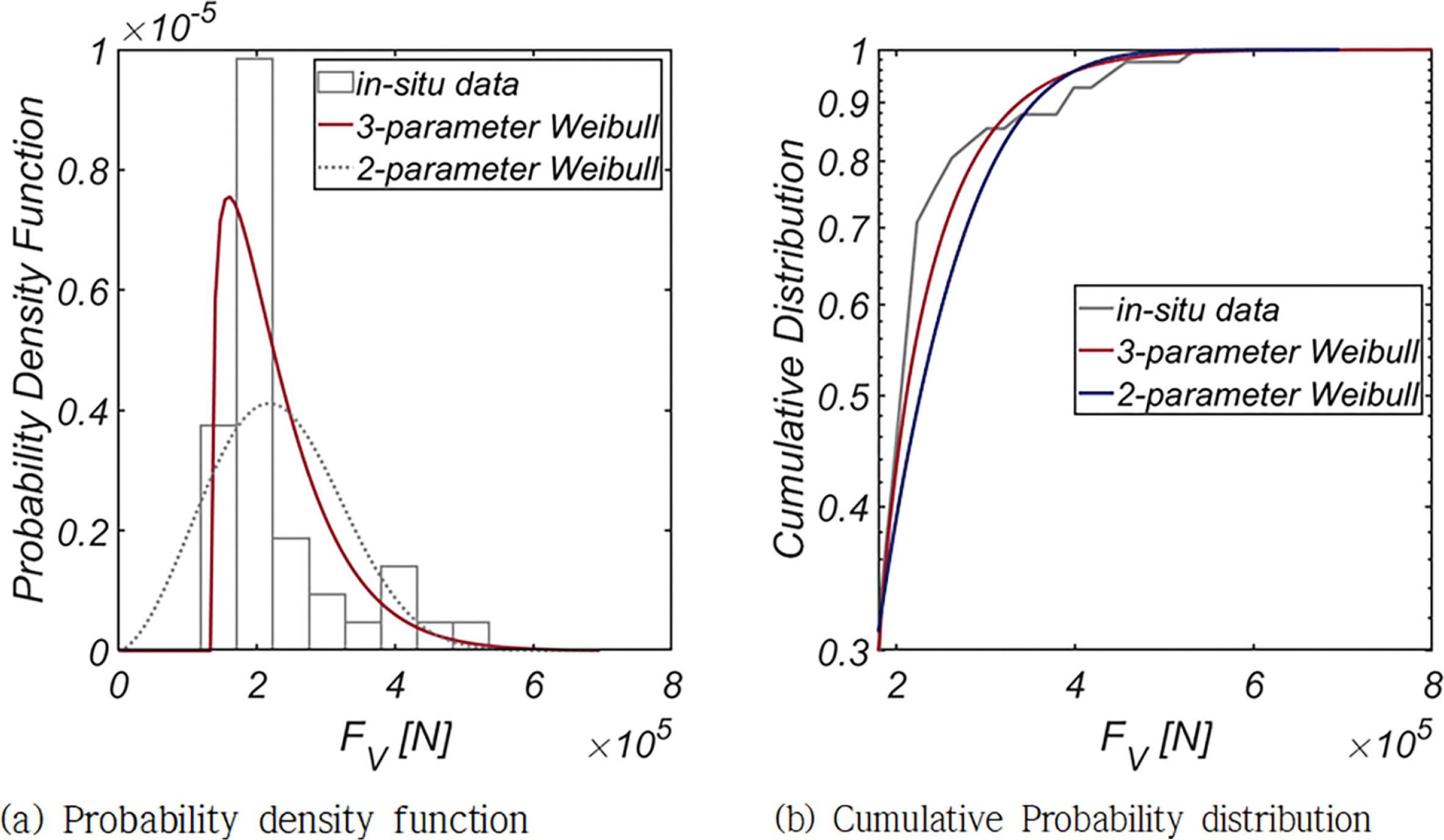
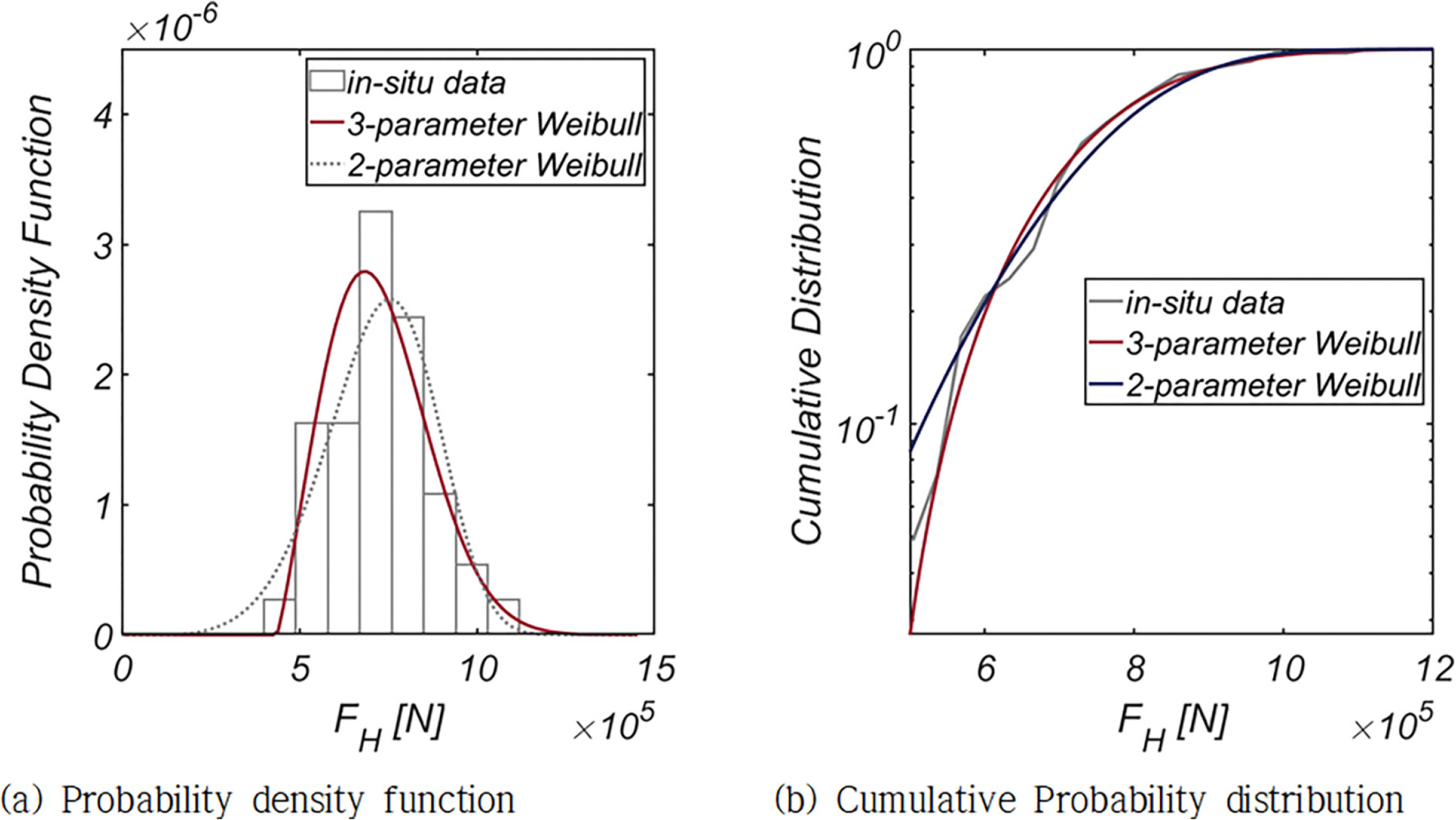
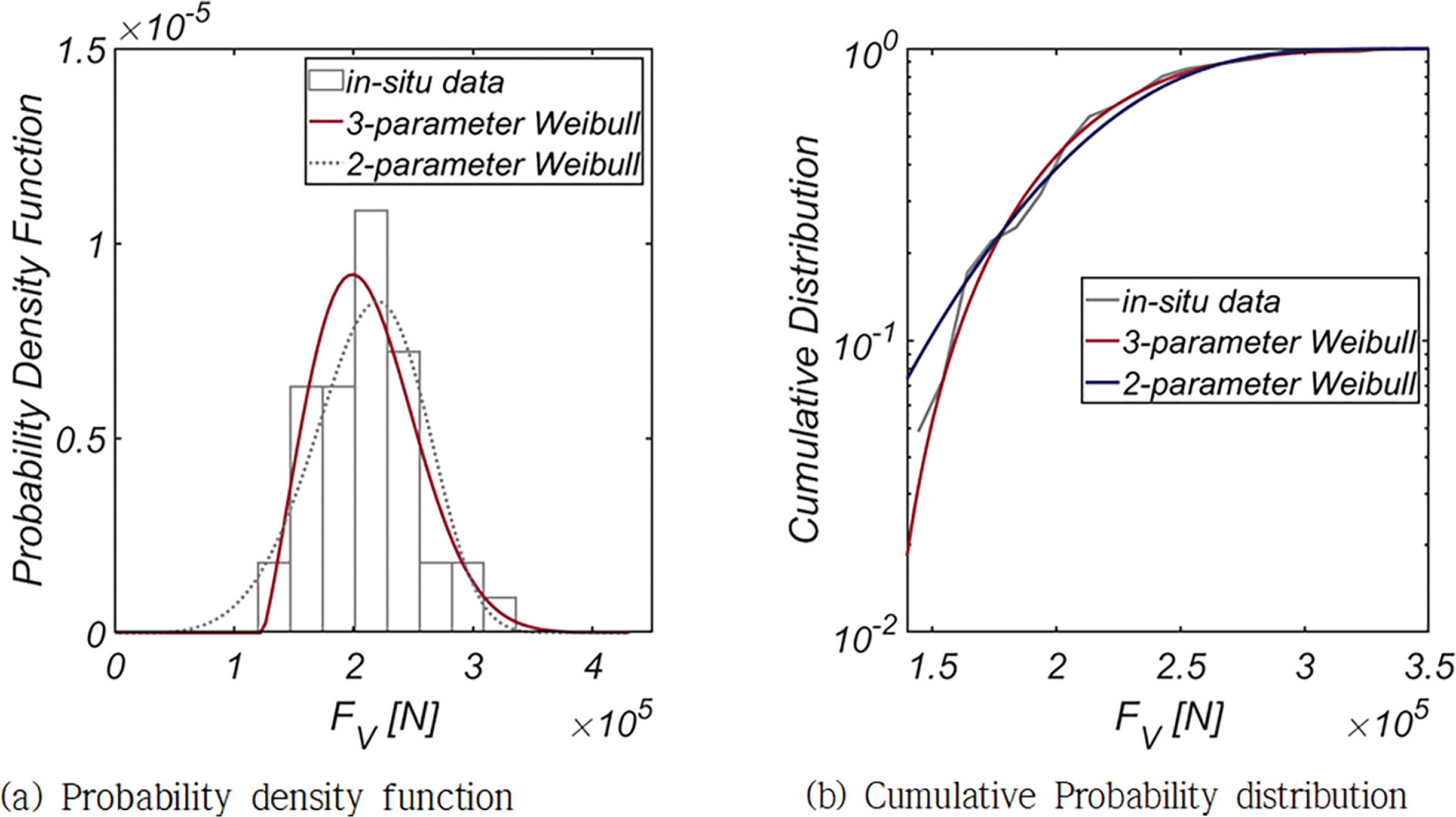
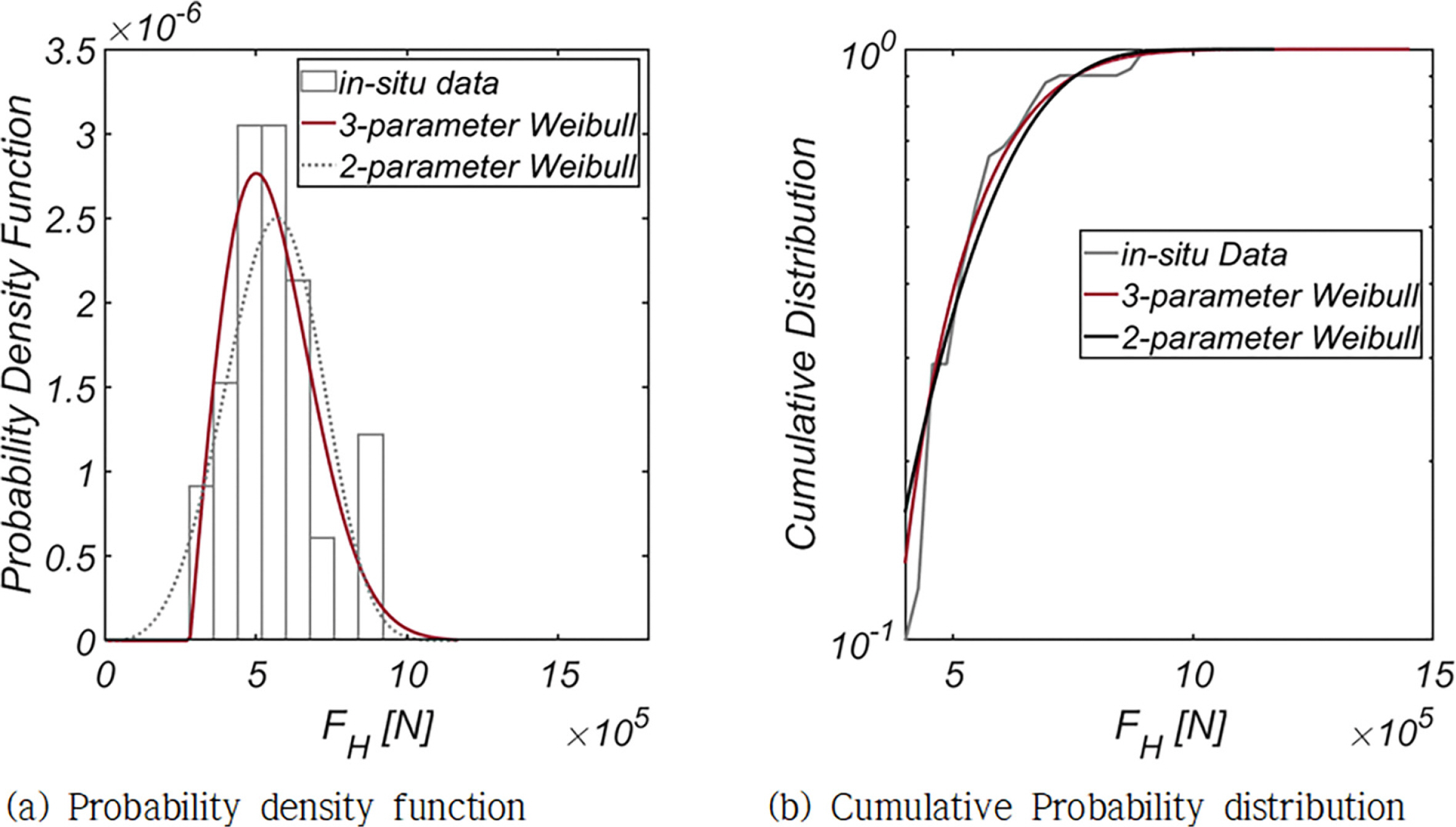
Fig. 5, 6에는 FH와 FV의 확률분포와 누가 확률분포를 정리하였으며, 기저 확률분포로는 대표적 극치분포로 알려진 Weibull 분포 계열을 사용하였다. 기저 확률분포로 Location Coefficient가 추가된 Three-parameter Weibull 분포를 사용하는 경우 적합도가 현저하게 개선되어, Location Coefficient가 우리나라 해양환경에 내재한 불규칙성을 해역별로 차별화할 수 있는 중요한 확률 모수인 것은 분명해 보인다.
Comparison of Weibull distribution of FH with in-situ data.
Probability density function of FV.
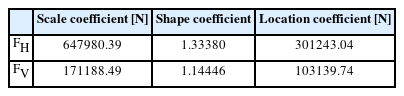
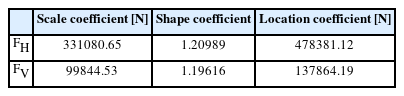
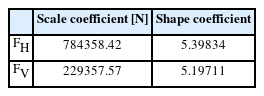
Table 1에는 in-situ wave data와 Matlab 기반 Statistics and Machine Learning Toolbox 중 최대가능도법[MLE, Maximum Likelihood Estimates]를 활용하여 산출한 Three-parameter Weibull 분포의 확률 모수인 Location, Scale, Shape Coefficients 를 수록하였다.
List of probability coefficients of 3-parameter Weibull distribution for wave force FH and lifting force FV [HaeunDae]
3.3.2 여수
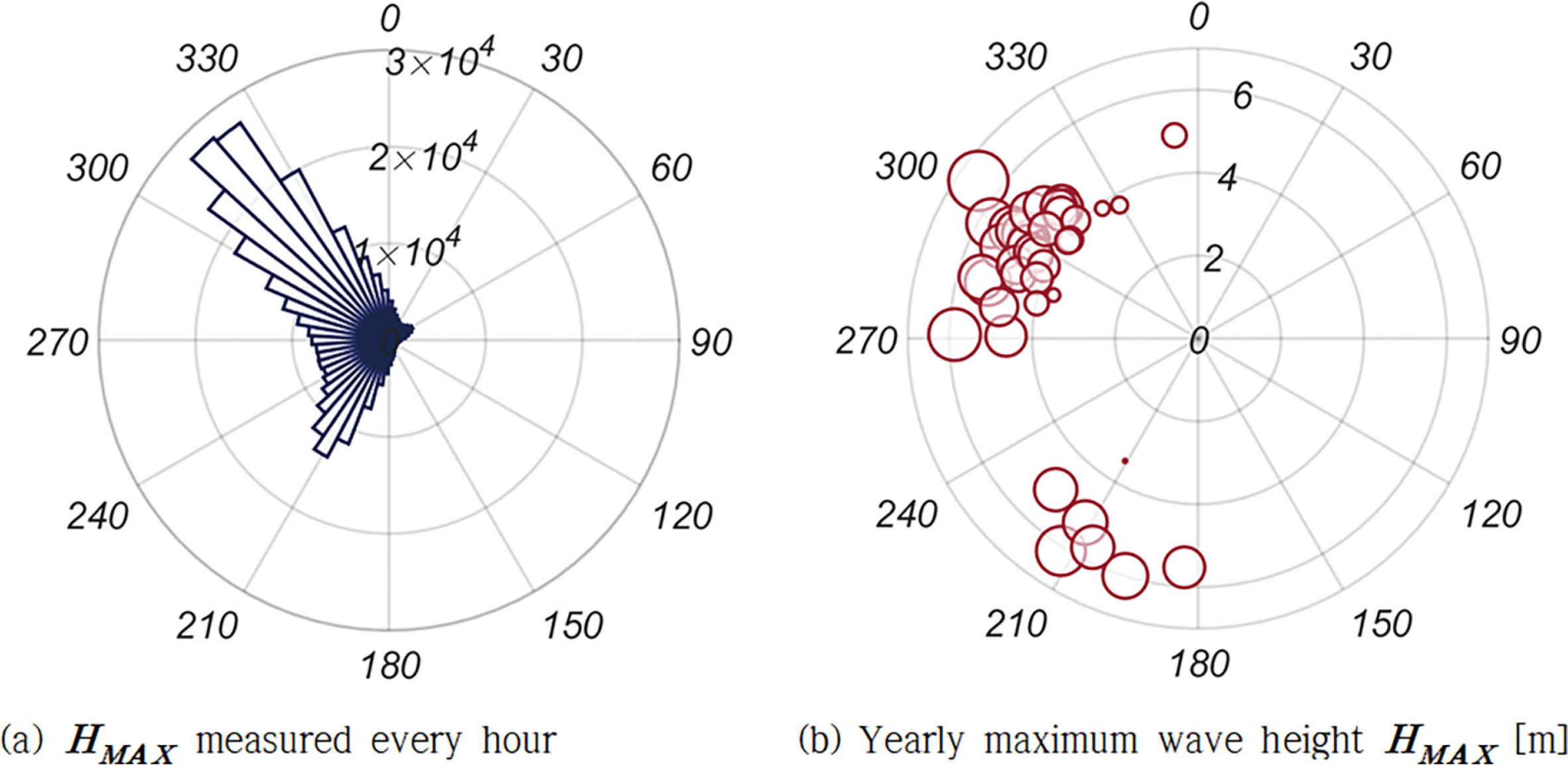
Fig. 7에는 HMAX, 파랑 진행 방향 파력 FH, 양력 FV의 1979.1.1부터 2019.12.31까지의 시계열자료를 도시하였다 [Grid NO 91-3]. Fig. 8(a)에는 한 시간 간격으로 계측된 파랑을 대상으로 한 파랑 장미도, Fig. 8(b)에 41개의 년 최대파랑을 대상으로 한 파랑 장미 도를 정리하였다. Fig. 8(b)에서 원점으로부터의 거리는 파고[m], 원의 면적은 주기를 나타낸다. 대부분의 년 최대파랑은 SSE 계열에서 발생하는 것을 확인할 수 있다.
Time series of measured HMAX, FH, and FV from 1979.1.1. to 2019.12.31.
Wave rose at the sea off YeoSu.
Fig. 9에는 HMAX와 주기 Tpeak의 결합확률 분포, HMAX와 Tpeak 상관관계 회귀분석 결과를 도시하였으며, 해운대에서도 관측되었듯 파고가 거친 경우 파고와 주기의 상관 정도가 옅어지는 것을 확인할 수 있다. 회귀분석 결과를 정리하면 다음과 같다.
Joint distribution of yearly maximum wave height HMAX and its associated period Tpeak, and the inter-correlation between HMAX and Tpeak.
Fig. 10, 11에는 FH와 FV의 확률분포와 누가 확률분포를 정리하였으며, 기저 확률분포로는 해운대 전면해역과 같이 Weibull 분포 계열을 사용하였다. 해운대 전면해역과 유사하게 기저 확률분포로 Three-parameter Weibull 분포를 사용하는 경우 적합도가 현저하게 개선되는 것을 확인할 수 있다. 나머지 확률 모수는 해운대와 비슷한 값을 지니나, Scale Coefficient는 현저하게 큰 값을 지니며, 이는 두껍고 긴 꼬리를 지닌 확률밀도함수를 결과하여 상대적으로 거친 해양환경이 해운대에 비해 자주 발생하는 것을 알 수 있다. 이러한 성정의 해양환경은 우리의 경험적 인식에 정확히 부합한다.
Comparison of Weibull distribution of FH with in-situ wave data.
Probability density function of FV.
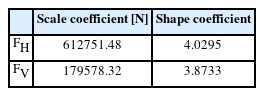
Table 2에는 in-situ wave data와 Matlab 기반 Statistics and Machine Learning Toolbox 중 최대가능도법[MLE, Maximum Likelihood Estimates]를 활용하여 산출한 Three-parameter Weibull 분포의 확률 모수인 Location, Scale, Shape Coefficient를 수록하였다.
List of probability coefficients of three-parameter Weibull distribution for wave force FH and lifting force FV [YeoSu]
3.3.3 목포
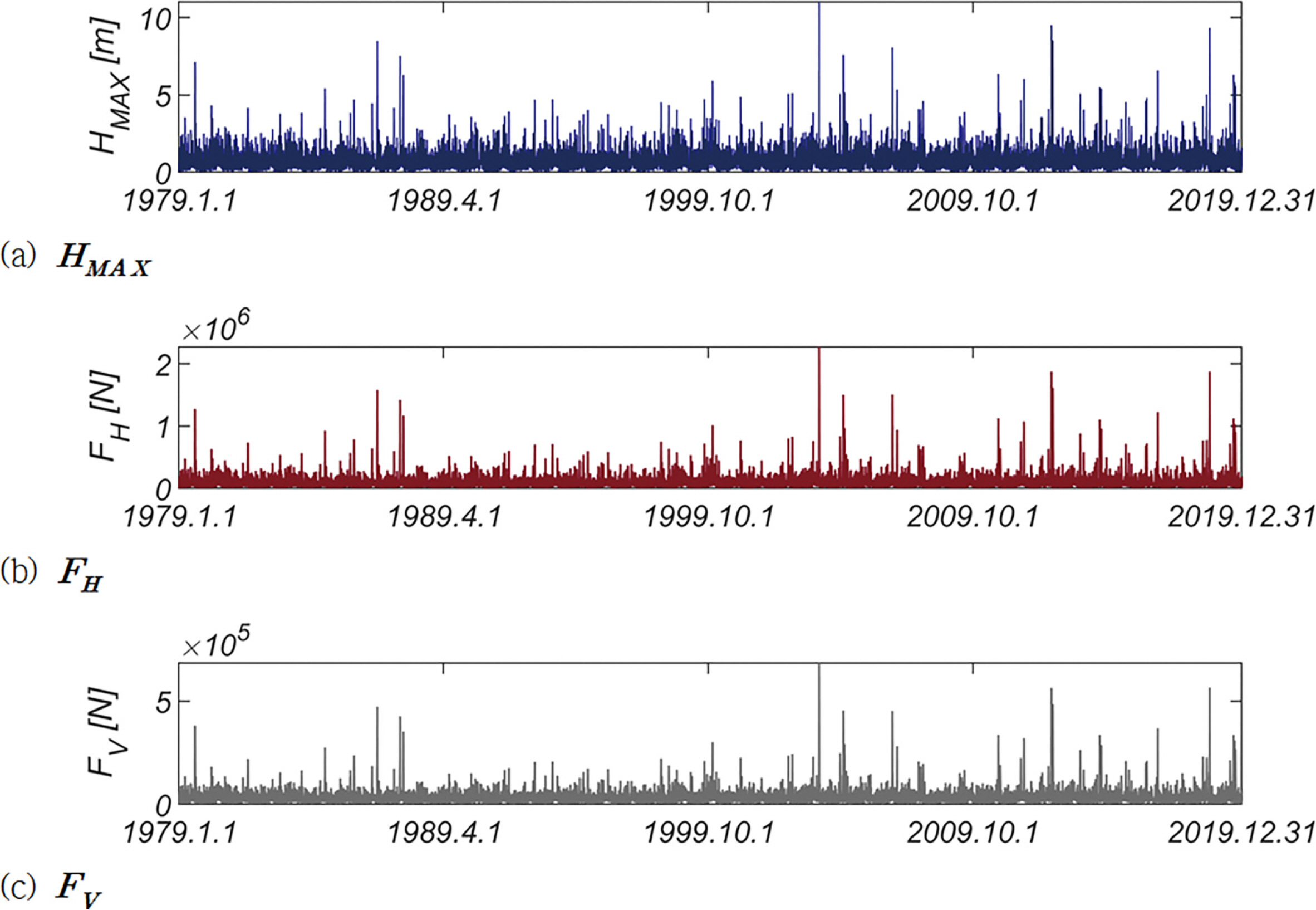
Fig. 12에는 HMAX, 파랑 진행 방향 파력 FH, 양력 FV의 1979.1.1부터 2019.12.31까지의 시계열자료를 도시하였다 [GRID NO 55-2]. Fig. 13(a)에는 한 시간 간격으로 계측된 파랑을 대상으로 한 파랑 장미도, Fig. 18(b)에 41개의 년 최대 파랑을 대상으로 한 파랑 장미 도를 도시하였다. Fig. 13(b)에서 원점으로부터의 거리는 파고[m], 원의 면적은 주기를 나타낸다.
Time series of measured HMAX, FH, and FV from 1979.1.1. to 2019.12.31.
Wave rose at the sea off MokPo.
Wave rose at the sea off GunSan.
대부분의 년 최대파랑은 NW 계열에서 발생하는 것으로 보이며, 출현 빈도는 상대적으로 낮으나 SSW 계열로부터 접근하는 파랑이 길고 파고가 월등하게 큰 것을 확인할 수 있다. 이러한 성정은 군산 전면해역에서도 일부 관측할 수 있으며, 목포 전면해역에서는 남해와 서해의 해양환경이 혼재한다는 사실을 함의한다. 여기서 파고가 엇비슷하더라도 NW 계열의 년 최대파랑이 SSW 계열의 파랑보다 상대적으로 짧아 서해의 경우 파랑의 성장이 취송거리에 제약을 받을 것이라는 우리나라 해안공학계에의 일반적인 추정을 정량적으로 확인할 수 있어 상당히 흥미롭다.
Fig. 14에는 HMAX와 주기 Tpeak의 결합확률 분포, HMAX와 주기 상관관계 회귀분석 결과를 도시하였으며, 해운대와 여수에서도 관측되었듯 파고가 거친 경우 파고와 주기의 상관 정도가 옅어지는 것을 확인할 수 있다. 회귀분석 결과를 정리하면 다음과 같다.
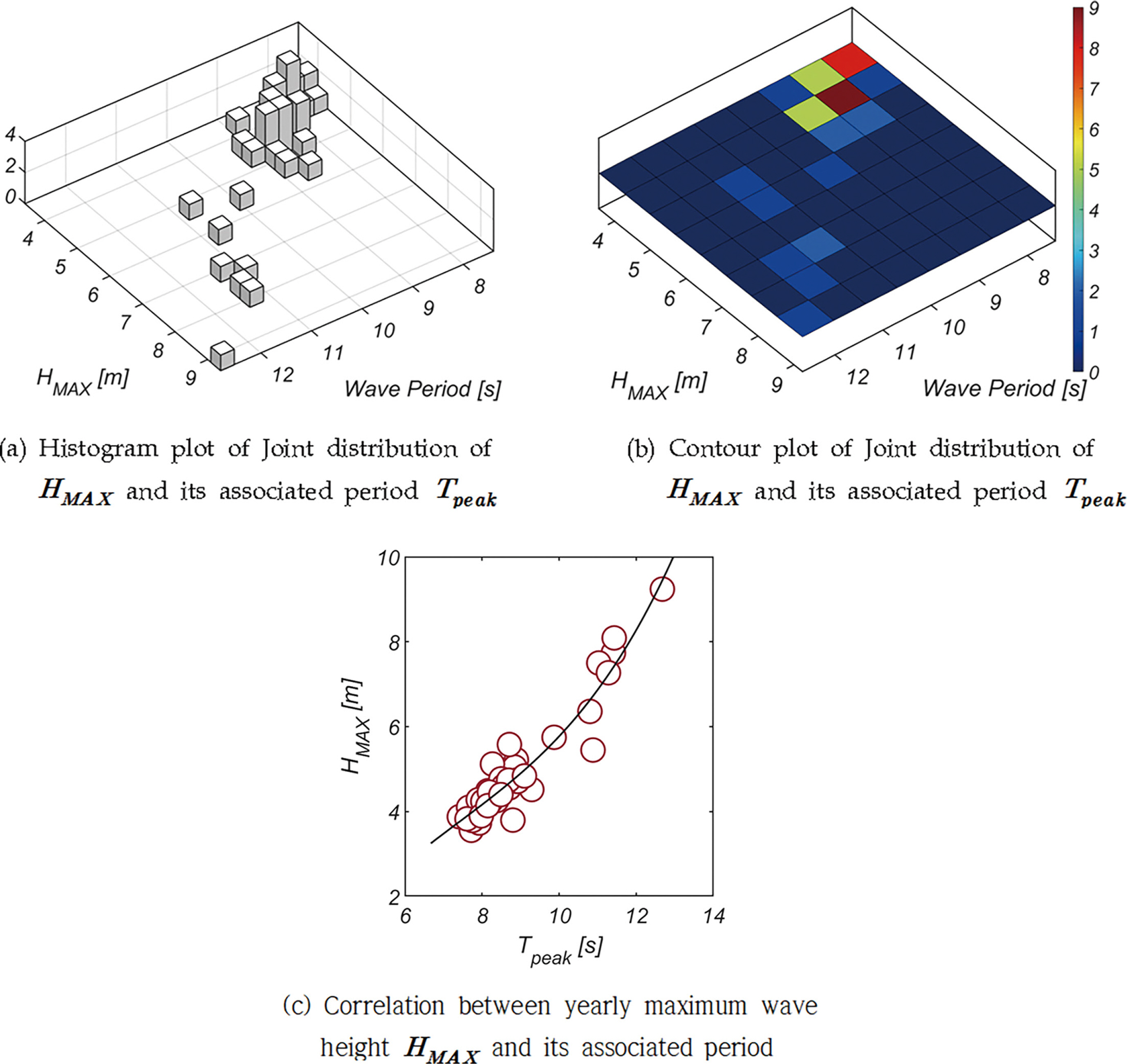
Joint distribution of yearly maximum wave height HMAX and its associated period Tpeak, and the inter-correlation between HMAX and Tpeak.
Fig. 15, 16에는 FH와 FV의 확률분포와 누가 확률분포를 정리하였으며, 기저 확률분포로는 해운대, 여수, 군산 전면해역과 같이 Weibull 분포계열을 사용하였다. 해운대, 여수 전면 해역과 유사하게 기저 확률분포로 Three-parameter Weibull 분포를 사용하는 경우 적합도가 현저하게 개선되었다. Scale Coefficient는 군산 전면해역과 유사하게 작은 값을 지녀, 변동성이 남해에 노출된 해운대, 여수에 비해 확연하게 적은 것으로 보이나, Shape Coefficient가 본 논문에서 다룬 네 해역 중 가장 작은 값을 지녀 확률 질량이 파력이 작은 쪽으로 편향되는 정도가 가장 큰 것을 확인할 수 있다. 이에 비해 Location Coefficient는 다른 해역에 비해 큰 값을 지닌다. 전술한 확률 모수 값은 목포 전면해역에는 남해와 서해의 해양환경이 혼재한다는 것을 의미하며 이러한 현상은 목포의 지리적 위치를 상기하면 수용 가능한 결과로 판단된다. 이러한 추론의 근거는 Fig. 13에 제시된 파랑 장미 도에서도 찾을 수 있다.
Comparison of Weibull distribution of FH with in-situ data.
Probability density function of FV.
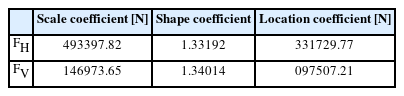
Table 3에는 in-situ wave data와 Matlab 기반 Statistics and Machine Learning Toolbox 중 최대가능도법[MLE, Maximum Likelihood Estimates]를 활용하여 산출한 3-parameter Weibull 분포의 확률 모수인 Location, Scale, Shape Coefficient를 수록하였다.
List of probability coefficients of 3-parameter Weibull distribution for wave force FH and lifting force FV [MokPo]
3.3.4 군산
Fig. 17에는 HMAX, 파랑 진행 방향 파력 FH, 양력 FV의 1979.1.1.부터 2019.12.31까지의 시계열자료를 도시하였다[GRID NO 42-1]. Fig. 18(a)에는 한 시간 간격으로 계측된 파랑을 대상으로 한 파랑 장미도, Fig. 18(b)에 41개의 년 최대 파랑을 대상으로 한 파랑 장미 도를 도시하였다. Fig. 18(b)에서 원점으로부터의 거리는 파고 [m], 원의 면적은 주기를 나타낸다.
Time series of measured HMAX, FH, and FV from 1979.1.1. to 2019.12.31.
대부분의 년 최대파랑은 NWW 계열에서 발생하는 것을 확인할 수 있으며, 출현 빈도는 상대적으로 낮으나 SW 계열로부터 비교적 큰 파랑이 과거 일곱 차례에 걸쳐 접근한 것을 알 수 있으나, 파고의 세기는 NWW 계열 파랑을 상회하는 것으로 보이지는 않았으며 이러한 성정은 군산 전면해역에서는 서해의 해양환경이 미세하게 우월하다는 사실을 함의한다.
Fig. 19에는 HMAX와 주기 Tpeak의 결합확률 분포, HMAX와 주기 상관관계 회귀분석 결과를 도시하였으며, 파고가 온화한 경우 파고와 주기는 선형 비례하는 것을 확인할 수 있다. 회귀분석 결과를 정리하면 다음과 같다.
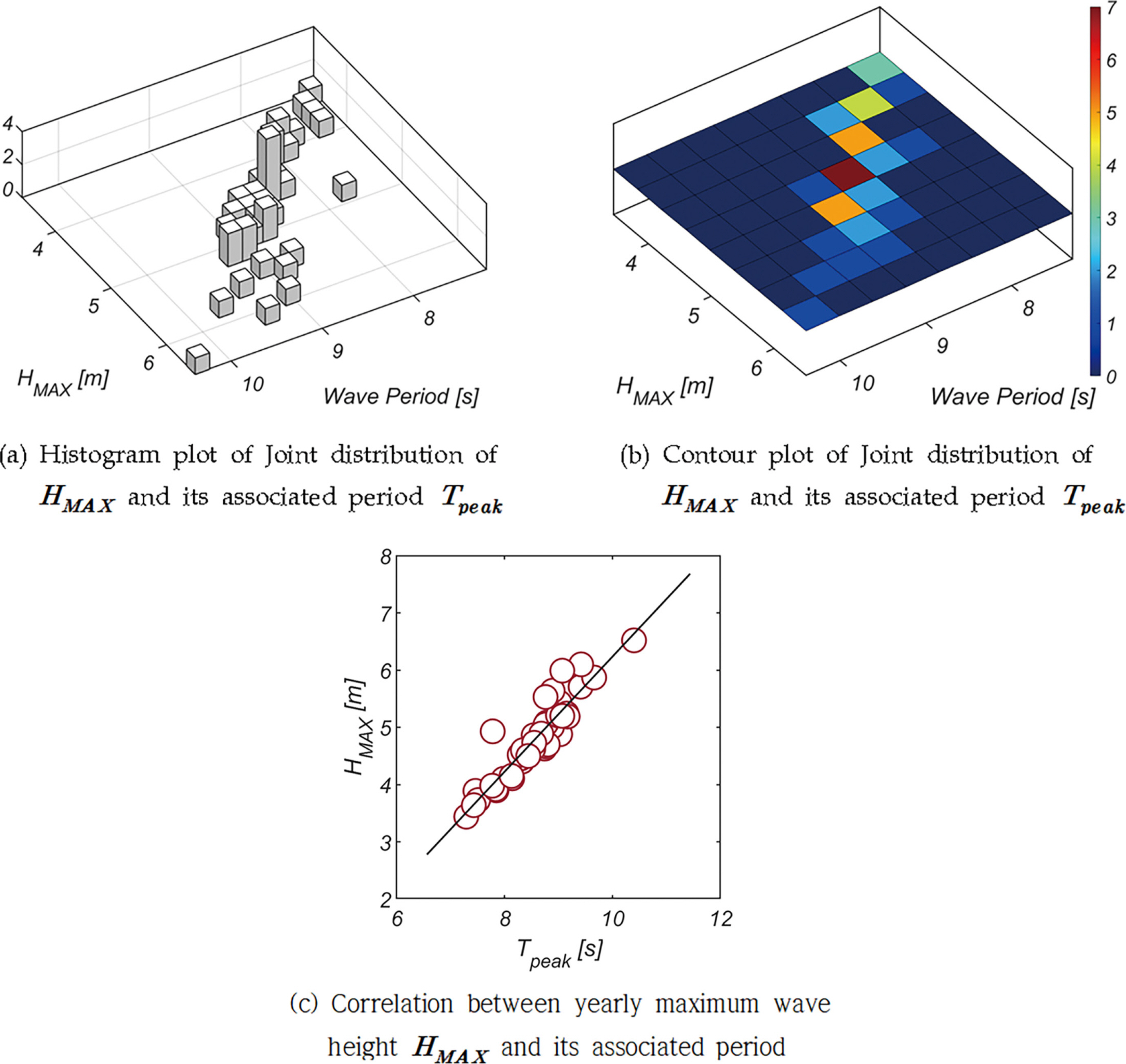
Joint distribution of yearly maximum wave height HMAX and its associated period Tpeak, and the inter-correlation between HMAX and Tpeak.
Fig. 20, 21에는 FH와 FV의 확률분포와 누가 확률분포를 정리하였으며, 기저 확률분포로는 해운대, 여수 전면해역과 같이 Weibull 분포계열을 사용하였다.
Comparison of Weibull distribution of FH with in-situ data.
Probability density function of FV.
해운대, 여수 전면해역과 다르게 기저 확률분포로 Twoparameter Weibull 분포를 사용하는 경우 적합도가 현저하게 개선되었다. Scale Coefficient가 상대적으로 작은 값을 지녀, 변동성이 해운대, 여수에 비해 확연하게 적은 것을 알 수 있으며, Shape Coefficient가 네 해역 중 가장 큰 값을 지녀 확률 질량이 파력이 작은 쪽으로 편향되는 정도가 가장 작았다. 이러한 확률 모수 값은 군사 전면해역에서 다른 해역에 비해 덜 거칠고 엇비슷한 해양환경이 자주 발생하는 것을 함의하며, 이러한 거동 특성은 우리나라 해안공학계에서 합의된 경험적 인식에 정확하게 부합하여 본 연구에서 개발한 파력 확률모형이 해역별로 각기 다른 우리나라 해양환경을 정확하게 기술할 수 있는 것으로 판단된다.
Table 4에는 in-situ wave data와 Matlab 기반 Statistics and Machine Learning Toolbox 중 최대가능도법[MLE, Maximum Likelihood Estimates]를 활용하여 산출한 Two-parameter Weibull 분포의 확률 모수인 Scale, Shape Coefficient를 수록하였다.
List of probability coefficients of Three-parameter Weibull distribution for wave force FH and lifting force FV [GunSan]
List of probability coefficients of Two-parameter Weibull distribution for wave force FH and lifting force FV [GunSan]
3.3.5 인천
Fig. 22에는 HMAX, 파랑 진행 방향 파력 FH, 양력 FV의 1979.1.1부터 2019.12.31까지의 시계열자료를 도시하였다[GRID NO 22-1]. Fig. 23(a)에는 한 시간 간격으로 계측된 파랑을 대상으로 한 파랑 장미도, Fig. 23(b)에 41개의 년 최대 파랑을 대상으로 한 파랑 장미 도를 도시하였다. Fig. 23(b)에서 원점으로부터의 거리는 파고 [m], 원의 면적은 주기를 나타낸다.
Time series of measured HMAX, FH, and FV from 1979.1.1. to 2019.12.31.
Wave rose at the sea off InCheon.
대부분의 년 최대파랑은 SSW, SW 계열에서 발생하였으며, 서해 깊숙이 위치한 지형적 특성상 파고는 상대적으로 작았으나, 긴 파랑도 다수 관측되어 서해를 따라 북진하는 태풍과 관련된 파랑 사상으로 보인다. 목포 전면해역에서도 관측되듯 파고가 엇비슷한 경우 NW 계열의 년 최대파랑이 SSW, SW 계열의 파랑보다 상대적으로 짧아 파랑의 성장이 취송거리에 제약을 받는다는 사실을 다시 한번 확인할 수 있다.
Fig. 24에는 HMAX와 주기 Tpeak의 결합확률 분포, HMAX와 주기 상관관계 회귀분석 결과를 도시하였다. 파고가 온화한 경우 파고와 주기는 선형 비례한다는 것을 다시 한번 확인할 수 있으며, 회귀분석 결과를 정리하면 다음과 같다.
Joint distribution of yearly maximum wave height HMAX and its associated period Tpeak, and the inter-correlation between HMAX and Tpeak.
Fig. 25, 26에는 FH와 FV의 확률분포와 누가 확률분포를 정리하였으며, 기저 확률분포로는 해운대, 여수, 목포, 군산 전면해역과 같이 Weibull 분포계열을 사용하였다. 군산 전면해역과 유사하게 기저 확률분포로 Two-parameter Weibull 분포를 사용하는 경우 적합도가 현저하게 개선되었다. Scale Coefficient가 본 논문에서 다룬 해역 중 가장 작은 값을 지녀, 변동성이 해운대, 여수에 비해 확연하게 적은 것을 알 수 있으며, Shape coefficient가 상대적으로 큰 값을 지녀 확률 질량이 파력이 작은 쪽으로 편향되는 정도가 작은 것을 확인할 수 있으며, 이러한 수치는 인천의 상대적으로 온화한 해양환경을 정확하게 반영하고 있는 것으로 보인다.
Comparison of Weibull distribution of FH with in-situ data.
Probability density function of FV.
Table 5에는 in-situ wave data와 Matlab 기반 Statistics and Machine Learning Toolbox 중 최대가능도법[MLE, Maximum Likelihood Estimates]를 활용하여 산출한 Two-parameter Weibull 분포의 확률 모수인 Scale, Shape Coefficient를 수록하였다.
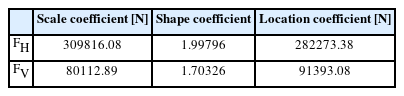
List of probability coefficients of Three-parameter Weibull distribution for wave force FH and lifting force FV [InCheon]
List of probability coefficients of Two-parameter Weibull distribution for wave force FH and lift FV [InCheon]
5. 결 론
우리나라 해안공학계에 신뢰성 기반설계가 시작된 지는 불과 십여 년에 불과하여 개선의 여지가 상당해 보인다. 개선이 필요해 보이는 부분이 다수 있으나 그중 해역별로 다른 우리나라 해양환경이 지니는 추계학적 성정을 담아낼 수 있는 확률모형, 파력과 양력의 상관관계 등은 우리나라에서 선호하는 항 외곽시설 구조양식인 직립식 방파제 활동 파괴 신뢰성 해석에 상당한 영향을 미치는 것으로 추정되나 아직 이렇다 할 연구성과가 없어 관련 연구가 시급해 보인다. 검토 결과 우리나라는 파고와 주기의 상관 정도가 해역별로 상당히 다른 것으로 나타났다. 이러한 성정은 파력이 작용하는 공간적 범위가 주기에 의해 결정된다는 사실을 상기하면 파고에만 천착하여 마련된 기존의 신뢰성 기반 설계법으로는 해역별로 현저하게 다른 우리나라 해양환경에 내재한 추계학적 특성을 담아내기 힘들다는 사실을 함의한다.
이러한 인식에 준거하여 본 논문에서는 해역별로 파고와 주기가 결과하는 파력과 양력에 대한 확률모형을 개발하였다. 우리나라 해양환경에 최적화된 확률모형은 장기 파랑 관측자료(WINK, Jeong et al., 2018)로부터 생성한 파력과 양력의 연 최댓값 시계열자료를 빈도 해석한 결과로부터 산출하였다. 파력과 양력 년 최댓값이라는 확률변수의 기저 확률분포로는 대표적 극치분포로 알려진 Three-parameter Weibull 분포를 사용하였으며, 확률 모수는 in-situ wave data와 Matlab 기반 Statistics and Machine Learning Toolbox 중 최대가능도법[MLE, Maximum Likelihood Estimates]를 활용하여 산출하였다.
해석 결과 남해안의 거친 해양환경은 큰 변동성을 지니며 이로 인해 상대적으로 큰 Scale Coefficient와 1.3 전후의 Shape Coefficient로 특정할 수 있는 것을 확인하였다. 1.3 전후의 Shape Coefficient가 암시하듯 상당한 확률 질량이 좌측으로 편향되어 확률 밀도함수는 긴 꼬리를 지니며 이러한 성정으로 인해 거친 해양환경이 자주 발생하는 남해의 해양환경을 상당한 정도로 기술할 수 있는 것을 확인하였다. 이에 비해 서해안의 상대적으로 온화한 해양환경으로 작은 변동성을 지니며 이는 작은 Scale Coefficient, 2.0 전후의 Shape Coefficient, 큰 Location Coefficient로 이어지는 것을 확인하였다. 전술한 확률 모수 값은 서해안의 덜 거칠고 엇비슷한 해양환경의 일반적인 성정과 정확히 일치하여 본 연구에서 개발한 파력과 양력 확률모형이 해역별로 다른 우리나라 해양환경을 정확하게 기술할 수 있는 것으로 보인다. 남해안과 서해안이 만나는 목포 전면해역의 경우 작은 Scale Coefficient, 1.2 전후의 Shape Coefficient, 큰 Location Coefficient 값으로 특정되었다. 이러한 Shape Coefficient 값은 본 논문에서 다룬 네 해역 중 가장 작은 것으로, 이는 확률 질량이 파력이 작은 쪽으로 편향되는 정도가 가장 크다는 것을 의미한다. 전술한 확률 모수 값은 목포 전면해역에는 남해와 서해의 해양환경이 혼재한다는 것을 의미하며 이러한 현상은 목포의 지리적 위치를 상기하면 수용 가능한 결과로 판단된다.
감사의 글
본 연구는 2022년도 서울시립대학교의 지원으로 수행되었으며 지원에 감사드립니다.