선형기계학습모델을 이용한 자갈해빈상에서의 쇄파지표 예측
A Study on the Predictions of Wave Breaker Index in a Gravel Beach Using Linear Machine Learning Model
Article information
Abstract
지금까지 쇄파는 발생기구의 본질적인 복잡성으로 인해 실내수리모형실험을 통해 쇄파파고 및 쇄파수심 등의 쇄파지표 예측을 위한 많은 경험식이 제안되어 왔다. 하지만, 자갈해빈에 대한 쇄파의 특성 및 쇄파지표예측을 위한 연구는 거의 수행되어 있지 않았다. 본 연구에서는 자갈해빈을 대상으로 쇄파파고 및 쇄파수심의 예측을 위하여 회귀 또는 분류 문제와 관련된 다양한 연구 분야에서 높은 예측 성능을 보이는 대표적인 선형기반 기계학습기법에 기반한 쇄파지표를 예측하고자 하였다. 먼저, 자갈해빈에 대하여 기존에 제안된 쇄파지표의 경험식의 적용성을 검토하고 기존의 경험식의 자갈해빈의 쇄파지표 예측성능의 한계성을 극복하기 위하여 다양한 선형기반 기계학습 알고리즘을 적용하여 쇄파지표 예측모델을 구축하였다. 구축된 기계학습모델 중 자갈해빈에서 발생하는 쇄파파고 및 쇄파수심에 대한 높은 예측성능을 보인 모델을 기반으로 손쉬운 계산이 가능한 쇄파지표에 대한 새로운 산정식을 제안하였고 수리모형실험결과 및 기존의 경험식과 비교하고 새롭게 제안한 쇄파지표의 예측성능을 검증하였다. 본 연구에서 제안한 쇄파지표에 대한 경험식은 단순한 다항식임에도 불구하고 자갈해빈에 대한 양호한 예측성능을 보였다.
Trans Abstract
To date, numerous empirical formulas have been proposed through hydraulic model experiments to predict the wave breaker index, including wave height and depth of wave breaking, due to the inherent complexity of generation mechanisms. Unfortunately, research on the characteristics of wave breaking and the prediction of the wave breaker index for gravel beaches has been limited. This study aims to forecast the wave breaker index for gravel beaches using representative linear-based machine learning techniques known for their high predictive performance in regression or classification problems across various research fields. Initially, the applicability of existing empirical formulas for wave breaker indices to gravel seabeds was assessed. Various linear-based machine learning algorithms were then employed to build prediction models, aiming to overcome the limitations of existing empirical formulas in predicting wave breaker indices for gravel seabeds. Among the developed machine learning models, a new calculation formula for easily computable wave breaker indices based on the model was proposed, demonstrating high predictive performance for wave height and depth of wave breaking on gravel beaches. The study validated the predictive capabilities of the proposed wave breaker indices through hydraulic model experiments and compared them with existing empirical formulas. Despite its simplicity as a polynomial, the newly proposed empirical formula for wave breaking indices in this study exhibited exceptional predictive performance for gravel beaches.
1. 서 론
쇄파는 연안에서 발생하는 대부분의 물리현상과 직·간접 적으로 관련되어 있으므로 쇄파에 대한 예측은 해안·항만공학 분야에서 매우 중요하다. 또한, 쇄파대 내에서는 파고분포에 대하여 적용 가능한 Ralyeigh 분포를 적용할 수 없으며, 쇄파 발생 시에는 파랑에너지의 일부가 소산하여 파랑의 에너지 방향집중도에도 영향을 미친다. 이러한 이유로 쇄파에 대한 정의를 처음으로 제안한 Stokes(1880)의 연구 이후로도 쇄파를 예측하고 발생기구를 규명하기 위한 지속적인 연구가 이루어져 왔지만 여전히 해안·항만공학분야에 있어서 매우 도전적인 과제 중의 하나이다.
Iversen(1951)은 처음으로 쇄파 현상을 재현하기 위해 실내 수리모형실험을 수행하였으며, 최근에도 다양한 조건에서 쇄파와 관련된 수리모형실험이 활발히 수행되고 있다. 이와 같은 다양한 수리모형실험의 결과들을 바탕으로 쇄파 발생 시 주요한 변수인 쇄파파고와 쇄파수심을 정량적으로 평가하기 위한 많은 경험식들이 제안되어왔다. 우리나라의 항만 및 어항 설계기준에서도 Goda(1970)의 연구결과를 기반으로 한쇄파파고 및 쇄파수심에 대한 도해법을 제공하고 있다. 그러나 대다수의 쇄파 관련 수리모형실험들은 주로 모래로 구성된 사빈이나 불투과성 사면을 대상으로 수행되었으며, 상대적으로 큰 입경과 높은 공극률을 갖는 자갈해빈에 대한 쇄파 연구는 여전히 부족한 실정이다. Lee et al.(2007)의 연구에 따르면 투수성이 높은 자갈해빈의 경우, 전빈의 지하수위가 사면에서의 파동장에 영향을 미칠 수 있음을 지적하고 있어 모래로 구성된 사빈이나 불투과성 사면에서 발생하는 쇄파기구와는 상이할 것으로 판단된다. 우리나라의 자갈해빈은 Fig. 1에 보인 바와 같이 주로 동남해안과 남해안 도서지역에 분포되어 있으며, 이러한 자갈해빈에 관한 연구는 주로 해빈에서의 입도분포 및 퇴적물의 이동양상에 중점을 두고 수행되어 왔다(Koh et al., 1993). 하지만, 자갈해빈의 변형에 직접적인 영향을 미치는 자갈해빈에서의 쇄파에 관한 연구는 거의 수행되고 있지 않는 실정이다.
Aspects of gravel beaches in Korea (left: Ulsan, http://www.news33.net, Right: Wando, https://www.newspim.com).
한편, 지금까지 제안된 쇄파지표에 관한 다양한 경험식들은 Liu et al.(2011)의 연구에 체계적으로 정리되었다. Liu et al.(2011)은 쇄파지표에 관한 실험기반의 경험식들을 관련 변수 및 실험식의 형태에 따라 McCowan-type(McCowan, 1984), Miche-type(Miche, 1944), Goda-type(Goda, 2010) 및 Munktype(Munk, 1949)의 4가지 형식으로 분류하고, 기존 실험데이터에 대하여 각각의 경험식의 예측성능을 비교·검토하였다. 그 결과, 바닥경사에 따른 쇄파지표의 오차는 다소 발생하지만 심해파형경사와 바닥경사를 주요 파라메타로 하는 Goda-type의 경험식이 비교적 높은 예측성능을 보임을 확인하였다. 또한, Liu et al.(2011)은 바닥경사에 따른 Goda-type 경험식의 쇄파지표 오차를 제거하기 위하여 천해조건에서 선형파이론의 파속을 이용하여 바닥경사에 독립된 쇄파지표 산정식을 제안하였다. Rattanapitikon and Shibayama(2006)는 기존의 쇄파지표 경험식들이 주로 쇄파파고와 쇄파수심의 비(ratio)에 대한 것임을 지적하고 각각의 물리량에 대한 양해적 산정이 가능한 경험식을 제안하고 기존의 수리모형 실험결과를 양호하게 재현함을 보였다. Goda(2010)는 초기의 Goda 경험식(Goda, 1970)이 급경사를 갖는 바닥경사에서 쇄파지표의 예측성능이 낮음을 보완하기 위해 경험식의 계수 값을 수정한 수정 Goda 쇄파지표식을 제안하였다. 또한, Xie et al.(2019)는 쇄파수심을 고정도로 예측하기 위해 천수방정식으로부터 쇄파에 대한 해석해를 유도하고 기존의 수리모형실험결과를 적용하여 쇄파수심에 대한 반경험식을 제안하였다.
한편, 최근에는 입력자료와 출력자료로부터 통계적 구조를 검색하여 입력과 출력 사이의 일정한 규칙이나 패턴을 생산하는 인공지능(Artificial Intelligence, AI)의 한 분야인 기계 학습(Machine Learning, ML)이 다양한 학문 및 산업분야에서 적극적으로 활용되고 있다. 기계학습은 과거 사용자가 물리적인 현상에 대하여 예측 알고리즘을 개발하고 프로그래밍 과정을 통해 계산기의 연산성능을 활용하여 물리적인 현상을 분석하고 예측하는 전통적인 연구방법과 상반되는 개념이다. 이러한 기계학습에 대한 시도는 일찍이 컴퓨터에 체스 게임을 학습시킨 Samuel(1959)의 연구에서 시작되었으나 자료에 대한 저장비용이 급격하게 감소하기 시작한 과거 십여년 전부터 급속하게 기계학습을 포함한 인공지능을 활용한 연구사례가 증가하고 있다. 최근 들어서는 해안 및 항만공학 분야에서도 기계학습을 활용하여 Lee et al.(2020)은 해양기상자료로부터의 항내파고를 신속하게 예측하였으며, Park et al.(2022)은 진해만 내의 해양환경 모니터링 자료로부터 용존 산소농도 및 빈산소수괴 발생을 예측하는 등 다양한 물리현상을 예측하려는 시도가 꾸준하게 증가하고 있다(Kim et al., 2010, Kim and Suh, 2011, Lee et al., 2020).
따라서, 본 연구에서는 기계학습을 이용하여 자갈해빈에서 발생하는 쇄파지표(쇄파파고 및 쇄파수심)에 대한 새로운 산정식을 제안한다. 특히, 본 연구에서 제안하는 쇄파지표에 대한 산정식은 개념설계 단계에서 쇄파파고와 쇄파수심에 대해 손쉬운 계산이 가능하도록 양해적으로 계산 가능한 선형식을 제안한다.
2. 쇄파자료 수집
본 연구에서는 자갈해빈을 대상으로 쇄파에 관한 수리모형실험을 수행한 Lee et al.(2007) 및 Lara et al.(2006)의 실험 결과를 이용하여 자갈해빈에서의 쇄파특성을 재분석하고 기계학습의 학습자료로 이용하였다. Lee et al.(2007)은 자갈해빈에서 지하수위와 해수면의 차이에 따른 전빈에서의 파동장 변화와 지형변동에 미치는 영향을 실험적으로 검토하였으며, Lara et al.(2006)은 자갈해빈의 경사가 파형의 변화 및 쇄파에 미치는 영향에 대한 실험연구를 제시하였다. 이하에 Lee et al.(2007) 및 Lara et al.(2006)의 수리모형실험에 대한 개요를 간략히 기술한다.
2.1 수리모형실험의 개요
Lee et al.(2007)의 수리모형실험은 길이 30 m, 폭 0.7 m, 높이 0.9 m인 2차원 단면조파수로에서 수행되었으며, 조파수로를 파랑의 진행방향으로 폭 0.3 m와 0.4 m로 분할하고 분할된 수로내에 중앙입경 d50 = 5 mm의 자갈을 이용하여 1/7, 1/10 및 1/12의 사면경사를 각각 구성하였다. 또한, 자갈해빈의 지하수위를 모의하기 위하여 해빈의 배후에 별도의 지하수위 조절용 수조를 제작하여 설치하였다. 아크릴로 제작된 지하수위 조절용 수조는 펌프에 의해 수조내부의 수위를 조절하였으며, 이를 통해 자갈해빈에서의 지하수위를 모의하였다.
Lara et al.(2006)은 수로바닥에서부터 자갈을 이용하여 사면을 구성한 Lee et al.(2007)의 실험과는 상이하게 길이 24 m, 폭 0.6 m, 높이 0.8 m의 제원을 갖는 단면조파수로 내에 아크릴로 1/20의 불투과 경사면을 구성한 후에 d50 = 19 mm 및 39 mm의 자갈을 이용하여 두께 11 cm의 자갈해빈을 구성하였다. Lee et al.(2007)과 Lara et al.(2006)의 단면조파수로의 실험개요를 Fig. 2에 보인다.
Sketch of the experimental setup.
2.2 실험조건 및 실험방법
Lee et al.(2007)은 정수심 h를 40.0 cm로 고정하고 자갈해빈의 경사면을 1/7, 1/10 및 1/12로 변화시켜 각각의 사면경사에 대하여 입사파고 Hi는 3.0~8.0 cm, 주기 T는 1.0~2.0 s 범위에서 11종류를 발생시켰다. 실험케이스는 바닥경사 1/7의 경우 469 케이스, 1/10의 경우 180 케이스, 1/12의 경우 186 케이스의 수리모형실험을 수행하였다. 실험방법은 수로내에 설치한 자갈해빈의 배후에 수위를 먼저 상승시켜 자갈해빈 내의 수위가 충분하게 안정된 후에 조파를 실시하였다. 모든 실험조건에 대하여 쇄파점 부근에서 초고속 비디오카메라(DITECT, HAS-500)를 이용하여 200 fps로 촬영하였으며 쇄파파고 Hb 및 쇄파수심 hb을 영상해석으로부터 산출하였다(Fig. 3 참조). Lee et al.(2007)은 모든 실험조건에 대하여 영상해석으로부터 쇄파파고 Hb 및 쇄파수심 hb을 해석하여 총 835개의 쇄파 데이터를 제공하였으나, 본 연구에서는 지하수위의 영향을 고려하지 않는 총 315개의 실험 데이터를 이용하였다.
An example of water surface profile taken with a digital high-speed camera.
Lara et al.(2006)는 정수심 h = 40.0 cm 조건하에서 Stokes 5차파와 Cnoidal파를 조파하였으며, 입사파고와 주기를 변화시켜 총 12종류의 입사파를 발생시켰다. 자갈해빈상에서 쇄파의 형상을 관찰하기 위하여 경사면에 저항식 수위계를 이용하여 총 20개소에서 수면형상을 측정하였으며, 비디오 이미지도 쇄파정보를 식별하는 데 사용하였다. 본 연구에서는 Lara et al.(2006)의 실험결과 중 경사면에서 쇄파가 발생한 16케이스에 대한 실험데이터를 이용하였다. 이상과 같이 수집된 자갈해빈에 대한 쇄파 실험 데이터를 정리하여 Table 1에 보인다.
Summary of the experimental results for wave breaker index
3. 자갈해빈에서의 쇄파특성
3.1 쇄파예측을 위한 기존 경험식 고찰
쇄파파고에 대한 Miche(1944)의 식(1)이 처음으로 제안된 이후로 다수의 연구자들이 쇄파와 관련한 다양한 수리모형실험을 수행하여 축적된 실험결과를 기반으로 한 많은 경험식이 제안되어 왔다(LeMehaute and Koh, 1967; Goda, 1970; Komar and Gaughan, 1972; Sunamura and Horikawa, 1974; Ostendorf and Madsen, 1979; Rattanapitikon et al., 2003; Rattanapitikon and Shibayama, 2006, Camenen and Larson, 2007; Goda, 2010; Xie et al., 2019).
여기서, Hb는 쇄파파고, hb는 쇄파수심(바닥경사면에서부터 정수면까지의 연직거리로 정의됨), Lb는 쇄파수심에서 파장이다. LeMehaute and Koh(1967)는 바닥의 기울기를 고려하지 못한 Miche(1944)의 제안식을 보완하기 위하여 심해파형경사와 바닥경사를 동시에 고려한 식(2)의 쇄파파고에 대한 경험식을 제안하였으며, Ostendorf and Madsen(1979)는 바닥경사에 따른 쇄파파고를 고려하기 위하여 Miche(1944) 식을 수정하여 식(3)과 같은 경험식을 제안하였다.
여기서, m은 바닥경사, H0는 심해파고, L0는 심해파장이다.
이후에, Rattanapitikon and Shibayama(2006)는 기존의 많은 수리모형 실험자료를 수집하여 심해파형경사를 이용한 식(4)의 쇄파파고와 식(5)의 쇄파수심에 대한 식을 제안하였으며, Camenen and Larson(2007)은 심해파형경사와 바닥경사를 동시에 고려할 수 있는 식(6)을 제안하였다.
Goda(2010)는 급한 바닥경사에 대한 쇄파 예측성능을 향상시키기 위해 기존의 Goda 쇄파식(Goda, 1970)을 수정하여 쇄파수심과 심해파장과 간의 비율을 파라미터로 하는 식(7)을 제안하였다.
여기서, A는 상수로 규칙파와 불규칙파에 따라 각각 0.17과 0.12를 갖는다. 한편, Liu et al.(2011)은 바닥경사에 독립적인 쇄파파고 및 쇄파수심을 산정하기 위하여 천해에서 선형파이론의 파속을 이용하여 다음과 같은 경험식을 제안하였다.
여기서, λb = Hb/Lb, Lb는 쇄파점에서의 파장, ψb = gHb/Cb, g는 중력가속도, Cb는 쇄파 시 파속으로 다음의 식(9)로 정의된다.
최근에 Xie et al.(2019)은 쇄파수심 산정을 위해 식(10)과 같은 반경험 공식을 제안하였다.
위에 기술한 대표적인 쇄파파고 및 쇄파수심에 대한 경험식 이외에도 수리모형 실험결과를 이용하여 통계적 분석 또는 선형이론을 결합한 다양한 경험식이 제안되어 왔다. Liu et al.(2011)은 제안된 경험식을 쇄파지표에 대한 정의와 입력 변수에 따라 다음과 같이 McCowan, Miche, Goda 및 Munk 형식으로 구분하고 형식별 예측특성을 검토하였다.
여기서, α(m, λo)와 β(m, λo)는 제안된 경험식에 따른 입력변수의 조합이며, m은 바닥구배, λo는 심해파형경사 Ho/Lo이고, γ은 제안된 경험식에 따라 결정되는 지수이다. Liu et al.(2011)의 연구에 의하면 Miche와 Goda 형식을 갖는 쇄파지표에 대한 경험식이 입력변수들과의 관계를 가장 잘 설명할 수 있는 반면에 McCowan과 Munk 형식을 갖는 경험식은 쇄파지표의 예측편차가 크게 발생하는 것으로 알려져 있다. 하지만, Miche와 Goda 형식의 경험식들은 쌍곡선함수와 지수함수를 포함하고 있고, 입력변수로 쇄파수심 hb를 포함하고 있어 쇄파지표에 대한 간단한 산정이 곤란하다. 반면, McCowan과 Munk 형식의 경우 입력변수로 바닥경사와 심해파형경사만을 사용하므로 쇄파지표의 산정이 간단하지만 Liu et al.(2011)이 지적한 바와 같이 예측성능이 저하될 수 있다.
3.2 기존 쇄파지표식의 재현성
자갈로 구성된 사면상에서 발생하는 쇄파는 불투과면 또는 모래로 구성된 사빈상에서 발생하는 쇄파와는 저질의 투수성 등의 차이 등으로 인해 서로 다른 특성을 갖을 것으로 예상된다. 본 연구에서는 먼저 불투과면(고정상) 또는 모래로 구성된 사빈을 대상으로 수행된 수리모형 실험결과로부터 유도된 대표적인 쇄파지표 경험식을 대상으로 자갈해빈에서의 쇄파지표에 대한 적용성을 검토하였다.
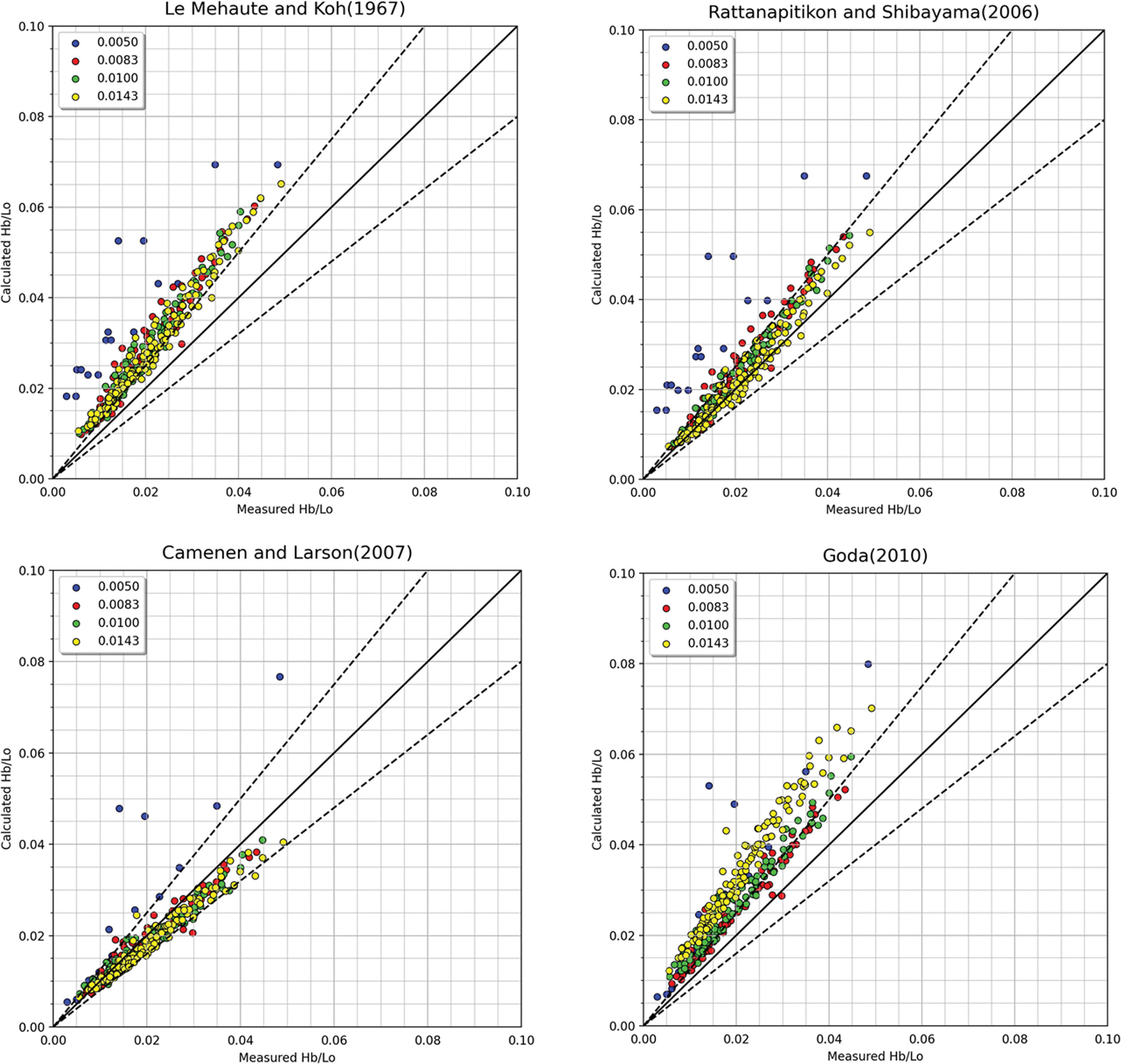
Fig. 4는 앞서 기술한 LeMehaute and Koh(1967), Rattanapitikon and Shibayama(2006), Camenen and Larson(2007) 및 Goda(2010)에 의해 각각 제안된 경험식에 따른 쇄파지표의 예측성능 비교를 위해 무차원 쇄파파고 Hb/Lo로 동일하게 변환시킨 결과를 나타낸다. 그림 중의 쇄파파고는 바닥경사별로 표기하였으며, 점선은 예측결과에 대한 ±20% 오차를 나타낸다.
Comparisons between wave breaking height formula and experimental data.
Fig. 4에서 자갈해빈에서 발생하는 쇄파파고의 예측결과를 분석한 결과, LeMehaute and Koh(1967)에 의해 제안된 경험식에 따른 쇄파파고는 실험결과를 전체적으로 과대평가하고 있으며, 특히 바닥경사가 완만한 경우에는 과대평가되는 경향을 보인다. Rattanapitikon and Shibayama(2006)의 경험식은 LeMehaute and Koh(1967)의 경험식에 비해 상대적으로 쇄파파고를 양호하게 예측하고 있지만 여전히 전반적으로 과대평가되고 있다. 또한, Camenen and Larson(2007)의 경험식은 오히려 쇄파파고를 전체적으로 과소평가하고 있으며, Goda(2010)의 경험식은 LeMehaute and Koh(1967)의 예측결과와 유사한 경향을 보인다.
Fig. 5는 앞서 기술한 쇄파파고와 유사하게 쇄파수심에 대하여 Rattanapitikon and Shibayama(2006) 및 Xie et al.(2019)의 경험식을 적용하여 실험 데이터와 비교한 결과이다. 쇄파수심에 대한 예측결과는 쇄파파고의 예측결과에 비해 실험결과를 양호하게 재현하고 있음이 확인되나 Rattanapitikon and Shibayama(2006)와 Xie et al.(2019)의 쇄파수심에 대한 경험식은 쇄파수심이 증가할수록 과대평가하고 있으며, 특히 Xie et al.(2019)의 경우 쇄파수심이 얕을수록 실험결과를 과소평가하는 경향을 보인다.
Comparisons between wave breaking depth formula and experimental data.
4. 기계학습을 통한 쇄파지표 예측모델
4.1 기계학습모델
본 연구의 목표는 간편한 산술 계산이 가능한 쇄파지표 산정식을 제안하는 것이므로, 이를 위해 쇄파지표와의 선형성과 상관성이 높은 것으로 알려진 심해파형경사 Ho/Lo와 사면경사 m을 입력변수로 하는 다음의 선형 기계학습모델을 적용하였다.
여기서, Γb = Hb/Lo와 Ωb = hb/Lo는 기계학습의 목표변수로 무차원 쇄파파고와 쇄파수심을 각각 나타내며, w = [w0, w1, w2]는 기계학습을 통해 산정되는 가중치(이하 회귀계수)에 대한 열벡터이다. 입력변수는 각각의 입력자료에 대해 유사한 정도의 특성(분포) 스케일이 반영되도록 정규화하는 과정(예로 최소-최대정규화(Min-Max normalization) 혹은 z-점수정규화(z-score normalization) 등이 필요하지만 본 연구는 선형모델에 기반한 기계학습으로부터 회귀계수를 산정하는 것이 목적이므로, 정규화를 적용하지 않은 원시자료를 이용하였다.
본 연구에서는 기존 쇄파 실험 데이터를 기반으로 쇄파지표를 예측하는 모델을 구축하기 위해 지도학습(supervised learning) 방법을 적용하였으며, 이하에 본 연구에서 적용한 기계학습모델을 간단히 기술한다. 지도학습에 적용되는 일반적인 선형회귀모델(linear regression model, 이하 LM)은 입력변수에 대한 결과값을 예측하는 가설(hypothesis) H(x)과 실제 결과값 y의 차이를 최소화기 위해 학습된다. 이 과정에서 손실함수(loss function)로는 평균제곱오차(mean squared error, MSE)인 식(13)을 사용한다.
MSE를 이용하는 LM은 훈련 데이터에 과도하게 적합될 수 있으므로 과대적합(over-fitting)을 방지하기 위해 MSE에 패널티(penalty)항을 도입하여 회귀계수의 크기를 제어하는 규제형 선형회귀모델(regularized linear regression model, 이하 RM)이 사용된다. RM에는 적용되는 패널티 항에 따라 릿지회귀(ridge regression), 라쏘회귀(lasso regression) 엘라스틱 넷(Elastic Net) 등의 방법들이 제안되어 있으나 여기서는 L2-norm을 패널티 항으로 사용하는 릿지회귀(ridge regression, 이하 RR)를 선택하였다.
여기서, α는 경험적으로 결정되어야 하는 하이퍼 파라미터(hyper parameter)이다.
또한, MSE를 손실함수로 사용하는 LM과 RR은 이상값(outlier)에 의해 손실함수가 크게 증가할 수 있으므로, 이를 방지하기 위해 일정 범위 ∊을 기준으로 하는 평균절대오차(mean absolute error, 이하 MAE)를 MSE와 함께 손실함수로 사용하는 식(15)의 후버회귀(Huber regression, HR)를 사용하였다.
마지막으로, 선형모델에 더하여 노이즈가 많은 입력 데이터로부터 회귀계수를 예측하는 방법인 란삭(random sample consensus, 이하 RANSAC, Fishler and Bolles, 1981) 알고리즘을 추가로 적용하였다. RANSAC은 입력 데이터에 이상점(outlier)이 존재한다고 가정하고, 무작위로 추출된 자료집합에 대한 반복적인 학습을 수행하는 방법이다. RANSAC에서 반복학습의 횟수는 하이퍼 파라미터이며, 학습 알고리즘은 LM을 이용하였다.
4.2 기계학습과 하이퍼마라미터 최적화
기계학습을 위해 쇄파 실험 데이터 중 60%를 무작위로 선택하여 훈련 데이터로 사용하였으며, 나머지 40%는 학습된 모델의 성능평가에 활용하였다. 그러나, 고정된 평가 데이터를 사용할 경우에는 모델이 해당 데이터에 과도하게 적합될 우려가 있으므로 과대적합을 방지하기 위해 교차검증(cross validation)을 적용하였다. 이를 통해 제한된 실험 데이터에서 과소적합(under-fitting)을 방지할 수 있는 장점이 있다. 교차 검증 방법으로는 k-fold, leave-p-out, leave-one-out 및 계층별 k-fold 등이 제안되어 있지만(Arlot and Celisse, 2010), 본 연구에서는 가장 일반적으로 사용되는 k-fold(k = 5) 교차검증을 선택하였다. 이 방법은 훈련 데이터를 k개의 부분으로 나누고, 각 반복에서 하나의 부분을 평가 데이터로 사용하고 나머지 부분을 훈련데이터로 사용하여 모델을 학습한다.
기계학습모델의 예측성능을 향상시키기 위해 학습 알고리즘의 작동을 제어하는 하이퍼 파라미터의 최적화가 필수적이다. 하이퍼 파라미터 최적화는 사용자가 최적의 조합을 직접 결정하는 수동검색(manual search), 모든 하이퍼 파라미터 조합에서 최적의 값을 찾는 격자검색(grid search), 그리고 해당 하이퍼 파라미터 범위에서 무작위로 추출하여 최적의 값을 찾는 무작위검색(random search) 등의 다양한 방법이 존재한다(Bergstra and Bengio, 2012). 격자검색은 하이퍼 파라미터를 균등하게 분포시켜 최적화를 시도하여 균일한 검색 범위를 제공하는 반면에 무작위 검색은 중요한 하이퍼 파라미터에 대해 보다 조밀하게 검색할 수 있는 장점이 있다. 본 연구에서는 제한된 수의 하이퍼 파라미터를 가진 선형 알고리즘을 적용하였기 때문에 균일한 검색범위를 제공하는 격자검색을 선택하였다.
4.3 기계학습을 이용한 쇄파지표의 예측결과
본 연구에서는 전술한 바와 같이 선형기반 모델의 기계학습 알고리즘인 선형회귀모델(LRM), 규제선형회귀모델(RR), 후버회귀모델(HR), 란삭회귀모델(RANSAC)을 활용하여 쇄파지표를 예측하였다. 이러한 기계학습 알고리즘의 성능평가는 평균 제곱근 오차(Root Mean Square Error; RMSE)를 실험 데이터의 평균치로 정규화한 산포지수(Scatter Index, SI)와 모델의 추정정도가 목표값을 표현하는 적합정도를 나타내는 결정계수 R2를 이용하였다.
여기서, xi는 목표값, yi는 예측값,
Fig. 6은 각 모델별 평가 데이터에 대한 무차원 쇄파파고 Γb의 예측결과를 나타내며, 하이퍼 파라미터 조정에 따른 각 모델의 최적 예측성능의 결과를 도시한 것이다. 그림에서 점선은 ±20%의 오차범위를 나타내며, 결정계수 R2와 산포지수 SI를 함께 제시하였다. 적용된 기계학습 모델별들의 결정계수 및 산포지수를 고려할 때, 자갈해빈에 대한 쇄파파고의 예측성능은 선형회귀모델(LRM)이 가장 우수한 성능을 보여주며, 규제선형회귀모델(RR)은 모델 중에서 가장 낮은 예측성능을 나타낸다. 또한, 본 연구에서 구체적으로 제시하지 않았지만 심해파형경사만을 입력변수로 고려한 예측모델과 바닥경사를 동시에 고려한 모델 간에는 결정계수가 약 10% 정도의 예측성능 차이가 있음을 확인하였다.
Wave breaking height prediction by each model.
Fig. 7은 Fig. 6과 동일하게 각 모델별 평가 데이터에 대한 무차원 쇄파수심 Ωb의 예측결과를 나타낸다. 쇄파파고와 유사하게 선형회귀모델(LRM)이 쇄파수심에 대한 실험결과를 잘 재현하고 있으며, 규제선형회귀모델(RR)은 모델 중에서 가장 낮은 예측성능을 보인다. 한편, 쇄파파고에 대한 예측결과와는 달리 쇄파수심에 대해서는 심해파형경사만을 입력변수로 고려한 예측모델과 바닥경사를 동시에 고려한 모델 간 예측성능의 차이가 크지 않음을 확인하였다.
Wave breaking height prediction by each model.
Table 2와 3은 쇄파파고와 쇄파수심 예측을 위해 각 모델별 알고리즘에 따른 회귀계수와 결정계수의 결과를 정리하여 보인다.
Summary of ML prediction results for breaking wave height
Summary of ML prediction results for breaking water depth
4.4 새로운 쇄파지표식 제안
앞서 기술한 선형기반의 ML 알고리즘 중에 훈련 및 평가데이터에 대하여 쇄파파고 및 쇄파수심 모두 LRM이 양호한 예측성능을 보였다. 쇄파파고 및 쇄파수심에 대해 예측된 각각의 회귀계수를 이용하여 손쉬운 계산이 가능한 새로운 쇄파지표 산정식을 제안하였다. 쇄파파고 및 쇄파수심에 대한 산정식은 다음의 식 (18)과 같다.
제안된 쇄파지표식은 바닥경사와 심해파형경사와의 함수로만 선형적으로 구성되어 있어 직관적으로 쇄파지표를 예측할 수 있다. 제안된 쇄파지표식의 예측성능을 비교하기 위해 대표적인 경험식인 Goda(2010)가 제안한 쇄파파고에 대한 경험식(식(7))과 Xie et al.(2019)가 제안한 쇄파수심에 대한 경험식(식(10))과의 성능을 비교하였다.
Fig. 8과 Fig. 9는 자갈해빈에 대한 모든 쇄파 데이터를 사용하여 쇄파파고 및 쇄파수심의 예측결과를 비교한 것으로, 실험결과와의 오차 및 예측성능을 MSE와 결정계수로 표기하였다. Fig. 8에서 본 연구에서 제안한 쇄파파고의 경험식은 경우 바닥경사 m = 0.05인 경우와 쇄파파고가 Γb ≥ 0.01의 특정 범위에서 실험결과를 과대평가하는 경향이 있으나, 전체적으로 실험결과를 양호하게 예측하고 있음을 확인할 수 있다. 바닥경사 m = 0.05인 경우에 대한 쇄파파고 예측성능의 저하는 Lara et al.(2006)의 실험결과로 단지 16개의 실험 데이터만을 이용하였으므로 충분한 학습이 이루어지지 않았을 것으로 판단된다. 한편, Goda(2010)의 경험식은 자갈해빈에 비해 공극율이 작은 사빈에 대한 실험결과를 기반으로 제안된 경험식이므로 모든 바닥경사에서 실험결과를 과대평가하고 있다. 쇄파수심에 대한 예측결과인 Fig. 9에서도 본 연구에서 제안한 쇄파수심의 경험식은 쇄파파고에 대한 예측결과와 유사한 경항을 보이고 있으며, 특히 바닥경사가 완만한 m = 0.05에서 쇄파수심을 과대평가하고 있음을 알 수 있다. 한편, Xie et al.(2019)의 경험식은 쇄파수심지표 Ωb ≤ 0.03일 때 쇄파수심을 과소평가하고 Ωb ≥ 0.03일 때 쇄파수심을 과대평가하고 있음이 확인된다. Goda(2010) 및 Xie et al.(2019)의 경험식 이외에도 본 연구에서 제시한 식(18)에 의한 쇄파지표에 대한 예측결과의 오차정도를 정량적으로 확인하기 위해 식(19)를 이용하여 오차해석을 수행하였으며, 그 결과를 Table 4에 보인다.
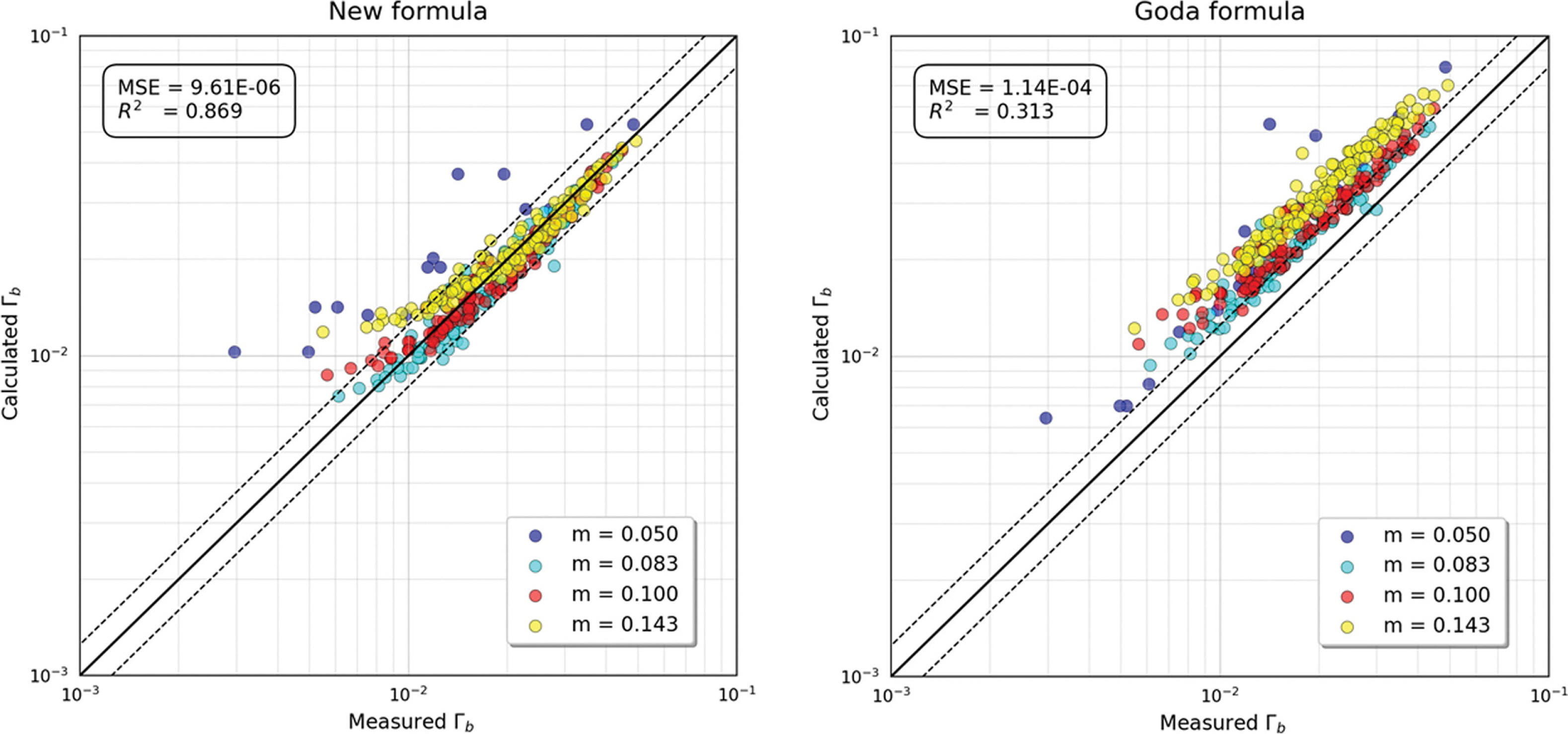
Comparison between the proposed formula and the Goda (2010) formula regarding wave breaking height.
Comparison between the proposed formula and the Rattanapitikon and Xie et al. (2019) formula regarding breaking water depth.
Results of error analysis
여기서, Φ는 쇄파파고 Γb 또는 쇄파수심 Ωb이며, Erms는 평균제곱근오차, Ebias는 편향, Esd는 표준편차, n은 데이터 수, 그리고 아래첨자 cal과 mea는 각각 예측값과 실험값을 의미한다.
Table 4에 보인 오차해석 결과로부터 본 연구에서 제시한 자갈해빈에 대한 쇄파지표 산정식은 간단한 선형식임에도 불구하고 기존의 경험식에 비해 쇄파지표의 예측성능이 향상됨을 확인할 수 있다. 또한, Goda(2010)의 경험식의 경우 쇄파파고를 과대평가하는 경향을 양의 편향에서 재확인되며, Xie et al.(2019) 및 식(18)의 쇄파수심에 대한 경험식은 쇄파수심을 약간 과소평가하고 있음을 음의 편향에서 확인할 수 있다. 결과적으로 본 연구에서 제안한 쇄파지표 산정식의 경우 결정계수를 기준으로 쇄파파고의 경우 12.0~177.6%, 쇄파수심의 경우 9.1~9.6% 정도의 예측성능이 향상되었음을 확인하였다.
5. 결론 및 향후과제
본 연구에서는 해안구조물의 설계와 연안표사문제 등 다양한 해안물리현상과 밀접한 쇄파를 대상으로 쇄파파고와 쇄파수심으로 대표되는 쇄파지표를 예측하기 위해 기계학습을 적용하였다. 특히, 본 연구에서는 자갈해빈에서 발생하는 쇄파지표를 대상으로 입력변수와 출력변수 사이의 관계가 설명 가능한 선형모델을 기반으로 쇄파예측을 수행하였다. 기계학습을 위한 학습 데이터와 평가 데이터는 자갈해빈을 대상으로 한 기존의 쇄파 연구로부터 획득한 수리모형실험 데이터를 활용하였다. 자갈해빈에서 발생하는 쇄파지표의 예측을 위해 기존의 수리모형실험결과와 기제안된 기존의 경험식과 비교·검토한 결과, 제안된 쇄파지표 경험식은 주로 사면이나 불투과 경사면에 대한 수리모형실험결과를 기반으로 하고 있어 상대적으로 공극이 높은 자갈해빈에 대한 쇄파파고 및 쇄파수심의 예측성능이 낮음을 확인하였다. 자갈해빈에서 발생하는 쇄파지표 예측을 위해 선형적인 기계학습 알고리즘에 기반한 모델을 사용하여 쇄파지표의 예측성능을 비교하였다. 쇄파파고 및 쇄파수심에 대한 예측결과에서 선형회귀모델이 가장 뛰어난 예측성능을 나타내었기에 각 알고리즘에 기반한 회귀계수를 활용하여 쇄파지표 산정식을 제안하였다. 본 연구에서 새롭게 제안한 쇄파지표 예측식과 기존 경험식과의 예측성능을 비교하였으며 예측성능은 전체 데이터를 이용하여 비교하였다. 새롭게 제안한 자갈해빈에 대한 쇄파지표 경험식은 실험결과를 양호하게 예측하였으며, 쇄파파고에 비해 쇄파수심의 예측성능이 상대적으로 높게 나타났다.
본 연구에서 제안된 자갈해빈에 대한 쇄파지표 예측식은 바닥경사와 심해파형경사만을 이용하여 간편하게 산술적으로 쇄파파고와 쇄파수심을 산정할 수 있으므로 설계단계에서 유용하게 활용될 수 있을것으로 기대된다. 그러나, 본 연구에서 제안한 기계학습 모형은 제한된 수리모형실험결과에 의존하여 학습되었으므로 모델의 입력변수로 저질의 특성이 고려되지 않았으며, 저질의 입경별 공극율(또는 투수계수) 또는 복합입경에 대한 쇄파지표 예측성능은 담보할 수 없다. 따라서, 향후 자갈해빈에 대한 보다 다양한 추가적인 수리모형실험을 수행하여 저질의 특성까지 고려될 수 있는 모델의 구축이 요구된다.
Acknowledgements
본 연구는 2021학년도 한국해양대학교 신진교수 정착연구지원사업 연구비 및 해양수산과학기술진흥원(KIMST)의 “월파 정량 관측 기술 개발(20220180)” 사업의 지원을 받아 수행된 연구이며, 연구비 지원에 감사드립니다.