2.1 실험시설 및 실험단면

수리모형실험은 Fig. 2에 제시된 바와 같이 길이 50 m, 폭 1 m, 최대 높이 1.8 m의 제원을 갖는 2차원 단면조파수로에서 수행되었다. 조파수로의 좌측 끝으로부터 4.1 m 이격된 위치에는 서보모터(Servo motor)로 구동되는 피스톤 형식의 조파기가 설치되어 있으며, 조파수조 양끝단에는 반사파 제어를 위한 소파제가 설치되어 있다. 조파수조의 바닥은 수조의 좌측 끝으로부터 10 m부터 16 m 구간까지 1:20의 경사면으로 이루어져 있어 16 m 이후 구간부터는 조파기가 설치된 수조바닥에 비해 0.3 m 높아진다. 본 수리모형실험에서는 18~22 m 구간에 1:20의 경사면을 추가로 설치하였으며, 22 m 이후 구간부터는 조파기가 설치된 위치의 수조바닥에 비해 0.5 m 높은 일정수심의 고정상을 구성하였다.

Fig. 2.

Plan and side views of wave flume (unit: mm).

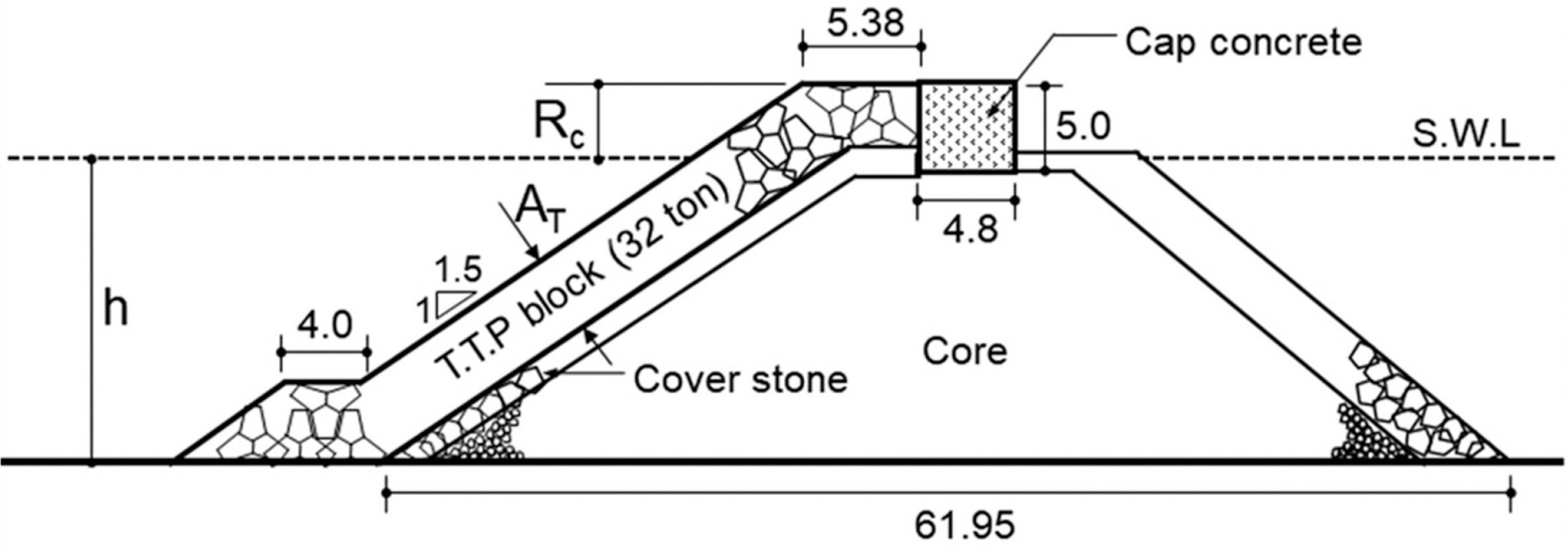
실험 대상구조물은 우리나라 호안구조물로 가장 광범위하게 적용되어 있는 사석경사제를 대상으로 하였으며, 구조물의 전면은 테트라포드 32 ton급으로 피복된 형상을 고려하였다. 구체적인 실험대상 구조물의 제원을 Fig. 3에 보인다. 또한, 피복된 사석경사제는 Lee and Kim(2023)이 적용한 경사식구조물과 동일하게 정수면으로부터 피복블록 상단까지의 높이와 상치구조물의 여유마루고가 일치하는 R_c = A_c 조건이다. Fig. 3의 사석경사제에 대하여 Froude 상사에 기초한 1/50 축척을 적용하여 실험모형을 제작하였으며, 모형구조물은 조파수로 내에 조파판으로부터 37 m 이격된 거리에 설치하였다. 모형구조물의 전면으로부터 4 m 이격된 거리부터 조파판 방향으로 연속으로 4대의 용량식 파고계를 설치하여 Mansard amd Funke(1980)에 의해 제안된 입·반사 분리를 통해 파고와 주기 정보를 분석하였다. 조파수로 내에 설치된 실험대상 구조물 및 월파량 측정을 위한 수로(chute)와 월파 집수함의 사진을 Fig. 4에 제시한다.

Fig. 3.

Cross-section sketch of model structure (unit: m).

Fig. 4.

Installation of the model structure and overtopping tank in the flume.

2.2 실험조건 및 월파량 측정방법

실험파는 Bretschneider-Mitsuyasu 스펙트럼을 이용하여 불규칙파를 생성하였으며, 유의주기 T_s에 따라 실험대상구조물에서 월파가 발생하도록 파고에 대한 조파신호를 조정하여 실험을 수행하였다. 모형구조물의 주요형상제원을 포함한 실험파의 제원을 Table 1에 제시한다. Table 1에 보인 유의파고 H_m0 및 평균파고 T_m은 전술한 입·반사 분리를 통한 입사파의 주파수 스펙트럼을 이용하여 식(1)에 의해 산정하였다.

Table 1.

Experimental conditions for irregular waves and geomerirc parameters of model structure

여기서, m_n은 스펙트럼 모멘트로 식(2)로 산정된다.

여기서, m_n은 에너지 밀도 스펙트럼의 n차 모멘트이며, f는 주파수, S는 스펙트럼 밀도이다.

Table 1에서 R_c는 정수면으로부터 구조물의 마루높이까지의 연직거리인 여유마루고이며, A_T는 소파블록의 피복층 두께이다. 수리모형실험은 Table 1에 제시한 조건에 따라 총 75 case의 실험을 수행하였으며, 월파량은 유의파를 기준으로 총 300파 동안 조파하여 시간 평균한 단위폭당 평균월파량 q(m³/s·m)으로 산정하였다.

월파량 측정은 Fig. 4와 같이 구조물 배후에 길이 122 cm, 높이 61 cm, 폭 55 cm 월파집수함(overtopping tank)을 설치하여 계측하였으며, 월파집수함은 구조물 마루에 설치된 폭 31 cm의 월파수로(overtopping chute)와 연결되어 있다. 월파집수함에는 용량식 수위계를 설치하여 월파량의 측정정도를 높였다.

3.1 기존 월파량 경험식의 분류

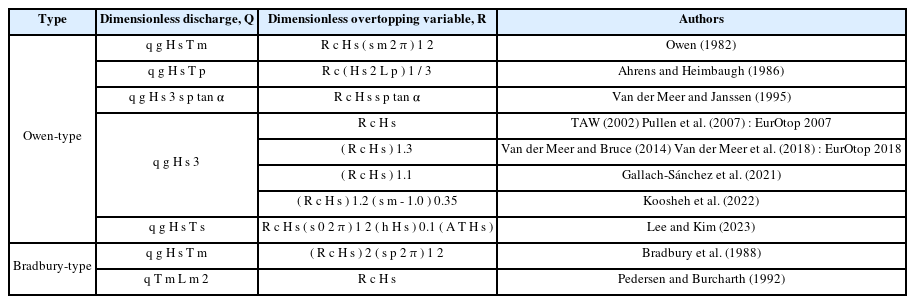
월파량에 대한 Goda(1970), Battjes(1974) 및 Owen(1980)의 연구 이후로 사석경사제에서 발생하는 월파량을 산정하기 위한 다양한 경험식들이 제안되었다(van Gent et al., 2022). 사석경사제의 월파량 산정을 위한 경험식의 형식은 지수 함수를 이용한 식(3)의 Owen-type과 멱함수 형태인 식(4)의 Bradbury-type으로 구분될 수 있다.

여기서, Q는 무차원 월파량, R은 구조물의 무차원 여유마루 고, 입사파고 및 파형경사로 구성된 무차원 변수(이하 월파 변수로 정의), γ는 경사입사파 혹은 구조물 사면에서의 조도 영향이 고려 가능한 영향계수, a 및 b는 상수이다.

Table 2에 지금까지 제안된 대표적인 월파량 경험식을 각각의 형식별로 정리하여 나타낸다. Table 2에서 T_m은 스펙트럼 평균주기, s_m(= 2πH_s/g Tm2)과 Lm(- g Tm2/2π)은 각각 평균주기 T_m에 해당하는 심해파형경사와 파장, g는 중력가속도, L_p(= g Tp2/2π·[tanh(4π²h/ Tp2g)]^1/2)는 첨두주기 T_p에 해당하는 천해파장, s_m-1,0(= 2πH_s/g Tm2_-1,0)은 스펙트럼으로부터 산정되는 평균주기 T_m-1,0 = m_-1/m₀에 해당하는 심해파형경사, s₀(= 2πH_s/g Ts2)는 유의파주기에 해당하는 파형경사, s_p(= 2πH_s/g Tp2)는 첨두주기에 해당하는 파형경사를 각각 나타낸다.

Table 2.

Existing empirical formulas for estimating overtopping discharge on rubble-mound structures

3.2 월파량 실험결과

Table 2에 제시한 많은 경험식 중에서 EurOtop 2018 매뉴얼은 CLASH 프로젝트에 기반한 데이터베이스로부터 다양한 형상에 대한 월파량 경험식을 제공하고 있어 최근 들어 활발히 활용되고 있다. EurOtop 2018 매뉴얼에서는 사면경사가 1:2~1:4/3인 경사식구조물을 대상으로 경사면의 조도영향 계수 γ_f의 영향을 고려하여 식(5)와 같은 경험식을 제안하고 있다.

식(5)에서 조도영향계수 γ_f는 피복된 블록의 종류 및 형태에 따라 0.38~0.60의 범위로 피복되지 않은 경사면의 경우 γ_f = 1이다. 본 연구에서 적용한 테트라포드의 경우 γ_f = 0.38을 제시하고 있으며, Cube 블록의 2단 적층인 경우 γ_f = 0.47을 제안하고 있다.

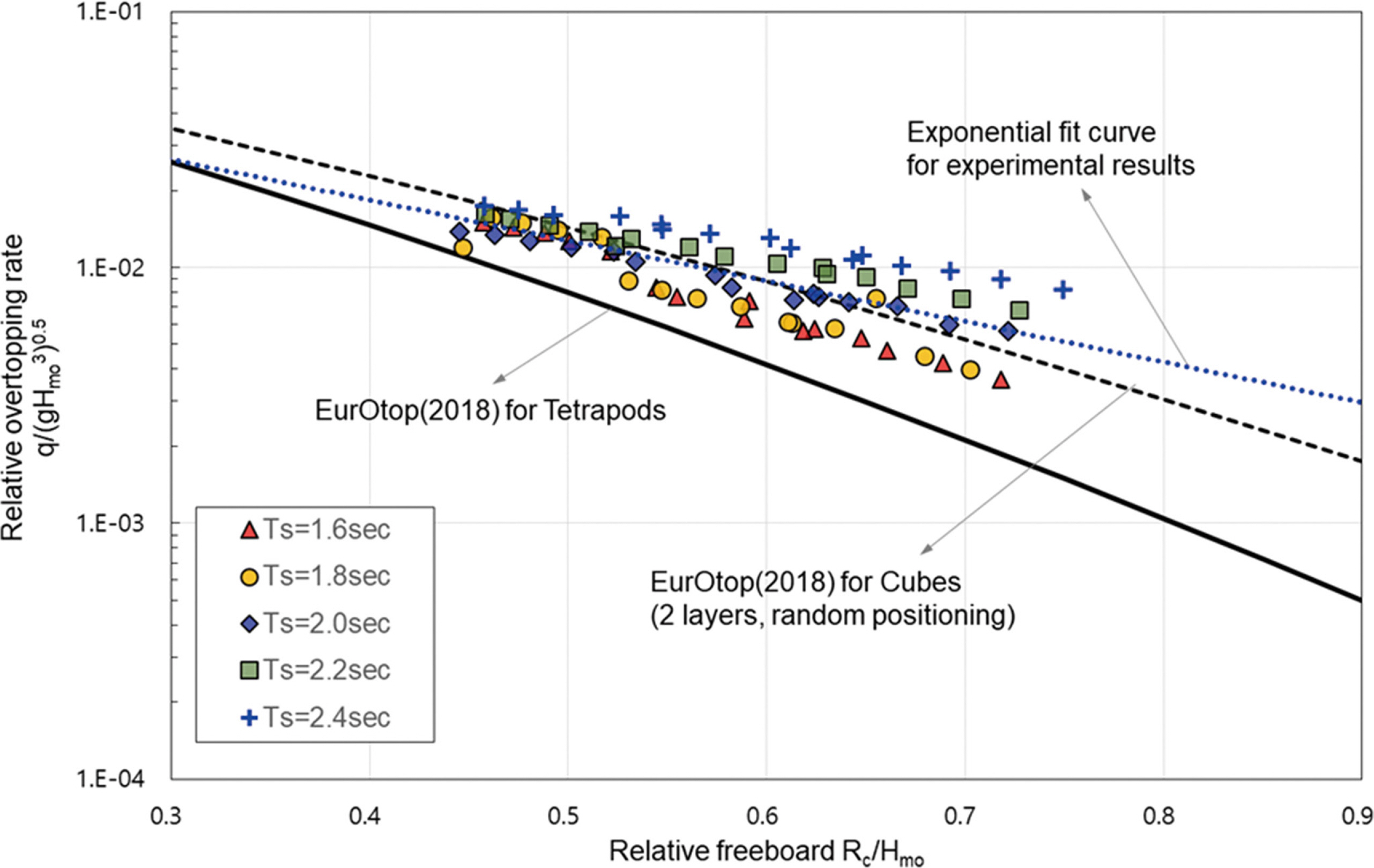
Fig. 5는 상대적으로 낮은 여유마루고를 갖는 0.45 < R_c/H_s < 0.75의 범위에서 수행된 월파량 실험결과와 EurOtop(2018)에서 제안하고 있는 식(5)에 의한 월파량 산정결과를 비교하여 나타낸 것이다. EurOtop(2018)의 월파량 경험식에서 제안된 조도영향계수 γ_f는 상치구조물의 여유마루고와 피복층의 높이가 동일한 R_c = A_c 조건이며, 본 연구의 실험조건과도 동일하다.

Fig. 5.

Comparisons of overtopping discharges between experimental results and EurOtop manual.

Fig. 5에서 확인되는 바와 같이 테트라포드로 피복된 사면경사에 대한 식(5)에 의한 EurOtop(2018)의 월파량 경험식은 실험결과를 과소평가하고 있으며, 피복블록의 형태가 상이하지만 오히려 큐브블록이 2층으로 적층된 조건이 실험결과를 가장 양호하게 재현하고 있음을 알 수 있다. 이는 테트라포드가 2층으로 적층되어 있는 사석경사제를 대상으로 0.77 < R_c/H_s < 1.63 범위에서 수리모형실험을 수행한 Lee and Kim(2023)의 연구결과와 유사한 경향을 보였다. Lee and Kim(2023)은 테트라포드로 2층 피복된 사석경사제에 대한 EurOtop(2018) 매뉴얼의 월파량 경험식의 경우 유의파주기에 따라 상이하지만 상대적으로 단주기의 경우에서는 γ_f = 0.4(투과성 체제에 피복석이 2층 피복된 조건), 상대적으로 장주기의 경우에서는 γ_f = 0.55(불투과성 제체에 피복석이 2층 피복되어 있는 조건)를 적용하는 것이 실험결과를 양호하게 재현할 수 있음을 제안하였다. Jung and Yoon(2019)의 연구에서도 소파블록에 의해 피복된 경우 EurOtop(2018)에서 제안한 조도영향계수를 적용하는 경우 실제 월파량을 과소평가 할수 있음을 지적하였다. 또한, Lee and Kim(2023)의 실힘결과와 유사하게 유의파주기가 길어짐에 따라 발생 월파량이 다소 증가하는 경향을 보였으나, R_c/H_s < 0.5 이하에서는 유의파주기에 따른 월파량 차이가 현저하게 감소함을 알 수 있다.

4.1 무차원 변수와 월파량과의 상관관계

Fig. 6은 본 연구의 수리모형실험에서 계측된 월파량을 Table 2에 제시한 Owen-type과 Bradbury-type의 월파량 경험식에서 사용한 무차원 월파변수 R 및 무차원 월파량 Q를 이용하여 도시한 결과이다. 단, 제안된 월파량 산정식에 대한 조도영향계수는 서로 상이하므로 γ_f = 1을 적용하였다. 한편, Table 2에 보인 바와 같이 월파량를 예측하기 위해 불규칙파에 대한 주파수 스펙트럼의 기여도를 평가하기 위해 다양한 주기가 적용되고 있음을 알 수 있다. Van Gent(1999)는 주파수 스펙트럼에서 첨두주기 T_p 또는 유의주기 T_s에 비해 장주기에 가중치를 부여하는 T_m-1,0이 월파에 대한 스펙트럼 형태의 영향을 설명하는데 가장 적합한 주기임을 제안하였다. 그러나, 실제 해안구조물의 설계 시에는 유의주기 Ts가 사용되며, Goda(2010)에 따르면 단일 첨두주기를 갖는 주파수 스펙트럼의 경우 스펙트럼의 평균주기 T_m-1,0와 유의주기 T_s가 거의 동일함을 지적하고 있다. 따라서, 본 연구에서는 스펙트럼으로부터 산정되는 T_m-1,0을 대신하여 유의주기 T_s를 적용하여 기존 경험식을 평가하였다.

Fig. 6.

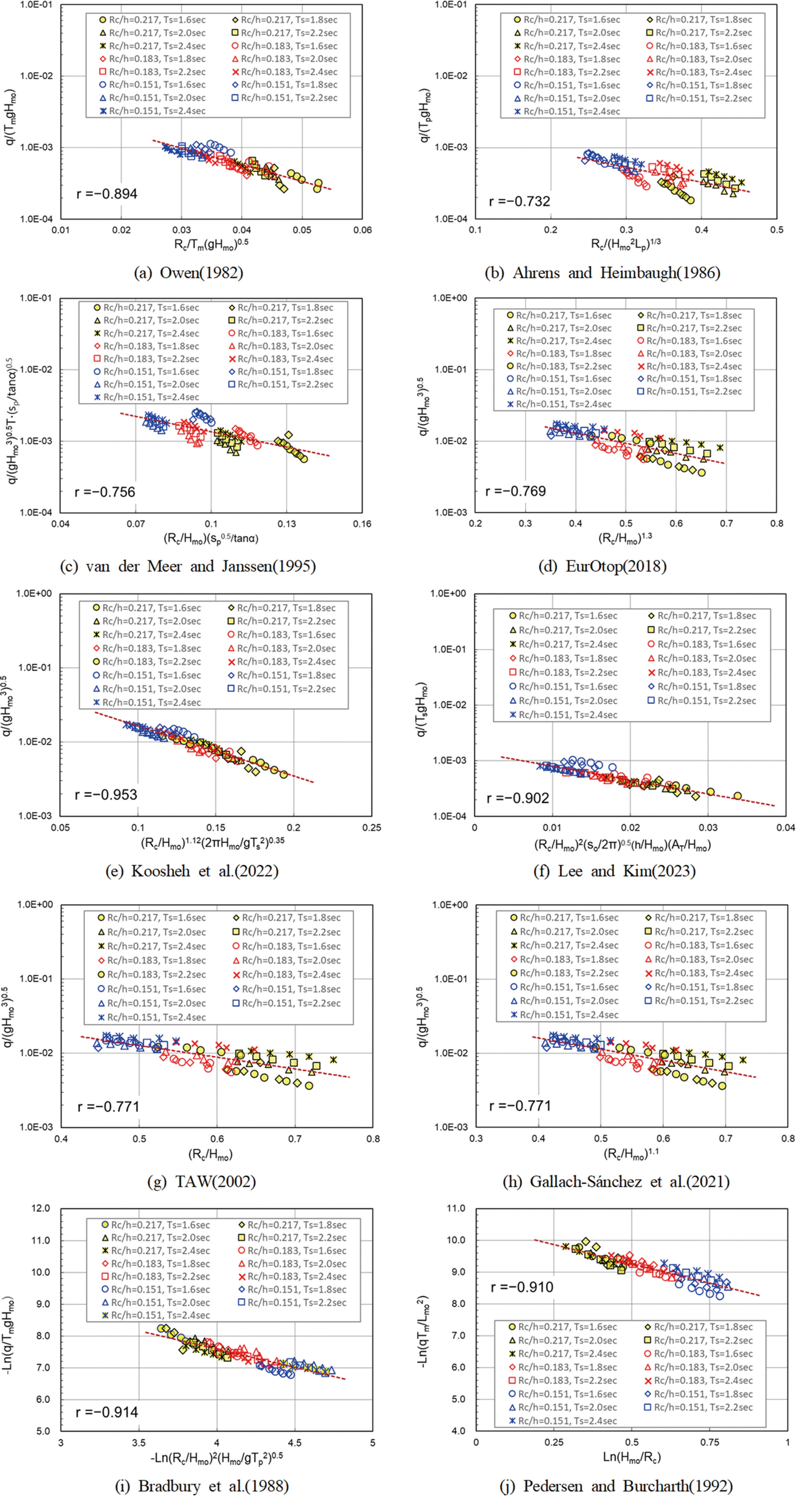
Comparison of overtopping discharge results using dimensionless variables of existing empirical formulae.

Owen-type의 월파량 경험식 가운데 Ahrens and Heimbaugh (1986)의 무차원 월파변수 R을 적용한 Fig. 6(b)가 가장 낮은 상관계수인 |r| = 0.732로 분석되었다. 반면에, Koosheh et al.(2022)의 경험식은 상관계수가 |r| = 0.953으로 본 연구의 실험결과를 가장 잘 재현하였으며, Lee and Kim(2023)의 경험식이 |r| = 0.902로 다음으로 높은 상관계수를 보였다. 또한, EurOtop(2018)의 경우 v0.769로 Owen-type의 월파량 경험식 가운데 상대적으로 낮은 상관계수를 보였으며, 전체적으로 무차원 월파변수 R에 주기의 영향이 고려된 경험식이 파고만을 고려한 경험식에 비해 높은 상관관계를 갖는 것으로 분석되었다. Bradbury-type의 월파량 경험식의 경우 Owen-type의 경험식에 비해 단순한 멱함수의 형태를 갖지만 Bradbury et al.(1988)과 Pedersen and Burcharth(1992)의 경우 각각 |r| = 0.914 및 0.910의 높은 상관관계를 나타냈다.

4.2 월파량 산정식 제안

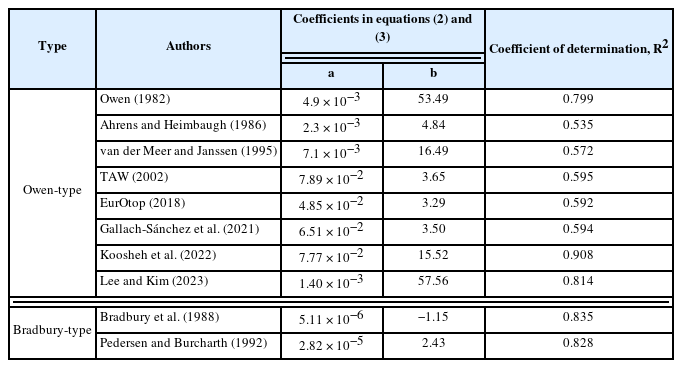
기존 월파량 경험식의 무차원 월파변수와 월파량과의 관계를 회귀분석하여 산정된 식(3)과 식(4)의 계수값을 결정계수와 함께 Table 3에 정리하여 제시한다. 비록 제한된 월파량 경험식을 대상으로 예측성능을 분석하였지만 Bradbury-type의 경험식은 일정한 상관계수를 보인 반면에 Owen-type의 경험식은 사용된 무차원 월파변수에 따라 월파량 예측정도의 편차가 발생함을 Table 3의 결정계수로부터 확인된다.

Table 3.

Coefficients in existing empirical formulas based on experimental results

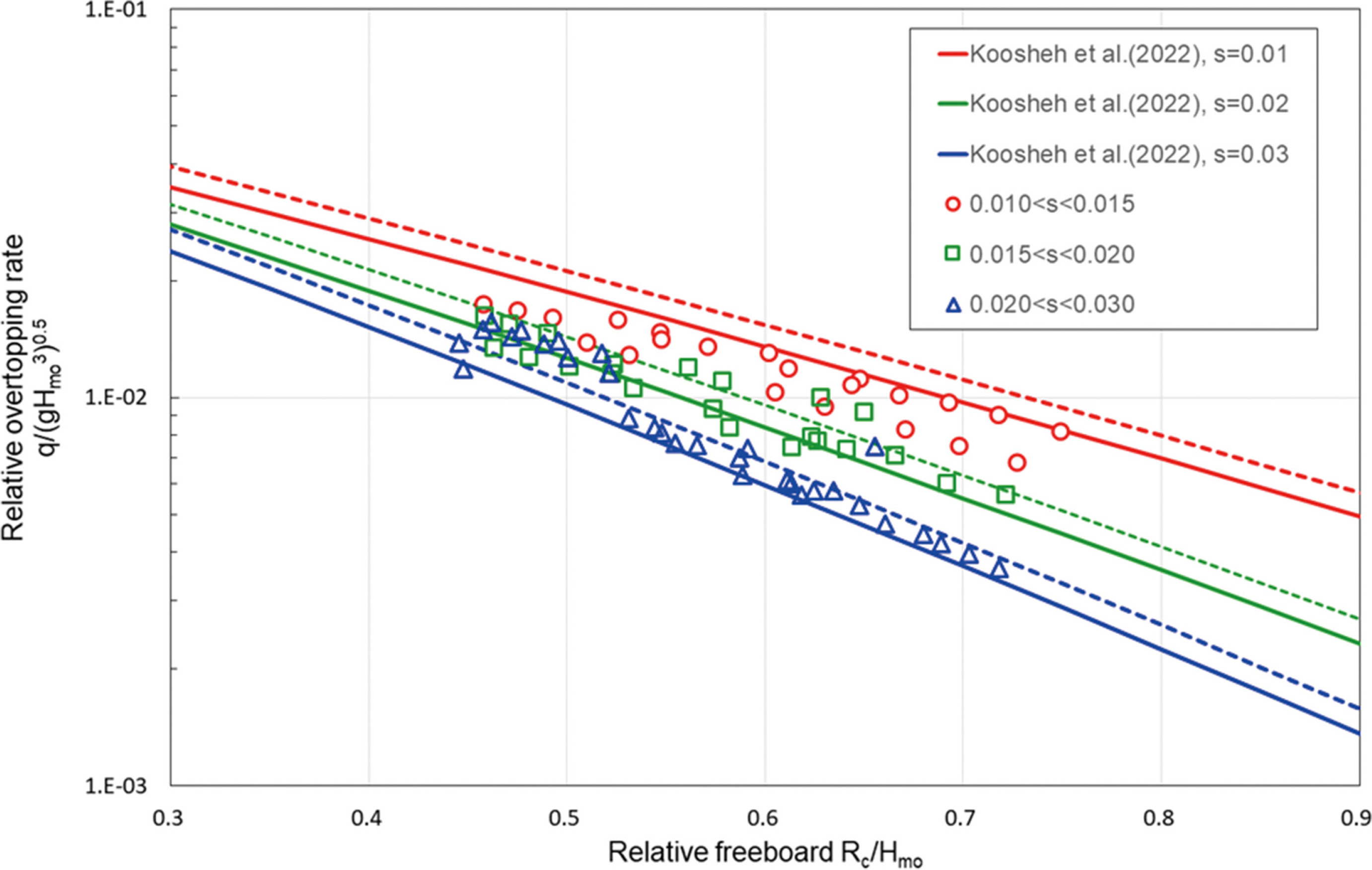
Fig. 7은 Table 3에 제시한 월파량 산정식 중에서 무차원 여유마루고와 월파량의 상관관계가 높게 나타난 Owen-type(Koosheh et al., 2022; Lee and Kim, 2023)과 Bradbury-type(Bradbury et al., 1988; Pedersen and Burcharth, 1992)의 경험식에 대한 월파량 예측결과를 수리모형실험결과와 비교한 것이다. 경험식에 따른 상호비교를 위해 무차원 월파량은 Q = q/ gHs3으로 비교하였다. Owen-type의 경험식에서는 Koosheh et al.(2022) 및 Lee and Kim(2023)의 결정계수가 각각 R² = 0.908과 R² = 0.814로 Koosheh et al.(2022)의 무차원 월파변수를 이용한 월파량 경험식이 보다 양호한 결과를 보였다. Bradbury-type의 경험식에서는 Bradbury et al.(1988)과 Pedersen and Burcharth(1992)의 결정계수가 각각 R² = 0.835와 R² = 0.828로 Bradbury et al.(1988)의 무차원 월파변수가 월파량의 변동성을 상대적으로 잘 설명하고 있음을 알 수 있다.

Fig. 7.

Comparison of overtopping discharge results using dimensionless variables of existing empirical formulae.

4.3 월파량 산정식에 대한 오차해석 및 성능평가

전술한 바와 같이 본 연구에서 분석한 기존 월파량 경험식 가운데 Owen-type의 Koosheh et al.(2022)의 경험식이 가장 높은 결정계수를 보였으나 결정계수만으로는 예측성능을 평가하기 곤란하다. 따라서, 월파량 예측에 대한 경험식의 오차 정도를 정량적으로 분석하기 위해 식(5)를 이용하여 오차해석을 수행하였으며, 예측 정확도의 성능평가는 식(6)과 같이 평균제곱근오차(Root Mean Square Error, RMSE)를 실험결과의 평균치로 정규화한 산포지수(Scatter Index, SI)와 예측값과 실험결과의 적합정도를 나타내는 Nash-Sutcliffe 효율 지수(Nash-Sutcliffe Efficiency, NSE)를 적용하였다.

여기서, Q_cal와 Q_mea는 각각 월파량 산정식 및 실험결과에 따른 무차원 월파량이며, E_rms는 평균제곱근오차, E_bias는 편향(Bias), E_sd는 표준편차(Standard Deviation, SD), n은 데이터 수를 나타낸다.

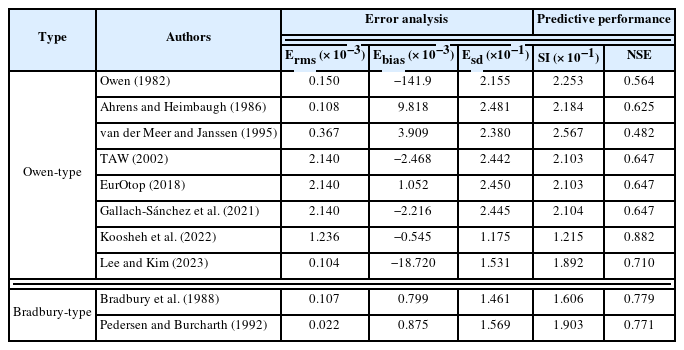
Table 4는 Table 3에서 제시한 월파량 산정식의 오차해석과 예측성능에 대한 결과를 나타낸다. 오차해석 중에서는 RMSE는 무차원 월파변수로 R_c/H_s 만을 이용한 TAW(2002), Gallach-Sánchez et al.(2021) 및 EurOtop(2018)의 경험식이 비교적 예측오차가 크며, Pedersen and Burcharth(1992)의 오차가 가장 작았다.

Table 4.

Summary of error analysis and predictive performance of wave overtopping discharge formulae

오차의 일관된 경향을 나타내는 편항은 무차원 월파변수와 월파량의 상관관계가 높게 나타난 Owen-type(Koosheh et al., 2022; Lee and Kim, 2023)의 경우 음의 편향으로 실험결과를 다소 과소평가하는 경향을 보이며, Bradbury-type(Bradbury et al., 1988; Pedersen and Burcharth, 1992)의 경우는 반대로 실험결과를 과대평가하는 경향을 보였다. 또한, 가장 작은 편향과 표준편차를 갖는 Koosheh et al.(2022)이 오차 변동성이 가장 적음을 알 수 있다. 월파량 예측 정확도의 성능평가를 위한 SI와 NSE에서는 Owen-type 및 Bradbury-type의 경험식 가운데 Koosheh et al.(2022)과 Bradbury et al.(1988)의 경험식이 높은 예측성능을 보였다. 이상으로부터 본 연구에서 검토한 상대적으로 낮은 여유마루고를 갖는 R_c/H_s < 0.75의 범위에서 테트라포드로 피복된 사석경사제에 대한 월파량 예측은 Koosheh et al.(2022)의 무차원 월파변수를 도입하는 경우가 가장 높은 예측정도를 나타냄을 확인하였으며, 실험결과로부터 제안된 Owen-type의 월파량 경험식은 다음과 같다.

여기서, s₀는 심해파형경사로 s₀ = 2πH_s/g Ts2이며, 식(7)로부터 산정되는 무차원 월파량 Q_cal = q/ gHs3와 실험결과인 Q_mea와의 비가 평균값 1.0을 갖는 정규분포로 가정하면 식(7)의 계수에 대한 표준편차는 σ(0.0777) = 0.0095와 σ(15.52) = 0.121이다. EurOtop(2018)과 유사한 준확률론적 접근방법(semi-probabilistic approach)으로 각 계수의 표준편차만큼의 안전계수를 적용하면 식(8)과 같다.

Fig. 8은 식(7) 및 식(8)에 의해 산정된 무차원 월파량과 수리모형실험에서 계측된 월파량을 파형경사의 계급별로 비교하여 도시한 결과이다. 그림 중의 실선은 식(7)에 의한 결과이며, 점선은 표준편차만큼의 안전계수를 적용한 식(8)에 의한 결과이다. 식(7)의 경우 낮은 파형경사에서 실험결과를 약간 과대추정하고 높은 파형경사에서는 과소평가하고 있으나 전체적으로 파형경사에 따른 월파량의 실험결과를 양호하게 산정할 수 있음을 알 수 있다. 또한, 안전계수를 적용한 식(8)은 낮은 파형경사에서 월파량을 과대평가할 수 있지만 설계적인 관점에서 월파량예측에 활용될 수 있을 것으로 판단된다.

Fig. 8.

Comparisons of overtopping discharges between experimental results and a new Owen-type formula.