수평 감쇠판이 부착된 폰툰형 부유식 구조물의 수리모형실험
Hydraulic Model Tests for a Pontoon-Type Floating Structure with a Horizontal Damping Plate
Article information
Abstract
본 연구에서는 수평 감쇠판을 부착한 폰툰형 부유식 구조물의 운동 저감 효과를 분석하기 위해 수리모형실험을 수행하였다. 일반 직사각형 폰툰형 부유식 구조물 및 수평 감쇠판이 부착된 폰툰형 구조물을 1/20의 축척을 적용하여 제작하였고, 규칙파 및 불규칙파 조건에서의 운동 응답을 계측하였다. 실험체별 16개 파랑 조건에 대한 계측 결과의 비교로부터 직사각형 폰툰형 부유체에 수평 감쇠판을 설치한 경우 수평 감쇠판이 설치되지 않는 조건 대비 응답이 평균 5 ~ 10 % 감소시킬 수 있음을 확인하였다.
Trans Abstract
In this study, hydraulic model tests were conducted to investigate the effect of a horizontal damping plate on the motion of the pontoon-type floating structure. The floating structures with and without the horizontal damping plates were fabricated with the scale of 1/20 and their motion responses to the regular and irregular wave conditions were investigated. From the comparison for the responses of each model with 16 wave conditions, it could be known that the damping plate made the response of the the pontoon to be smaller by about 5 to 10 % compared with the normal rectangular pontoon.
1. 서 론
1.1 연구배경 및 목적
방파제와 같은 외곽시설은 파랑으로부터 해안 시설물의 보호 및 안정화를 목적으로 연안 해역에 설치되는 구조물이다. 최근 기후변화에 따른 해상환경 변화와 해수면 상승으로 인해 파랑의 강도와 빈도가 증가함에 따라 항만 시설물에 미치는 피해는 증가하고 있으며(Choi et al., 2019; Ministry of Oceans and Fisheries, 2021), 이에 따라 효율적이고 강화된 해안 보호시설에 대한 수요가 높아지고 있다. 외곽시설은 중력식과 부유식으로 구분될 수 있으며, 부유식 구조물은 수심이 깊어질수록 중력식 대비 시공성 및 경제성 측면에서 유리하고 해역 보호 외에 낚시, 레저 등의 다양한 목적으로 활용할 수 있어 장점이 있다. 경남 통영과 마산의 강재 부유식 방파제 시공을 시작으로 콘크리트(경남 고성 당항포) 및 PE(전남 장성) 등 여러 재질의 부유체의 설치 사례가 확인되고 있고, 다양한 형상의 부유식 방파제 적용을 위한 연구가 이뤄지고 있다.
먼저 해상 부유 구조물의 사용 재료 또한 다양한 변화 노력이 있어 왔다. 전통적으로 강재, 경량 콘크리트-강재, 경량 철근콘크리트-강재를 사용한 부유 구조물이 제안되거나 실제 적용되었으며, 철근 및 강재를 FRP 등으로 대체하는 방법도 제안된 바 있다(KIOST, 2016). 최근에는 국내 수상 태양광 시설 및 수변공간 수요가 증가됨에 따라 폴리에틸렌(Polyethylene: PE) 부력체를 해상에도 적용하고자 하는 연구도 이뤄지고 있다. 해상에 노출된 PE 부력체는 내구성 및 연결부 구조적 안전성 문제에 취약하므로, 이를 해결하기 위해 복합소재 부유체(Lee et al., 2023) 및 콘크리트-PE 부유체(Park et al., 2022; Kim and Jeong, 2023)가 제안되기도 하였다.
또한 형상 개선을 통한 부유구조물의 운동 저감을 위한 연구도 지속해 이뤄지고 있으며, 여러 연구에서 부유체 자체 형상을 달리 고안하거나 감쇠판 도입 등 부가 부재 부착 방법이 제안되었다. 먼저 폰툰형 구조물에 수직판(Hong, 2012)을 부착하거나 폰툰과 반잠수식 부유체 형상을 혼합한 하이브리드형(Lee et al., 2013) 부유식 구조물에 대한 수치해석적 연구가 수행된 바 있으며, Jung et al.(2006)은 일본의 표준 부유식 방파제 형상 사례에 착안하여 PE 재질의 파이프와 시트를 조합한 부유식 방파제를 제안하기도 하였다. 해양플랫폼 및 부유식 풍력 구조물 등의 수요가 높아짐에 따라 부유체 크기 및 자중을 줄이기 위해 폰툰형 부유체(Chen et al., 2012) 및 원통형 부유체(Cho, 2011; Sudhakar and Nallayarasu, 2014; Lim et al., 2015; Lopez-Pavon and Souto-Iglesias, 2015; Bezunartea-Barrio at al., 2020)에 감쇠판을 적용한 운동 저감 효과를 분석하는 연구도 다수 수행된 바 있다. 그러나 대부분 원통형 부유체의 운동 저감을 위한 연구이며, 부유식 구조물에 적합한 폰툰형 부유체에 대한 연구는 상대적으로 부족한 실정이다. 최근 Park et al.(2022)이 포텐셜 기반 수치해석 모델을 사용해 폰툰형 부유식 구조물에 적용되는 수평 감쇠판의 길이 영향을 분석하고, Pitch 저감을 위해 파랑 조건별 수평 감쇠판의 길이 선정이 중요함을 밝혔으나, 실험을 통한 수평 감쇠판의 거동 규명에 관한 연구는 부재한 상황이다.
본 연구는 감쇠판의 적용이 부유식 구조물의 운동 응답에 미치는 영향을 수리모형실험을 통해 분석하였다. 단순한 직사각형 단면의 폰툰형 부유식 구조물 대비 감쇠판이 설치된 부유체의 운동 감소 효과를 확인하기 위하여 다양한 파랑 조건과 길이가 다른 수평 감쇠판을 적용하였다.
2. 실험시설 및 실험조건
2.1 실험대상 및 축소모형
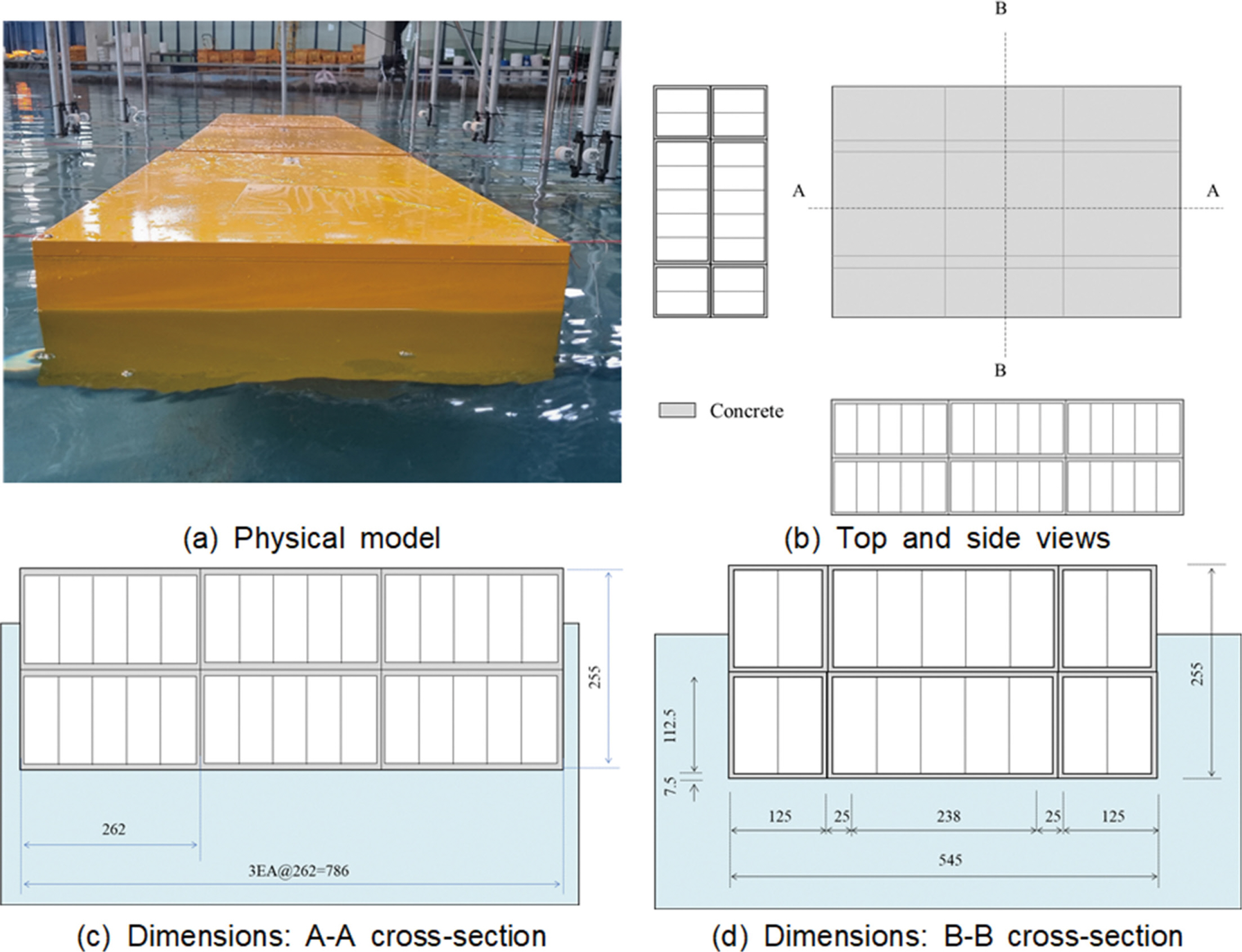
본 연구에서 다루고자 하는 부유 구조물은 단위 모듈로 구성된다. 실제 각 단위 모듈은 실제는 철근 콘크리트 재질로 제작하여 해양 외력에 대한 내구성을 확보하도록 하며, 다수의 단위 부유체 모듈 간 결합을 통해 확장성을 높임으로써 다양한 용도로 활용될 수 있다. 본 연구의 실험 대상인 부유식 구조물은 Fig. 1와 Fig. 2와 같이 단위 모듈을 수직 및 수평으로 결합해 형성되며, 이때 실제 제원은 약 15 m(가로) × 10 m(세로) × 5 m(높이)이다.
Reference floating structure: Model A.
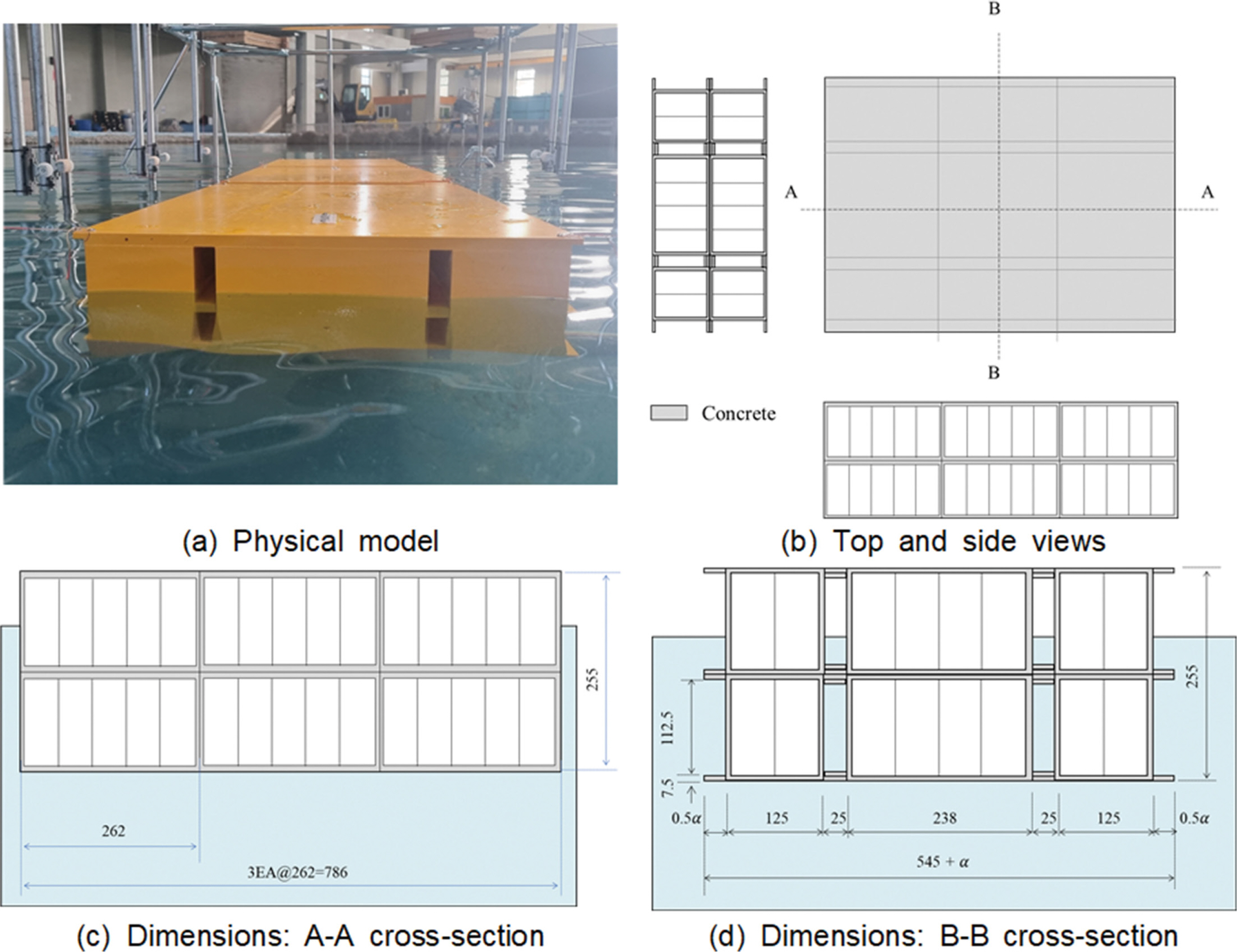
Floating structure with horizontal damping plates: Models B and C (α: Lengths of the damping plates).
해당 부유체의 수리적 거동에 수평 감쇠판이 미치는 영향을 분석하기 위해 서로 다른 수평 감쇠판 길이를 갖는 부유체에 대한 축소 모형을 제작해 수리모형실험을 수행하였다. 실험체는 목표 흘수 원형상 3.566 m를 달성하도록 실험 축척 1/20의 Froude 상사 법칙에 따라 설계 및 제작하여 Table 1의 크기와 중량을 충족하도록 하였다. 각 실험체는 아크릴판으로 정밀 가공하였으며, 아크릴판 접합부의 물의 유입을 방지하도록 방수 처리를 실시해 실험체 내부의 기밀이 유지되도록 하였다.
Geometry and weight property of small-scaled models for wave reducer unit.
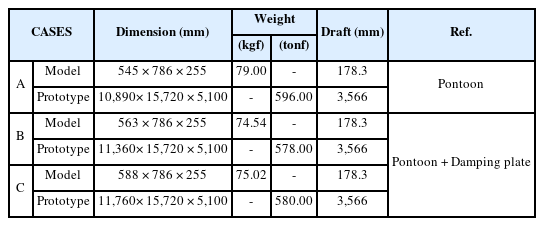
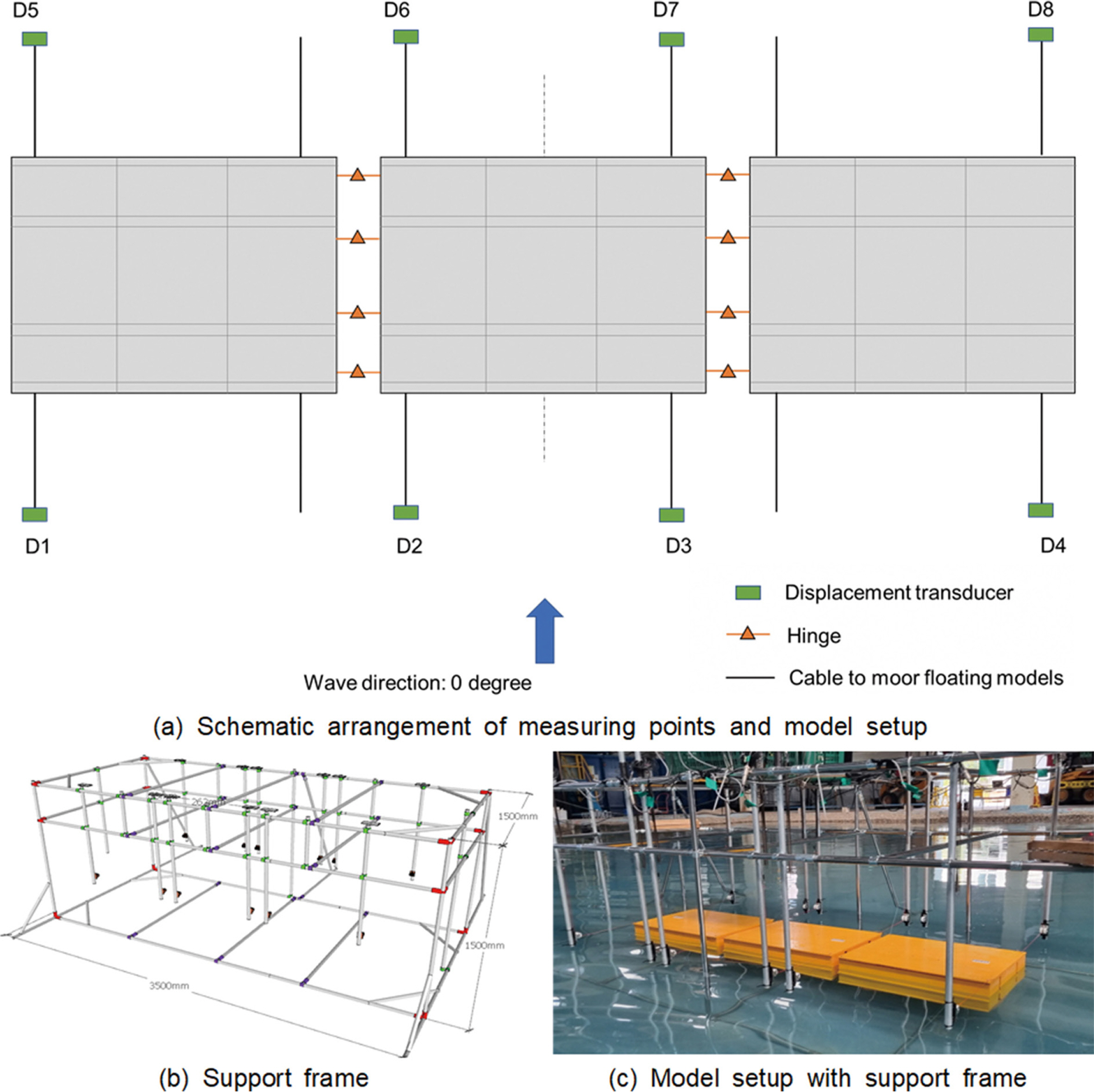
Table 1에 정리된 바와 같이 축소 모형 A, B, C는 서로 다른 길의 수평 감쇠판 조건을 적용하였으며, A는 수평 감쇠판 길이가 0인 일반 직사각형 폰툰, B와 C는 길이가 서로 다른 수평 감쇠판이 부착된다. 여기서 A는 수평 감쇠판의 영향을 판단하기 위한 기준 부유체로 수평 감쇠판이 없는 일반 직사각형 폰푼 부유체이며, B와 C는 수평 감쇠판 존재 및 크기 규모에 따른 부유체의 운동 응답 영향을 분석하기 위해 고안하였다. 수리 실험 시 같은 유형의 부유체 모형을 Fig. 3(a)와 같이 가로 방향으로 3개씩 배치하고 각 부유체를 힌지로 연결하여 실험체 간 수평 및 수직 운동은 상호 구속되나, 회전에 대해서는 자유롭게 운동할 수 있도록 하였다. 또한 실험체의 운동 계측을 위한 계측기를 비롯한 제반 도구를 배치할 수 있도록 지그를 제작 설치하였으며, 실험체는 계류선을 통해 지그에 연결되도록 하였다(Fig. 3(b) and Fig 3(c)). 여기서 실험체의 계류 방식은 이완계류(Catenary mooring) 또는 긴장계류(Tension leg mooring)에 해당하지 않으며, 계류선이 지그 프레임의 고정 도르래와 계류선 끝단에 강성이 낮은 스프링(Stiffness: 58 N/m)를 통해 부유체가 최대한 자유 운동에 가깝게 움직일 수 있도록 하였다(Fig. 4 and Fig. 5).
Test model setup.
Photos for wave basin and model test.
Schematic diagram for the motion of the floating structure and the definition of mixed displacement.
2.2 실험시설 및 파랑조건
수평 감쇠판이 부착된 폰툰형 부유체와 일반 폰툰형 부유체의 수리 거동을 구현하기 위해 한국건설기술연구원 방파제실험동에서 수리실험을 수행하였다. 해당 실험수조의 제원은 가로와 세로가 각각 50 m, 깊이가 1.2 m이며, 평면조파 제어시스템을 통해 규칙 및 불규칙 조건의 입력 파랑의 조파가 가능하다(Fig. 4). 본 실험시설 내 조파기를 통해 Table 2에 나타낸 파랑을 재현하였으며, 구조물 설치 수심을 0.5 m로 하였다. 입사파향에 따른 실험체의 거동을 조사하기 위해 파향선을 기준으로 0o 및 45o 방향으로 Table 1의 실험체를 배치해 실험을 실시하였다. Table 2에 나타낸 규칙파와 불규칙파 실험체의 변위를 측정하였으며, 규칙파와 불규칙파의 조파 지속시간은 각각 3분, 5분이며, 실험 케이스당 1회 응답을 측정하였다.
Regular and irregular wave conditions
2.3 부유체 운동에 대한 수평 감쇠판의 영향 평가 방법
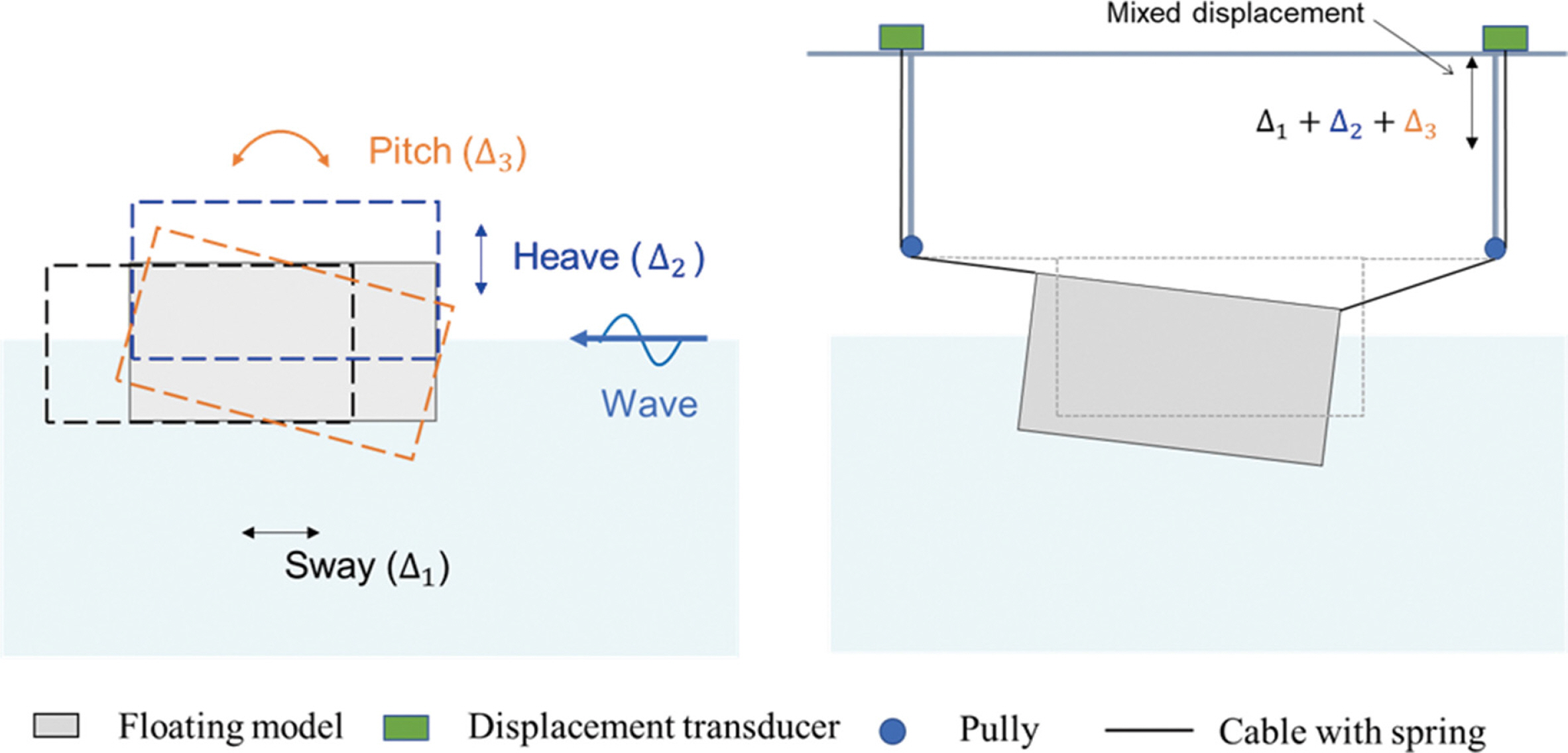
수평 감쇠판 부착에 따른 부유체 운동 저감 효과를 확인하기 위해 계류선 스프링과 전기저항식 변위계를 연결하여 Fig. 5와 같이 케이블의 수직 변위량을 계측하였다. 여기서 Fig. 5는 지그에 부착된 실험체의 운동 및 계측을 설명하기 위한 모식도이다. Fig. 5에 나타낸 계측장비의 성능 및 설치의 한계로 인해 입사 파랑에 대한 실험체의 복합적인 거동이 계측되므로, Sway, Heave, Pitch 등에 대한 개별 거동 측정은 불가능하며 운동 성분별로 응답 특성 변화를 추적하는 것은 한계가 있다. 따라서 실험 계측 결과는 파랑 진행 방향에 대해 실험체에서 발생할 수 있는 복합 변위(Mixed displacement)를 사용해 부유체의 운동 응답을 계측하였다. 복합변위는 부유체의 6자유도 운동이 모두 합쳐진 전체적인 운동을 의미한다. 따라서 부유체의 6자유도 성분별로 구체적인 운동 저감 효과를 규명하기에는 부족하지만, 본 논문의 주요 목적인 수평 감쇠판 도입에 따른 부유체의 전반적인 운동 저감 효과를 평가하기 위한 물리량으로는 충분히 활용 가능하다.
추가로 본 실험은 Fig. 3과 같이 3개 부유체를 힌지로 연결해 부유체별로 응답을 계측할 수 있게 설계하였으나, 좌우 외측 부유체의 계측 결과는 중앙 부유체 대비 대표적인 운동 응답을 나타내기 어렵다고 판단된다. 따라서 Fig. 3에 나타낸 8개 변위계 중 중앙 실험체에 부착된 4개로부터 계측된 운동 응답을 이용하여 수평 감쇠판의 영향을 평가하였다. 먼저, 중앙부 4개 변위계의 시간 이력 응답에 대한 진폭 평균값(average level)을 실험체별로 각각 산정하였다(Fig. 3(a): D2, D3, D6, D7). 다음으로, 실험체별 4개 변위계의 진폭 평균값을 평균하였으며, 이를 실험체의 파랑 조건별 동적 거동에 대한 대표값인 운동 지수로 활용하였다. 여기서 운동 지수는 측정된 복합 변위 응답 진폭 평균에 대한 평균이므로, 단위는 mm 이며, 파랑조건에 대한 진폭 최댓값 대신 평균값을 사용한 이유는 실험체의 동적 응답에 대한 극단값의 영향을 배제하기 위함이다. 위와 같이 산정된 실험체 간 운동 지수를 비교함으로써 수평 감쇠판 길이가 부유식 구조물의 운동 응답 감소에 미치는 영향을 분석하였다.
3. 실험 결과
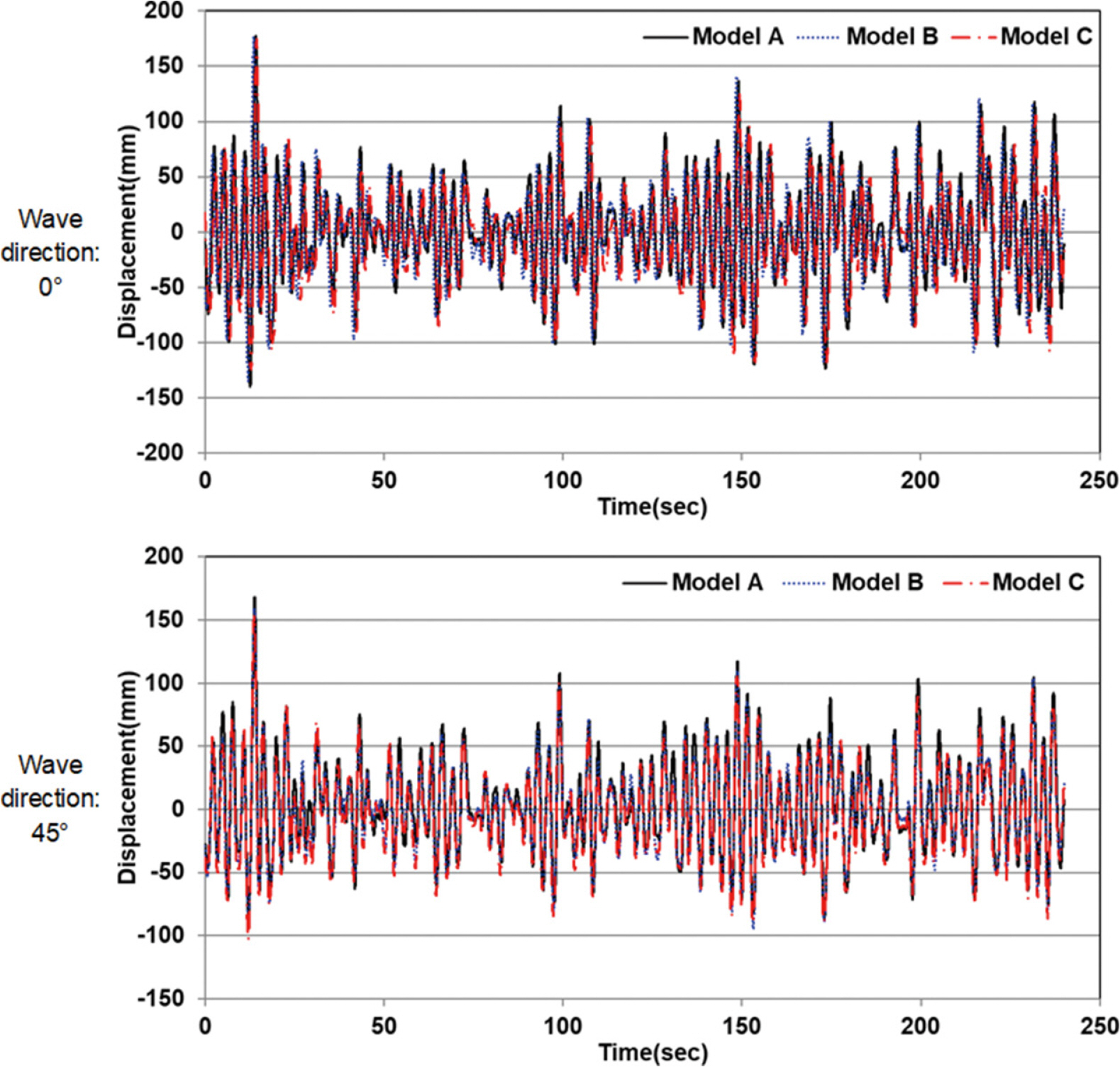
Figs. 6과 7은 Table 2의 여러 규칙파와 불규칙파 조건 가운데 각각의 4번 파랑하중케이스에 대한 실험체 A, B, C에서 복합 변위 응답을 보여준다. 먼저 Fig. 6은 규칙파 조건에서의 실험체 응답으로 운동 주기가 파랑 주기에 근사하게 나타나며, 응답 진폭도 규칙적인 특성을 보여주었다. 최대 진폭은 규칙파의 경우 파랑 방향 0o와 45o에 대해 100 mm, 75 mm 전후의 진폭을 나타내었으며, 불규칙파의 경우, 파랑 방향에 관계없이 최대 150 mm 전후의 진폭을 나타냈다.
Vertical displacements of models: Case 4 of regular wave condition (RE4).
Vertical displacements of models: Case 4 of irregular wave condition (IR4).
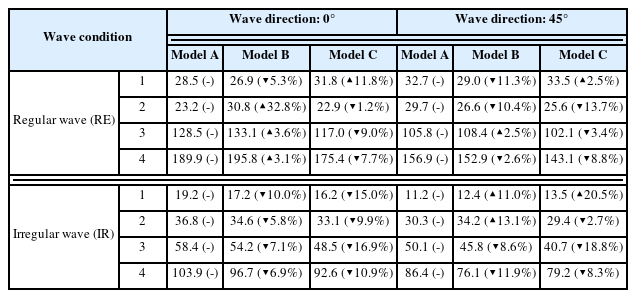
나머지 규칙파 및 불규칙 파랑 조건에 대한 실험체의 응답 또한 유사한 경향을 보여주었으며, 전체 파랑 조건에 대한 실험체 A, B, C의 운동 지수를 산출해 Table 3에 나타냈다. 수평 감쇠판이 있는 부유체 입사 파랑의 방향이 0o 일 때 규칙파와 불규칙파에 대해 약 5.3~9.0% 및 5.8~16.9%의 진폭 저감 효과를 각각 보였고, 입사방향이 45o 일 때 2.6~13.0% 및 2.7~18.8%의 진폭 저감 효과를 나타내었다. 그러나 응답이 오히려 증가하는 결과도 확인되었다. 파랑 방향 0o 일 때 규칙파에 대해 3.1~32.8%, 파랑방향 45o 일 때 규칙파와 불규칙파에 대해 각각 2.5%, 11.0~20.5%의 폰툰형 대비 응답 증폭이 확인되었다. 비록 실험체 응답의 감소와 증폭이 혼재되어 있으나, 실험체에 대한 16개 파랑 조건 가운데 Model B와 Model C의 응답이 감소한 파랑 케이스가 각각 10, 13건이고, 파랑방향 0o의 RE2와 파랑방향 45o의 IR1과 IR2를 제외하고 폰툰형 대비 응답 증폭이 5% 이하이다. 따라서 전반적으로 수평 감쇠판 도입에 따른 부유체의 운동 저감 효과는 존재하는 것으로 판단되며, 저감율의 최대/최소값을 제외하면 폰툰형 대비 5~10%의 응답 진폭 감소 효과가 있다고 파악된다.
Motion index of test models for regular and irregular wave conditions (unit: mm).
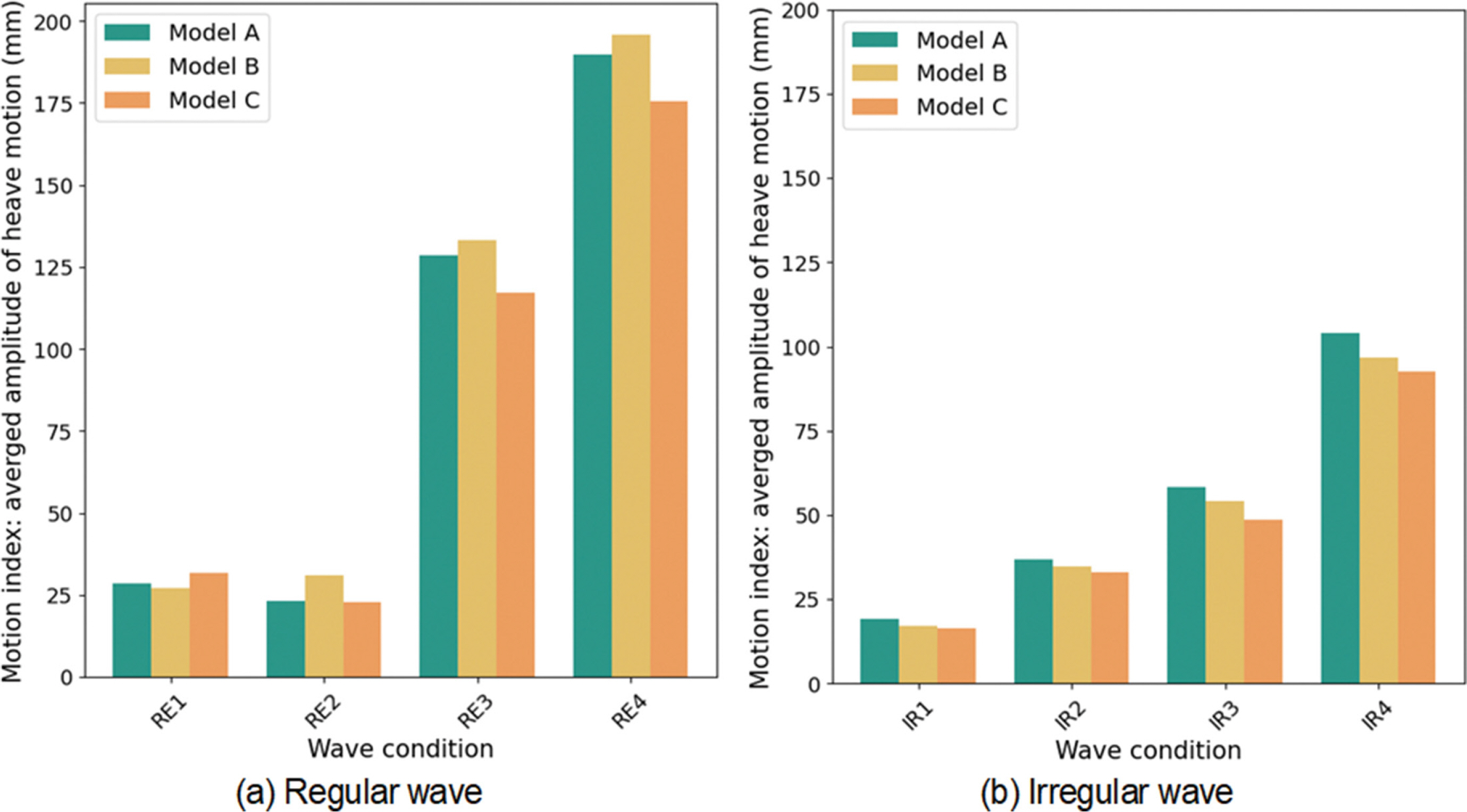
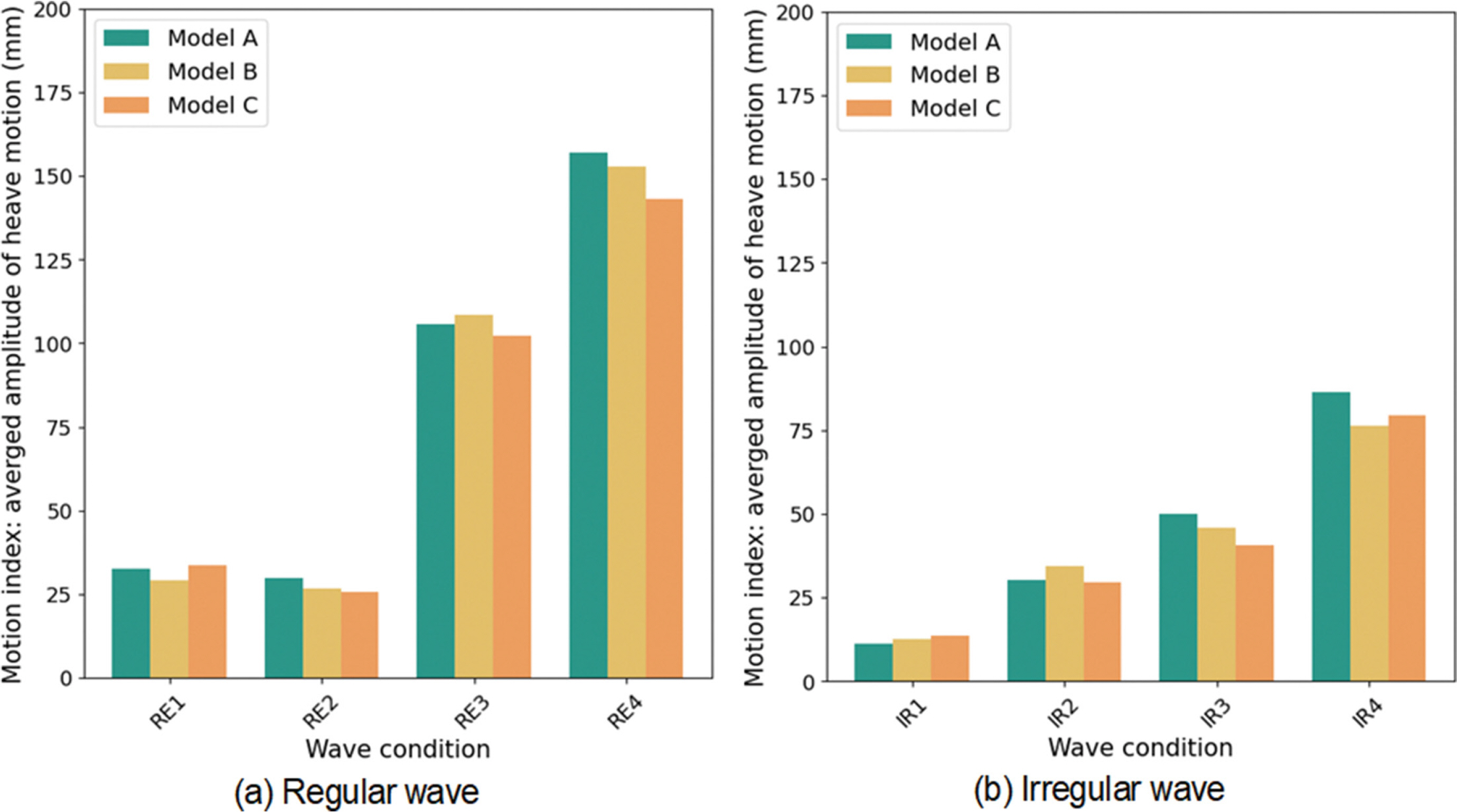
그러나 폰툰형 부유체(Model A) 대비 수평 감쇠판 길이 변화에 비례한 운동 감소 효과는 확인하지 못하였다. 이러한 결과는 Fig. 8과 Fig. 9의 파랑 조건별 운동 지수를 통해 명확히 확인된다. 수평 감쇠판의 길이가 증가할수록 평균 운동 진폭이 일관되게 감소하는 현상은 파랑방향 0o의 IR1~ IR4 조건에서만 존재하였고, 파랑방향 45o 조건에서 평균 운동 진폭 감소는 RE2, RE4, IR3, IR4에서만 확인되었다. 나머지 파랑조건에 대한 실험체의 응답은 수평 감쇠판 적용에 따라 오히려 응답이 모두 증가하거나(파랑방향 45o의 IR1), 응답의 증감이 혼재되고 있다. 파고가 높고 장주기일수록 최대 응답 진폭이 증가하는 경향이 있음을 확인할 수 있으나, 파장 대비 파고 비에 대한 상관성은 응답 경향성은 확인되지 않았다. 규칙파의 경우 파랑 방향이 0o일 때 실험체의 평균 진폭이 45o 대비 크게 나타났으나, 불규칙파는 IR4 조건을 제외하고 실험체의 평균 진폭의 크기는 유사하였다. 수평 감쇠판 적용에 따른 효과는 Table 3에 나타낸 바와 같이 일관성을 확인하기 어려웠으나, 수평 감쇠판의 길이가 가장 긴 Model C는 RE1를 제외하고 폰툰형 대비 모두 감소하고 있어 파랑주기 9초 이상에서 운동 저감 효과가 있음을 보여주고 있다. 반면 수평 감쇠판의 길이가 Model C의 절반인 Model B는 일관된 경향성을 보이지 못하였고, 오히려 평균 응답이 증가한 경우가 확인되고 있다.
Comparison of motion index: wave direction of 0°.
Comparison of motion index: wave direction of 45°.
상기의 실험결과 분석을 통해, 전반적으로 수평 감쇠판 도입을 통해 부유체의 운동 응답을 감소시키는 효과가 확인되나 일관된 경향성이 나타나지 않는 원인은 다음과 같이 추정된다. 첫째로 실험 특성상 완벽한 설계 파랑의 재현에는 한계가 존재하므로, 실험체 응답 측정 시 일부 반사파 잔존 등이 계측 결과에 영향을 미쳤을 가능성이 있다. 둘째로, 파랑 주기 대비 수평 감쇠판의 크기가 작아 감쇠 효과가 분명하게 드러나지 못했을 가능성이 있다. 감쇠판이 부착된 원통형 부유체에 대한 기존 연구 결과(Cho, 2011; Lim et al., 2015)는 감쇠판의 크기가 일정 이하이면 감쇠판의 운동 저감 효과는 미미하나 일정 이상부터 감쇠 효과가 크게 증가함을 밝히고 있다. 비록 이들 연구가 비점성 유체 및 심해파 조건의 수치해석 모델을 사용해 직접적인 비교는 어렵겠으나, 본 실험의 수평 감쇠판의 길이 영향의 경향성이 뚜렷하게 나오지 못한 원인 중 하나로 본 구조체(폰툰) 대비 감쇠판의 크기가 파랑 조건 대비 충분히 크지 않았을 가능성이 있다. 가령, Lim et al.(2015)의 경우 원통형 부유체 직경 대비 감쇠판 길이 비를 달리하여 원통형 부유체 대비 Heave Response Amplitude Operator(RAO) 변화를 분석하였는데, 직경 대비 감쇠판 길이비가 1.25 이하일 때는 원통형 대비 Heave RAO가 증가하였으나 1.25 이상부터는 원통형 대비 작아지며 감쇠판의 길이 증가가 운동 응답의 감소로 이어졌다. 선행 연구 결과의 분석을 통해 감쇠판의 길이가 응답 감소에 유리할 것으로 판단되나, Park et al.(2022)이 언급한 바와 같이 부유체로 둘러싸인 유체 영역에서의 유체 공진이 가능하므로 수평 감쇠판의 길이 증가가 반드시 부유체의 안정성으로 연결되지 않을 수 있다. 따라서 대상 해역의 파랑 주기 범위를 고려한 수평 감쇠판의 적정 길이 선정이 필요할 것으로 판단된다.
4. 결 론
본 논문은 수평 감쇠판을 부착한 폰툰형 부유체의 운동 저감 효과를 분석하기 위해 수리실험을 수행하였다. 감쇠판의 도입 효과를 분석하기 위해 서로 다른 길이의 감쇠판이 부착된 축소 실험체를 3차원 조파수조에 설치하고 규칙파 및 JONSWAP 스펙트럼을 적용한 불규칙파 조건에서의 운동 저감 효과를 비교 분석하였다. 규칙파 및 불규칙파에서의 실험체 운동은 감쇠판 도입으로 인해 여러 파랑 조건에서 폰툰형 대비 전반적으로 응답이 감소하는 경향을 확인할 수 있었으나, 감쇠판 길이 변화에 따른 뚜렷한 경향성은 확인할 수 없었다. 부유체 관련 선행연구 결과와의 비교 분석을 통해 폰툰형 부유체의 감쇠판 도입을 통한 자세 안정성 개선 시 설치 해역의 파랑 주기를 고려한 수평 감쇠판의 길이 선정이 필요함을 확인할 수 있었다.
본 연구는 폰툰형 부유체의 수평 감쇠판 적용 효과 및 도입 가능성을 실험적으로 확인할 수 있었다는 점에서 의미가 있다고 판단하며, 폰툰형 부유체의 자세 안정성 개선에 참고할 수 있는 기초자료로 활용이 가능할 것으로 판단된다. 본 연구의 구조물은 정온도가 확보된 항내에서 부유식 방파제로의 사용 목적으로 설계되었으며, 이에 따라 실험도 대상 지역(항내)에서 발생 가능한 파랑 조건을 대상으로 하였다. 본 실험 통해 확인한 정온 해상조건에서의 수평 감쇠판에 의한 부유체 동요 저감 효과에 근거하여, 보다 험한 해상조건으로의 확장 적용도 기술적으로 가능할 것으로 판단된다. 본 연구는 계측 방법의 제약으로 수평 감쇠판에 의한 부유체 운동 저감 효과를 복합 변위로 평가하였다. 수평 감쇠판 도입으로 인한 전반적인 부유체 운동 변화를 정량화 하였으나, 복합 변위 사용으로 인해 특정 운동 성분별 감소 효과까지는 규명하지 못하여, 수평 감쇠판에 의한 주요한 운동 응답 저감 매커니즘까지 도출할 수 없었다. 향후 여러 실험 및 수치 해석 등의 연구를 통해 다양한 파랑 및 수평 감쇠판 조건의 폰툰형 부유체의 응답을 평가할 필요가 있으며, 이를 바탕으로 폰툰형 부유체에 대한 수평 감쇠판의 적용 효과를 보다 명시적으로 규명할 수 있을 것으로 생각된다.
Acknowledgements
본 연구는 서울대학교 부유식인프라연구단을 통한 국토교통부/국토교통과학기술진흥원(과제번호 RS-2023-00250727, 신소재 기반 부유식 구조체 기술개발) 및 과학기술정보통신부/한국건설기술연구원의 연구비지원사업(과제번호 2023-001, 하이브리드 부유체의 해상 적용성 확장을 위한 모듈연결 및 자세 안정성 향상 기술개발)의 지원을 받았습니다.