해양 및 대기 순환 수치모델에 사용하는 연직 좌표계에 대한 고찰

A Review on the Vertical Coordinate Systems used in Oceanic and Atmospheric Circulation Numerical Model

Article information

J Korean Soc Coast Ocean Eng. 2024;36(4):158-166

Publication date (electronic) : 2024 August 31

doi : https://doi.org/10.9765/KSCOE.2024.36.4.158

HyukJin Choi ^*, Shin Taek Jeong^,^**, Hong-Yeon Cho ^***, Dong-Hui Ko ^****

^*Chief Executive Officer, Coast and Ocean Technology Research Institute

^**Advisor, Coast and Ocean Technology Research Institute, A-2511 Hyundai Knowledge Industrial Center, 70 Dusan-ro Geumcheon-gu, Seoul 08584, Korea

^***Principal Research Scientist and Professor, Marine Bigdata and AI Center, Korea Institute of Ocean Science and Technology, Univ. of Science and Technology

^****Principal Research Scientist, Ocean Space Development and Energy Research Department, Korea Institute of Ocean Science and Technology

최혁진^*, 정신택^,^**, 조홍연^***, 고동휘^****

^*(주)해안해양기술 대표

^**(주)해안해양기술 고문

^***한국해양과학기술원 해양빅데이터·AI센터 책임연구원

^****한국해양과학기술원 해양공간개발·에너지연구부 책임연구원

Corresponding author: Shin Taek Jeong, Advisor, Coast and Ocean Technology Research Institute, A-2511 Hyundai Knowledge Industrial Center, 70 Dusan-ro Geumcheon-gu, Seoul 08584, Korea, Tel: +82-2-2104-6632, Fax: +82-2-2104-6601, stjeong@wku.ac.kr

Received 2024 July 29; Revised 2024 August 23; Accepted 2024 August 23.

Abstract

순환 모델 연구를 위한 수치 방법에서는, 증가하는 온실가스 배출에 대한 해양과 대기의 물리적 반응을 모의하기 위해 다양한 연직 좌표계를 사용한다. 본 연구에서는 해양 및 대기 순환 수치모델에 자주 사용하는 4종류의 연직좌표계, 즉 고도, 일반, 압력, 그리고 무차원 연직좌표계에 대하여 소개한다. 최종적으로, 연직좌표계로 표현된 정수압 방정식, 연직속도, 수평방향 운동방정식, 그리고 연속방정식을 도입하고, 연직좌표계에 대한 장단점을 정리하여, 수치모형 개발 정확성을 도모하였다.

Trans Abstract

In a numerical method for the study of the circulation model, various vertical coordinate systems are used to simulate the physical response of the ocean and atmosphere to the increasing greenhouse gas emission. In this study, four types of vertical coordinate systems frequently used in oceanic and atmospheric circulation numerical models, i.e., height, general, pressure, and normalized vertical coordinate systems, respectively are introduced. Finally, the hydrostatic pressure equation, vertical velocity, equation of horizontal motion, and continuity equation expressed in a vertical coordinate system were introduced, and the pros and cons of the vertical coordinate system were summarized to promote the accuracy of numerical model development.

Keywords: 순환 모델; 연직 좌표계; 정수압 방정식; 연직속도; 수평방향 운동방정식; 연속방정식

Keywords: the circulation model; vertical coordinate systems; hydrostatic pressure equation; vertical velocity; equation of horizontal motion; continuity equation

1. 서론

최근 기후변화로 인하여 세계 해수면 상승은 급격히 가속화되고 있으며, 이러한 해수면 상승은 직접적으로 국토유실과 연안지역의 침수와 범람 위험을 증가시키는 요인이 된다. 이에 따라 IPCC 제6차 보고서의 SSP(Shared Socioeconomic Pathways)를 적용한 우리나라 주변 해역의 해수면 상승에 대한 관심이 고조되고 있다.

해양 및 대기의 운동은 유체역학, 열역학방정식 등으로 설명되는 물리 법칙의 적용을 받는다. 이러한 기본방정식들은 잘 알려져 있으나 비선형 편미분방정식 형태가 대부분이기 때문에 수치해석을 이용하여 구한 수치해를 이용하여 자연현상을 규명하고 있다. 산이나 연안 등의 지형을 대상으로, 유한차분 수치해석을 적용하는 경우, 절단오차를 제거하는 것이 불가능하다. 따라서 지형과 연직좌표계 선택을 통합하여 신중하게 검토한다.

대기 및 해양모델링에 있어서 다양한 연직좌표계를 사용하고 있다. 수치모델링시 연직 좌표계로서는 직교좌표계에서 연직상향 방향을 기준으로 하는 z 좌표계를 많이 사용하였다. 그러나, 연직좌표계로서 압력 연직 좌표계를 사용하면 정수압 근사 등의 관계식이 매우 간단하게 표현되는 등의 장점이 있기 때문에, 다양한 연직좌표계에 대한 이론적 연구를 수행한다.

Sutcliffe(1947)은 고도를 연직축으로 사용하는 z좌표계를 대신하여 압력 p를 연직축으로 사용하는 방법을 제안하였다. 이 방법은 저면 경계조건을 항상 격자와 일치시켜 오차를 축소하는 방법으로 이후 다양한 방법이 제시되었다. Phillips(1957)는 압력을 무차원화한 변수 v를 도입하였고, 이후 고도를 무차원화한 변수, 등온위를 무차원화한 변수 등 다양한 방법으로 변형된 연직 좌표계를 제시하였다(Kasahara, 1974; Sundqvist, 1979). Arakawa and Lamb(1977), Simmons and Burridge(1981), Arakawa and Konor(1996) 등은 혼합 좌표계를 사용한 수치모형을 제시하였다. 한편, 다양한 연직좌표계를 해양모델링에 적용한 예는 Kowalik and Murty(1993), Haidvogel and Beckmann(1999), Mellor et al.(2002), Chandrasekar(2022) 등이 있다. 본 연구에서는 주로 대기 및 해양모델링에서 사용하는 다양한 연직좌표계에 대하여 검토하였다.

유체역학에 사용하는 기본방정식과 다양한 연직좌표계를 검토하고, 부록 A-D에서는 주요 관계식 유도 과정을, 부록 E에서는 사용한 기호를 정리하였다.

2. 고도 연직좌표계를 이용하여 표현한

기본 방정식 동쪽, 북쪽, 그리고 상향 방향을 양으로 하는 직교좌표계 x, y, z와 시간 t를 사용하여 수평방향 운동방정식을 기술하면 다음과 같다.

(1a) dVdt+fk+V=-1ρ∇p+F

단,

(1b) V=ui+vj,∇=i∂∂x+j∂∂yddt=∂∂t+V⋅∇+w∂∂z

여기서, i, j, k는 각각 x, y, z 축 방향의 단위벡터; ∇는 수평방향 델 연산자, V는 수평방향 속도, u와 v는 V의 x, y 방향 속도 성분, w는 연직 속도, d/dt는 전미분, f는 코리올리 매개변수(≡ 2Ωsinζ), Ω는 지구 자전 각속도, ζ는 고도, ρ는 밀도, p는 압력 그리고 F는 단위 질량당 마찰력이다.

정수압 방정식은 다음과 같다.

(2) ∂p∂z=-ρg

여기서, g는 중력가속도이고, 식(2)는 연직방향 운동의 좋은 근사식이 된다. 정수압 방정식(2)는 높이와 압력을 연결하는 관계를 제공하여 다양한 연직좌표계에서 많이 사용하고 있다.

한편, 연속방정식은 다음과 같다(부록 A 참조).

(3a) ddtlnρ+∇⋅V+∂w∂z=0

또는,

(3b) ∂ρ∂t+∇⋅(ρV)+∂(ρw)∂z=0

고도 연직좌표계(Height vertical coordinate system, or Geometric vertical coordinate system)로 표현된 기본방정식들은 간단하고 잘 알려져 있지만, 수치모델링을 하는 경우, 격자 선정에 따른 지형 및 경계조건 처리시 문제가 발생하기 때문에 주의가 필요하다(Kasahara, 1974).

3. 일반 연직좌표계를 이용하여 표현한 기본 방정식

변환된 좌표계를 이용하여 표현한 물리적인 값들은 원래 좌표계를 사용하여 표현한 경우와 동일하여야 한다. 정수압 방정식(2)를 보면 고도에 따른 압력변화가 단조 감소하는 것을 알 수 있다. 따라서 원좌표계인 고도를 대신하여 압력(pressure, p)을 변환 좌표계로 활용할 수 있고, 이는 다양한 종류의 지배방정식을 단순화할 수 있는 장점을 갖는다. 압력과 같이 새로운 좌표계로 변환하는 경우, 임의의 새로운 변수 s를 고려할 수 있다.

z – system은 독립변수 x, y, z, t로 구성된 고도 좌표계로 가정하고, 반면에 s – system은 독립변수 x, y, s, t로 구성된 일반 연직좌표계(generalized vertical coordinate system)로 가정하면 다음 식(4), (5)와 같이 표현된다.

(4) s=s(x,y,z,t)

(5) z=z(x,y,s,t)

이 경우, 임의의 종속변수 A(예를 들면, u, v, w, ρ, p 등)는 식 (6), (7)과 같이 표현된다.

(6) A(x,y,s,t)=A[x,y,z(x,y,s,t),t]

(7) A(x,y,z,t)=A[x,y,s(x,y,z,t),t]

새로운 좌표계 s를 이용하여 편도함수를 표현하면 식(8), (9)와 같다.

(8) ∂A∂s=∂A∂z∂z∂s

(9) ∂A∂z=∂A∂s∂s∂z

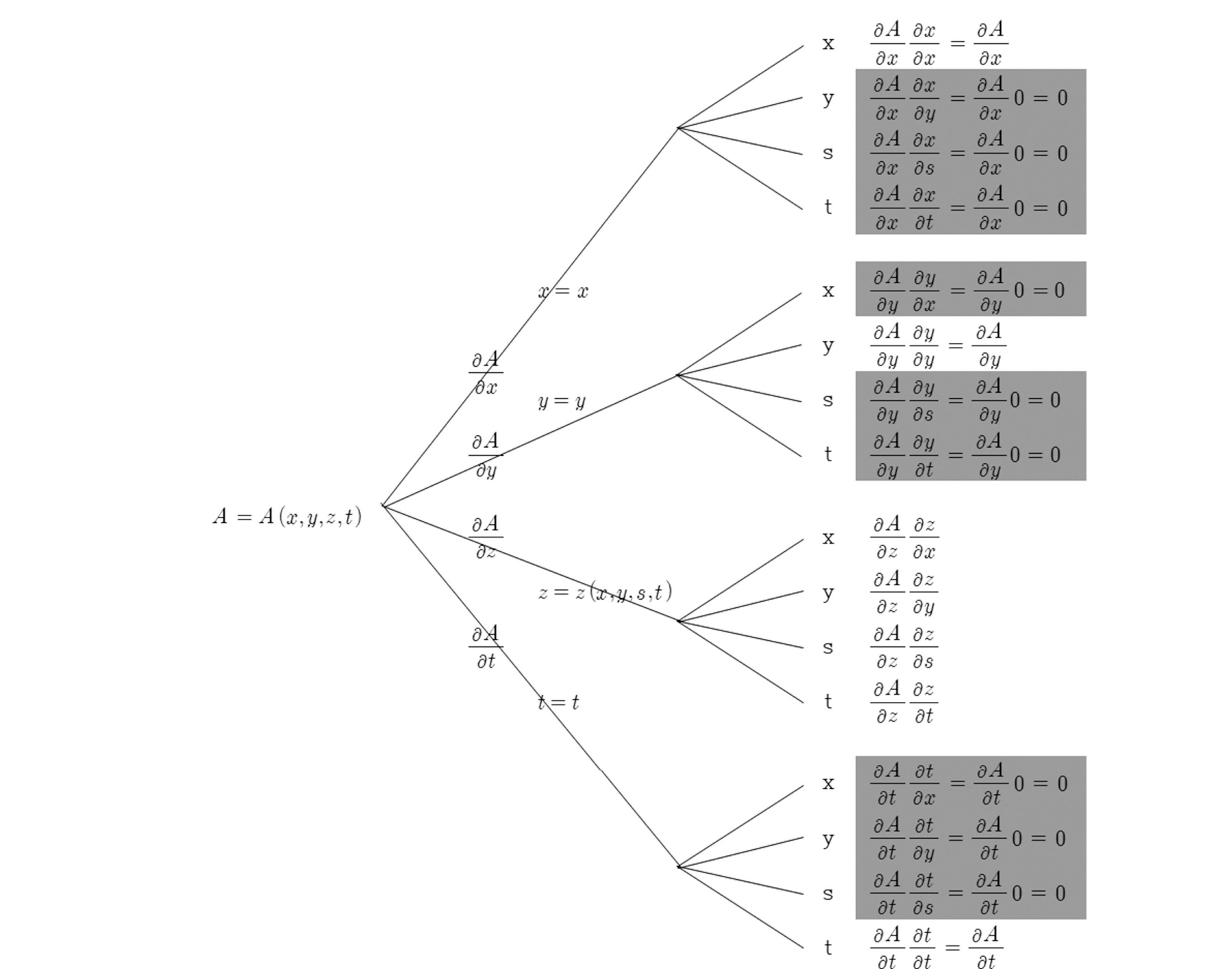
종속변수 A의 c(여기서 c는 x, y, 혹은 t)에 대한 편도함수는 chain rule을 이용하여 다음과 같이 표현된다.

(10) (∂A∂c)s=(∂A∂c)z+∂A∂z(∂z∂c)s

(11) (∂A∂c)z=(∂A∂c)s+∂A∂s(∂s∂c)z

위 식들의 아래 첨자 s, z는 편미분시 이들 첨자 변수를 상수로 간주한다는 것을 의미하며, 식(10), (11)은 식(8), (9)를 사용하면 식(12), (13)으로 표현된다(부록 B 참조).

(12) (∂A∂c)s=(∂A∂c)z+∂s∂z(∂z∂c)s∂A∂s

(13) (∂A∂c)z=(∂A∂c)s+∂z∂s(∂s∂c)z∂A∂z

한편, 편미분 관계식(10), (11)을 이용하면 종속변수 A의 수평 방향 기울기(∇A)는 다음 식과 같이 된다.

(14a) ∇sA=∇zA+∂A∂z∇sz

(14b) ∇zA=∇sA-∂A∂z∇sz

(15a) ∇zA=∇sA+∂A∂s∇zs

(15b) ∇sA=∇zA-∂A∂s∇zs

편미분 관계식(12)를 이용하면 변수 A의 수평방향 기울기는 다음 식과 같이 된다.

(16a) ∇sA=∇zA+∂s∂s∂A∂s∇sz

(16b) ∇zA=∇sA-∂s∂z∂A∂s∇sz

식(10), (11)에서 변수 c를 t로 바꾸면, 다음과 같은 시간 미분 관계식을 구할 수 있다.

(17) (∂A∂t)s=(∂A∂t)z+∂A∂z(∂z∂t)s

(18) (∂A∂t)z=(∂A∂t)s+∂A∂s(∂s∂t)z

식(9), (15a), (18)을 식(1b)에 대입하여 정리하면 다음과 같이 새로운 좌표계 s에 대한 전미분 관계식을 구할 수 있다.

(19) dAdt=(∂A∂t)z+V⋅∇zA+w∂A∂z =[(∂A∂t)s+∂A∂s(∂s∂t)z]+V⋅[∇sA+∂A∂s∇zs]+w(∂A∂s∂s∂z) =(∂A∂t)s+V⋅∇sA+[(∂s∂t)z+V⋅∇zs+w∂s∂z]∂A∂s

일반 연직좌표계에서의 전미분은 정의로부터 다음 식(20)과 같이 표현된다.

(20) dAdt=(∂∂t)s+V⋅∇sA+s˙∂A∂A

여기서, ṡ (= ds/dt)는 일반 연직좌표계에서의 연직유속이다.

ṡ 와 z축 좌표계에서의 연직유속 w (= dz/dt)와의 관계식은 식(19)와 식(20)을 비교하여 다음과 같이 표현된다.

(21a) s˙=dsdt=[(∂s∂t)z+V⋅∇zs+w∂s∂z]

이 식은 z축 좌표계에서의 연직유속 w를 대신하는 일반 연직좌표계에서의 연직유속 ṡ 이다. 한편, 식(14b), (17)을 식(21a)에 대입하여 정리하면, 다음과 같이 표현된다(Kasahara, 1974).

(21b) s˙=dsdt=(∂s∂t)z+V⋅∇zs+w∂s∂z =[(∂s∂t)s-∂s∂z(∂z∂t)s]+V⋅[∇ss-∂s∂z∇sz]+w∂s∂z =w∂s∂z-∂s∂z(∂z∂t)s-V⋅∂s∂z∇sz+[(∂s∂t)s+V⋅∇ss]s˙=dsdt=∂s∂z[w-(∂z∂t)s-V⋅∇sz]

기본방정식들을 새로운 s 좌표계를 사용하여 표현하면 다음과 같다.

1) 정수압 방정식(식(2)와 식 (8) 사용)

(22) ∂p∂s=∂p∂z∂z∂s=-ρg∂z∂s

2) 수평방향 운동방정식(식(1a)와 식 (16b) 사용)

(23) dVdt+fk×V=-1ρ∇sp+1ρ(∂s∂z)∇zz∂p∂s+F

또한, 정수압 방정식(22)를 식(23)에 대입하여 정리하면 다음과 같은 정수압 평형상태의 수평방향 운동방정식을 구할 수 있다.

(24) dVdt+fk×V=-1ρ∇sp-g∇sz+F

3) 연속방정식(식 (3a), (12) 사용, 부록 C 참조)

(25) [∂∂t(ρ∂z∂s)]s+∇s⋅(ρV∂z∂s)+∂∂s(ρs˙∂z∂s)=0

또한, 정수압 평형상태의 연속방정식은 식(22)를 식 (25)에 대입하여 다음과 같이 표현된다.

(26) [∂∂t(ρ∂z∂s)]s+∇s⋅(ρV∂z∂s)+∂∂s(ρs˙∂z∂s)=0[∂∂t(-1g∂p∂s)]s+∇s⋅(-V1g∂p∂s)+∂∂s(-1gs˙∂p∂s)=0[∂∂t(∂p∂s)]s+∇s⋅(V∂p∂s)+∂∂s(s˙∂p∂s)=0[∂∂s(∂p∂t)]s+∇s⋅(V∂p∂s)+∂∂s(s˙∂p∂s)=0

4. 압력 연직좌표계를 이용하여 표현한 기본 방정식

압력은 고도를 대신하여 사용하기 편리한 수직 좌표계이다. 정수압 근사법을 사용하는 경우 압력과 고도 사이의 관계는 정수압 방정식(2)로 표현된다. 고도 연직좌표계에서 연직 속도, w는 dz/dt로 정의하였으나, 압력 연직좌표계(Pressure vertical coordinate system), p에서 연직속도는 ω ≡ dp/dt로 정의하며, 단위는 Pa/s이다. w와 ω의 관계 식은 다음과 같다.

(27) ω=dpdt=∂p∂t+u∂p∂x+v∂p∂y+w∂p∂z

정수압 상태를 가정하면 위의 식은

(28) ω≃-ρgw

가 된다. 압력 연직좌표계 p에서 전미분은 다음과 같다.

(29) ddt=(∂∂t)p+V⋅∇p+(ω∂∂p)p

기본방정식들을 새로운 p 연직좌표계를 사용하여 표현하면 다음과 같다.

1) 정수압 방정식

(30) ∂φ∂p=-α

여기서, Φ는 geopotential(Φ = gz), a는 비체적(a = 1/ρ)이다.

2) 수평방향 운동방정식(식(23)에 s = p 대입)

(31) dVdt+fk×V=-1ρ∇pp+1ρ(∂p∂z)∇pz∂p∂p+FdVdt+fk×V=-g∇pz+F

3) 연속방정식(식(25)에 s = p 대입, 혹은 식(26)에 s = p 대입)

(32) [∂∂t(ρ∂z∂p)]p+∇p⋅(ρV∂z∂p)+∂∂p(ρp˙∂z∂p)=0∂ρ∂t∂z∂p+ρ∂∂t(∂z∂p)+∇p⋅(ρV∂z∂p)+∂∂p(ρp˙∂z∂p)=0∂z∂p∂p∂t+∇p⋅(ρV∂z∂p)+∂∂p(ρp˙∂z∂p)=0(-1ρg)∂ρ∂t-1g∇p⋅V-1g∂∂pp˙=0∇p⋅V+∂ω∂p=0

식(31), (32)는 정수압 평형상태와 동일한 관계식이다. 부록 D에 식 (32)를 유도하는 다른 방법을 정리하였다.

5. 무차원 압력좌표계를 이용하여 표현한 기본 방정식

압력 연직좌표계는 지형적인 변화가 큰 지역(산 혹은 연안 등)을 수치모의하는 경우, 하단 경계조건의 복잡성 때문에 문제가 발생한다. 이러한 문제를 해결하기 위하여 무차원 압력(Normalized pressure coordinate system), 즉 ‘시그마(σ)’를 도입하여(Phillips, 1957), 지구의 표면과 격자면이 일치하도록 모형을 구성한다. 여기서, σ = p/p_s이고, p_s(x, y, t)는 지표면 압력이다. 지표면에서는 σ = 1이고, 상단에서는 p= 0, σ = 0이므로, 상단 및 하단 경계조건은 σ˙=0이다. 보다 일반적으로는 상단면 압력 p_T가 일정하다고 가정하는 경우,

(33) σ=p-pTps-pT=p-pTπ

로 표현된다(Kasahara, 1974; Kalnay, 2002). p_T = 0까지 상단 경계를 확장하는 경우, 식(33)은 Phillips(1957)가 제안한 식과 동일하다. 연직방향 속도 σ˙는 식(33)을 시간에 대하여 미분하여 다음과 같은 결과를 얻을 수 있다.

(34) σ˙=ddt(p-pTπ)=1π2[π(dpdt-dpTdt)-(p-pT)dπdt] =1π2[πdpdt-(p-pT)dπdt] =1π[dp-(p-pT)πdπdt]σ˙=1π(dpdt-σdπdt)

식(33)으로부터 ∂p/∂σ = π이므로, 이 관계식을 이용하여 기본방정식들을 새로운 σ 좌표계를 사용하여 표현하면 다음과 같다.

1) 정수압 방정식

(35) ∂φ∂σ=∂φ∂p∂p∂σ=-σπ

2) 수평방향 운동방정식(식(23)에 s = σ 대입)

(36) dVdt+fk×V=-1ρ∇σp+1ρ(∂σ∂z)∇σz∂p∂σ+F

또한, 정수압 평형상태의 수평방향 운동방정식은(24)에 s = σ를 대입하여 구할 수 있다.

(37) dVdt+fk×V=-σ∇πρ-g∇σz+F

3) 연속방정식(식(25)에 s = σ 대입)

(38) [∂∂t(ρ∂z∂σ)]σ+∇σ⋅(ρV∂z∂σ)+∂∂σ(ρσ˙∂z∂σ)=0

또한, σ 연직좌표계에서의 정수압 평형상태 연속방정식은 식(26)에 s = σ를 대입하여 정리하면 다음과 같이 된다.

(39) [∂∂σ(∂p∂t)]σ+∇σ⋅(V∂p∂σ)+∂∂σ(σ˙∂p∂σ)=0[∂∂t(∂p∂σ)]σ+∇σ⋅(V∂p∂σ)+∂∂σ(σ˙∂p∂σ)=0∂π∂t+∇σ⋅(πV)+π∂σ˙∂σ=0

6. 결론 및 토의

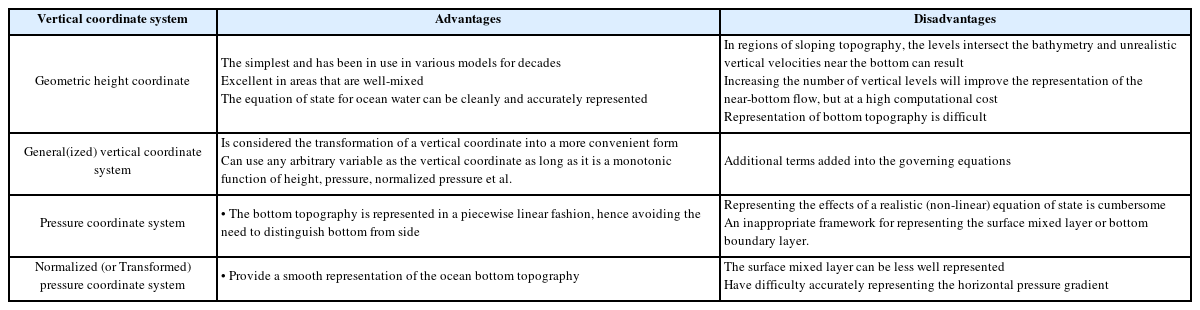
해양 및 대기 수치모델링에서 다양한 연직좌표계를 사용하고 있다. 본 연구에서는 자주 사용되는 4종류의 연직좌표계에 대하여 정수압 방정식, 연직속도, 수평방향 운동방정식, 연속방정식 등을 소개하였다. 전술한 연직좌표계에 대한 검토 결과를 Table 1에, 또한 Table 2에는 각각의 장단점을 정리하였다(Kasahara, 1974; Song and Haidvogel, 1994; Kalnay, 2002; Chandrasekar, 2022).

Table 1.

Summary of properties of some vertical coordinate systems.

Table 2.

Summary of properties of some vertical coordinate systems.

고도 연직좌표계를 사용하는 경우에 비하여 다른 종류의 연직좌표계를 사용하는 경우, 수평방향 운동방정식, 연속방정식, 그리고 연직방향 유속방정식 등이 더 복잡한 형태로 표현된다. 특히 수평방향 운동방정식중 압력경도에 의한 힘 항에는 좌표변환으로 고도 또는 해저면 기울기 항이 추가되어(식(23), (36), (37) 참조), 유한차분을 이용한 수치모형을 사용하는 경우, 절단오차가 더 커지게 된다. 이러한 문제를 해결하기 위하여 Mesinger는 ‘에타’라 지칭하는 계단형-산악 좌표계를 도입하였다(Kalnay, 2002). 무차원 압력좌표계는 압력을 무차원하여 사용하지만, 압력대신 고도를 무차원화하여 사용하기도 한다(Mellor et al., 2002; Shchepetkin and McWilliams, 2003; Shchepetkin and McWilliams, 2009).

한편, Haidvogel et al.(2008)은 연직확산계수(Vertical Stretching Factor)를 도입하여 기존의 무차원 압력좌표계를 수정하였고, Klemp(2011)는 고도 또는 해저면 경사가 급한 경우 발생하는 수치해석상의 문제점을 극복하기 위하여 고도 연직좌표계를 기본으로 하는 혼합 연직좌표계를 제안하였다.

이러한 연직좌표계를 사용하는 수치예측기법은 차후 위성 및 레이더와 같은 원격 센서 등에서 가능한 많은 정보를 추출할 수 있는 정교한 관측시스템을 활용한 자료동화 방법과 더불어 더욱 활성화될 수 있다. 이를 위해서는 다양한 연직좌표계의 도입, 수치모형 기법시 필요한 일관성(consistency), 정확도(accuracy), 안정성(stability) 확보, 급격한 지형 변화 적용 등에 적합한 수치모형 개발 등이 필요하다. 최종적으로는, 대기-해양-육지 결합 상세 수치모형을 개발하여 연안재해, 유류오염, 해난사고, 해양오염, 기후변화에 따른 해수면 상승 등의 현안 문제를 해결할 수 있다.

References

Arakawa A., Konor C.S.. 1996;Vertical differencing of the primitive equations based on the charney-phillips grid in hybrid σ-p vertical coordinates. Mon. Wea. Rev 124(3):511–528.

Arakawa A., Lamb V.R.. 1977;Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in Computational Physics 17:173–265.

Chandrasekar A... 2022. Numerical Methods for Atmospheric and Oceanic Sciences Cambridge University Press.

Haidvogel D.B., Beckmann A.. 1999. Numerical Ocean Modeling London, UK: Imperial College Press.

Haidvogel D.B., Arango H., Budgell W.P., Cornuelle B.D., Curchitser E., Di Lorenzo E., Fennel K., Geyer W.R., Hermann A.J., Lanerolle L., Levin J., McWilliams J.C., Miller A.J., Moore A.M., Powell T.M., Shchepetkin A.F., Sherwood C.R., Signell R.P., Warner J.C., Wilkin J.. 2008;Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the regional ocean modeling system. J. Comp. Phys 227(7):3595–3624.

Kalnay E.. 2002. Atmospheric modeling, data assimilation and predictability Cambridge University Press.

Kasahara A.. 1974;Various vertical coordinate systems used for numerical weather prediction. Mon. Wea. Rev 102(7):509–522.

Klemp J.B.. 2011;A terrain-following coordinate with smoothed coordinate surfaces. Mon. Wea. Rev 139(7):2163–2169.

Kowalik Z., Murty T.S.. 1993. Numerical Modeling of Ocean Dynamics World Scientific.

Mellor G., Häkkinen S., Ezer T., Pachen R.. 2002;A generalization of a sigma coordinate ocean model and an intercomparison of model vertical grids. Ocean Forecasting: Conceptual Basis and Applications :55–72.

Phillips N.A.. 1957;A coordinate system having some special advantages for numerical forecasting. J. Met. Soc 14:184–185.

Shchepetkin A.F., McWilliams J.C.. 2003;A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. J. Geophys. Res 108(C3):3090.

Shchepetkin A.F., McWilliams J.C.. 2009;Correction and commentary for “Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the regional ocean modeling system” by Haidvogel et al., J. Comp. Phys. 227, pp. 3595–3624. J. Comp. Phys 228:8985–9000.

Simmons A.J., Burridge D.M.. 1981;An energy and angular-momentum conserving vertical finite-difference scheme and hybrid vertical coordinates. Mon. Wea. Rev 109(4):758–766.

Song Y.T., Haidvogel D.. 1994;A semi-implicit ocean circulation model using a generalized topography following coordinate system. J. Comput. Phys 115:228–244.

Sundqvist H.. 1979;Vertical coordinates and related discretization. Numerical Methods Used in Atmospheric Models 2:3–50.

Sutcliffe R.C.. 1947;A contribution to the problem of development. Q. J. R. Meteorol. Soc 73:370–383.

Appendices

부록 A. 연속방정식 (3a), (3b) 유도

3차원 직교좌표계에서 질량보전식은 다음과 같다.

(dmdt)system=ddt(ρδxδyδz)=0

상기 식을 전개하면

ddt(ρδxδyδz)=0dρdtδxδyδz+d(δx)dtρδyδz+d(δy)dtρδxδz+d(δz)dtρδxδz=01δxδyδz[dρdtδxδyδz+d(δx)dtρδyδz+d(δy)dtρδxδz+d(δz)dtρδxδz]=0dρdt+[ρd(δx)dt1δx+ρd(δy)dt1δy+ρd(δz)dt1δz]=0dρdt+(ρδuδx+ρδvδy+ρδwδz)=0

위의 식에서 미소량들에 대한 극한을 구하면, 다음과 같이 표현된다.

dρdt+(ρ∂u∂x+ρ∂νδy+ρ∂w∂z)=0

부록 B. (9), 식(10), (12)유도

따라서,

(3a) dρdt+(ρ∂u∂x+ρ∂v∂y+ρ∂w∂z)=0dρdt+ρ∇⋅V+ρ∂w∂z=01ρdρdt+∇⋅V+∂w∂z=0ddtlnρ+∇⋅V+∂w∂z=0

혹은,

(3b) dρdt+(ρ∂u∂x+ρ∂v∂y+ρ∂w∂z)=0(∂ρ∂t+u∂ρ∂x+v∂ρ∂y+w∂ρ∂z)+(ρ∂u∂x+ρ∂v∂y+ρ∂w∂z)=0∂ρ∂t+(u∂ρ∂x+ρ∂u∂x)+(v∂ρ∂y+ρ∂v∂y)+(w∂ρ∂z+ρ∂w∂z)=0∂ρ∂t+∂(ρu)∂x+∂(ρv)∂y+∂(ρw)∂z=0∂ρ∂t+∇⋅(ρV)+∂(ρw)∂z=0

Fig. B1.

Tree diagram for a function of four variables.

Table B1.

The formulas for the four partial derivatives of A = A(x, y, z, t).

부록 C. 식(25)유도

(3a) dlnρdt+∇⋅V+∂w∂z=0

(25) dlnρdt+∇s⋅V−(∂s∂z)(∇sz)⋅∂V∂s +∂s∂z[ddt(∂z∂s)+∂V∂s⋅∇sz]+∂s˙∂s=0dlnρdt+∇s⋅V+∂s∂z[ddt(∂z∂s)]+∂s˙∂s=0dlnρdt+∇s⋅V+ddt[ln(∂z∂s)]+∂s˙∂s=0ddt[lnρ+ln(∂z∂s)]+∇s⋅V+∂s˙∂s=0ddt[ln(ρ∂z∂s)]+∇s⋅V+∂s˙∂s=01(ρ∂z∂s)∂∂t(ρ∂z∂s)+∇s⋅V+∂s˙∂s=0∂∂t(ρ∂z∂s)+(ρ∂z∂s)∇s⋅V+(ρ∂z∂s)∂s˙∂s=0[∂∂t(ρ∂z∂s)]s+∇s⋅(ρV∂z∂s)+∂∂s(ρs˙∂z∂s)=0

부록 D. 식(32)유도

압력좌표계에서 질량보전식은 다음과 같다.

(D1) (dmdt)system=ddt(ρδxδyδz)=0

정수압 평형상태의 경우, δp = ρgδz이므로, 위의 식은 다음과 같이 된다.

(D2) ddt[ρδxδy(−δpρg)]=ddt(δxδyδp)=0

상기 식을 전개하면

(D3) ddt(δxδyδp)=0d(δx)dtδyδρ+d(δy)dtδxδp+d(δp)dtδxδy=0d(δx)dt1δx+d(δy)dt1δy+d(δp)dt1δp=0δ(dx)dt1δx+δ(dy)dt1δy+δ(dp)dt1δp=0δuδx+δvδy+δωδp=0

여기서, ω ≡ dp/dt는 압력 연직좌표계에서 연직속도이다. 위의 식에서 미소량들에 대한 극한을 구하면, 다음과 같이 표현된다.

(32) ∂u∂x+∂v∂y+∂ω∂p=0∇p⋅V+∂ω∂p=0

식(32)는 압력좌표계의 연속방정식으로 유체의 압축성에 대한 가정이 필요하지 않고, 식 자체가 매우 간단하게 표현된다.

부록 E. List of notation

List of Symbols

any scalar function

variable representing x, y, or tfor partial differentiation

friction force per unit mass

Coriolis parameter

earth’s gravity

i, j, k

unit vectors in x–, y–, and z– coordinates

pressure, pressure coordinate system

general(ized) vertical coordinate

time

u, v

x– and y – components of V

horizontal velocity

= dz/dt, vertical velocity in z coordinate

x, y, z

Cartesian coordinates directed eastward, northward and upward

Greek symbols

= 1/ρ, specific volume

increment

geographical latitude

= p_x − p_T

density

=p−pTps−pT=p−pTπ, normalized pressure coordinate system

= gz, geopotential

= dp/dt, vertical velocity in p coordinate

Other symbols

∇

horizontal del operator

d/dt

total derivative

(·)

= d()/dt

Subscripts

evaluated at the earth’s surface

evaluated at the model top

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Chapter	Vertical coordinate system		Hydrostatic equation	Vertical velocity	Continuity equation
Chapter	Name	Symbol	Hydrostatic equation	Vertical velocity	Continuity equation
2	Geometric height coordinate	z	∂p∂z=-ρg	w=dzdt	Eq. (3a), (3b)
3	General(ized) vertical coordinate system	s	∂p∂s=-ρg∂z∂s	dsdt=(dsdt)z+V⋅∇zs+w∂s∂z	Eq. (26)
4	Pressure coordinate system	p	∂φ∂p=-α	ω=dp/dt≈ρgw	Eq. (32)
5	Normalized (or Transformed) pressure coordinate system	σ	∂φ∂σ=-πα	σ˙=dσdt =1π(dpdt-σdπdt)	Eq. (38)

Vertical coordinate system	Advantages	Disadvantages
Geometric height coordinate	The simplest and has been in use in various models for decades Excellent in areas that are well-mixed The equation of state for ocean water can be cleanly and accurately represented	In regions of sloping topography, the levels intersect the bathymetry and unrealistic vertical velocities near the bottom can result Increasing the number of vertical levels will improve the representation of the near-bottom flow, but at a high computational cost Representation of bottom topography is difficult
General(ized) vertical coordinate system	Is considered the transformation of a vertical coordinate into a more convenient form Can use any arbitrary variable as the vertical coordinate as long as it is a monotonic function of height, pressure, normalized pressure et al.	Additional terms added into the governing equations
Pressure coordinate system	• The bottom topography is represented in a piecewise linear fashion, hence avoiding the need to distinguish bottom from side	Representing the effects of a realistic (non-linear) equation of state is cumbersome An inappropriate framework for representing the surface mixed layer or bottom boundary layer.
Normalized (or Transformed) pressure coordinate system	• Provide a smooth representation of the ocean bottom topography	The surface mixed layer can be less well represented Have difficulty accurately representing the horizontal pressure gradient

∂A∂x=∂A∂x+∂A∂y∂y∂x+∂A∂z∂z∂x+∂A∂t∂t∂x∂A∂x=∂A∂x+∂A∂z∂z∂x	⇒	(∂A∂x)s=const=(∂A∂x)z=const+∂A∂z(∂z∂x)s=const
∂A∂y=∂A∂x∂x∂y+∂A∂y∂y∂y+∂A∂z∂s∂y+∂A∂t∂t∂y∂A∂y=∂A∂y+∂A∂z∂s∂y	⇒	(∂A∂y)s=const=(∂A∂y)z=const+∂A∂z(∂z∂y)s=const
∂A∂s=∂A∂x∂x∂s+∂A∂y∂y∂s+∂A∂z∂z∂s+∂A∂t∂t∂s∂A∂s=∂A∂s∂s∂z	⇒	∂A∂s=∂A∂z(∂z∂s)
∂A∂t=∂A∂x∂x∂t+∂A∂y∂y∂t+∂A∂z∂z∂t+∂A∂t∂t∂t∂A∂t=∂A∂t+∂A∂z∂z∂t	⇒	(∂A∂t)s=const=(∂A∂t)z=const+∂A∂z(∂z∂t)s=const
(10) (∂A∂c)s=const=(∂A∂c)z=const+∂A∂z(∂z∂c)s=const , where c can be x, y, or t. (9) ∂A∂z=∂A∂s(∂s∂z) (12) (∂A∂c)s=const=(∂A∂c)z=const+∂A∂s∂s∂z(∂z∂c)s=const