2.1 실험시설

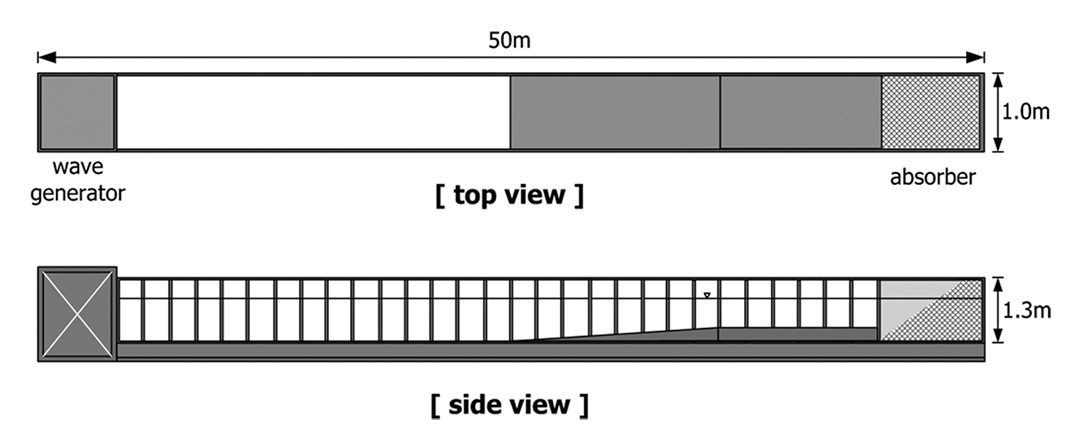
본 실험은 전남대학교 해안항만실험센터의 흐름수로와 2차원 조파수로에서 수행되었다. 사용된 흐름수로의 제원은 폭 2 m, 길이 100 m, 높이 3 m이며, 재현가능한 정상상태(steady state condition)의 최대유속은 2 m/sec이다. 그리고 경사식구조물을 대상으로 한 월파량 계측실험은 폭 1 m, 길이 50 m, 높이 1.3 m의 조파수로를 이용하였다. 사용된 조파수로에는 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다. 또한 조파판 전면에 부착된 파고계를 이용하여 독취한 자료를 바탕으로 반사파 흡수식 제어가 가능하고 수로 양쪽 끝부분에는 소파시설이 설치되어 있다. 설치된 조파기의 성능은 최대파고 0.7 m, 재현가능 주기 0.5~5 sec이다. 본 실험에서 실험파 설정시 사용된 파고계는 용량식으로서 계측범위는 ±0.75 m이며, 압력측정에 사용된 압력계의 독취율은 1 kHz이다. 그리고 월파량은 월파량 수집장치를 이용하여 계측하였으며, 월파수집 탱크, 수중펌프 및 유량계로 구성되어 있다. Fig. 1은 조파수로의 개념도이다.

Figure 1.

Experimental facility.

2.2 실험파 및 실험단면

월파량 계측방법의 적정성 검토를 위한 실험파는 Table 1에 제시되어 있으며, 규칙파와 불규칙파를 적용하였다. 규칙파의 목표주기(T) 및 목표파고(H)는 각각 T = 1.6~3.2 sec, H = 14~24 c m 범위이며, 주기는 ΔT = 0.2 sec 간격, 파고는 ΔH = 2 cm 간격으로 설정하였다. 그리고 불규칙파를 적용한 실험파의 목표 유의주기(T_S) 및 유의파고(H_S)는 각각 T_S = 1.56~2.40 sec, H_S = 8~20 c m 범위이며, 유의주기는 ΔT_S = 0.28 sec 간격, 유의파고는 ΔH_S = 2 cm 간격으로 설정하였다. 불규칙파는 Bretschneider-Mitsuyasu 주파수 스펙트럼을 이용하였다. 구조물 전면수심(d)이 40 cm이기 때문에 적용된 실험파 중 일부는 쇄파조건에 해당된다.

Table 1.

Target wave conditions in the experiment

본 실험은 주어진 파랑조건에 대해 월파량을 계측하여 월파량을 산정하는 경험식을 도출하는 것이 아니라 직접 계측된 월파량과 간접적인 방법으로 추정된 월파량을 비교 검토하여 월파량 계측방법의 적정성을 검토하는 것이 주된 목적이며, 동일한 파랑조건에서도 계측시간을 변경하여 다양한 월파량을 계측하고, 추정된 월파량과 비교하였다.

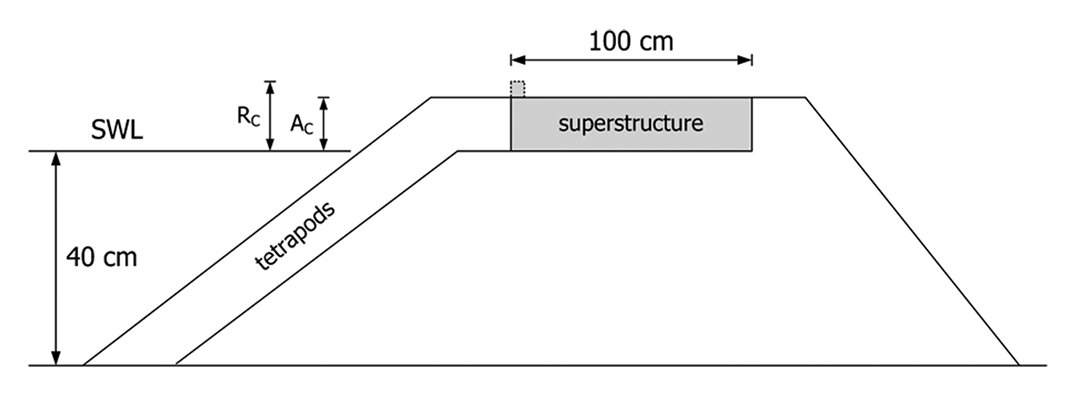
본 실험에 적용된 실험단면은 Fig. 2와 같다. Fig. 2에서 R_C는 여유고(freeboard), A_C는 피복재 상단고(armor block height)이며, 전사면에 테트라포드가 1:1.5의 경사로 피복된 경사식구조물 단면이다. 본 실험에서 적용한 모형구조물의 기하학적 제원으로 피복재 상단고는 A_C = 10 cm로 고정하고, 여유고는 R_C = 10 cm와 14 cm를 적용하여 파라펫(parapet)의 유무에 따른 영향도 검토하였다. 이는 월파수괴의 산란이 발생하는 경우에도 월파량 계측방법이 적정한지 평가하기 위해 파라펫이 설치된 조건을 포함한 것이다. 그리고 상치콘크리트의 폭은 100 cm이다.

Figure 2.

Cross-section of model structure.

3.1 압력-유속 관계 도출 실험

월파량을 추정하는데 있어 월파된 수괴의 유속을 측정하는 것이 가장 중요하다. 구조물 상치콘크리트 상부에 유속계를 직접 설치하는 방안을 고려해 볼 수 있지만, 1차원 프로펠러 유속계의 경우에는 흐름이 지나간 후에도 프로펠러의 관성에 의해 유속이 발생되는 문제점이 있고, 2차원 초음파 유속계의 경우에는 검출부가 수중에 있어야 하는데 상치콘크리트 상부에 설치하게 되면 월파가 발생하지 않을 때는 공기중에 노출되는 문제점이 있다. 따라서 본 연구에서는 공기중과 수중에서 적용 가능한 압력계를 이용하는 방안을 수립하였다. 즉, 유속별 압력을 측정하여 압력-유속 관계를 사전에 정립하고, 월파수괴에 의해 발생되는 압력을 계측한 후 이를 유속으로 환산하여 연속방정식을 적용하는 방법을 고안하였다. 이러한 방법을 적용하기 위해서는 압력과 유속의 상관관계를 사전에 확보하여야 하며, 이를 위해 흐름수로를 이용한 실험을 수행하게 되었다.

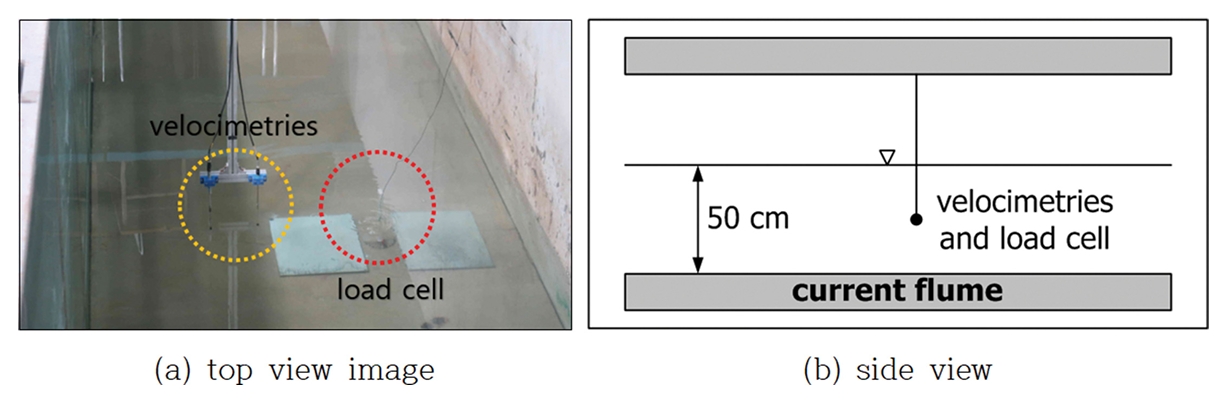
압력-유속의 관계정립을 위해 흐름수로 내에 Fig. 3과 같이 압력계(로드셀, Bongshin DBCM)와 2차원 초음파 유속계(KENEK VP1200)를 배치하였다. 흐름실험시 수심은 50 cm이며, 유속계와 압력계는 바닥으로부터 25 cm 위치에 설치하였다. 유속계는 1차원 프로펠러 유속계와 2차원 초음파 유속계를 동시에 설치하여 실험을 수행하였으나, 최종적으로는 2차원 유속계의 자료를 이용하였다. 압력을 계측하기 위해 사용된 계측기는 로드셀(load cell)이며, 계측된 힘을 표면적으로 나누어 압력으로 환산하였다. 흐름발생장치를 이용하여 유속 0~1.8 m/sec 범위에서 유속을 단계별로 증가시켜 해당 유속에서의 압력을 계측한 후 압력-유속 관계를 도출하였다. 하나의 유속조건에서 압력을 계측한 후, 다음 단계의 유속을 발생시키기 위해서는 흐름발생장치의 출력을 약간 증가시키면 된다. 증가된 유속이 정상상태에 도달되었는지 유속계의 계측자료를 확인한 후 유속과 압력을 10 sec 동안 동시 계측하였으며, 각각의 계측자료를 평균하여 사용하였다. 그리고 월파는 구조물에 경사지게도 발생하므로 이를 고려하기 위해 로드셀의 각도를 변화시킨 실험도 수행하였다.

Figure 3.

Position of velocimetries and load cell.

3.2 월파량 추정 실험

본 방법은 상치콘크리트 후면에서 월파수괴의 압력을 측정하고, 압력-유속 관계로부터 도출된 유속과 월파수괴의 단면적을 곱한 연속방정식을 이용하여 월파량을 추정하는 것이다. 이를 위해서는 월파수괴에 의한 압력과 월파수괴의 높이 측정이 필요하다.

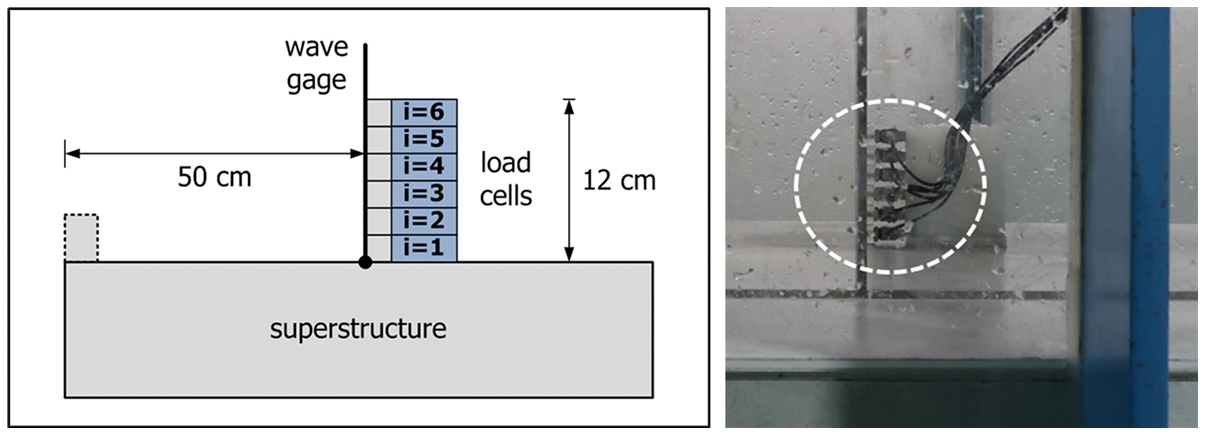
Fig. 2와 같은 경사식구조물 상치콘크리트 상부에 Fig. 4와 같이 수위계(파고계)와 로드셀을 상치콘크리트 선단으로부터 50 cm 떨어진 동일한 선상에 설치하였다. 월파수괴의 높이는 파고계를 이용하여 계측하였으며, 압력계측은 압력-유속 관계식 도출에 사용되었던 로드셀을 이용하였다. 로드셀은 연직방향으로 6개를 설치하였고, 로드셀의 검출부에 높이 1.9 cm의 패널을 부착하여 전체 높이가 12 cm가 되도록 하였다. 높이 1.9 cm의 패널을 이용한 것은 각각의 로드셀에 작용하는 압력을 계측하기 위해서는 로드셀간 계측부가 약간 이격되어 있어야 하기 때문이다. 본 실험에서는 계측기 위치에서 월파수괴의 높이가 12 cm 이하가 되는 조건의 파랑을 적용하였다. 만약 월파수괴의 높이가 이보다 높다면 로드셀을 추가로 설치하면 된다.

Figure 4.

Position of wave gage and load cells on the superstructure.

Fig. 5는 경사식구조물 상부에 로드셀과 파고계(수위계)를 설치한 장면이다. 파고계는 일정 부분이 수중에 잠겨있어야 하므로 상치콘크리트 상부에 홈을 두어 파고계 하단이 홈 속에 위치하도록 설치하고, 홈에 물을 채워 수중조건으로 구성하였다. 실험전 상부 홈의 수위가 상치콘크리트 상단면의 높이와 같은지 확인하고, 낮을 경우에는 물을 보충하여 높이를 동일하게 하였다.

Figure 5.

Image of model structure and measuring device setup.

Fig. 6은 예비실험 장면으로서. ①은 로드셀 위치, ②는 파고계 위치이다. ①의 위치에서 확인할 수 있는 것과 같이 월파수괴가 로드셀에 부딪친 후 상부로 솟구치는 것을 확인할 수 있다. 이러한 경우에 실제 월파수괴 높이보다 위에 위치한 로드셀에 압력이 계측되게 되며, 이는 실제 월파수괴에 의한 압력은 아니다. 본 실험에서는 월파량 추정을 위한 분석 시 파고계(수위계)로부터 계측된 월파수괴 높이보다 높은 위치에서의 압력값이 존재하는 경우에는 해당되는 로드셀의 수위값을 0으로 처리하여 산정유량이 0이 되도록 하였다. 여러 조건에 대한 예비실험을 수행하여 도출된 문제점을 보완한 후 본 실험을 수행하였다.

Figure 6.

Image of model test.

본 실험은 계측된 월파량과 추정된 월파량을 비교하여 본 연구에서 제안한 월파량 계측방법의 적정성을 평가하기 위한 것으로 다양한 파랑조건의 적용 뿐만 아니라 동일한 파랑조건의 경우에도 계측시간을 서로 다르게 하여 월파량을 계측하는 실험을 수행하였다. 압력-유속 관계 도출실험에서와 같이 구조물에 경사지게 입사하는 월파조건에 대한 실험은 로드셀의 각도를 변화시켜 수행하였다. 본 실험에서는 β = 0° (직각입사), 30° 및 60° 조건에 대해 수행하였다.

본 연구에서 제안한 압력-유속 관계식과 월파수괴의 높이를 이용하는 방법은 다음 식을 이용하여 월파량의 체적을 추정하게 된다.

상기 식에서 v_i는 각 로드셀에 계측된 압력으로부터 압력-유속 관계를 이용하여 산정된 유속([L/T]), Δh_i는 로드셀 전면부에 부착된 패널에 월파수괴가 접하는 높이([L]), 즉 패널 전체에 월파수괴가 접하는 경우에는 패널의 높이이고, 패널 일부에만 접하는 경우에는 패널하단에서 월파수괴가 접하는 위치까지의 높이, Δt는 독취율(sampling rate)에 대응하는 시간 간격([T]), w는 월파량 수집장치의 폭([L])이며, V_E는 추정 월파량으로서 체적([L³])으로 나타난다. 이러한 추정 월파량(V_E)과 모형실험에서 직접 계측한 월파량(V_M)을 비교하여 제안된 방법의 적정성을 검토하였다. 전술한 바와 같이 로드셀에 의한 처오름으로 인해 월파수괴의 높이보다 높은 곳에 위치하는 로드셀에서의 압력이 존재하는 경우가 있으며, 이러한 경우에는 해당되는 패널의 Δh_i를 0으로 처리하여 산정유량이 0이 되도록 하였다.

4.1 압력-유속 관계실험 결과

압력-유속 관계실험은 흐름수로를 이용하여 수행하였으며, 흐름의 진행방향과 로드셀의 검출부가 이루는 각도는 β = 0° (직각조건)~60°까지 15° 단위로 수행하였다.

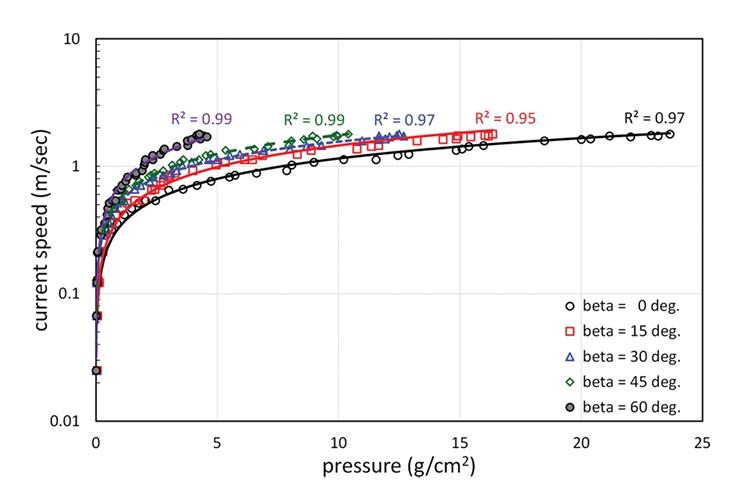
Fig. 7은 압력-유속 관계실험의 결과를 도시한 것이다. 유속은 약 1.8 m/sec까지 적용하였으며, 흐름방향과 로드셀 검출부의 각도가 증가할수록 압력-유속의 관계가 민감함을 알 수 있다. 전체적으로 실험자료의 상관관계는 R² = 0.95~0.99로서 상당히 높게 나타났다. 직각조건(β = 0°)의 경우와 β = 60°의 경우를 비교해 보면 β = 60° 조건에서는 작은 압력의 변화에도 유속의 변화폭이 크며, 이는 로드셀이 경사지게 배치됨으로 인해 유속증가에 따른 압력의 증가가 크지 않기 때문이다. 따라서 흐름방향과 로드셀이 이루는 각도가 증가할수록 압력-유속의 관계가 민감해지기 때문에 월파량 추정값의 변동성이 다소 증가할 수 있는 여지가 있다. 본 실험에서는 Fig. 7에 도시된 회귀선에 해당되는 압력-유속 관계 회귀식을 이용하였으며, 회귀식도 실험결과와 일정 수준 차이가 있기 때문에 이 또한 월파량 추정값의 변동성에 영향을 미치게 된다.

Figure 7.

Test results for pressure-current speed relationship.

Fig. 7에 제시된 압력-유속 관계결과는 절대적인 결과가 아니며 사용하는 압력계에 따라 달라질 수 있으므로 본 연구에서 제안하는 방법을 적용할 경우에는 사전에 사용하는 압력계와 유속 간의 상관관계를 정립하여야 한다.

4.2 월파량 추정실험 결과

월파량 추정실험은 Fig. 2의 경사식구조물을 대상으로 Table 1에 제시된 파랑조건을 적용하여 수행하였다. 월파량 추정실험은 규칙파를 적용한 단일파 조건(case RS)과 연속파 조건(Case RC), 불규칙파를 적용하고 파라펫이 없는 조건(case IW)과 파라펫이 설치된 조건(case IP)을 대상으로 하였고, 흐름방향과 로드셀이 이루는 각은 β = 0°, 30°, 60°를 적용하였다. 여기서, β = 0°는 상치콘크리트에 파랑이 직각으로 입사하는 조건이고, β = 30°와 60°는 경사지게 입사하는 조건이다.

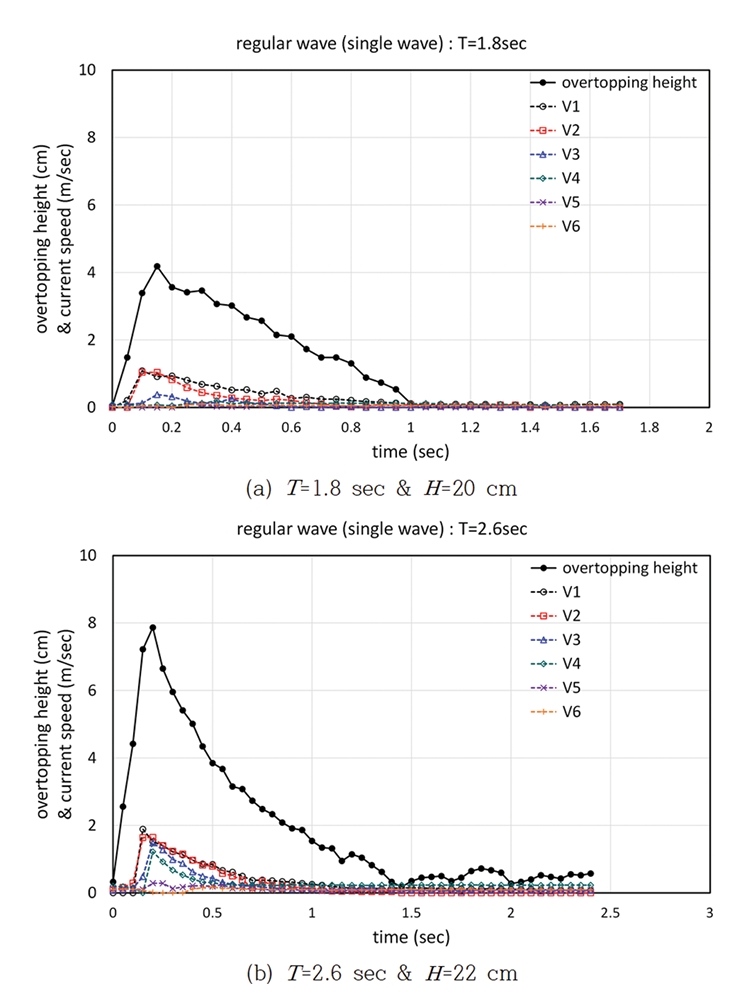
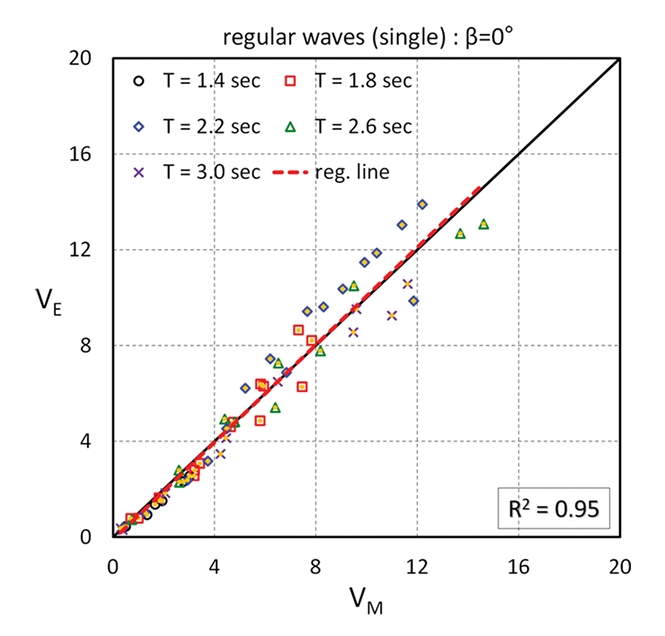
규칙파를 적용한 단일파 조건(case RS) 실험은 파랑이 구조물의 마루높이를 상회하여 월파가 발생되는 조건에서 1회의 월파에 대한 월파량을 계측하여 추정값과 비교한 것이다. Fig. 8은 구조물의 마루높이와 피복재의 상단고가 동일한 R_C = A_C 조건에서 case RS에 대한 실험결과 중 두가지 파랑조건에 대한 월파고 및 각 높이별 유속의 시계열을 도시한 것이다. Fig. 8(b)는 Fig. 8(a)에 비해 파고도 높고, 주기도 긴 경우로서 월파수괴가 상치콘크리트에 낙하한 후에도 월파수괴 높이의 변동이 발생하고 있음을 알 수 있다. Fig. 8을 살펴보면 월파수괴의 유속은 상치콘크리트 상부면과 인접한 위치에서 빠르며 연직방향으로 올라 갈수록 유속이 작아지는 것을 확인할 수 있다. Fig. 9는 β = 0°인 경우에 case RS 조건에 대한 계측 월파량(V_M)과 추정 월파량(V_E)을 비교한 것으로서 상관계수는 R² = 0.95로 분석되었다. 전체적으로 월파량이 증가할수록 V_E/V_M의 변동성이 증가함을 알 수 있으며, V_E/V_M = 0.70~1.21 범위이고 (V_E/V_M)_ave = 0.97로 분석되었다. 월파량이 많은 경우에 변동성은 일정 수준 존재하지만 회귀선으로 살펴본 전반적인 경향은 비교적 적정하다고 판단된다. case RS 실험에서는 계측기의 독취율(sampling rate)로 20 Hz를 적용하였지만, 다소 부족하다는 판단을 하였다. 월파수괴의 유속이 빠르기 때문에 독취율도 오차에 일정수준 영향을 미쳤을 것으로 판단하여 후속 실험에서는 50Hz의 독취율을 적용하였다.

Figure 8.

Time series of overtopping height and current speed for case RS.

Figure 9.

Comparison of the measured (V_M) and the estimated (V_E) overtopping volumes for case RS & β = 0°.

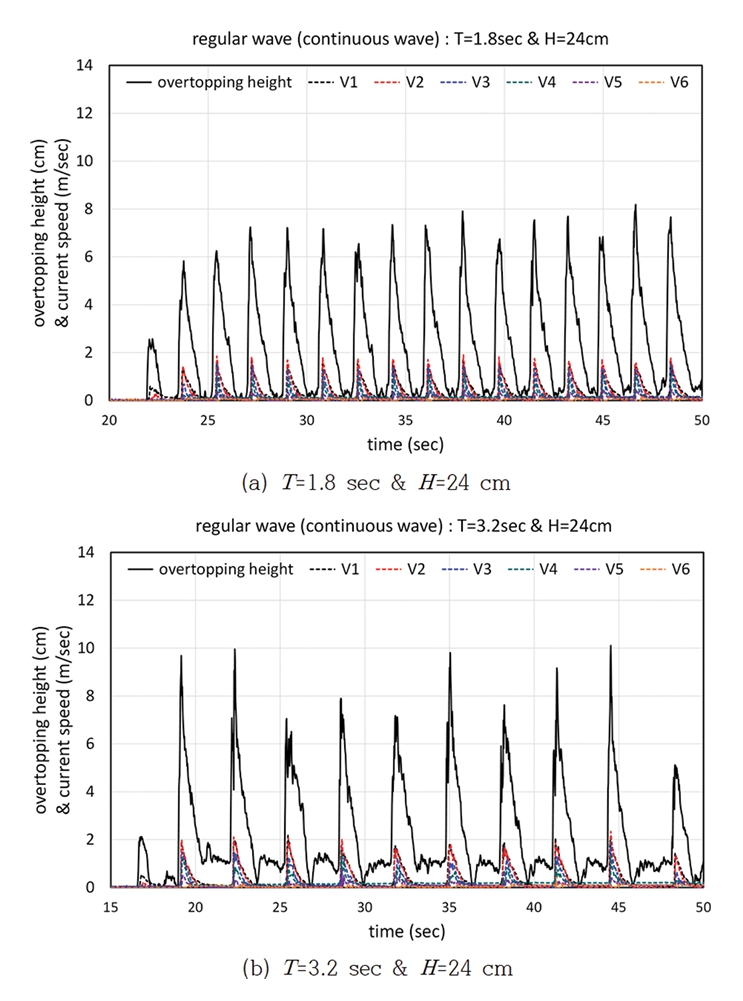
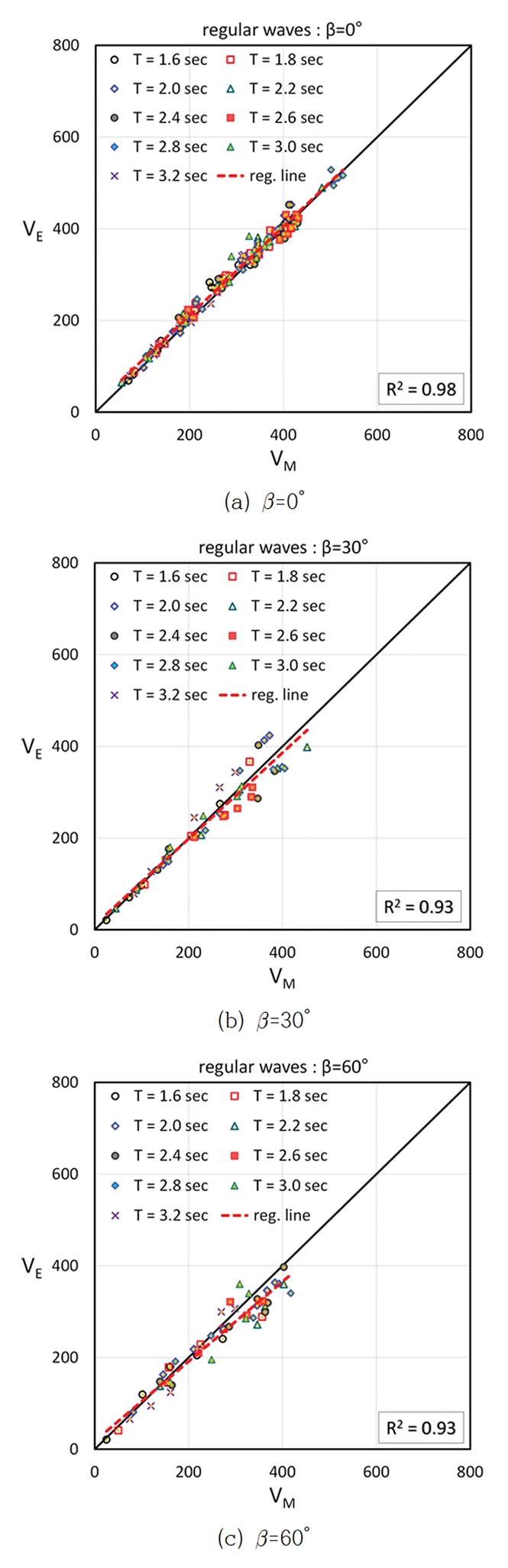
규칙파를 적용한 연속파 조건(Case RC) 실험은 일정시간 동안 발생한 월파량 전체를 비교하는 실험이다. Fig. 10은 구조물의 마루높이와 피복재의 상단고가 동일한 R_C = A_C 조건에서 Case RC에 대한 실험결과 중 두가지 파랑조건에 대한 월파고 및 각 높이별 유속의 시계열을 도시한 것이다. Fig. 11은 Case RC 실험에서 β = 0°, 30°, 60°인 경우의 계측 월파량(V_M)과 추정 월파량(V_E)을 비교한 것으로서 입사각별로 약간의 차이는 있지만 계측량과 추정량의 상관계수는 R² = 0.93~0.98로 분석되었다. β = 0° 조건에서는 계측된 월파량과 추정된 월파량이 상당히 잘 일치하는 것을 알 수 있지만, β가 증가할수록 상관계수는 상대적으로 작아지고 계측량이 측정량에 비해 약간 크게 나타나는 것을 볼 수 있다. Fig. 7에서 살펴본 바와 같이 β가 증가하게 되면 작은 압력의 변화에도 유속의 변화가 크기 때문에 상대적인 차이가 크게 나타나는 것으로 판단된다. Case RC 실험에서 β = 0° 조건의 경우에 (V_E/V_M)_ave = 1.04, β = 30° 조건의 경우에 (V_E/V_M)_ave = 0.99, β = 60° 조건의 경우에 (V_E/V_M)_ave = 0.95로 나타났으며, β가 증가할수록 추정량이 계측량보다 약간 작아지는 경향을 보이지만 본 연구에서 제안한 방법은 충분한 정도로 적용 가능함을 알 수 있다.

Figure 10.

Time series of overtopping height and current speed for Case RC.

Figure 11.

Comparison of the measured (V_M) and the estimated (V_E) overtopping volumes for Case RC.

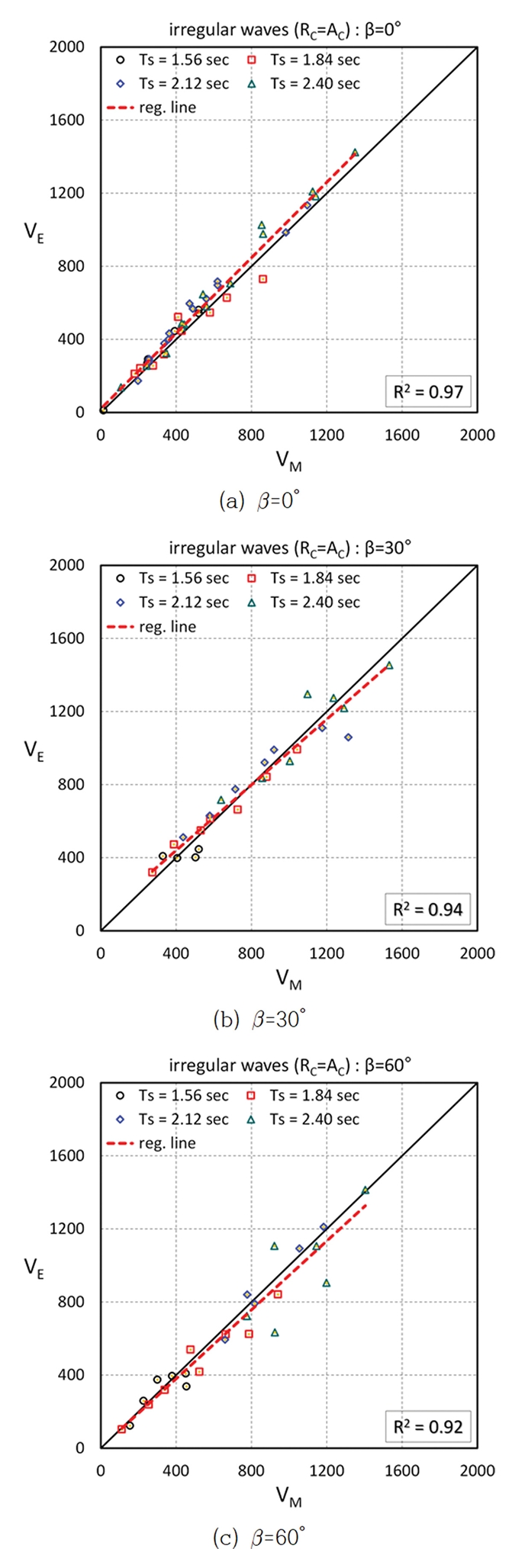
Fig. 12는 구조물의 마루높이와 피복재의 상단고가 동일한 R_C = A_C 조건에서 불규칙파를 적용한 case IW 실험의 결과를 도시한 것이다. β = 0°, 30°, 60°인 경우의 계측 월파량(V_M)과 추정 월파량(V_E)은 입사각별로 약간의 차이는 있지만 계측량과 추정량의 상관계수는 R² = 0.92~0.97로 분석되었다. 입사각이 증가할수록 추정량 보다는 계측량이 다소 많아지는 경향을 보이고, 실험자료의 분산 또한 커짐을 알 수 있다. 분석결과의 회귀선을 살펴보면 월파량이 상대적으로 많을 때 상대적인 차이가 커짐을 알 수 있다. case IW 실험에서 β = 0 o 조건의 경우에 (V_E/V_M)_ave = 1.08, β = 30° 조건의 경우에(V_E/V_M)_ave = 1.02, β = 60° 조건의 경우에 (V_E/V_M)_ave = 0.95로 나타났다. 즉, β = 0°인 경우에는 월파수괴가 로드셀에 부딪칠 때 충격적인 성분이 다소 포함됨으로 인해 압력이 크게 계측되고, 이로 인해 유속이 빠르게 산정되었기 때문으로 판단된다.

Figure 12.

Comparison of the measured (V_M) and the estimated (V_E) overtopping volumes for case IW.

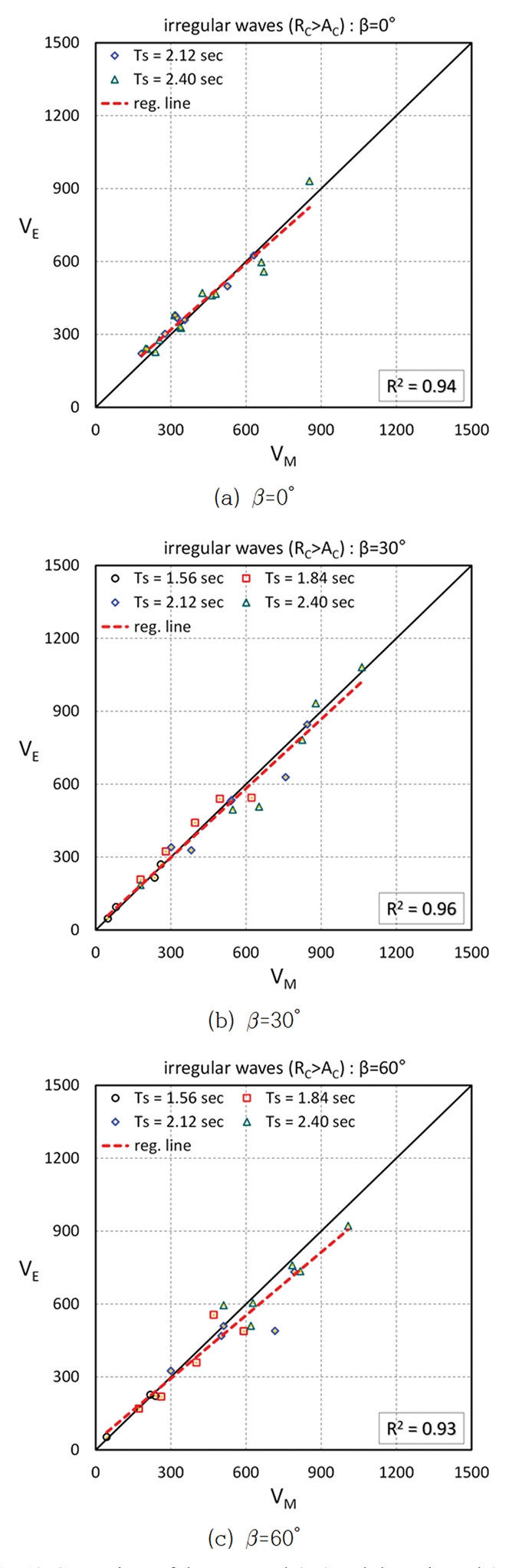
Fig. 13은 구조물의 마루높이가 피복재의 상단고보다 높은 R_C > A_C 조건에서 불규칙파를 적용한 case IP 실험의 결과를 도시한 것이다. β = 0° 조건의 경우에 파라펫 설치로 인해 상대적으로 긴 주기에서만 월파가 발생하였으며, β = 30°와 60° 실험에서는 구조물의 마루높이를 약간 낮추어 여러 실험파 조건에서 월파가 발생되도록 하였다. β = 0°, 30°, 60°인 경우의 계측 월파량(V_M)과 추정 월파량(V_E)의 상관계수는 R² = 0.93~0.96으로 분석되었다. 그리고 case IP 실험에서 β = 0° 조건의 경우에 (V_E/V_M)_ave = 1.05, β = 30° 조건의 경우에 (V_E/V_M)_ave = 1.00, β = 60° 조건의 경우에 (V_E/V_M)_ave = 0.96으로 나타났다. case IP 실험은 파라펫이 설치됨으로 인해 월파수괴의 거동이 다소 복잡하고 산란되는 경우이지만 평균 관점에서 충분한 정도로 월파량의 추정이 가능할 것으로 판단된다.

Figure 13.

Comparison of the measured (V_M) and the estimated (V_E) overtopping volumes for case IP.

본 연구에서 제안한 월파량 계측방법의 적정성을 검토하기 위해 경사식구조물을 대상으로 규칙파와 불규칙파를 적용한 수리모형실험을 수행하였다. 실험결과에 따르면 제안된 방법의 적용 가능성은 충분하다고 판단된다. 계측량과 추정량의 오차는 전술한 요인이 있지만, 추가적으로는 압력-유속 관계 도출시 적용한 정상상태 흐름과 실제 월파시 발생하는 유속의 비정상상태 조건에 의한 차이도 일부 영향을 미쳤을 것으로 생각된다.