Article information

Abstract

Trans Abstract

1. 서 론

항만구조물의 외곽시설은 크게 직립식구조물과 경사식구조물로 구분할 수 있으며, 파랑외력에 대해 안정하게 설계 및 건설되어야 한다. 직립식구조물에 작용하는 파랑외력은 Goda의 파압 산정식(Goda, 1974, 2010)을 이용하는 것이 일반적이며, 직립식구조물 전면에 소파블록이 전사면 피복되는 경우에는 Takahashi et al.(1990)의 파압저감계수를 Goda의 파압 산정식에 적용하여 작용파압을 산정하고 있다. Goda의 파압 산정식은 충격쇄파 조건에는 적용이 어렵다는 한계가 있지만 일반적인 대부분의 조건에는 보편적으로 사용되고 있다. 상대적으로 수심이 낮은 곳에 건설되는 경사식구조물은 설계 시 안정성 확보측면에서 항내외측 피복재 및 상치콘크리트의 안정, 제체침하, 선단세굴, 제체활동 등을 검토하여야 한다. 경사식구조물의 안정확보 측면에서 대부분의 요소 항목에 대한 검토 방안이 정립되어 있지만 상치콘크리트의 안정을 검토하는 방법론은 아직 미흡한 점이 있다. 즉, 파랑외력이 경사식 구조물에 작용하는 경우에 구조물의 최상부에 설치되는 상치콘크리트에 작용하는 파력을 산정하는 방법에 대해서는 명확하게 정립되어 있지 않다. 국내 항만 및 어항 설계기준·해설(MOF, 2020)에는 경사식구조물의 상치콘크리트에 작용하는 파력을 산정할 수 있는 지침이 부재한 실정으로서 설계시 필요한 작용파압은 직립식구조물에 작용하는 파압을 산정하는 Goda의 파압 산정식과 Takahashi et al.(1990)의 파압저감계수를 적용하여 간접적으로 산정하고 있다.

경사식구조물의 설계시 필요한 항목 중, 상치콘크리트 안정 확보와 관련하여 상치콘크리트에 작용하는 수평파압에 대한 국내 연구는 미미하지만, 해외에서는 지속적으로 수행되고 있다. 대표적인 연구로는 Pedersen(1996)의 연구를 들 수 있으며, 여러 후속 연구는 Pedersen의 연구성과를 기반으로 하고 있다. Nørgaard et al.(2013)은 Pedersen의 파압산정식이 천해조건시와 노출부(파라펫 구간)의 파압을 과대평가함을 지적하고, Pedersen이 제안한 식을 수정하였다. 또한 Martin et al.(1999)은 규칙파를 적용한 실험을 통해 상치콘크리트에 작용하는 파압에 대한 결과를 제시하였다. 이외에도 여러 연구자들에 의해 경사식구조물의 상치콘크리트에 작용하는 파압에 대한 연구가 수치해석 및 수리실험을 통해 수행되어 왔다(Guanche et al., 2009; Chen et al., 2015; Contestabile et al., 2017; Doorslaer et al., 2017; Jacobsen et al., 2018; Molines et al., 2018; Aniel-Quiroga et al., 2019; van Gent and van der Werf, 2019; Formentin et al., 2021; Han et al., 2022). Aniel-Quiroga et al.(2019)은 고립파를 이용하여 지진해일시 상치콘크리트에 작용하는 파압에 대한 연구를 수행하였으며, van Gent and van der Werf(2019)는 경사식방파제 상치콘크리트에 작용하는 파랑의 입사각 영향을 검토하였다. 대부분의 해외 연구성과는 주피복재로 피복석을 사용한 조건으로서 국내에서 일반적으로 사용되는 테트라포드와 같은 콘크리트 이형블록이 피복된 조건에 대한 추가적인 성과도출이 요구된다.

국내 연구로서 Lee et al.(2021)은 불규칙파 조건에서 테트라포드가 피복된 경사식구조물의 상치콘크리트에 작용하는 파압 산정을 위해 2차원 수리모형실험을 수행하였으며, 실험결과를 이용하여 새로운 파압보정계수를 제안하였다. 즉, 주된 실험목표는 Takahashi et al.(1990)의 파압보정계수를 대체하기 위한 것으로서 피복부와 노출부를 구분하여 각각의 새로운 파압보정계수를 제안하였으며, 노출부에서 상당히 큰 파압이 작용함을 보였다. 그러나 경사식구조물의 상치콘크리트에 작용하는 파압에 대한 국내 연구는 여전히 미흡한 실정이다.

본 연구에서는 경사식구조물의 상치콘크리트에 작용하는 수평파압 산정식을 도출하기 위해 규칙파를 적용한 2차원 수리 실험을 수행하고 그 결과를 분석하였다. 비쇄파조건에서 규칙파의 파고와 주기를 변경시키며 실험을 수행하였으며, 계측은 파력계를 이용하였다. 실험은 1:1.5 경사의 테트라포드가 2층 피복된 조건의 단면을 대상으로 하였다. 실험결과는 Goda의 파압 산정식(Goda, 1974, 2010) 및 Takahashi et al.(1990)의 파압보정계수를 적용한 결과(G&T)와 본 실험결과를 비교하였으며, 규칙파 조건에서 상치콘크리트에 작용하는 수평파압 산정 경험식을 제안하였다.

2. 실험시설 및 실험조건

2.1 실험시설

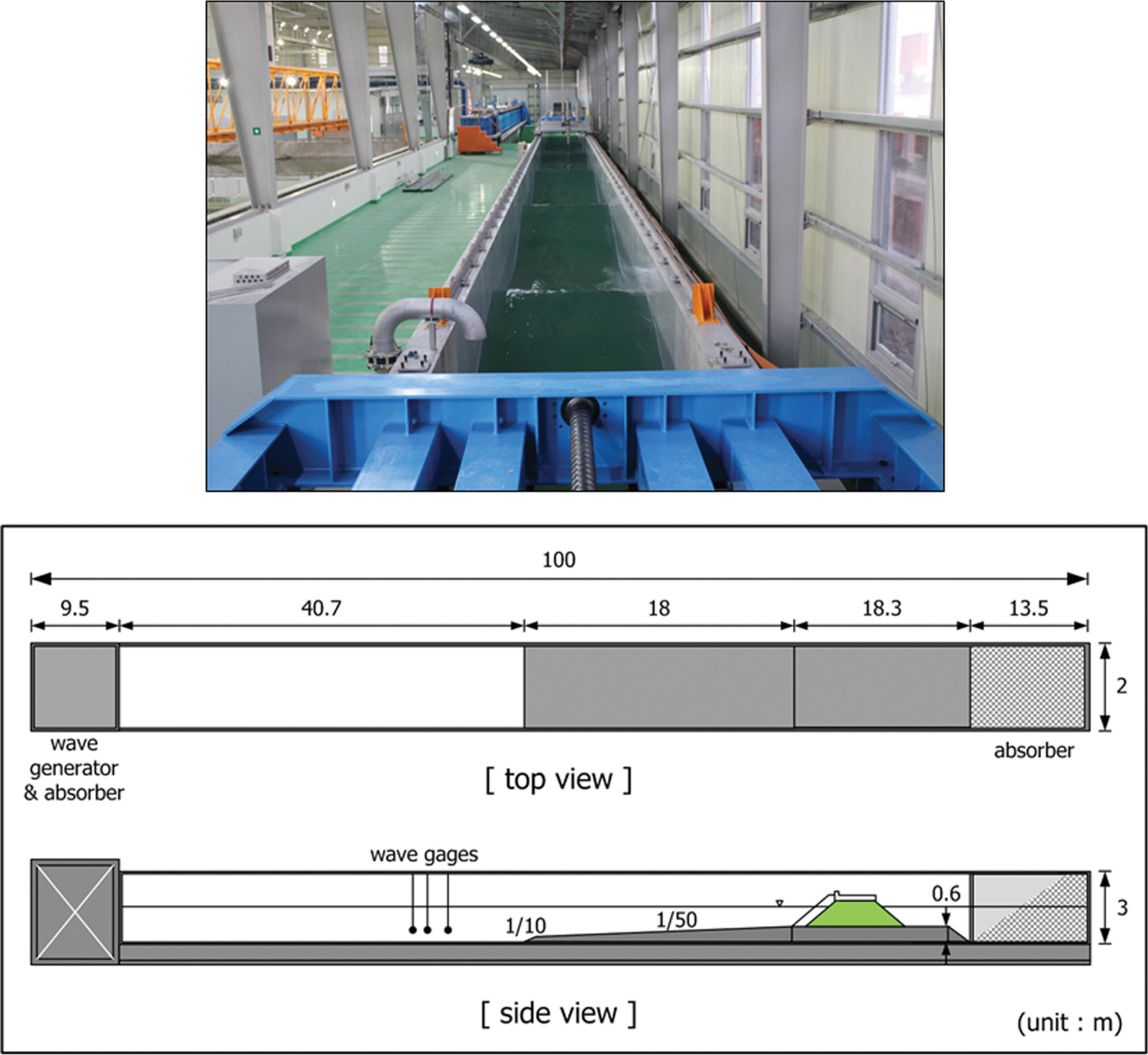
본 실험은 전남대학교 해안항만실험센터 2차원 수로에서 수행되었으며, 사용된 단면수로의 제원은 폭 2 m, 길이 100 m, 높이 3 m이며, 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다. 그리고 조파판 전면에 부착된 파고계를 이용하여 독취된 자료를 바탕으로 반사파 흡수식 제어가 가능하고 수로 양쪽 끝부분에 소파시설이 설치되어 있다. 설치된 조파기의 성능은 최대파고 1.3 m, 재현가능 주기는 0.5~10 sec이며, Fig. 1은 단면수로의 개념도이다. 본 실험에서 자유수면계측에 활용된 파고계는 용량식 파고계로서 계측범위는 ±0.75 m, 독취율은 50 Hz이며, 파력계측을 위해 사용된 로드셀(Bongshin DBCM)의 독취율은 1 kHz이다.

Fig. 1.

Experimental facilities.

2.2 실험조건

실험에 적용된 실험파 및 실험수심은 Table 1에 제시되어 있다. 구조물 설치위치에서의 수심(d)은 0.8 m, 실험파의 목표 주기(target wave period, T₀)는 T₀ = 1.6, 2.0, 2.4, 2.8, 3.2, 3.6, 4.0 sec, 목표 파고(target wave height, H₀)는 H₀ = 32, 36, 40, 44 cm를 적용하였다. 실험은 축척 1/25 개념으로 계획함으로 인해 원형상 목표 주기는 T₀ = 8, 10, 12, 14, 16, 18, 20 sec, 원형상 목표 파고는 H₀ = 8, 9, 10, 11 m이다. 목표 파고와 주기를 대상으로 실험파를 설정하더라도 동일한 제원을 가지는 파랑을 재현하기는 어렵다. 본 실험에서 설정된 실험파의 파고 및 주기는 목표 제원과 약간의 차이가 있지만 최대한 목표값에 근사하도록 설정하였다. 실험결과 분석에서는 목표 파랑제원이 아닌 실험파 설정시의 파랑제원(T, H)을 이용하여 결과를 분석하였다. 본 실험은 경사식방파제 상치콘크리트에 작용하는 수평파력을 계측하는 것으로서 파랑제원별로 규칙파 5개가 작용하는 시간동안 수평파력을 계측하고, 이를 평균하여 해당 제원의 파랑 작용시의 수평파력으로 설정하였다. 수평파력 계측에 적용된 5개의 규칙파는 실험파 설정시의 시간대와 동일한 파랑이다. 즉, 5개의 파랑이 작용하는 시간동안 계측된 수평파력을 평균한 후, 이를 수평파압으로 환산하였다.

Table 1.

Test wave conditions and water depth

2.3 실험단면 및 계측방법

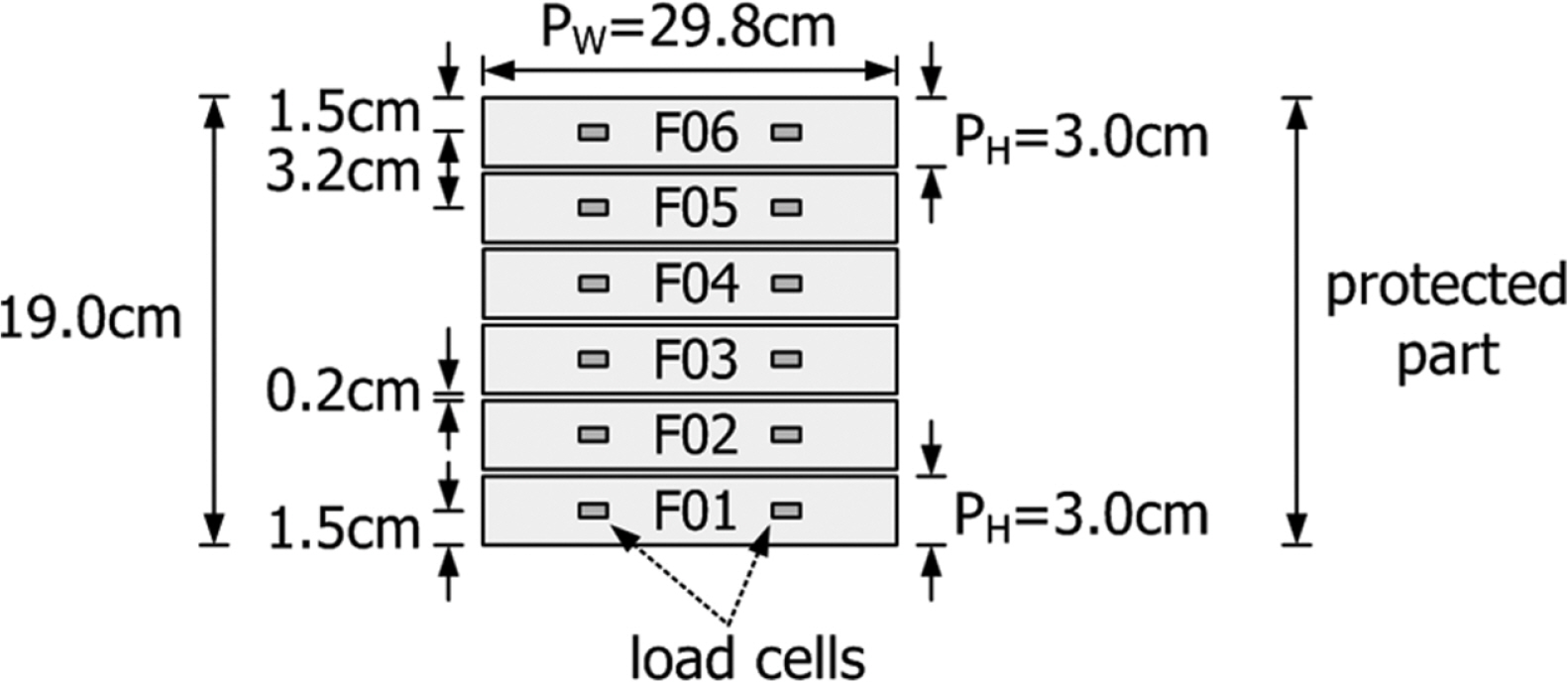
본 실험에 적용된 단면은 Fig. 2와 같으며, 주피복재로 테트라포드가 2층 피복되고, 사면경사가 1:1.5인 단면이다. Fig. 2에서 G_W은 피복재 상단 어깨폭으로서 G_W = 22.0 cm(G_W/D_n = 2.37)이며, R_C는 여유고, A_C(-)와 A_C(+)는 각각 정수면으로부터의 피복재 하단고와 상단고이다. 여기서, D_n은 피복재의 공칭길이(= V^1/3)이며, V는 피복재의 체적이다. 그리고 실험에 적용된 여유고(R_C 또는 A_C(+))는 A_C(+) = 21.7~34.0 cm이고, 피복재 하단고(A_C(-))는 AC() = 2.5~14.8 cm이다. 따라서 목표 파랑제원이 아닌 설정된(분석에 사용되는) 실험파의 파랑제원을 적용할 경우, A_C(+)/H = 0.36~1.15, A_C(-)/H = 0.04~0.50에 해당된다.

Fig. 2.

Cross-section of model structure.

Fig. 3은 상치콘크리트 전면에 설치되는 로드셀의 배치와 수평파력 계측을 위한 패널(panel)을 도시한 것이다. 상치콘크리트 전면에 6개의 패널(P_W = 2 9.8 cm(폭), P_H = 3 cm(높이))을 설치하였고, 패널간 간격은 0.2 cm를 두어 패널간의 접촉이 없도록 하였으며, 최하단 패널과 중간피복층 상단과도 접촉되지 않도록 하였다. 각 패널에 2개의 파력계(load cell)를 설치함에 따라 전체 12대의 로드셀이 활용되었다. Pedersen(1996)과 Nørgaard et al.(2013)은 파압계(pressure gage)를 이용하여 수평파압을 계측하였다. 파압계를 활용할 경우에 파압계 설치위치에 따라 서로 다른 파압이 계측될 수 있다. 즉, 파압계가 피복재 후면에 위치하는 경우와 공극에 위치하는 경우에 따라 서로 다른 파압이 계측될 수 있다. Pedersen(1996)과 Nørgaard et al.(2013)은 이를 보완하기 위해 상치콘크리트 기준선방향(파봉선 방향)으로 동일 높이에 대해 2~3개의 파압계를 설치하여 계측된 각각의 파압을 평균하여 사용하였다. 2~3개의 파압계를 동일 높이에 설치하여 평균하더라도 계측 파압이 적정한가에 대한 의문은 여전히 남게 되지만, Pedersen과 Nørgaard et al.은 피복재로 피복석을 이용하였기 때문에 상대적으로 잘 짜여지는 피복석의 특성상 전술한 문제점은 어느 정도 상쇄되었을 것으로 판단된다. 본 연구에서는 공극이 상대적으로 큰 테트라포드를 피복재로 사용하였기 때문에 파압계를 활용했을 때의 문제점을 보완하기 위해 일정 면적을 가지는 패널을 설치하고, 패널에 작용하는 수평파력을 계측한 후 각 패널의 면적으로 나누어 수평파압으로 환산하는 방법을 채택하였다(Fig. 3 참조). 결과분석시에는 동일한 패널에 설치된 로드셀에서 계측된 수평파력의 시계열을 합산한 후, 밴드패스 필터(bandpass filter)를 사용하여 노이즈 성분 등을 제거한 후 분석하였다.

Fig. 3.

Positioning of panel and load cells on the crown wall.

3. 계측자료 분석

본 실험에서는 실험파 설정시와 동일한 시간대에 진행하는 5개의 파랑으로부터 수평파력(F)을 계측한 후, 이를 수평파압 (p)으로 환산하였다. 분석된 수평파압은 무차원 수평파압(= p/ ρgH)으로 환산하였으며, 여기서 ρ는 유체의 밀도, g는 중력가속도이고 H은 설정된 실험파의 파고이다. 수평파력 계측시 적용된 독취율은 500 Hz이다. 분석된 결과를 도시할 때, 종축은 정수면으로부터 계측점까지의 높이(z), 횡축은 무차원 수평파압으로 나타내었으며, 본 실험결과(exp.)와 현행 설계법(G&T)의 결과를 비교 도시하였다.

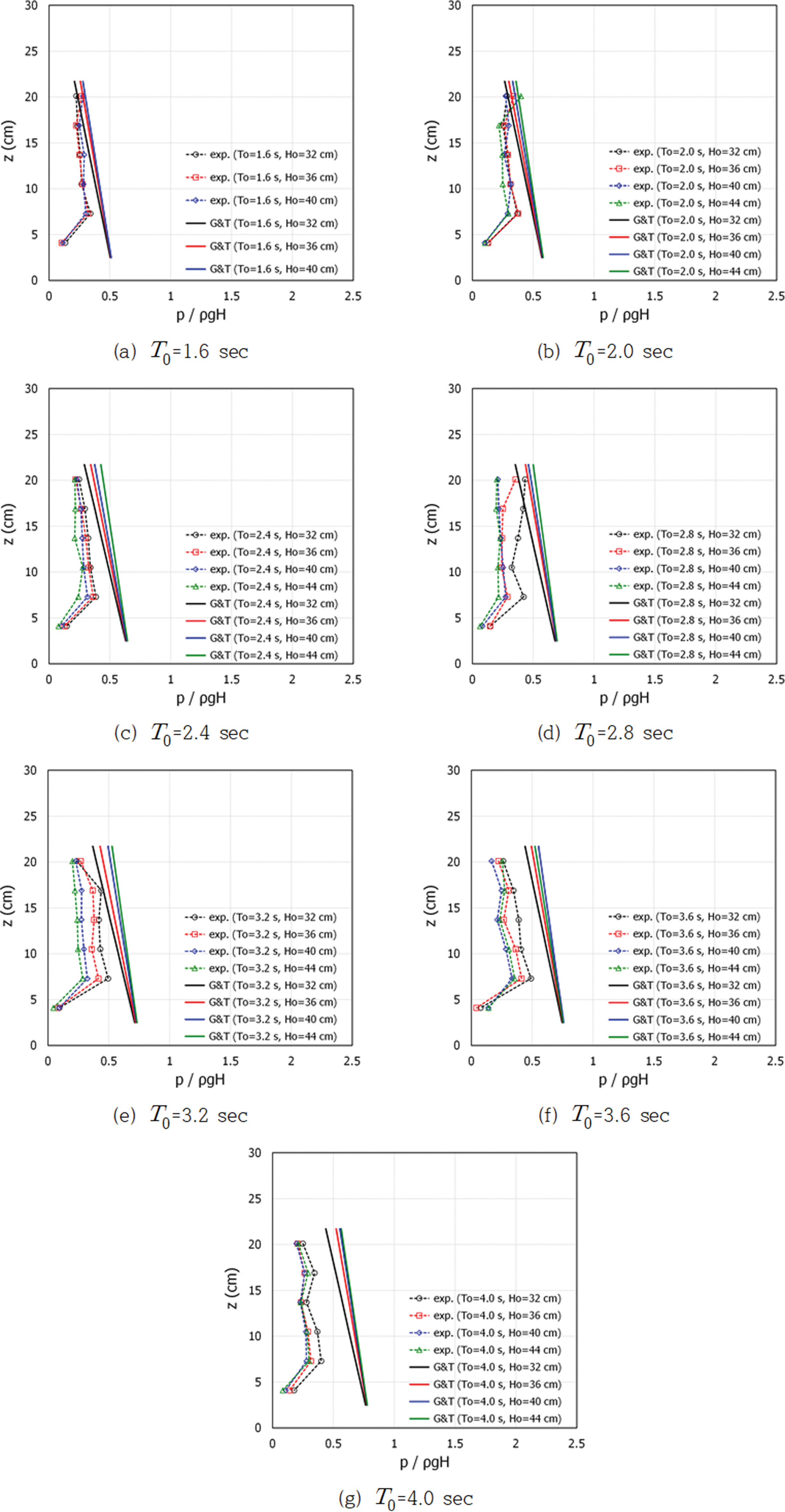
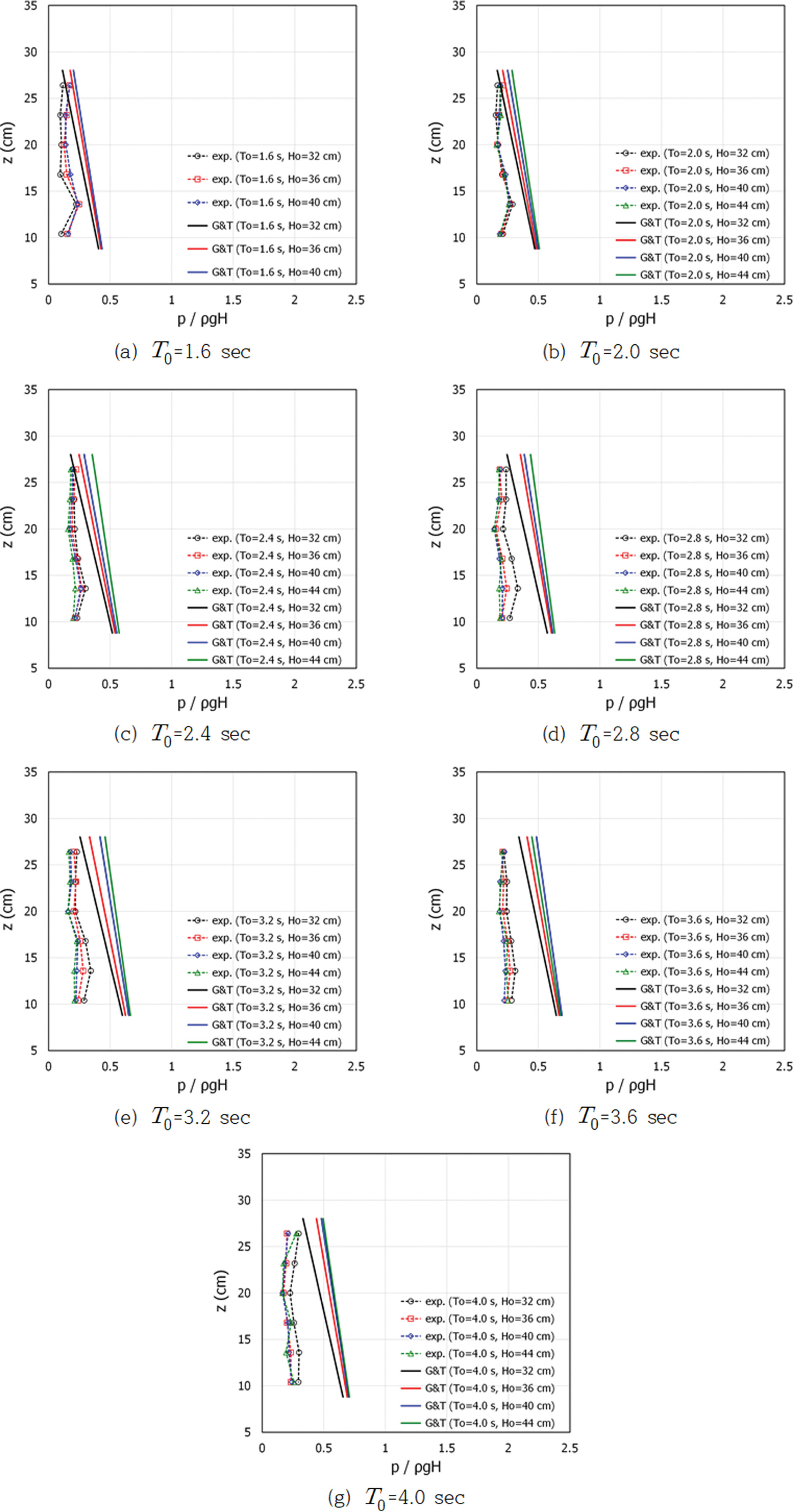
Figs. 4~6은 수행된 실험조건 중 일부를 도시한 것으로서 피복재 상단 어깨폭(G_W)이 G_W = 22.0 cm(G_W/D_n = 2.37)인 조건에서 피복재 하단고(A_C(-))에 따른 주기별 무차원 수평파압을 본 실험결과와 G&T의 결과를 비교한 것이다. Fig. 4는 A_C(-) = 2.5 cm, A_C(+) = 21.7 cm, Fig. 5는 A_C(-) = 8.8 cm, A_C(+) = 28.0 cm, Fig. 6은 A_C(-) = 14.8 cm, A_C(+) = 34.0 m의 결과이다.

Fig. 4.

Vertical profiles of measured data and G&T’s results for A_C(−) = 2.5 cm.

Fig. 5.

Vertical profiles of measured data and G&T’s results for A_C(−)= 8.8 cm.

Fig. 6.

Vertical profiles of measured data and G&T’s results for A_C(−) = 14.8 cm.

Fig. 4는 A_C(-) = 2.5 cm이고 A_C(+) = 21.7 cm인 실험결과(exp.)와 현행 설계법(G&T)에 의한 결과를 비교한 것으로서 전체적으로 현행 설계법에 의한 무차원 수평파압보다 작게 계측되었다. 연직방향의 무차원 수평파압 분포를 살펴보면 가장 아래 지점의 무차원 수평파압은 상대적으로 작게 계측되었으나, 그 외 계측점에서의 무차원 수평파압 분포는 거의 일정함을 알 수 있다. 가장 낮은 계측점의 수평파압이 작게 계측된 것은 정수면 인근 위치이기 때문에 경사면에서 처오른 파랑의 영향이 크지 않기 때문으로 판단된다. Fig. 5는 A_C(-) = 8.8 cm이고 A_C(+) = 28.0 cm인 실험결과(exp.)와 현행 설계법(G&T)에 의한 결과를 비교한 것으로서 무차원 수평파압의 분포는 Fig. 4의 결과와 유사하지만, 피복재가 정수면으로부터 높아짐으로 인해 전체적인 무차원 수평파압의 크기는 감소하였다. 또한 Fig. 4의 결과와는 달리 가장 낮은 계측점에서의 수평파압도 다른 계측점에서의 수평파압과 크기가 유사함을 알 수 있다. Fig. 6은 본 실험조건 중 피복재가 정수면으로부터 가장 높은 곳에 위치하는 A_C(-) = 14.8 cm, A_C(+) = 34.0 cm 조건인 실험결과(exp.)와 현행 설계법(G&T)에 의한 결과를 비교한 것으로서 무차원 수평파압은 Fig. 4과 Fig. 5의 결과에 비해 상당히 감소하는 것을 확인할 수 있다. 타 조건과는 달리 주기가 길어지는 경우에 최상단에 위치한 계측점에서의 수평파압이 타 계측점보다 크게 분석되었으며, 이는 피복재 상단고가 증가함으로 인해 제체 사면에서 처오른 파랑이 월파되지 못하고 최상부를 타격하기 때문으로 판단된다.

규칙파를 적용한 수평파압 계측결과(exp.)는 현행 설계법(G&T)에 의한 결과보다 전체적으로 작게 나타났으며, 일부 조건에서만 유사한 크기를 보였다. 본 실험결과를 이용하여 규칙파 작용시 상치콘크리트에 작용하는 수평파압 산정 경험식을 도출하고자 한다.

4. 결과 분석

본 실험에서는 상치콘크리트 전면 전체가 테트라포드로 피복된 경우에 대해 규칙파를 적용한 수평파력 계측실험을 수행하였고, 분석된 결과를 이용하여 상치콘크리트에 작용하는 수평파압을 산정할 수 있는 경험식을 제시하고자 한다. Figs. 4~6에 나타난 바와 같이 무차원 수평파압의 연직방향 변화는 크지 않으므로 전체를 평균한 수평파압으로 산정식을 도출하여도 큰 문제는 없을 것으로 판단된다.

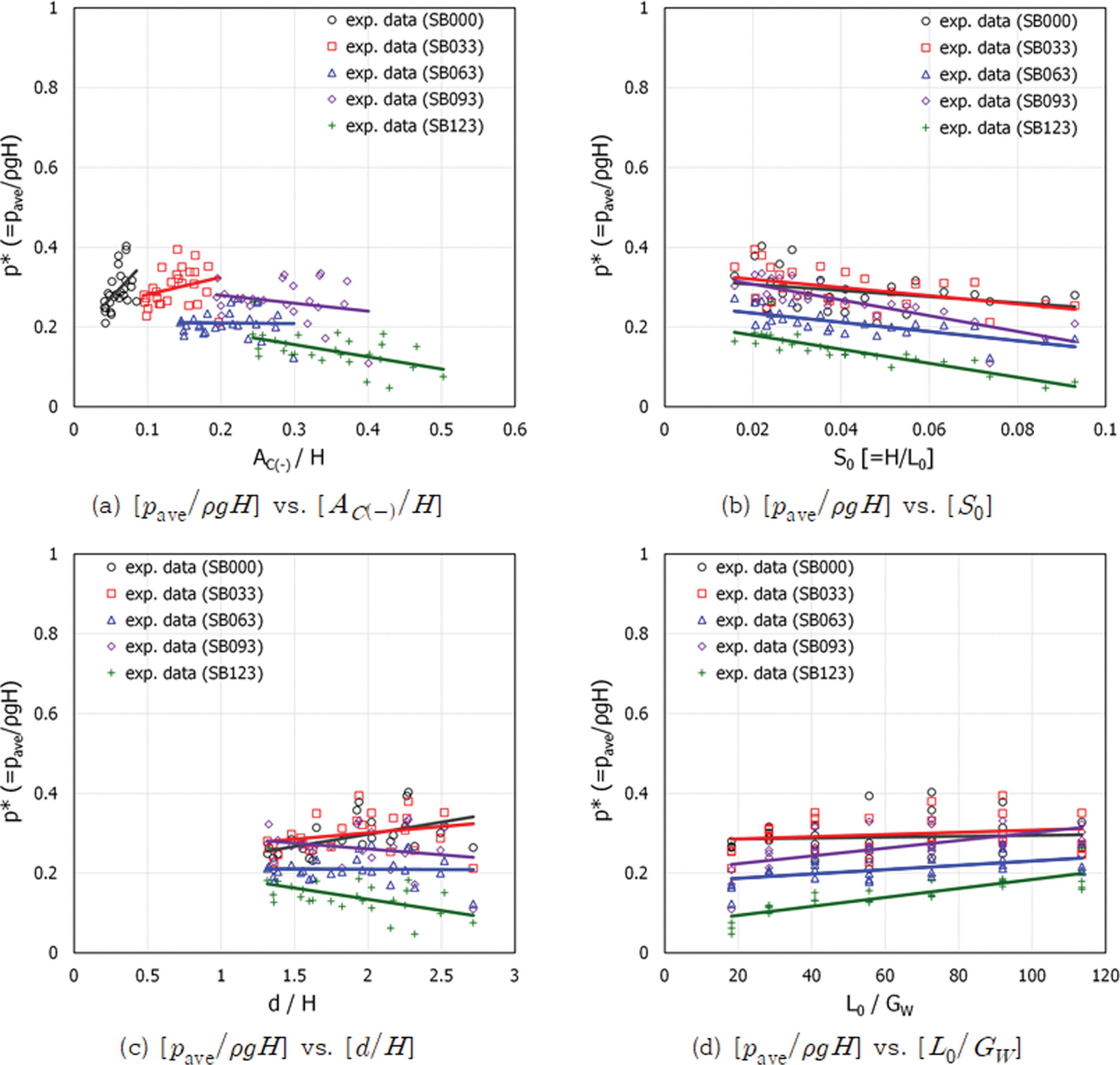
Fig. 7은 무차원 수평파압(p* = p_ave/ρgH)을 상대 피복재 하단고(A_C(-)/H), 파형경사(S₀ = H/L₀), 상대수심(d/H) 및 상대 피복재 어깨폭(L₀/G_W)에 대해 도시한 것이다. Fig. 7(a)는 상대 피복재 하단고에 대한 무차원 수평파압의 변화를 도시한 것으로서 상대 피복재 하단고에 따라 무차원 수평파압의 변화 기울기가 다소 상이한 결과를 보인다. 상대 피복재 하단 고가 낮은 경우에는 상대 피복재 하단고[A_C(-)/H]에 따라 무차원 수평파압이 증가하는 경향이고, 높은 경우에는 감소하는 경향이다. Fig. 7(b)는 파형경사에 대한 무차원 수평파압의 변화를 도시한 것으로서 피복재 하단고와 관계 없이 파형 경사가 증가할수록 무차원 수평파압은 감소하는 경향을 보인다. Fig. 7(c)는 상대수심에 대한 무차원 수평파압의 변화를 도시한 것으로서 피복재 하단고가 낮은 경우에는 증가하고, 높은 경우에는 감소하는 경향을 보인다. Fig. 7(d)는 상대 피복재 어깨폭에 대한 무차원 수평파압의 변화를 도시한 것으로서 피복재 하단고와 관계 없이 파장이 증가할수록, 즉 주기가 증가할수록 무차원 수평파압은 증가하는 경향을 보인다. 상대 피복재 하단고, 파형경사, 상대수심 및 상대 피복재 어깨폭에 대한 무차원 수평파압의 변화 기울기는 크지 않지만, 정수면으로부터의 피복재 높이에 따른 차이는 명확하게 나타났다.

Fig. 7.

Relationship between dimensionless horizontal wave pressure and dimensionless parameters.

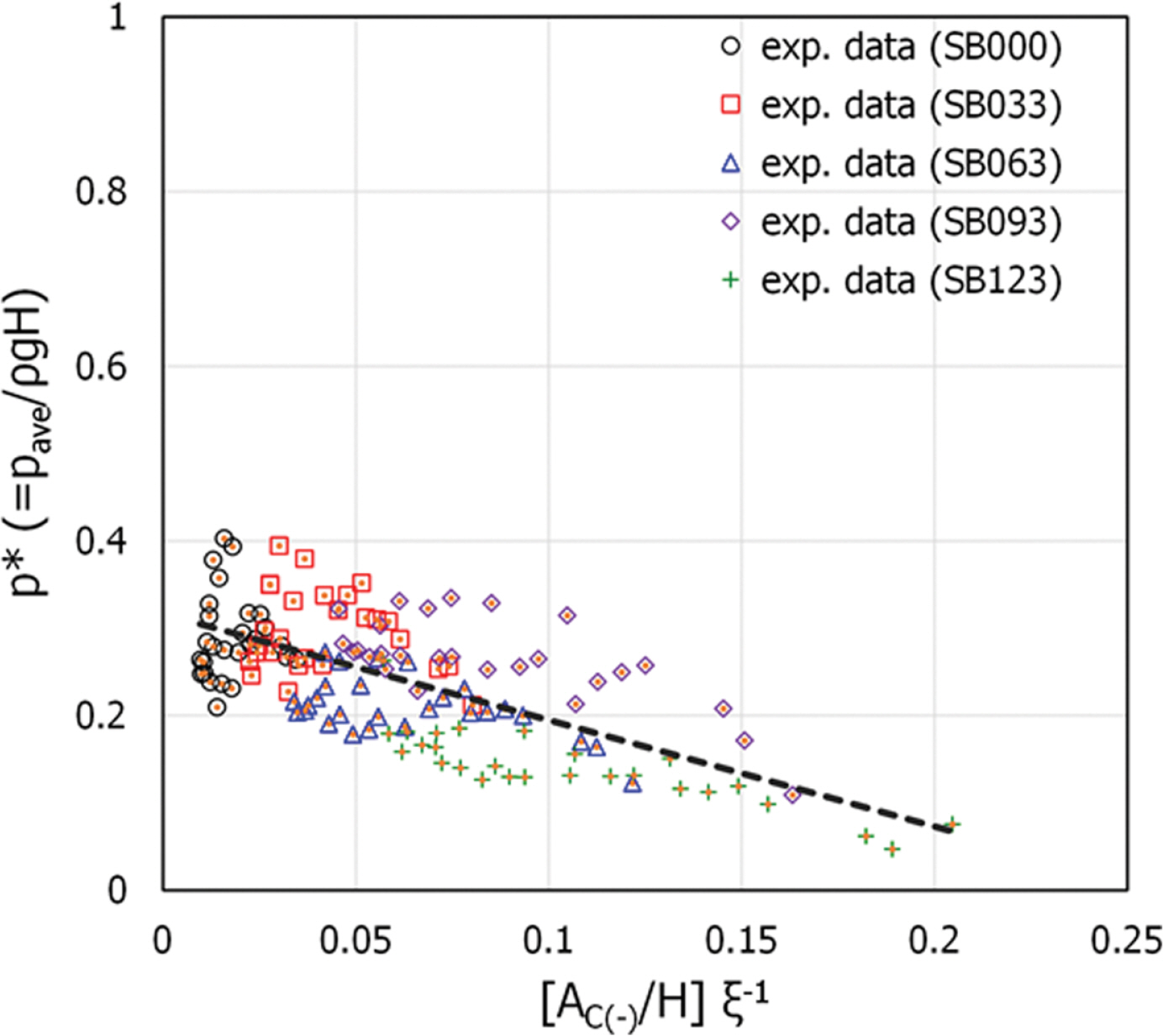
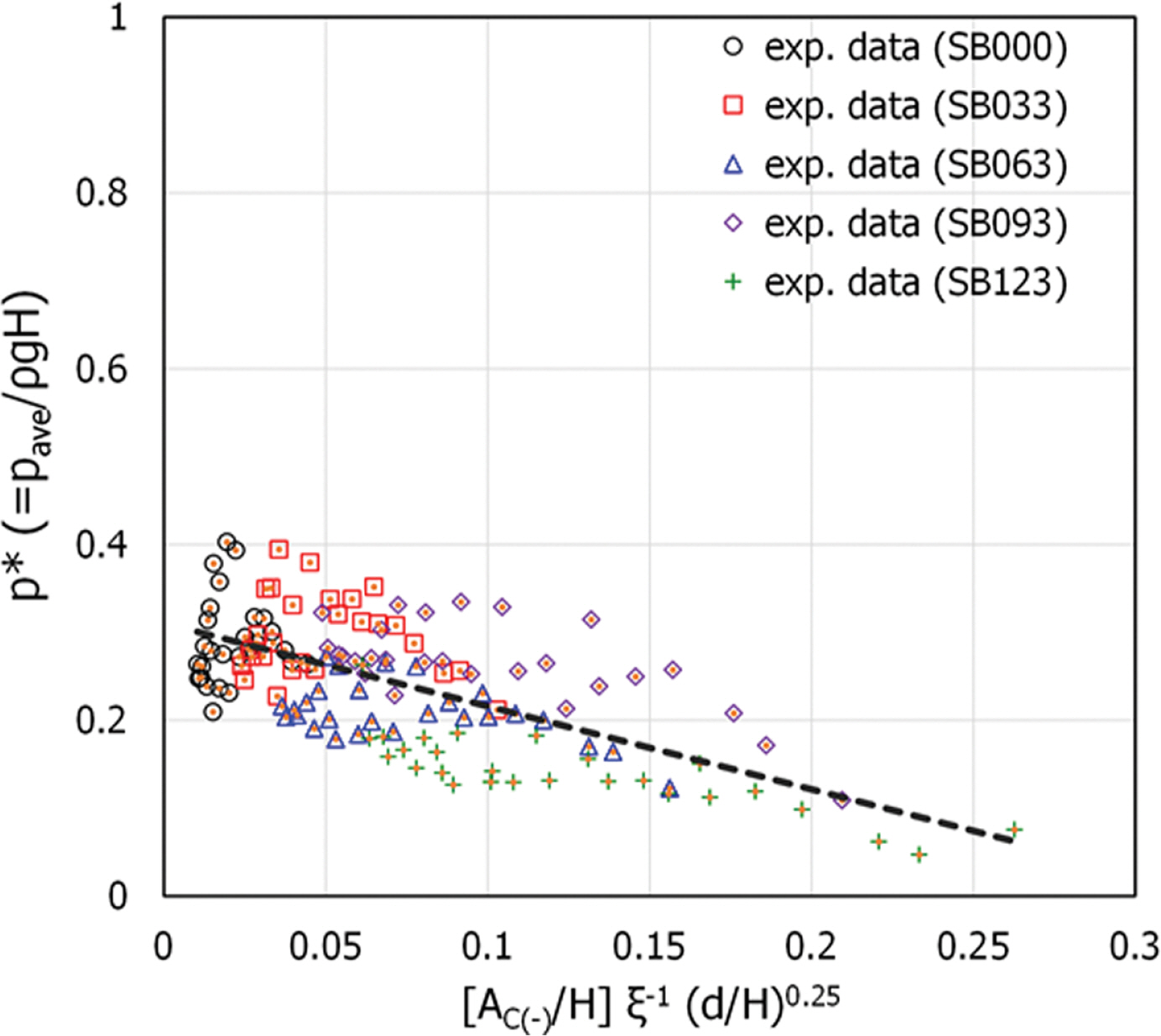
Fig. 8은 무차원 수평파압을 상대 피복재 하단고와 가중치를 적용한 쇄파 유사성 매개변수(ξ)의 곱에 대해 도시한 것이고, Fig. 9는 상대 피복재 하단고에 가중치를 적용한 쇄파 유사성 매개변수 및 상대수심의 곱에 대해 도시한 것이다. Fig. 8 및 Fig. 9에서 무차원 수평파압과 무차원 변수들의 곱에 대한 회귀식의 결정계수(R²)는 각각 R² = 0.47 및 R² = 0.45로 나타났으며, 수평파압의 분산이 커서 낮은 결정계수를 보였다. 여기서, 쇄파 유사성 매개변수(surf similarity parameter)는 ξ = tanα/ H/L0이고, tanα는 제체 사면경사이다.

Fig. 8.

Relationship between dimensionless horizontal wave pressure and (A_C(−)/H)ξ⁻¹.

Fig. 9.

Relationship between dimensionless horizontal wave pressure and (A_C(−)/H)ξ⁻¹ (d/H)^0.25.

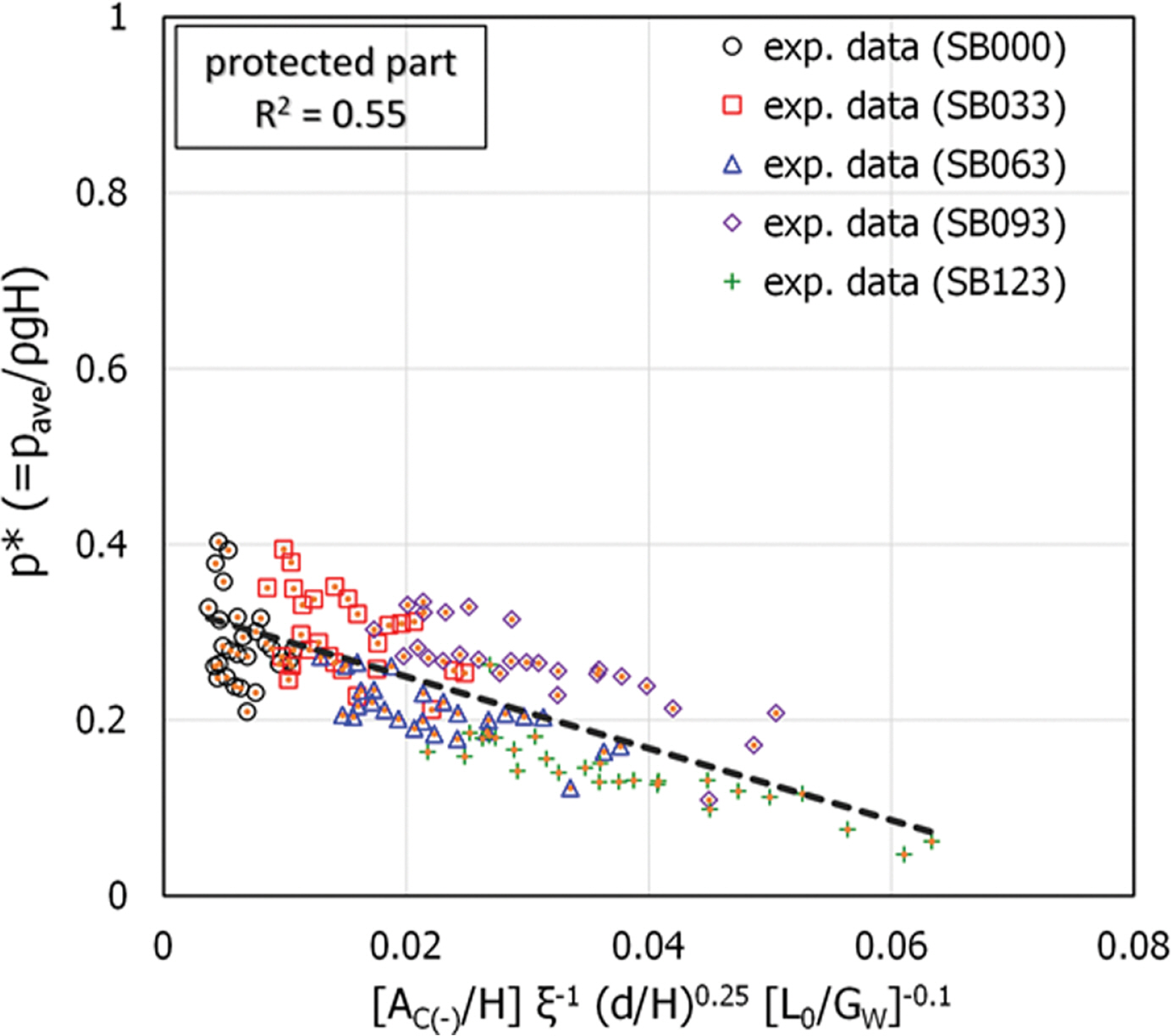
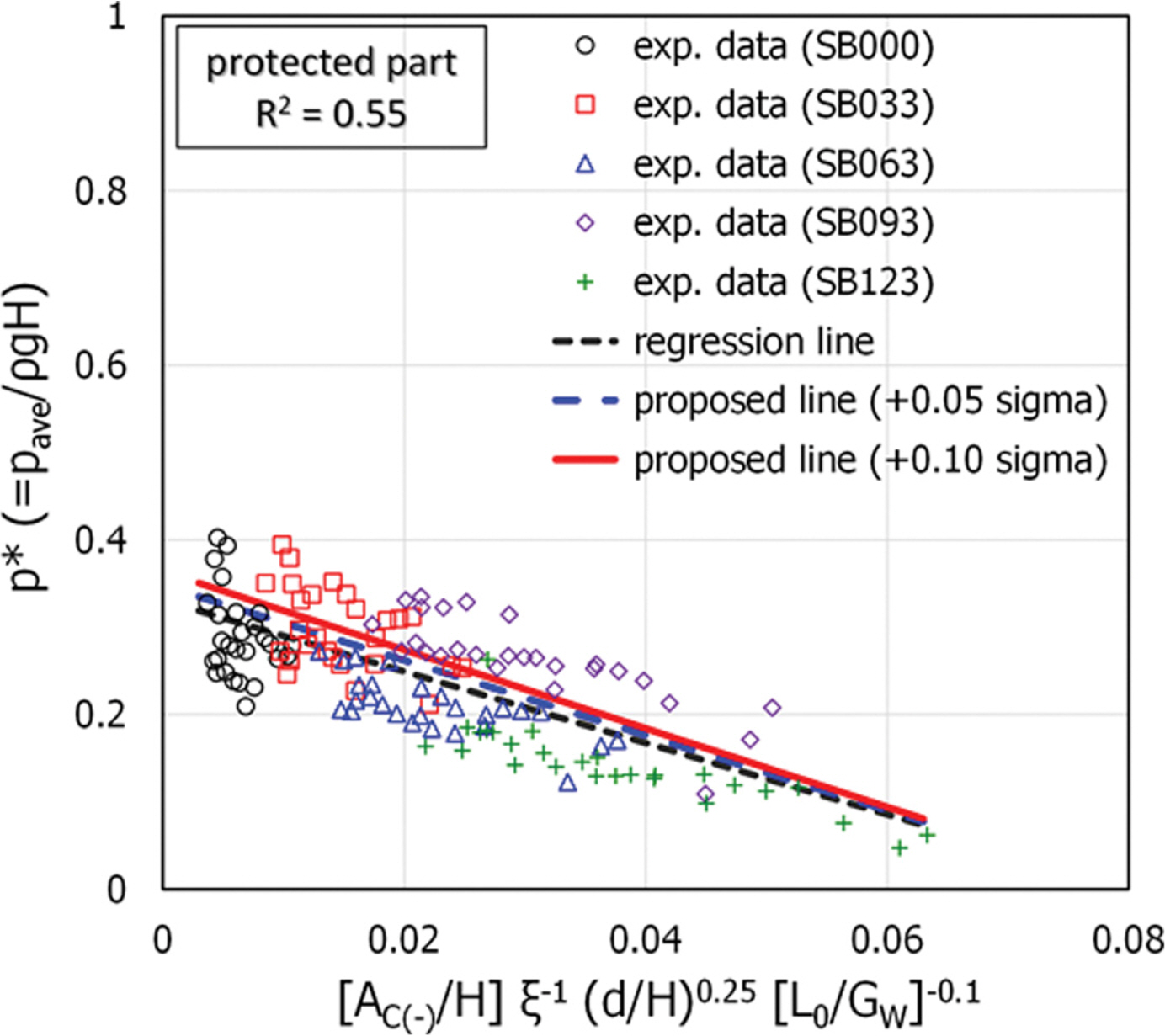
Fig. 10은 무차원 수평파압을 상대 피복재 하단고에 가중치를 적용한 쇄파 유사성 매개변수, 상대수심 및 파장의 영향을 도시한 것이다. 무차원 수평파압과 무차원 변수들의 곱에 대한 회귀식의 결정계수(R²)는 R² = 0.55로 나타났으며, 파장이 결정계수의 증가에 일정부분 영향을 미치는 것으로 나타났다.

Fig. 10.

Relationship between dimensionless horizontal wave pressure and [A_C(−)/H]ξ⁻¹ (d/H)^0.25 [L₀/G_W]^−0.1.

Fig. 11은 무차원 수평파압 제안결과를 도시한 것으로서 본 실험결과에 대한 회귀식과 무차원 수평파압 실험결과에 0.05σ 및 0.1σ를 더한 제안식의 결과를 비교하여 도시하였다. 여기서, σ는 무차원 수평파압 실험결과의 표준편차이다. Fig. 11에 도시된 무차원 수평파압 산정 경험식은 다음과 같다.

Fig. 11.

Results of dimensionless horizontal wave pressure acting on crown wall.

• 무차원 수평파압 실험결과 회귀식

• 무차원 수평파압 실험결과+0.05σ 회귀식

• 무차원 수평파압 실험결과+0.10σ 회귀식

• 무차원 수평파압 제안식의 적용범위

수평파압 분석에서 무차원 변수인 상대수심(d/H) 및 상대 피복재 어깨폭(L₀/G_W)은 실험결과와 경험식의 상관도를 향상시키는데 큰 영향을 미치지 않았다. 그러나 본 제안식에서 상대수심 및 상대 피복재 어깨폭을 도입한 것은 향후 쇄파 및 피복재 어깨폭의 변화에 따른 영향을 고려하기 위함이다.

5. 결 론

현행 항만 및 어항 설계기준·해설(MOF, 2020)에는 경사식 구조물의 상치콘크리트에 작용하는 수평파압을 산정할 수 있는 지침이 정립되어 있지 않아 직립식구조물에 작용하는 Goda의 파압 산정식(Goda, 1974, 2010)과 직립식구조물 전면에 소파블록이 전사면 피복되었을 때의 Takahashi et al.(1990)의 파압저감계수를 사용하여 수평파압을 산정하고 있는 실정으로서 설계지침으로 명확하게 정립되어 있지 않다. 또한 설계지침의 부재로 인해 간접적으로 파압을 산정하여 사용하고 있는 실정이지만 직립식구조물에 작용하는 파압특성이 경사식구조물에도 동일한가에 대한 의문은 남아 있다. 따라서 경사식구조물의 특성이 반영된 수평파압의 산정이 가능한 방법의 정립이 필요한 실정이다.

본 연구에서는 경사식구조물의 상치콘크리트에 작용하는 수평파압을 규칙파를 적용하여 검토하였다. 적용된 경사식구조물은 테트라포드가 2층 피복되고, 피복재 상단고와 마루높이가 동일한 조건이다. 경사식구조물의 상치콘크리트에 작용하는 수평파압 산정을 위해 2차원 수리모형실험을 수행하였으며, 도출된 결과를 요약하면 다음과 같다.

(1) 상치콘크리트에 작용하는 수평파압은 피복재 높이가 증가할수록 감소하고, 파형경사가 증가할수록 감소하는 경향을 보인다. 또한 상대수심이 증가할수록 감소하는 경향을 보이고, 주기가 증가할수록 증가하는 경향을 보인다.

(2) 규칙파 조건에서 상치콘크리트에 작용하는 수평파압은 실험결과에서 0.1(표준편차의 10%) 상향한 조건의 다음과 같은 산정식을 제안하고자 한다.

(3) 제안식의 적용범위는 다음과 같다.

본 연구에서는 규칙파를 적용하여 경사식구조물의 상치콘크리트에 작용하는 수평파압에 대한 수리모형실험을 수행하고, 수평파압 산정식을 제안하였다. 계측된 수평파압의 변동성이 다소 크게 나타났지만 수평파압의 분포 및 수평파압에 미치는 영향변수 등은 검토가 가능하였다. 본 실험결과는 마루높이와 피복재 상단고가 동일한 조건으로서 추후 마루높이가 피복재 상단고보다 높은 조건에 대한 검토도 필요하다. 또한 상치콘크리트에 작용하는 양압력에 대한 검토도 추가로 필요하다고 판단된다. 본 논문에서는 규칙파를 적용하여 상치콘크리트에 작용하는 수평파압 산정을 위한 경험식을 제안하였으나, 실제 해역에서는 불규칙파가 작용하기 때문에 실무적인 적용 측면에서는 다소 미흡한 실정이지만, 상치콘크리트에 작용하는 수평파압 경험식의 도출 가능성은 확인하였다.

본 연구와 관련하여 일련의 실험이 진행 중에 있으며, 최종목표는 실무 적용성을 위해 불규칙파를 적용한 수평파압 및 양압력을 산정할 수 있는 경험식을 제안하는 것으로서 이에 대한 결과는 추후 제시하고자 한다.

Article information Continued