2.1 파형 경사 자료

파형경사는 유의파고와 파장의 비율로 정의되는 변수를 의미하며, 파장 계산에 필요한 주기와 수심은 기상부이에서 제공하는 자료를 이용하였다. 파장은 미소진폭파(선형파) 이론으로 유도되는 분산 관계식(dispersion relationship; Holthuijsen, 2007)을 이용하여 추정하였다. 본 연구에서 파형경사 변수 생성에 이용한 자료는 KMA에서 운영하는 기상부이 31개 지점의 2023년 관측자료이다(Fig. 1, Table 1 참조). 본 연구에서 대상으로 하는 파형경사는 관측자료에서 제공하는 파고(H_m0, H_s), 첨두주기(T_p) 정보를 추출하여 생성한 파형경사(파생변수, 다수의 관측 변수를 조합하여 생성되는 또 하나의 변수) 자료이다. 한 지점에서 생성되는 파형경사 자료는 1년 동안 1시간 간격의 관측자료로 생성되므로, 결측이 없는 경우, 전체 8,760개가 생성된다. 2023년 관측 기간이 1년에 크게 못 미치는 3개 지점(남해 244, 고성, 삼척 – KOB 111, Goseong, Samcheok)은 분석에서 제외하였다. 또한 파고가 제로(H_s = 0)인 자료는 분석에서 제외하였으며, 본 연구에서 사용한 28개 지점의 기본 통계정보를 추정하여 제시하였다(Table 2 참고). 표에서 볼 수 있는 바와 같이 정점 2, 3, 11번에서 보이는 높은 첨도는 평균 영역(몸통 부분, body)에서 크게 벗어나는 꼬리(tail) 부분에 위치한 파형경사 자료에 의한 영향으로 간주할 수 있다(De Carlo, 1997; Westfall, 2014). 한편, 정점 14번(서귀포)의 음수로 추정된 왜도는 왼쪽으로 치우친(left-skewed) 분포로 판단할 수 있으며, 오른쪽으로 치우친(right-skewed) 다른 21개 지점과는 매우 다른 특이한 분포 형태를 보이고 있음을 알 수 있다. 이 정점에 대한 심층 분석이 요구되나, 본 연구에서는 전체적인 특성 파악에 중점을 두어 진행하기 때문에 제외하였다.

Figure 1.

Location map of the KMA ocean monitoring stations.

Table 1.

Basic information of the KMA monitoring stations

Table 2.

Basic statistical measures of the wave steepness

2.2 분포 추정 방법

파형경사의 분포는 대표적인 비모수 추정 방법에 해당하는 Kernel 분포 추정형태를 기준으로 이용하였으며, 모수적인 분포 추정함수는 Cho(2021b), Cho and Park(2024) 등이 우리나라 동해 연안에서 파형경사 분포로 제안한 바 있으며, 다수의 첨두 및 변곡(reflection) 형태 재현이 가능한 Gauss 혼합(Gaussian mixture distribution, 이하 GMD) 함수(모형)을 선택하여 수행하였다. GMD 모형은 서로 다른 평균, 표준편차를 가지는 다수의 정규분포함수를 선형조합(혼합, mixtures)하는 모형으로 조합하고자 하는 개수와 각각의 정규분포함수에 대한 가중계수를 이용하여 표현할 수 있다(식(1) 참고). GMD 모형의 적절한 개수를 판단하는 절대적인 기준은 없으나, 실질적이고 적절한 추정이 요구된다. 본 연구에서는 GMD 모델 개수를 추정 대상이 되는 파형 경사 자료에 분류 모형을 적용하여 가장 적절하다고 판단되는 분류 개수로 결정하였다. 분류개수 결정에 사용한 방법은 K-평균 분류기법(kmeans clustering), 성능판단에 사용한 기준 지수는 Silhoutte 점수를 이용하였다. 본 연구의 분석 작업은 R 프로그램(R Core team, 2024)을 이용하여 수행하였으며, 세부 수행과정에서 사용한 패키지 및 함수를 명시하였다. 최적 분류 개수 결정에는 ‘NbClust’ 패키지의 NbClust() 함수를 사용하였으며, 인덱스 옵션으로 Silhouette 지수를 선택하였다(Charrad, 2014).

Gauss 혼합 분포모형의 매개변수는 최우도법 기반의 EM(expectation & maximization) 알고리즘(Jun, 2012; Oh, 2008)을 이용하여 추정하였다. 매개변수 추정에 사용한 함수는 Kernel 분포함수, Gauss 혼합 분포함수에 대하여 각각 ‘stats’ 패키지 density() 함수; ‘mixtools’ 패키지의 normalmixEM() 함수를 이용하였다(R Core Team, 2024; Milard, 2013; Benaglia et al., 2009).

여기서, f_m(x) = 파형경사 변수(x)의 확률밀도함수로 평균과 표준편차가 다른 다수의 정규분포함수를 선형조합한 함수, m = GMD 모형을 구성하는 정규분포 함수의 개수이며, λ_k = k 번째 가중계수이고, 각각의 정규분포 함수는 아래와 같다(식 (2) 참고).

여기서, μ_k, σ_k = 각각 k번째 정규분포 함수의 평균, 표준편차이다.

따라서 추정하여야 하는 매개변수의 개수는 가중계수의 제약조건 하나를 반영하면 3m – 1개가 된다. 매개변수 추정은 최우도법(max. likelihood method) 기반으로 수식을 구성하며, 구성되는 다수의 변수를 포함하는 비선형 연립방정식의 해는 EM(expectation and maximization) 알고리즘으로 추정한다. 매개변수 최적 추정에 이용되는 우도, 로그우도(log-likelihood) 계산은 다음 수식을 이용한다.

Log-likelihood,

여기서 n = 파형경사 자료의 개수이다.

3.1 파고-주기 분포함수

파형경사는 파고와 파장으로 정의되지만, 파장은 대표적인 파랑 관측에 해당하는 정점 관측으로는 계측할 수 없다. 일반적으로 제공되는 주기와 수심 그리고 선형파 이론에서 유도되는 분산관계식(dispersion relationship; σ² = gktanh(kh), σ = 2π/T = wave frequency, k = 2π/L = wave number, T = wave period(s), L = wave length(m), h = water depth(m))을 이용하여 파장을 추정하고, 그 추정된 파장을 이용하여 파형경사 정보를 생산한다. 따라서 자료의 관점에서는 파형경사 변수 생성에 이용되는 파고와 주기의 결합확률 분포에서 파형경사 변수가 차지하는 위치는 중요한 특성이므로, 해당 변수를 양쪽 꼬리 부분에서 분석하였다(Fig. 2, Fig. 3 참고). 또한, 파고와 주기의 관계를 추가적으로 분석하기 위해 Fig. 4에 이를 도시하였다. 그림에서 볼 수 있는 바와 같이, 파고는 잔잔한 해역에 해당하는 정점 10, 26번(신안, 풍도)에서는 파고가 전반적으로 매우 작게 나타나고 있다(Fig. 2 참고). 한편, 주기의 하한 경계는 2.0초 정도로 판단되며, 이는 해수면 고도 관측 간격(∆t)이 1.0초 조건에서 관측되는 경우에 해당한다. 분해 가능한(주파수 해상도, resolution) 최대 주파수(Nyquist frequency)는 1/(2∆t)로 계산되며, ∆t = 1.0 조건에서 Nyquist 주파수의 역수로 가장 작은 주기 2.0(초)가 계산된다. 또한 주기자료에서 보여지는 부등 간격의 주기 자료는 스펙트럼법을 이용하는 경우, Nyquist 주파수를 스펙트럼 분석에 사용하는 해수면 자료 개수 또는 그 이하의 수준(스펙트럼의 Smoothing 정도로 인한 주파수 해상도 저하)으로 등분하고, 그 등분된 주파수 영역에서 첨두주파수를 산정하고, 그 주파수를 이용하여 첨두주기를 산정하는 경우 발생하는 현상이다. 첨두주파수 영역은 상대적으로 작은 주파수 영역으로 그 주파수의 역수를 취하는 경우, 급격하게 증가하는, 큰 간격을 가지는 주기 산정이 불가피하다. 이러한 조건에서 파형경사의 상한, 하한 5% 정도에 해당하는 파형경사를 도시한 그림(상한 파형경사는 red c ircle; 하한 파형경사는 blue circle)에서 보면, 주기에 대한 파고 변수의 상한-하한경계에 위치하고 있음을 알 수 있다(Fig. 4 참고). 그리고 상한경계의 경우, 주기 증가에 따라 파고, 파형경사가 뚜렷하게 증가하는 경향을 보이기 때문에, 파고-주기 등과 같은 다변량(multi-variate) 조건에서 적절한 조합을 이용하여 하나의 파생 변수(derivative variables)를 구성하는 경우 차원 축소 효과도 기대할 수 있다. 본 연구에서는 그 후보로 파형경사를 제안한다.

Figure 2.

Density plot of the wave height data (x-axis – wave height (unit: m), y-axis – probability).

Figure 3.

Density plot of the peak wave period data (x-axis – wave period (unit: s), y-axis – probability).

Figure 4.

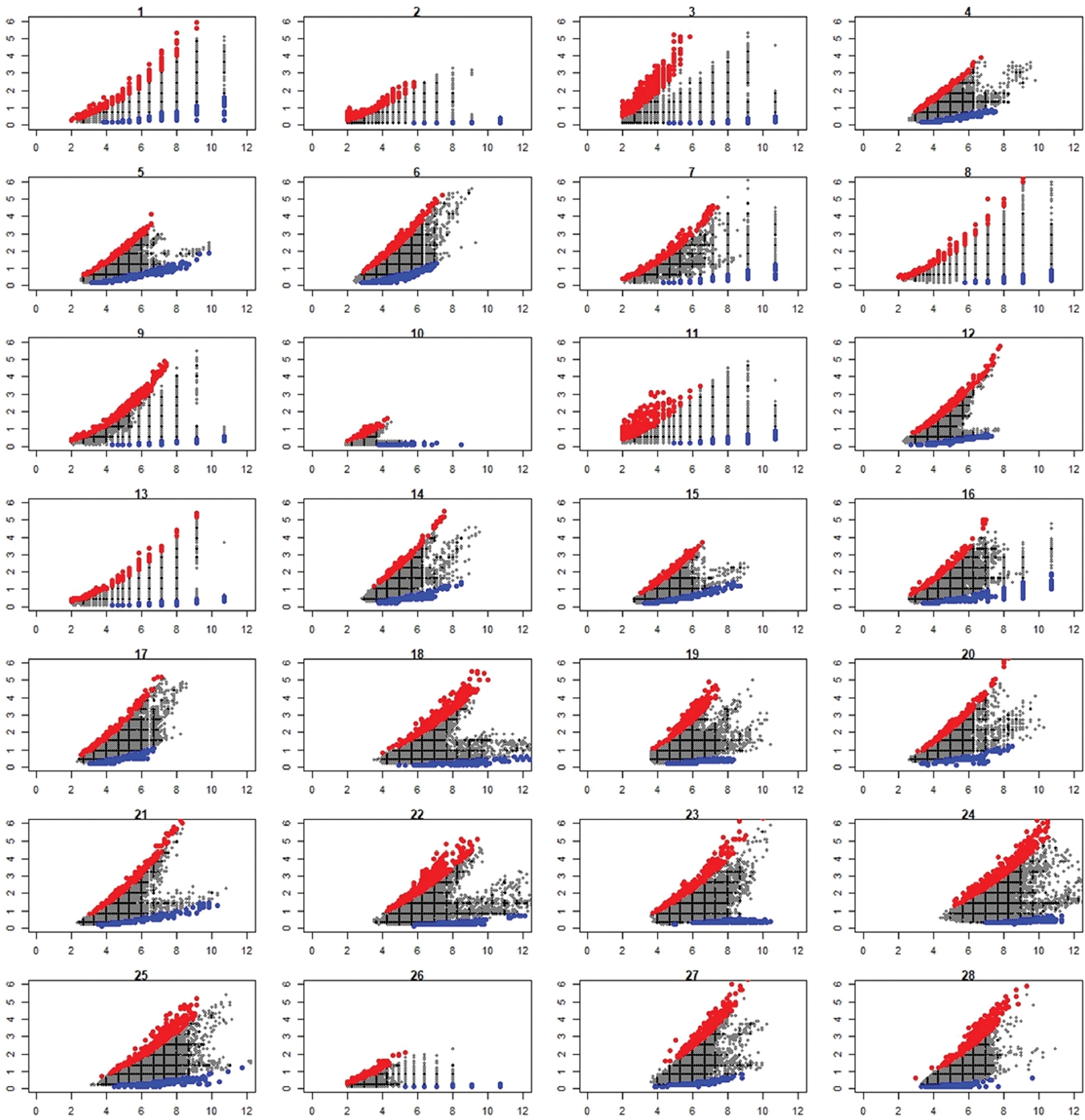
Scatter plot of the wave height and period (Symbols: blue circle = below 5% quantiles, red circle = above 95% quantiles of the wave steepness data points) (x-axis – wave period (unit: s), y-axis – wave height (unit: m)).

주기 분포는 주기가 대략 6초 정도를 넘어서는 영역에서 불연속적인 분포양상을 보이고 있음, 이는 주파수 해상도(0.01 정도) 관점에서 보면 6초는 0.17 정도, 이후 보다 저주파수 영역이 장주기 영역에 해당하는데, 주파수 영역이 0.16부터 0.05 수준까지 등간격으로 감소하는 경우, 그에 해당하는 주기는 6.25, 6.67, 7.14, 7.69, 8.33, 9.09, 10.00, 11.11, 12.50, 14.29, 16.67, 20.00 간격으로 변화하는 영향이 반영된 것으로 판단된다. 스펙트럼 기법을 이용하여 첨두 주파수를 추정하여, 첨두주기를 역산하는 경우, 발생하게 되는 수치적인 문제이다. 이를 방지하기 위해서는 첨두 주파수 정보에 해상도 수준의 흐트림(jittering) 크기를 적용하여 주기를 추정하여야 연속적인 주기분포 형태를 얻을 수 있다.

3.2 파형경사의 분포함수 추정

파형경사의 분포 추정 과정은 다음과 같은 세부 단계로 구분한다. 비모수 기법을 이용한 분포 형태 추정, 분류기법을 이용한 파형경사 자료의 최적 분류개수 추정, 추정된 분류개수(m)에 해당하는 GMD 모델(이하 GMD(m) 표기)의 매개변수 추정 및 분포 적합 검정으로 구성된다. 이상의 과정을 종합하여 파형경사 GMD(m) 분포함수와 기준이 되는 분포함수를 비교하여 도시하였다(Fig. 5 참고). 파형경사의 최적 분류개수는 정점 11번(추자도의 경우, 3개)을 제외하고는 모두 2개가 최적으로 결정되어, GMD(2) 모델 조건에서 추정된 모델 매개변수를 정리-제시하였다(Table 3 참고). 물론, 자료의 분류개수가 증가하는 경우, 추정하여야 하는 매개변수도 증가하고, 매개변수 추정에 필요한 계산량도 증가하는 단점이 있으나, 전체적인 분류 성능은 꾸준하게 점점 작아지는 정도이지만 증가하는 경향을 보이고 있음도 확인하였다. 그러나 매개변수 추정이 점점 국지적인 최적(local optimum)에 도달하는 가능성도 존재하기 때문에, 수렴을 보장하는 EM 알고리즘을 능가하는 가용한 매개변수 추정 기법의 부재를 고려하면, 대략 2개 또는 3~4개 정도로 GM 개수로 실질적인 측면에서 한정할 필요가 있을 것으로 판단된다.

Figure 5.

Gaussian mixture distribution plot for the wave steepness (k = 2).

Table 3.

Optima parameters of the Gaussian two-mixtures distribution, GMD(2)

3.3 파형경사의 상관분석

파고와 주기 자료로부터 생성되는 파형경사 정보가 어떤 변수가 더 우세한 영향을 미치는지, 또는 어떤 방식으로 영향을 주는지를 파악하기 위해, 전통적으로 널리 사용되는 선형 상관계수(Pearson correlation coefficient)와 대표적인 순위 상관계수인 Spearman 및 Kendall 상관계수를 이용하여 분석하였다(Kendall, 1938, 1945). 또한 국지적인 비선형 상관 분석이 가능한 MIC(maximum information coefficient; Reshef et al., 2011) 정보를 추정하여 분석에 이용하였다. 상관계수 추정결과는 Table 4에 제시하였다. MIC 상관계수는 ‘minerva’ 패키지에서 제공하는 mine() 함수를 이용하여 계산하였다(Albanese et al., 2012).

Table 4.

Correlation coefficients and maximum information coefficients of the wave parameters

4.1 분포 형태에 따른 분류

파형경사는 대부분이 뚜렷한 단봉(single peak, single-modal) 형태의 분포라기보다는 다봉(multi-peak, multi-modal) 분포 형태 또는 단봉 형태분포의 결합으로 형성되는 변곡형태를 가지는 분포 형태를 보이기 때문에 적절한 첨두 개수의 추정을 선행하고, 매개변수 추정이 진행되어야 한다. Cho(2021b)는 동해 연안 파형경사 분포를 GMD(3) 모형으로 제안하였으나, 본 연구에서 전체적으로 적절한 첨두 개수를 분류 관점에서 평가한 결과, GMD(2) 모형이 적합한 모델로 파악되었다. 파형경사 분포함수의 적합 수준은 다수의 정규분포를 조합하는 GMD(m) 모형을 사용하면 점차로 증가하지만, 매개변수 추정이 불안정해지거나, 수렴조건을 만족할 때까지 과도한 반복 연산이 요구되는 단점이 있다. 따라서 첨두의 개수 2개를 기준으로 3개, 4개 정도 수준으로 확장하여 분포 적합수준을 높이는 방법도 목적에 따라 필요할 것으로 판단된다.

한편 왜도 계수를 이용한 분포함수 형태 분석도 유효한 것으로 판단된다. 파형경사의 분포형태는 왜도로도 판단할 수 있는 바와 같이, S-14번 서귀포 정점을 제외하고는 전반적으로 ‘positive(right)-skewed’ 형태를 보이고 있는 것으로 파악되었다. 그림에서도 볼 수 있는 바와 같이 서귀포 정점을 제외하고는 ‘치우친’ 형태 관점에서는 대부분의 지점에서 낮은 파형경사가 우세하고, 높은 파형경사 부분은 긴 꼬리를 가지고 있는 것으로 파악되었다(Fig. 5). S14 정점과 다른 지점과의 두드러진 환경 특성 차이가 보이지 않기 때문에 이 정점의 파형경사 분포는 검토가능한 모든 변수 등을 고려하여 국지적인 측면에서 보다 상세한 검토가 필요할 것으로 판단된다. 한편 첨두의 편평(peak flatness) 정도 또는 첨두 개수의 관점에서 개략적인 형태를 보면, 하나의 첨두가 우세하게 드러나는 분포와 그 첨두 분포가 뭉개어지는, Cho(2021b) 논문에서 언급한 확률 고원(probability pleatu) 또는 다수의 첨두로 구성되는 분포형태가 대등한 정도로 발생하고 있음을 알 수 있다. 첨두의 분리로 구성되는 multi-modal분포 형태는 두드러진 파형경사의 발생빈도가 크기 때문으로, 작은 파형경사와 높은 파형경사 또는 다수의 동등하게 발생하는 다소 복잡하고, 혼합된 분포형태를 보이고 있음을 알 수 있다.

따라서 다수의 첨두를 반영하는 Gaussian Mixture 분포함수 추정이 가능하고, 실제로 최적 모델(분포함수) 선정 기준이 되는 AIC(Akaike information criteria), BIC(Bayesian information criteria) 수치 관점에서 보다 다수의 첨두를 이용하는 분포함수가 분포함수 적합 측면에서는 우수한 것으로 판단되지만, 실질적인 측면에서 매개변수 추정에 과도한 반복 연산이 요구되고, 국지적으로 과도한 적합 형태를 보이고 있는 것으로 파악되어 본 연구에서는 첨두개수를 2개, 3개로 한정하여 비교 분석을 수행하였다. 각각의 조건에서 최적 추정한 매개변수 정보는 다음과 같다(Table 3).

4.2 파형경사와 파랑변수의 상관분석

파형경사 변수와 이를 생성하는 데 사용된 파고 및 주기 변수를 대상으로 상관계수를 분석하면, 어느 변수가 파형경사에 더 큰 영향을 미치는지와 그 영향의 유형을 판단할 수 있다.

Table 4에서 볼 수 있는 바와 같이 전반적으로 파고는 양의 상관을 가지고, 주기는 음의 상관을 가지는 것으로 파악되었으며, 비선형 상관(연관, association) 분석이 가능한 MIC 관점에서는 파고-주기 상관계수에 비하여, 파고-파형경사, 주기-파형경사 모두 높은 상관계수를 보이는 것으로 파악되었다. 수심의 영향은 전체적으로 미미한 수준으로 판단된다. 한편 그림(Fig. 4)에서 볼 수 있는 바와 같이 각각 상위 1%, 하위 1% 파형경사에 해당하는 지점을 파고-주기 scatter 도시에 중첩한 결과, 높은 파형경사는 파고-주기의 상한 경계 부분에 자리잡고 있으며, 낮은 파형경사는 하한 경계 부분에 위치하고 있음을 알 수 있다. 파고에 따른 일반적인 주기 증가 경향은 상한 경계 형성에 직접적으로 기여하고 있는 것으로 판단되며, 이 영역을 벗어나는 파형은 쇄파 등의 영향으로 사라지기 때문에 관측에서 감지되지 않는 것으로 판단할 수 있다.