2.1 실험 시설 및 모형

수리실험의 세부 사항은 Oh and Lee(2020)에 제시되어 있지만 본 논문에서 이후의 설명을 위해 주요 사항을 아래에 제시하였다. 실험은 길이 50 m, 폭 1.2 m, 높이 1.6 m인 2차원 조파수조(Oh and Lee, 2018)에서 수행되었다. 케이슨 모형은 아크릴로 제작되었으며 길이는 0.45 m, 폭은 0.4 m이고 높이는 각각 0.5 m와 0.6 m인 두 개의 모형이 제작되었다. 케이슨 모형의 전면은 12개의 독립적인 판으로 구성하였으며, 각 판의 중앙에는 초소형 파압계를 설치하여 케이슨 전면에 작용하는 파압을 계측하였다. 또한 케이슨 모형 양 옆으로 크기가 같은 케이슨 모형을 추가로 배치하였으나, 양쪽에 배치된 모형에는 파압계가 설치되지 않았다. 실험 모형은 조파판으로부터 28 m 지점에 설치되었고 조파수조 내 파고 계측을 위해 총 13개의 파고계가 사용되었다.

2.2 실험 조건 및 변수 정의

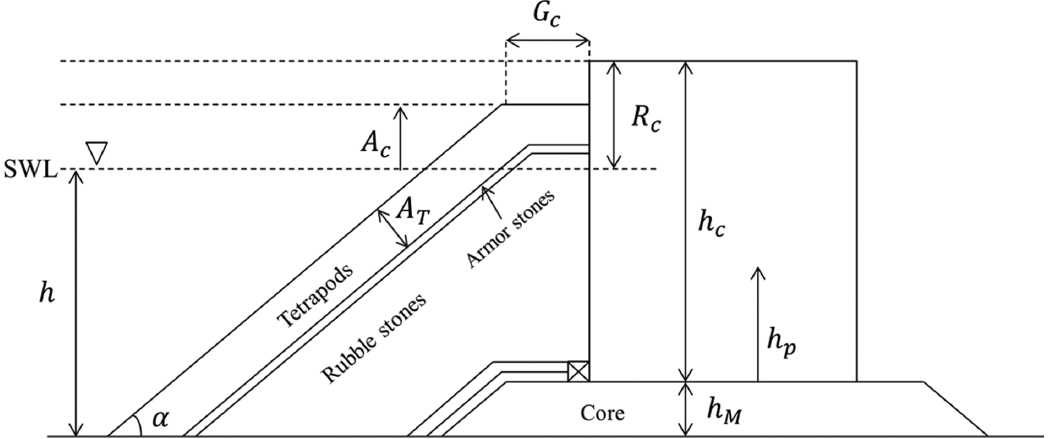
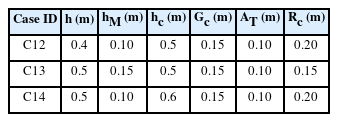
Fig. 1은 수평혼성제와 관련된 기하학적 변수들의 정의를 나타낸다. h는 수심, h_c는 케이슨의 높이, h_p는 케이슨의 바닥에서부터 임의의 지점까지의 높이, A_c는 정수면으로부터 소파공 상단까지의 높이, R_c는 정수면으로부터 케이슨 상단까지의 높이, G_c는 소파공의 어깨폭, A_T는 소파블록의 피복층 두께를 각각 의미한다. Table 1에는 실험 케이스별로 주요 변수들의 값을 제시하였다.

Figure 1.

Parameters related to the geometry of the horizontal composite breakwater.

Table 1.

Summary of the geometrical parameters in the experimental setup

한편, Oh and Lee(2020)는 케이슨 전면이 보강된 높이에 따라 피복의 정도를 표현할 수 있는 무차원 변수인 피복 (coverage rate, C_R)을 케이슨 전체 높이에 대한 소파공 높이로 정의한 바 있으며 이를 식으로 표현하면 다음과 같다.

소파공이 케이슨 전면의 상당 부분을 피복하도록 설치되는 것이 일반적이므로, 피복률을 위와 같이 정의할 경우 C_R의 적용 범위가 1에 가까운 좁은 범위로 제한된다는 한계점이 있다. 실제로 Oh and Lee(2020)에서도 0.7 ≤ C_R ≤ 1.0의 범위에 대해서 파압보정계수를 제시하였다.

이러한 점을 고려하여 본 연구에서는 정수면으로부터 소파공 상단까지의 높이(A_c)를 여유고(R_c)로 나눈 무차원 변수로 새롭게 피복률을 정의하였다.

즉, 식(2)에서는 케이슨 전면이 소파공으로 전혀 피복되지 않은 경우에 C_R = 0이 되지만, 식(3)에서는 소파공 높이가 정수면과 일치할 경우에 C_R = 0이 된다. 피복층이 케이슨 마루높이까지 완전히 피복된 경우에는 두 식 모두 C_R = 1로 같다.

Fig. 2에는 6개의 서로 다른 피복률로 보강된 케이슨 실험 조건을 제시하였다. Fig. 2(a)는 케이슨 전면이 피복되지 않은 조건(T01), Fig. 2(f)는 케이슨 마루높이까지 완전히 피복된 조건(T11)에 해당된다. 한편, Fig. 2(b) 및 2 (c)는 A_C가 R_C보다 15 cm 낮은 조건(T13)이며, 이 높이 차이는 실험에 사용된 테트라포드 모형 공칭직경의 두 배에 해당한다. A_C와 R_C의 차이는 같더라도 R_C의 높이가 서로 다르기 때문에 C_R 값이 차이가 나게 된다. Fig. 2(d) 및 2(e)는 A_C가 R_C보다 테트라포드 모형 공칭직경에 해당하는 7.5 cm 낮은 조건(T12)에 해당한다. 마찬가지로, 두 조건의 C_R 값은 서로 다르다. Fig. 3에는 Fig. 2(b) 및 Fig. 2(f) 조건의 실험 장면을 나타내었다.

Figure 2.

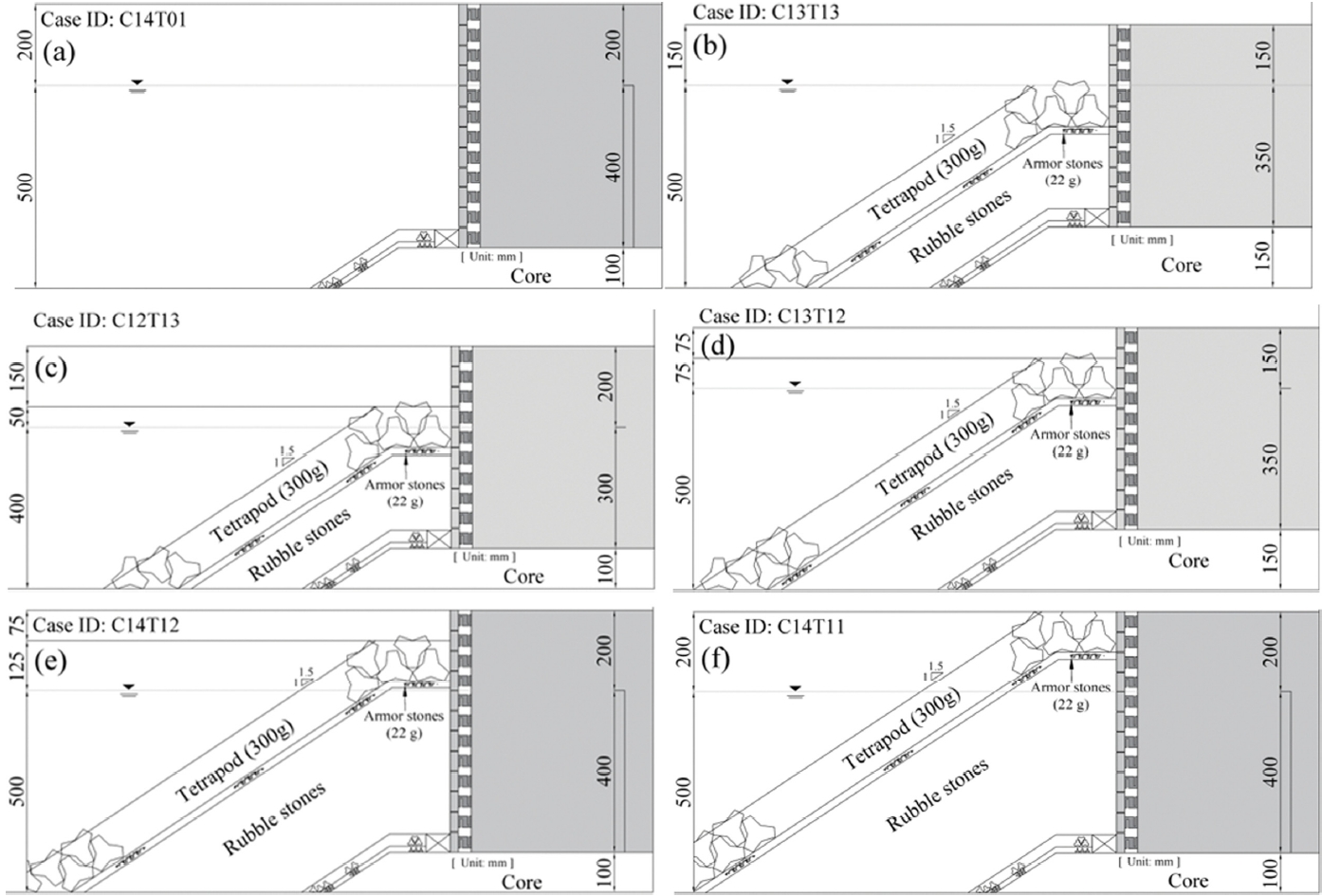
Six experimental layouts illustrating different coverage ratios in front of the caisson model (C_R): (a) no coverage, (b) C_R = 0, (c) C_R = 0.25, (d) C_R = 0.50, (e) C_R = 0.625, (f) C_R = 1.0.

Figure 3.

Photographs of the models: (a) C13T13 (C_R = 0) and (b) C14T11 (C_R = 1.0).

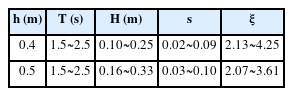
수리실험은 주기와 파고가 서로 다른 20개의 규칙파를 이용하여 수행되었다. 실험파 주기는 1.5 s부터 2.50 s까지 0.25 s 간격으로 설정되었으며, 쇄파 및 비쇄파 조건이 모두 포함될 수 있도록 각 주기별로 4개의 서로 다른 파고를 적용하였다. Table 2에는 주기 및 파고 외에 파형 경사(s)와 쇄파지수(surf-similarity parameter, ξ)의 범위도 함께 제시하였다.

Table 2.

Parameter ranges of the test waves used in the experiment

3.1 수평 파압 분포의 매개변수화

본 연구에서는 Oh and Lee(2000)의 분석 방법과 동일하게 케이슨 바닥으로부터 임의의 높이까지의 연직거리(h_p)를 케이슨 전체 높이(h_c)로 나누어 무차원화한 변수인 h_p/h_c에 따른 파압 분포에 근거하여 수평 파압 매개변수화를 시도하였다. 케이슨에 작용하는 수평 파압은 케이슨 전면이 피복된 실험조건(T11, T12, 그리고 T13)에서 계측된 값을, 피복되지 않은 실험 조건(T01)에서의 값으로 나누어 무차원화하였다. Fig.4에는 이렇게 계산된 무차원 파압의 연직분포를 나타내었다. 파란색 점은 실험에서 파압계로 계측된 지점별 최대파압을 무차원화한 값을 나타내며, 검은색 실선은 각 높이별 계측 파압의 평균값(μ)에 표준편차(σ)의 절반을 더한 값을 의미한다. 이는 통계적으로는 파압 계측 데이터 중 상위 33%에 해당하는 값으로, 파압 평균값을 사용하는 것에 비해 파압을 더 보수적으로 평가하는 것이다.

Figure 4.

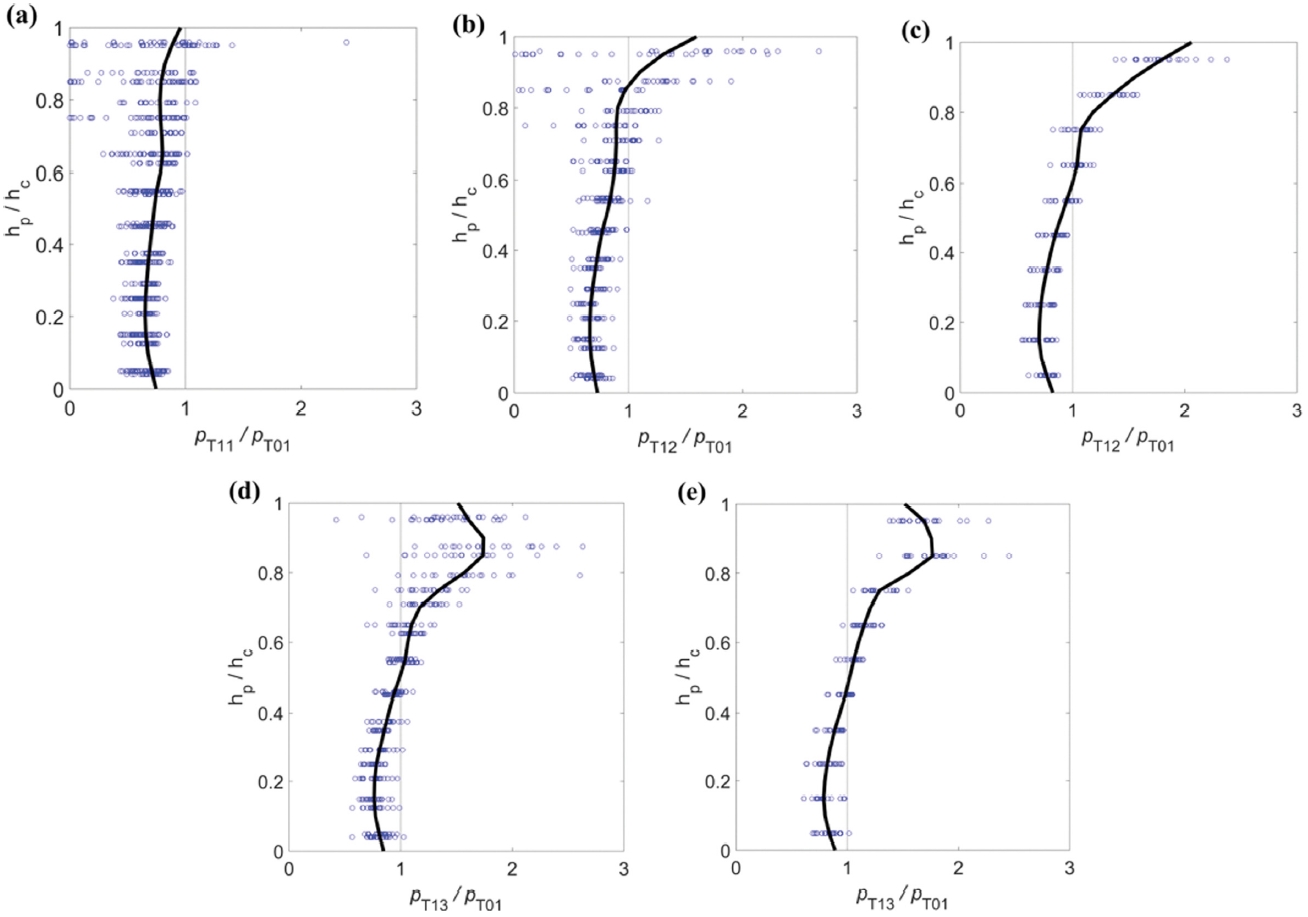
Non-dimensionalized horizontal wave pressures for different coverage ratios. (a) C_R = 1.0, (b) C_R = 0.625, (c) C_R = 0.50, (d) C_R = 0.25, and (e) C_R = 0.

Fig. 4(a)로부터 케이슨 전면이 완전히 피복된 경우에는 케이슨 전면을 따라 모든 높이에서 검은색 실선으로 나타낸 값이 1보다 작음을 확인할 수 있다. 이는 케이슨 전면이 마루 높이까지 완전히 피복되면 모든 구간에서 파압이 저감됨을 의미한다. Fig. 4(b)~(e)에는 케이슨 전면이 부분적으로 피복된 경우의 무차원 파압 분포도를 제시하였고, 이 경우 케이슨 상단 구간에 작용하는 파압이 피복이 이루어지지 않은 경우(T01)에 비해 더 크게 작용하는 현상이 나타났다. 이것은 케이슨 마루높이까지 완전 피복되지 않았을 경우 케이슨 상단 노출부에 충격성 파압이 작용하기 때문이다. 파압의 첨두값은 피복률이 상대적으로 커서 노출부가 작은 조건에서는 케이슨 최상단에서 나타났으며(Fig. 4(b)~(c)), 피복률이 상대적으로 작아서 노출부가 더 큰 조건에서는 케이슨 최상단보다 약간 아래 위치에서 나타났다(Fig. 4(d)~(e)). 한편, Fig.4(a)~(e)로부터 케이슨 바닥 근처에 작용하는 파압은 피복률의 차이에 따라서 크게 달라지지 않음을 확인할 수 있다.

당초 수리실험은 Oh and Lee(2020)에 제시된 것처럼 케이슨 전체 높이를 기준으로 70%와 85% 피복률을 대상으로 이루어졌지만, 본 연구에서 피복률 C_R을 식(3)과 같이 새롭게 정의하여 실험 데이터를 재분류하게 되면서 Fig. 4에 보인 것처럼 C_R 값에 따라 사용되는 데이터 개수에 차이가 있고, 이로 인해 데이터의 분포 범위에도 차이가 있다. 특히, Fig. 4(b)의 경우 실험 조건에 따라 케이슨 상단 노출부에 상대적으로 강한 충격파 성격의 파력이 작용하는 경우와 사면 상에서 소파가 이루어져 매우 약한 파력이 작용하는 경우가 공존함에 따라 데이터의 분산성이 상대적으로 크게 나타났다.

이처럼 계측된 실험 데이터에서 파압의 분산성이 크게 나타나는 이유는 Table 1에 제시된 것처럼 마운드 높이, 케이슨 높이 등 제원이 서로 다른 실험 단면에 대해서 다양한 파고 및 주기 조건의 실험파가 작용함에 따라 케이슨 전면 피복부에서의 소파 특성이 매우 큰 편차를 나타내기 때문이다. 그렇기 때문에 예를 들어 쇄파지수 또는 파형경사 등의 파라메터에 따라 파압 특성이 어떻게 구별되는지 분석해 보는 것도 의미가 있을 것이다. 그러나 파압의 변동성이 매우 크기때문에 이러한 파라메터를 모수화한 파압 저감계수를 도출하는 것은 매우 어렵고 훨씬 더 많은 실험 데이터가 필요하게 될 것이다. 이러한 점을 고려하여 본 연구에서는 Fig. 4에 검은색 실선으로 제시된 평균적인 파압 분포를 기준으로 수평 파압 보정계수를 도출하였다.

3.2 수평 파압 보정계수 도출

Fig. 5에는 Fig. 4의 검은색 실선을 점선으로 표시했고, 이 점선을 선형적으로 근사화한 회귀선(fitted line)을 빨간색 실선으로 나타내었다. 피복률(C_R)에 따른 파압 분포를 고려하여 케이슨 전체 높이를 4개의 Zone(0 < h_p/h_c ≤ 0.3, 0.3 < h_p/h_c ≤ 0.7, 0.7 < h_p/h_c ≤ 0.85, 0.85 < h_p/h_c ≤ 1.0)으로 나누어 회귀선을 제시하였다. 이를 바탕으로 각각의 피복률에 따라 케이슨 전면에 작용하는 무차원 파압을 수식(4)~(7)처럼 나타낼 수 있다. C_R = 0인 경우와 C_R = 0.25인 경우는 두 조건 차이에 따른 파압 분포가 거의 다르지 않아 식(7)과 같이 하나의 식으로 나타내었다. 또한, 케이슨 전면이 완전히 피복된 경우(C_R = 1.0)에는 Zone 1~3까지 무차원 파압의 변화가 크지 않아 0.75의 단일값으로 제시되었다.

Figure 5.

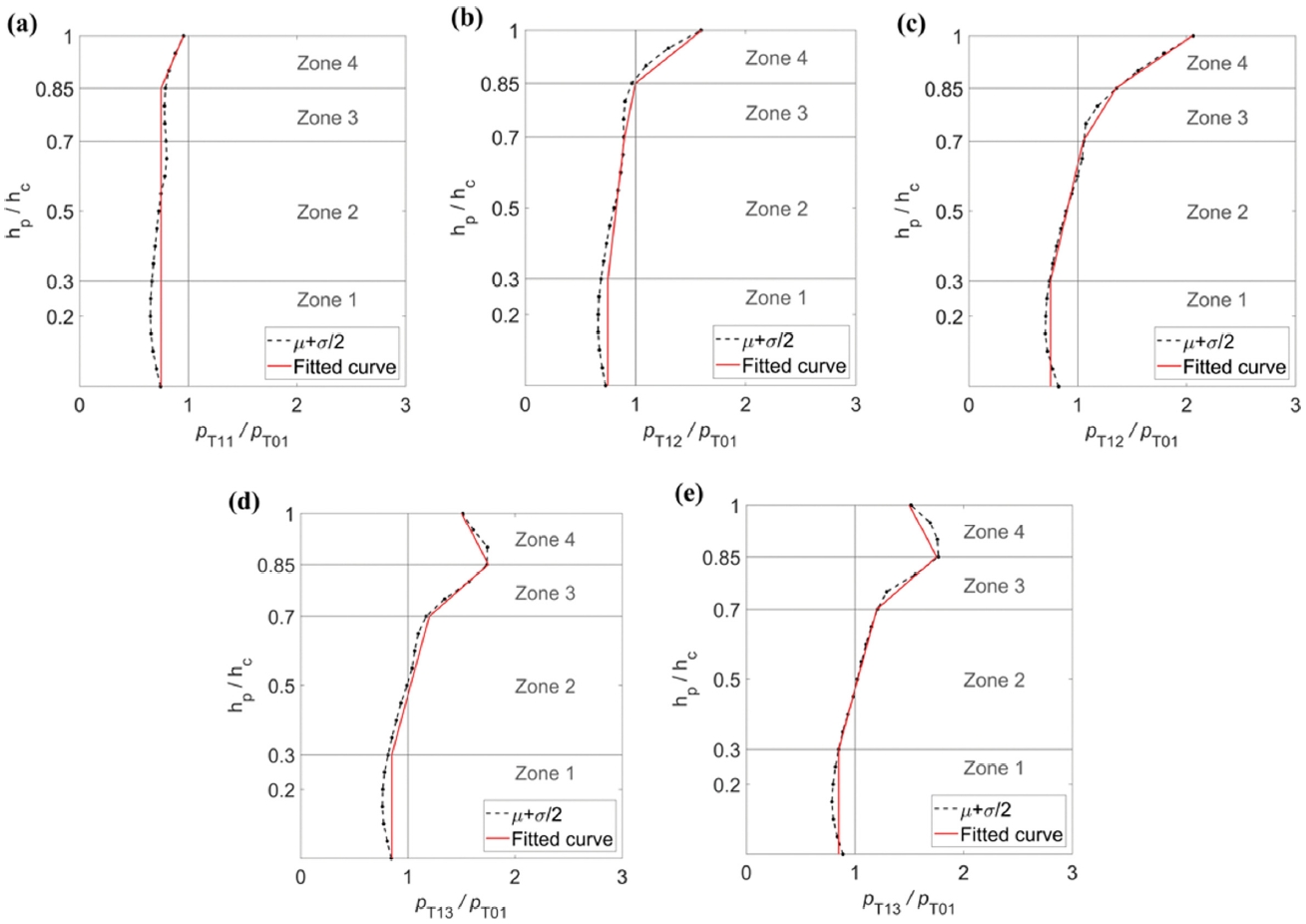
Separation of zones for parameterization of dimensionless horizontal wave pressures for different coverage ratios. (a) C_R = 1.0, (b) C_R = 0.625, (c) C_R = 0.50, (d) C_R = 0.25, (e) C_R = 0.

when C_R = 1.0

when C_R = 0.625

when C_R = 0.5

when C_R = 0 and C_R = 0.25

Table 3에는 4개로 구분된 Zone 각각에 대해 식(4)~(7)로부터 피복률에 따른 무차원 파압의 평균값을 계산하여 나타내었다. Zone 1에서 Zone 4로 갈수록(h_p/h가 증가할수록) 무차원 파압 값도 증가하며, 이러한 경향은 피복률(C_R)이 낮을수록 더 뚜렷하게 나타난다. 무차원 파압은 케이슨 전면이 피복된 경우의 파압을 피복이 이루어지지 않은 조건의 파압으로 나눈 비율을 의미하고, 후자의 경우 Goda파압식에 대응된다. 따라서, 무차원 파압 값은 사석마운드 위 소파블록으로 피복되는 수평혼성제의 수평 파압 보정계수로 정의할 수 있으며, 본 연구에서는 이 보정계수를 λ_C 기호로 표현하였다.

Table 3.

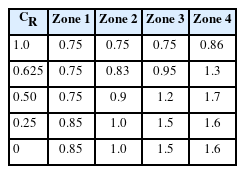
Average values of the normalized horizontal wave pressures calculated from the fitted lines from Zone 1 to 4 for different coverage ratio

Fig. 6에는 Table 3에 제시된 피복률(C_R)에 따른 구간별 무차원 파압의 평균값, 즉 파압 보정계수(λ_C) 값들을 나타내었다. 또한, Zone 1부터 Zone 4까지 각 구간별로 λ_C의 데이터를 바탕으로 각 구간별로 λ_C의 경향을 보여주는 선형 근사화 결과를 실선으로 함께 나타내었다. 그리고 실선으로 나타낸 4개의 선형 근사식을 식(8)에 수식으로 제시하였다. 따라서, 식(8)에 의해 사석마운드 위 소파블록으로 피복되는 수평 혼성제에 작용하는 파압을 다양한 피복률 조건에 대해 추정할 수 있다. Oh and Lee(2020)와 피복률(C_R)에 대한 정의가 다르기 때문에 식(8)에 제시된 파압 보정계수(λ_C) 산정식은 피복률(C_R)이 0부터 1까지 범위에서 적용 가능하다.

Figure 6.

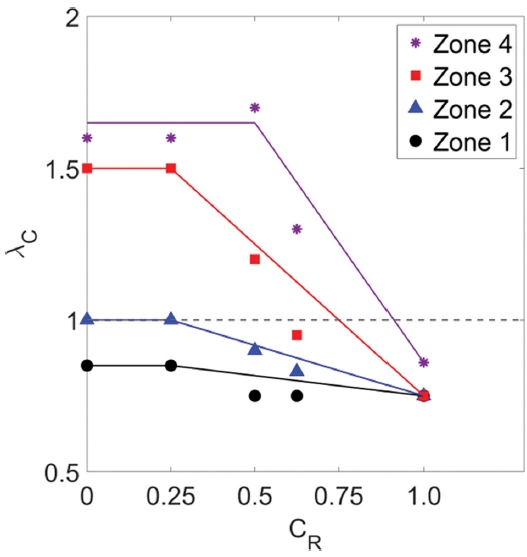
The mean values of C and their fitted lines for Zone 1 to 4 depending on the different coverage rates.

for 0 ≤ C_R ≤ 1

Fig. 7에는 식(8)을 사용하여 계산된 수평파력과 실험을 통해 계측된 값을 비교한 결과를 나타내었다. 세 가지 실험 단면(C12~ C14)에 대해서 케이슨 전면의 소파공에 의한 피복률(C_R)이 서로 다른 조건 (T11~T13)에 대해서 실험 계측값과 식(8)에 의한 추정값이 전반적으로 잘 일치하는 결과가 나타났다. Fig. 7에 제시된 결과는 Oh and Lee(2020)와 거의 차이가 없었으며, 이러한 결과는 C14 실험 단면에 대해서 본 연구에서 제안한 수평파압 보정계수 산정식과 선행 연구(Oh and Lee, 2020)의 산정식을 직접 비교한 Fig. 8에서도 확인된다. 따라서 본 연구에서 새롭게 제안된 식(8)에 의한 파압 저감계수가 경사식 마운드로 피복된 수평혼성제에 작용하는 파압을 잘 예측함과 동시에 현업에서 사용하기에 더 넓은 피복률 범위(0 ≤ C_R ≤ 1)에 대해 적용 가능하다는 것을 보여준다.

Figure 7.

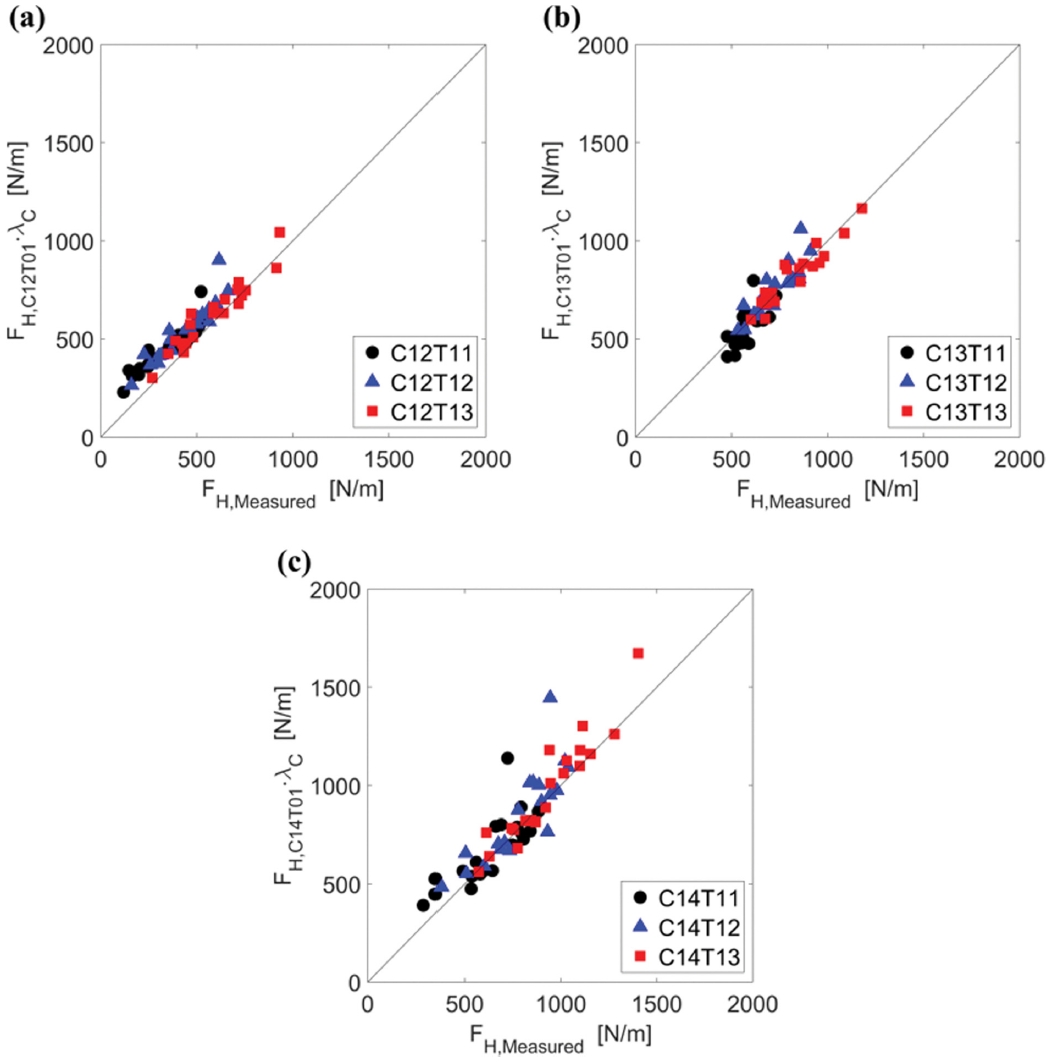
Comparison of horizontal wave forces calculated from the experiment with the estimates by Equation (8).

Figure 8.

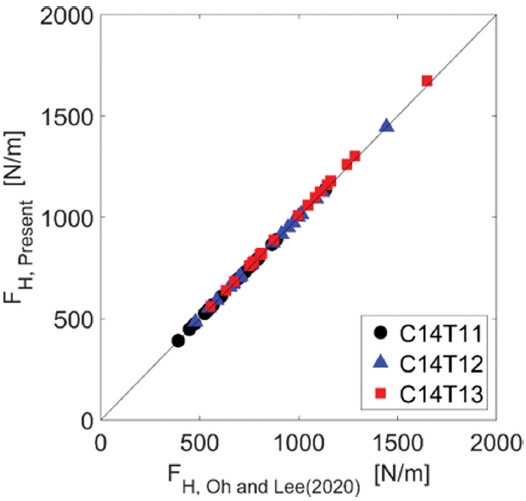
Comparison of the horizontal wave forces estimated by the empirical formula suggested in the present study and Oh and Lee (2020).

한편, 본 연구에서는 규칙파 실험을 통해 수평혼성제에 작용하는 수평파압을 산정하였는데, 불규칙파에 대해서도 본 연구 결과를 적용하는 것이 가능할 것이다. Goda 공식으로 널리 알려져있는 무공케이슨 작용 수평파압은 Goda(1974)의 규칙파 실험 결과로부터 도출되었지만, 불규칙파에 대해서도 최대파고(H_max)를 기준으로 적용되고 있으며 다수의 현장 관측 결과 등을 통해 그 적용성이 검증된 바 있다. 본 연구에서 제안하는 수평파압 보정계수인 λ_C도 근본적으로 무공케이슨에 작용하는 수평파압을 기준으로 경사식 마운드로 피복될 경우의 상대적인 파압 크기 변화를 나타내는 값이므로 Goda의 파압 공식과 비슷한 맥락에서 적용 가능할 것으로 추정된다. 다만, 불규칙파에 대한 수리실험을 수행하여 엄밀하게 검증하는 추가 연구가 이루어진다면 더 바람직할 것이다.