분산보정기법을 사용한 수정 COMCOT 수치모형의 검증
Verification of Corrected COMCOT Numerical Model Using Dispersion Correction Method
Article information
Abstract
현재까지 COMCOT 수치모형에 의한 지진해일 모의는 대부분 선형 또는 비선형 천수방정식을 사용해왔다. COMCOT 수치모형에는 공간에 따라 변하는 수심에도 적용가능한 분산보정기법이 적용되어 있으나, 이 방법을 사용하기 위해서는 수치모형의 소스코드 수정이 동반되어야 한다. 본 연구에서는 분산보정기법이 적용되도록 수정한 COMCOT 수치모형을 사용하여 분산효과를 고려한 지진해일을 모의하였다. 수정한 COMCOT 수치모형을 해석해와 비교하여 검증하였으며, 1983년 동해중부 지진해일에 적용하여 관측치와 비교, 검증하였다.
Trans Abstract
Tsunami simulations based on the COMCOT numerical model have predominantly used either linear or nonlinear shallow water equations. Although COMCOT includes a dispersion correction scheme applicable to regions with varying bathymetry, its application requires corrections to the model’s source code. In this study, a corrected version of COMCOT, where the dispersion correction scheme is properly implemented, is used to simulate tsunami propagation with dispersion effects. The corrected model is validated against analytical solutions and further evaluated by comparing the simulation results with observational data from the 1983 Akita Tsunami event.
1. 서 론
2004년 인도네시아 수마트라 지진해일, 2011년 동일본 지진해일, 2018년 인도네시아 술라웨시 지진해일 등 대형 지진해일이 전 세계적으로 지속적으로 발생함에 따라 국내에서도 지진해일에 대한 사회적 관심과 우려가 커지고 있다. 특히 2011년 3월 11일에 발생한 동일본 대지진 및 지진해일은 일본에서 2만명이 넘는 인명피해와 막대한 경제적 피해를 초래하였고, 후쿠시마 원전사고를 발생시켜 전 세계적으로 지진해일의 위험성을 다시 한번 일깨워 준 계기가 되었다.
동일본 지진해일은 일본 동북부 해역에서 발생하여 우리나라에는 그 영향이 매우 작았지만(Bae et al., 2012), 동해 동연부(일본 서해안)와 류큐 트렌치에서 지진해일이 발생할 경우 우리나라에도 영향을 줄 수 있다. 동해 동연부는 유라시아판과 북미판의 경계에 속하며, 1940년, 1964년, 1983년, 1993년에 동해 동연부에서 지진해일이 발생하여 우리나라에 내습한 기록이 있다. 특히 1983년에 발생한 동해중부 지진해일(아키타 지진해일)은 우리나라 동해안에 내습하여 5명의 인명피해를 발생시켰으며, 선박의 파괴 및 가옥의 파손 등 약 3억 7천여만원의 재산피해를 발생시켰다. 1993년에 발생한 북해도 지진해일은 우리나라에서 인명피해는 없었지만, 선박의 파괴 등 약 4억원의 재산피해가 발생하였다. 최근 2024년 1월 1일에도 일본 이시카와현 노토반도에서 지진해일이 발생하여 우리나라 동해안에 내습하였고, 우리나라는 별다른 피해가 없었지만, 묵호 관측소에서 최대 82 cm의 해일고를 기록하였다.
우리나라 동해안에 내습하는 지진해일의 피해를 예방하기 위해서는 무엇보다도 동해를 전파하는 지진해일을 정확히 모의할 수 있어야 하는데, 동해의 중앙에는 반경 300 km, 정상부 수심 300~400 m 정도의 수중고원(submerged plateau)인 대화퇴가 있어 이 대화퇴를 통과하는 지진해일은 굴절, 회절 및 부분반사 등 매우 복잡한 전파과정을 거치므로 이러한 물리적인 현상을 모의할 수 있어야 한다. 또한, 동해에서 발생하는 지진해일은 조석에 비하여 파장이 짧아 상대적으로 분산성이 강하므로 먼 거리를 전파하는 경우 물리적인 분산효과를 고려하여 해석해야 한다(Yoon, 1999; Yoon et al., 2002).
분산효과를 고려한 지진해일을 해석하기 위하여 방정식 자체에 물리적인 분산항이 있는 Boussinesq 방정식을 지배방정식으로 하는 수치모형을 사용하는 것이 적합하지만, Boussinesq 방정식의 물리적인 분산항을 수치오차 없이 정확히 모의하기 위해서는 상대적으로 작은 격자를 사용하여야 한다. 더불어 물리적인 분산항에는 고차의 미분항을 포함하고 있어 더욱 복잡한 계산과정이 추가된다. 이에 따라 Boussinesq 수치모형은 계산양이 방대해질 수 밖에 없는데, 최근에는 이러한 단점을 해결하기 위하여 GPU(Graphic Processing Unit) 연산이 가능한 Boussinesq 수치모형(Yuan et al., 2020)도 개발되었다. 하지만, 해안에서 지진해일의 천수효과로 인한 파장의 재현, 지진해일의 처오름 모의 등을 위한 상세한 모의를 위해서는 4.5~20 m까지의 상세한 격자간격(Yoon et al., 2002; Bae et al., 2012; Choi et al., 2012)을 사용해야만 하는데, GPU 연산이 가능한 수치모형을 사용한다 하더라도 이러한 상세격자간격으로 동해 전체영역을 구성하는 것은 매우 비효율적이다. 또한, 동해의 지진해일 예측을 위하여 적용되는 지진단층은 지진규모, 단층의 위치, 주향각, 경사각, 경사방향, 변위분포 등에 따른 불확실성이 많아서 동해에 내습하는 지진해일을 평가하기 위해서는 이러한 변수들에 따른 다양한 경우의 지진단층 파라미터에 따른 지진해일을 모의해야만 한다. 따라서, 다양한 경우의 지진해일 모의를 위한 수치모형은 가능한 효율적이면서도 물리적인 특성을 정확히 모의할 수 있어야 한다.
COMCOT 수치모형 버전 1.7(Wang, 2009)에는 분산보정기법(Yoon, 2002; Wang, 2008)이 적용되어 Boussinesq 수치모형보다 상대적으로 큰 격자간격을 사용하면서 물리적인 분산효과를 고려한 지진해일을 모의할 수 있으며, 격자접속방법을 사용하여 광역에서부터 최상세역까지 격자간격을 줄여가며 효율적으로 지진해일을 모의할 수 있다. 하지만, COMCOT(Wang, 2009)에서 분산보정기법을 사용하기 위해서는 수치모형의 수정이 동반되어야 한다. 현재까지 COMCOT은 대부분 선형 또는 비선형 천수방정식으로 모의한 결과가 제시되어 있고(Mulia et al., 2016; Ramalho et al., 2018; Syamsidik et al., 2019; Shi et al., 2024), 아직까지 분산보정기법을 사용한 COMCOT의 검증사례는 제시된 결과가 없다. 본 연구에서는 분산보정기법을 사용하기 위해 COMCOT 버전 1.7을 수정한 후, 이를 해석해(Carrier, 1991)와 비교하여 검증하였고, 1983년에 발생한 동해중부 지진해일을 모의하여 관측치와 비교하였다.
2. COMCOT 수치모형
COMCOT(COrnell Multi-grid COupled Tsunami model) 수치모형은 미국의 코넬대학교에서 개발한 지진해일 수치모형으로 지진해일 해석에 많이 활용되어 왔다. COMCOT은 천수방정식을 기반으로 한 수치모형이며, Wang(2009)은 Yoon(2002) 또는 Wang(2008)이 제안한 분산보정기법을 COMCOT에 적용하여 분산효과를 고려한 지진해일을 모의할 수 있도록 개선하였다. 2장에서는 COMCOT의 지배방정식에 해당하는 천수방정식과 적용된 분산보정기법을 제시한다.
2.1 천수방정식
COMCOT에서 모의하는 선형 천수방정식은 식(1)~(3)과 같다.
여기서, η는 정수면으로부터 수면변위, h는 수심, g는 중력가속도, P = hu, Q = hv이다. u와 v는 각각 x, y 방향의 수심평균유속을 의미한다.
COMCOT에서 모의하는 비선형 천수방정식은 식(4)~(6)과 같다.
여기서, H = η + h이며, Fx 와 Fy 는 각각 x, y 방향의 바닥 마찰항을 의미하고 식(7), (8)과 같다.
여기서, μ은 Manning의 조도계수를 의미한다. 본 연구에서 식(1)과 (4)의 우변항에 제시된 시간에 따른 수심 변화는 고려하지 않았다.
COMCOT에서 선형 천수방정식 및 비선형 천수방정식에 대한 수치해석방법은 시간과 공간에 대하여 교호격자(staggered grid)를 사용하는 leap-frog 기법을 사용하였으며, 자세한 설명은 Wang(2009)에 제시되어 있으므로 본 논문에서는 생략한다.
2.2 분산보정기법
식(1)~(3)을 leap-frog 기법으로 차분화하면, 수치근사에 의한 절삭오차(truncation error)로 생긴 수치분산항이 나타나는데, 이 수치분산항을 선형 Boussinesq 방정식의 물리적인 분산항과 인위적으로 같아지도록 할 수 있다. 즉, 식(9)를 이용하여 수심 h와 시간간격 Δt에 대하여 격자간격 Δx를 사용하면, 수치분산항이 물리적인 분산항을 대체하게 되어 격자의 x와 y 방향에 대해서는 분산효과가 고려된다. 하지만, 격자의 대각선 방향의 분산을 고려하기 위해서는 추가적인 보정항을 필요로 한다(Cho, 1995; Cho and Yoon, 1998).
Cho and Yoon(1998)은 leap-frog 기법으로 차분화시킨 선형 천수방정식의 수치분산이 모든 방향에 대해 물리적인 분산과 근접하게 되도록 일정 수심과 등간격 격자 가정하에 대각선 방향의 분산보정항을 추가하였고, 선형천수방정식에 대한 Cho and Yoon(1998)의 분산보정항이 추가된 유한차분식은 식(10)~(12)와 같다.
여기서, 상첨자 n은 시간단계, 하첨자 i와 j는 각각 x와 y 방향의 격자점 번호를 의미한다. 식(11)과 (12)의 γ = 1이고, 격자간격 Δx는 식(9)를 이용하여 결정한다.
식(10)~(12)는 일정한 수심을 가정하였으나, 실제 수심은 공간에 따라 변하므로 식(9)에 의한 분산효과를 고려하기 위해서는 수심변화에 따라 격자간격도 달라져야 한다. 하지만, 등간격을 사용하는 유한차분법의 경우 수심변화에 따라 식(9)를 만족하는 격자간격과 실제 수치계산에 사용되는 격자간격이 다르므로 실제 물리적으로 발생하는 분산 효과와 다른 오차가 발생하게 된다. 이러한 오차를 보정하기 위하여 Yoon (2002)은 실제 격자간격(Δx, Δy) 대신 가상의 격자간격(Δx*, Δy*)으로 식(9)를 계산하는 방법을 제안하였다.
Yoon(2002)이 제안한 분산보정기법에 따른 유한차분식은 식(13)~(15)와 같다.
여기서, Δx* (= Δy*)은 분산효과를 만족시키기 위하여 식(16)과 같이 계산된다.
실제 격자간격이 Δx (= Δy)일 때 가상의 격자간격과 실제 격자간격의 비 α를 식(17)과 같이 정의하며, 식(14)와 (15)에서 γ = α2일 때 선형 Boussinesq 방정식의 해와 근접한 해를 계산할 수 있다(Yoon, 2002; Yoon et al., 2002).
또한, 식(13)~(14)의 하첨자 *F, *B은 x 방향으로 전방(forward), 후방(backward)의 가상격자점을 의미하고, 가상격자점에서의 차분은 3차의 보간함수를 사용하여 식(18), (19)와 같이 계산한다.
여기서, A1 = (α2 - 1)/(24Δx), A2 = 3(9 - α2)/(24Δx)이다. 식(13), (15)의 하첨자 *U, *L은 y 방향으로 상부(upper)와 하부(backward)의 가상격자점을 의미하고, 이에 대한 차분은 x 방향으로 계산하는 방법과 동일하게 적용된다.
Yoon(2002)의 방법은 3차의 보간함수를 사용함에 따라 주변 4개의 격자점을 이용하므로 0 < α ≤ 3의 범위이며, α >
여기서, δ = α2/4이다. 상기의 식들에 대한 유도과정 및 자세한 설명은 Cho(1995), Cho and Yoon(1998), Yoon(2002)에 제시되어 있으므로 본 논문에서는 생략한다.
COMCOT user manual(Wang, 2009)에서 분산보정기법을 사용하기 위한 설정방법은 따로 제시되어 있지 않지만, COMCOT에서 분산보정기법을 사용하기 위해서는 제어문서(comcot.ctl)에서 지배방정식 관련 매개변수를 2 또는 3으로 설정해야 한다. 또한, COMCOT에서는 dispersion.f90의 subroutine MASS_C_D와 MOMT_C_D에서 MASK라는 변수에 따라 분산효과를 고려하는 방법이 다르게 적용되어 있다. 예를 들어, (i,j) 격자점에서 MASK(i,j)=0일 때는 Cho and Yoon(1998)의 분산보정기법이 사용되고, MASK(i,j)=1일 때는 Yoon(2002)의 분산보정기법이 사용된다. MASK 변수는 dispersion.f90의 subroutine ALPHA에서 정의되는데, Do문 안에서 항상 MASK(:,:)=0으로 초기화되는 오류가 있어 본 연구에서는 Yoon(2002)의 분산보정기법을 사용하기 위하여 Do문 안에서 초기화되는 명령문을 삭제하였다. Subroutine MASS_C_D와 MOMT_C_D에서 INTP=2인 경우 Wang(2008)의 분산보정기법을 사용하는데, 본 연구에서는 INTP=1로 설정하여 Yoon(2002)의 분산보정기법을 사용한 COMCOT의 검증을 수행하였다.
추가적으로, Yoon(2002)의 분산보정기법 적용 시 경계에서 발생하는 수치적인 오류를 제거하기 위하여 완전반사경계조건(Toro, 2001)을 적용하였고, subroutine CONMOME에서 비선형 천수방정식에 적용된 식(6)과 (8)의 바닥마찰항에 대하여 원래의 식이 모의될 수 있도록 오류를 수정하였다.
3. Carrier(1991)의 해석해를 이용한 수정 COMCOT 수치모형의 검증
Carrier(1991)는 초기 수면변위가 Gauss 분포인 가상의 지진해일을 사용하여 지진해일의 전파과정에서 분산효과를 설명할 수 있는 해석해를 제시하였다. Carrier(1991)가 사용한 수면변위의 초기조건은 식(22)와 같다.
여기서, a는 Gauss 분포의 반지름이고,
식(22)의 초기조건에 대한 선형 Boussinesq 방정식의 해석해는 식(23)과 같다.
여기서, J0는 0차 제1종 Bessel 함수이다.
3절에서는 분산보정기법을 사용하도록 수정된 COMCOT을 사용하여 초기 수면변위가 Gauss 분포인 가상의 지진해일 전파에 대한 수치모의를 수행한 후, Carrier(1991)에 의한 선형 Boussinesq 방정식의 해석해와 검증하였다. 수치모형의 검증을 위해 사용된 해석조건 및 매개변수는 다음과 같다(Yoon, 1999, 2002).
식(23)의 h는 수심이며, h = 600 m, 1,200 m, 1,800 m의 3가지 경우에 대하여 수정된 COMCOT의 검증을 수행하였다.
Fig. 1에 h = 600 m인 경우에 대하여 t = 6,000 sec일 때의 수정 전 COMCOT과 본 연구를 통해 수정된 COMCOT의 결과를 해석해와 비교하여 제시하였다. Fig. 1에 제시한 θ는 x 축과 이루는 각도를 의미한다. 실제 수치모의에 사용된 격자간격은 2,500 m이고, 식(16)에 의한 격자간격은 1,285.3 m이다. 실제 격자간격이 식(16)에 의한 격자간격보다 크므로 Cho and Yoon(1998)의 분산보정기법을 사용하는 수정 전 COMCOT에서는 분산이 과대하게 계산되지만, Yoon(2002)의 분산보정기법을 사용할 수 있도록 수정된 COMCOT에서는 모든 방향에서 해석해와 잘 일치하는 결과를 보인다.
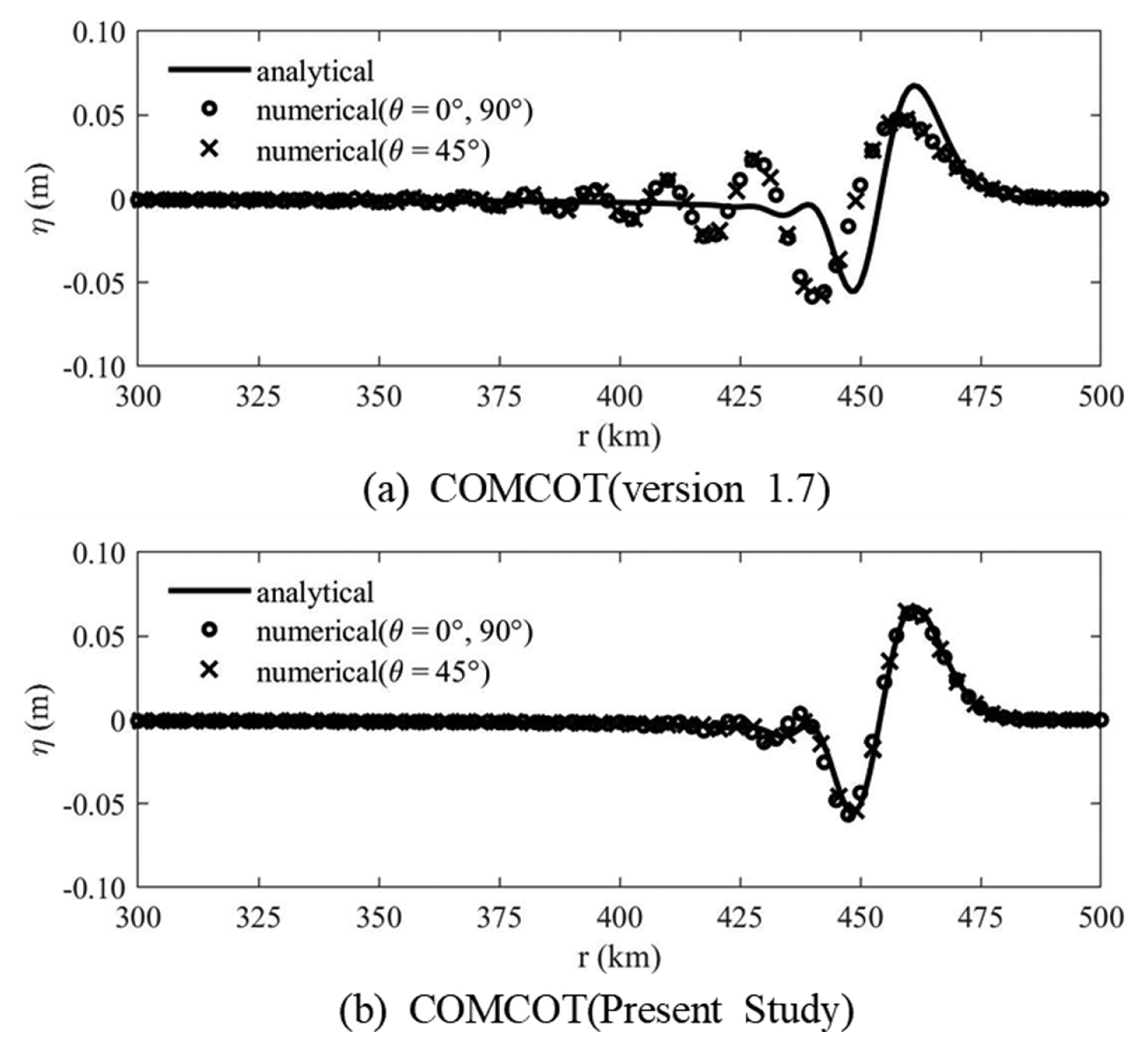
Comparison of numerical solutions with analytical solution of Carrier (1991) for the case of h = 600 m.
Fig. 2는 h = 1,200 m인 경우이며, t = 6,000 sec일 때의 수치모형 결과와 해석해를 비교하였다. 실제 수치모의에 사용된 격자간격은 2,500 m이고, 식(16)에 의한 격자간격은 2,486.7 m이다. h = 600 m인 경우와 다르게, 실제 격자간격과 식(16)에 의한 격자간격이 비슷하므로 Cho and Yoon(1998)의 분산보정기법을 사용하는 수정 전 COMCOT의 결과와 Yoon(2002)의 분산보정기법을 사용할 수 있도록 수정된 COMCOT 결과 모두 해석해와 동일한 분산효과가 나타난다.
Comparison of numerical solutions with analytical solution of Carrier (1991) for the case of h = 1,200 m.
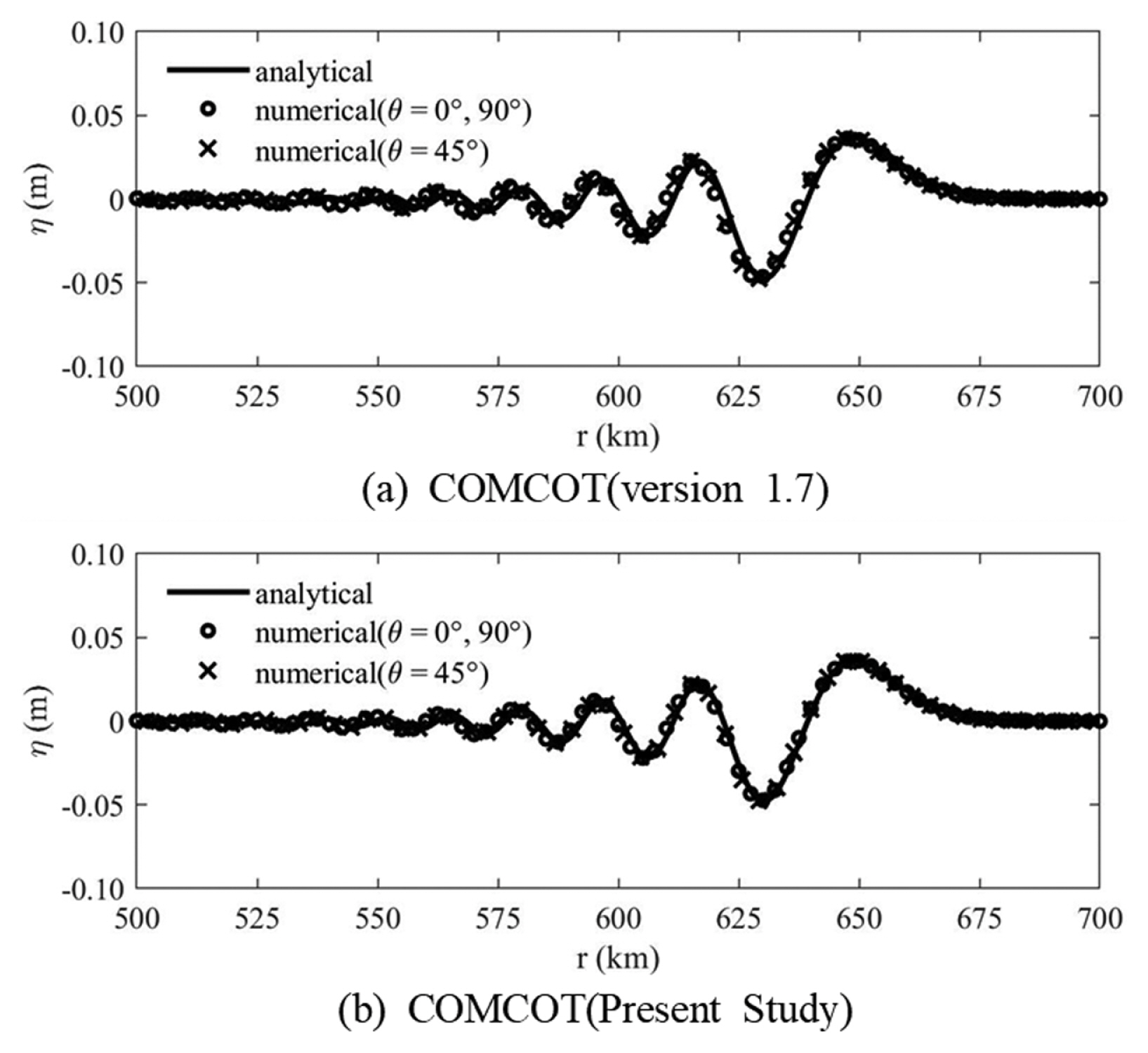
Fig. 3에 h = 1,800 m인 경우에 대하여 t = 6,000 sec의 수치모형 결과와 해석해를 비교하였다. 실제 수치모의에 사용된 격자간격은 2,500 m이고, 식(16)에 의한 격자간격은 3,687.4 m이다. 실제 격자간격이 식(16)에 의한 격자간격보다 작으므로 Cho and Yoon(1998)의 분산보정기법을 사용하는 수정 전 COMCOT의 결과에서는 분산이 작게 계산되었으나 Yoon(2002)의 분산보정기법을 사용할 수 있도록 수정된 COMCOT에서는 해석해와 만족할만한 일치를 보인다.
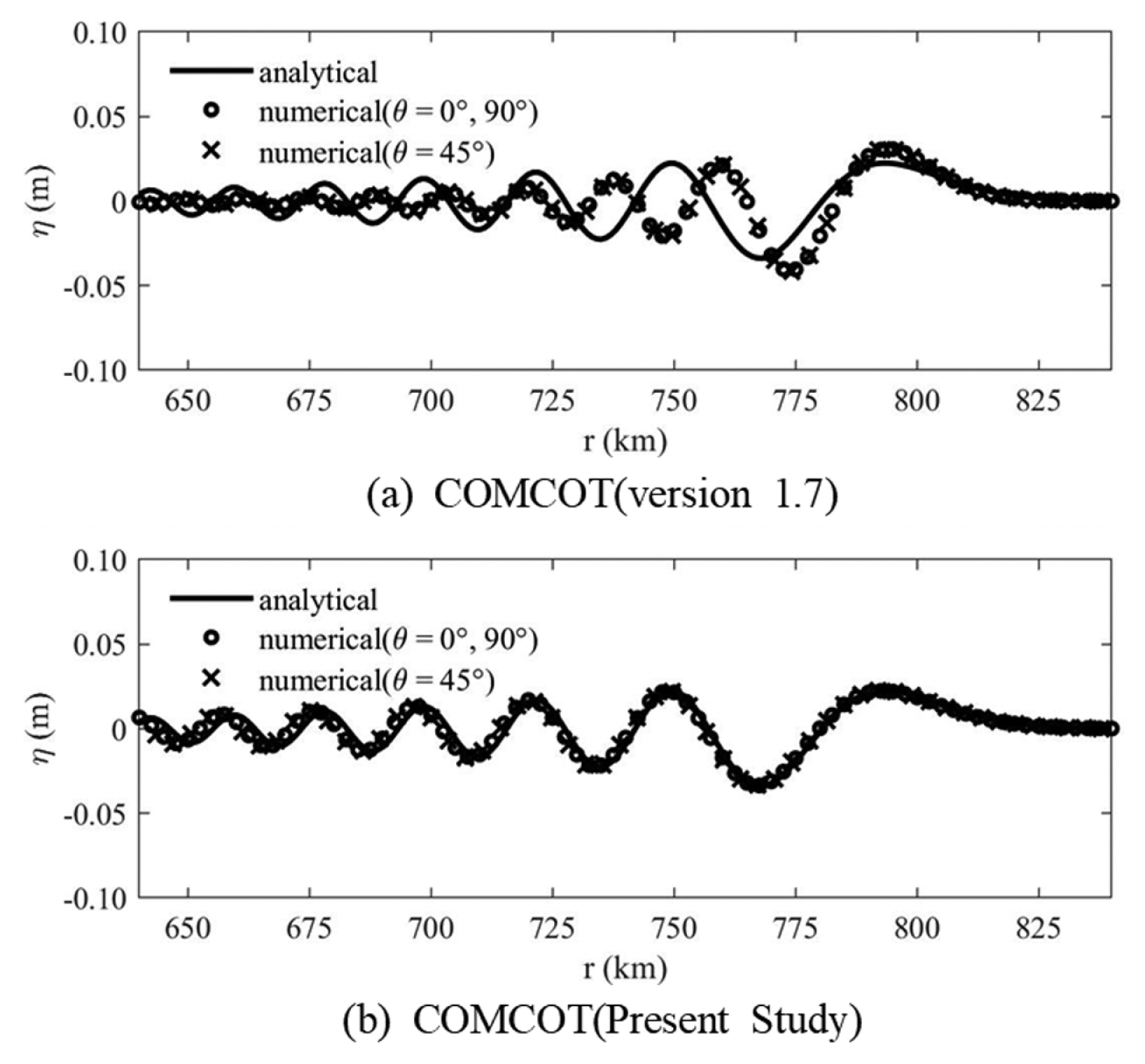
Comparison of numerical solutions with analytical solution of Carrier (1991) for the case of h = 1,800 m.
4. 1983년 동해중부 지진해일 모의를 통한 수정 COMCOT 수치모형의 검증
본 연구를 통해 수정한 COMCOT을 이용하여 1983년에 발생한 동해중부 지진해일을 모의하였다. 수치모형의 결과를 속초, 포항, 울산 검조소의 관측치와 비교하여 수치모형의 검증을 수행하였다. 검증에 사용된 속초, 포항, 울산 검조소의 관측치는 Lim et al.(2008)에 제시된 값을 사용하였다.
COMCOT은 구면좌표계에도 적용가능하도록 개발되었으나, 본 연구에서는 3절에서 해석해와 검증된 직각좌표계의 수정된 COMCOT을 사용하여 1983년 동해중부 지진해일을 모의하였다. 직각좌표계에서 모의하지만, 지구곡면효과를 고려할 수 있도록 Yoon(2002)과 Lim et al.(2008)이 제안한 방법을 적용하였다. Yoon(2002)과 Lim et al.(2008)에 따라 경도 격자간격(Δψ)을 일정한 값으로 설정하고, 위도 격자간격(ΔΦ)은 격자간격이 국부적으로 정사각격자(Δx = Δy)가 되도록 식(25)와 (26)을 이용하여 계산하였다.
여기서, R(= 6.378 × 106 m)은 지구의 반지름이고, Φ와 ψ는 각각 위도와 경도를 의미한다.
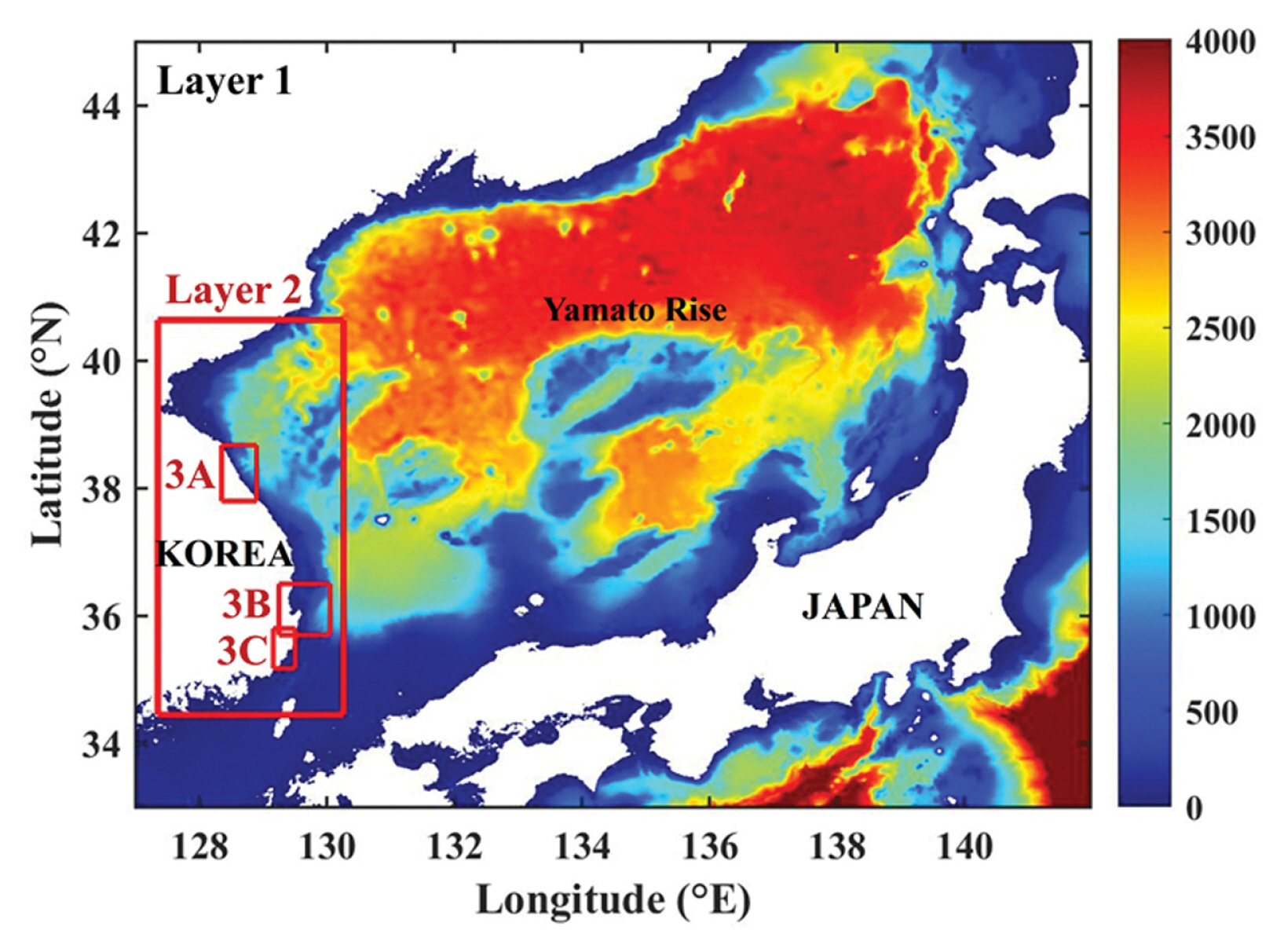
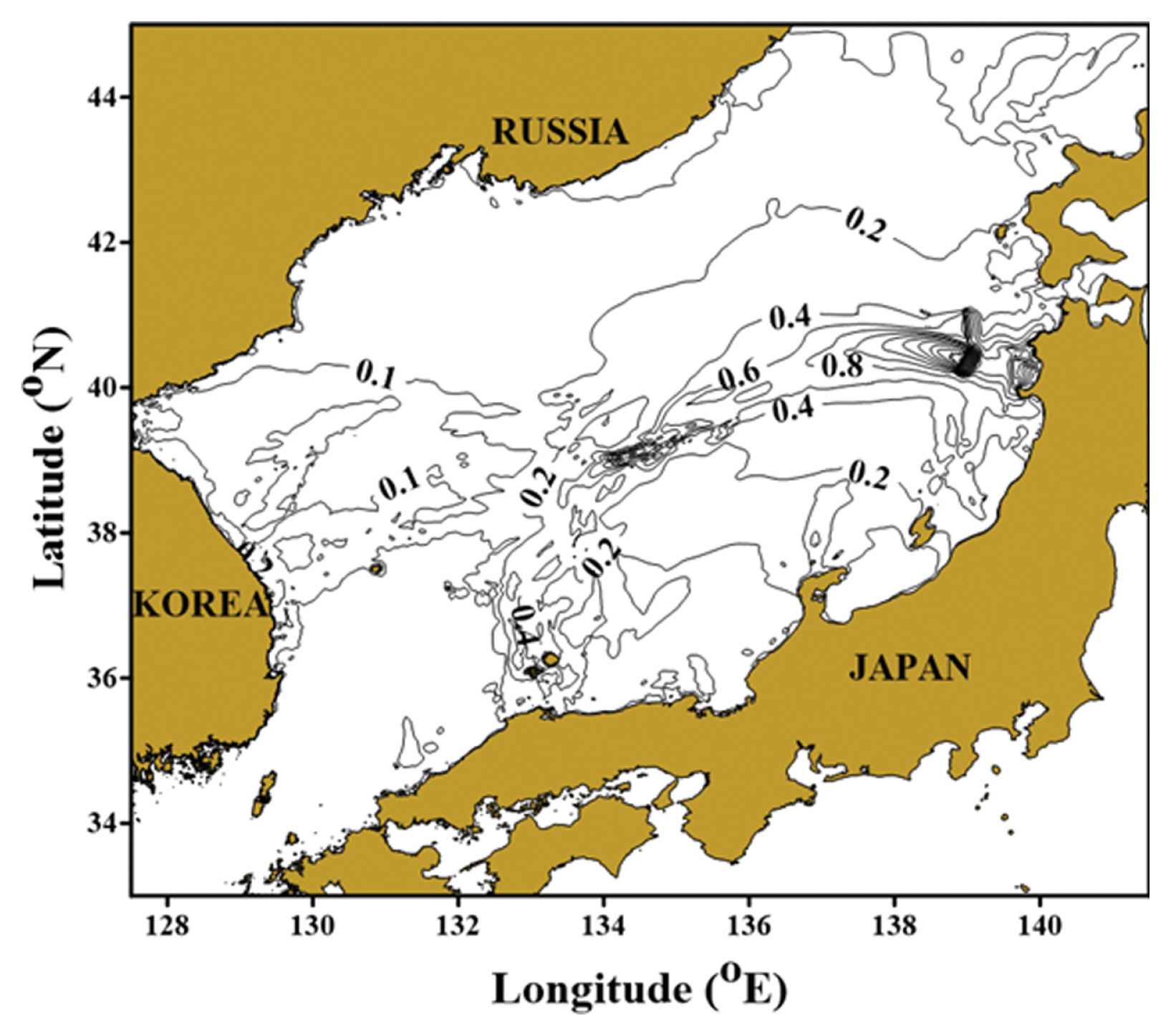
전체 모의영역은 경도 127~142oE, 위도 33~45oN의 해역으로 설정하였으며, Fig. 4에 전체모의영역에 대한 수심분포를 제시하였다.
Computational domains and bathymetry (unit: m).
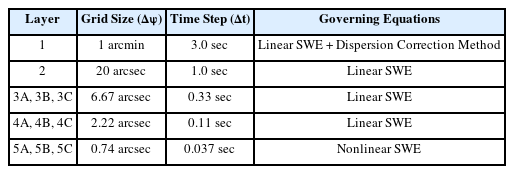
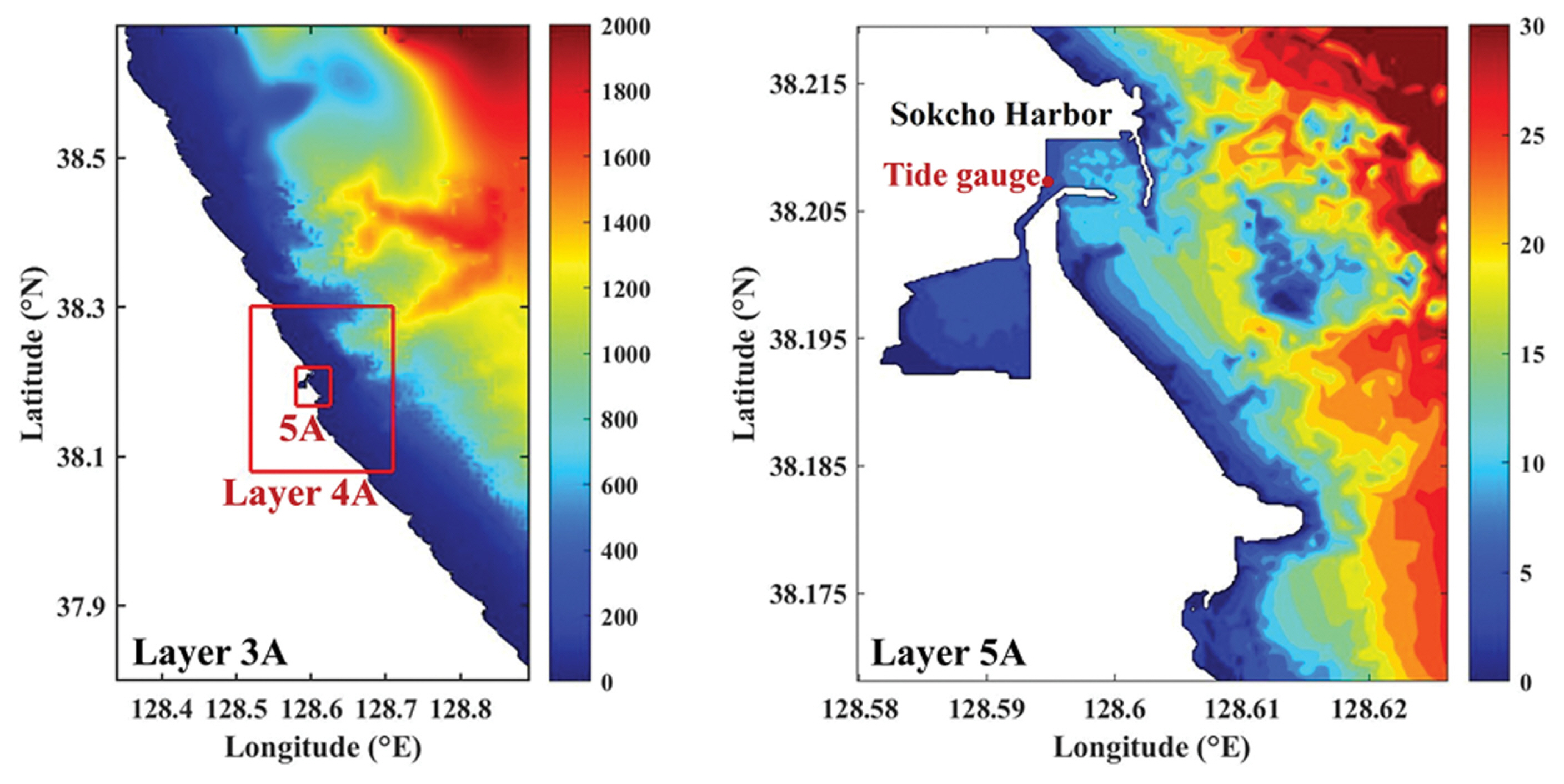
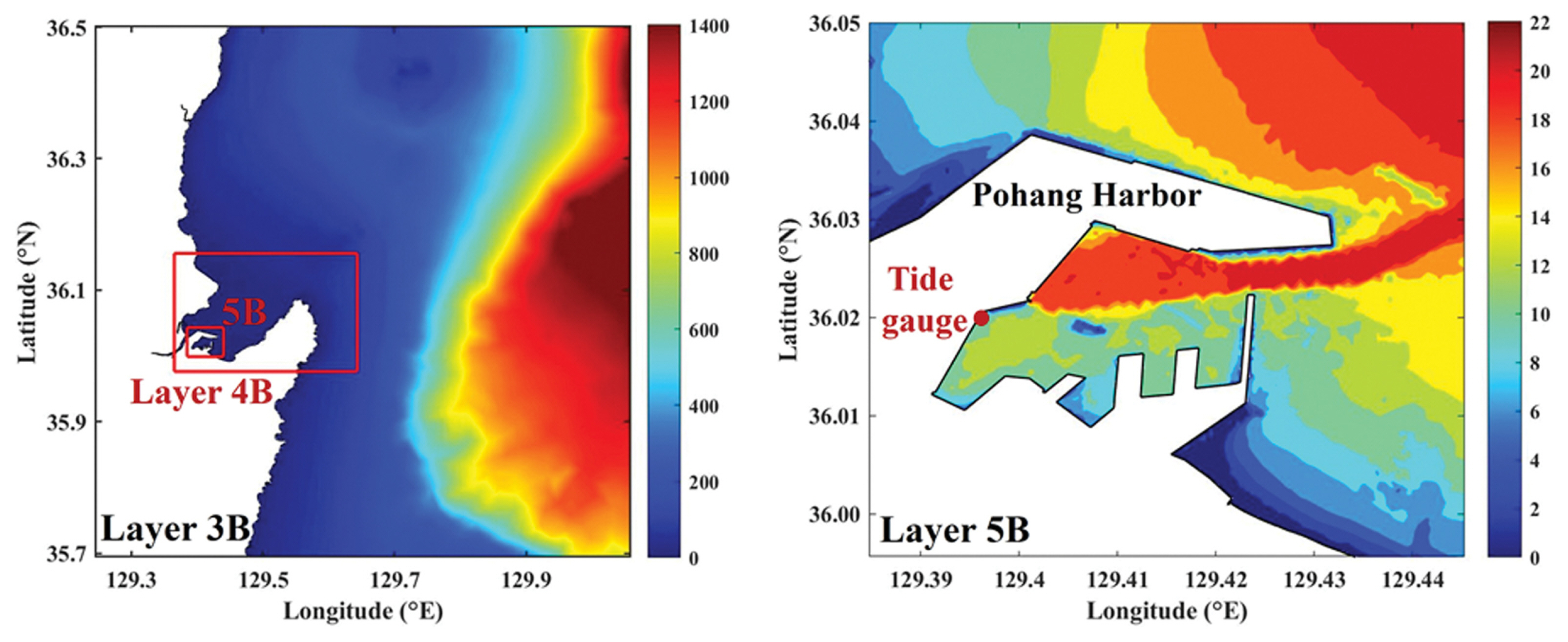
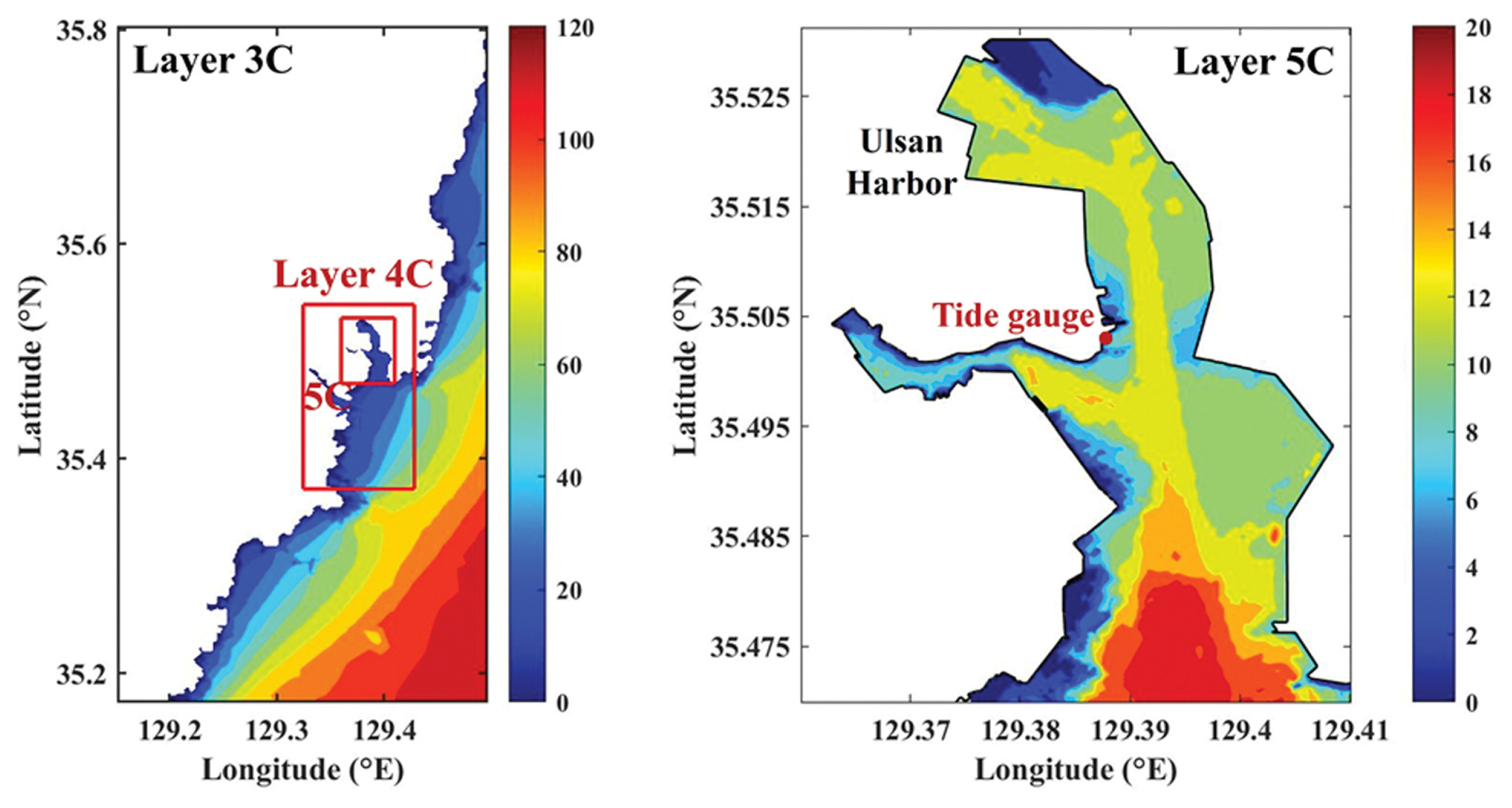
진원지에서 발생한 지진해일은 우리나라 연안으로 전파해오면서 수심 감소로 인하여 파장이 짧아지므로 세밀한 격자를 구성해야만 지진해일을 정확히 재현할 수 있다. 전체 모의영역을 세밀한 격자로 구성하는 것은 상당히 비효율적이므로 효율적인 수치모의를 위하여 Yoon(2002)과 Lim et al.(2008)의 모의방법과 같이 Layer 1에서 Layer 5까지 5개의 영역을 격자접속방법을 사용하여 모의하고, 전체 모의영역인 Layer 1에서 최상세 모의영역인 Layer 5까지 격자간격을 1/3씩 줄여 세밀한 격자를 구성하였다. 속초(Layer 3A, 4A, 5A), 포항(Layer 3B, 4B, 5B), 울산(Layer 3C, 4C, 5C) 검조소의 관측치와 비교하기 위한 각 모의영역의 격자간격 및 시간간격을 Table 1에 제시하였다. 또한, 각각의 검조소의 관측치와 비교하기 위한 모의영역과 수심분포를 Fig. 5~7에 제시하였고, Lim et al.(2008)의 관측치가 제시된 검조소의 위치를 함께 제시하였다. 각 모의영역의 수심자료는 Seo(2008)의 KorBathy30s과 한국해양개발의 최신 수심자료를 사용하였다.
Simulation information for Sokcho, Pohang, and Ulsan harbors
Computational subdomains and bathymetry around Sokcho harbor (unit: m).
Computational subdomains and bathymetry around Pohang harbor (unit: m).
Computational subdomains and bathymetry around Ulsan harbor (unit: m).
동해 동연부에서 발생되어 동해를 전파하는 지진해일은 파장이 비교적 짧고, 먼 거리를 전파하므로 물리적인 분산효과를 고려해야 한다(Yoon, 2002). 또한, 수심이 얕은 연안해역을 제외하면 대부분의 해역에서 수심에 비해 수면변위가 작으므로 비선형성을 무시할 수 있다. 이에 따라 전체 모의영역인 Layer 1 영역은 분산보정기법이 적용된 선형천수방정식으로 지진해일을 모의하였다. 지진해일이 수심이 얕은 연안 해역에 도달하면 얕은 수심의 영향으로 비선형성과 바닥마찰의 영향이 증가하는 반면, 분산효과는 감소하므로 Layer 5 영역은 비선형 천수방정식으로 지진해일을 모의하였다.
초기수면변위는 단층 파라미터를 사용한 Mansinha and Smylie(1971)의 해석해를 사용하였다. 1983년 동해중부 지진해일에 대한 단층 파라미터는 Aida(1984)에 의해 Table 2와 같이 제시된다. 초기 단위폭당 유량인 P와 Q는 모두 0으로 가정하였다. Layer 1 영역의 경계 전면에서는 sponge layer(Shi et al., 2016)를 적용하여 경계에서의 반사파가 발생하지 않도록 하였다. 또한, Yoon(2002)의 분산보정기법은 수심이 완만히 변하는 가정 하에 유도된 기법이므로 수심이 급변하는 부근에서 발생할 수 있는 수치적인 불안정성을 완화시키기 위하여 평활화 방법(Lim, 2001; Yoon et al., 2002)을 적용하였다. 수치모의는 총 400분 동안 수행하였다.
Fault parameters for 1983 Tsunami (Aida, 1984)
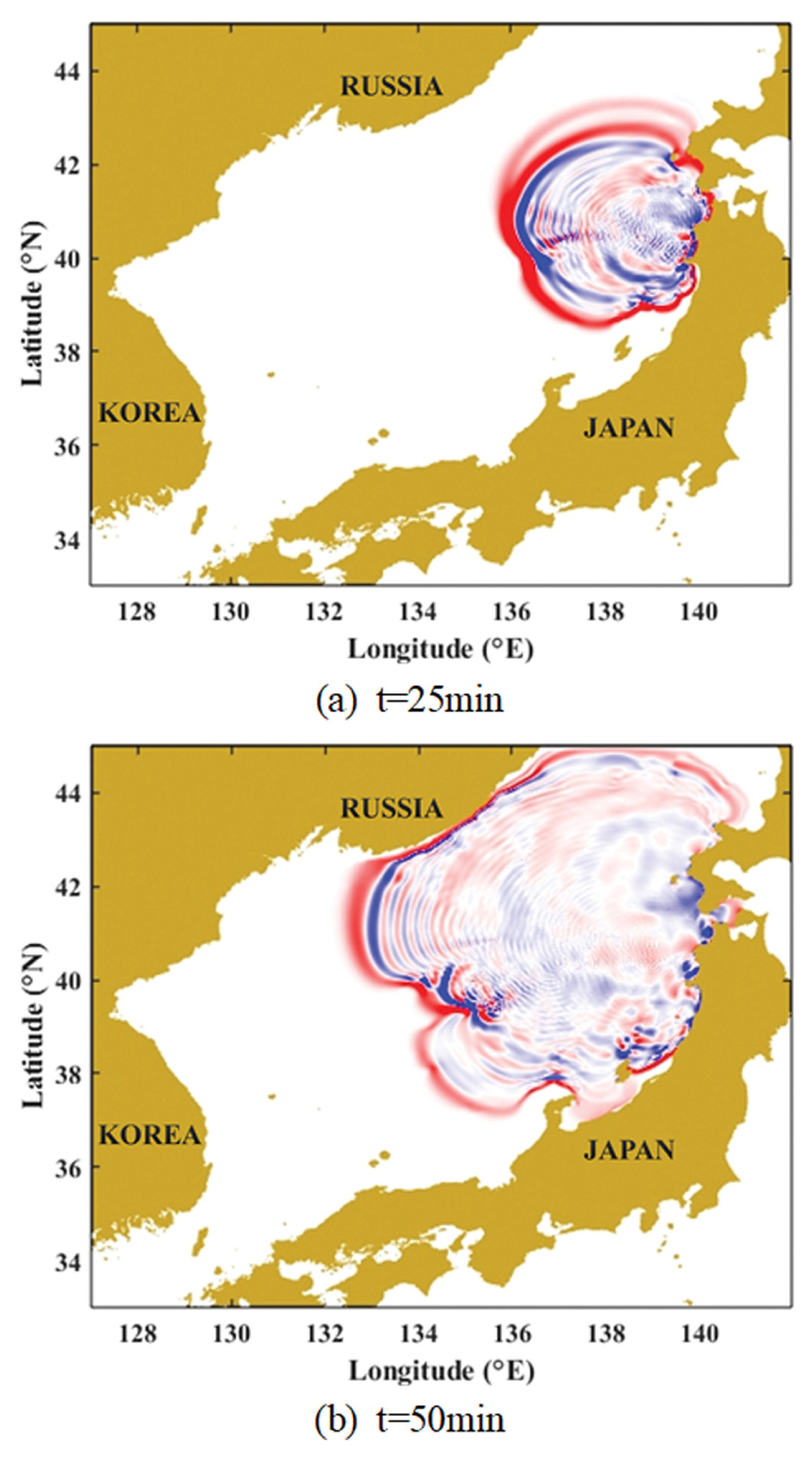
동해상을 전파하는 지진해일에 대하여 Yoon(2002)의 분산보정기법을 사용하도록 수정된 COMCOT의 결과를 Fig. 8에 제시하였다. Yoon(2002)에 제시된 결과와 비슷하게 동해상을 전파하는 지진해일은 러시아와 대화퇴(Yamato Rise) 사이에서 분산효과에 의해 여러 개의 파로 나뉘어져서 진행하는 결과가 나타난다.
Results of free surface elevation by corrected COMCOT using dispersion correction scheme.
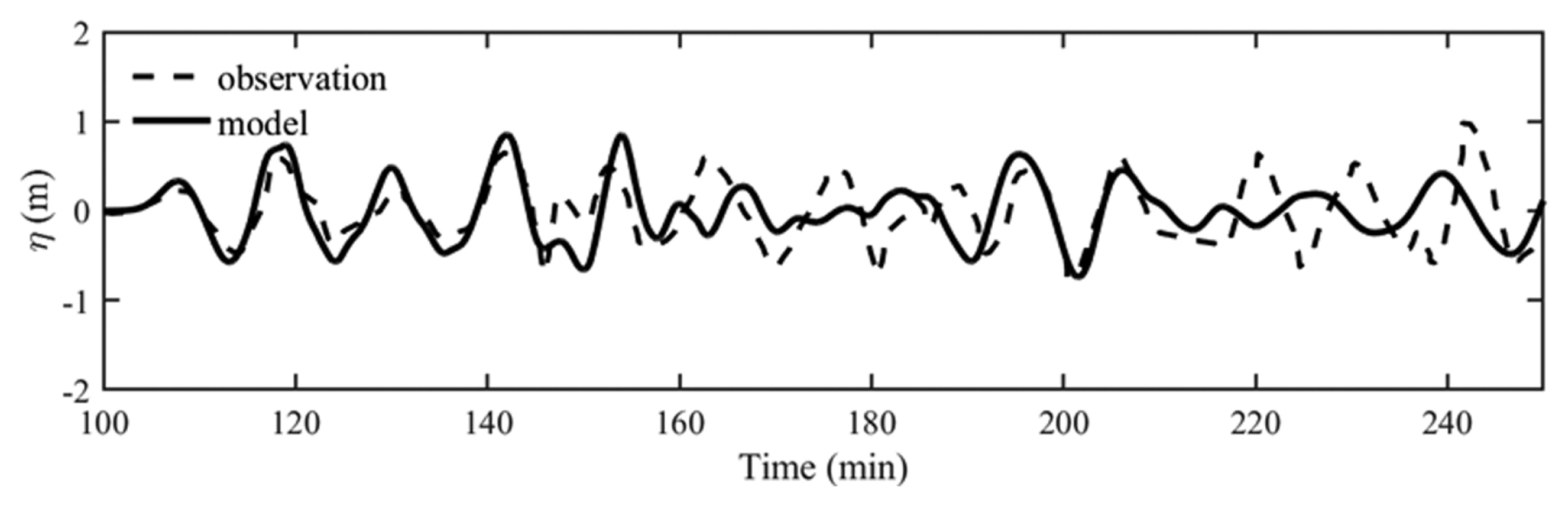
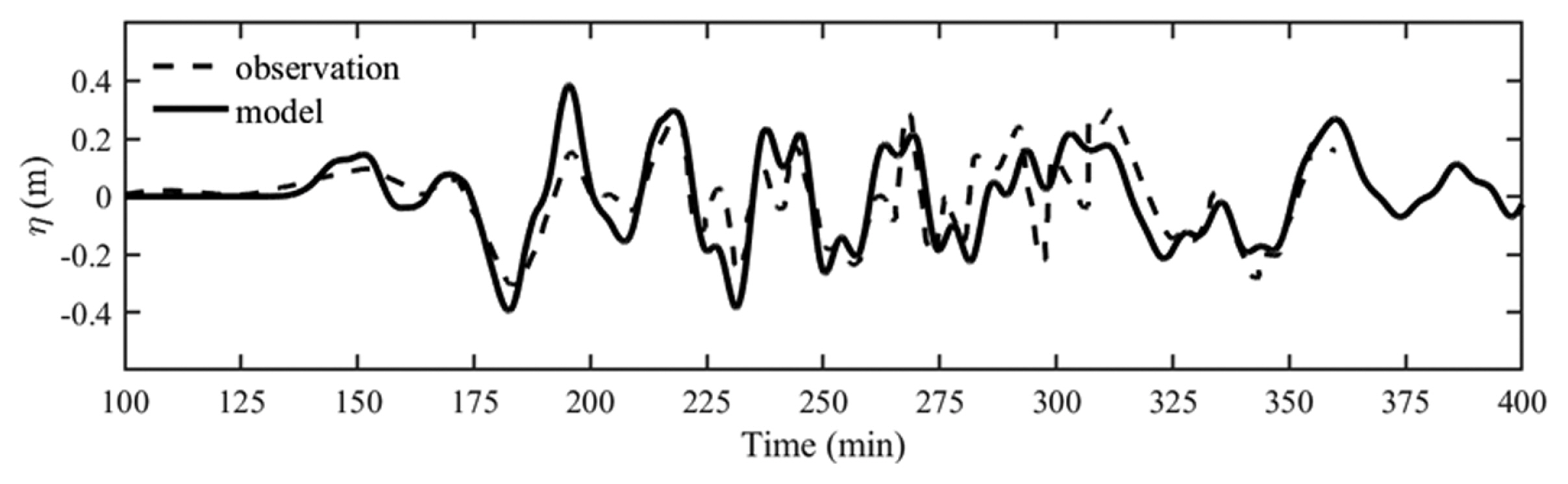
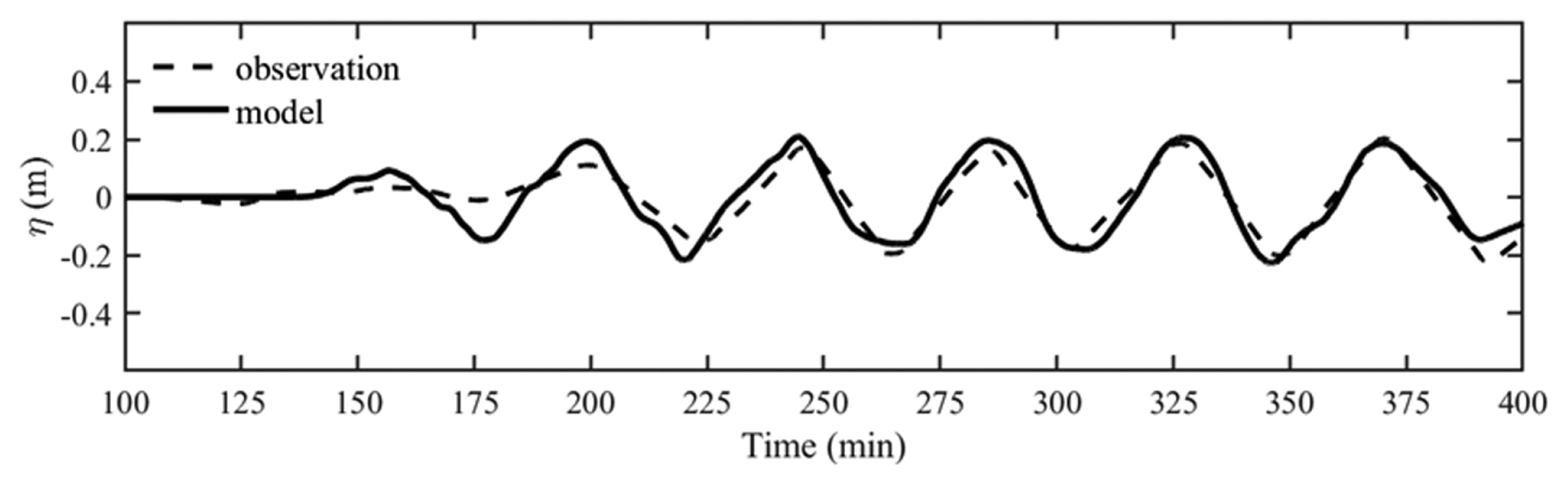
속초, 포항, 울산 검조소의 관측치와 비교한 결과를 각각 Fig. 9~11에 제시하였다. 각 검조소에서 지진해일의 첫 파가 도달하는 시간은 관측치와 대체적으로 일치한다. 속초 검조소와 울산 검조소의 관측치와 수치모형 결과는 전반적으로 상당히 잘 일치하는 것을 확인할 수 있다. 속초 검조소의 경우, 포항 및 울산 검조소에 비하여 지진해일의 진폭이 상대적으로 높게 나타나는데, Fig. 12에 제시된 최대 수면변위 결과를 참고하면 동해를 통과하는 지진해일은 동해 중앙의 해저에 형성된 대화퇴에 의하여 주로 일본 남측으로 굴절되고, 나머지 일부가 동해안으로 내습하기 때문에 속초에는 남측에 위치한 포항과 울산보다 상대적으로 높은 진폭의 지진해일이 내습한다. 울산 검조소의 경우, Fig. 11에 제시된 지진해일의 평균주기는 대략 43분이고, Fig. 7에 제시된 울산만(Layer 5C)의 수심이 12 m, 길이가 7,000 m인 사각형만으로 가정할 경우, 파랑이 x 방향으로만 자유진동한다면, 이 때의 고유주기는 약 43분이 되는데, Yoon(2002)에 제시된 사항과 비슷하게 고유주기와 계산된 주기는 대체적으로 일치하는 결과를 보인다. 포항 검조소의 수치모형 결과는 관측치와 약간의 차이는 있지만, 비슷한 수위 변화를 재현하고 있다.
Comparison between numerical and observed time histories of surface elevation at Sokcho harbor.
Comparison between numerical and observed time histories of surface elevation at Pohang harbor.
Comparison between numerical and observed time histories of surface elevation at Ulsan harbor.
Calculated maximum water levels by 1983 Tsunami (unit: m).
5. 결 론
현재까지 COMCOT은 대부분 선형 또는 비선형 천수방정식을 이용하여 지진해일에 대한 수치모의 결과가 제시되어 왔다. 본 연구에서는 동해 동연부에서 발생하여 분산효과가 고려된 지진해일을 모의하기 위하여 기존의 COMCOT(Wang, 2009)에서 Yoon(2002)의 분산보정기법이 실질적으로 반영되지 못한 점을 수정하였고, 수치모형의 일부를 개선한 COMCOT의 수치모의 결과를 제시하였다.
해석해가 존재하는 Gauss 분포의 초기 수면변위 문제를 모의한 결과, 수정 전 COMCOT에서는 식(9)를 만족하지 않는 Δx를 사용할 경우 해석해와 차이가 나타났으나, 본 연구를 통해 수정한 COMCOT에서는 해석해와 만족할만한 일치를 보였다.
또한, 수정한 COMCOT을 이용하여 1983년에 발생한 동해중부 지진해일을 모의한 결과, 동해상을 전파하는 지진해일은 분산효과에 의해 여러 개의 파로 나뉘어 진행하는 결과가 확연히 나타났다. 속초, 포항, 울산 검조소의 관측치와 수치모의 결과를 비교한 결과, 관측치와 대체적으로 잘 일치하는 결과를 보였다. 추후, 수정한 COMCOT을 이용하여 2011년 동일본 지진해일을 포함한 과거 지진해일 사례를 추가적으로 수치모의하여 관측치와 비교, 검증할 계획이다.