국내 연안 유의파고 관측자료의 최적 확률분포 추정 및 평가
Estimation and Assessment on the Optimal Probability Distribution of the Monitoring Wave Height Data in the Korean Coast
Article information
Abstract
파랑 자료의 확률분포 모델 추정은 파랑 자료가 어떤 확률적 성질을 가지는지 이해하고, 공학적 설계 변수의 정량적 평가를 가능하게 한다. 이에 본 연구에서는 국내 연안 20개 정점에서 관측된 유의파고 자료를 기반으로 최적 확률분포를 추정하고, 그 자료의 확률적 특성과 꼬리 거동을 분석하였다. 확률분포모델로는 총 9개(Normal, Log-normal, Weibull-3, Gamma-3, Generalized Gamma, Generalized Beta-2, Johnson SB, Generalized Hyperbolic, Extended Generalized Inverse Gaussian)의 모델을 이용하였으며, 각 분포의 매개변수 추정법으로는 최대우도추정법을 사용하였다. 모델의 성능을 평가하기 위한 적합도 검정 방법으로는 Kolmogorov-Smirnov 검정과 Kullback-Leibler Divergence 지표를 사용하였으며, Q-Q plot을 통해 확률 분포 꼬리 영역에서의 적합성을 분석하였다. 그 결과, Generalized Hyperbolic, Johnson SB, Generalized Gamma 분포가 많은 지점에서 높은 적합도를 보였으며, 복수의 형상 매개변수를 갖는 확률분포들이 유의파고의 비대칭성과 꼬리 특성을 잘 설명하는 것으로 나타났다. 그러나, 일부 확률분포 모델에서는 극단 분위수 영역에서 유의파고를 과소 또는 과대 추정하는 경향을 보여 유의파고 자료를 보다 정확하게 설명하기 위해서는 대상 지점의 파랑 자료에 적합한 확률분포를 추정하여 사용하는 것이 적절할 것으로 판단되었다.
Trans Abstract
The estimation of probability distribution models for wave data enables an understanding of the probabilistic characteristics of wave conditions and the quantitative evaluation of engineering design variables. In this study, the optimal probability distributions were fitted using by significant wave height data observed at 20 points around the Korean coast, and the probabilistic characteristics and tail behaviors of the data were analyzed. A total of nine distribution models were considered, including the Normal, Log-normal, Weibull-3, Gamma-3, Generalized Gamma, Generalized Beta-2, Johnson SB, Generalized Hyperbolic, and Extended Generalized Inverse Gaussian distributions. The parameters for each distribution were estimated using the Maximum Likelihood Estimation (MLE) method. To evaluate the performance of each model, goodness-of-fit tests such as the Kolmogorov–Smirnov test and the Kullback–Leibler divergence metric were used, and Q-Q plots were employed to assess the fit in the tail regions of the distributions. As a result, the Generalized Hyperbolic, Johnson SB, and Generalized Gamma distributions showed high goodness-of-fit at many stations. Distributions with multiple shape parameters were found to effectively capture the asymmetry and tail characteristics of the significant wave height data. However, some distribution models tended to underestimate or overestimate the extreme quantile regions. Therefore, it is considered appropriate to select and apply the probability distribution model that best fits the wave data at each target site in order to more accurately describe the characteristics of significant wave heights.
1. 서 론
파랑은 해안 및 항만 구조물의 설계, 선박 설계 등에 있어서 매우 중요한 설계 변수로 작용하며, 시시각각 변동하는 파랑의 불확실성을 정량화하기 위한 노력이 지속적으로 요구되고 있다. 특히 해역별 파랑 특성은 지형과 기상에 따라 다르기 때문에 각 해역의 파랑 특성은 관측 자료를 기반으로 확률분포 특성을 이해하는 것은 중요하다(Young et al., 2011; Young and Ribal, 2019; Haselsteiner and Thoben, 2020; Shamshirband et al., 2020; Dehghan et al., 2022). 이러한 유의파고의 확률적 특성을 정량적으로 표현하기 위한 대표적인 방법으로는 확률분포 모델을 활용한 통계적 접근이 주로 사용되고 있으며, 이는 파랑의 발생 빈도, 크기 및 극치값 등을 포괄적으로 설명할 수 있다는 점에서 널리 사용되고 있다(Ferreira and Soares, 1999; Ferreira and Soares, 2000). 또한 다양한 분야의 국제표준에서는 대상 해역의 극치해상상태를 평가하기 위한 방법으로 I-FORM(Inverse-First Order Reliability Method) 기법을 이용한 환경 등고선 작도를 적극적으로 권장하고 있다. 이때 입력변수로 사용되는 파고, 주기 등의 해양환경변수는 서로 다른 확률분포 특성을 가지며, 이들의 분포 형태는 등고선의 위치와 형상에 결정적인 영향을 미친다. 따라서 각 변수에 대해 통계적 적합도가 검증된 확률분포를 적용하는 것은 필수적이다(Mackay and Haselsteiner, 2021; Clarindo and Soares, 2024). 최근에는 Log-normal 분포 및 Weibull-3 분포와 같이 주로 사용되는 분포보다는 보다 정확한 분포 형상 조절이 가능하며, 극치영역의 재현성이 높은 4~6개의 매개변수를 갖는 비교적 복잡한 확률분포를 적용하여 유의파고 분포를 정확하게 추정하는 연구가 활발히 이루어지고 있다(Wu et al., 2016; Soukissian, 2021). 특히 Weibull-3의 경우, 낮은 파고 영역에서의 과대 추정과 높은 파고 영역에서의 과소 추정이 빈번하게 발생한다는 단점이 있다. 이는 상대적으로 적은 매개변수의 개수로 분포의 형상을 재현함에 있어 유연성이 제한되며, 실제 유의파고 확률분포의 비대칭성과 꼬리 두께를 충분히 반영하지 못한다는 한계를 갖는다(James and Panchang, 2022; Vanem and Fazeres-Ferradosa, 2022).
한편, Soukissian(2021)은 그리스 해역 4개 지점, 미국 NCDC 부이 4개 지점을 대상으로 복수의 매개변수를 갖는 다양한 확률분포 모델을 적용하여 유의파고의 적합도를 비교하였으며, 확률분포 모델 식의 매개변수 수가 증가할수록 분포 형상에 대한 조절 능력이 향상되어 유의파고의 비대칭적 분포 특성 및 극치 영역을 보다 정확하게 재현하고 있음을 확인한 바 있다. 또한, Wu et al.(2016)은 기존의 Rayleigh 및 Weibull 분포가 수심이 얕은 해역에서 발생하는 쇄파고의 분포를 추정하기 위해 유의파고의 중심 및 꼬리 부분을 각각 Weibull 분포와 Generalized Pareto 분포로 적용하여, 두 분포를 하나의 연속된 모델로 유연하게 결합한 Weibull-Generalized Pareto(WGP) 분포를 제안하였다. 제안된 WGP 모델은 유의파고를 기준으로 두 분포가 자연스럽게 적용되도록 설계됐으며, 기존 모델보다 극치 영역의 파고 분포를 더욱 정밀하게 재현하는 것으로 나타났다. 한편, 국내에서 수행된 유의파고 확률분포 추정과 관련된 연구를 살펴보면, Jeong et al.(2015)는 국내 동해안에 위치한 대진 연안의 장기 파랑 특성을 분석하기 위하여 약 7년간 관측된 유의파고와 첨두주기를 대상으로 최적 확률분포를 추정한 바 있다. 이 과정에서 사용된 후보 분포함수는 Kernel, Generalized Gamma, Generalized Extreme Values(GEV) 분포를 사용하였으며, 최소제곱법과 최대우도추정법을 사용하여 각각의 분포함수 내 매개변수를 추정하였다. 또한, Ko et al.(2017)에서는 중규모 유럽 기상예보센터 재분석 자료를 활용하여 국내 연안 유의파고의 확률 분포 특성을 검토하기 위해 Lognormal, Weibull 및 GEV 분포를 적용하였으며, 각각의 확률분포의 매개변수 추정을 위해 최대우도추정법이 사용된 바 있다. 아울러, Lee et al.(2024)의 경우, 유의파고와 첨두주기 사이의 결합확률분포 분석을 위하여 Normal, Lognormal, Gamma, Weibull-3 분포를 후보 분포로 결정하여 최대우도추정법을 통해 최적 확률분포를 추정한 바 있다. 유의파고에 대한 적합 확률분포 추정은 주로 국외에서 활발하게 수행되고 있으나, 국내에서는 대부분 특정 해역을 대상으로 특정 분포를 적용하거나, 비교적 간단한 형태의 분포 모델을 적용한 경우가 대부분이다.
이에 따라 본 연구에서는 우리나라 연안 20개 지점에서 관측된 유의파고 관측자료를 활용하여 Log-normal, Weibull-3, Gamma-3 분포와 더불어 4~6개의 매개변수를 가지는 대표적인 확률분포함수를 대상으로 최적 분포함수를 추정하였으며, 매개변수는 최대우도추정법을 이용하였다. 또한 추정된 분포 함수에 대한 분포 적합 검정은 KS 방법으로 수행하였으며, Kullback-Leibler Divergence 측도를 이용하여 모든 지점의 유의파고 분포에 대한 적합 수준을 정량적으로 평가하였다. 또한, 평가된 분포함수에 대하여 Q-Q(Quantile-Quantile) 플롯을 이용하여 유의파고의 극단값에 해당하는 꼬리 거동을 검토하였으며, 적합 확률분포 평가 결과를 바탕으로 지점별로 최적 또는 적합 상위 분포함수의 특성 및 순위에 대한 종합 평가를 실시하여 국내 지점 별 적합한 분포함수 순위를 제시하였다.
2. 관측자료 및 방법
2.1 국내 파랑 관측자료
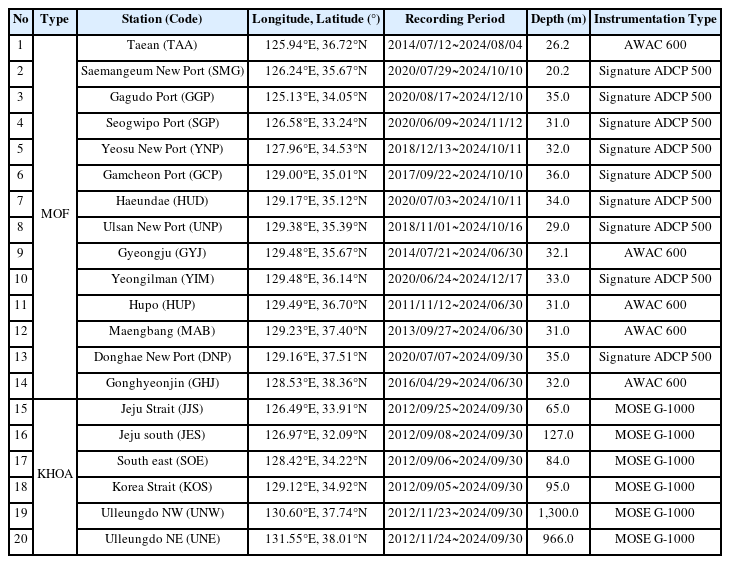
본 연구에서는 전국 파랑 관측 자료 제공 시스템(WINK: Wave Information Network of Korea)에서 제공하는 해양수산부(MOF) 및 국립해양조사원(KHOA)에서 관측한 자료를 대상으로 유의파고의 분포함수 추정을 수행하였다. 해양수산부는 전국 34개 지점에서 AWAC 600, Signature ADCP 500 등의 파랑 관측 장비를 활용하여 유의파고 및 주기 등 파랑 자료를 30분 간격으로 수집하고 있으며, 관측 기간은 최소 약 3개월에서 최대 12년 이상으로 지점에 따라 차이를 보이고 있다. 국립해양조사원은 6개의 대형 해양관측부이에서 파랑 관측을 수행하고 있으며, 파랑 관측은 GPS 방식인 Datawell 사에서 개발한 MOSE G-1000을 통해 수면위 3.5 m에서 관측을 수행한다. 또한, 대형 해양관측부이에서 관측되는 파랑 자료의 관측 간격은 30분 간격, 최대 관측 기간은 약 12년이다.
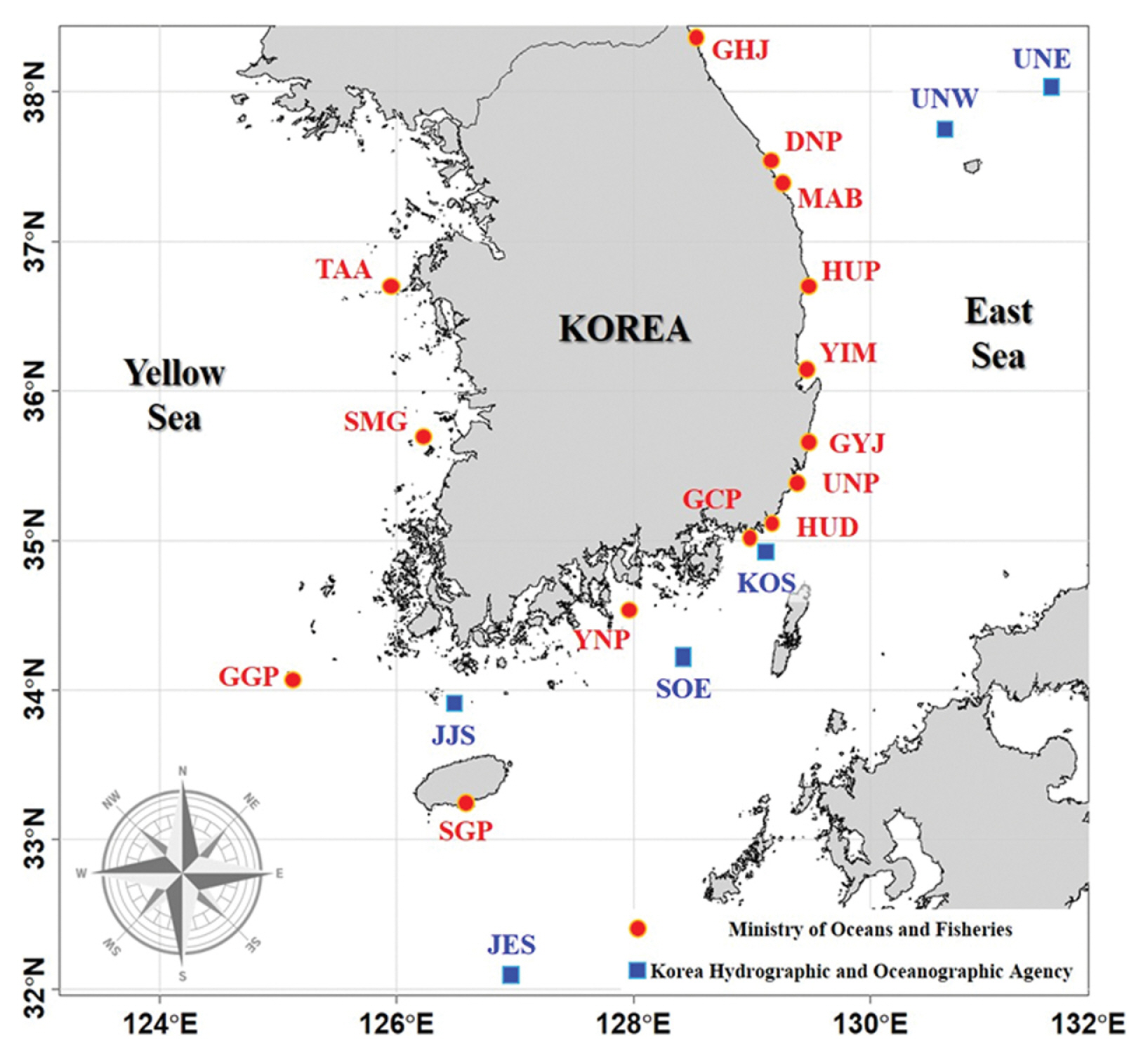
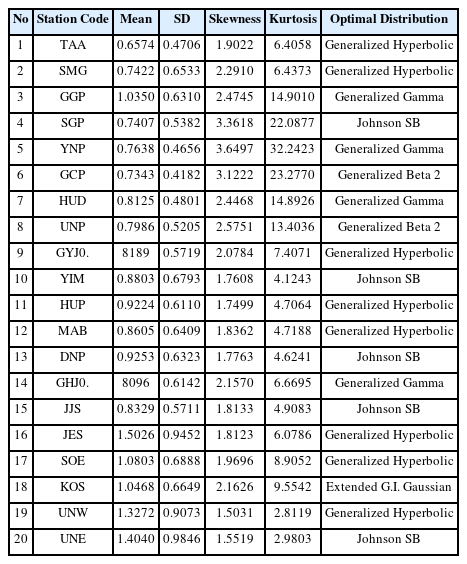
본 연구에서 선정한 분석 대상 지점은 관측 기간이 3년 이상인 지점으로 한정하였으며, 이는 유의파고의 통계적 신뢰도를 확보하기 위해 최소 3년 이상의 관측 기간이 필요하다는 선행 연구를 근거로 결정하였다(Cho et al., 2013). 한편, 분석에 사용된 해양수산부와 국립해양조사원의 유의파고 자료는 기관별로 산출 방식에 차이가 있으며, 해양수산부에서 관측된 유의파고의 경우, 스펙트럼 분석법을 이용하고 있으며, 국립해양조사원의 경우, 파열 분석법을 이용한다. 분석 대상 지점의 위치도 및 관측 정보는 다음 Fig. 1 및 Table 1과 같다.
Locations of significant wave height observation sites (Red circle: MOF; Blue squares: KHOA).
Summary of significant wave height observation sites
2.2 유의파고 확률분포 후보 함수
본 연구에서는 유의파고의 최적 확률분포를 추정하기 위해 Normal 분포, Log-normal 분포, Weibull-3 분포, Gamma-3 분포를 이용하였다. 또한, 보다 다양한 확률분포를 적용하기 위하여 4-매개변수 기반의 Johnson SB 분포, Generalized beta distribution of the 2-kind 분포 및 Generalized Gamma 분포, 5-매개변수 기반의 Generalized Hyperbolic 분포와 6-매개변수 기반의 Extended Generalized Inverse Gaussian 분포를 후보 분포함수로 선정하였다.
이에 각각의 분포에 대한 설명 및 확률밀도함수는 다음과 같으며, 분포 추정 대상이 되는 유의파고 변수(H)는 일반적으로 이용되는 변수기호(x, 변수집합기호 X)를 사용하고, 확률밀도함수와 누적확률분포함수의 기호는 각각 f, F 기호를 사용하였다. 또한, dF(x)/dx = f(x) 조건은 두 함수의 관계를 의미하는 제약조건임을 의미한다.
1) Normal Distribution (N)
정규분포는 가장 널리 사용되는 연속 확률분포로, 평균, 분산 두 개의 매개변수를 가지며 데이터가 평균값을 중심으로 대칭적으로 분포하는 특성을 가지며, 다음 식(1)과 (2)와 같이 표현할 수 있다.
여기서, a, b는 각각 분포함수의 위치 매개변수(location parameter), 척도 매개변수(scale parameter)를 의미하며, 분포함수에 종속된다. 이어지는 분포함수에서도 같은 의미의 매개변수에 해당한다. Φ는 표준정규분포의 누적분포함수를 의미한다(Patel and Read, 1996).
2) Log-normal Distribution (LN)
로그정규분포는 변수의 로그(x' = lnx)가 정규분포를 따르는 분포로, 변수변환에 따른 분포추정을 적용하면 유의파고와 같이 비대칭적이고 양의 값으로만 정의되는 경우에 적합하며, 다음 식(3)과 (4)와 같이 표현할 수 있다(Athanassoulis et al., 1994).
3) Gamma-3 Distribution (G3)
Gamma 분포는 변수가 양의 실수 범위(x - a > 0)에서 정의되며, 위치, 척도, 형상 매개변수에 따라 분포의 형태가 달라지는 비대칭 분포로서, 기본 형태인 척도, 형상 매개변수에 위치매개변수를 도입하는 3개의 매개변수를 가지는 분포함수이다. G3 함수는 형상 매개변수(k, shape parameter)를 포함하는 형태로 다음 식(5)와 (6)과 같이 표현할 수 있다(Bobee and Ashkar, 1991).
여기서, Γ(·)는 감마함수, γ(·, ·)는 하위(lower) 불완전 감 마함수를 의미한다.
4) Weibull-3 Distribution (W3)
Weibull-3 분포는 형상, 척도 및 위치 매개변수로 구성되며, 다양한 분포 형태를 표현할 수 있는 유연성을 가진다. 특히 해당 분포는 유의파고 표현에 있어 널리 사용되고 있으며, 다음과 같은 조건(x - a > 0)에서 다음 식(7)과 (8)과 같이 표현할 수 있다(Weibull, 1951; Rao and Hamed, 2000).
5) Generalized Beta distribution of the 2-kind Distribution (GB)
제 2종 GB 분포의 경우, 이전의 분포와는 달리 형상 매개변수를 세분화하는, 다수의 형상매개변수를 도입하는 형태의 함수이다. 이 분포함수는 3개의 형상 매개변수와 1개의 척도 매개변수(b)를 통해 다양한 분포 형태(형상)를 비교적 정확히 표현할 수 있으며, 특히 왜도 및 첨도가 큰 분포에 적합한 장점이 있다. GB 분포는 다음과 같이 표현이 가능하며, 형상 매개변수는 k, p, q 기호로 추가하여 표현한다(식(9)와 (10) 참조).
여기서, B(p, q)는 Beta 함수, Iz(p, q)는 불완전 베타 함수를 정규화한 불완전 Beta 함수를 의미하며, 형상 매개변수를 입력으로 요구하며, 다음 식(11)과 (12)와 같이 표현된다(McDonald and Xu, 1995).
여기서, t = (x/b)k, z = t/(1 + t)이다.
6) Johnson SB Distribution (JSB)
Johnson SB 분포는 각각 하나의 위치 매개변수(a), 척도 매개변수(b), 그리고 두 개의 형상 매개변수(p, q)를 포함하는 4-매개변수 분포로서, 분포의 비대칭성 및 첨도 조절이 가능한 구조를 가지며, 다음 식(13)과 (14)와 같이 표현할 수 있다.
이 분포에서 위치 매개변수인 a는 분포의 시작점을 조절하는 매개변수로서 변수는 a ≤ x ≤ a + b 범위로 한정된다. 형상 매개변수 중 p는 분포의 기울기 또는 첨도를 조절하는 등 분포의 폭과 관련된 매개변수이다(Johnson, 1949).
7) Generalized Gamma Distribution (GG)
Generalized Gamma 분포는 네 개의 매개변수(위치 및 척도 매개변수와 두 개의 형상 매개변수; a, b, p, q 기호 사용)로 구성된 분포로서, 다양한 분포 형태를 표현할 수 있는 확률 분포이며, 다음 식(15)와 (16)과 같이 표현된다(Stacy, 1962; Lawless, 1980).
8) Generalized Hyperbolic Distribution (GH)
Generalized Hyperbolic 분포는 총 다섯 개의 매개변수(위치, 척도 매개변수와 3개의 형상 매개변수; a, b; k, p, q)를 가지며, 분포의 형태, 비대칭성, 척도 및 위치를 조절할 수 있는 확률분포이다. 특히, 해당 분포는 Normal Inverse Gaussian, Hyperbolic, Student-t 분포 등의 특수한 형태를 포함하고 있어, 유의파고와 같이 꼬리가 두껍고 비대칭적인 관측자료를 재현하는데 적합하며, 분포함수는 다음 식(17)과 (18)과 같이 표현할 수 있다.
여기서,
9) Extended Generalized Inverse Gaussian Distribution (EGIG)
이 분포는 총 6개의 매개변수(위치, 척도 매개변수, a, b; 4개의 형상매개변수, k, s, p, q)를 포함하는 확률분포로서, 유의파고와 같이 비대칭적이며, 긴 꼬리를 가지는 자료에 적합하게 설계되었다. 이 분포는 일반화된 역 감마 분포와 비슷한 형태를 가지며, Bessel 함수 기반의 정규화 상수를 포함하여 다양한 분포 형태를 재현할 수 있다. 이러한 분포는 다음 식(19)와 (20)과 같이 표현할 수 있다.
여기서, 형상 매개변수의 경우, k, s는 분포 꼬리의 두께 및 비대칭을 조절하는 Shape-Scale 역할을 하며, p는 중심 및 꼬리 부분의 곡률을 결정하고, q는 분포의 첨도 및 분포 형태의 전반적인 형상을 결정한다. 또한, 해당 분포는 GH 분포와 마찬가지로 복잡한 함수 형태로 인해 누적분포함수 수식은 존재하지 않으며, 수치 적분 또는 경험 누적분포를 통해 근사적으로 계산하게 된다(Shakil et al., 2010; Gupta and Viles, 2011, 2012; Low et al., 2017).
2.3 최대우도추정법
확률분포 모델의 매개변수를 추정하기 위해서는 최소제곱법, 확률가중모멘트법, 최대우도추정법 등이 주로 이용된다. 최소제곱법은 추정 방법이 비교적 간단하고 직관적이나 편향(bias)이 발생하는 단점이 있으며, 확률가중모멘트법은 자료의 극단값에 덜 민감한 장점이 있다. 그러나 두 방법 모두 분포의 수학적 특성과 자료의 통계적 특성을 적절하게 반영하지 못하는 경우가 발생할 수 있으며, 특히 매개변수의 수가 증가할수록 추정의 정확도와 안정성에 한계를 보인다(Clauset et al., 2009; Katalinic and Parunov, 2020). 반면, 최대우도추정법은 주어진 자료에 대해 가능도(likelihood)를 극대화하는 통계적인 개념을 기반으로 하는 방식으로 복잡한 형태의 확률분포에 대하여 일관성있고 효율적이며 통계적으로 신뢰할 수 있는 추정을 가능하게 한다(Clauset et al., 2009; Pascal et al., 2013; Soukissian, 2021).
본 연구에서는 유의파고의 적합 확률분포를 추정하기 위해 최대우도추정법(MLE, Maximum Likelihood Estimation)을 이용하였다. 최대우도추정법은 관측자료에 가장 유사한, 관측자료가 독립이라는 조건에서 모든 자료의 발생확률을 최대화하는 조건에서 확률분포의 매개변수를 추정하는 통계적 방법이다. 특정 확률밀도함수 f(Hi|θ)에 대하여, 관측값 Hi(i = 1, 2, …, n, n = 자료의 개수)가 독립적으로 추정되었다고 가정하면, 우도함수(L)는 다음 식(21)과 같이 정의된다.
계산의 효율성을 위하여 일반적으로 로그우도 함수를 사용하며, 이는 다음 식(22)와 같이 표현할 수 있다.
최대우도추정법은 상기 로그우도함수를 최대화하는 모수 벡터(θ = θk, k = 1, 2, …, np, np = 추정 매개변수의 개수)를 추정하는 문제로서, 이는 다음 식(23)과 같이 정리된다.
일반적으로 로그우도함수는 비선형함수형태이기 때문에, 해석적으로 극대값을 구할 수 있는 경우가 제한된다. 따라서 수치적 최적화 기법을 이용한 추정이 수행된다. 특히, 본 연구와 같이 다수의 매개변수를 갖는 확률분포의 경우, 매개변수의 상·하한 경계 조건을 고려할 수 있는 최적화 알고리즘인 L-BFGS-B(Limited-memory Broyden-Fletcher-Goldfarb-Shanno with Bounds) 기법을 활용하여 최대우도 추정을 수행하였다(Byrd et al., 1995; Nocedal and Wright, 2006).
2.4 적합도 검정 및 적합 측도 평가
유의파고 변수에 대한 후보 확률분포의 분포 적합 평가를 위하여 본 연구에서는 널리 이용되는 Kolmogorov-Smirnov 검정 기법을 이용하였다. 더불어, 이 검정을 통과한 후보 분포에 대해서는 Kullback-Leibler Divergence 측도를 이용하여 후보 분포함수 간의 분포 적합 정도와 순위를 결정하는데 이용하였다.
1) Kolmogorov-Smirnov 분포 적합 검정
유의파고의 확률분포 적합성을 정량적으로 평가하기 위해 Kolmogorov-Smirnov 검정(KS 검정)을 이용하였다. KS 검정은 일반적으로 분포 적합성 검정을 위한 방법으로 널리 사용되는 방법으로서, 경험 누적분포함수와 이론 누적분포함수 간의 차이를 기반으로 통계적 유의성을 평가한다(Massey, 1951; Conover, 1999; Press, 2007). 이 검정의 귀무가설은 검정 대상이 되는 “후보 분포함수와 기준이 되는 데이터 기반 분포함수와는 유의미한 차이는 없다.” 이므로, p-value 기반 판정의 경우에는 p < 0.05(유의수준 = 0.05) 조건에서 귀무가설을 기각할 수 있다. 본 연구에서는 각 후보 확률분포에 대해 KS 검정통계량을 이용하여 p-value를 산정하였으며, 5% 유의수준에서 p-value가 0.05 이상인 경우, 해당 분포가 적합하다고 판단하였다.
2) Kullback-Leibler Divergence 측도
KS 검정을 통과한 후보 확률분포에 대하여, 추가적인 적합성 비교평가를 정량적으로 수행하기 위하여 Kullback-Leibler Divergence(KL-Divergence) 측도를 이용하였다. 이 방법은 경험적 확률분포와 후보 확률분포 간의 차이를 정량적으로 평가하는 지표로서, 다음 식(24)를 이용하여 각 확률분포의 기준 분포에 대한 차이를 정량화된 수치로 계산할 수 있다. 이 수치를 이용하여, 후보 분포함수의 적합 순위를 결정하였다(Belov and Armstrong, 2011; Wu et al., 2016).
여기서, P(xi)는 관측된 유의파고의 확률밀도함수, Q(xi)는 후보 분포의 확률밀도함수를 의미하며, xi는 분포 비교가 수행되는 구간으로 전체 파고 범위 영역을 유한한 구간(xi, i = 1, 2, …, m)으로 구분한 유의파고를 의미한다. 또한, 보다 정밀한 적합 확률분포를 평가하기 위하여 각 후보 확률밀도함수와 유의파고 관측자료 사이의 결정계수(r2) 및 평균제곱근 오차(RMSE)를 보조적으로 산정하여 제시하였다. 아울러, 평균제곱근오차는 유의파고와 후보 확률밀도함수 사이의 꼬리 영역을 평가하기 위해 사용된 Q-Q 플롯 분석의 평가지표로 활용하였다. 결정계수 및 평균제곱근오차는 다음 식(25)~(27)을 활용하였다.
여기서, xi는 유의파고,
여기서, fobs(xi)는 유의파고의 확률밀도함수, ffit(xi)는 후보확률밀도함수, n은 비교 구간의 개수를 의미하며, Qobs, i는 누적확률의 관측 분위수, Qfit, i는 Qobs, i에 대응되는 이론 분위수, n은 분위수 비교 지점의 개수를 의미한다.
3. 분포함수 매개변수 추정 및 분포 적합 검정 결과
3.1 분포함수 매개변수 최적 추정 결과
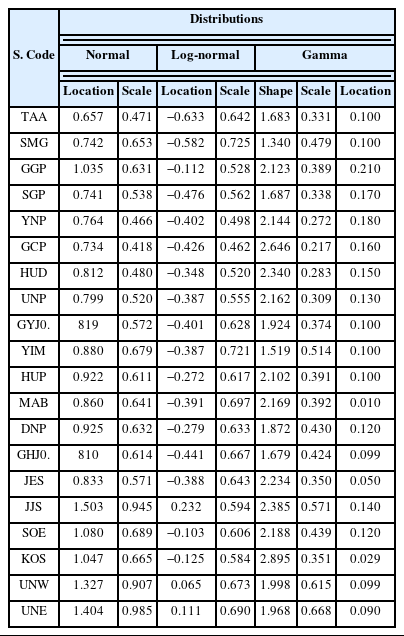
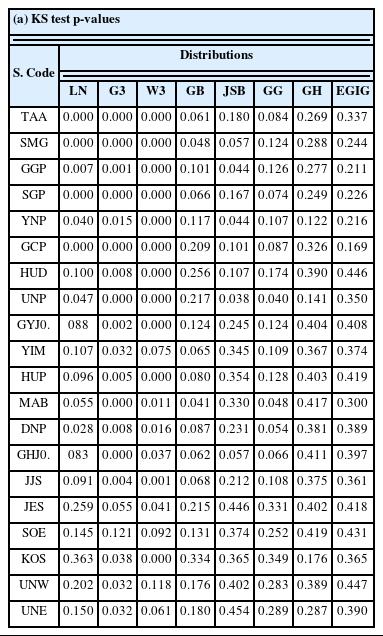
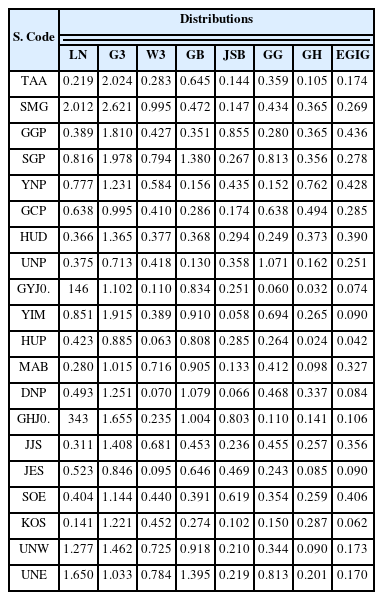
본 연구에서는 우리나라 연안 20개 지점을 대상으로 유의파고 관측자료에 적합한 확률분포함수를 평가하기 위하여 다양한 매개변수를 갖는 총 9개의 후보 확률분포함수를 적용하였다. 각 분포함수에 대한 매개변수는 최대우도추정법을 통해 산정하였으며, 모든 지점에서 산정된 모든 후보 분포함수 매개변수 값은 Appendix A에 제시하였다. 아울러, 최적 추정된 분포함수에 대한 KS 분포 적합 검정 결과(p-value)와 분포함수 사이의 적합 정도 비교를 위한 KL Divergence(DKL) 측도를 추정한 결과는 Appendix B에 제시하였다.
비교평가 지표를 분석한 결과, GH 분포는 전체 20개 지점 중 8개 지점(40%)에서 적합 분포로 선정되었으며, 가장 많은 지점에서 유의파고 관측자료를 잘 재현하는 것으로 나타났다. JSB 분포는 5개 지점(25%)에서 최적 분포로 도출되었으며, GG 분포는 총 4개 지점(20%)에서 적합한 결과를 보였다. 아울러, GB 분포는 2개 지점(10%), EGIG 분포는 1개 지점(5%)에서 각각 최적 분포로 평가됨에 따라 전반적으로 분포의 적합도는 해역 및 지점별로 상이하게 나타났다. 또한, 각각의 지점에서 평가된 적합 확률분포의 결정계수는 0.98 이상으로 매우 높게 나타났으며, 평균제곱근오차는 0.01~0.09 m 수준으로 매우 낮게 나타남에 따라 적합하게 평가된 확률분포의 재현성은 우수한 것으로 판단된다(Table 2 참조).
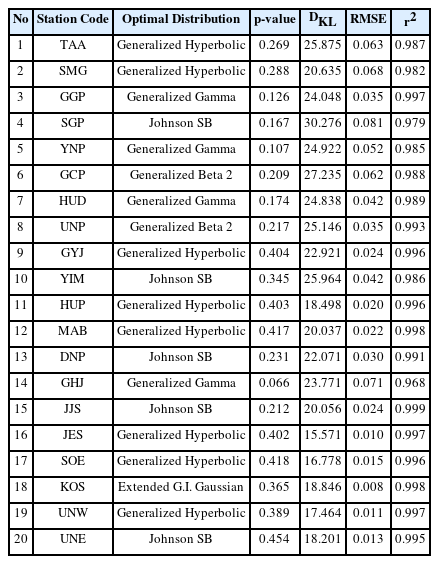
The best fitted probability distribution with the corresponding p-value of the KS test, the KL-divergence measures for the twenty sites in Korea
한편, 본 연구에서는 총 20개 지점에 대해 9개의 확률밀도함수를 적용하여 적합도를 평가하였으며, 이 중 적합 확률분포로 선정된 GH, JSB, GG, GB 및 EGIG 분포에 대하여 대표 결과를 Fig. 2에 제시하였다. 각 분포별로는 해당 분포의 적합도가 가장 높은 1개 지점을 선정하였으며, 선정된 지점은 해역별 최소 1개 지점이 포함되도록 결정하였다.
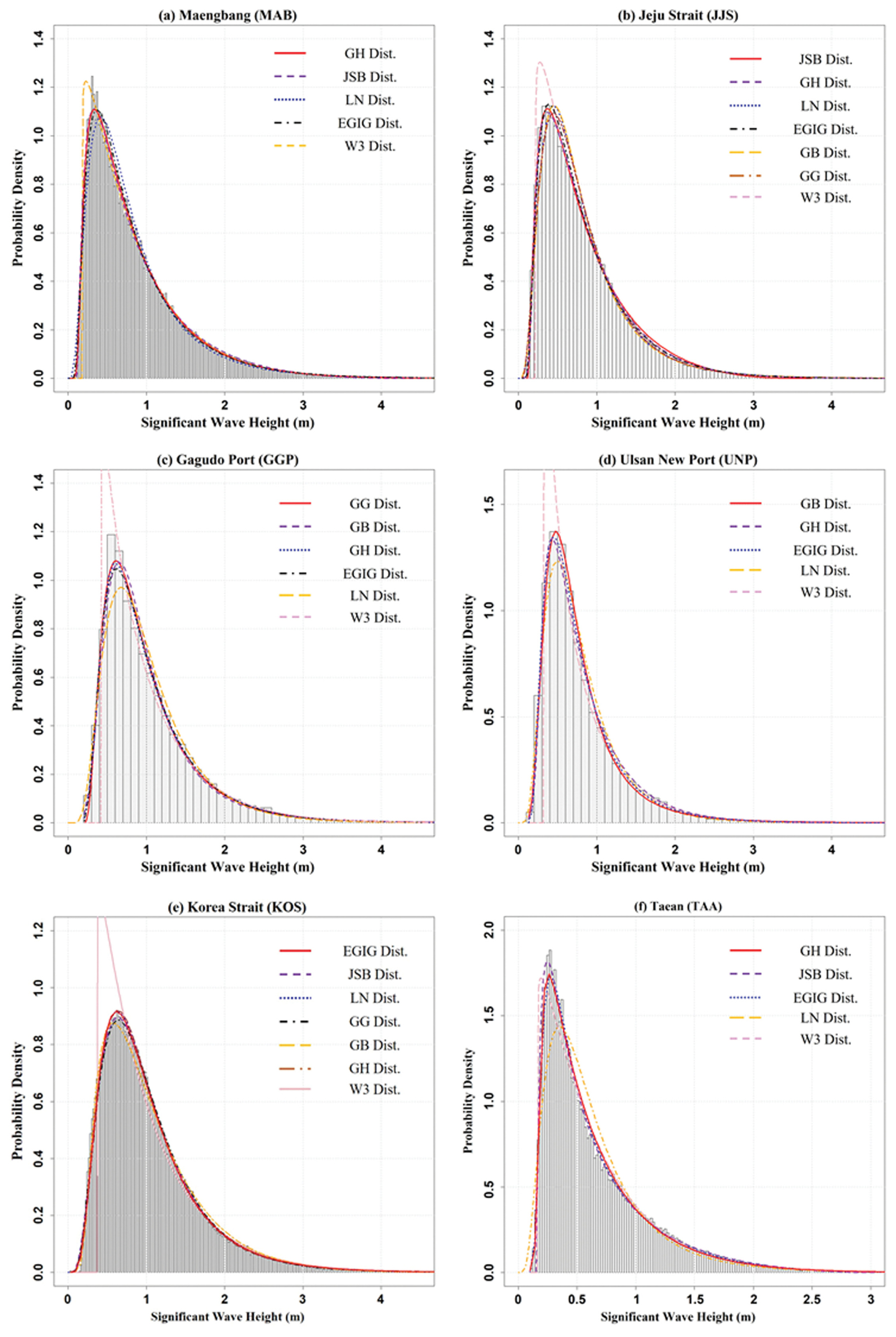
Histogram and fitted probability density functions of significant wave height for representative stations.
각 지점에서 최적 확률분포로 추정된 분포들은 대체로 유의파고 분포의 첨두 부분을 정확하게 재현하고 있으며, 특히 중심부에서 꼬리 영역으로 확장되는 구간에 대해 전반적으로 우수한 적합도를 보이는 것으로 나타났다. 또한, Appendix B에 제시한 바와 같이 모든 지점에서 4개 이상의 매개변수를 갖는 확률분포는 대부분 p-value 값이 0.05 이상인 것으로 나타났으며, 상대적으로 2, 3 매개변수 기반의 확률분포는 유의파고 확률분포 추정에 비교적 적합하지 않은 것으로 나타났다. Fig. 2와 Appendix B에서 확인할 수 있듯이, 일반적으로 유의파고 분석에 활용되는 LN 및 W3 분포는 분포의 중심부와 꼬리 영역에서의 분포 형태를 충분히 재현하지 못하여 다수의 매개변수를 갖는 분포들에 비해 전반적인 적합성이 낮은 것으로 확인됐다.
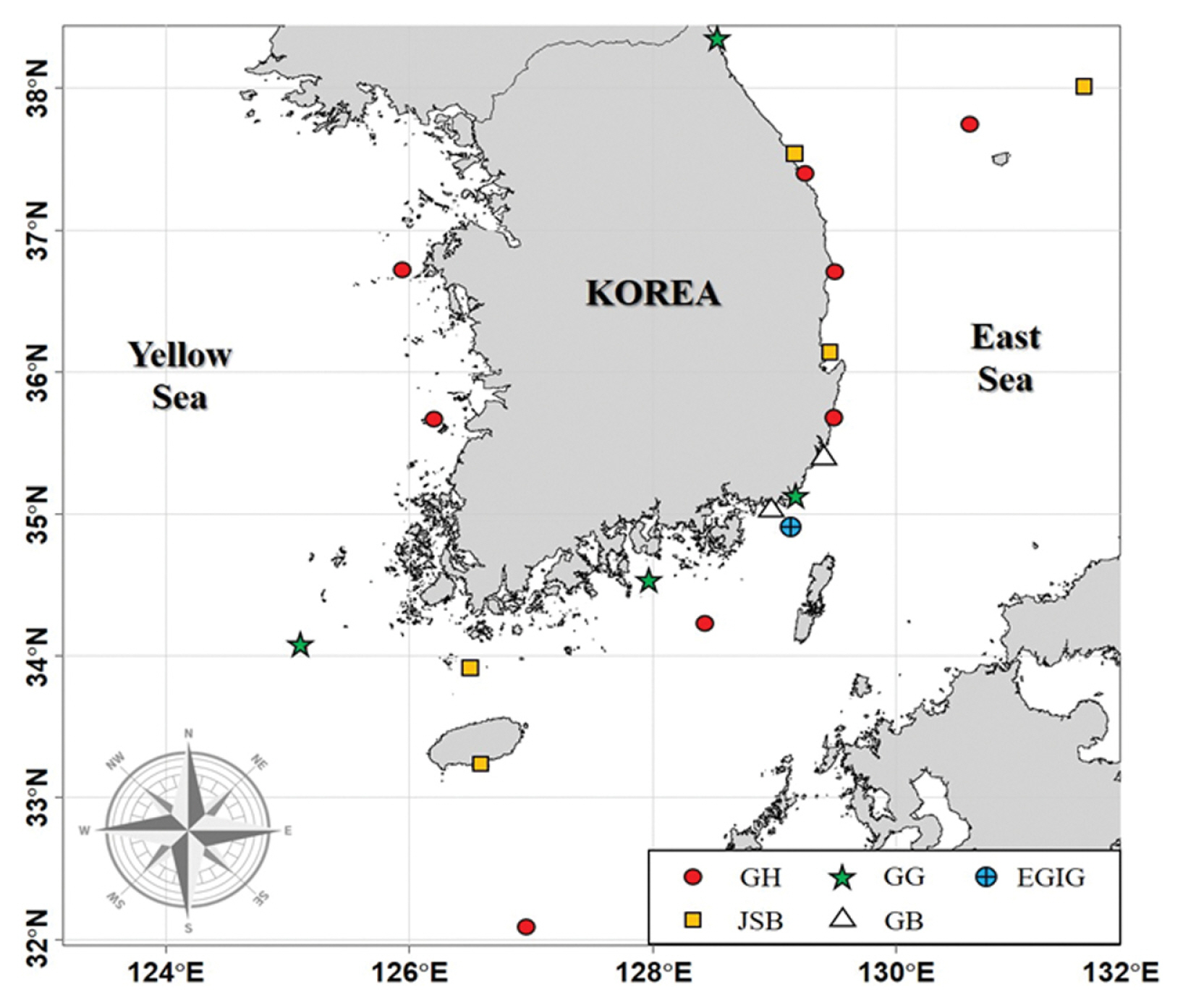
지점에 따라 평가된 적합 확률분포의 공간 분포는 다음 Fig. 3과 같다. GH 분포는 서해안과 동해안 및 남해안 일부 지점에서 주로 우세하게 나타났으며, 전반적으로 국내 연안 전역에서 광범위하게 분포하는 경향을 보였다. JSB 분포의 경우, 주로 동해안과 제주 해역 인근에서 주로 적합한 결과를 보임에 따라 지역적 집중도가 GH 분포에 비해 비교적 뚜렷한 것으로 나타났으며, GB 분포는 동해 남부 연안의 일부 지점에서만 최적 분포로 평가된 것으로 나타났다. GG 분포는 서해, 남해, 동해에서 적합한 것으로 나타나 뚜렷한 공간적 경향은 나타나지 않았으며, EGIG 분포는 대한해협 하나의 지점에서 적합 분포로 평가됐다.
Spatial distribution of optimal probability distributions of significant wave height around Korean coast.
3.2 유의파고 확률분포의 꼬리 영역 재현성 검토 결과
확률분포함수는 분포의 중심부 영역에 대해서는 일반적으로 높은 적합도를 보이지만, 꼬리 영역에 대해서는 통계적으로 불확실성이 증가함에 따라 적합도가 저하되는 한계가 존재한다. 이러한 한계를 보완하고 각 후보 분포의 꼬리 영역 재현성을 보다 정밀하게 검토하기 위하여, 본 연구에서는 분위수를 기반으로하는 Q-Q(Quantile-Quantile) 플롯을 이용한 분석을 수행하였다. Q-Q 플롯은 후보 확률분포의 이론 분위수와 관측자료의 분위수를 비교함으로서 전반적인 분포 적합도를 직관적으로 판단할 수 있으며, 특히 극단값이 위치한 꼬리 영역에 대한 검토가 가능하여 널리 사용되고 있다(Soukissian, 2021).
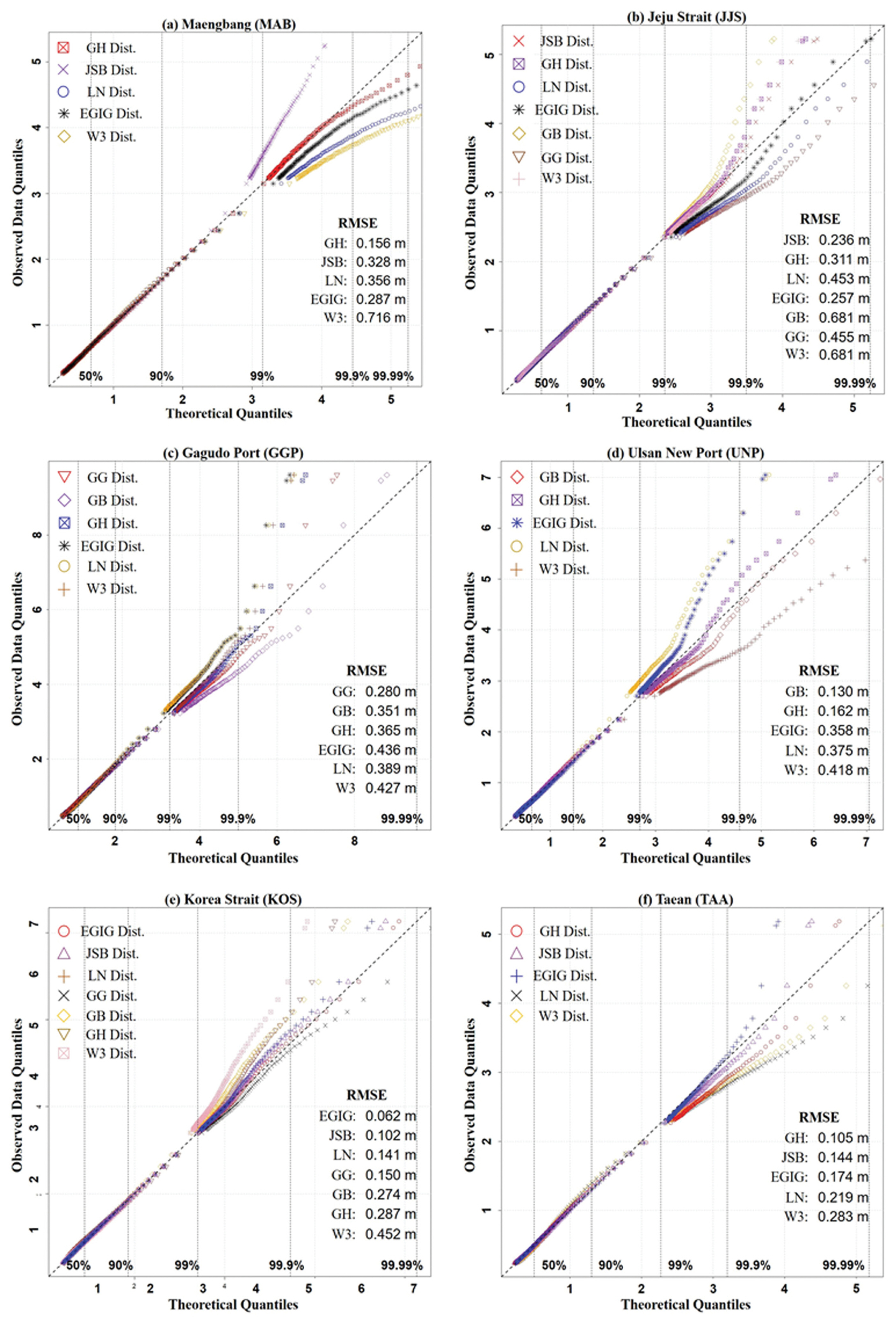
아울러 Fig. 2에서 제시한 지점에 대하여 Q-Q 플롯을 가시화하였으며, 각 후보 분포 별 분위수와 관측값 분위수 사이의 RMSE를 산정하여 수치적 적합도를 정량적으로 비교하였다(Fig. 4 참조). 분석 결과, 대체로 99% 분위수 이하 구간에서는 대체로 후보 분포 간 뚜렷한 차이는 보이지 않았으나, 99% 이상의 분위수 구간에서는 분포 별 꼬리 영역의 재현성 차이가 뚜렷하게 나타나는 경향을 보였다. MAB 지점에서는 GH 분포가 RMSE 0.156 m로 가장 낮은 값을 보였으며, 전반적인 적합 성능이 우수하였으나, 99.99% 분위수 이상의 극치 영역에서는 관측값을 과대 추정하는 경향이 나타났다. JJS 지점의 경우, JSB 분포는 99.9% 분위수까지는 안정적인 적합도를 보였으나, 보다 높은 분위수 영역에서는 EGIG 분포가 극단값을 보다 정밀하게 재현하는 것으로 나타났으며, EGIG 분포의 RMSE는 0.257 m로서 JSB 분포와 유사한 수준을 보였다. GGP 지점에서는 GG 분포가 RMSE 0.280 m로 가장 낮은 값을 보이며 상대적으로 우수한 재현성을 보였으나, 모든 후보 분포에서 99.9% 이상 분위수에서는 극단값을 전반적으로 과소 추정하는 경향을 보였다. UNP 지점의 경우, GB 분포가 RMSE 0.130 m로 가장 낮은 값을 보였으며, GH와 EGIG 분포에 비해 전반적인 적합도가 우수하고, 99.99% 수준에서도 극단값을 비교적 안정적으로 재현하는 결과를 보였다. KOS 지점의 경우 EGIG 분포가 유의파고의 극단값을 가장 잘 재현하는 것으로 나타났으며, 서해안에 위치한 TAA는 GH 분포가 극단값을 잘 설명하는 것으로 나타났다. 또한, Fig. 4에 제시하지 않은 지점에 대하여 Q-Q 플롯의 RMSE 분석 결과를 Appendix C에 제시하였다.
Q-Q plots comparing observed and theoretical quantiles of significant wave height for representative stations using fitted probability distributions.
4. 최적 분포함수 평가 및 토의
후보 분포함수를 이용한 분포 적합 성능평가 측도를 분석한 결과, 복잡한 형태의 확률 분포가 더 많은 형상 매개변수를 포함함으로써 분포의 비대칭성 및 꼬리 거동까지 유연하게 조절할 수 있기 때문에 기존 단순 분포보다 유의파고 확률분포를 정확하게 재현하는 것으로 판단된다. 한편, EGIG 분포는 6개의 매개변수를 갖는 복잡하지만 유연한 구조를 갖는 분포임에도 불구하고, 1개의 지점에서 적합한 분포로 평가됐다. 이는 과도한 유연성이 관측자료의 통계적 특성을 초과해 모델이 과적합되었거나, 상대적으로 많은 매개변수로 인해 수렴 안정성 문제가 발생했을 가능성이 있다. 또한, 매개변수의 수가 증가함에 따라 매개변수 간 상관성이 높아져 추정 과정이 복잡해지고, 최적화 과정에서 수렴이 불안정하거나 비일관적인 결과가 산출될 가능성이 있으므로, 추정된 최적 매개변수에 대한 해석에 주의가 필요하며, 보다 정확한 적합도 평가가 이루어져야 할 필요가 있다(Lubke and Campbell, 2016; Ying, 2019; Kiraly and Hangya, 2022).
한편, 유의파고의 전체 자료를 대상으로 추정된 최적 확률분포를 기반으로 정확한 극값을 추정하는 것은 자료의 독립성과 등질성의 문제로 권장되지 않는다(Goda, 2010; Vanem, 2015; Takbash and Young, 2019). 그러나, 최근 해양 구조물 설계 관점에서 요구되는 등고선 접근법은 전체 자료에 대한 최적 확률분포를 추정하여 분석하는 방법으로서 이를 정확히 재현하기 위해서는 정확한 확률밀도함수를 추정하는 것이 필요하다. 이에 따라 본 연구에서는 Q-Q 플롯 방법을 통해 확률분포 꼬리 영역의 재현성을 검토하였다. Fig. 4에 제시된 바와 같이 대체로 복수의 매개변수를 가지고 있는 후보 확률분포인 GH, JSB, GB, GG, EGIG 분포들은 분위수 99.99% 이상에서 관측치와 비교적 유사한 꼬리 거동을 보이는 것으로 나타났다. 본 연구에서 검토한 확률분포의 꼬리 거동 특성은 유의파고의 최적 확률분포를 추정하기 위한 초기적인 평가이며, 극값에 대한 정확한 분석을 위해서는 극치파랑분석을 추가로 수행하는 것을 권장한다.
본 연구에서 국내 연안 20개 지점에 대하여 평가된 적합 확률분포의 특성을 확인하기 위해 평균, 표준편차, 왜도(Skewness), 첨도(Kurtosis)를 산정하여 유의파고의 형상 특성을 검토하였으며, 그 결과는 다음 Table 3에 제시하였다. 대부분의 지점에서 유의파고의 평균은 0.65~1.40 m, 표준편차는 0.42~0.98 m 범위로 나타났으며, 대체로 수심이 깊은 지점에서 상대적으로 높은 평균값과 큰 변동성을 보였다. 왜도는 모든 지점에서 1.5 이상으로 나타나 유의파고 분포가 평균보다 작은 값에 집중되고, 일부 큰 파랑이 꼬리 영역에 존재하는 우측 왜도 형태를 보였다. 분포의 비대칭 정도를 나타내는 통계량인 왜도와 분포의 뾰족함과 꼬리 영역의 두께를 나타내는 지표인 첨도를 검토한 결과, 왜도와 첨도는 각각 1.5~3.6, 2.8~32.2의 범위로 나타났으나, 해역 및 적합 분포에 따른 뚜렷한 경향은 확인되지 않았다. 이는 파랑 분포의 비대칭성과 첨두 특성이 지역적인 해황 조건보다는 수심, 해저지형, 풍향 분포, 태풍 등 국지적 요인에 더 민감하게 반응하기 때문인 것으로 판단된다(Annenkov and Shrira, 2014; Abroug et al., 2022). 이는 동일 해역 내에서도 해상조건의 불균질성으로 인해 확률분포의 형태가 다양하게 나타날 수 있음을 의미한다.
Statistical characteristics of significant wave heights at 20 coastal sites around Korea
5. 결론 및 제언
유의파고의 확률분포 추정은 파랑에너지 자원량 평가, 해양 및 항만 구조물 설계 등 다양한 분야에서 활용됨에 따라 이를 정확하게 추정하고 분석하는 것은 필수적이다. 본 연구에서는 우리나라 연안을 대상으로 다양한 형태의 확률분포 모델을 적용하여 유의파고에 대한 적합 확률분포를 추정하고, 꼬리 영역의 거동 및 해역별 특성을 검토하였다.
국내에서 유의파고 확률분포 추정에 주로 사용되는 LN, W3 분포는 일부 지점을 제외하고 대부분 통계적으로 유의한 적합도를 확보하지 못했으며, 특히 분포의 중심 및 전체 영역의 재현에 한계가 있는 것으로 나타났다. 반면, 6-매개변수 기반의 EGIG 분포, 5-매개변수 기반의 GH 분포, 4-매개변수 기반의 JSB, GG, GB 등 복수의 매개변수를 가진 분포들은 높은 적합도를 보였으며, 유의파고의 중심값 및 전체 분포 특성을 보다 정밀하게 재현하는 것으로 나타났다.
그러나, 확률밀도함수만으로는 판단하기 어려운 꼬리 영역의 적합성을 정량적으로 평가하기 위해 Q-Q 플롯을 활용한 추가 분석을 수행하였다. 분석 결과, 대부분의 분포는 99% 분위수 이내에서는 관측자료와 유사한 경향을 보였으나, 분위수가 증가하여 극단값에 가까워질수록 분포 간 적합도 차이가 나타났다. 이는 매개변수가 많은 확률분포가 전반적인 분포 형태를 잘 재현하더라도, 꼬리 영역까지 일관되게 적합하기에는 한계가 있음을 의미한다. 아울러, 유의파고 확률분포 추정 시에는 하나의 분포에 의존하기보다는 다양한 매개변수를 갖는 확률분포를 충분히 고려하는 것이 필요하다고 판단되며, 확률분포 모델 선택 시 단순 매개변수 개수에 의존하는 것이 아닌 해당 분포의 구조, 안정성 등을 종합적으로 고려할 필요가 있다. 그럼에도 불구하고, 전체 유의파고 자료에 대하여 단일 확률분포를 적용해야 하는 경우에는, 본 연구에서 가장 높은 적합도를 보인 Generalized Hyperbolic(GH) 또는 Johnson SB(JSB) 분포를 사용하는 것이 가장 합리적인 선택으로 판단된다. 반면, 극치해상상태 분석이나 재현빈도 산정 등 극한 영역을 대상으로 하는 경우에는, 극치분포에 주로 활용되는 분포를 사용하는 것이 바람직할 것으로 판단된다.
본 연구에서 평가된 적합 확률분포 평가 결과는 향후 극치해상상태 분석 및 신뢰성 기반의 해양 구조물 설계, 해상 작업 가능성 평가 등 다양한 실무 분야에 활용될 수 있을 것으로 기대된다. 특히, 국제표준문서에서 권장하는 등고선 접근법 분석 시, 입력변수인 유의파고에 대한 정량적 분포 정보로서 실질적인 근거를 제공할 수 있을 것으로 판단된다. 향후, 유의파고 확률분포의 특성이 관측 기간, 계절에 따라 어떤 변화를 보이는지에 대한 추가적인 검토가 필요할 것으로 보이며, 울릉도, 제주도 등 연안에 비해 상대적으로 심해에 위치한 지점에 대하여 수심 및 해저지형 등 물리적 요인을 고려한 확률분포 비교 연구가 필요할 것으로 판단되며, 확률밀도함수의 매개변수를 추정하기 위해 사용된 최대우도추정법 외에 최소제곱법, 확률가중모멘트법 및 L-Moment 법 등을 적용한 추가적인 연구가 필요할 것으로 사료된다.
Notes
감사의 글
본 연구는 산업통상자원부의 신재생에너지 핵심기술개발 사업인 “해상풍력 해상보증조사(MWS) 기술지침서 국내 표준화 개발(과제번호: RS-2025-02313959)” 과제의 일환으로 수행되었습니다. 연구비 지원에 감사드립니다.
References
Appendices
Appendix
Estimated parameters of 9 probability distribution for each observation sites
Goodness-of-fit results and Kullback-Leibler divergence measures
Quantile-Quantile RMSE analysis results