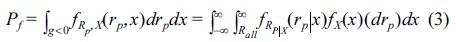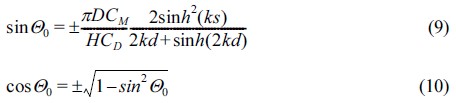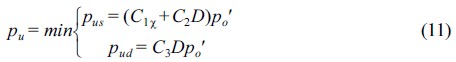2.1 극치응답비를 이용한 신뢰성 해석

지지구조물의 동적 응답은 지지구조물의 역학적 특성, 지반물성 그리고 설계하중 등의 설계변수에 의해 결정되며, 신뢰성 해석을 위한 지지구조물의 한계상태방정식은 식(1)과 같이 정의할 수 있다.

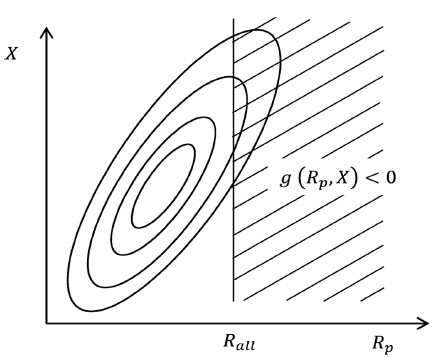
여기서, R_all은 구조물 응답에 대한 허용치, R_P(X)는 설계변수에 의한 지지구조물의 동적 피크응답이며 일반적인 확률밀도함수 형태는 Fig. 1과 같다.

Fig. 1.

A typical probability density function of peak response.

Fig. 1에서 R_p는 지지구조물의 피크응답을 의미한다. 그러나 지반의 강성, 풍속 등 설계변수(X)에 의해 R_p의 확률밀도 함수는 달라지며, X에 따른 확률밀도 함수는 Fig. 2와 같다.

Fig. 2.

PDFs of R_p for different X′s .

따라서, R_p와 X의 결합 확률밀도함수는 식(2)와 같이 정의될 수 있다.

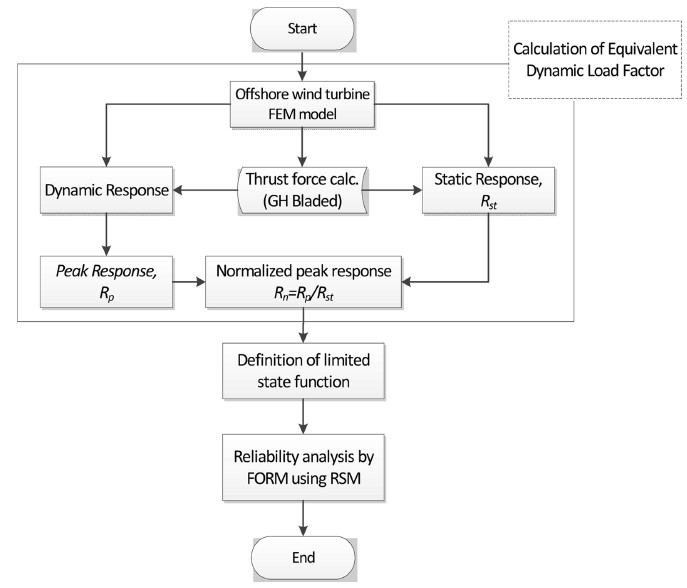
Fig. 3은 확률밀도함수 f_Rp, _X(r_p,x)를 나타낸 것이며, 빗금 친 영역은 한계상태함수가 음수가 되는 부분으로 파괴영역에 해당하기 때문에 파괴확률은 식(3)과 같이 표현할 수 있다.

Fig. 3.

Contour plot for f_Rp, _X( r_p, x).

위 조건에서 파괴확률 계산을 위해 확률변수로 고려되는 설계변수(X)에 따른 동적 피크응답을 구해야 하지만, 반복적인 동적 구조해석을 수행해야 하므로 어려움이 따른다. 이에 파괴확률(P_f)을 쉽게 구할 수 있도록 식(4)와 같이 동적응답계수 R_n을 정의하였다.

여기서, R_st는 설계조건에서의 정적응답이며, 지반물성 및 파랑, 풍하중 등에 대한 종속변수이다. 설계변수의 변동성에 따른 지지구조물의 동적 특성 변화가 크지 않은 경우 동적 피크응답과 정적응답은 비례할 수 있다는 가정에 식(4)의 개념을 적용하면, 한계상태함수는 식(5)와 같이 다시 쓸 수 있다.

R_n과 X의 결합된 확률밀도함수를 표준정규분포 확률변수 공간에 도시하면 Fig. 4와 같다.

Fig. 4.

Contour plot for f_Rn′,_X′ (r_n′, x′).

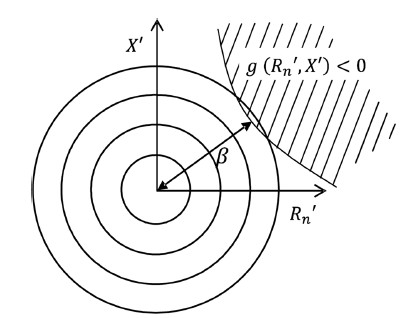
표준정규분포 확률변수의 공간에서 원점으로부터 파괴면 까지의 최단거리인 신뢰도지수를 산정하는 일계신뢰도법(First Order Reliability Method, FORM)을 통해 파괴확률을 계산할 수 있다. GH_Bladed를 통해 추력을 계산하고 정적/동적구조해석 결과를 이용한 신뢰성해석 과정을 흐름도로 나타내면 Fig. 5와 같다.

Fig. 5.

Flowchart for reliability analysis.

실제 구조물을 대상으로한 동적 구조해석에는 과도한 해석시간이 소요되므로 검증을 위한 모델은 1자유도계 시스템으로 가정하였으며, 질량(M) 1095.156 ton, 강성(K) 3.059 MN/m, 감쇠비(ζ )는 1%로 5MW 해상풍력터빈의 1차 고유진동수에 맞춰 모델링 하였다. 동적해석에 사용된 불규칙 파는 유의파고 7.9 m, 피크주기 15.19 sec로 Jonswap spectrum을 통해 생성하였으며, 모리슨 방정식(Morison et al., 1950)을 사용하여 계산하였다. 해석에 사용된 확률변수는 강성(K)과 동적응답계수(R_n)로 Table 1과 같다.

Table 1.

Distribution of random variables

Monte Carlo Simulation(MCS) 및 FORM을 사용하여 신뢰성해석을 수행하였으며, 각 한계상태 함수는 허용변위(0.038m)기준으로 식(6), (7)와 같이 정의하였다.

신뢰성 해석을 통해 계산된 파괴확률은 Table 2와 같고, 파괴확률의 절대오차는 0.067%로 허용 가능한 오차라고 판단된다.

Table 2.

Reliability analysis results

2.2 동적 피크응답에 대한 분포 추정

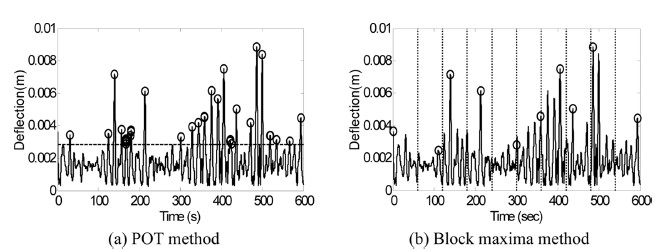
지지구조물의 동적 피크응답의 분포함수는 파랑 및 풍하중 등에 의한 동적응답을 분석함으로써 구할 수 있으며, 동적응답으로부터 피크응답의 분포를 추정하는 방법으로는 Block maxima와 Peak-Over-Threshold(POT) 방법이 주로 사용되고 있다. Block maxima 방법은 시간이력응답을 일정 블록(Block) 크기로 분할하고 각 블록에서 최대값을 통해 분포함수를 추정하는 방법이며, POT 방법은 미리 정의된 임계값을 초과하는 모든 피크점을 가지고 분포함수를 추정하는 것이다. Block maxima와 POT 방법의 샘플링 예를 나타낸 Fig. 6에서 볼 수 있듯이 Block maxima 방법에서는 block내부에서 하나의 최대값을 선택하기 때문에 다른 피크값들은 무시된다는 단점이 있지만 블록 크기를 줄임으로써 해결 할 수 있다. 그리고 POT 방법은 임계값에 따라 추정된 분포함수가 종속되기 때문에 임계값의 결정은 매우 중요한 요소이지만, 적절한 임계값을 구하는 것은 쉽지 않다는 제한사항이 있다.

Fig. 6.

Extreme value sampling.

2.3 파랑하중

지지구조물에 작용하는 파력 계산시 모리슨 방정식(Morison et al., 1950)이 사용되었으며, 작용하는 하중으로 인한 부재의 거동을 고려할 경우 단위 길이당 작용하는 힘 f_W는 식(8)과 같은 형태로 나타낼 수 있다.

여기서, C_D, C_M은 항력계수와 관성력계수, ρ_w는 해수의 밀도, D는 해양부착생물을 포함한 부재의 유효직경, A는 수직축에 투영된 부재 단면적, U는 부재축 직각방향의 물 입자 속도 성분이다. 식(8)을 통한 정적 파랑하중 계산시 물 입자의 속도를 부재 거동에 대한 상대속도로 고려하기 위해 고려된 부재의 속도성분인 는 무시된다. 그리고 물 입자 운동에 대한 위상(Phase)은 선형 파랑이론에 근거하여 Sine과 Cosine 함수로 정의되며, 파력이 최대가 되는 위상은 식(9),(10)과 같다.

2.4 모래지반에 대한 P-y 곡선

지반의 모델링은 구조물과의 상호작용을 고려하기 위해 비선형 스프링으로 모델링 하였다. 모래지반에서 구조물 변위와 지반반력의 비선형 관계를 정의하는 P-y 곡선은 API에서 제시한 방법에 따라 계산하였다(API RP 2A-WSD, 2007).

여기서, p_u는 지반의 극한지지력, s와 d는 각각 얕은 기초와 깊은 기초, C_i는 모래지반의 내부마찰각에 의해 결정되는 계수, D는 기초 파일의 직경, χ는 해저면을 기준으로 한 깊이, p_o'는 유효 흙덮기압이며, 비선형 P-y 관계는 API기준에 따라 식(12)과 같이 정의된다.

여기서, A는 동적 또는 정적하중 계수, k는 초기 지반반력계수, y는 수평 변위이다.

2.5 응답면 기법(Response surface method,RSM)

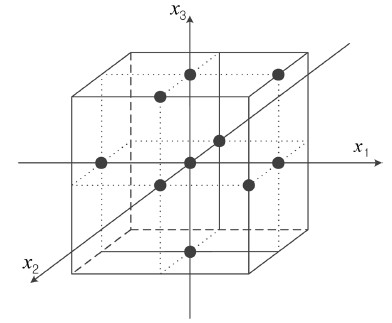
신뢰도 지수 산정을 위해서는 설계변수에 의해 정의되는 한계상태함수가 양함수로 표현 가능한 형태여야 한다. 그러나 한계상태함수가 식(5)와 같이 설계변수에 의해 종속되는 음함수로 존재하는 경우 Scheuller et al.(1987)에 의해 제안된 응답면 기법을 사용하여 한계상태함수를 양함수로 근사화 할 수 있다. 응답면은 표본점 선정 후 각 표본점에서의 구조해석을 통해 구할 수 있으며, 표본점 선정은 식(13)과 같이 확률변수의 평균 또는 중심으로부터 일정 거리만큼 떨어져 있는 점을 취하는 방법을 사용하였다(Khuri and Cornell, 1996).

여기서, 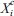는 확률변수의 평균 또는 중심이 되는 점으로 매회 갱신되는 파괴점, σ_Xi는 X_i의 표준편차, h_i는 확장폭 그리고 I_i scattering index 이며, Saturated Design 에 의한 구조해석점을 정규화된 공간에 도시하면 Fig. 7과 같다.

Fig. 7.

Saturated design using full second order polynomial with cross terms.

3.1 지지구조물 및 지반조건

수치해석은 5-MW급 해상풍력터빈을 대상으로 하였으며, 지지구조물은 Fig. 8과 같이 서남해안의 풍속, 수심 및 파고 등을 고려하여 설계된 4-Leg 재킷(Jacket) 구조로 Pin pile을 삽입하여 암반과 그라우팅되는 형태이다.

Fig. 8.

Front view of jacket structure.

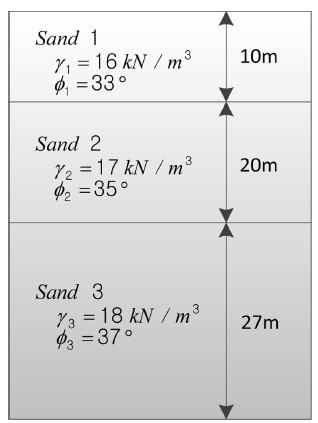
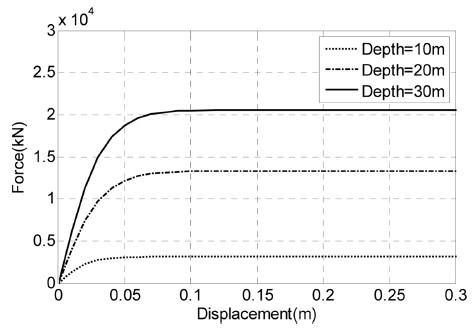
NREL 5-MW 해상풍력터빈 모델(Jonkman et. al., 2009)을 참조하였으며, 로터(Rotor)와 너셀(Nacelle), 타워(Tower) 그리고 지지구조물의 질량은 각각 350 ton, 391 ton, 265 ton 이다. 지반은 Fig. 9와 같이 각각 다른 유효단위중량(γ_i) 및 내부마찰각(φ_i)을 갖는 다층 모래지반으로 구성하였고, 이에 따라 계산된 P-y 곡선은 Fig. 10과 같다.

Fig. 9.

Soil properties.

Fig. 10.

P-y curves for API sand(cyclic loading conditions).

3.2 유한요소 모델링 및 고유치 해석

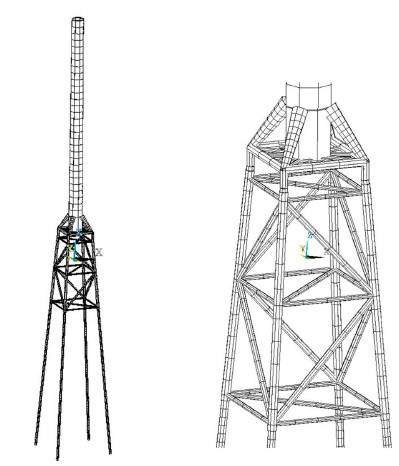
범용 유한요소해석 프로그램인 Ansys 12.0을 사용하여 유한요소 모델 및 구조해석을 하였다(ANSYS user’s manual, Ver. 12.0). 블레이드(Blade) 및 너셀(Nacelle)은 집중질량으로 고려되었으며, 재킷(Jacket) 및 타워(Tower)는 보(Beam)요소를 사용하여 Fig. 11과 같이 모델링 하였다.

Fig. 11.

FEM model.

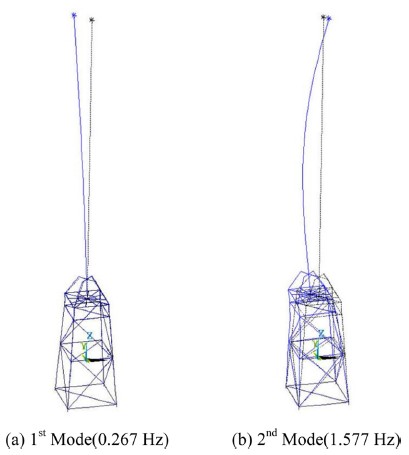
지반부분에 사용된 비선형 스프링은 1 m 간격으로 모델링되었으며, 고유치 해석 결과 모드 형상은 Fig. 12와 같고, 고유 진동수는 각각 0.267 Hz, 1.577 Hz로 나타났다.

Fig. 12.

Mode shapes.

3.3 환경하중

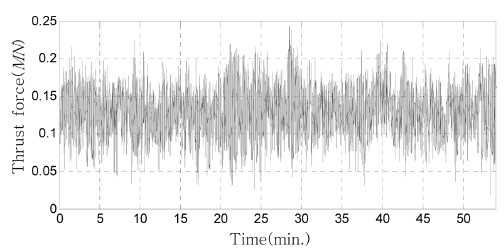
풍하중의 분포를 구하기 위해 GH_Bladed(Bladed Multibody dynamics user manual, Ver. 4.4)를 사용하였으며, 바람장 생성시 IEC 61400-1(IEC 61400-1 Ed.3, 2005) CLASS II 등급에 해당하는 설계풍속 42.5 m/sec, 난류강도(I_ref)는 0.12로 설정되었다. Fig. 13은 1시간 동안 시뮬레이션을 통해 계산된 추력을 나타낸 것이다.

Fig. 13.

Thrust force time history.

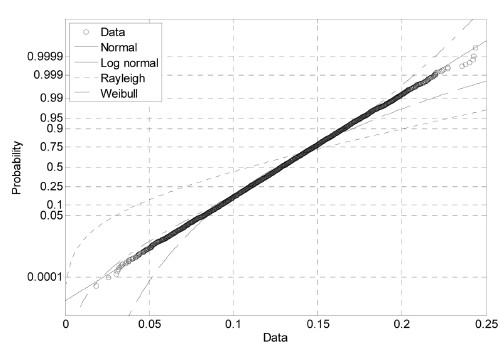
정적하중으로 고려된 추력은 Fig. 14와 같이 정규분포 확률변수로 추정되었으며, 평균은 0.129 MN, 변동계수(COV)는 0.22 이다.

Fig. 14.

Probability plot for thrust force.

타워(Tower)에 작용하는 풍하중을 계산하기 위해서는 풍속이 필요하며, 작용하는 추력에 해당하는 풍속은 식(14)를 통해 계산할 수 있다.

여기서, F_fh는 추력에 대한 누적확률분포함수이고, F_V은 풍속의 누적확률분포함수이다.

타워(Tower)에 작용하는 단위 길이당 풍하중은 식(15)와 같이 계산할 수 있다.

여기서, ρ_air는 공기의 밀도, C_t는 타워(Tower)의 항력계수, V는 풍속, z는 해수면으로부터 높이, D는 타워(Tower)의 직경이다. 그리고 해상풍력터빈의 작동상태 및 해상환경조건을 정리하면 Table 3과 같다.

Table 3.

Design environmental condition

3.4 동적구조해석 및 피크응답의 분포

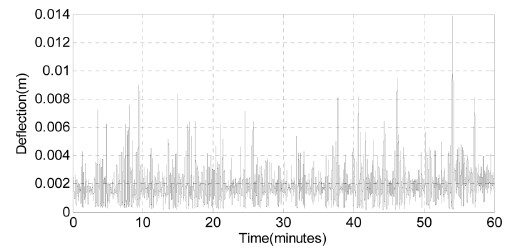
설계 파랑 및 풍하중에 대한 해상풍력터빈의 동적구조해석을 수행하였다. 시뮬레이션 시간은 1시간이며, mud-line에서의 시간이력 수평변위 응답은 Fig. 15와 같다. 해석에 사용된 PC는 OS Windows7 64bit, CPU Quad core(3.4 GHz) 환경이며, 해석에 약 13시간 30분이 소요되었다. 따라서 해상풍력터빈의 신뢰성 해석시 동적 구조해석을 직접 사용하여 파괴확률을 산정하는 것은 사실상 불가능하다.

Fig. 15.

Dynamic response of support structure at mud-line.

Block maxima 방법을 사용하여 피크응답에 대한 확률분포를 추정하였으며, block 크기는 1분이다. 그 결과 Fig. 16과 같이 Log normal 분포가 적합한 것으로 나타났다.

Fig. 16.

Probability plot for peak response.

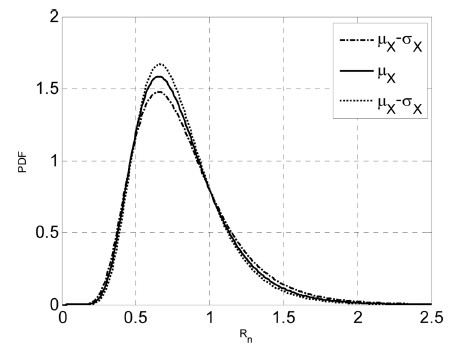
Fig. 17과 Table 4는 설계변수(X) 변화에 따른 동적응답계수(R_n)의 확률밀도함수와 그에 대한 확률분포 모수이며, 확률밀도함수는 거의 동일한 형태를 유지하는 것을 알 수 있다. 이는 설계변수 변화에 V F 따른 동적피크응답이 크거나 작게 나타날 수 있지만 그에 따라 정적인 응답 또한 동적피크응답에 대해 유사한 비율로 증가 또는 감소한다는 의미이다. 그러므로 임의의 설계조건에서 정적응답과 정의된 동적응답계수를 통해 동적응답을 예측하는 방법이 적용 가능하다는 것을 입증하고 있다.

Fig. 17.

PDFs of normalized peak response under different environmental load.

Table 4.

Mean and standard deviation for the lognormal distributions.

3.5 신뢰성 해석 Level II(FORM)

FORM을 사용하여 신뢰성 해석을 수행하였으며, 해석에 사용된 확률변수는 Table 5와 같다. 동적응답계수는 동적응답의 분석을 통해 Log normal 분포로 고려되었으며, 지반의 단위중량 및 추력은 정규분포, 그리고 지반의 내부마찰각은 상한과 하한이 정해진 Beta분포로 가정하였다.

Table 5.

Distribution of random variables

한계상태함수는 식(16)과 같이 mud-line에서 지지구조물의 허용 수평변위를 사용하여 정의하였다.

여기서 f_w는 모리슨 방정식에 의해 계산된 파력으로 지지구조물에 분포하중으로 적용되었으며, 파력 산정시 사용된 재현주기 50년에 해당하는 유의파고(H_s)는 상수로 가정하였다.

허용 수평변위인 R_all은 교량설계에 적용되는 AASHTO LRFD Bridge Design Specification를 준용하여 38 mm로 결정하였다.

신뢰성해석 결과 신뢰도지수(β)는 Fig. 18과 같이 약 40번의 반복과정 이후 6.0493으로 수렴되었다. 신뢰도지수의 수렴이 비교적 느린 이유는 내부마찰각이 상한과 하한이 정해져 있는 Beta분포로 고려되었기 때문이다.

Fig. 18.

Reliability analysis by FORM.

각 확률변수의 민감도계수(Sensitivity factors) 및 Most probable failure point(MPFP)는 Table 6과 같다. Table 6에 나타난 민감도 계수 및 MPFP를 통해 알 수 있듯이 동적응답계수가 가장 주요한 요인이며, 그 다음으로 풍하중인 것을 알 수 있다. 그리고 지반 물성 관련 확률변수 중 표층의 지반내부마찰각인 φ₁을 제외한 다른 확률변수의 민감도는 매우 작은 것으로 나타났다.

Table 6.

Sensitivity factors and most probable failure points

3.6 접근방법의 제한사항

설계변수(X) 변화에 따른 동적응답계수(R_n)의 확률밀도함수들을 비교한 결과 Fig. 17에서와 같이 거의 동일한 형태를 유지하는 것을 알 수 있었기 때문에 본 연구에서는 해상풍력터빈 지지구조물의 동적응답계수(R_n)가 일정하다고 가정하였다. 그러나 설계변수(X)에 따른 구조물의 동/정적 응답 비선형성이 큰 경우에는 검증되지 않았다. 따라서, 이 방법은 대상이 되는 구조물의 비성형성을 주의 깊게 식별한 후 적용해야 한다.