Numerical Simulation of Dynamic Response of Seabed and Structure due to the Interaction among Seabed, Composite Breakwater and Irregular Waves (I)
불규칙파-해저지반-혼성방파제의 상호작용에 의한 지반과 구조물의 동적응답에 관한 수치시뮬레이션 (I)
Article information
Abstract
Seabed beneath and near coastal structures may undergo large excess pore water pressure composed of oscillatory and residual components in the case of long durations of high wave loading. This excess pore water pressure may reduce effective stress and, consequently, the seabed may liquefy. If liquefaction occurs in the seabed, the structure may sink, overturn, and eventually increase the failure potential. In this study, to evaluate the liquefaction potential on the seabed, numerical analysis was conducted using the expanded 2-dimensional numerical wave tank to account for an irregular wave field. In the condition of an irregular wave field, the dynamic wave pressure and water flow velocity acting on the seabed and the surface boundary of the composite breakwater structure were estimated. Simulation results were used as input data in a finite element computer program for elastoplastic seabed response. Simulations evaluated the time and spatial variations in excess pore water pressure, effective stress, and liquefaction potential in the seabed. Additionally, the deformation of the seabed and the displacement of the structure as a function of time were quantitatively evaluated. From the results of the analysis, the liquefaction potential at the seabed in front and rear of the composite breakwater was identified. Since the liquefied seabed particles have no resistance to force, scour potential could increase on the seabed. In addition, the strength decrease of the seabed due to the liquefaction can increase the structural motion and significantly influence the stability of the composite breakwater. Due to limitations of allowable paper length, the studied results were divided into two portions; (I) focusing on the dynamic response of structure, acceleration, deformation of seabed, and (II) focusing on the time variation in excess pore water pressure, liquefaction, effective stress path in the seabed. This paper corresponds to (I).
Trans Abstract
해양 및 해안구조물 하부의 해저지반에 장시간 지속적인 고파랑이 작용하는 경우 진동성분과 잔류성분으로 구성되는 과잉간극수압의 증가에 따른 유효응력의 감소로 인하여 해저지반내에 액상화의 가능성이 나타나고, 일단 액상화가 발생되면 그의 진행에 따라 구조물의 침하 혹은 전도에 의해 종국적으로 구조물이 파괴될 가능성이 높아지게 된다. 본 연구에서는 2차원수치파동수로를 혼상류해석과 불규칙파동장으로 확장한 수치해석법을 적용하여 불규칙파동장하에서 해저지반상 및 혼성방파제의 표면상에서 시간변동의 동파압과 유속에 의한 전단응력을 산정하고, 그 결과를 지반의 동적거동을 정밀하게 재현할 수 있는 유한요소법에 기초한 탄소성해저지반응답용의 수치해석프로그램에 입력치로 적용하여 불규칙파동장에서 해저지반내에서 과잉간극수압 및 유효응력의 시공간적인 변화, 이로 인한 액상화, 그리고 지반의 시간변형과 케이슨의 시간변위 및 변위가속도 등을 정량적으로 평가한다. 이로부터 혼성방파제 전면 및 후면 하부의 해저지반내에서 액상화 가능성을 확인할 수 있었고, 이에 따라 액상화된 토립자는 흐름에 대한 저항력을 상실하므로 액상화된 지반은 세굴가능성이 클 것으로 판단된다. 또한, 액상화된 지반은 강도의 현저한 저하로 구조물의 진동변위가 증폭되고, 더불어 혼성방파제의 안정성에 큰 영향을 미칠 것으로 예상된다. 여기서, 본 연구의 전체 내용을 지면관계상 두 부분으로 나누며, 전반부를 (I)로 하여 구조물의 동적변위와 변위가속도 및 지반변형을 중심으로 다루고, 후반부를 (II)로 하여 지반내에서 간극수압의 시간변동, 액상화 및 유효응력경로 등을 상세히 다루며, 본 연구는 전반부인 (I)에 해당한다.
1. 서 론
방파제와 같은 해안구조물 근방에서는 연안지형과 지반의 특성 및 파랑과 흐름의 성질에 따라 자연적 및 인위적인 요인들이 복잡하게 작용하여 국부적인 침식(세굴) 및 퇴적, 그리고 광역에 걸친 지형변동이 여러 가지 형태로 발생 및 발달하며, 이러한 지형변동은 연안의 해저지반을 끊임없이 변화시키는 것으로 보고되고 있다(MOLIT, 2010). 연안역에서 지형변동의 한 원인으로 각종 개발사업과 관련된 방파제와 안벽으로 대표되는 인공구조물의 건설에 따른 해역환경변화를 들 수 있지만, 근래 또 다른 하나의 원인으로 파동에 의한 해저지반의 액상화가 지목되고 있다.
고파랑이 장시간 지속되는 경우 해저지반내 과잉간극수압의 증가에 따른 유효응력의 감소로 해저지반이 액상화될 수 있고(Tsuruya and Krezumi, 1990), 일단 액상화가 발생되면 토립자는 흐름에 대한 저항력을 상실하므로 지형변동이 발생된다. 특히, 파동으로 인한 지반액상화는 방파제에서 사석마운드부의 침하 혹은 케이슨의 침하와 전도 등을 야기하여 종국적으로 구조물의 파괴와 같은 큰 피해를 초래할 수 있다.
이에 대한 대표적인 경우로 1978년에 포르투칼 Cape Sines에 있는 Sines방파제가 해저지반의 액상화에 의해 침하된 피해사례가 잘 알려져 있고(Burcharth, 1987), 또한 유사한 피해사례가 세계 각지에서 많이 보고되어 있다(Burcharth, 1987; Oumeraci, 1994; Zen and Umehara, 1986; Okusa, 1984). 우리나라의 경우 최근 2003년 태풍 매미의 내습시 남해안에 해안구조물의 침하에 따른 많은 피해와 2012년 태풍 볼라벤 내습시 제주도 서귀포항 방파제의 피해사례를 대표적으로 들 수 있을 것이다.
지반액상화와 직접적인 연관을 갖는 파동에 기인한 지반내 과잉간극수압변동은 진동성분(oscillatory pore water pressure)과 잔류성분(residual pore water pressure)으로 구분될 수 있고, 각각은 서로 다른 방법으로 예측된다. 진동성분에 대해서는 대표적으로 다공질탄성지반(porous elastic seabed)과 압축성유체에 기초한 Madsen(1978), Yamamoto et al.(1978), Tsai and Lee(1995), Jeng and Hsu(1996), Jeng(1997), 경계층근사를 적용한 Mei and Foda(1981), 해저지반내 흙의 포화도에 대한 중요성을 입증한 Okusa(1985) 및 교차비등방해저지반(cross-anisotropic seabed)에 대한 Kianto and Mase(1999), Yuhi and Ishida(2002) 등의 연구를 들 수 있으며, 이는 지반내의 연직깊이에 따라 간극수압의 변화에서 진폭의 감쇠와 위상지연이 수반된다.
또한, 잔류성분은 반복하중하에 흙의 수축에 의해 야기되는 과잉간극수압의 축적으로 발생되며(Seed and Rahman, 1978; Sumer and Fredsøe, 2002), 파작용시간에 비례하여 축적되는 경향을 나타낸다. 파동으로 인한 과잉간극수압의 축적에 대한 메커니즘의 규명에는 지진시 지반내에서 발생되는 과잉간극수압과 유효응력과의 관계(Seed et al., 1975)가 고려되고 있다. 이에 대한 연구로 해석해를 나타낸 McDougal et al.(1989), Cheng et al.(2001), Chen et al.(2005), Jeng et al.(2006, 2010), Jeng and Seymour(2007), 반복전단응력의 분포와 과잉간극수압소산을 고려하여 1차원유한요소모델을 확립한 Seed and Rahman(1978) 및 Laplace변환을 사용하여 중복파동으로 인한 액상화에 탄소성모델을 적용한 Sekiguchi et al.(1995) 등을 들 수 있고, 수치해석모델의 개발에 관해서는 Miyamoto, et al.(2004), Sassa and Sekiguchi(1999, 2001), Sassa et al.(2001) 등의 연구가 있다.
한편, 방파제와 같은 해안구조물이 설치된 해역에서 해저지반내 과잉간극수압 등의 동적거동을 검토한 연구로, 다공질탄성지반의 가정하에 얻어지는 Biot의 압밀방정식(Biot, 1941)을 기초방정식으로 2차원 혹은 3차원파동장에 설치된 방파제 주변에서 지반내 유효응력, 진동 및 잔류간극수압 등의 동적응답과 액상화 가능성을 평가한 Mase et al.(1994), Ulker et al.(2010), Li and Jeng(2008) 및 Ye et al.(2014), 그리고, 포텐셜이론에 기초한 Li and Jeng(2008) 등을 예로 들 수 있다.
이상에서 기술된 진동 및 잔류과잉간극수압 등과 같은 해저지반의 동적거동을 해석한 연구예는 모두가 규칙파를 대상으로 하고 있다. 주지의 사실로, 실제 파동은 불규칙파동에 보다 가깝고, 따라서 불규칙파동장을 대상으로 해저면과 구조물에 작용하는 불규칙파압과 전단응력 등을 적용하여 해저지반내 간극수압, 변위 및 액상화 등과 같은 물리량의 동적거동 특성을 명확히 평가할 필요가 있다. 따라서, 본 연구에서는 2차원수치파동수로를 불규칙파동장으로 확장한 수치해석법(Lee et al., 2013)으로부터 해저지반상 및 혼성방파제 표면에서 시간변동의 불규칙파압 및 유속에 의한 전단응력을 산정하고, 그 결과를 지반의 동적거동을 정밀하게 재현할 수 있는 수치 해석프로그램(Finite element analysis LIquefaction Program(이하 FLIP); Iai et al., 1992a, 1992b)의 외력으로 사용하여 해저지반내에서 진동과잉간극수압, 잔류과잉간극수압, 유효응력, 액상화, 지반변형 및 케이슨의 변위에 대한 시간변화와 주파수스펙트럼의 분석으로부터 불규칙파랑-지반-혼성방파제의 상호작용특성을 정량적으로 평가한다.
여기서, 본 연구의 전체 내용을 지면관계상 두 부분으로 나누며, 전반부를 (I)로 하여 구조물의 동적변위와 변위가속도 및 지반변형을 중심으로 다루고, 후반부를 (II)로 하여 지반 내에서 간극수압의 시간변동, 액상화 및 응력경로 등을 다루며, 본 연구는 전반부인 (I)에 해당한다.
2. 수치해석이론의 개요
2.1 2D-NIT모델에 의한 파동장해석의 개요
본 연구의 2D-NIT모델(Lee et al., 2013)은 기존의 2차원 수치파동수로모델(CDIT, 2001)을 기체와 액체의 거동을 동시에 해석하는 혼상류 및 불규칙파동장으로 확장한 모델로, 자유표면의 해석모델에 VOF법(Hirt and Nichols, 1981)을, 난류모델에는 k−ε모델을 각각 적용하고 있다. 하지만, 본 연구에서는 단순한 불투과연직케이슨의 혼성방파제가 설치된 비쇄파 파동장의 경우 유의한 난류성분이 발생되지 않을 것으로 판단되고, 또한 계산시간을 고려하여 난류모델을 적용하지 않는 것으로 한다. 따라서, 파동장해석은 2차원비압축성의 점성유체를 대상으로 한 연속식과 PBM (Porous Body Model; Sakakiyama and Kajima, 1992)으로 확장한 Navier-Stokes방정식에 기초한다. 여기서, 2D-NIT모델에 의한 수치동수로에서 각 경계조건 및 불규칙파의 조파 등에 관한 보다 상세한 정보는 Lee et al.(2013)을 참조바란다. 그리고, 후술하는 해저지반거동과 파동장과의 간섭에 의한 파동장의 변화는 무시된다.
2.2 FLIP모델에 의한 해저지반거동해석의 개요
FLIP모델(Iai et al., 1992a, 1992b)은 다중전단메커니즘을 이용한 2차원유효응력의 유한요소해석모델로, 이 모델에서는 원형고정경계를 전단변형영역과 무한개의 가상스프링경계의 연결로 정의되는 이동절점으로 나타낸다. 여기서, 각 스프링은 여러 방향을 갖는 실제 단순전단메커니즘이라고 할 수 있고, 이는 지반에서 흙의 탄소성에 관한 응력-변형율관계를 잘 모사할 수 있다.
과잉간극수압은 반복전단작용에 의해 발생되는 흙의 체적 변형과 간극률 및 간극수의 체적탄성계수와의 관계로부터 산정되고, (+)다일러턴시의 영향은 Iai et al. (1992a, 1992b)에 의해 제안된 액상화프론트(liquefaction front)를 이용하여 반복전단작용에 의한 흙의 유효응력감소에 의해 유발되는 반복 변동(cyclic mobility) 및 액상화거동을 재현할 수 있다. 보다 상세한 이론적인 배경은 FLIP모델(Iai et al., 1992a, 1992b)혹은 Lee et al.(2014)을 참조바란다.
3. 수치해석
3.1 수치해석결과의 검증
전술한 바와 같이 FLIP모델(Iai et al., 1992a, 1992b)은 지반내 간극수를 압축성으로, 그리고 흙골격을 탄소성체로 각각 가정하며 지진시 액상화에 따른 지반과 구조물의 안정성을 검토하기 위하여 개발된 유한요소기반프로그램이며, 지진시 구조물의 손상에 대한 계측결과와 비교 및 검토로부터 그의 타당성이 검증되었다(Sawada et al., 2000; Ozutsmi et al., 2002; Iai et al., 1992a, 1992b). 그리고, 불규칙파랑을 대상으로 하는 2D-NIT모델은 모델의 개발과정(Lee et al., 2013)에서 파-구조물의 상호간섭에 의한 파변형과 월파량 등에 대해 검증되었다. 또한, 해저지반과 상부파동장이 접하는 경계면상에서 시간변동의 압력과 유속에 의한 전단응력을 2DNIT모델로부터 산정하고, 이를 해저지반상에 외력치로 하여 FLIP으로부터 산출되는 과잉간극수압과 유효응력 등의 수치해석결과를 기존의 해석해(Yamamoto et al., 1978)와 실험결과(Chang et al., 2007)와 비교 및 검토한 Lee et al.(2014)에 의해 충분히 검증되었기 때문에 본 논문에서는 검증에 대한 반복적인 기술을 생략하는 것으로 한다.
3.2 계산조건
3.2.1 파동부에서 계산조건
Fig. 1 같은 일정수심 h의 불규칙파동장에 설치된 혼성방파제를 대상으로 2D-NIT모델(Lee et al., 2013)로부터 해저면에서 파동으로 인한 동파압과 전단응력을 도출하기 위하여 저면유속을 산정하였다. 그림에서 사석마운드부의 높이 h2는 5 m, 케이슨의 폭 b와 높이 h1+h3은 각각 20 m이며, 파동장에서 격자간격은 수평 및 연직 모두 0.5 m로 설정되었다. 불규칙파랑의 수치해석에 적용된 입사파의 제원은 다음의 Table 1과 같고, 표에서 Run-4의 경우는 월파가 발생하는 케이스이다.
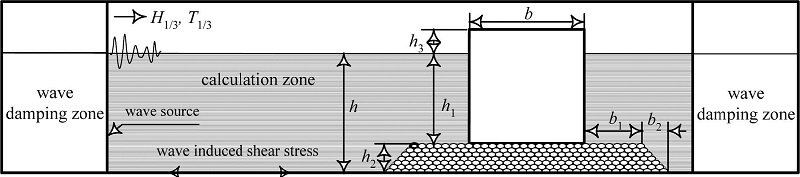
Schematic diagram of the numerical wave tank domain used for this numerical simulation (h = 20m, h1 = 15 m, h2 = 5 m, h3 = 5 m, b = 20m, b1 = 10 m, b2 = 5 m).
3.2.2 지반부에서 계산조건
이상에서 제시된 불규칙파랑의 입사조건과 구조물의 형상 및 크기를 2D-NIT모델에 적용하여 파동부의 해저면에서 유속에 의한 전단응력 및 파압을 산정하고, 이를 지반해석프로그램 FLIP모델(Iai et al., 1992a, 1992b)에 지반상면에서 입력치로 적용한다. 그리고, FLIP모델에 동시에 적용되는 사석마운드부 및 해저지반부의 물성치는 다음의 Table 2와 같다. Fig. 2는 FLIP에 적용되는 해저면에서 파압과 유속에 의한 전단응력의 입력위치, 구조물 침하량의 산정위치 N1과 N2 및 모래지반내 과잉간극수압의 산정위치 P.1에서부터 P.21까지를 나타내며, 지반부에서 수치해석의 격자간격은 가변격자로 수평과 연직 모두 최소 1 m, 최대 2 m로 각각 설정되었다.
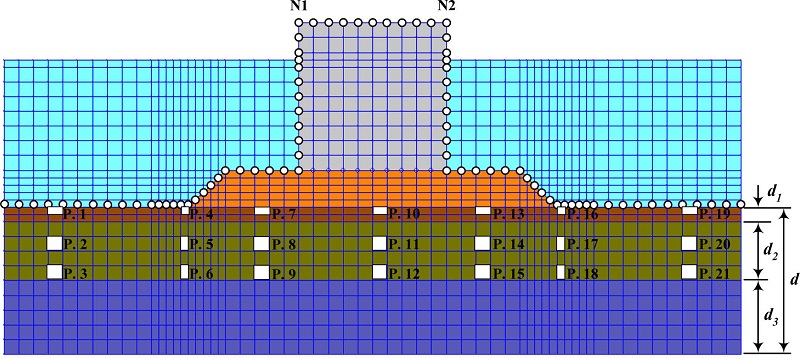
Schematic diagram of the breakwater and ground formation domain used for this numerical simulation(d = 20 m, d1(sand 1) = 2 m, d2(sand 2) = 8 m, d3(sand 3) = 10 m)(N1 and N2: measuring points of caisson displacements, ○ : input points of wave pressures and shear stresses, P.1~P.21 : measuring points of excess pore water pressures).
3.3 불규칙파랑의 조파
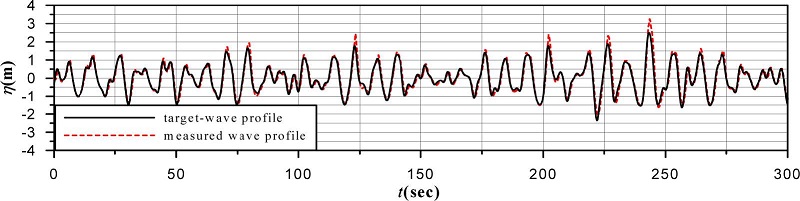
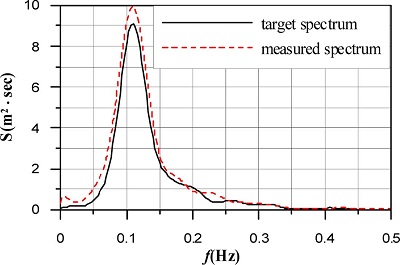
H1/3= 3m, T1/3= 10 sec의 불규칙파랑에 대해 조파기에 입력한 Bretschneider-Mitsuyasu스펙트럼(Mitsuyasu, 1970)에 의한 목표파형(target wave profile)과 조파판 바로 전면에서 얻어진 측정파형(measured wave profile)과의 비교를 나타낸 일례가 Fig. 3이다. 그림으로부터 시간변동에 따른 두 파형의 위상 및 수위변화가 매우 잘 일치하는 것을 알 수 있고, 더불어 300초의 많은 시간경과에 대해서도 평균수위의 변화가 발생되지 않는 안정된 파형이 얻어지는 것을 확인할 수 있다. 수위변동의 피크에서 측정파형이 목표파형보다 다소 큰 값을 나타내는 것을 볼 수 있으며, 따라서 Fig. 8의 수위변동에 기초한 Fig. 4의 주파수스펙트럼에서 측정스펙트럼이 목표스펙트럼보다 다소 큰 파랑에너지를 나타내지만, 피크주파수의 발생위치 및 주파수의 변동에 따른 스펙트럼의 변화양상은 잘 일치하는 것으로 판단된다.
Vertical displacements according to change of significant wave heights at points N1 and N2 of caisson.
3.4 구조물의 동적거동
불규칙파동장을 해석하기 위한 2D-NIT모델(Lee et al., 2013)과 탄소성지반에서 다중전단메커니즘에 관한 유효응력 해석을 기반으로 유한요소해석법을 적용하는 FLIP모델(Iai et al., 1992a, 1992b)로부터 이하에 나타내는 해저지반상 구조물의 수평변위와 침하량 및 응답가속도, 그리고 지반변형을 수치적으로 계산하였다. 이 때, 상부경계, 하부경계 및 좌우경계로 구분되는 지반경계에 대해 하부경계조건은 수직 및 수평변위의 구속조건으로, 좌우경계조건은 수직변위의 허용과 수평변위의 구속조건으로 각각 모델링하였으며, 파동부에서 불규칙파랑해석으로부터 산출되는 해저면에서 시간변동의 동파압과 유속에 의한 전단응력을 상부경계면에 경계치로 입력하였다.
이하에서 제시되는 결과들은 해저표면상에서 유속으로 인한 전단응력을 고려하지 않은 결과로, 전단응력을 고려한 경우와의 차이는 거의 나타나지 않았다는 점을 부기하여 둔다.
3.4.1 케이슨의 동적변위
직립케이슨 천단상의 양쪽 가장자리 N1과 N2 지점에서 시간경과에 따른 수평변위(활동)의 시계열을 나타낸 것이 Fig. 5이며, 그림에서는 유의파고를 H1/3= 3m로 일정하게 유지하고 유의주기를 T1/3= 7,10,13s로 변화시켰다. 먼저, N1에서 수평변위를 살펴보면 유의주기가 길어질수록 진동성분 및 잔류성분의 수평변위가 커지는 것을 알 수 있고, 이는 기본적으로 유의주기가 길수록 작용파력이 커지기 때문이다. 시간경과에 따른 진동 및 잔류성분 모두는 t > 300s에서 급격히 커지는 경향을 나타내며, 특히 잔류수평변위는 입사파진행방향의 역방향((-)변위)으로 치우치게 되고, 이러한 상태는 시간경과에 따라 점점 심화되는 경향을 나타낸다. 이것은 후술하는 바와 같이 t > 300s에서 발생되는 액상화 혹은 근접된 액상화에 의해 지반저향력이 감소되고, 이로부터 입사파진행방향의 역방향으로 전도되는 회전변위와 연성된 수평변위가 점점 커지기 때문인 것으로 판단된다. 또한, N2에서 수평변위를 살펴보면 유의주기의 변화에 따른 수평변위 및 시간경과에 따른 진동성분과 잔류성분에 대한 수평변위의 변화과정은 N1의 경우와 거의 동일하다는 것을 알 수 있다.
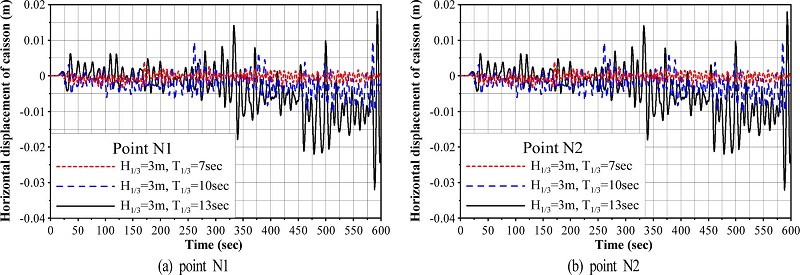
Horizontal displacements according to change of significant wave periods at points N1 and N2 of caisson.
동일한 유의주기 T1/3= 10 s에 대해 유의파고를 H1/3= 3m에서 H1/3= 6m로 변화시킨 경우 N1과 N2 지점에서 시간경과에 따른 수평변위의 시계열을 나타낸 것이 Fig. 6이다. 그림에서 연직축스케일은 Fig. 10의 경우를 50배하여 나타내었기 때문에 Fig. 5에서 주어지는 H1/3= 6m, T1/3= 10 s에 대한 수평변위는 Fig. 6의 연직축스케일에서는 매우 작게 나타난다는 것을 유의바란다. 여기서, H1/3= 6m, T1/3= 10 s는 입사파랑이 케이슨 천단상을 월파하는 경우이며, 그림으로부터 유의파고의 증가 및 그로 인한 월파에 의해 매우 큰 수평변위가 나타나며, 특히 t > 250s에서 급격한 증폭현상을 나타낸다. 이는 전술한 바와 같이 지반액상화의 영향이 반영되었기 때문이며, 일단 액상화가 발생하게 되면 수평변위는 수평파력의 영향을 크게 받아 진동성분이 크게 발달하는 반면, 지반액상화가 발생되기 전의 t < 250s에서는 작용파력에 대한 케이슨의 관성저항이 크기 때문에 수평변위가 상대적으로 작게 나타난다. 여기서, N1과 N2 지점에서 수평변위는 Fig. 5의 경우와 같이 동일하게 나타나며, 각각 t > 250s의 영역에서 평균수평변위는 (-)값을 나타내므로 역시 케이슨은 입사파진행 방향의 역방향으로 치우치게 된다.

Horizontal displacements according to change of significant wave heights at points N1 and N2 of caisson.

Spectrum of vertical displacements according to change of significant wave periods at points N1 and N2 of caisson.
Fig. 7은 N1과 N2 지점에서 시간경과에 따른 연직변위(침하)의 시계열을 나타낸 것으로, Fig. 5와 동일하게 유의파고를 H1/3= 3m로 일정하게 유지하고 유의주기를 T1/3= 7, 10, 13s로 변화시킨 경우의 결과를 나타낸다. 그림으로부터 N1과 N2 지점 모두는 t~30s에서 미소하지만 급격한 침하((-)변위)를 나타내는 것을 알 수 있다. 이것은 본 수치계산에서 사석마운드부와 케이슨을 t = 0s에 지반부상에 일시에 거치하였기 때문에 이로 인한 침하량이 반영된 것으로 판단되지만, 기초가 모래지반으로 구성되어 있기 때문에 그 값은 0.5 cm보다 작은 미소한 값을 나타낸다. 여기서, 수평변위와 유사하게 유의주기가 증가함에 따라 진동침하량과 잔류침하량 모두 커지며, 유의주기 T1/3= 13s의 경우에 현저하게 나타난다. 시간의 경과에 따른 잔류침하량의 변화양상을 살펴보면 t = 300s 이전에는 점진적인 증가를 나타내지만, t = 300s 이후, 특히 T1/3= 13s의 경우는 급격히 침하되는 것을 알 수 있다. 이것은 수평변위에서 언급한 바와 같이 액상화 혹은 근접한 액상화에 따른 지반저항력의 저하에 기인하는 현상으로, 일단 액상화 혹은 액상화에 근접된 지반에서는 연직상재하중에 대한 지반저항력이 많이 상실되므로 시간경과에 따라 지속파랑하중에 의해 침하량이 점차 증대되는 것으로 판단된다. 특히, Fig. 12(a)와 (b)의 비교로부터 케이슨 천단상의 N2보다 N1 지점에서 보다 큰 침하량을 나타내므로 결국 케이슨은 파진행방향의 역방향으로 전도되는 것을 알 수 있고, 이와 연성되어 파진행방향의 역방향으로 수평변위가 발생되는 결과를 초래한다. 여기서, N2보다 N1 지점에서 큰 침하량을 나타내는 것은 후반부 (II)에서 기술된 바와 같이 케이슨하 후면지반부보다 전면지반부에서 상대적으로 액상화의 범위가 넓고, 또한 액상화의 심도가 깊기 때문이다.
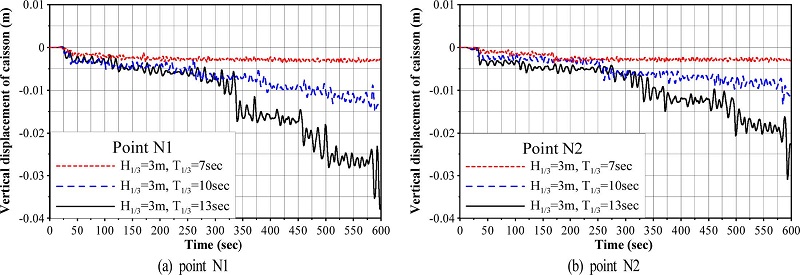
Vertical displacements according to change of significant wave periods at points N1 and N2 of caisson.
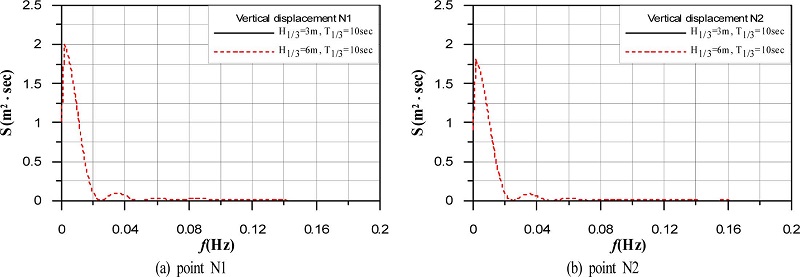
Spectrum of vertical displacements according to change of significant wave heights at points N1 and N2 of caisson.
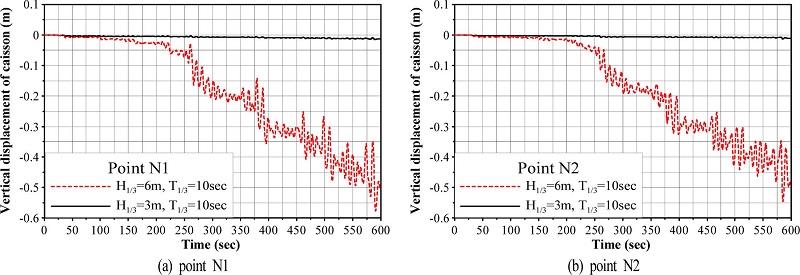
한편, 동일한 유의주기 T1/3= 10s에 대해 유의파고를 H1/3 = 3 m에서 H1/3= 6m로 변화시킨 경우에 케이슨의 침하량을 나타낸 결과가 Fig. 8에 제시되어 있다. 그림에서 연직축스케일은 Fig. 7의 경우를 10배하여 나타내었기 때문에 Fig. 7에서 주어지는 H1/3= 6m, T1/3= 10s에 대한 수평변위는 Fig. 8의 연직축스케일에서는 매우 작게 나타난다는 것을 유의바란다. 여기서, 전술한 바와 같이 H1/3= 6m, T1/3= 10s의 경우는 케이슨 천단상을 통한 월파가 발생되는 케이스로, 그림으로부터 유의파고의 증가 및 그로 인한 월파에 의해 매우 큰 침하량이 나타나고, 특히 t > 250s에서 급격히 증대되는 것을 알수 있다. 이는 전술한 바와 같이 지반액상화의 영향이 직접적으로 반영되었기 때문이며, 일단 액상화가 발생하게 되면 잔류침하량이 발달하는 것을 Fig. 8의 결과로부터 알 수 있다. 또한, Fig. 8(a)와 (b)를 비교하면 케이슨 천단상의 N2보다 N1 지점에서 보다 큰 침하량을 나타내므로 결국 케이슨은 파진행방향의 역방향으로 전도되는 것을 알 수 있다.
3.4.2 케이슨의 동적변위에 대한 주파수스펙트럼
Fig. 5와 7에서 제시하는 케이슨 천단상 N1 및 N2 지점에서 수평 및 침하변위로부터 산정된 변위스펙트럼을 다음의 Fig. 9와 10에 도시한다. 먼저, Fig. 9의 수평변위스펙트럼을 살펴보면 N1 및 N2 지점에서 주파수의 변화에 따른 수평변위스펙트럼의 값 및 그의 변화과정이 완전히 일치하는 것을 알 수 있고, 이러한 결과는 Fig. 5로부터 간단히 유추될 수 있다. 그림에서 f < 0.02 Hz에서 주어지는 피크치는 잔류수평 변위성분을 나타내는 것으로, 유의주기가 길어질수록 이의 값은 점차적으로 증대되고, 이 경향은 전술한 Fig. 5의 경우와 또한 일치한다. 특히, 유의주기대에서 진동수평변위성분이 피크치를 나타내며, 유의주기가 짧을수록 혹은 유의주파수(T1/3 = 7 s→f = 0.14 Ηz; T1/3= 10s→f = 0.1 Hz; T1/3= 13s→f = 0.077 Hz)가 길수록 피크치는 작아지고, 경우에 따라 잔류성분보다 진동성분이 커지는 케이스도 볼 수 있다.
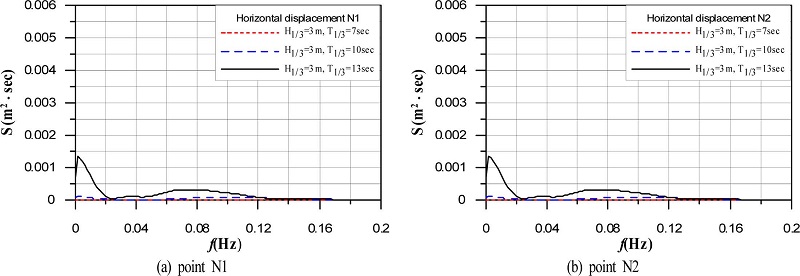
Spectrum of horizontal displacements according to change of significant wave periods at points N1 and N2 of caisson.
유기주기의 변화에 따른 침하량의 주파수스펙트럼을 나타낸 Fig. 10을 검토한다. 그림으로부터 N1 지점에서 침하량이 N2의 경우보다 전체적으로 크게 나타나는 것을 알 수 있고, 이는 Fig. 6으로부터도 역시 확인될 수 있다. 한편, 유의주기가 길어질수록 유의주기에서 진동성분의 피크치가 커지지만, f < 0.02 Hz에서 주어지는 잔류침하량과의 차이는 줄어드는 경향을 나타내며, 이는 Fig. 9의 수평변위스펙트럼에서 언급한 결과와 동일하다.
유의파고의 변화에 따른 수평변위 및 침하량의 주파수스펙트럼을 나타낸 결과가 Fig. 11과 12이다. 그림에서 H1/3 = 3m, T1/3= 10s의 결과는 H1/3= 6m, T1/3= 10s의 경우에 비해 미소하기 때문에 그래프상에서는 값이 주어지지 않는다. H1/3= 6m, T1/3= 10s는 전술한 바와 같이 케이슨 천단상으로 월파가 발생되는 경우로, 전체적으로 잔류성분보다는 진동성분의 에너지가 크다는 것을 알 수 있고, 게다가 유의주파수 대에서 진동성분의 피크치가 나타나지 않고 보다 짧은 주파수대에서 피크치가 나타나는 것을 알 수 있다. 이러한 결과는 유의주기대에서 큰 파고성분은 월파될 가능성이 보다 크기 때문에 상대적으로 파고가 작은 긴 주기대의 파랑에 의한 수평변위가 크게 나타나기 때문인 것으로 판단된다. 하여튼, 월파 유무에 관계없이 N1과 N2 지점 모두에서 수평변위스펙트럼은 동일하게 나타나는 것을 알 수 있다.
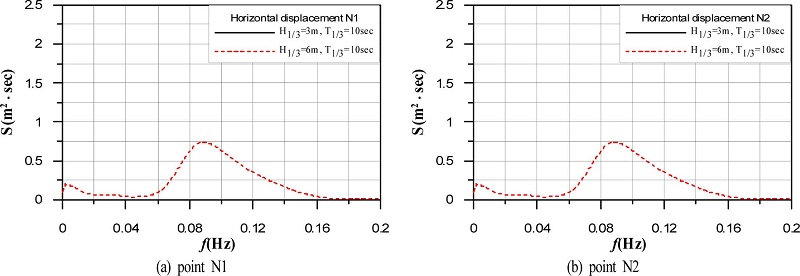
Spectrum of horizontal displacements according to change of significant wave heights at points N1 and N2 of caisson.
침하량주파수스펙트럼을 살펴보면 수평변위의 경우와 같이 H1/3= 3m, T1/3= 10s의 결과는 값이 미소한 관계로 그래프상에서 나타나지 않는다. 침하의 경우 전체적으로 진동성분보다는 잔류성분의 에너지가 매우 크게 나타나는 것을 알 수 있고, 진동성분은 수평변위의 경우보다 더 짧은 주파수대에서 피크치가 나타나는 것을 볼 수 있다. 잔류성분의 피크주파수는 Fig. 10의 경우와 거의 동일한 값을 나타내지만, 에너지는 월파가 발생되는 H1/3= 6m, T1/3= 10s의 경우가 매우 큰 값을 나타낸다. 이러한 사실로부터 케이슨 천단상으로의 월파를 적극적으로 억제할 필요가 있는 것으로 판단된다. 그리고, Fig. 7, 8 및 10에서와 같이 N2보다는 N1 지점에서 더 큰 잔류성분의 에너지가 나타나므로 월파가 발생하는 경우에도 케이슨이 파진행방향의 역방향으로 전도된다는 것을 또한알 수 있다.
3.4.3 케이슨의 동적변위가속도
케이슨 천단상 N1과 N2 지점에서 변위가속도(응답가속도)를 나타낸 것이 Fig. 13과 14로, Fig. 13이 수평변위가속도를, Fig. 14가 침하가속도를 각각 나타낸다. 먼저, 수평변위가속도를 살펴보면 N1과 N2 지점에서는 모든 유의주기에 대해 동일한 값을 나타내는 것을 알 수 있고, 이는 전술한 수평변위로부터도 간단히 유추될 수 있는 결과이다. 하지만, 유의주기별로 시간경과에 따른 수평가속도의 변화양상은 상이하고, T1/3= 7s의 경우 시간경과에 따라 안정된 변화값을 나타내지만, T1/3= 10,13s의 경우 시간경과에 따라 점차로 증대되는 값의 변화추이를 나타낸다. 이러한 변화과정은 Fig. 5에서 주어진 수평변위에서 가속도성분을 나타내지 않는 잔류성분을 제외한 변동성분만을 고려하면 쉽게 이해되는 현상이다.
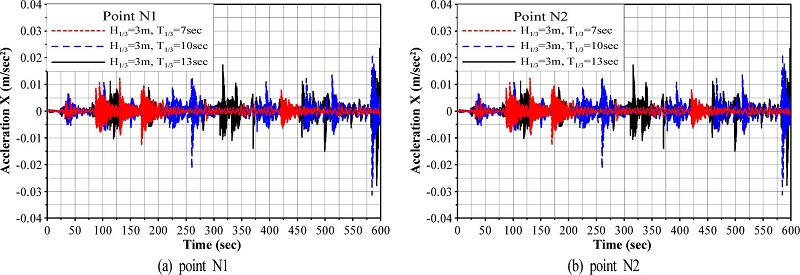
Horizontal accelerations according to change of significant wave periods at points N1 and N2 of caisson.
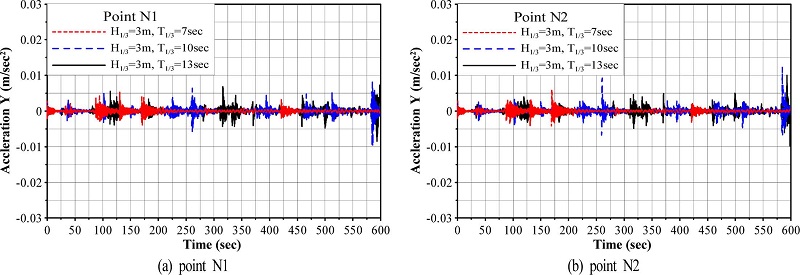
Vertical accelerations according to change of significant wave periods at points N1 and N2 of caisson.
또한, Fig. 14의 침하가속도를 살펴보면 수평의 경우와 매우 유사한 거동을 나타내지만, 그의 변화치가 상대적으로 작다는 것을 알 수 있다. 전술한 케이슨의 침하 및 수평변위의 시간변화특성과 비교하여 수평변위가속도 및 침하가속도에는 매우 짧은 주기를 갖는(고주파수) 작은 크기의 가속도성분이 동시에 포함되어 나타나는 것을 볼 수 있으며, 이러한 진동성분은 규칙파의 해석(Lee et al., 2014)에서도 지적되고 있는 바와 같이 파압의 영향을 직접적으로 받는 방파제 등의 해안구조물에서 실제로 확인되는 현상이다.
다음으로, 일정한 유의주기 T1/3= 10s에 대해 유의파고를 변화시킨 H1/3= 3m와 H1/3= 6 m의 경우 N1과 N2 지점에서 수평변위가속도와 침하가속도를 제시한 결과가 Fig. 15와 16이다. 그림에서 연직축스케일은 Fig. 13과 14의 경우를 10배 이상으로 하여 나타내었기 때문에 Fig. 13과 14에서 주어지는 H1/3= 3m, T1/3= 10s에 대한 수평변위 및 침하량은 매우 작게 나타난다는 점을 유의바란다. 전제적으로 주어지는 경향은 수평변위가속도가 침하가속도보다 매우 크고, 동일한 유의주기에 대해 유의파고가 증가함으로써 수평변위가속도 및 침하가 속도 모두 매우 큰 값을 나타내며, 특히 수평변위가속도에서 이러한 현상이 현저하다는 것을 알 수 있다. 특히, t = 250s 근방의 수평변위가속도에서 급격한 값의 증폭이 나타나고, 이후 시간경과에 따라 변동치가 점차 누적되는 경향을 나타낸다. 이러한 결과는 전술한 바와 같이 지반액상화와 직접적인 연관을 가지며, 일단 액상화된 지반상에 놓인 구조물은 파랑외력에 대한 저항력을 많이 상실한다는 것을 역으로 알 수 있다.

Horizontal accelerations according to change of significant wave heights at points N1 and N2 of caisson.
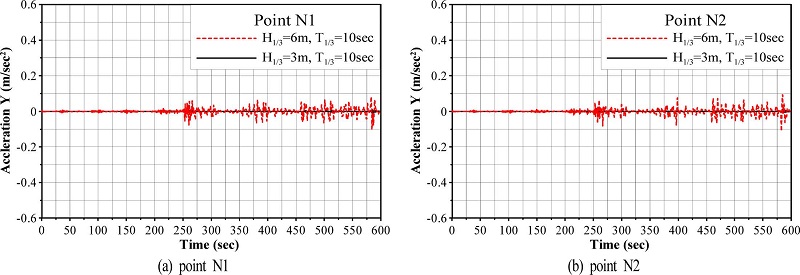
Vertical accelerations according to change of significant wave heights at points N1 and N2 of caisson.
3.4.4 케이슨의 동적변위가속도에 대한 주파수스펙트럼
다음으로, Fig. 13과 14에서 주어진 수평변위 및 침하량의 가속도를 주파수스펙트럼으로 나타낸 Fig. 17과 18의 결과를 검토한다. 먼저, 수평변위의 가속도스펙트럼을 살펴보면 각각의 피크치에 해당하는 주파수는 해당하는 유의주파수보다 약간 큰 값을 나타내므로 유의주기보다 짧은 주기대에 수평변위의 가속도에너지가 집중되고, 피크치의 값은 유의주기가 길수록 작아진다는 것을 알 수 있다. 이러한 것은 Fig. 18의 침하량가속도스펙트럼에서도 동일하게 확인되는 현상이다. 하지만, 전술한 Fig. 13과 14에서 알 수 있는 바와 같이 N1과 N2 지점에서 수평변위의 가속도스펙트럼은 서로 동일하게 나타나지만, 침하량의 경우는 N1보다 N2의 피크치에서 약간 작은 값을 나타내며, 전체 주파수영역에서 수평변위의 가속도스펙트럼은 침하량의 경우보다 훨씬 큰 값을 나타낸다. 특히, f > 0.2 Hz의 주파수영역에서 수평변위가속도스펙트럼 Fig. 17은 고주파수대에 여러 피크치가 주어지며, 이러한 결과는 Fig. 13에 주어진 고주파수대의 작은 진동성분에 의해 나타나는 결과이다.

Spectrum of horizontal accelerations according to change of significant wave periods at points N1 and N2 of caisson.
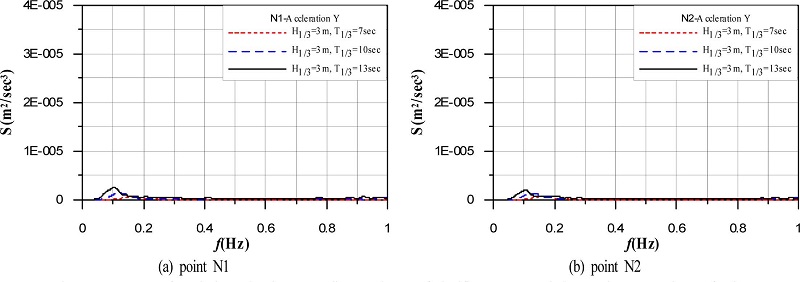
Spectrum of vertical accelerations according to change of significant wave periods at points N1 and N2 of caisson.
유의파고의 변화에 따른 수평변위 및 침하가속도를 주파수스펙트럼으로 나타낸 결과가 Fig. 19와 20이다. 두 결과에서 H1/3= 3m의 경우는 H1/3= 6m에 비해 매우 작은 가속도를 나타내므로 그래프상에서 값이 주어지지 않고, 침하가속도의 주파수스펙트럼에서는 H1/3= 6m의 경우도 매우 작은 값을 나타내며, 이는 Fig. 15와 16으로부터 쉽게 납득될 수 있을 것이다. 수평변위의 경우 유의주파수에서 조금 큰 주파수에서 스펙트럼의 피크치를 나타내는 것을 알 수 있고, 비월파의 Fig. 17의 경우와 같이 고주파수대에서 가속도성분이 또한 나타나고, 보다 큰 에너지를 가진다는 것을 알 수 있다.
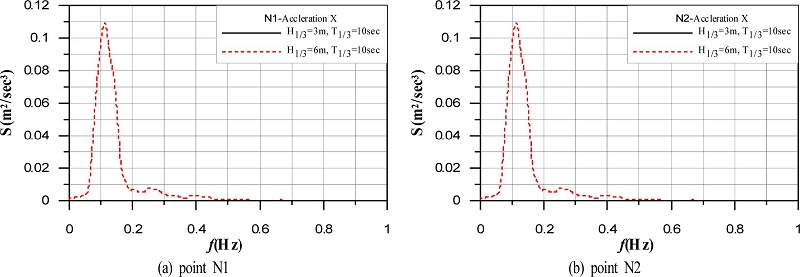
Spectrum of horizontal accelerations according to change of significant wave periods at points N1 and N2 of caisson.
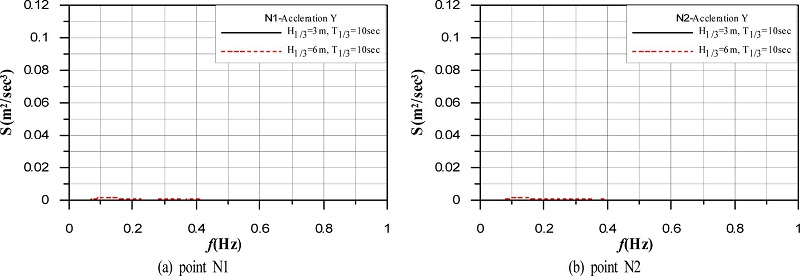
Spectrum of vertical accelerations according to change of significant wave periods at points N1 and N2 of caisson.
3.4.5 케이슨 및 주변지반에서 최종변형의 공간분포
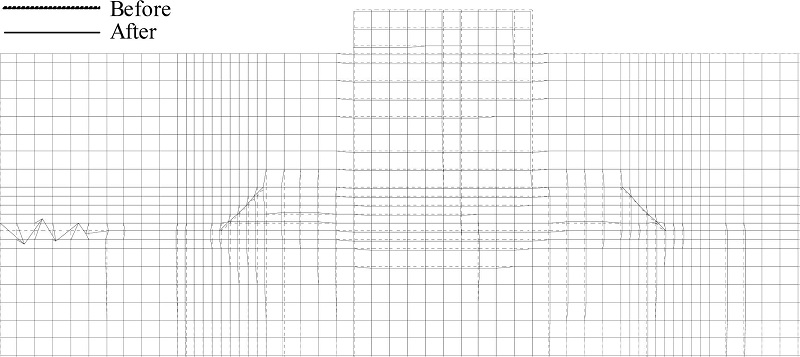
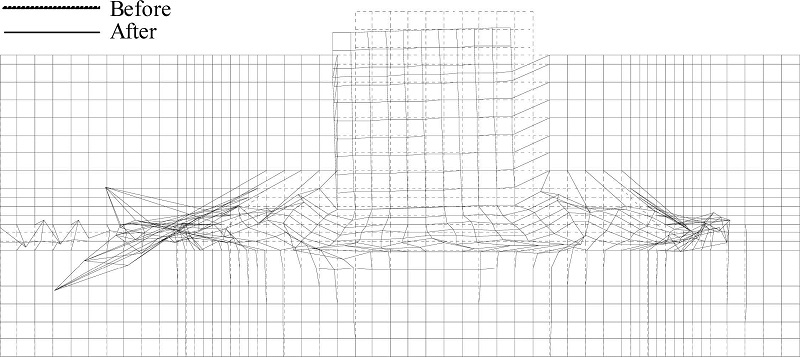
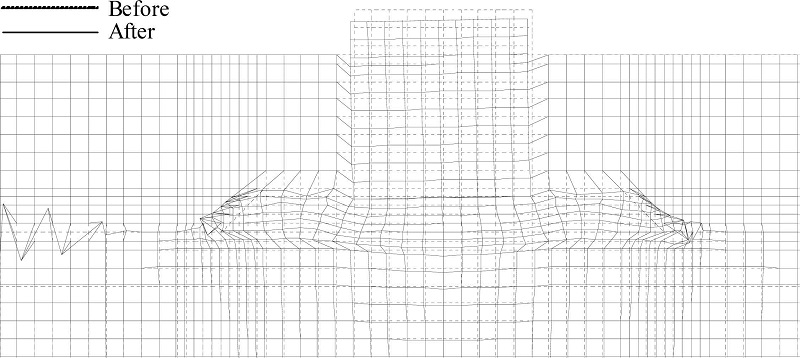
이상에서 언급한 직립케이슨의 수평변위와 침하량 및 언급되지 않은 해저지반의 각 절점에서 수평 및 연직변위까지 포함하여 수치계산의 최종수행시점에서 얻어진 최종변형단면을 나타낸 것이 Fig. 21~24이다. 여기서, 각 절점에서 변위량이 작기 때문에 Fig. 21~23은 결과치를 50배, Fig. 24는 5배하여 나타낸 것임을 유의하기 바란다. 전체적으로 케이슨 하부의 사석마운드부에서 약간의 침하와 동시에 파진행방향의 역방향으로 수평변위(활동)와 회전변위(전도)가 발생되고, 동일한 유의파고에 대해서는 유의주기가 길수록, 그리고 동일한 유의주기에 대해서는 유의파고가 클수록 큰 변형이 발생되는 것을 시각적으로 확인할 수 있다. 사석마운드부는 케이슨의 하부에 놓이게 되므로 케이슨의 침하량과 거의 동일한 변화 경향을 나타내지만, 유의파고와 유의주기가 클수록 비탈면과 그의 근방에서 큰 수평변위를 나타내며, 연직변위의 경우 케이슨 전방의 사석마운드부는 약간 위로 부상하는 반면, 후방의 사석마운드부는 아래로 약간 침하하는 경향을 나타낸다. 여기서, 비월파의 경우 케이슨의 후방에서는 거의 파랑이 존재하지 않는다는 점을 고려하면 후방 사석마운드부에서 변형은 케이슨의 변형에 의한 결과로 나타나는 것으로 판단된다. 해저지표면상에서 변위는 케이슨 전방의 중복파동장에서 크게 나타나고, 이는 사석마운드부의 전방비탈면에서 다소 이격된 거리에서 발생하는 것을 알 수 있다.
케이슨 및 지반변형이 매우 크게 나타나는 Fig. 24의 경우는 월파가 발생된 결과로, 그림에서 케이슨 전면의 사석마운드는 거의 파괴상태에 도달한 것으로 보인다. 하여튼, 모든 케이스에서 케이슨은 파진행방향의 역방향으로 전도되고, 케이슨 전후의 사석마운드부, 특히 비탈면에서 큰 변형이 발생되지만, 모래로 구성된 지반부는 상대적으로 작은 변형을 나타낸다. 여기서, 월파가 발생되는 경우는 상대적으로 모래지반에서 변형이 상대적으로 매우 작다는 특징을 볼 수 있다.
4. 결 론
본 연구에서는 규칙파랑을 대상으로 혼성방파제의 지반변형과 과잉간극수압변동 등을 포함한 동적해석에서 기수행된 2D-NIT모델 및 FLIP모델의 검증결과를 근거(Lee et al., 2014)로, 불규칙파동장하 해저지반-혼성방파제의 상호작용에 의한 지반과 구조물의 동적응답에 관한 수치시뮬레이션을 수행하였다. 수치계산에서는 규칙파동장에서와 동일하게 2D-NIT모델로부터 일정수심의 불규칙파랑작용하에 해저면상에서 동파압, 그리고 저면유속으로부터 전단응력을 산정하고, 이를 탄소성지반의 다중전단메커니즘에 관한 유효응력해석을 기반으로 유한요소해석법을 적용하는 FLIP모델에 입력치로 적용하였다. 이로부터 전반부 (I)에서는 해저지반상 혼성방파제에서 케이슨의 동적거동(변위와 응답가속도) 및 케이슨과 사석마운드부를 포함한 주변지반변형을 중심으로 수치모델링하여 결과들의 상세한 비교, 분석 및 검토를 수행하였다. 이로부터 얻어진 중요한 사항을 다음에 요약하여 기술한다.
(1) 해저표면상에서 전단응력을 고려한 경우와 고려하지 않은 경우 혼성방파제에서 케이슨의 변위와 응답가속도 및 케이슨과 사석마운드부를 포함한 주변지반변형에서 유의한 결과의 차이를 나타내지 않았다.
(2) 케이슨의 수평변위는 유의주기가 길수록, 그리고 유의파고가 클수록 큰 진동성분과 잔류성분을 나타내며, 검토된 모든 케이스에서 케이슨은 파진행방향의 역방향으로 변위가 발생된다.
(3) 침하량의 경우도 수평변위와 같이 유의주기와 유의파고가 클수록 큰 진동 및 잔류성분을 나타내지만, 상대적으로 진동성분은 작아지고, 특히 잔류성분이 탁월하게 나타나며, 모든 케이스에서 케이슨이 파진행방향의 역방향으로 전도되는 결과를 나타낸다.
(4) 케이슨 천단상으로 월파가 발생되는 경우 피크수평변위를 나타내는 주기는 파의 유기주기보다 길다는 것을 스펙트럼해석으로부터 확인할 수 있다.
(5) 응답가속도에서 수평성분이 침하성분보다 탁월하고, 유의주기와 유의파고가 클수록 큰 값을 나타내는 것이 전체적인 경향이다. 한편, 월파가 발생되는 경우 파작용 초기에는 케이슨의 관성저항에 의해 수평응답가속도가 매우 작은 값을 나타내지만, 지반액상화가 발생되는 시점부터 급격히 증대되는 현상을 나타낸다. 또한, 수평응답가속도에서는 무시될 수 없는 고주파수대의 진동성분이 발생되는 것을 스펙트럼분석으로부터 확인할 수 있다.
(6) 월파가 발생되는 경우 케이슨의 큰 변위 및 사석마운드부의 큰 변형을 유발하지만, 지반변형은 상대적으로 작아진다.
이상에서 논의된 2D-NIT모델과 FLIP모델에 의한 본 논문의 타당성은 기존의 수리실험과 해석결과와의 비교 및 규칙파에 대한 선행연구로부터 검증되었지만, 향후 수리모형실험을 수행하여 보다 심층적으로 불규칙파랑에 의한 2D-NIT모델과 FLIP모델에 의한 결과의 타당성을 검토하고자 한다.
Acknowledgements
이 연구는 해양수산부/한국해양과학기술진흥원의 연구과제(PJT200538)로 수행된 연구임.