2.1 결정론적 설계법

결정론적 설계법에서 케이슨의 활동에 대한 안정성은 식 (1)로 정의된다. 안전율이 1.2보다 클 경우 케이슨이 활동에 대하여 안정한 것으로 판단한다.

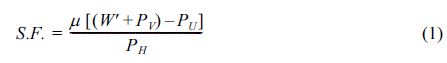
여기서 μ는 케이슨과 사석 마운드 사이에서의 마찰계수, W'는 케이슨의 수중 중량, P_H는 케이슨에 작용하는 수평 파력, P_U는 양압력, P_V는 유수실 하부에 작용하는 파력을 의미한다.

2.2 성능 설계법

성능 설계법에서는 케이슨 방파제가 약간의 활동이 발생하더라도 제 기능을 유지할 수 있다고 본다. 케이슨의 활동량은 다음과 같은 운동방정식으로부터 계산할 수 있다.

여기서 W는 공기 중 케이슨의 중량, g는 중력 가속도, M_a는 부가질량(= 1.0855 ρ₀h'²), ρ₀는 해수의 밀도, h'은 케이슨 저면에서 설계조위까지의 거리, xG는 케이슨의 수평변위, P_R은 마찰 저항력(= μ(W'+P_V − P_U))을 나타낸다. 파력의 시계열을 기초로 하여 파력이 마찰 저항력을 초과하면 활동이 일어나는 것으로 보고 위 식을 두 번 수치 적분하여 활동량을 구한다. 기대활동량은 구조물의 수명 동안 발생하는 활동량을 누적시키는 일련의 과정을 5000번 반복하여 이를 평균함으로써 구한다. Takahashi et al. (2001)은 Table 1과 같이 기대활동량에 대한 안정성 기준을 제안하였다. Table 1과 같이 누적활동량의 발생확률을 고려하지 않고 단지 기대활동량만 안정성의 기준으로 채택한 경우 보통의 중요도를 가지는 구조물의 허용 기대활동량은 0.3 m 이하인 것으로 보고 본 연구에서 사용한다.

Table 1.

Allowable expected sliding distance by Takahashi et al. (2001)

한편, Goda (2001)와 Kim and Suh (2009)는 누적활동량의 평균값인 기대활동량 대신 식 (3)과 같이 허용누적활동량의 초과확률을 사용할 것을 제안하였다.

여기서 n_e는 구조물 수명 동안의 총 누적활동량이 허용활동량을 초과한 횟수이며, N은 총 모의 횟수이다. Shimosako and Tada (2004)는 케이슨 방파제의 활동 파괴에 대하여 관측치를 토대로 Table 2와 같이 구조물의 중요도와 한계상태에 따라 허용활동량의 초과확률 기준을 제안하였다. 보통의 중요도의 구조물에서 구조물의 수명 동안의 허용활동량을 초과하는 확률은 복구가능 한계상태(0.1 m), 극한 한계상태(0.3 m), 붕괴 한계상태(1.0 m)에서 각각 30, 10, 그리고 5%를 제시하고 있다. 본 연구에서는 결정론적 설계법에서의 안전율 1.2가 성능설계법에서 구조물의 중요도가 보통이라고 보고 복구가능 한계상태 및 극한 한계상태에 대해서 해석을 수행하였다.

Table 2.

Acceptable exceedance percentage of total sliding distance for breakwaters of different levels of importance, as proposed by Shimosako and Tada (2004)

3.1 설계파

일반적으로 케이슨 방파제의 파괴는 설계 파고에 상응하는 고파랑에 의해 발생한다. 따라서 년 최대 심해파고를 계산에 사용해도 충분한 것으로 간주한다. 보통 방파제 설계의 심해 파고는 장기간의 관측 또는 후측에 의한 극치 파랑자료를 이용하여 얻어지는 극치 파고분포에 따라 결정된다.

본 연구에서는 식 (4)의 심해파고 극치분포함수인 Weibull 분포를 사용한다. 여기서 X는 년 최대 심해 유의파고를 의미하고, α, ξ, 그리고 κ는 각각 척도, 위치, 형상 모수를 나타낸다. 확률파는 Kim (2005)의 연구에서 사용된 50년 재현주기의 설계 유의파고 6.5 m에 해당되는 것으로서 Weibull분포의 척도, 위치, 형상 모수는 각각 2.005, 1.595, 1.525를 사용한다.

한편, Suh et al. (2010)은 우리나라 연안에서의 관측 및 후측자료, 일본의 장기간 실측자료 등을 분석하여 설계파에 근접하는 고파랑에 대해서 Goda (2003)가 제안한 식과 Shore Protection Manual (U.S. Army, 1977)에서 제안한 식을 평균한 식을 다음과 같이 유의파고-유의파주기 관계에 사용할 수 있음을 보였다.

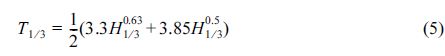
심해파향은 바닥경사가 일정한 해안에 직각으로 입사하는 일방향 불규칙 파랑에 대해서 고려한다. 조위는 저조위와 고조위 사이에서 정현파형의 변화를 갖는 것으로 가정한다. 따라서, 0과 2π사이에서 균등한 분포를 따르는 난수를 추출하여 정현곡선의 위상을 결정한 후 이를 이용하여 평균해면에 대한 조위의 표본 η를 계산한다.

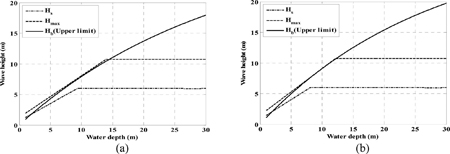
심해에서 방파제 위치까지 파랑변형을 계산하기 위해 해안선과 평행한 등심선을 갖는 해안에 직각으로 입사하는 불규칙 파랑에 대하여 Goda (1975)의 모형을 사용한다. 환산 심해파고(H₀')는 Modified BM 스펙트럼과 Mitsuyasu-type 방향 분산 함수를 이용하여 계산한다. 방파제 위치에서의 유의파고가 정해지면 방파제의 활동을 유발하는 정도의 큰 태풍이 년간 1회 내습했을 때 그 태풍에 의해 약 1000파가 발생 된다는 가정하에 태풍 작용시간 동안의 개별파를 Rayleigh분포로 가정하여 추출한다. 추출된 개별파고가 쇄파고(H_b)보다 클 경우 개별파고 대신에 쇄파고를 사용한다. 쇄파고는 Goda(1974)가 제안한 방법을 사용하였다. Fig. 1는 바닥경사 1/50과 1/20에 대하여 Goda (1975)의 모형을 이용하여 구한 파고를 수심에 따라 나타낸 것이다. 여기서 바닥경사가 1/50인 경우에는 14 m, 1/20인 경우에는 12 m 이내에서 쇄파대가 형성됨을 알 수 있다.

Fig. 1.

Wave heights in different water depths on a coast with (a) bottom slope of 1/50, (b) bottom slope of 1/20.

3.2 파력 및 시계열

유공케이슨 방파제에 작용하는 파력은 Takahashi et al. (1991)이 다양한 실험 조건에서 수리모형실험을 수행하여 제안하였다. 이 방법은 파가 작용하는 상태를 Fig. 2에서와 같이 압파 I, 압파 IIa, 그리고 압파 IIb 등으로 구분한다. 압파 I은 파가 전면 유공벽에 처음 부딪히는 순간으로 유공벽과 하부의 무공벽에 파압이 작용하고 케이슨 저면에는 양압력이 작용한다. 압파 IIa의 상태는 파가 전면 유공벽을 지나 유수실 후면벽에 부딪히는 순간으로 이 때는 전면벽은 물론 후면벽에도 파압이 미치며 유수실 하부에는 수위증가로 인한 압력증가가 발생한다. 압파 IIb는 앞서 압파 IIa의 상태를 지나 파가 중복파 형태를 띄는 순간이다. 파력 계산식은 일반적으로 사용되어지는 무공케이슨 방파제의 식과 동일하다. 하지만, 이때 적용되는 형상보정계수 λ₁, λ₂, 그리고 λ₃는 Takahashi et al. (1991)이 제안한 Table 3과 같이 파압의 작용상태에 따라 다르게 적용한다. Table 3에서 B', L'은 각각 유수실의 폭에 전면벽의 두께를 합한 거리, 유수실 내 수심(d') 에서의 파장이다. 여기서 유의할 점은 압파 IIa의 후면벽 보정계수 λ_R2산정 시 필요한 충격파 보정계수 α*를 계산할 때 수심 d에 유수실 내수심 d'을, 파장 L에 유수실 내 수심을 이용한 L'을, 그리고 B_M에 B' − (d − d')을 사용한다는 것이다.

Fig. 2.

Phase difference for wave action on a perforated caisson defined by Takahashi et al. (1991).

Table 3.

Correction coefficients for perforated caissons given by Takahashi et al. (1991)

Kim (2005)은 무공케이슨 방파제의 파력의 시계열 계산방법과 Takahashi et al. (1991)이 제안한 유공케이슨 방파제의 파압 계산 식을 결합하여 유공케이슨 방파제에 작용하는 파력의 시계열 계산방법을 제안하였다. 즉, 유공케이슨 방파제에 위상차를 가지고 작용하는 압파 I, 압파 IIa, 압파 IIb의 파력을 두개의 충격파와 한 개의 중복파 형태로 다음과 같이 나타내었다.

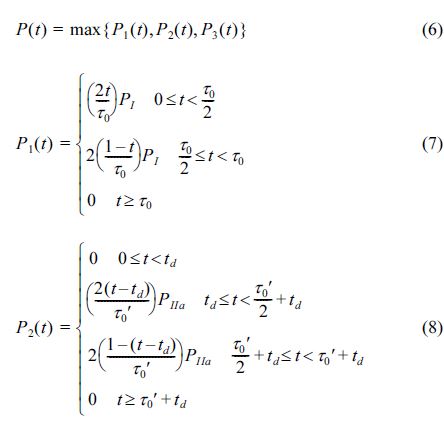
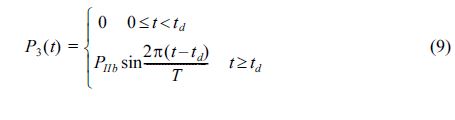
여기서, P_I, P_IIa, 그리고 P_IIb는 Table 3의 보정계수를 이용하여 구한 최대파력 값이다. td는 파력 P₁(t)와 P₂(t)의 발생 시차, τ₀′은 압파 IIa의 지속시간으로 다음과 같이 구할 수 있다.

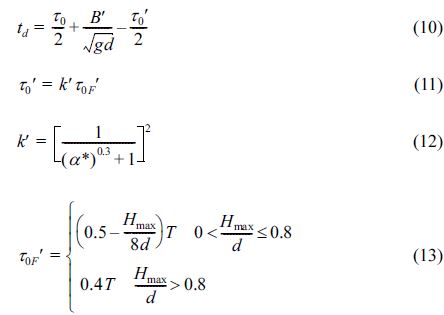
식 (11)-(13)에는 방파제 위치에서의 수심 h 대신 유수실내 수심 d'을 사용한다. 식 (13)에서 파고는 엄밀하게 말하면 마운드 위에서의 값을 의미하지만 마운드 상에서의 파고 변화가 무시할 만큼 작다는 가정하에 방파제 전면 해저면에서의 파고를 사용한다(Kim, 2005). 유공케이슨에 작용하는 양압력 U(t)는 수평파력의 시계열과 같은 방법으로 구할 수 있다.

유공케이슨 방파제는 무공케이슨 방파제와 달리 케이슨에 작용하는 파력을 저감시켜줄 수 있는 유수실이 존재한다. 유수실 하부에 작용하는 힘은 유수실 내의 수위 증가로 인해 발생하며 이는 케이슨의 안정성을 증가시켜 준다. 유수실 하부의 힘은 충격파가 후면벽에 부딪히는 순간(t_d+ τ₀'/2)의 최대값(P_IIaM)과 중복파가 최대로 되는 순간(t_d+ Τ/4)의 값(P_IIbM)을 이용하여 삼각형 분포로 가정하여 전개하였다(Kim, 2005).

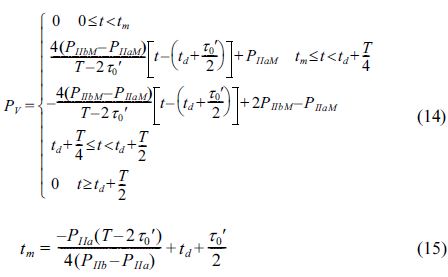
여기서 t_m 은 유수실 수위증가로 유수실 하부에 연직 압력이 발생하기 시작하는 시간이다.

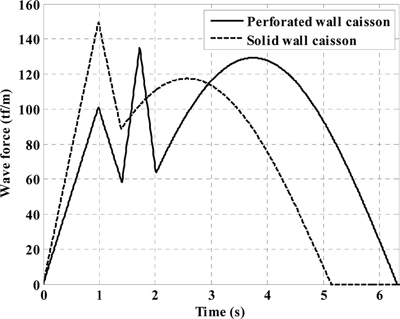
Fig. 3은 같은 파랑 조건에서 유공케이슨 방파제와 무공케이슨 방파제의 수평파력 시계열을 비교한 것이다. 유공케이슨 방파제는 전면의 소파구조로 인한 파력감쇄효과가 있어 무공케이슨 방파제보다 더 작은 파력 값을 보이며, 무공케이슨 방파제와는 다르게 충격파의 영향이 줄어든 것을 확인할 수 있다. 시계열의 형태로부터 구조물의 형상에 따라 충격파가 지배적인지 중복파가 지배적인지를 알 수 있다.

Fig. 3.

Comparison of time series for horizontal wave force between perforated wall caisson and solid wall caisson breakwater. (H_s = 6.5m, T_s = 10.27 s).

3.3 설계 변수의 통계적 특성

설계 변수의 불확실성은 다음 식과 같이 평균(μ_Xi)과 표준편차(σ_Xi)로 나타냈으며, 각 변수들에 대한 통계적 특성들은 Table 4에 제시하였다.

Table 4.

Statistical characteristics of design variables

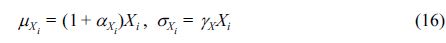
여기서 X_i, σ_Xi, 그리고 γ_Xi는 각각 설계변수, 편의, 그리고 변동계수를 의미한다. 한편 정규분포의 확률적 변동을 부여할 시 음의 무한대에서 양의 무한대까지 추출되므로 발생 불가능한 설계값이 추출될 수 있다. 이러한 단점을 극복하고자 Kim and Takayama (2003)는 수평파력과 마찰계수에 대해 Takayama and Ikeda (1992)의 실험 자료를 바탕으로 상한 x₁과 하한 x₂를 사용하여 이중절단정규분포의 사용을 제안하였다. 본 연구에서는 마찰계수와 유공케이슨 방파제의 수평파력에 대해서 이중절단정규분포를 사용하였고 나머지 설계변수에 대해서는 실험 자료가 부족하여 정규분포의 가정을 그대로 사용하였다.

식 (17)의 이중절단정규분포의 확률밀도함수 fDTN(x)는 정규분포의 확률밀도함수 f (x)와 식 (18)과 같은 관계를 가진다. 한편, 이중절단정규분포의 누적분포함수 FDTN(x)는 정규분포의 누적분포함수 F(x)로 다음과 같이 표현된다.

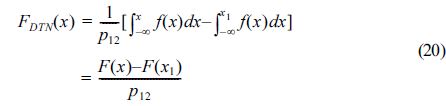
상한과 하한이 결정되면 F(x₁)과 p₁₂를 각각 계산할 수 있다. 또한 이중절단정규분포의 난수 r(0 ≤ r ≤ 1)은 정규분포로 생성되는 난수 r'과 다음과 같은 관계를 가진다.

따라서 이중절단정규분포의 변수 X를 다음과 같이 산정할 수 있다.

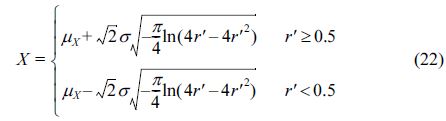
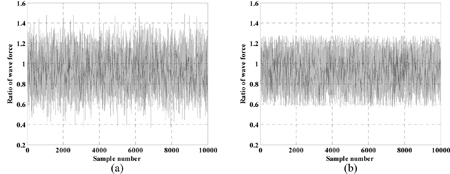
Fig. 4는 실험값에 대한 관측치의 비로 나타낸 유공케이슨 방파제에 작용하는 수평파력을 무작위로 추출한 것이다. Takayama and Ikeda (1992)는 유공케이슨 방파제의 수평파력에 대한 상한과 하한을 1.28, 0.57로 제안하였다. Fig. 4는 이중절단정규분포를 사용하여 물리적으로 발생 가능성이 희박한 상한과 하한 밖의 값을 제거하여 합리적인 값을 추출할 수 있음을 보여준다. 마찰계수 역시 Takayama and Ikeda(1992)가 제안한 상한(1.43)과 하한(0.71)사이에서 추출되었다.

Fig. 4.

Random samples of wave force using (a) normal distribution and (b) doubly-truncated normal distribution.

4.1 방파제 설계 조건

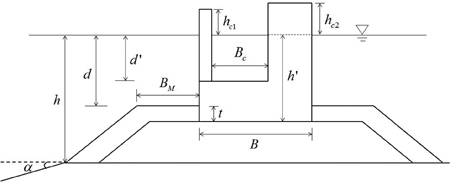
Fig. 5는 전형적인 유공케이슨 방파제의 단면 형상이며, Table 5는 본 연구에서 사용한 방파제의 설계 조건이다. 여기서 t는 피복층 두께를 의미한다. 결정론적 설계법과 성능 설계법을 비교하기 위하여 결정론적 설계법에서의 정적 활동 안전율을 1.0부터 1.3까지는 0.1간격으로, 1.3부터 1.9까지는 0.2 간격으로 변화시켜 가면서 각각의 안전율을 만족하는 케이슨의 폭을 결정하고 이에 대한 성능설계를 수행하였다. 방파제 설치위치에서의 수심은 DL(-)14 m에서부터 DL(-)30 m까지는 4 m 간격으로 하였으며, DL(-)10 m부터 DL(-)14 m까지는 2 m 간격으로 하였다. 바닥경사는 1/50과 1/20, 두 가지 경우에 대해서 계산을 수행하였으며, 마운드 상단의 수심과 방파제 전면에서의 수심의 비(h′/h)는 0.7, 유수실 안에서의 수심과 마운드 상단의 수심의 비 (d′/h′)는 0.5로 하였다. 케이슨의 유수실 폭은 유수실 폭과 파장의 비 (B_c/L)가 0.12가 되도록 하였으며, 이는 유수실 폭을 크게 늘리지 않으면서 반사율을 상당히 줄일 수 있는 값이다. 기초 마운드 위의 어깨폭은 어깨폭과 파장의 비 (B_M/L)가 0.05인 값을 사용하였다. 설계 고조위는 DL(+)0.66 m로 가정하였다. 전면 유공벽 상단의 높이는 0.5 H_1/3, 후면벽 상단의 높이는 0.6 H_1/3으로 결정하였다. 전면 유공부의 유공률(ε)은 최소 반사율을 보이는 30%의 값을 사용하였다

Fig. 5.

Typical cross-section of perforated-wall caisson breakwater.

Table 5.

Computational and geometric design conditions

4.2 모델의 검증

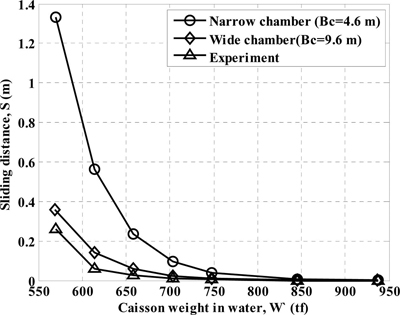
본 연구에서 사용할 모델을 검증하기 위하여 Report for Basic Design of a Breakwater Protecting New Marine Town, Hydraulic Model Test-II (Cross-Sectional Stability Test) KORDI (1992)의 수리모형 실험 결과와 비교하였다. 실험에서 사용한 표준 단면은, 전면 유수실 상부가 막힌 형태의 종 slit유공케이슨 방파제의 제 2안이다. 모형의 축척은 1/50이다. 실험파의 제원은 불규칙파를 조파하였으며 100년 빈도 설계파에 해당하는 유의파고 9.5 m, 유의주기 15 s, 그리고 조파시간은 유의주기의 380배이다. 모델 검증을 위해 사용된 조건들은 수리실험에서 사용한 대부분의 조건들과 같은 조건으로 하였으며, 개별파의 주기는 유의주기 15 s에 변동계수 0.1을 부여하였다. 기대활동량은 기존의 성능설계법에서는 1000개의 개별파를 생성시키지만, 검증 단계에서는 실험의 조건을 따르기 때문에 유의주기의 380배 동안의 총 활동량을 5000번 반복 계산하여 평균한 활동량으로 산정하였다. 수리모형실험에서 사용된 유공 케이슨은 중간 유공벽에 의해 유수실이 전후 2개로 분리된 2중 유수실을 가지고 있다. 각 유수실의 폭은 4.6 m이며, 전면 및 중간 유공벽의 두께는 각각 0.8 m, 0.4 m이다. 본 연구에서 사용된 Takahashi et al. (1991)의 파압 공식은 단일 유수실에 대하여 제안된 식이기 때문에 다음과 같은 두 가지 경우에 대하여 계산을 수행하였다. 첫번째는 폭 4.6 m의 전면 유수실만 있고 후면 유수실을 돌로 속채움한 Narrow chamber이며, 두번째는 중간 유공벽이 없고 유수실 폭이 9.6 m인(즉, 4.6 × 2 + 0.4 = 9.6) Wide chamber이다. Fig. 6는 수리모형 실험 결과와 본 연구에서 사용한 모델의 결과를 비교한 것이다.

Fig. 6.

Comparison of sliding distance versus caisson weight in water between experiment and calculation.

본 연구에서 사용된 모델의 결과가 실험 결과에 비해 크게 나타나는 것을 알 수 있다. 이는 실험에서 사용된 케이슨은 유수실이 2개로 이루어져 있어서 파를 2번 소산시키는 효과가 있기 때문인 것으로 추정된다. Narrow chamber의 경우는 후면 유수실을 속채움하여 케이슨 중량이 증가했음에도 불구하고 전면벽과 후면벽에 작용하는 파력의 위상차가 작아서 두 힘이 동시에 작용하여 상대적으로 큰 활동량이 산정된 것을 알 수 있다. Wide chamber의 경우는 중간 유공벽에 의한 파 에너지 소산 효과를 고려하지 못하기 때문에 수리모형실험 결과보다 약간 큰 활동량이 계산되었으나, 실험결과와 유사한 경향성을 보인다.

4.3 계산 결과

본 연구에서는 기존의 무공케이슨 방파제에 대한 성능 설계법을 유공케이슨 방파제로 확장하여 연구를 수행하였기 때문에, 우선 무공케이슨과 유공케이슨의 결과를 비교한다. Fig. 7과 Fig. 8은 무공케이슨 방파제와 유공케이슨 방파제에 대한 계산 결과를 수심에 대해서 각각의 안전율에 따라 나타낸 것이다. 계산은 기대 활동량, 극한 한계상태 및 복구가능 한계상태일 때의 초과확률 등 3가지에 대해서 수행하였으나 여기서는 복구가능 한계상태에서의 초과확률만 제시하였다. 수심이 감소함에 따라 초과확률이 감소하다가 바닥경사 1/50인 경우 14 m부터, 1/20인 경우 12 m부터 다시 증가한다. 수심 14 m와 12 m는 바닥경사 1/50과 1/20일 때 쇄파가 시작되는 지점이다(Fig. 1 참조). 쇄파대 바깥쪽에서는 수심이 감소함에 따라 초과확률이 감소한다. 이는 Fig. 1에서도 알 수 있듯이, 수심이 증가함에 따라 개별파의 쇄파한계파고가 증가하여 파고가 높은 개별파가 많이 발생하기 때문이다. 이와 같은 결과는 Suh et al. (2013)에 무공케이슨 방파제에 대해서도 보여진 바 있다. 쇄파대 안쪽에서는 수심이 얕아질수록 초과확률이 증가한다. 이는 수심이 얕아질수록 케이슨의 활동을 유발할 수 있는 정도의 파고 생성 범위가 좁아져, 상대적으로 쇄파한계파고에 가까운 값들의 발생 빈도가 높아지기 때문인 것으로 판단된다.

Fig. 7.

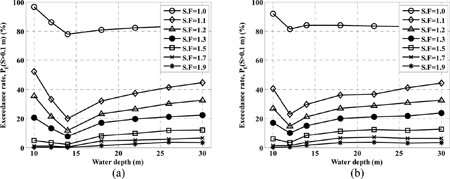
Exceedance percentage (S > 0.1 m) of solid-wall caisson breakwater in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

Fig. 8.

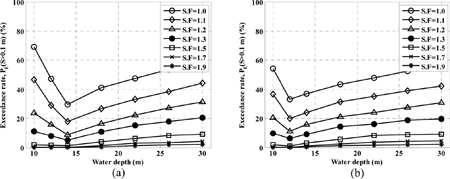
Exceedance percentage (S > 0.1 m) of perforated-wall caisson breakwater in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

계산 결과에서 알 수 있듯이, 무공케이슨 방파제에 적용하던 성능설계법을 유공케이슨 방파제에 확장하여 적용하더라도 그 결과의 경향성이 같기 때문에 본 연구에서 사용한 유공케이슨 방파제의 성능 설계 방법이 오류가 없음을 확신할 수 있다.

Fig. 9와 Fig. 10은 중요도가 보통인 구조물의 복구가능 한계상태의 경우(누적활동량 0.1 m 이상일 비율이 30% 이하), 무공케이슨 방파제와 유공케이슨 방파제의 초과확률을 나타낸 것이다. 무공케이슨 방파제의 경우 바닥경사가 1/50일 때 수심 10, 26, 30 m에서 현행 설계법의 기준인 안전율 1.2보다 높은 안전율에서 초과확률 30%를 만족시킨다. 바닥경사가 1/20일 때에는 수심 26, 30 m에서 기존 안전율 1.2보다 높은 안전율에서 초과확률 30%를 만족시킨다. 유공케이슨 방파제의 경우 바닥경사 1/50과 1/20일 때의 조건 모두 30 m를 제외한 전 수심에 걸쳐 기존 안전율 1.2보다 작은 안전율에서 초과확률 30%를 만족시킨다. 허용 기대활동량과 극한한계상태에서의 계산 결과 역시 비슷한 양상을 보인다.

Fig. 9.

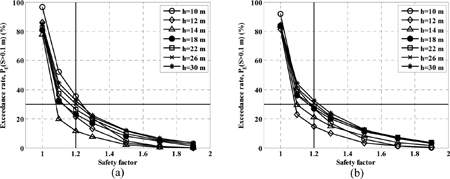
Exceedance percentage (S > 0.1 m) of solid-wall caisson breakwater for different safety factors in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

Fig. 10.

Exceedance percentage (S > 0.1 m) of perforated-wall caisson breakwater for different safety factors in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

Fig. 11~Fig. 13은 무공케이슨 방파제와 유공케이슨 방파제의 계산 결과를 정리하여 비교 분석한 것이다. Fig. 11은 허용 기대활동량 0.3 m를 만족할 때의 정적 활동 안전율을 수심에 따라 무공케이슨 방파제와 유공케이슨 방파제에 대해 비교한 것이다. 바닥경사 1/50과 1/20일 경우 모두 쇄파대 내에서는 무공케이슨 방파제의 안전율과 유공케이슨 방파제의 안전율이 비슷한 경향을 보이며, 쇄파대 바깥쪽에서는 무공케이슨 방파제의 안전율이 유공케이슨 방파제보다 더 크게 나타난다. Fig. 12은 중요도가 보통인 구조물의 극한한계상태 설계조건을 만족할 때의 정적 활동 안전율을 수심에 따라 무공케이슨 방파제와 유공케이슨 방파제에 대해 비교한 것이다. Fig. 13는 중요도가 보통인 구조물의 복구가능한계상태 설계조건을 만족할 때의 정적 활동 안전율을 수심에 따라 무공케이슨 방파제와 유공케이슨 방파제에 대해 비교한 것이다. 두 조건 모두 바닥경사 1/50과 1/20일 경우 모두 전 수심에 걸쳐 무공케이슨 방파제의 안전율이 유공케이슨 방파제보다 더 크게 나타난다.

Fig. 11.

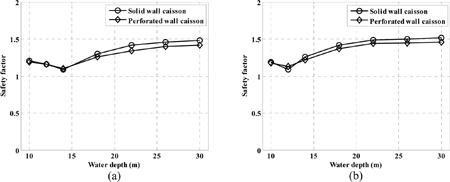
Comparison of safety factors corresponding to allowable expected sliding distance of 0.3 m in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

Fig. 13.

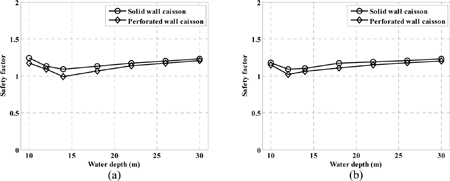
Comparison of safety factors corresponding to exceedance percentage for repairable limit state in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

Fig. 12.

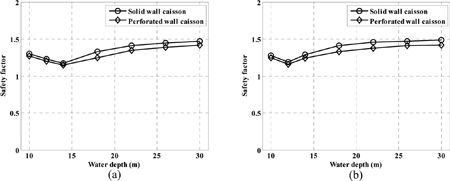
Comparison of safety factors corresponding to exceedance percentage for ultimate limit state in different water depths of (a) bottom slope = 1/50 and (b) bottom slope = 1/20.

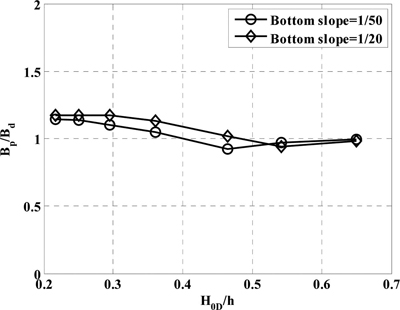
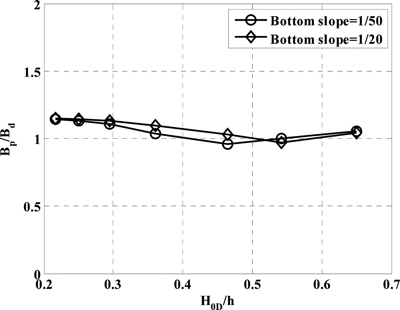
Fig. 14~Fig. 16는 수심의 변화에 따른 케이슨의 폭을 성능설계법과 결정론적 설계법에 대해 비교한 것이다. 여기서 H_0D는 심해 설계파고, B_p는 성능 설계법으로 계산한 유공케이슨의 폭, B_d는 결정론적 설계법에서 안전율 1.2를 만족할때의 유공케이슨의 폭을 나타낸다. 무차원 케이슨 폭B_p/B_d가 1보다 작다는 것은 성능 설계법이 결정론적 설계법보다 더 작은 폭을 요구하여 경제적임을 의미한다. Fig. 14은 허용 기대활동량이 0.3 m를 만족하는 경우의 무차원 케이슨 폭을 수심의 변화에 따라 나타낸 것이다. 허용 기대활동량이 0.3 m를 만족하는 경우, 쇄파대 내를 제외한 모든 수심에서 성능설계법이 결정론적 설계법보다 더 큰 폭을 요구하여 비경제적임을 알 수 있다. Fig. 15는 극한 한계상태에서 초과확률 10%를 만족하는 경우의 무차원 폭을 수심의 변화에 따라 나타낸 것이다. 극한 한계상태를 만족하는 경우, 두가지 바닥경사 모두 쇄파가 일어나는 지점을 제외한 모든 수심에서 성능설계법이 결정론적 설계법보다 더 큰 폭을 요구하여 비 경제적임을 알 수 있다. Fig. 16는 복구가능 한계상태에서 초과확률이 30%를 만족하는 경우의 무차원 폭을 수심의 변화에 따라 나타낸 것이다. 복구가능 한계상태에서는 두 가지 바닥경사 모두 전 수심에서 성능설계법이 결정론적 설계법보다 더 작은 폭을 요구하여 경제적임을 알 수 있다. 결과에 대한 경향성은 허용 기대활동량과 극한 한계상태일 때가 거의 유사하며, 복구가능 한계상태일 때에는 바닥경사에 따른 차이가 거의 없고 수심이 가장 큰 경우와 가장 작은 경우 1.0에 가까운 무차원 폭을 보이며 그 사이에서는 1.0보다 작은 값을 보인다. 하지만 Kim and Suh (2009)의 연구에서도 알 수 있듯이, 허용 기대활동량에 대한 평가보다는 초과확률에 대한 결과로 평가하는 것이 더 합리적일 것으로 판단된다.

Fig. 14.

Dimensionless caisson width based on expected sliding distance of 0.3 m.

Fig. 16.

Dimensionless caisson width based on repairable limit state (Exceedance percentage of 30% for total sliding distance).

Fig. 15.

Dimensionless caisson width based on ultimate limit state (Exceedance percentage of 10% for total sliding distance).