Analytical Method of Partial Standing Wave-Induced Seabed Response in Finite Soil Thickness under Arbitrary Reflection
임의반사율의 부분중복파동장에서 유한두께를 갖는 해저지반 내지반응답의 해석법
Article information
Abstract
Most analytical solutions for wave-induced soil response have been mainly developed to investigate the influence of the progressive and standing waves on the seabed response in an infinite seabed. This paper presents a new analytical solution to the governing equations considering the wave-induced soil response for the partial standing wave fields with arbitrary reflectivity in a porous seabed of finite thickness, using the effective stress based on Biot's theory (Biot, 1941) and elastic foundation coupled with linear wave theory. The newly developed solution for wave-seabed interaction in seabed of finite depth has wide applicability as an analytical solutions because it can be easily extended to the previous analytical solutions by varying water depth and reflection ratio. For more realistic wave field, the partial standing waves caused by the breakwaters with arbitrary reflectivity are considered. The analytical solutions was verified by comparing with the previous results for a seabed of infinite thickness under the two-dimensional progressive and standing wave fields derived by Yamamoto et al.(1978) and Tsai & Lee(1994). Based on the analytical solutions derived in this study, the influence of water depth and wave period on the characteristics of the seabed response for the progressive, standing and partial standing wave fields in a seabed of finite thickness were carefully examined. The analytical solution shows that the soil response (including pore pressure, shear stress, horizontal and vertical effective stresses) for a seabed of finite thickness is quite different in an infinite seabed. In particular, this study also found that the wave-induced seabed response under the partial wave conditions was reduced compared with the standing wave fields, and depends on the reflection coefficient.
Trans Abstract
파-지반의 상호작용 해석에 지금까지는 대부분 무한두께를 갖는 해저지반 상의 진행파와 무한두께 혹은 유한두께의 해저지반 상에서 완전중복파에 대해서만 해석해가 제안되어 있다. 본 연구에서는 임의반사율의 부분중복파동장에 선형파 이론과 유한두께를 갖는 해저지반에 Biot(1941) 3차원 압밀이론 및 지반탄성론에 기초한 유효응력 개념을 각각 적용하여 지반 내 동적응답에 관한 해석해를 새롭게 유도하며, 이에 수심과 반사율만을 변화시킴으로서 기존의 해석해가 간단히 얻어지기 때문에 그의 적용성이 보다 넓다. 본 해석해의 타당성은 무한지반 상의 진행파동장 및 완전중복파동장에 대한 Yamamoto et al.(1978) 및 Tsai & Lee(1994)의 해석해와 비교·검토로부터 검증된다. 또한, 본문에서는 유한깊이를 갖는 해저지반 상의 진행파동장, 완전중복파동장 및 임의반사율의 부분중복파동장에 대해 수심과 주기의 변화에 따른 본 해석해의 변화특성을 면밀히 검토한다. 이로부터 유한깊이의 지반은 무한두께의 경우와는 매우 상이한 지반응답(간극수압, 전단응력, 수평 및 연직 유효응력)을 나타내고, 반사율의 함수인 부분중복파동장에서 지반응답은 완전중복파동장에서의 값보다 일반적으로 작은값을 나타낸다는 것을 확인할 수 있었다.
1. 서 론
1970년대 Liu(1973), Moshagen & Tørum(1975), Nakamura(1973), Sleath(1970), Massel(1976) 등은 불변형의 강체투과지반을 가정하여 해저지반 내 흐름문제를 연구하였으며, 여기서 Moshagen & Torum(1975)과 Nakamura(1973)의 연구를 제외하면 모두 비압축성의 간극수를 가정하였다. 그러나, 간극수의 흐름, 체적변화와 변형은 해저지반에서 동시에 발생되므로 모든 영향을 설명하기 위해서는 유체 및 투과매체에 관한 복합거동을 보다 현실적으로 고려할 수 있는 수학모델에 기초를 두어야 한다.
Biot(1941)는 일찍이 투과매체에 탄성거동과 간극유체에 압축성 및 간극수의 흐름에 Darcy법칙을 고려한 3차원 압밀이론을 제안하였다. 이후에 Yamamoto et al.(1978)와 Madsen(1978)은 파동으로 인한 해저지반 내 파랑응답에 대해 Biot(1941)의 3차원 압밀이론에 기초한 선구적인 연구를 수행하였으며, 미소진폭파, 진행파 및 무한깊이의 균질지반이라는 제한된 조건 아래 해석해를 유도하였다. 또한, Tsui & Helfrich(1983), Maeno & Hasegawa(1987), Okusa(1985), Zen & Yamazaki (1990) 등은 진행파동으로 인한 해저지반 내 간극 수압변동을 원형조건 아래 실험적으로 조사하였으며, 이러한 연구결과들은 이후 수치해석결과의 검증자료로 활용되었고, 구조물이 설치된 파동장에서 지반응답해석이나 소성지반으로의 수치해석에 초석이 되었다. 한편, 최근 Jeng & Rahman(2000)은 유한깊이의 진행파동에서 지반응답에 관한 기초방정식에 관성력을 항을 고려한 해석을 수행하여 지반응답 특성을 검토하였다.
또한, 근래 무한두께를 해저지반 상의 2차원 완전중복파동장에 대해 Tsai & Lee(1994)가 해석해를 유도하고 있고, 또한 무한두께 혹은 유한두께의 지반을 대상으로 3차원 파동장에서 단파정파(short-crested waves)에 대해 Hsu et al.(1993), Tsai(1995) 및 Jeng & Hsu(1996)가 해석해를 유도하고 있지만, 임의반사율을 갖는 부분중복파동장에는 적용될 수 없는 단점이 있다. 여기서, 완전중복파동을 가정한 것은 방파제에 의한 반사를 완전반사로 고려하기 때문이지만, 실제로 방파제에 의한 반사가 완전반사라는 것은 이상적인 조건이므로 본 연구에서는 방파제에 의한 반사율을 임의반사율로 규정하여 보다 현실적인 관점에서 해석해를 유도한다. 이 때, 임의반사율의 부분중복파동장에 선형파 이론과 유한두께를 갖는 해저지반에 Biot(1941)의 3차원 압밀이론 및 지반탄성론에 기초한 유효응력 개념을 각각 적용하여 지반 내 동적응답에 관한 해석해를 새롭게 유도하며, 이에 수심과 반사율만을 변화시킴으로서 기존의 해석해가 간단히 얻어지기 때문에 본 연구의 해석해는 보다 넓은 적용성을 갖는 것으로 판단된다.
이러한 결과들은 무한지반 상의 진행파에 대한 Yamamoto et al.(1978)의 결과 및 무한지반 상의 완전중복파에 대한 Tsai & Lee(1994)의 결과와 비교하여 해석해의 정당성을 입증하고, 더불어 임의반사율의 부분중복파동장과 유한두께의 지반에 적용하여 수심과 주기의 변화에 따른 본 해석해의 변화특성을 면밀히 검토한다.
파동으로 인한 간극수압의 해석에 사용되는 부분중복파 시스템의 정의도와 좌표계를 Fig. 1에 나타낸다. 여기서, z축은 유체-해저지반의 접면에서 상방이 (+)이고, L은 파장, d는 수심으로 정의된다. 파고는 (1 + KR)H로 주어지며, KR은 복소반사율, H는 입사파고를 나타내고, 여기서 KR= 1의 경우는 완전중폭파로 파고는 2H로 되고, KR= 0의 경우는 진행파로 파고는 H로 된다. 해저지반의 토층은 유한두께 h를 가지며, 수리학적으로 등방균질불포화지반을 가정한다. 또한, 간극유체의 운동은 Darcy법칙을 따르는 것으로 가정된다. Biot의 압밀이론에 기초하면(Verruijt, 1969), 압축성다공질매체에서 압축성간극유체의 간극수압에 대한 2차원 저류방정식은 다음과 같이 주어질 수 있다.
Definition sketch of partial standing wave system in Cartesian coordinates.
여기서, P는 정수압을 초과하는 파동으로 인한 (과잉)간극수압이고, K는 흙의 투수계수, γ는 간극수의 단위중량, n′는 흙의 공극률, t는 시간이다. β는 간극유체의 압축률로 포화도와 겉보기 체적탄성계수와 관련된다. 그리고, 식(1)에서 ε은 다음의 식에 의해 정의되는 체적변형율이다.
여기서, (ξ, 1)는 (x, z)방향의 지반변위이다.
유효응력 개념과 Hooke법칙으로부터 다음의 평형방정식을 나타낼 수 있다.
여기서, μ는 흙의 Poisson비, G는 흙의 전단탄성계수이며, 이들과 흙의 탄성계수 E 사이에는 다음의 관계식이 성립된다.
특정의 경계조건과 연관하여 식(1), (3) 및 (4)를 풀면 간극수압과 지반변위가 얻어질 수 있다. 선형파 이론으로부터 임의 복소반사율 KR을 갖는 일정수심 d의 부분중복파동장에서 z = 0인 해저면 상에서 간극수압 Pb는 다음과 같이 주어질 수 있다.
여기서, p0= ρgH/2cosh kd이며, k는 파수, ω는 각주파수, Re는 복소함수의 실수부분, 
이다.
파동으로 인한 간극수압과 지반변위는 불투과·불변형 경계면 z = −h에서 다음과 같이 가정된다.
한편, 지반 내의 유효응력 및 전단응력은 Hooke법칙에 의해 다음과 같이 유도될 수 있다.
여기서, (σ′x σ′z)는 (x, z)방향의 유효응력, τ는 전단응력을 나타낸다.
그리고, 유효응력과 전단응력에 대한 경계조건으로 다음이 고려된다.
식(6)으로부터 간극수압과 지반변위에 관한 해가 다음과 같은 조화함수형을 갖는 것으로 가정될 수 있다.
여기서, 첨자 1과 2는 각각 진행성분과 반사성분을 의미한다.
식(13)과 (14)를 (2)에 대입하여 다음을 얻는다.
이하에서는 지배방정식(1), (3) 및 (4), 그리고 경계조건식(6), (7), (11)이 선형이므로 입사성분과 반사성분을 분리하여 전개할 수 있다. 미지수가 P1 ξ1 χ1, P2 ξ2 χ2의 2조 3개로 구성되므로 식(1)~(4)에 (12)~(15)를 고려하고, 다소 번잡한 과정을 통하여 하나의 미지수에 관한 지배방정식을 나타낼 수 있다. 여기서, 지반 수평변위의 입사성분 ξ1및 반사성분 ξ2에 관한 각각의 지배방정식을 나타내면 다음의 식으로 주어질 수 있다.
여기서,
여기서, mv는 압밀시험으로부터 결정되는 체적감소계수로 다음과 같이 정의된다.
식(16)은 6계 상미분방정식으로 다음과 같은 해를 갖는 것으로 가정될 수 있다.
식(19)를 (16)에 대입하면 r에 관한 6차 결정방정식을 얻을 수 있고, 이의 해로 
가 얻어지므로 일반해로 다음을 가정할 수 있다.
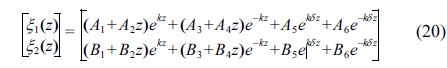
식(20)을 경계조건식(6), (7), (11)에 대입하여 다음과 같이 입사 및 반사성분에 대한 2조의 6원 1차 연립방정식을 도출할 수 있다.
여기서,
이상의 입사 및 반사성분에 대한 2조의 6원 1차 연립방정식에서 계수들이 갖는 특정한 성질로부터 A1= - B1, A2= −B2, A3= - B3, A4= - B4, A5= - B5, A6 = -B6의 관계가 성립 되므로 실질적으로는 입사성분 혹은 반사성분 하나만을 해석하면 된다. 이러한 결과를 식(12)~(14)에 적용하면 보다 간략화된 다음의 관계식을 도출할 수 있다.
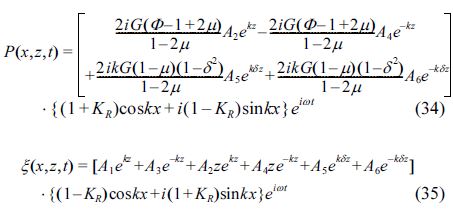
또한, 식(34)~(36)을 (8)~(10)에 대입하여 다음과 같은 수평 및 연직 유효응력과 전단응력을 나타낼 수 있다.
식(21)~(26)의 6원 1차 연립방정식은 매트릭스 계산의 간단한 컴퓨터 프로그램을 이용하여 미정계수 A1 A2 …… A6을 쉽게 산정할 수 있고, 이 값을 식(34)~(39)에 적용함으로서 간극수압, 지반변위, 수평 및 연직 유효응력과 전단응력 등을 산정할 수 있다.
3. 해석결과
3.1 무한지반의 진행파동장
진행파동장은 반사파성분이 존재하지 않기 때문에 본 연구의 결과에 복소반사율을 KR= 0으로 고려하고, 동시에 무한두께이므로 A3=A4=A6 = 0을 적용한다. 이로부터 진행파동장에서 무한두께의 균질등방지반에 관한 지반응답의 해석해를 유도한 Yamamoto et al.(1978)의 결과와 본 결과를 비교한 것이 Fig. 2이다.
Progressive wave-induced pore water pressure and effective stresses in the infinite soil thickness (t/T = 0).
그림에서 파동조건은 수심 d = 45 cm, 파고 H = 5.0 cm, 주기 T = 1.0 s이고, 완전포화토에 대한 해저지반의 물성치는 투수계수 K = 1.2×10-4cm/s, Poisson비 μ = 0.3, 공극율 n' = 0.38이며, 특히 간극수의 압축률 β(= 1/K', K'는 간극수의 겉보기 체적탄성계수)과 흙의 전단탄성계수 G와의 곱이 Gβ = 0으로 구성되는 흙이 강성을 갖지 않는 경우를 적용한 결과이다. 여기서, Gβ = 0의 경우는 촘촘한 모래지반을 제외한 대부분의 흙에서 실질적으로 적용될 수 있다(Yamamoto et al., 1978).
그림으로부터 해저표면에서 간극수압 |P|/p0는 1의 값을 나타내고, 연직깊이가 깊어질수록 급격히 감소하는 것을 알 수 있고, 또한 수평 및 연직 유효응력 |σ′x|/p0및 |σ′z|/p0와 전단응력 |τx|/p0는 해저표면에서 0의 값을 취하지만, 연직깊이가 깊어질수록 kz > -1까지는 증가하고, kz = -1에서 최대치 0.36을 나타내며, kz < -1에서는 감소하는 경향을 나타낸다. 이러한 변화과정에서 본 해석해의 결과와 Yamamoto et al.(1978)에 의한 해석결과가 완전히 일치한다는 것을 확인할 수 있다.
이상에서 얻어지는 결과는 Yamamoto et al.(1978)도 지적하고 있는 바와 같이 흙입자를 강체로, 간극수를 비압축으로 가정한 Putnam(1949)의 결과와 지반을 탄성 연속체로, 간극내에서 비배수를 가정한 Prévost et al.(1975)의 결과와 일치한다.
3.2 무한지반의 완전중복파동장
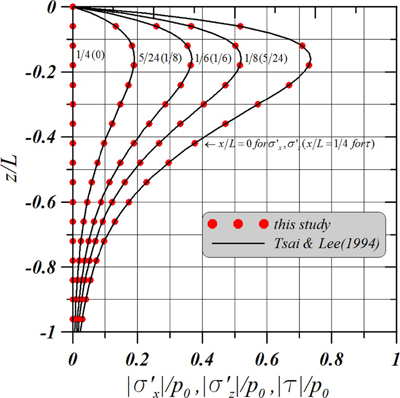
완전중복파동장에서 무한두께를 갖는 지반 내에서 동적응답은 본 연구결과에 복소반사율 KR= 1과 A3 = A4 = A6 = 0을 적용하면 간단히 해가 얻어질 수 있다. 이로부터 완전중복파동장에서 무한두께의 균질등방지반 내 동적응답에 관한 해석해를 유도한 Tsai & Lee(1994)의 결과와 본 결과를 비교한 것이 Fig. 3과 4이다.
Standing wave-induced pore water pressure in the infinite soil thickness (t/T = 0).
Standing wave-induced effective and shear stresses in the infinite soil thickness (t/T = 0).
그림에서 파동조건은 수심 d = 45 cm, 파고 H = 5.0 cm, 주기 T = 1.0 s이고, 완전포화토에 대한 해저지반의 물성치는 투수계수 K = 1.2×10-4cm/s, Poisson비 μ = 0.3, 공극율 n' = 0.38이며, 특히 간극수의 압축률 β과 흙의 전단탄성계수 G와의 곱이 Gβ = 0으로 구성되는 역시 흙의 강성이 없는 경우를 적용한 결과이다. 여기서, Fig. 3이 간극수압을, Fig. 4가 수평 및 연직 유효응력과 전단응력을 각각 나타낸다. 완전중복파동장이므로 Fig. 3에서는 위치 x/L에 따라 간극수압이 상이하고, x/L= 0인 완전중복파의 배에서 x/L = 1/4인 마디로 전이될수록, 그리고 연직깊이가 깊어질수록 감소하는 경향을 나타낸다. 또한, 수평 및 연직 유효응력 σ′x및 σ′z도 완전중복파의 배에서 마디로 전이될수록 감소하는 경향을 나타내지만, 연직 깊이 z/L > -0.159의 범위에서는 증가하고, z/L = -0.159에서 최대치를 나타낸 이후에 감소한다. 여기서, 전단응력의 경우는 유효응력과 동일한 값의 변화를 나타내지만, 마디에서 최대치를, 배에서 최소치를 각각 나타내므로 유효응력과는 위상 차이가 존재하며, 이러한 변화과정에서 본 해석결과는 Tsai & Lee(1994)의 결과와 완전히 일치하는 것을 알 수 있다.
3.3 유한지반의 진행파동장
유한두께의 해저지반을 갖는 진행파동장이므로 본 연구결과에 KR= 0을 적용한다. 이하에서는 무차원 연직깊이 z/h에 따른 무차원 간극수압 |P| p0, 수평 및 연직 유효응력|σ′x|/p0및 |σ′z|/p0와 |τ|/p0전단응력 의 변화를 분석·검토 한다. 이 때, 파동조건은 수심 d = 45 cm, 파고 H = 5.0 cm이고, 완전포화토에 대한 해저지반의 물성치는 투수계수K = 1.2×10-4cm/s, Poisson비 μ = 0.3, 공극율 n' = 0.38이며, 특히 간극수의 압축률 β과 흙의 전단탄성계수 G와의 곱이 Gβ = 0인 경우를 적용한 결과이다.
(1) 지반두께의 변화
Fig. 5는 입사파 주기를 T = 1.2 s로 일정하게 유지한 상태에서 파라미터로 해저지반두께를 변화시킨 경우의 결과이다. 간극수압은 전체적으로 연직깊이가 해저표면에서 불투과·불변형으로 깊어짐에 따라 감소하며, 지반두께에 따른 간극수압 및 변화의 차이가 크다는 것을 확인할 수 있다. 특히, 지반두께가 얕아질수록 전 연직깊이에 따른 간극수압의 분포가 상당히 커지지만, 그의 변화는 작아지고, 궁극적으로는 균등분포에 가까워지는 결과를 나타낼 것으로 추정되며, 이는 파동에서 수심과 파장과의 관계에서 보이는 물입자 궤적운동과 유사한 현상이다. 결국, 지반 내에서 연직깊이가 깊어질수록 간극수의 운동이 작아지고, 이에 따른 간극수의 침투가 어려워져 파동으로 인한 간극수압의 영향이 작아지게 된다. 한편, 무한두께의 경우 Fig. 2에 나타낸 바와 같이 연직깊이가 깊을수록 간극수압은 0으로 수렴되는 경향을 나타내지만, 유한의 경우는 특정한 값으로 수렴되고, 그 특정치는 지반두께가 얕을수록 보다 큰 값을 나타낸다.
Progressive wave-induced pore water pressure, effective and shear stresses under the different finite soil thickness (t/T = 0).
연직 유효응력의 변화를 살펴보면 해저표면에서 연직 유효 응력은 모두 0을 나타내고, 연직깊이가 깊을수록 증가하지만, 특정한 깊이에서 최대치를 나타낸 이후 다시 감소하는 경향을 나타낸다. 지반두께에 따른 각 최대치는 지반두께의 증감에 따른 일정한 경향을 나타내지는 않고, 본 계산에서는 h = 100 cm의 경우가 가장 큰 최대치를 나타내며, 각 최대치를 나타내는 연직위치는 지반두께가 두꺼울수록 보다 지표면에 가까워지는 경향을 볼 수 있다. 그리고, 지반두께가 두꺼워질수록 무한두께의 지반에서와 같이 불투과·불변형층 근방에서는 0에 근접하고, 동시에 그의 변화율도 0에 접근하는 경향을 볼 수 있다. 여기서, 지반 내에서 연직 유효응력이 발생하는 것은 파동의 파봉과 파곡에서 수위의 시간변동에 따른 압력차이로 연직방향으로 간극수의 흐름이 발생되기 때문이며, 하향침투(파봉시)인 경우 유효응력의 증가를, 상향침투(파곡시)인 경우 유효응력의 감소로 나타난다.
다음으로, 수평 유효응력의 경우는 h = 50 cm의 경우와 같이 해저표면에서 반드시 0으로 주어지지 않는 결과는 연직 유효응력의 경우와 상이하지만, 이는 식(11)에서와 같은 수평 유효응력에 관한 경계조건식이 부과되지 않았기 때문이다. 그 상당히 커지지만, 그의 변화는 작아지고, 궁극적으로는 균등분포에 가까워지는 결과를 나타낼 것으로 추정되며, 이는 파동에서 수심과 파장과의 관계에서 보이는 물입자 궤적운동과 유사한 현상이다. 결국, 지반 내에서 연직깊이가 깊어질수록 간극수의 운동이 작아지고, 이에 따른 간극수의 침투가 어려워져 파동으로 인한 간극수압의 영향이 작아지게 된다. 한편, 무한두께의 경우 Fig. 2에 나타낸 바와 같이 연직깊이가 깊을수록 간극수압은 0으로 수렴되는 경향을 나타내지만, 유한의 경우는 특정한 값으로 수렴되고, 그 특정치는 지반두께가 얕을수록 보다 큰 값을 나타낸다.
연직 유효응력의 변화를 살펴보면 해저표면에서 연직 유효응력은 모두 0을 나타내고, 연직깊이가 깊을수록 증가하지만, 특정한 깊이에서 최대치를 나타낸 이후 다시 감소하는 경향을 나타낸다. 지반두께에 따른 각 최대치는 지반두께의 증감에 따른 일정한 경향을 나타내지는 않고, 본 계산에서는 h = 100 cm의 경우가 가장 큰 최대치를 나타내며, 각 최대치를 나타내는 연직위치는 지반두께가 두꺼울수록 보다 지표면에 가까워지는 경향을 볼 수 있다. 그리고, 지반두께가 두꺼워질수록 무한두께의 지반에서와 같이 불투과·불변형층 근방에서는 0에 근접하고, 동시에 그의 변화율도 0에 접근하는 경향을 볼 수 있다. 여기서, 지반 내에서 연직 유효응력이 발생하는 것은 파동의 파봉과 파곡에서 수위의 시간변동에 따른 압력차이로 연직방향으로 간극수의 흐름이 발생되기 때문이며, 하향침투(파봉시)인 경우 유효응력의 증가를, 상향침투(파곡시)인 경우 유효응력의 감소로 나타난다.
다음으로, 수평 유효응력의 경우는 h = 50 cm의 경우와 같이 해저표면에서 반드시 0으로 주어지지 않는 결과는 연직 유효응력의 경우와 상이하지만, 이는 식(11)에서와 같은 수평 유효응력에 관한 경계조건식이 부과되지 않았기 때문이다. 그러나, 나머지 지반두께에 대해서는 연직 유효응력과 후술하는 전단응력과 같이 해저표면에서 0의 값을 나타내고, 궁극적으로는 Fig. 2에 나타내는 무한두께의 지반에서와 같이 세 개 모두 동일한 값을 나타낼 것으로 추정되며, 또한 Fig. 5에서도 h = 300 cm의 경우는 수평 및 연직 유효응력과 전단응력의 분포형상과 그의 값이 거의 동일하다는 것을 확인할 수 있으므로 이는 무한두께에 가까운 지반이라고 판단된다. 여기서, 지반 내에서 수평 유효응력의 변화가 발생하는 것은 파동의 파봉과 파곡에서 수위의 공간변동에 따른 압력차로 수평방향으로 간극수의 흐름이 발생되기 때문이다.
전단응력은 지반두께가 두꺼워질수록 전술한 두 유효응력의 변화과정과 매우 유사하지만, 반면에 지반두께가 얕을수록 세 개의 변화과정은 매우 상이한 것을 알 수 있다. 여기서, 식(11)과 같은 조건식 때문에 해저표면에서 전단응력이 0의 값을 나타내는 것은 연직 유효응력과 동일하다.
이상으로부터 지반두께가 두꺼워질수록 지반 내에서 동적응답이 무한수심에 가까워지는 거동을 확인할 수 있고, 이로부터 무한두께의 지반을 파동에서와 유사하게 h/L > 1/2로 규정하는 것(McDougal et al.(1989), Jeng(1997))은 타당한 것으로 판단된다.
(2) 주기의 변화
Fig. 6은 해저지반두께 h를 100 cm로 동일하게 유지한 상태에서 파라미터로 입사파의 주기를 변화시킨 경우의 결과이다. 간극수압은 각 주기에 대해 모두 연직깊이가 깊을수록 감소하는 경향을 나타내고, 주기가 짧을수록 연직깊이에 따라 보다 작은 값을 나타낸다. 이것은 주기가 짧을수록 파수 k가 커지고, 동시에 해저지반의 상대두께 kh의 값이 커지므로 무한두께의 지반에 가까워지기 때문이다. 따라서, 입사주기가 짧아지는 것은 결국 지반두께가 두꺼워지는 효과를 나타내게 되며, 이러한 관점에서 고찰하면 Fig. 5와 6의 두 값은 궁극적으로 지반응답에 유사한 영향을 미치는 상이한 두 파라미터에 의해 결과적으로 유사한 변화과정을 나타내는 것으로 추정된다.
Progressive wave-induced pore water pressure, effective and shear stresses in the finite soil thickness under the different wave period (t/T = 0).
수평 및 연직 유효응력과 전단응력의 변화에서도 주기가 긴 경우는 보다 얕은 유한두께에서 지반응답을, 반면에 주기가 짧은 경우는 보다 무한두께에 접근하는 지반응답을 나타내는 것을 알 수 있고, 이러한 거동은 전술한 간극수압의 변화에서 지적한 것과 동일한 현상이다. 궁극적으로 무한두께의 해저지반에서는 연직깊이에 따라 수평 및 연직 유효응력과 전단응력은 동일한 분포와 값을 가지지만, 유한두께의 해저지반에서는 Fig. 5에서도 언급한 바와 같이 입사주기가 길어질수록 각각 매우 상이한 분포와 값을 나타내고, 특히 수평 유효응력에서는 해저표면에서 0이 되지 않는 경우도 발생한다. 따라서, 무한두께의 해저지반에 대한 결과를 유한두께에 그대로 적용하는 경우는 큰 오차를 나타낼 우려가 있고, 특히 지반두께가 얕을수록 각각의 지반응력 자체가 상이할 수도 있다는 점에 유의할 필요가 있다.
3.4 유한지반의 완전중복파동장
유한두께의 해저지반을 갖는 완전중복파동장이므로 본 연구결과에 KR= 1을 적용하며, 적용한 파동조건과 완전포화토에 대한 해저지반의 물성치는 유한지반의 진행파동장의 경우와 동일하다.
(1) 지반두께의 변화
Fig. 7는 입사파 주기를 T = 1.2 s로 일정하게 유지한 상태에서 파라미터로 해저지반두께를 변화시킨 경우의 결과이다. 완전중복파동장이기 때문에 배와 마디 사이 x의 위치에 따라 간극수압, 수평 및 연직 유효응력과 전단응력이 변동하며, 여기서는 Fig. 3에서 나타낸 바와 같이 간극수압과 수평 및 연직 유효응력이 최대로 되는 x/L = 0 (전단응력은 0을 나타낸다)과 전단응력이 최대로 되는 x/L = 1/4(간극수압과 수평 및 연직 유효응력은 0을 나타낸다)에서 값을 제시한다. 간극수압 |P|/p0의 변동을 살펴보면 모두 z = 0에서 2의 값을 나타내고, 연직깊이가 깊어지면서 감소하는 경향을 보인다. 이는 Fig. 3에서도 지적한 바와 같이 완전중복파이기 때문에 수위변동이 진행파의 2배로 증가되고, 파동으로 인한 지반 내 간극수압은 연직깊이가 깊어질수록 감쇠되기 때문이다. 여기서, 지반두께에 따른 차이는 기본적으로 Fig. 5의 경우와 거의 유사하지만, 완전중복 파동장이기 때문에 역시 값이 2배로 되어 있다는 것을 확인할 수 있다. 지반두께가 얕아질수록 불투과·불변형 간극수압이 0으로 되지 않으며, 연직으로 균등분포에 가까워지는 경향을 나타내고, z = −h의 불투과·불면형면에서 P = 0를 나타내는 무한두께의 경우보다 훨씬 큰 값의 분포를 볼 수 있다.
Standing wave-induced pore water pressure, effective and shear stresses under the different finite soil thickness (t/T = 0).
수평 및 연직 유효응력의 경우도 진행파동장에 대한 Fig. 5의 변화과정과 거의 동일하지만, 역시 완전중복파동장이기 때문에 값이 2배로 주어진다는 것을 알 수 있다. 연직 유효응력은 해저표면에서 모두 0을 나타내고, 연직깊이가 깊을수록 증가하지만, 특정한 깊이에서 최대치를 나타낸 이후 다시 감소하는 경향을 나타낸다. 지반두께에 따른 각 최대치는 지반두께의 증감에 따른 일정한 경향을 나타내지는 않으며, h = 100 cm의 경우가 가장 큰 최대치를 나타내고, 각 최대치를 나타내는 연직위치는 지반두께가 두꺼울수록 보다 지표면에 가까워지는 무한두께를 갖는 해저지반응답에 근접한다. 또한, 지반두께가 두꺼워질수록 무한두께의 지반에서와 같이z = −h인 불투과·불변형층 근방에서는 0에 근접하고, 동시에 그의 변화율도 0에 접근하는 현상을 볼 수 있다. 수평 유효응력의 경우 h = 50 cm의 해저표면에서 0이 아닌 것은 연직 유효응력의 경우와 다르지만, 나머지 지반두께에 대해서는 연직 유효응력과 거의 유사한 변동과정을 나타낸다. 그리고, 최대치는 지반두께가 두꺼울수록 작아지지만, 결국에는 무한두께의 값에 수렴할 것으로 추정된다.
전단응력을 살펴보면 유효응력 및 간극수압과 동일하게 Fig. 5의 변화과정과 거의 동일하고, 또한 값이 2배로 된다는 것을 확인할 수 있고, 지반두께가 두꺼울수록 최대값의 크기가 증가하며, 최대값이 나타나는 연직깊이는 지표면에 가까워진다. 이러한 결과는 유효응력에서도 확인되는 현상이다.
이상으로부터 유한지반의 완전중복파동장에서는 유한지반의 진행파동장에서 값의 2배로 나타나고, 무한지반의 완전중복파와 매우 다른 지반응답을 나타낸다는 것을 알 수 있다.
(2) 주기의 변화
Fig. 8은 일정한 해저지반두께 h = 100 cm에 대해 파라미터를 입사파 주기로 하여 T = 0.6 s에서 1.6 s까지 변화시킨 경우의 결과이다. 여기서, 배와 마디 사이의 수평위치에 따라 간극수압, 수평 및 연직 유효응력과 전단응력이 변동하는 완전중복파동장이므로 x/L = 0에서 간극수압과 수평 및 연직 유효응력(이 때, 전단응력은 0이다)을, x/L = 1/4에서 전단응력(이때, 간극수압과 수평 및 연직 유효응력은 0이다)을 제시한다.
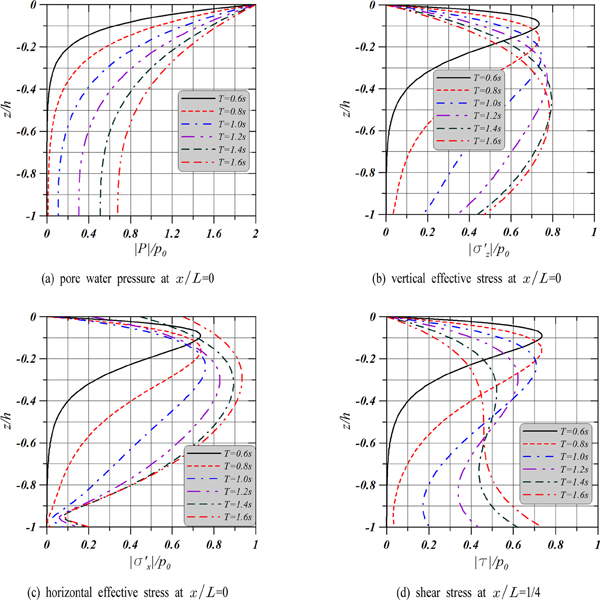
Standing wave-induced pore water pressure, effective and shear stresses in the finite soil thickness under the different wave period (t/T = 0).
먼저, 간극수압 |P|/p0의 변동을 살펴보면 모두 z = 0에서 2의 값을 나타내고, 연직깊이가 깊어질수록 감소하는 경향을 보이며, z = −h인 불투과·불변형면에서 간극수압의 변화율이 0으로 나타난다. 이러한 원인은 경계조건으로 z = 0에서 동파압이 간극수압으로 주어지고, 불투과·불변형면상에서 간극수압의 연직변화율이 0이라는 경계조건이 부과되며, 또한 완전중복파동장이기 때문이다. 입사주기에 따른 차이는 기본적으로 진행파동장에 관한 Fig. 6의 경우와 거의 유사한 변화과정을 나타내지만, 완전중복파동장이기 때문에 2배의 값을 취하는 것을 확인할 수 있다. 특히, 입사주기가 길수록 지반두께 h가 얕아지는 Fig. 7의 효과를 나타낸다는 사실에 비추어 볼 때 무한두께의 지반을 h/L > 1/2로 규정하는 것(McDougal et al.(1989), Jeng(1997))은 완전중복파동장에서도 타당한 것으로 판단된다. 또한, 주기의 변화는 간극수압과 후술하는 수평 및 연직 유효응력과 전단응력의 변화에 매우 민감하다는 사실을 확인할 수 있고, 더불어 지반두께가 얕을수록 무한두께의 경우와는 매우 상이한 지반응답을 나타낸다는 사실에 유의할 필요가 있다.
다음으로 수평 및 연직 유효응력과 전단응력에 대한 결과를 보면 Fig. 6에서 언급된 진행파동장에서 값의 2배로 주어지며, 연직깊이 및 입사주기의 변화에 따른 응력의 변화과정은 Fig. 6의 경우와 완전히 동일하다는 것을 알 수 있다. 이러한 결과는 Fig. 6과 동일한 파동장과 지반물성치를 적용하였고, 완전중복파동장이기 때문이다. 따라서, 유효응력과 전단응력도 간극수압과 동일하게 해저지반에서 경계조건으로 부과되는 동파압의 크기에 비례하므로 완전중복파동장에서 간극수압과 지반응력의 최대치는 진행파동장에서 얻어지는 값의 2배로 된다는 사실을 간단히 추정할 수 있다.
3.5 유한지반의 부분중복파동장
유한두께의 지반을 갖는 부분중복파동장에서 지반 내 간극수압과 지반응력을 검토하기 위하여 적용한 파동조건과 해저지반에서 물성치는 전술한 유한지반의 진행파동장과 완전중복파동장의 경우와 동일하다. 부분중복파동장이므로 복소반사율 KR의 값에 따라 많은 케이스의 결과를 도출할 수 있지만, KR= 0과 1인 경우는 앞에서 서술된 진행파동장과 완전중복파동장으로 귀결되고, 따라서 유한지반의 부분중복파동장에서 지반응답으로 여기서는 지면관계상 KR= 0.7의 경우에 한정하여 논의하는 것으로 한다.
(1) 지반두께의 변화
Fig. 9의 결과는 부분중복파의 배 위치인 x/L = 0에서 간극수압, 유효응력 및 전단응력을 나타낸 것이다. 그림으로부터 부분중복파의 경우는 유한두께의 완전중복파동장에서와 달리 x/L = 0에서 전단응력이 0으로 되지 않고 약간의 값을 가진다는 것을 확인할 수 있다. 이는 x/L = 0의 경우 식(39)로부터 sin kx는 0으로 되지만 (1 – KR)coskx – 1–KR ≠ 0으로 주어지기 때문이다. 전술한 완전중복파동장에서는 KR= 1이므로 (1 – KR)coskx의 항도 0으로 되어 전단응력이 0으로 된다.
Partial standing wave-induced pore water pressure, effective and shear stresses under the different finite soil thickness at x/L = 0 (t/T = 0).
지반두께 및 연직깊이의 변화에 따른 간극수압과 수평 및 연직 유효응력의 변화양상은 전술한 완전중복파와 동일한 과정을 나타내지만, 부분반사에 의해 해저지반 상에서 경계조건으로 부과되는 동파압이 약간 작은 값으로 주어지기 때문에 간극수압과 수평 및 연직 유효응력의 값도 약간 작은 값을 나타낸다. 그리고, 진행파동장에서 무한두께의 지반에 대한 정의 h/L > 0.5(McDougal et al.(1989), Jeng(1997))는 부분중복 파동장에서도 그대로 적용될 수 있는 것으로 판단된다.
한편, Fig. 10의 결과는 부분중복파의 마디 위치인 x/L = 1/4에서 간극수압, 유효응력 및 전단응력을 나타낸 것이다. 그림으로부터 부분중복파의 경우는 유한두께의 완전중복파동장에서와 달리 x/L = 1/4에서 간극수압과 수평 및 연직 유효응력이 0으로 되지 않고 약간의 값을 가진다는 것을 확인할 수 있다. 이는 식(34), (37) 및 (38)로부터 coskx는 0으로 되지만 (1 − KR)sinkx = 1 – KR ≠ 0으로 주어지기 때문이다. 역시 완전중복파동장에서는 KR= 1이므로 ( 1 – KR)sinkx의 항도 0으로 되어 간극수압, 유효응력 및 전단응력은 0으로 된다. 동일하게, 지반두께 및 연직깊이의 변화에 따른 전단응력의 변화양상은 전술한 완전중복파와 동일한 과정을 나타내지만, 부분 반사라는 조건에 의해 전단응력의 값도 약간 작은 값을 나타낸다.
Partial standing wave-induced pore water pressure, effective and shear stresses under the different finite soil thickness at x/L = 1/4 (t/T = 0).
(2) 주기의 변화
Fig. 11은 입사주기를 파라미터로 부분중복파의 배 위치인 x/L = 0에서 간극수압과 수평 및 연직 유효응력을, x/L = 1/4에서 전단응력을 나타낸 것이다. 입사주기의 변화에도 전술한 Fig. 10에서와 같이 x/L = 0에서 전단응력이, x/L = 1/4에서 간극수압과 수평 및 연직 유효응력이 0의 값을 취하지 않고 약간의 값을 나타내는 것이 확인되지만, 여기서는 지면관계상 제시하지 않는다. 그림으로부터 입사주기 및 연직깊이의 변화에 따른 간극수압, 수평 및 연직 유효응력, 그리고 전단응력에서 그의 변화양상은 부분중복파에서도 전술한 완전중복파와 동일한 과정을 나타내지만, Fig. 9와 10에서와 같이 각각 약간 작은 값을 나타낸다.
Partial standing wave-induced pore water pressure, effective and shear stresses in the finite soil thickness under the different wave period (t/T = 0).
4. 맺음말
본 연구에서는 임의반사율과 유한두께의 지반을 대상으로 해저지반 내 동적응답에 관한 해석해를 유도하였고, 산정된 결과에 대해 기존 무한두께의 진행파와 완전중복파의 해석결과와 비교하여 본 해석해의 타당성을 입증하였다. 그리고, 유한두께의 진행파동장, 완전중복파동장 및 임의반사율을 갖는 부분중복파동장에 각각 적용하여 간극수압, 수평 및 연직 유효응력, 그리고 전단응력에서 지반두께 및 입사주기의 변화에 따른 그들의 변화특성을 명확히 규명하였다. 이로부터 유한두께의 해저지반에서는 무한두께의 경우와는 매우 상이한 지반응답을 나타내는 것을 확인할 수 있었고, 완전중복파동에서는 진행파동장에서의 값에 2배가, 부분중복파동장에서는 완전중복파동장에서의 값보다 작고, 동시에 진행파동장에서의 값보다 큰 값을 갖는 지반응답특성을 또한 확인할 수 있었다.
이러한 변화특성을 나타내는 본 해석해는 완전반사에 가까운 직립안벽이나 방파제에서부터 저반사의 투수성 구조물에 이르기까지 넓은 범위의 해저지반에 적용될 수 있을 것으로 판단되고, 동시에 지반두께가 상대적으로 얕은 해역에 구조물이 설치될 수 있다는 점을 고려하면 깊은 해저지반과 더불어 얕은 해저지반에도 그 적용성이 확대될 수 있을 것으로 판단된다.
여기서, 저반사의 투수성구조물이 설치된 부분중복파동장에서 반사율의 변화에 따른 해저지반 내 지반응답의 변동특성은 지면관계상 충분히 논의되지 못하였다는 점을 부기하여둔다.
Acknowledgements
이 연구는 해양수산부/한국해양과학기술진흥원의 연구과제(PJT200538)로 수행된 연구임.